INTRODUCTION

In many systems described by equations of the reaction–advection–diffusion type and having two stable equilibrium positions, sharp transition layers occur between these positions provided that the diffusion coefficient is small as compared to the reaction coefficient. Such equations are singularly perturbed and have a small parameter at the highest derivative. They appear in many applied problems, in particular, in physics of semiconductors when modeling the field distribution and density of carriers inside the semiconductor [1] (see the work and references therein). Note that the problem posed in Section 2 arises in the search of the electric field strength distribution inside a semiconductor with a region of negative differential conductivity by use of the drift–diffusion model (see [2], Sect. 2).

The problem of transition layer motion in singularly perturbed equations of the reaction–diffusion and reaction–advection–diffusion types was studied in works [3–5, 7, 8]. To my knowledge, the last results related to spatially inhomogeneous problems with coefficients periodically dependent on time are contained in [5, 7].

In [6], the existence of a stable periodic internal layer was shown in the reaction–diffusion problem with periodic coefficients, where, in contrast to Eq. (1) studied in this work, the coefficient \({\varepsilon}^{2}\) stands at the time derivative. It is also known (see [5]) that in the initial boundary value problem corresponding to the equation from [6] in which the front at the initial time instant is already formed and is situated at a finite distance from the stable periodic front, the rate of attraction of this front to the periodic one exceeds the periodic motion speed of the latter by an order of magnitude. In [5], such two motions were called fast and slow.

It turns out that the layer for Eq. (1) moves with a speed the order of which at any time instant coincides with the order of the speed of the periodic layer motion, i.e., only slow motion occurs. As well, the abovementioned passage to another time scale leads to a significant change in the condition of asymptotic stability of the periodic solution (cf. the inequality in requirement \(Y_{3}\) in [6] and condition (A4) of this work).

1 FORMULATION OF THE PROBLEM

In this work, we are interested in solutions of the following singularly perturbed boundary value problem

$$Nu:=\varepsilon^{2}\frac{\partial^{2}u}{\partial x^{2}}-\varepsilon\frac{\partial u}{\partial t}-\varepsilon A(x,t,\varepsilon)\frac{\partial u}{\partial x}$$
$${}-f(u,x,t,\varepsilon)=0,$$
$$x\in(-1,1),$$
$$\frac{\partial u}{\partial x}(-1,t,\varepsilon)=0,\quad\frac{\partial u}{\partial x}(1,t,\varepsilon)=0,$$
(1)

which is considered at \(t\in\mathbb{R}\) and condition of periodicity in time

$$u(x,t,\varepsilon)=u(x,t+T,\varepsilon),\quad x\in[-1,1],\quad t\in\mathbb{R}$$

or at \(t>0\) with the initial condition

$$u(x,0,\varepsilon)=u_{00}(x,\varepsilon),\quad x\in[-1,1].$$

Here, \({\varepsilon}\in(0,{\varepsilon}_{0}]\), \({\varepsilon}_{0}>0\) is a small parameter.

We suppose that the following conditions are satisfied:

(A1) Functions \(A(x,t,\varepsilon)\) and \(f(u,x,t,\varepsilon)\) are \(T\)-periodic in \(t\) and sufficiently smooth in their domains of definition.

(A2) Let the degenerate equation \(f(u,x,t,0)=0\) have exactly three \(T\)-periodic in \(t\) solutions \(u=\varphi^{(\pm,0)}(x,t)\), and for any \((x,t)\in[-1,1]\times\mathbb{R}\) the following inequalities are satisfied:

$$\varphi^{(-)}(x,t)<\varphi^{(0)}(x,t)<\varphi^{(+)}(x,t),$$
$$f_{u}(\varphi^{(\pm)}(x,t),x,t,0)>0,$$
$$f_{u}(\varphi^{(0)}(x,t),x,t,0)<0.$$

We are interested in solutions having a moving sharp internal transition layer near a certain point \(x=\hat{x}(t,{\varepsilon})\), which occurs from the root \(\varphi^{(-)}(x,t)\) of the degenerate equation to the root \(\varphi^{(+)}(x,t)\). Such solutions are called step-type contrast structures.

To start with, we clarify the conditions of the existence of periodic solutions that are asymptotically stable in the sense of Lyapunov.

2 PERIODIC SOLUTIONS

The statement of the problem in the periodic case has the form

$$\varepsilon^{2}\frac{\partial^{2}u}{\partial x^{2}}-\varepsilon\frac{\partial u}{\partial t}-\varepsilon A(x,t,\varepsilon)\frac{\partial u}{\partial x}-f(u,x,t,\varepsilon)=0,$$
$$(x,t)\in D_{t}=(-1,1)\times\mathbb{R},$$
$$\frac{\partial u}{\partial x}(-1,t,\varepsilon)=0,\quad\frac{\partial u}{\partial x}(1,t,\varepsilon)=0,\quad t\in\mathbb{R},$$
$$u(x,t,\varepsilon)=u(x,t+T,\varepsilon),\quad x\in\bar{D}_{t}.$$
(2)

2.1 Construction of the Formal Asymptotics of the Solution

The asymptotics of the solution of problem (2) is sought in the standard form [9, 10]:

$$U^{(\pm)}(x,t,\varepsilon)=\bar{u}^{(\pm)}(x,\varepsilon)+Q^{(\pm)}(\xi,t,\varepsilon)$$
$${}+R^{(\pm)}\left(\eta^{(\pm)},t,\varepsilon\right),\quad(x,t,\varepsilon)\in D_{t}^{\pm}\times(0,\varepsilon_{0}].$$
(3)

Here, \(D_{t}^{(-)}:=[-1,\hat{x}]\times\mathbb{R}\), \(D_{t}^{(+)}:=[\hat{x},1]\times\) \(\mathbb{R}\), \({\bar{u}}^{\left(\pm\right)}\left(x,\varepsilon\right)=\bar{u}_{0}^{(\pm)}(x)+\varepsilon\bar{u}_{1}^{(\pm)}(x)+...\) is the regular part of the expansion, the functions \({Q}^{\left(\pm\right)}\left(\xi,t,\varepsilon\right)=Q_{0}^{\left(\pm\right)}\left(\xi,t,\varepsilon\right)+\varepsilon Q_{1}^{\left(\pm\right)}\left(\xi,t,\varepsilon\right)+...\) describe the behavior of the solution in a neighborhood of the transition point \(\hat{x}(t,\varepsilon),\) \(\xi=\displaystyle\frac{x-\hat{x}(t,\varepsilon)}{\varepsilon}\) is the stretched variable of the transition layer; the functions \(R\left(\eta^{(\pm)},t,\varepsilon\right)={R}_{0}\left(\eta^{(\pm)},t\right)+\varepsilon{R}_{1}\left(\eta^{(\pm)},t\right)+...\) describe the behavior of the solution in neighborhoods of the boundary points of the segment \([-1;1],\) and \(\eta^{(\pm)}=\frac{x\mp 1}{\varepsilon}\) are the stretched variables near the points \(x=\pm 1\), respectively.

Note that the functions \(\bar{u}_{i}(x,t)\) and \({R}\left(\eta^{(\pm)},t\right)\) are determined in the standard way (see [9])) and \({\bar{u}_{0}}^{\left(\pm\right)}(x,t)=\varphi^{\left(\pm\right)}(x,t),\) \({R}\left(\eta^{(\pm)},t\right)=O({\varepsilon})\) by virtue of the Neumann boundary conditions, i.e., there appears a weak boundary layer.

The position of the internal transition layer is determined from the condition of \(C^{1}\)-joining of asymptotic representations \(U^{(-)}(x,t,\varepsilon)\) and \(U^{(+)}(x,t,\varepsilon)\) at the transition point \(\hat{x}(t,\varepsilon):\)

$${U}^{\left(\pm\right)}\left(\hat{x}(t,\varepsilon),t,\varepsilon\right)=\varphi^{(0)}(\hat{x}(t,\varepsilon),t),$$
(4)
$$\varepsilon\frac{\partial}{\partial x}{U}^{\left(-\right)}(\hat{x}(t,\varepsilon),t,\varepsilon)=\varepsilon\frac{\partial}{\partial x}{U}^{\left(+\right)}(\hat{x}(t,\varepsilon),t,\varepsilon).$$
(5)

The transition point \(x=\hat{x}(t,\varepsilon)\) is sought in the form of expansion in powers of the small parameter \(\varepsilon\):

$$\hat{x}(t,\varepsilon)=x_{0}(t)+\varepsilon x_{1}(t)+\dots\,.$$
(6)

Coefficients of this expansion are determined when constructing the asymptotics. Note that, in contrast to the approach expounded, e.g., in [8], we do not begin with expansion of the transition point \(\hat{x}(t,\varepsilon)\) in powers of \(\varepsilon\) in the asymptotics of the solution. This simplifies the algorithm of constructing the asymptotics.

The problems for the functions \(Q_{0}^{\left(-\right)}\left(\xi,t,\varepsilon\right)\) have the form

$$\frac{\partial^{2}Q_{0}^{\left(\pm\right)}}{\partial\xi^{2}}+\left(\frac{\partial\hat{x}(t,\varepsilon)}{\partial t}-A(\hat{x}(t,\varepsilon),t,0)\right)\frac{\partial Q_{0}^{\left(\pm\right)}}{\partial\xi}$$
$${}=f(\varphi^{\left(\pm\right)}(\hat{x}(t,\varepsilon),t)+Q_{0}^{\left(\pm\right)},\hat{x}(t,\varepsilon),t,0),$$
$$Q_{0}^{(\pm)}(0,t,\varepsilon)+\varphi^{(\pm)}(\hat{x}(t,\varepsilon),t)=\varphi^{(0)}(\hat{x}(t,\varepsilon),t),$$
$$Q_{0}^{\left(-\right)}\left(\pm\infty,t,\varepsilon\right)=0.$$
(7)

Let us introduce an operator \(D\) which acts by the following rule:

$$D\hat{x}:=\frac{\partial\hat{x}(t,\varepsilon)}{\partial t}-A(\hat{x}(t,\varepsilon),t,0).$$
(8)

Let us introduce functions

$$\tilde{u}^{(\pm)}\left(\xi,\hat{x},t\right)=\varphi^{(\pm)}(\hat{x}(t,\varepsilon),t)+Q_{0}^{(\pm)}(\xi,t,\varepsilon),$$
$$\tilde{v}^{(\pm)}\left(\xi,\hat{x},t\right)=\frac{\partial\tilde{u}^{(\pm)}}{\partial\xi}(\xi,\hat{x},t),\quad\xi\in[0,\pm\infty).$$
(9)

Problems (7) in notations (9) take the form

$$\frac{\partial^{2}\tilde{u}^{(\pm)}}{\partial\xi^{2}}+D\hat{x}\frac{\partial\tilde{u}^{(\pm)}}{\partial\xi}=f(\tilde{u}^{(\pm)},\hat{x},t,0),$$
$$\tilde{u}^{(\pm)}(0,\hat{x},t)=\varphi^{(0)}(\hat{x},t),$$
$$\tilde{u}^{(\pm)}(\pm\infty,\hat{x},t)=\varphi^{(\pm)}(\hat{x},t).$$
(10)

Together with problems (10), we consider the problem

$$\frac{\partial^{2}\hat{u}}{\partial\xi^{2}}+W\frac{\partial\hat{u}}{\partial\xi}=f(\hat{u},\hat{x},t,0),$$
$$\hat{u}(0,\hat{x},t)=\varphi^{(0)}(\hat{x},t),$$
$$\hat{u}(\pm\infty,\hat{x},t)=\varphi^{(\pm)}(\hat{x},t).$$
(11)

Problem (11) was studied in detail in [3], and we present the result we require as a lemma.

Lemma 1. For any \(\hat{x}\in(-1,1)\), \(t\in\mathbb{R}\), there exists a unique quantity \(W\) such that problem (11) has a unique smooth monotonic solution \(\hat{u}(\xi,\hat{x},t)\) satisfying the estimate

$$|\hat{u}(\xi,\hat{x},t)-\varphi^{(\pm)}(\hat{x},t)|<C\exp(-{\kappa|\xi|}),$$

where \(C\) and \(\kappa\) are some positive constants. The function \(W(\hat{x},t)\) is determined by the following expression:

$$W(\hat{x},t)=\frac{\int\limits^{\varphi^{(+)}(\hat{x},t)}_{\varphi^{(-)}(\hat{x},t)}f(u,\hat{x},t,0)du}{\int\limits^{+\infty}_{-\infty}\left(\frac{\partial\hat{u}}{\partial\xi}(\xi,\hat{x},t)\right)^{2}d\xi}.$$

The smoothness of the function \(W(\hat{x},t)\) coincides with the smoothness of the function \(f(\hat{u},\hat{x},t,0)\) with respect to the arguments \((\hat{x},t)\).

Since the functions \(f\) and \(A\) are \(T\)-periodic in \(t\), the function \(W\) also has this property. Let the following requirements be satisfied.

(A3) Let the problem

$$\frac{dx}{dt}=W(x,t)+A(x,t,0),$$
(12)
$$x(t)=x(t+T)$$
(13)

have a solution \(x=x_{0}(t)\): \(-1<x_{0}(t)<1\), \(t\in\mathbb{R}\).

(A4) Let \(x_{0}(t)\) satisfy the condition

$$\int\limits_{0}^{T}\left.\frac{\partial}{\partial x}\bigg{(}W(x,t)+A(x,t,0)\bigg{)}\right|_{x=x_{0}(t)}dt<0.$$
(14)

It is well known that the inequality in condition (A4) guarantees asymptotic stability in the sense of Lyapunov for the periodic solution \(x_{0}(t)\).

Let (10.a) denote problems (10) in which \(\hat{x}\) is everywhere replaced by \(x_{0}(t)\) or, in other words, \({\varepsilon}=0\) is set. As follows from Lemma 1 and condition (A3), problems (10.a) are uniquely solvable because condition \(D\hat{x}_{0}(t)=W(x_{0}(t),t)\) is satisfied. At the same time, \(\frac{\partial\tilde{u}^{(+)}}{\partial\xi}(0,x_{0}(t),t)-\frac{\partial\tilde{u}^{(-)}}{\partial\xi}(0,x_{0}(t),t)=0\), \(t\in\mathbb{R}\). By virtue of the supposed smoothness of the coefficients \(f\) and \(A\) (see condition (A1)), problems (10) are a regular perturbation of problems (10.a) and, therefore, they are also uniquely solvable. Note that, by virtue of representation (6), we now have \(\frac{\partial\tilde{u}^{(+)}}{\partial\xi}(0,\hat{x}(t,{\varepsilon}),t)-\frac{\partial\tilde{u}^{(-)}}{\partial\xi}(0,\hat{x}(t,{\varepsilon}),t)=O({\varepsilon})\).

Thus, construction of the transition layer function in the zero order has been completed. The transition layer functions of the first and subsequent orders are found by the standard algorithm (for more details, see, e.g., [8]) and their construction is not presented here.

2.2 Asymptotic Approximation of the Front Position

The unknown coefficients of the expansion \(x_{i}(t)\), \(i=1,2...\), are determined from joining conditions (5) for derivatives of asymptotic expansions. Let us introduce a function

$$H(\varepsilon,t):=\varepsilon\left(\frac{\partial U^{(+)}}{\partial x}(\hat{x},t,\varepsilon)-\frac{\partial U^{(-)}}{\partial x}(\hat{x},t,\varepsilon)\right)$$
$${}=H_{0}(\varepsilon,t)+\varepsilon H_{1}(\varepsilon,t)+\varepsilon^{2}H_{2}(\varepsilon,t)+...,$$
(15)

where

$$H_{0}(\varepsilon,t)=\frac{\partial Q_{0}^{\left(+\right)}}{\partial\xi}(0,t,\varepsilon)-\frac{\partial Q_{0}^{\left(-\right)}}{\partial\xi}(0,t,\varepsilon),$$
$$H_{1}(\varepsilon,t)=\frac{\partial\varphi^{\left(+\right)}}{\partial x}(\hat{x},t)-\frac{\partial\varphi^{\left(-\right)}}{\partial x}(\hat{x},t)$$
$${}+\left(\frac{\partial Q_{1}^{\left(+\right)}}{\partial\xi}(0,t,\varepsilon)-\frac{\partial Q_{1}^{\left(-\right)}}{\partial\xi}(0,t,\varepsilon)\right),$$

and so on. Condition of \(C^{1}\)-joining (5) is expressed by the equality \(H(\hat{x},t,\varepsilon)=0.\) By virtue of Lemma 1 and condition (A3) with allowance for the expansion of the transition point (6), this equality is satisfied in the order \(\varepsilon^{0}\).

Analysis of problems (10), (11) shows that the function \(H_{0}\) can be represented in the form

$$H_{0}(\varepsilon,t)=\left(D\hat{x}-W(\hat{x},t)\right)\frac{1}{\tilde{v}(0,\hat{x},t)}$$
$${}\times\int\limits_{-\infty}^{+\infty}\tilde{v}^{2}(\xi,\hat{x},t)e^{(D\hat{x})\xi}d\xi+O(\varepsilon^{2}).$$
(16)

As follows from expansion (15) and representation (16), the high-order terms \(x_{i}(t),i\geqslant 1\) in (6) can be found from the following linear periodic problems:

$$\frac{dx_{i}}{dt}+\bigg{(}\left.\frac{\partial}{\partial x}\bigg{(}W(x,t)+A(x,t,0)\bigg{)}\right|_{x=x_{0}(t)}\bigg{)}x_{i}(t)$$
$${}=G_{i}(t),$$
(17)
$$x_{i}(t)=x_{i}(t+T),$$
(18)

where \(G_{i}(t)\) are known functions. Solvability of these problems is guaranteed by condition (A4).

2.3 Justification of the Formal Asymptotics

Let us put \(X_{n}(t,{\varepsilon})=\sum_{i=0}^{n}\varepsilon^{i}x_{i}(t)\), \(\xi=\) \(\frac{x-X_{n}(t,{\varepsilon})}{\varepsilon}.\) The curve \(X_{n}(t,{\varepsilon})\) divides the domain \(\bar{D}_{t}\) into two subdomains \(\bar{D}_{tn}^{(-)}:(x,t)\in[-1,X_{n}(t,{\varepsilon})]\times\mathbb{R}\) and \(\bar{D}_{tn}^{(+)}:(x,t)\in[X_{n}(t,{\varepsilon}),1]\times\mathbb{R}.\) Let us define functions

$$U_{n}^{(\pm)}(x,t,\varepsilon)$$
$${}=\sum\limits_{i=0}^{n}\varepsilon^{i}(\bar{u}_{i}^{\left(\pm\right)}(x,t)+Q_{i}^{\left(\pm\right)}(\xi,t,\varepsilon)+R_{i}^{\left(\pm\right)}(\eta^{(\pm)},t)),$$
$$(x,t)\in\bar{D}_{tn}^{(\pm)},$$

where \(\hat{x}(t,\varepsilon)\) entering into the expressions for the transition layer functions are replaced by \(X_{n}(t,{\varepsilon}).\) Let us denote

$$U_{n}(x,t,\varepsilon)$$
$${}=\begin{cases}U_{n}^{(-)}(x,t,\varepsilon),\quad(x,t)\in\bar{D}_{tn}^{(-)},\\ U_{n}^{(+)}(x,t,\varepsilon),\quad(x,t)\in\bar{D}_{tn}^{(+)}.\end{cases}$$
(19)

To prove the existence of the solution in the form of a moving front, we use the asymptotic method of differential inequalities (see [11]). Let us define a function \({x}_{\beta}(t,\varepsilon)=X_{n+1}(t,{\varepsilon})-\varepsilon^{n+1}\delta(t),\) where the positive function \(\delta(t)>0\) is defined below. We construct the upper solution \(\beta_{n}(x,t,{\varepsilon})\) in each of the domains \(\bar{D}_{t\beta}^{(-)}:(x,t)\in[-1,{x}_{\beta}(t,{\varepsilon})]\times\mathbb{R}\) and \(\bar{D}_{t\beta}^{(+)}:(x,t)\in[{x}_{\beta}(t,{\varepsilon}),1]\times\mathbb{R}.\) Let us introduce a stretched variable \(\xi_{\beta}=\frac{x-{x}_{\beta}(t,{\varepsilon})}{\varepsilon}.\) The upper solution of problem (2) is constructed in the form

$$\beta_{n}^{(\pm)}(x,t,\varepsilon)=U_{n+1}^{(\pm)}|_{\xi_{\beta}}+\varepsilon^{n+1}\left(\mu+q^{(\pm)}\left(\xi_{\beta},t,\varepsilon\right)\right)$$
$${}+\varepsilon^{n+1}(e^{\kappa_{0}\eta^{(+)}}+e^{-\kappa_{0}\eta^{(-)}}),\quad(x,t)\in D_{t\beta}^{(\pm)}.$$
(20)

By \(U_{n+1}^{(\pm)}|_{\xi_{\beta}}\) we mean the functions \(U_{n}^{(\pm)}(x,t,\varepsilon)\) in which the argument \(\xi\) in the transition layer functions is replaced by \(\xi_{\beta}\) and \(X_{n+1}\) is replaced by \(x_{\beta}\). The functions \(q^{(\pm)}\left(\xi_{\beta},t,{\varepsilon}\right)\) are necessary to eliminate residual errors which appear when the operator acts on the upper solution and are determined in the standard way [8]. The lower solution \(\alpha_{n}^{(\pm)}(x,t,{\varepsilon})\) is constructed similarly. All necessary conditions for the upper and lower solutions are checked in the standard way similarly to [6, 8]. Here, we check only the derivative jump condition. We have

$$\varepsilon\left[\left.\frac{\partial\beta_{n}^{(+)}}{\partial x}\right|_{x=x_{\beta}}\right]_{-}^{+}$$
$${}=-{\varepsilon^{n+1}}\frac{L(x_{0},t)}{{\tilde{v}\left({0,x_{0},t}\right)}}\bigg{(}\frac{d\delta}{dt}+\bigg{(}\left.\frac{\partial}{\partial x}\bigg{(}W(x,t)+A(x,t,0)\bigg{)}\right|_{x=x_{0}(t)}\bigg{)}\delta(t)+\frac{F(x_{0},t)}{L(x_{0},t)}\bigg{)}+O(\varepsilon^{n+2}),$$
$$\text{where}\quad F(x_{0},t)=\mu\Bigg{[}\displaystyle\bar{f}_{u}^{\left({\pm}\right)}\left({x_{0},t}\right)\int\limits_{\pm\infty}^{0}{\tilde{v}^{\left({\pm}\right)}\left({\sigma,x_{0},t}\right)e^{(Dx_{0})\sigma}d\sigma}\Bigg{]}^{+}_{-},$$
$$L(x_{0},t)=\int\limits_{-\infty}^{+\infty}\tilde{v}^{2}(\xi,x_{0},t)e^{(Dx_{0})\xi}d\xi>0.$$
(21)

We define the function \(\delta(t)\) as a solution of the problem

$$\frac{d\delta}{dt}+\left.\frac{\partial}{\partial x}\bigg{(}W(x,t)+A(x,t,0)\bigg{)}\right|_{x=x_{0}(t)}\delta(t)$$
$${}+\frac{F(x_{0},t)}{L(x_{0},t)}=\sigma,$$
(22)
$$\delta(t)=\delta(t+T),$$
(23)

where \(\sigma\) is a sufficiently large positive quantity. As can be easily shown, it follows from condition (A4) that the solution of this problem exists and is everywhere positive. Therefore, the expression in the right-hand side of equality (21) is negative due to \(\sigma>0\) at sufficiently small \({\varepsilon}\).

Thus, based on the well-known comparison theorems from [12], one can state that there exists a \(T\)-periodic in \(t\) solution of the problem satisfying the inequality \(\alpha_{n}(x,t,{\varepsilon})\leqslant u(x,t,{\varepsilon})\leqslant\beta_{n}(x,t,{\varepsilon})\). Using the method of contracting barriers (see, e.g., [13]), it is easy to prove that this solution is asymptotically stable in the sense of Lyapunov with the attraction domain of at least \([\alpha_{1}(x,0,{\varepsilon});\beta_{1}(x,0,{\varepsilon})]\) the width of which is \(O({\varepsilon})\). Thus, the following theorem is proved:

Theorem 1. Suppose that conditions (A1)–(A4) are satisfied. Then there exists a \(T\)-periodic in \(t\) solution \(u_{p}(x,t,\varepsilon)\) of problem (2) for which the estimate

$$|u_{p}(x,t,{\varepsilon})-U_{n}(x,t,{\varepsilon})|=O({\varepsilon}^{n+1})$$

is valid.

In addition, the solution \(u_{p}(x,t,{\varepsilon})\) is asymptotically stable in the sense of Lyapunov with the domain of stability with a width \(O({\varepsilon})\), and, therefore, it is unique in this domain.

3 THE MOTION OF THE FRONT IN THE INITIAL BOUNDARY VALUE PROBLEM

The following study of the initial boundary value problem is a direct development of results from [8] for the case of the presence of advection and a periodic dependence of the reaction and advection coefficients on time.

We suppose that conditions (A1)–(A4) are satisfied and study the motion of the formed front in the presence of periodic solutions mentioned in Theorem 1. We are interested in solutions that are attracted to the periodic solution \(u_{p}(x,t,{\varepsilon})\) as \(t\to\infty\) found in the previous section.

The statement of the initial boundary value problem has the form

$$Nu:=\varepsilon^{2}\frac{\partial^{2}u}{\partial x^{2}}-\varepsilon\frac{\partial u}{\partial t}-\varepsilon A(x,t,\varepsilon)\frac{\partial u}{\partial x}$$
$${}-f(u,x,t,\varepsilon)=0,$$
$$\quad x\in(-1,1),\quad t>0,$$
$$\frac{\partial u}{\partial x}(-1,t,\varepsilon)=0,\quad\frac{\partial u}{\partial x}(1,t,\varepsilon)=0,\quad t>0,$$
$$u(x,0,\varepsilon)=u_{00}(x,\varepsilon),\quad x\in[-1,1].$$
(24)

The asymptotics of the solution of problem (24) for which we introduce a notation \(\tilde{U}_{n}(x,t,{\varepsilon})\) has the same form as the asymptotics \(U_{n}(x,t,{\varepsilon})\) for the periodic solution \(u_{p}(x,t,{\varepsilon})\); in the latter, however, the transition layer coordinate is determined in a different way: \(\tilde{x}(t)=\tilde{x}_{0}(t)+{\varepsilon}\tilde{x}_{1}(t)+{\varepsilon}^{2}\tilde{x}_{2}(t)+...\) . Let the following condition be satisfied.

(A5) Let the problem

$$\begin{cases}\frac{dx}{dt}=W(x,t)+A(x,t,0),\\ x(0)=x_{00}\in(-1,1)\end{cases}$$
(25)

have a solution \(x=\tilde{x}_{0}(t)\): \(-1<\tilde{x}_{0}(t)<1\) at \(t\geqslant 0\); along with this, \(\lim\limits_{t\to\infty}(\tilde{x}_{0}(t)-x_{0}(t))=0\).

The limit relationship in (25) is the requirement that \(x_{00}\) must belong to the domain of influence of the asymptotically stable periodic solution \(x_{0}(t)\).

The functions \(\tilde{x}_{i}(t)\), \(i=1,2,...\), are defined as solutions of linear Cauchy problems for Eq. (17), in which \(x_{0}(t)\) is replaced by \(\tilde{x}_{0}(t)\), with the initial condition \(\tilde{x}_{i}(0)=0\).

Let \(\tilde{\alpha}_{n}(x,t,{\varepsilon})\) and \(\tilde{\beta}_{n}(x,t,{\varepsilon})\) denote the lower and upper solutions for problem (24), respectively. The upper and lower solutions for problem (24) are defined similarly to the definition used in the previous section. The main difference is only that the requirement of \(T\)-periodicity in \(t\) is replaced by condition

(A6) Let the inequality \(\tilde{\alpha}(x,0,{\varepsilon})\leqslant u_{00}(x,{\varepsilon})\leqslant\tilde{\beta}(x,0,{\varepsilon}),x\in[-1,1],{\varepsilon}\in(0,{\varepsilon}_{0}]\) be satisfied.

Fig. 1
figure 1

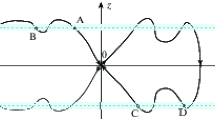
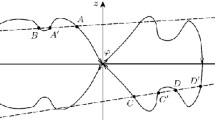
(a–f) Solutions of periodic problem (27) and corresponding initial boundary value problem as a function of coordinate \(x\) at different values of \(t\) with a step equal to \(1\). The dashed and dot-and-dash lines denote the numerical solutions of the corresponding initial boundary value problem that are attracted to the solution with the internal transition layer. The solid line is the zero-order asymptotics for the periodic solution \(u_{p}(x,t,{\varepsilon})\). Figure (e) depicts the corresponding solutions of Eq. (12) with the periodicity condition in time (the solid curve) and with the initial conditions \(x(0)=0.9\) (the dot-and-dash curve) and \(x(0)=-0.9\) (the dashed curve).

Full size image

The last condition means that the front is already formed at the initial time instant.

The upper solution is defined by expression (20) in which (1) functions \(x_{i}(t)\) are replaced by \(\tilde{x}_{i}(t)\), (2) function \(\delta(t)\) is replaced by function \(\tilde{\delta}(t)\) defined as a solution of the Cauchy problem for Eq. (22) in which \(x_{0}(t)\) is replaced by \(\tilde{x}_{0}(t)\) with the initial condition \(\tilde{\delta}(0)=\tilde{\delta}_{0},\) where \(\tilde{\delta}_{0}>0\) is a constant. One can show that, by virtue of conditions (A3)–(A5)

$$\delta_{1}<\tilde{\delta}(t)<\delta_{0},\quad t\geqslant 0,$$
(26)

where \(\delta_{0}\) and \(\delta_{1}\) are certain positive constants.

The lower solution \(\tilde{\alpha}(x,t,{\varepsilon})\) has a similar structure. It is seen that all conditions involved in the definition of the upper and lower solutions for problem (24) are satisfied for the functions \(\tilde{\alpha}(x,t,{\varepsilon})\) and \(\tilde{\beta}(x,t,{\varepsilon})\). It follows from the well-known comparison theorems (see [14]) that there exists a unique solution of initial boundary value problem (24) \(u(x,t,{\varepsilon})\in[\tilde{\alpha}(x,t,{\varepsilon}),\tilde{\beta}(x,t,{\varepsilon})]\), \(x\in[-1,1]\), \(t\geqslant 0,\) \({\varepsilon}\in(0,{\varepsilon}_{0}]\). As well, by virtue of condition (A5) and inequality (26), there exists \(t_{1}\) such that the inequalities \(\alpha_{1}(x,t_{1},{\varepsilon})<\tilde{\alpha}_{2}(x,t_{1},{\varepsilon})\leqslant u(x,t_{1},{\varepsilon})\leqslant\tilde{\beta}_{2}(x,t_{1},{\varepsilon})<\beta_{1}(x,t_{1},{\varepsilon})\) are valid for \(t\geqslant t_{1}\). These mean that the function \(u(x,t_{1},{\varepsilon})\) lies in the domain of influence of the stable solution \(u_{p}(x,t,{\varepsilon})\). Thus, the following theorem is valid:

Theorem 2. Suppose that conditions (A1)–(A6) are satisfied. Then there exists a unique solution \(u(x,t,\varepsilon)\) of problem (24) having an internal transition layer for which the estimate

$$|u(x,t,{\varepsilon})-\tilde{U}_{n}(x,t,{\varepsilon})|=O({\varepsilon}^{n+1})$$

is valid.

In addition,

$$\lim\limits_{t\to\infty}|u(x,t,{\varepsilon})-u_{p}(x,t,{\varepsilon})|=0.$$

4 EXAMPLE

Let us consider the problem

$$\varepsilon^{2}\frac{\partial^{2}u}{\partial x^{2}}-\varepsilon\frac{\partial u}{\partial t}$$
$${}+\varepsilon k(t)x\frac{\partial u}{\partial x}=\left(u^{2}-1\right)\left(u-\varphi^{(0)}(x,t)\right),$$
$$x\in(-1,1),\quad t\in\mathbb{R};$$
$$\frac{\partial u}{\partial x}(-1,t,\varepsilon)=0,\quad\frac{\partial u}{\partial x}(1,t,\varepsilon)=0,$$
$$u(x,t,\varepsilon)=u(x,t+2\pi,\varepsilon),$$
$$x\in[-1,1],\quad t\in\mathbb{R}.$$
(27)

For the zero-order asymptotics, we have an expression

$$U_{0}(x,t,{\varepsilon})=\tilde{u}(\xi,x_{0}(t),t)=\frac{C(x_{0},t)\exp(\sqrt{2}\xi)-1}{C(x_{0},t)\exp(\sqrt{2}\xi)+1},$$
$$C(x,t)=\frac{1+\varphi^{(0)}(x,t)}{1-\varphi^{(0)}(x,t)}.$$

The problem for the determination of the transition point \(x_{0}(t)\) corresponding to the periodic solution \(u_{p}(x,t,{\varepsilon})\) has the form

$$\frac{dx}{dt}=\sqrt{2}\varphi^{(0)}(x,t)-k(t)x,\quad t\in\mathbb{R},$$
(28)
$$x(t)=x(t+2\pi).$$
(29)

Let us put \(\varphi^{(0)}(x,t)=\frac{b}{\sqrt{2}}\sin{t}\), \(b=\text{const}<\sqrt{2}\); then, problem (28) takes the form

$$\frac{dx}{dt}+k(t)x=b\sin t,\quad t\in\mathbb{R},$$
(30)
$$x(t)=x(t+2\pi).$$
(31)

The solution of problem (30), (31) is written explicitly:

$$x_{0}(t):=\Phi(t)\frac{\Phi(2\pi)}{1-\Phi(2\pi)}\int\limits_{0}^{2\pi}\Phi^{-1}(s)b\sin{s}ds$$
$${}+\Phi(t)\int\limits_{0}^{t}\Phi^{-1}(s)b\sin{s}ds,$$
$$\Phi(t)=\exp{\left(-\int\limits_{0}^{t}k(s)ds\right)}.$$

Let the \(2\pi\)-periodic function \(k(t)\) be chosen such that the inequality

$$\int\limits_{0}^{2\pi}\left.\frac{\partial}{\partial x}\bigg{(}W(x,t)+A(x,t,0)\bigg{)}\right|_{x=x_{0}(t)}dt$$
$$=-\int_{0}^{2\pi}k(t)dt<0$$

is satisfied. In particular, if we choose \(k(t)=1\), we have \(x_{0}(t)=\frac{b}{\sqrt{2}}\sin(t-\pi/4).\) It is evident that conditions (A1)–(A4) are satisfied; therefore, the statement of Theorem 1 is valid for problem (27).

Let us now consider the initial boundary value problem corresponding to problem (27) with the initial condition

$$u(x,0,\varepsilon)=\tilde{u}\left(\frac{x-x_{00}}{{\varepsilon}},x_{00},0\right),$$
$$x\in[-1,1],$$
(32)

where \(x_{00}=x_{0}(0)+\Delta\), \(\Delta=\text{const}\). By virtue of linearity of problem (30) and fulfillment of condition (A4), its periodic solution \(x_{0}(t)\) is globally stable and, therefore, condition (A5) is also satisfied (at the same time, condition \(-1<\tilde{x}_{0}(t)<1\) is satisfied due to the choice of a sufficiently small \(\Delta\)). It is evident that condition (A6) is also satisfied. Thus, for the initial boundary value problem corresponding to problem (27) with initial condition (32), the statement of Theorem 2 is valid. The layer motion is shown in Fig. 1 (for \(k(t)\equiv 1\) and \(\varphi^{(0)}(x,t)=\frac{1}{2}\sin{t}\)).

CONCLUSIONS

As a result of the investigation, the existence theorems have been proved for an asymptotically stable periodic solution with an internal transition layer and for a nonstationary solution of the same type. Conditions providing the presence of an asymptotically stable periodic layer and conditions under which the solution in the form of the internal layer for the corresponding initial boundary value problem is attracted to it have been revealed. The further development of studying these problems may consist in the study of the layer generation problem, as well as in the passage to the multidimensional case.