INTRODUCTION

Periodic parabolic boundary value problems have been being intensively studied from both the theoretical and applied standpoints. A number of problem classes that are important for applications can be found, for example, in [1]. Evolution and periodic problems with analogous higher differential operators were considered in [3–6] based on the operator method under development, as well as their application in a number of applied physical problems. In applications, equations of this kind are called reaction-diffusion equations or reaction–diffusion–advection equations when they involve a term that describes transport. These equations are widely and successfully used in nonlinear wave theory and fluid dynamics (see, for example, [2–8]). In many cases, singularly perturbed problems of the considered type are used to describe processes with an intense reaction (source), namely, problems with a small-parameter coefficient of the higher differential operator. A characteristic feature of these problems is the existence of solutions with boundary and inner transition layers [9–11]. We also note that an analogous method was applied in [12] to study the asymptotic stability. Reaction–diffusion–advection equations often occur in applications, for example, in ecology when the variation in temperature or gas concentration in surface layers of the atmosphere is mathematically simulated, as well as in chemical kinetics and biological kinetics. In this work, we consider a new class of problems that have not been studied earlier, more precisely, problems multidimensional with respect to the spatial variable with boundary conditions singular with respect to the small parameter. This work develops and generalizes the result obtained in [13] for the one-dimensional case to the more complicated class of problems multidimensional with respect to the spatial variable. Problems with singularly perturbed conditions arise in many applications where reaction–diffusion equations are used as mathematical models. In particular, boundary conditions of such a type occur in the hydrodynamic variant of the Burgers equation (see, for example, [14]).

1 PROBLEM STATEMENT

We consider the following reaction–diffusion equation with a second-kind singularly perturbed boundary condition that naturally occurs in mathematical models with rapid flow across a boundary:

$$N_{\varepsilon}(u):=\varepsilon^{2}\left(\triangle u-\frac{\partial u}{\partial t}\right)-f(u,x,t,{\varepsilon})=0,$$
$$(x,t)\in D_{t}:=\{(x,t)\in R^{3}:x\in{D},t\in R\},$$
$${\varepsilon}\frac{\partial u}{\partial n}(x,t,{\varepsilon})=u_{\Gamma}(x,t),\quad x\in{\Gamma},t\in R,$$
$$u(x,t,{\varepsilon})=u(x,t+T,{\varepsilon}),\quad x\in\bar{D},t\in R,$$
(1)

where \(\triangle=\frac{\partial^{2}}{{\partial x_{1}}^{2}}+\frac{\partial^{2}}{{\partial x_{2}}^{2}}\), \(\frac{\partial}{\partial n}\) is the derivative with respect to the inner normal to the smooth boundary \(\Gamma\) of a given two-dimensional simply connected domain \(D\), and \({\varepsilon}>0\) is a small parameter.

The small parameter \({\varepsilon}\) in the boundary condition can be interpreted as intense sources at the boundary of the domain. Boundary conditions of this type are called singular, since the small parameter is in the denominator when the Neumann boundary condition is written in the standard form. Unlike the standard Neumann condition, when the boundary layer is weak (of order \({\varepsilon}\)), the boundary layer occurring in this case is of order 1 and as shown below has a more complex structure than that in the case of Dirichlet boundary conditions.

We assume that the following conditions hold:

(A1) Let \(f(u,x,t,\varepsilon)\) and \(u_{\Gamma}(x,t)\) be sufficiently smooth \(T\)-periodic (with respect to \(t\)) functions in the considered domain.

(A2) Let the degenerate equation \({f}(u,x,t,0)=0\) have a \(T\)-periodic (with respect to \(t\)) solution \(u=\varphi(x,t)\) such that

$$f_{u}(\varphi,x,t,0)>0,\quad x\in\bar{D},\quad t\in R.$$

We study the problem of the existence of a smooth periodic solution of problem (1) such that for any time \(t\), it tends to the root \(\varphi(x,t)\) in the interior of the domain \(D\) bounded by the curve \(\Gamma\) as \({\varepsilon}\to 0\) and abruptly changes in a neighborhood of \(\Gamma\), that is, that has a boundary layer.

2 CONSTRUCTION OF THE ASYMPTOTICS

2.1 Asymptotic Expansion of the Solution

To describe the boundary layer in a standard way we introduce a local system of coordinates. For the curve \(\Gamma\), we define the \(\delta\)-neighborhood \(\Gamma^{\delta}(t):=\{P\in D:dist(P,\Gamma)<\delta\}\), \(\delta=const>0\). Furthermore, in the \(\delta\)-neighborhood of \(\Gamma\), we introduce the local coordinates \((r,\theta)\), where \(\theta\in[0,\Theta)\) is the coordinate of the point \(M\in{\Gamma}\) such that \(dist\{x,\Gamma\}=dist\{x,M\}\); \(r=dist\{x,\Gamma\}\), \(x\in D\). We assume that the curve \(\Gamma\) is given parametrically as follows: \(x_{i}=X_{i}(\theta)\), \(i=1,2\); \(\mathbf{n}(\theta)=\{n_{1}(\theta),n_{2}(\theta)\}\) is the inner normal to \(\Gamma\) at \(M\). With a sufficiently small \(\delta\) (which is however finite and independent of \({\varepsilon}\)), there is a one-to-one correspondence between the coordinates \((x_{1},x_{2})\) and \((r,\theta)\):

$$x_{i}=X_{i}(\theta)+rn_{i}(\theta),\quad i=1,2.$$

We seek the asymptotics of the solution to problem (1) in the form

$$U(x,t,{\varepsilon})=\bar{u}(x,t,{\varepsilon})+\Pi(\xi,\theta,t,{\varepsilon}),$$
(2)

where the regular part has the form

$$\bar{u}(x,t,{\varepsilon})=\bar{u}_{0}(x,t)+{\varepsilon}\bar{u}_{1}(x,t)+$$
$${}\ldots+{\varepsilon}^{n}\bar{u}_{n}(x,t)+\ldots$$

and the boundary part in the neighborhood of \(\Gamma\) has the form

$$\Pi(\xi,\theta,t,{\varepsilon})=\Pi_{0}(\xi,\theta,t)$$
$${}+{\varepsilon}\Pi_{1}(\xi,\theta,t)+\ldots+{\varepsilon}^{n}\Pi_{n}(\xi,\theta,t)+\ldots,$$

where

$$\xi=\frac{r}{{\varepsilon}}.$$

Such a structure of the asymptotics is standard for problems with boundary layers and has been proposed by Tikhonov and Vasil’eva in their classical works (see [15]): the regular part of the asymptotics is intended to approximate the solution in the interior of the domain, while the boundary layer part is intended to approximate the solution near the boundary. The coefficients of the powers of \({\varepsilon}\) in the boundary layer part are called boundary functions.

In view of the features of a parabolic operator (see [16, 17]), the standard algorithm of the boundary function method (see [15, 16]) gives a sequence of problems to determine the coefficients of asymptotic series (2). In particular, we obtain the relation \(\bar{u}_{0}(x,t)=\varphi(x,t)\), while the terms \(\bar{u}_{i}(x,t)\) of higher orders can be derived from simple algebraic equations.

We will consider constructing the boundary layer functions in detail. The Laplace operator in the local coordinates \((r,\theta)\) has the form (see [15]) \(\triangle=\frac{\partial^{2}}{\partial r^{2}}+\triangle{r}\frac{\partial}{\partial r}+|\nabla\theta|^{2}\frac{\partial^{2}}{\partial\theta^{2}}+\triangle{\theta}\frac{\partial}{\partial\theta}\). When acting on the boundary layer functions, the differential operator \(D_{\varepsilon}:=\varepsilon^{2}\left(\triangle-\frac{\partial}{\partial t}\right)\) assumes the following form in the variables \((\xi,\theta,t)\):

$$D_{\varepsilon}=\frac{\partial^{2}}{\partial\xi^{2}}+{\varepsilon}s({\varepsilon}\xi,\theta)\frac{\partial}{\partial\xi}$$
$${}+{\varepsilon}^{2}\left(|\nabla\theta|^{2}\frac{\partial^{2}}{\partial\theta^{2}}+\triangle{\theta}\frac{\partial}{\partial\theta}-\frac{\partial}{\partial t}\right),$$

where \(s(r,\theta):=\triangle{r}(r,\theta).\) Let \({\mathbf{R_{0}(\theta)}}=\{X_{1}(\theta),X_{2}(\theta)\}\) be the radius vector of a point of the curve \(\Gamma\) with coordinate \(\theta\). We know (see [18]) that \(\triangle{r}(r,\theta)\) is the curvature of \(\Gamma_{r}:=\{x\in D:{}\{x_{1},x_{2}\}=\mathbf{R_{0}}(\theta)+r\mathbf{n}(\theta)\}\) at the point \((x_{1}(\theta),x_{2}(\theta))\).

We will determine the functions \(\Pi_{i}\) using the scheme of the algorithm proposed by A.B. Vasil’eva.

The term \(\Pi_{0}(\xi,\theta,t)\) is obtained from the problem

$$\frac{\partial^{2}\Pi_{0}(\xi,\theta,t)}{\partial\xi^{2}}=f(\varphi(0,\theta,t)$$
$${}+\Pi_{0}(\xi,\theta,t),0,\theta,t,0),\quad\xi>0,$$
$$\frac{\partial\Pi_{0}}{\partial\xi}(0,\theta,t)=u_{\Gamma}(\theta,t),$$
$$\Pi_{0}(+\infty,\theta,t)=0.$$
(3)

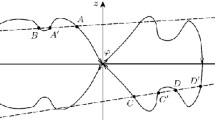
The differential equation in (3) is an autonomous second-order equation (\(\theta\) and \(t\) are parameters), which can be studied on the phase plane \((\Pi_{0},{\Pi_{0}^{\prime}})\), where the origin \((0,0)\) is a saddle-type equilibrium point (due to (A2)). Problem (3) has a solution in the case when a separatrix passing toward the saddle point \((0,0)\) intersects the horizontal line \(\Pi_{0}^{\prime}=u_{\Gamma}(\theta,t).\) This problem can have several solutions (see Fig. 1). We choose a solution according to the following condition.

(A3) We assume that for any fixed \((\theta,t)\in[0,\Theta)\times\mathbb{R}\), that problem (3) has a solution \(\Pi_{0}(\xi,\theta,t)\) that is monotonic with respect to \(\xi\) and satisfies the inequality

$$\Pi_{0}^{\prime\prime}(0,\theta,t)=f(\varphi(0,\theta,t)$$
$${}+\Pi_{0}(0,\theta,t),0,\theta,t,0)>0(<0),$$
$$\Pi_{0}(0,\theta,t)>0(<0).$$
Fig. 1
figure 1

The possible location of separatrices on the phase plane of problem (3). The upper and lower horizontal dotted lines correspond to positive and negative values of the function \(u_{\Gamma}(\theta,t)\).

Full size image

Several solutions \(\Pi_{0}(\xi,\theta,t)\) satisfying (A3) can exist. For example, when points \(A\), \(B\), \(C\), and \(D\) correspond to the argument \(\xi=0\) (Fig. 1), we obtain phase trajectories that are solutions of problem (3) that satisfy the condition (A3) when moving away from them along the corresponding separatrix toward the saddle point (0,0). The following estimates are known to hold (see [19]):

$$|\Pi_{0}(\xi,\theta,t)|\leq{C}e^{-k\xi},$$
(4)

where \(C\) and \(k\) are some positive constants.

We will show how to obtain the functions \(\Pi_{i}\), \(i=1,2\ldots\).

The functions \(\Pi_{1}\) are derived from the problem

$$\frac{\partial^{2}\Pi_{1}}{\partial\xi^{2}}-\frac{\partial\tilde{f}}{\partial u}\Pi_{1}=r_{1},$$
$$\frac{\partial\Pi_{1}(0,\theta,t)}{\partial\xi}+\frac{\partial\bar{u}_{0}}{\partial r}(0,\theta,t)=0,$$
$$\Pi_{1}(+\infty,\theta,t)=0,$$
$$r_{1}(\xi,\theta,t):=-\frac{\partial\Pi_{0}}{\partial\xi}(\xi,\theta,t)s(0,\theta)$$
$${}+\xi\left(\frac{\partial\tilde{f}}{\partial u}\frac{\partial\bar{u}_{0}}{\partial r}(0,\theta,t)+\frac{\partial\tilde{f}_{0}}{\partial r}\right)$$
$${}+\bar{u}_{1}(0,\theta,t)\frac{\partial\tilde{f}}{\partial u}+\frac{\partial\tilde{f}_{0}}{\partial\varepsilon},$$
(5)

where the symbol ‘‘\({\sim}\)’’ over a function means that its value is taken at the argument \((\Pi_{0}(\xi,\theta,t)+\bar{u}_{0}(0,\theta,t),0,\theta,t,0)\).

The solution of (5) under the condition that \((\Pi_{0}(\xi,\theta,t)\) is chosen according to the requirement (A3) is explicitly representable as (see [13])

$$\Pi_{1}(\xi,t)=\frac{z(\xi,\theta,t)}{\frac{\partial z}{\partial\xi}(0,\theta,t)}\bigg{\{}-\frac{\partial\overline{u}_{0}}{\partial r}(0,\theta,t)$$
$${}+\frac{1}{z(0,\theta,t)}\int\limits_{0}^{\infty}z(\chi,\theta,t)r_{1}(\chi,\theta,t)d\chi\bigg{\}}-z(\xi,\theta,t)$$
$${}\times\int\limits_{0}^{\xi}\frac{1}{z^{2}(\eta,\theta,t)}\left[\int\limits_{\eta}^{\infty}z(\chi,\theta,t)r_{1}(\chi,\theta,t)d\chi\right]d\eta,$$
(6)

where \(z(\xi,\theta,t)=\frac{\partial\Pi_{0}(\xi,\theta,t)}{\partial\xi}\).

For \(\Pi_{1}\), the estimate

$$|\Pi_{1}(\xi,\theta,t,{\varepsilon})|<{C_{1}}e^{-k_{1}\xi}$$

holds, where \(C_{1}\) and \(k_{1}\) are some positive constants.

The inner transition layer functions of higher orders are derived from problems analogous to the problems for \(\Pi_{1}\):

$$\frac{\partial^{2}\Pi_{i}}{\partial\xi^{2}}-\frac{\partial\tilde{f}}{\partial u}\Pi_{i}=r_{i},$$
$$\frac{\partial\Pi_{i}(0,\theta,t)}{\partial\xi}+\frac{\partial\bar{u}_{i+1}}{\partial r}(0,\theta,t)=0,$$
$$\Pi_{i}(+\infty,\theta,t)=0,$$
(7)

where \(r_{i}(\xi,\theta,t)\) are known functions. The solution of (7) can be written in an explicit form analogous to (6). We note that the inverse operator that specifies the solution of the problems for \(\Pi_{i}\) is monotonic, which is essentially used in proving the existence of the solution and its asymptotic Lyapunov stability.

We note that the \(\Pi\)-functions are formally defined for \(\xi\in R\); however, they actually make sense only for \(|\xi|\leq\frac{\delta}{{\varepsilon}}\). To smoothly extend them to the whole of the domain \(D\), the standard method of smoothing functions is used (see, for example, [15]).

Thus, we have completed a formal construction of the asymptotics of the solution with a boundary layer for problem (1).

3 JUSTIFICATION OF THE CONSTRUCTED ASYMPTOTICS

Let \(U_{n}(x,t,{\varepsilon})=\sum_{i=0}^{n}({\bar{u}_{i}(x,t)}+\Pi_{i}(\xi,\theta,t)){\varepsilon}^{i}.\) The following theorem states the main result of this section.

Theorem 1.If the conditions(A1–A3)are satisfied, then for sufficiently small \({\varepsilon}\), for each solution \(\Pi_{0}(\xi,\theta,t)\)of problem (3) chosen according to the condition (A3), there exists a relevant solution \(u(x,t,{\varepsilon})\)of problem (1) with a boundary layer such that the estimate

$$|{U_{n}(x,t,{\varepsilon})-u(x,t,{\varepsilon})}|<C{\varepsilon}^{n+1},$$
$$x\in\bar{D},\quad t\in R$$

holds.

Proof

We will prove this assertion based on the method of differential inequalities. As an upper solution, we choose the function

$$\beta_{n}(x,t,{\varepsilon})=\bar{u}_{0}(x,t)$$
$${}+{\varepsilon}\bar{u}_{1}(x,t)+\ldots+{\varepsilon}^{n+1}\bar{u}_{n+1}(x,t)+\Pi_{0}(\xi,\theta,t)$$
$${}+{\varepsilon}\Pi_{1}(\xi,\theta,t)+\ldots+{\varepsilon}^{n+1}\Pi_{n+1}(\xi,\theta,t)$$
$${}+{\varepsilon}^{n+1}(\gamma+\Pi_{\beta}(\xi,\theta,t)),$$

where the function \(\Pi_{0}\) is chosen according to the condition (A3), \(\gamma>0\) is a constant that provides the fulfillment of the necessary differential inequality and the functions \(\Pi_{\beta}\) are needed to compensate the changes due to \(\gamma\); these functions are derived from the problem

$$\frac{\partial^{2}\Pi_{\beta}}{\partial\xi^{2}}-\frac{\partial\tilde{f}}{\partial u}\Pi_{\beta}=r_{\beta},$$
$$\frac{\partial\Pi_{\beta}(0,\theta,t)}{\partial\xi}=-\delta,$$
$$\Pi_{\beta}(+\infty,\theta,t)=0,$$
(8)

where \(\delta>0\) is some constant and

$$\quad r_{\beta}(\xi,\theta,t){}{}=\gamma\bigg{(}\frac{\partial f}{\partial u}(\Pi_{0}(\xi,\theta,t)$$
$$+\bar{u}_{0}(0,\theta,t),0,t,0)$$
$${}-\frac{\partial f}{\partial u}(\varphi,0,t,0)\bigg{)}-M\exp(-k\xi).$$

It is straightforward to see that the coefficient of \(\gamma\) has an exponential estimate implied by (4). Therefore, we can choose a sufficiently large \(M>0\) and a sufficiently small \(k>0\) so that \(r_{\beta}(\xi,\theta,t)<0\).

Problem (8) is analogous to problem (7) and has the solution

$$\Pi_{\beta}(\xi,t)=\frac{z(\xi,\theta,t)}{\frac{\partial z}{\partial\xi}(0,\theta,t)}$$
$${}\times\bigg{\{}-\delta+\frac{1}{z(0,\theta,t)}\int\limits_{0}^{\infty}z(\chi,\theta,t)r_{\beta}(\chi,\theta,t)d\chi\bigg{\}}$$
$${}-z(\xi,\theta,t)\int\limits_{0}^{\xi}\frac{1}{z^{2}(\eta,\theta,t)}$$
$${}\times\left[\int\limits_{\eta}^{\infty}z(\chi,\theta,t)r_{\beta}(\chi,\theta,t)d\chi\right]d\eta.$$
(9)

Due to (A3), if \(\Pi_{0}(0,\theta,t)>0{}(<0)\), then the following inequalities are valid: \(\frac{\partial z}{\partial\xi}(0,\theta,t)=\Pi_{0}^{\prime\prime}(0,\theta,t)>0(<0)\), \(z(\xi,\theta,t)=\Pi_{0}^{\prime}(\xi,\theta,t)<0(>0)\), \(\xi\in[0,\infty)\), \(t\in\mathbb{R}\), \(\theta\in[0,\Theta)\). These inequalities and (9) imply that \(\Pi_{\beta}(\xi,\theta,t)>0\), \(\xi\in[0,\infty)\), \(t\in\mathbb{R}\), \(\theta\in[0,\Theta)\).

The lower solution \(\alpha_{n}(x,t,{\varepsilon})\) has an analogous structure such that \(r_{\alpha}(\xi,\theta,t)>0\), \(\Pi_{\alpha}(\xi,\theta,t)<0\), \(\xi\in[0,\infty)\), \(t\in\mathbb{R}\), \(\theta\in[0,\Theta)\); therefore, the upper and lower solutions are ordered.

To verify the necessary differential inequalities, we directly compute them analogously to [13]. For the upper solution, we have

$$N_{{\varepsilon}}\beta_{n}={\varepsilon}^{2}\bigg{(}\triangle-\frac{\partial}{\partial t}\bigg{)}\beta_{n}-f(\beta_{n},x,t,{\varepsilon})$$
$${}=-{\varepsilon}^{n+1}\bigg{(}{\frac{\partial\bar{f}}{\partial u}\gamma+M\exp(-k\xi)\bigg{)}}+O({\varepsilon}^{n+2}),$$

where the dash over a function means that its value is taken at the argument \((\bar{u}_{0},0,\theta,t,0)\). Due to (A2), for sufficiently small \(\varepsilon\), the inequality \(N_{{\varepsilon}}{{\beta}_{n}}<0\) holds for any \(\gamma>\text{0}\).

The inequality on the boundary is verified directly as follows:

$${{\varepsilon}}\frac{\partial\beta_{n}}{\partial r}(x_{\Gamma},t,{\varepsilon})=\frac{\partial\Pi_{0}}{\partial\xi}+{\varepsilon}^{n+1}\frac{\partial\Pi_{\beta}}{\partial\xi}+{\varepsilon}^{n+2}\frac{\partial u_{n+1}}{\partial r}$$
$${}=u_{\Gamma}(\theta,t)+{\varepsilon}^{n+1}\bigg{\{}-\delta+\frac{1}{z(0,\theta,t)}$$
$${}\times\int\limits_{0}^{\infty}z(\chi,\theta,t)r_{\beta}(\chi,\theta,t)d\chi\bigg{\}}+O({\varepsilon}^{n+2})\leq u_{\Gamma}(\theta,t).$$

The corresponding inequality for the upper solution can be verified analogously.

The known comparison theorems imply the existence of a solution of problem (1) that satisfies the inequality \(\alpha_{n}(x,t,{\varepsilon})\leq u(x,t,{\varepsilon})\leq\beta_{n}(x,t,{\varepsilon})\), where, as follows from the construction, we have \(\alpha_{n}(x,t,{\varepsilon})-\beta_{n}(x,t,{\varepsilon})=O({\varepsilon}^{n+1})\), which yields the assertion of the theorem.

4 THE ASYMPTOTIC STABILITY OF THE SOLUTION

Periodic solutions of problem (1) can be considered as solutions of the relevant initial boundary value problem on the semi-infinite time interval:

$$N_{\varepsilon}(v):=\varepsilon^{2}\left(\triangle v-\frac{\partial v}{\partial t}\right)-f(v,x,t,{\varepsilon})=0,$$
$$(x,t)\in D_{t+}:=\{(x,t)\in R^{3}:x\in{D},0<t<\infty\},$$
$${\varepsilon}\frac{\partial v}{\partial n}(x,t,{\varepsilon})=u_{\Gamma}(x,t),\quad x\in{\Gamma},t\in R,$$
$$v(x,0,{\varepsilon})=v^{0}(x,{\varepsilon}),\quad(x,y)\in\bar{D}.$$
(10)

Evidently, if \(v^{0}(x,{\varepsilon})=u(x,0,{\varepsilon})\), where \(u(x,t,{\varepsilon})\) is a solution of periodic problem (1), then problem (10) has the solution \(v(x,t,{\varepsilon})=u(x,t,{\varepsilon})\). Studying its stability is based on the asymptotic method of differential inequalities. We will seek the upper and lower solutions of problem (10) in the form \(\alpha(x,t,{\varepsilon})=u(x,t,{\varepsilon})+e^{-\Lambda({\varepsilon})t}(\alpha_{n}(x,t,{\varepsilon})-u(x,t,{\varepsilon}))\) and \(\beta(x,t,{\varepsilon})\!=\!u(x,t,{\varepsilon})+e^{-\Lambda({\varepsilon})t}(\beta_{n}(x,t,{\varepsilon})-u(x,t,{\varepsilon}))\), where \(\Lambda({\varepsilon})>0\) will be indicated below. It is obvious that \(\alpha<\beta\); to verify the classical theorems on differential inequalities for parabolic systems in [1], it suffices to show that \(N_{{\varepsilon}}\beta<0\) and \(N_{{\varepsilon}}\alpha>0\). By substituting the above expressions for \(\alpha\) and \(\beta\) and taking the fact into account that \(u\) is a solution of Eq. (1), we can easily derive the needed inequalities. As an example, the expression for \(N_{{\varepsilon}}\beta\) is transformed to the form (for brevity, we omit all arguments of the functions \(f\) and \(f_{u}\) except for the first one in the following formulas):

$$N_{{\varepsilon}}\beta=e^{{-\Lambda}t}\bigg{\{}\bigg{[}{\varepsilon}^{2}\bigg{(}-\frac{\partial\beta_{n}}{\partial t}+\triangle{\beta_{n}}\bigg{)}-f(\beta_{n})\bigg{]}$$
$${}+\bigg{[}{\varepsilon}^{2}\bigg{(}-\frac{\partial u}{\partial t}+\triangle{u}\bigg{)}-f(u)\bigg{]}$$
$${}+[f(\beta_{n})-f(u)-f_{u}^{*}\cdot(\beta_{n}-u)]+{\varepsilon}^{2}\Lambda(\beta_{n}-u)\bigg{\}}.$$

Here, the symbol ‘‘\(*\)’’ to the right of a function means that its value is taken at the argument \(u(x,t,{\varepsilon})+{\theta}e^{-\Lambda({\varepsilon})t}(\alpha_{n}(x,t,{\varepsilon})-u(x,t,{\varepsilon})\)), \(0<\theta<1\).

We use the fact that \({\varepsilon}^{2}\big{(}-\frac{\partial\beta_{n}}{\partial t}+\triangle{\beta_{n}}\big{)}-f(\beta_{n})=-{\varepsilon}^{n+1}\big{(}{\frac{\partial\bar{f}}{\partial u}\gamma+M\exp(-k\xi)\big{)}}+O({\varepsilon}^{n+2})\), where \(\gamma>0\), \(\beta_{n}-u=O({\varepsilon}^{n+1})\), and \(f(\beta_{n})-f(u)-f_{u}^{*}(\beta_{n}-u)=O({\varepsilon}^{2n+2})\); upon choosing \(\Lambda({\varepsilon})=\Lambda_{0}>0\) and a sufficiently large \(\gamma\), we obtain the relation \(N_{{\varepsilon}}\beta=e^{-\Lambda_{0}t}(-{\varepsilon}^{n+1}({\frac{\partial\bar{f}}{\partial u}\gamma+M\exp(-k\xi))}+O({\varepsilon}^{2n+2})+\Lambda_{0}O({\varepsilon}^{n+3}))<0\) for \(n\geq 0\). The inequality \(N_{{\varepsilon}}\alpha>0\) can be verified in an analogous way. Thus, each of the solutions whose existence is guaranteed by Theorem 1 is asymptotically Lyapunov stable with the domain of attraction at least \([\alpha_{0}(x,0,{\varepsilon}),\beta_{0}(x,0,{\varepsilon})]\), whose width is a quantity of order \(O({\varepsilon}^{1}).\)

Therefore, the following theorem is valid.

Theorem 2.We assume that the conditions(A1–A3)hold. Then, each solution \(u(x,t\text{,}\varepsilon)\)of problem (1) whose existence is guaranteed by Theorem 1 is asymptotically Lyapunov stable with the domain of stability at least \([\alpha_{0}(x,0,{\varepsilon}),\beta_{0}(x,0,{\varepsilon})]\); therefore, \(u(x,t,\varepsilon)\)is a unique solution of problem (1) in this domain.

Fig. 2
figure 2

The solid line is a part of the separatrix passing toward the saddle point \((0,0)\) on the phase plane \((\Pi_{0},{\Pi_{0}^{\prime}})\) of relevant problem (12). The dotted line corresponds to the initial condition for \(z=2.2(1+0.05\sin(2\pi t/T))\). The parameter \(t\) is \(0\).

Full size image
Fig. 3
figure 3

The zero-order asymptotics \(U_{0}(x_{1},0,\theta,0,{\varepsilon})\) for both stable boundary layer solutions of problem (11).

Full size image

4.1 An Example of a Boundary Layer Solution

We consider the problem

$$N_{\varepsilon}(u):=\varepsilon^{2}\left(\triangle u-\frac{\partial u}{\partial t}\right)-u(u+2)(u+3)=0,$$
$$(x,t)\in D_{t}:=\{(x,t)\in R^{3}:$$
$$x\in{D}=\{(x_{1},x_{2}):x_{1}^{2}+x_{2}^{2}<1\},t\in R\},$$
$$\quad{\varepsilon}\frac{\partial u}{\partial n}(x,t,{\varepsilon})=2.2(1+0.05\sin(2\pi t/T)),$$
$$\quad x\in{\Gamma},t\in R,$$
$$u(x,t,{\varepsilon})=u(x,t+T,{\varepsilon}),\quad x\in\bar{D},\quad t\in R,$$
(11)

where \(T=0.2,{\varepsilon}=0.1\).

We immediately note that this problem is radially symmetric, which means that the solution must be independent of the parameter \(\theta\), being the angle between the point \((x,y)\) and the \(Ox\) axis.

The degenerate equation \(u(u+2)(u+3)=0\) has three roots \(\varphi_{1}=-2\), \(\varphi_{2}=-3\), and \(\varphi=0\); it is well known that the points \((\varphi_{1},0)\) and \((\varphi,0)\) on the phase plane \((\Pi_{0},{\Pi_{0}^{\prime}})\) are saddle-type equilibrium points, while \(\varphi_{2}=-3\) is a center-type equilibrium point. We seek boundary layer solutions that are close to the root \(\varphi=0\) far from the boundary. The condition (A3) is satisfied by exactly two solutions of problem (8) corresponding to the phase trajectories started at the points \(A\) and \(B\) of intersection of the line \(z=u_{\Gamma}\) and the separatrix passing toward the saddle point \((0,0)\) (see Fig. 2).

The problem for \(\Pi_{0}\) assumes the form

$$\frac{\partial^{2}\Pi_{0}}{\partial\xi^{2}}=\Pi_{0}(\Pi_{0}+2)(\Pi_{0}+3),$$
$$\frac{\partial\Pi_{0}}{\partial\xi}(0,\theta,t)=2.2(1+0.05\sin(2\pi t/T)),$$
$$\Pi_{0}(+\infty,\theta,t)=0.$$
(12)

Then, the zero-order asymptotics of the solution is expressed as follows:

$$U_{0}(x_{1},x_{2},t,{\varepsilon})=\Pi_{0}\Big{(}\Big{(}1-\sqrt{x_{1}^{2}+x_{2}^{2}}\Big{)}/{\varepsilon},\theta,t\Big{)}.$$

Due to Theorems 1 and 2, there exist two asymptotically Lyapunov stable solutions \(u(x,t,{\varepsilon})\) of problem (11) that correspond to the above two solutions of problem (12) such that \(|U_{0}(x,t,{\varepsilon})-u(x,t,{\varepsilon})|=O({\varepsilon})\). Each of the solutions is locally unique in the domain indicated in Theorem 2.

Figure 3shows the zero-order asymptotics for both solutions.

CONCLUSIONS

This paper considers a new class of nonlinear problems in mathematical physics, which is important for many applications. Strict results are obtained concerning the stability of boundary layer solutions in the case of singularly perturbed Neumann boundary conditions. It is established that the behavior of the solution in the boundary layer for problems of this kind is much more complicated than that for problems with Dirichlet boundary conditions and common Neumann conditions. The result can be extended to singularly perturbed boundary conditions of the third kind and is a basis to study new applied problems. The results concerning the conditions of asymptotic stability of boundary layer solutions are also important in studying contrast structures (solutions with inner transition layers), since the limit discontinuous solution depends on the behavior in the boundary layer as well (see, for example, [16]).