Visualization of Black Hole Images

Abstract

A fast progress in the observational technologies in astrophysics provides the unique possibility for detailed observations of black holes in the nearest future. It would be possible to verify general relativity and its numerous modifications in the strong field limit by using observational data from the advanced cosmic interferometric observatories. We review the modeled images of the rotating black hole in different appropriate cases: the luminous distant background, the thin accreting disk and the luminous moving hot spots in relativistic jets along the black hole rotation axis.

1 INTRODUCTION

What is the genuine gravity theory? Nowadays we do not know the answer as on the quantum level and also on the classical one. General relativity perfectly explain all gravitational phenomena in the weak field limit. Meantime numerous modified gravity theories were proposed for understanding the physical properties of relativistic astrophysical objects and expanding Universe. The first serendipitous obser- vation by the Event Horizon Telescope collaboration in 2019 of the black hole shadow opens the unique window for verification of the general relativity and its modifications in the strong field limit. Here we shortly review the possible forms of astrophysical black hole images by using numerical models for photon geodesics (trajectories) in the Kerr metric.

Fig. 1

Classical black hole shadow [3] is viewed, which is a capture photon cross-section in the black hole gravitational field, if there is a luminous background far behind the black hole with respect to a distant observer. Schwarzschild case ($a=0$) is at left and extreme Kerr case ($a=1$) is at right. The disk inside a black hole shadow is an image of the black hole event horizon globe in the imaginative Euclidean space without gravity. Numerically calculated photon trajectories, producing the shadow edge, start from the luminous background far behind the black hole and finish very far from black hole.

Fig. 2

Lensed images (direct and two light echoes) of a compact star on the equatorial circular orbit with radius $r_{s}=20M_{\textrm{h}}G/c^{2}$ around extreme Kerr black hole, observed by a distant telescope in discrete time intervals. Images of the first and second light echoes are projected on the sky close to position of the classical black hole shadow [4]. The dashed circle here and in the all similar figures is an image of the black hole event horizon globe in the imaginative Euclidean space without gravity.

Fig. 3

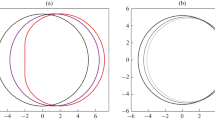
Reconstruction of the lensed event horizon image by detecting of photons emitted some probes very near to the event horizon in the Schwarzschild case (at left) and in extreme Kerr case (at right) [5–7]. The lensed event horizon image is projected on the sky inside the position of classical black hole shadow.

Fig. 4

Infall of the star into rotating black hole viewed by a distant observer in discrete time intervals [8].

Fig. 5

Direct image and first light echoes of the moving hot spot in the jet from black hole SgrA* (left) and M87* (right) in discrete time intervals [9, 10]. In the nearest future a crucial information for the verification of strong gravity will be provided by the detailed observations of black hole images including the motion of bright spots in jets.

2 INTEGRAL EQUATIONS FOR TEST PARTICLE MOTION

In our numerical calculations we use the integral form for the equations of motion for test particle geodesics (trajectories) in the Kerr metric derived by Brandon Carter [1]:

$${\int\hskip-11.0pt-}\frac{dr}{\sqrt{R(r)}}={\int\hskip-11.0pt-}\frac{d\theta}{\sqrt{\Theta(\theta)}},$$

(1)

$$\tau={\int\hskip-11.0pt-}\frac{r^{2}}{\sqrt{R(r)}}\,dr+{\int\hskip-11.0pt-}\frac{a^{2}\cos^{2}\theta}{\sqrt{\Theta(\theta)}}\,d\theta,$$

(2)

$$\phi={\int\hskip-11.0pt-}\frac{a(E(r^{2}+a^{2})-aL)}{\Delta\sqrt{R(r)}}\,dr$$

$${}+{\int\hskip-11.0pt-}\frac{L-aE\sin^{2}\theta}{\sin^{2}\theta\sqrt{\Theta(\theta)}}\,d\theta,$$

(3)

$$t={\int\hskip-11.0pt-}\frac{(r^{2}+a^{2})(E(r^{2}+a^{2})-aL)}{\Delta\sqrt{R(r)}}\,dr$$

$${}+{\int\hskip-11.0pt-}\frac{(L-aE\sin^{2}\theta)a}{\sqrt{\Theta(\theta)}}\,d\theta.$$

(4)

It is used the standard Boyer–Lindquist coordinates $(t,r,\theta,\phi)$ [2] and $\tau$ is a proper time of the massive ($\mu\neq 0$) particles or a corresponding affine parametri- zation for the massless ($\mu=0$) particles. In these equations $\Delta=r^{2}-2Mr+a^{2}$, $M$ is a black hole mass, $a=J/M$ is a black hole spin. We use the dimensional values: $r\Rightarrow r/M$, $t\Rightarrow t/M$ and similar ones. For example, $GM/c^{2}$ is the used unit for the radial distance, and, correspondingly, $GM/c^{3}$ is the used unit for the time intervals. Similarly, $a=J/M^{2}\leq 1$ (with $0\leq a\leq 1$) is the dimensionless value of the black hole spin. The event horizon radius of the rotating black hole in these units is $r_{\textrm{h}}=1+\sqrt{1-a^{2}}$. The test particle geodesics depend on the integrals of motion: $\mu$ is the particle mass, $E$ is the particle total energy, $L$ is particle azimuth angular momentum, and the very specific Carter constant $Q$, defining the non-equatorial motion of the test particle. The effective radial $R(r)$ and polar $\Theta(\theta)$ potentials here are

$$R(r)=(E(r^{2}+a^{2})-aL)^{2}$$

$${}-\Delta[\mu^{2}r^{2}+(L-aE)^{2}+Q],$$

(5)

$$\Theta(\theta)=Q-\cos^{2}\theta[a^{2}(\mu^{2}-E^{2})+L^{2}\sin^{-2}\theta].$$

(6)

The integrals in (1)–(4) are the path integrals along the test particle trajectories. For example, the path integrals in (1) reduce to the ordinary ones in the absence of both the radial and polar turning points along the particle trajectory:

$$\int\limits_{r_{0}}^{r_{s}}\frac{dr}{\sqrt{R(r)}}=\int\limits_{\theta_{0}}^{\theta_{s}}\frac{d\theta}{\sqrt{\Theta(\theta)}}.$$

(7)

Here, $r_{s}$ and $\theta_{s}$ are the initial radial and polar coordinates of the particle (e.g., photon), while $r_{0}\gg r_{\textrm{h}}$ and $\theta_{0}$ is the corresponding final (finishing) points on the trajectory (e.g., the photon detection point by a distant telescope). A little bit more complicated is a case with the only one turning point in the polar direction, $\theta_{\textrm{min}}(\lambda,q)$ (derived from the equation $\Theta(\theta)=0$). The corresponding line integrals in (1) are reduced to the following ordinary ones:

$$\int\limits_{r_{s}}^{r_{0}}\frac{dr}{\sqrt{R(r)}}=\int\limits_{\theta_{\textrm{min}}}^{\theta_{s}}\frac{d\theta}{\sqrt{\Theta(\theta)}}+\int\limits_{\theta_{\textrm{min}}}^{\theta_{0}}\frac{d\theta}{\sqrt{\Theta(\theta)}}.$$

(8)

The most cumbersome complicated case, which we consider here, is a particle trajectory with the one turning point in the polar direction, $\theta_{\textrm{min}}(\lambda,q)$ (derived from the equation $\Theta(\theta)=0$), and the one turning point in the radial direction, $r_{\textrm{min}}(\lambda,q)$ (derived from the equation $R(r)=0$). The corresponding path integrals in (1) in this case are reduced to the following ordinary ones:

$$\int\limits_{r_{\textrm{min}}}^{r_{s}}\frac{dr}{\sqrt{R(r)}}+\int\limits_{r_{\textrm{min}}}^{r_{0}}\frac{dr}{\sqrt{R(r)}}$$

$${}=\int\limits_{\theta_{\textrm{min}}}^{\theta_{s}}\frac{d\theta}{\sqrt{\Theta(\theta)}}+\int\limits_{\theta_{\textrm{min}}}^{\theta_{0}}\frac{d\theta}{\sqrt{\Theta(\theta)}}.$$

(9)

It is clear that the path integrals in Eqs. (1)–(4) for particle trajectories with additional turning points are reduced to the ordinary ones in similar ways.

3 IMAGES OF ASTROPHYSICAL BLACK HOLES

See in Figs. 1–5 images of astrophysical black holes modeled with using of the integral equations of motion for photons (1)–(4). Shapes of black hole images depend on the distribution of emitting matter around black holes. Classical black hole shadow, which is a capture photon cross-section [3], is viewed if there is a luminous background far behind the black hole. Meantime, the lensed image of the event horizon globe is viewed if there is luminous accreting matter near the event horizon.