Images of Black Holes Viewed by a Distant Observer

Abstract

We describe the possible forms of black hole images viewed by a distant observer (or a telescope) on the celestial sphere. These images are numerically calculated based on general relativity and the equations of motion in the Kerr–Newman metric. A black hole image is a gravitationally lensed image of the black hole event horizon. It may be viewed as a black spot on the celestial sphere, projected inside the position of a classical black hole shadow. In the nearest future it will be possible to verify modified gravity theories by observations of astrophysical black holes with Space Observatory Millimetron.

1 INTRODUCTION

How does a black hole look like? It is a standard question of both scientific experts and men in the streets. In this paper, the black hole images are calculated based on general relativity and the equations of motion in the classical Kerr–Newman metric [1–6] describing a rotating and electrically charged black hole (see Appendices A, B, C for details). These images are the gravitationally lensed images of a black hole event horizon.

Numerical supercomputer simulations of general-relativistic hydro-magnetic accretion onto a black (see, e.g., [7–13]) confirm the Blandford-Znajek mechanism [14] of energy extraction from fast rotating Kerr black holes. The crucial feature of this mechanism is an electric current flowing through the black hole immersed into an external poloidal magnetic field. This electric current heats the accreting plasma up to the nearest outskirts of the black hole event horizon. A very high luminosity of this hot accreting plasma will spoil some parts of the black spots in astrophysical black hole images.

Images of astrophysical black holes may be viewed as black spots on the celestial sphere, projected inside the possible positions of classical black hole shadows. See in Figs. 1, 2 some examples of classical black hole shadows.

It must be stressed that the shapes of discussed dark spots are independent from the distribution and emission of the accreting plasma. Instead, the corresponding shapes of dark spots are completely determined by the properties of the black hole gravitational field and the black hole parameters like the mass $M$ and the spin $a$. (Throughout this paper we use the standard dimensionless units with $GM/c^{2}=1$, where $G$ is the Newtonian gravitational constant, and $c$ the velocity of light.)

See in Fig. 3 an example of reconstruction of the spherically symmetric Shwarzschild black hole event horizon silhouette using 3D trajectories of photons (numerically calculated by using Careter), which start very near the black hole event horizon and are detected by a distant observer (or a distant telescope). Correspondingly, Fig. 4 shows an example of reconstruction of an extremely fast rotating Kerr black hole with spin $a=1$.

The trajectories of photons in all figures of this paper are calculated numerically by using the test particle equations of motion in the Kerr metric (see Appendices B and C). The event horizon silhouette (dark spot) is always projected on the celestial sphere within the classical black hole shadow.

Figure 1

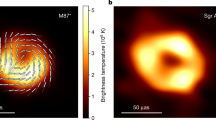
Some examples of classical black hole shadows are shown for the cases of supermassive black holes SgrA* and M87*. (a): Shadow of SgrA* (with a possible inclinations of the rotation axis with respect to the polar angle $\theta_{0}$) in the spherically symmetric Schwarzschild case $(a=0)$ is the black circle with a radius $r_{\textrm{sh}}=3\sqrt{3}\simeq 5.196$. The closed large curve is the shadow of an extremely fast rotating black hole $(a=1)$, and the closed smaller curve to the shadow of a moderately fast rotating black hole $(a=0.65)$. Note that the vertical size of the shadows, in the case of SgrA*, is independent from the values of spin $a$. (b): The corresponding forms of the shadow in the case of M87* (with possible inclinations of the rotation axis with respect to the polar angle $\theta_{0}=163^{\circ}$) for spin values $a=1$ (the largest closed curve), $a=0.75$, and $a=0$ (circle) of radius $r_{\textrm{sh}}=3\sqrt{3}$.

Figure 2

Numerical simulation of a compact spherical probe (neutron star or spaceship) orbiting around a fast rotating black hole ($a=0.9982$) in a circular orbit with the dimensionless radius $r=20$. One orbital period is shown in discrete time intervals. A distant observer is placed a little bit above the black hole equatorial plane. A direct image is shown as well as the first and second light echoes. The central gray region is the classical black hole shadow. The image of the second light echo is concentrated at the outskirts of the shadow. Gravitational lensing of the spherical probe in the black hole’s gravitational field (in the ellipsoidal approximation) is viewed by a distant observer as a deformation of the probe. For details see [15].

Figure 3

Reconstruction of the Schwarzschild black hole event horizon silhouette using 3D trajectories of photons (numerically calculated using the equations of motion in the Kerr metric), which start very near the event horizon and are detected by a distant observer (or telescope). The event horizon silhouette is always projected on the celestial sphere within the classical black hole shadow of radius $3\sqrt{3}$. Meanwhile, the corresponding radius of the event horizon silhouette is $r_{\textrm{h}}\simeq 4.457$ [21, 22].

Figure 4

Reconstruction of the extremely fast Kerr black hole ($a=1$) event horizon silhouette for the rotation axes orientation of the supermassive black hole SgrA*. 3D trajectories of photons (numerically calculated curves) are used, starting very near the black hole event horizon and detected by a distant observer (telescope). The nearest hemisphere of the event horizon is projected into the (light colored) disk with radius $r_{\textrm{EW}}\simeq 2.848$. The farthest hemisphere is projected into the hollow (dark disk with radius $r_{\textrm{eh}}\simeq 4.457$. It is a radius of the gravitationally lensed event horizon image. The reconstructed curves are the corresponding parallels and meridians at the gravitationally lensed image of the event horizon globe.

2 CLASSICAL BLACK HOLE SHADOW

Some examples of classical black hole shadows are shown in Fig. 1 for the cases of the supermassive black holes M87* at the center of galaxy M87 and SgrA* at the center of our native Milky Way galaxy. The left panel shows shadows of SgrA*, the right one those of M87*.

Figure 2 shows the results of a numerical simulation of the motion of a compact spherical probe (neutron star or spaceship) near a fast rotating black hole ($a=0.9982$) in a circular orbit with the dimensionless radius $r=20$.

The apparent shape of the black hole shadow, as seen by a distant observer in the equatorial plane is determined parametrically, $(\lambda,q)=(\lambda(r),q(r))$, from a simultaneous solution of the equations $V_{r}(r)=0$ and $[rV_{r}(r)]^{\prime}=0$ (see, e.g., [6, 17, 18]):

$$\lambda=\frac{-r^{3}+3r^{2}-a^{2}(r+1)}{a(r-1)},$$

(1)

$$q^{2}=\frac{r^{3}[4a^{2}-r(r-3)^{2}]}{a^{2}(r-1)^{2}}.$$

(2)

3 DARK SPOTS IN BLACK HOLE IMAGES

The form of a dark spot in the astrophysical black hole image, which is viewed by a distant telescope (observer) at the black hole equatorial plane, may be calculated by using Brandon Carter’s [4] integral equation of motion in the Kerr metric

$$\int\limits_{2}^{\infty}\frac{dr}{\sqrt{V_{r}}}=2\int\limits_{\theta_{\textrm{min}}}^{\pi/2}\frac{d\theta}{\sqrt{V_{\theta}}},$$

(3)

where $\theta_{\textrm{min}}$ is a turning point of the photon trajectory for a direct image in the polar direction (for details, see [19, 20]).

In the Schwarzschild case, a turning point is at the polar angle $\theta_{\textrm{min}}=\arccos\,(q/\sqrt{q^{2}+\lambda^{2}})$, where $q$ and $\lambda$ are the parameters of photon trajectories from Eq. (A.7). Respectively, from the right-hand-side integral in (3) is equal to $\pi/\sqrt{q^{2}+\lambda^{2}}$. The resulting numerical solution of the integral equation (3) provides the radius of the event horizon image $r_{\textrm{eh}}=\sqrt{q^{2}+\lambda^{2}}=4.457$. The nearest hemisphere of the event horizon is projected into a disk with radius $r_{\textrm{EW}}\simeq 2.848$. The farthest hemisphere is projected into the hollow dark disk with radius $r_{\textrm{eh}}\simeq 4.457$. It is a radius of the gravitationally lensed event horizon image. Figures 3 and 4 show the corresponding numerical solutions for the gravitationally lensed event horizon images in the Schwarzschild ($a=0$) and extremely fast Kerr rotation case ($a=1$), for the rotation axes orientation of the supermassive black hole SgrA*. The near hemisphere of the event horizon is projected by the lensing photons into the central (dark) region. Respectively the far hemisphere is projected into the hollow light colored region. The closed curves at the event horizon globe are the corresponding reconstructed parallels and meridians.

The event horizon globe of the Kerr black hole ($e=0$, $a\neq 0$), according to the general equation (A.4), is rotating as a solid body with an angular velocity

$$\Omega_{\textrm{h}}=\frac{a}{2(1+\sqrt{1-a^{2}})}.$$

(4)

Figure 5

3D picture of the supermassive black hole M87* with a supposed spin parameter $a=1$, surrounded by a thin accretion disk, which is supposed to be nontransparent. The largest closed curve is an outer boundary of the classical black hole shadow, viewed by a distant observer (telescope) in the celestial sphere. Two numerically calculated photon trajectories start from the inner boundary of the accretion disk (in the vicinity of the black hole event horizon equator) and arrive far from the black hole at the position of a distant observer.

Figure 6

Gravitationally lensed images, in discrete time intervals, of a small probe with a zero angular momentum ($\lambda=0$) and zero Carter constant ($q=0$), plunging into a fast rotating black hole. A distant observer is placed a little bit above the black hole equatorial plane. The probe is winding around the black hole equator One circle of this winding is shown. For details of numerical calculations and for animation see [30–35].

Figure 7

A composition of the Event Horizon Telescope image of supermassive black hole SgrA* [23–29] with the numerically modeled dark spot corresponding to the gravitationally lensed image of the event horizon globe with spin $a=1$. The closed purple curve is the outline of the classical black hole shadow. The magenta arrow is the direction of the black hole rotation axis. The magenta dashed circle is the position of the event horizon with radius $r_{\textrm{h}}=1$ in Euclidean space without gravity.

Figure 8

Superposition of the modeled dark spot with the Event Hotizon Telescope image of the supermassive black hole M87*. (a): $a=1$; (b): $a=0.75$. A $17^{\circ}$ inclination angle of the black hole rotation axis on the celestial sphere is supposed. Note that the size of the dark spot in the case of the rotation axis orientation of this black hole weakly depends on the value of the spin parameter $a$.

Figure 5 shows a 3D picture of the supermassive black hole M87* with a supposed spin parameter $a=1$, surrounded by a thin nontransparent accretion disk. An inclination angle of M87* rotation axis with respect to a distant observer is supposed to be near $17^{\circ}$. The arrows indicate the direction of the black hole rotation axis. The smallest black closed curve is the outer boundary of the dark spot which may be viewed by a distant observer at the celestial sphere. Two numerically calculated photon trajectories start from the inner boundary of the accretion disk (in the vicinity of the event horizon equator) and finish far from the black hole at the position of a distant observer. The largest closed curve in this 3D picture is the outer boundary of the classical black hole shadow. We remind the reader that black spots in the images of astrophysical black holes are always projected inside the possible positions of the black hole shadows. The dashed circle is a projection of the imaginary sphere with unit radius on the celestial sphere in the absence of gravity (i.e., in Euclidean space). The southern hemisphere of the gravitationally lensed event horizon globe may be viewed by a distant observer in the case of M87*.

Figure 6 shows, in discrete time intervals, gravitationally lensed images of a small probe (neutron star or space ship) with a zero angular momentum ($\lambda=0$) and a zero Carter constant ($q=0$), which is plunging into a fast-rotating black hole. A distant observer is placed a little bit above the black hole equatorial plane. The small probe is winding around the equator of the event horizon globe. One circle of this winding is shown. The escaping signals from this probe are exponentially fading in time. For numerical animation see [16].

Superpositions of the modeled dark spots with the Event Hotizon Telescope images of the supermassive black holes SgrA* and M87* are shown in Figs. 7 and 8.

4 DISCUSSION AND CONCLUSIONS

In this paper we discuss the possible shapes of black hole images, viewed by a distant observer, calculated based on general relativity and the equations of motion in the Kerr–Newman metric. The black hole image is a gravitationally lensed image of the black hole event horizon. It may be viewed as a black spot on the celestial sphere, projected inside the position of a classical black hole shadow. The event horizon silhouette (dark spot) is always projected on the celestial sphere within the classical black hole shadow.

Images of astrophysical black holes may be viewed as black spots on the celestial sphere, projected inside the possible positions of classical black hole shadows. The very high luminosity of the hot accreting plasma spoils some parts of the black spots in the astrophysical black hole images.

It must be stressed that the forms of the discussed dark spots are independent from the distribution and emission of the accreting plasma. Instead, the corresponding shapes of dark spots are completely determined by the properties of the black hole’s gravitational field and its parameters like the mass $M$ and spin $a$.

In the nearest future, it will be possible to verify modified gravity theories by observations of astrophysical black holes with the international Millimetron Space Observatory [39–42].

APPENDIX

1.1 A. THE KERR–NEWMAN METRIC

The line element of the classical Kerr–Newman metric [1–6] describing a rotating ($a\neq 0$) and electrically charged ($e\neq 0$) black hole, is

$$ds^{2}=-e^{2\nu}dt^{2}+e^{2\psi}(d\phi-\omega dt)^{2}$$

$${}+e^{2\mu_{1}}dr^{2}+e^{2\mu_{2}}d\theta^{2},$$

(A.1)

where

$$e^{2\nu}=\frac{\Sigma\Delta}{A},\quad e^{2\psi}=\frac{A\sin^{2}\theta}{\Sigma},\quad e^{2\mu_{1}}=\frac{\Sigma}{\Delta},$$

$$e^{2\mu_{2}}=\Sigma,\quad\omega=\frac{2Mar}{A},$$

$$\Delta=r^{2}-2Mr+a^{2}+e^{2},\quad\Sigma=r^{2}+a^{2}\cos^{2}\theta,$$

$$A=(r^{2}+a^{2})^{2}-a^{2}\Delta\sin^{2}\theta,$$

(A.2)

where $M$ is the black hole mass, $a=J/M$ is its specific angular momentum (spin), $e$ is its electric charge, $\omega$ is the frame-dragging angular velocity.

The roots of the equation $\Delta=0$ determine the black hole event horizon radius $r_{+}$ and the Cauchy radius $r_{-}$:

$$r_{+}=1\pm\sqrt{1-a^{2}-q^{2}}.$$

(A.3)

The event horizon of the Kerr–Newman black hole rotates as a solid body (i.e., independently from the polar angle $\theta$) with the angular velocity

$$\omega_{+}=\frac{2Mar_{+}}{(r_{+}^{2}+a^{2})^{2}}.$$

(A.4)

For particles moving near such a black hole, according to Carter’s equations of motion [4], there are the following integrals of motion: $\mu$ is the particle mass, $E$ is its total energy, $L$ is its azimuthal angular momentum, and $Q$ is the specific Carter constant, determining the non-equatorial motion. The corresponding radial potential $R(r)$ is

$$R(r)=P^{2}-\Delta[\mu^{2}r^{2}+(L-aE)^{2}+Q],$$

(A.5)

where $P=E(r^{2}+a^{2})-aL$. The polar potential $\Theta(\theta)$ is

$$\Theta(\theta)=Q$$

$${}-\cos^{2}\theta[a^{2}(\mu^{2}-E^{2})+L^{2}\sin^{-2}\theta].$$

(A.6)

The particle trajectories depend on three parameters:

$$\gamma=\frac{E}{\mu},\quad\lambda=\frac{L}{\mu},\quad q=\frac{\sqrt{Q}}{E}.$$

(A.7)

For massless particles like photons there are two parameters: $\lambda$ and $q$. The corresponding horizontal and vertical impact parameters, $\alpha$ and $\beta$, which are viewed on the celestial sphere by a distant observer placed at the polar angle $\theta_{0}$ are [17, 19, 20]

$$\alpha=-\frac{\lambda}{\sin\theta_{0}},\quad\beta=\pm\sqrt{\Theta(\theta_{0})}.$$

(A.8)

From an astrophysical point of view (see, e.g., [36–38]), the most probable are the cases of fast rotating supermassive black holes with spin values close to the maximum value, $a_{\textrm{max}}=1$.

1.2 B. EQUATIONS OF MOTION FOR TEST PARTICLES

The first-order differential equations of motion in the Kerr–Newman metric, derived by Brandon Carter [4], are

$$\Sigma\frac{dr}{d\tau}=\pm\sqrt{R(r)},$$

(B.1)

$$\Sigma\frac{d\theta}{d\tau}=\pm\sqrt{\Theta(\theta)},$$

(B.2)

$$\Sigma\frac{d\phi}{d\tau}=L\sin^{-2}\theta+a(\Delta^{-1}P-E),$$

(B.3)

$$\Sigma\frac{dt}{d\tau}=a(L-aE\sin^{2}\theta)+(r^{2}+a^{2})\Delta^{-1}P,$$

(B.4)

where $\tau$ is the proper time of a massive ($\mu\neq 0$) particle or an affine parameter of a massless ($\mu=0$) particle like a photon.

1.3 C. INTEGRAL EQUATIONS FOR TEST PARTICLE MOTION

For numerical calculations, very useful are the integral equations of motion corresponding to (B.1)–(B.4):

$$\not\negthickspace {\displaystyle \int}\frac{dr}{\sqrt{R(r)}}=\not\negthickspace {\displaystyle \int}\frac{d\theta}{\sqrt{\Theta(\theta)}},$$

(C.1)

$$\tau=\not\negthickspace {\displaystyle \int}\frac{r^{2}}{\sqrt{R(r)}}\,dr+\not\negthickspace {\displaystyle \int}\frac{a^{2}\cos^{2}\theta}{\sqrt{\Theta(\theta)}}\,d\theta,$$

(C.2)

$$\phi=\not\negthickspace {\displaystyle \int}\frac{aP}{\Delta\sqrt{R(r)}}\,dr+\not\negthickspace {\displaystyle \int}\frac{L-aE\sin^{2}\theta}{\sin^{2}\theta\sqrt{\Theta(\theta)}}\,d\theta,$$

(C.3)

$$t=\not\negthickspace {\displaystyle \int}\frac{(r^{2}+a^{2})P}{\Delta\sqrt{R(r)}}\,dr$$

$${}+\not\negthickspace {\displaystyle \int}\frac{(L-aE\sin^{2}\theta)a}{\sqrt{\Theta(\theta)}}\,d\theta.$$

(C.4)

The integrals in Eqs. (C.1)–(C.4) monotonically grow along the particle trajectory and change their sign at both the radial and polar turning points:

$$\int\limits_{r_{0}}^{r_{s}}\frac{dr}{\sqrt{R(r)}}=\int\limits_{\theta_{0}}^{\theta_{s}}\frac{d\theta}{\sqrt{\Theta(\theta)}},$$

(C.5)

where $r_{s}$ and $\theta_{s}$ are, respectively, the initial radial and polar particle coordinates, and $r_{0}\gg r_{\textrm{h}}$ and $\theta_{0}$ are the corresponding final particle coordinates. A more complicated case is with one turning point in the latitude (or polar) direction, $\theta_{\textrm{min}}(\lambda,q)$, which is a solution of the equation $\Theta(\theta)=0$. The corresponding ordinary integrals in Eq. (C.1) are written as

$$\int\limits_{r_{s}}^{r_{0}}\frac{dr}{\sqrt{R(r)}}=\int\limits_{\theta_{\textrm{min}}}^{\theta_{s}}\frac{d\theta}{\sqrt{\Theta(\theta)}}+\int\limits_{\theta_{\textrm{min}}}^{\theta_{0}}\frac{d\theta}{\sqrt{\Theta(\theta)}}.$$

(C.6)

We use these equations in our numerical calculations of photon trajectories, starting in the vicinity of the Kerr–Newman black hole and finishing at the position of a distant observer very far from the black hole.