Stochastic ordering results on extreme order statistics from dependent samples with Archimedean copula

Abstract

This paper considers parallel and series systems with heterogeneous components having dependent exponential lifetimes. The underlying dependence is assumed to be Archimedean and the component lifetimes are supposed to be connected according to an Archimedean copula. Sufficient conditions are found to dominate a parallel system with heterogenous exponential components, with respect to the dispersive order, by another parallel system with homogenous exponential components where the dependence structure between lifetimes of components is the same. We also compare two series systems (and two parallel systems) with general one-parameter dependent components and with respect to the usual stochastic ordering. Examples are given to illustrate the theoretical findings.

1 Introduction

Numerous researchers have examined stochastic comparisons between order statistics from specific families of distributions in the literature when the underlying random variables are either independent and identically distributed (i.i.d.) or independent but not identically distributed (i.n.i.d.). The reader is directed, among other sources, to [2] for a review of this subject. Stochastic orders of order statistics when underlying random variables induce certain dependent structures were examined by some authors. In this manuscript, we additionally validate several novel stochastic order outcomes amidst the most extensive order statistics. These results extend several established findings from i.n.i.d. to scenarios in which the random variables lack both identical distribution and independence. Order statistics constitute an important class of statistics in reliability and survival analysis to model the lifetime events. They have also been used frequently in the context of many reliability or survival models for the purpose of estimation of the parameters of the models. In the context of reliability engineering, a system with a k-out-of-n structure is a system which needs $(n-k+1)$ from its n components to be operational in order for the entire system to work, where $k=1,\ldots ,n$. The k-out-of-n system structure is a very popular type of redundancy in fault-tolerant systems. It finds wide applications in both industrial and military systems. Two cases of $k=1$ and $k=n$ which correspond to two extreme order statistics, i.e., $X_{1:n}$ and $X_{n:n}$, are well-known as the series and parallel system, respectively. Stochastic comparisons of series and parallel systems have been an attractive topic of research during recent decades (see, for instance, [6–10, 12, 14, 18], and [15]). For some stochastic comparisons of ordered random variables in the i.i.d. case, we refer the reader to [1, 4], and [5]. We first go over the definition of a copula function and also recall some concepts of stochastic orders before getting into their specific roles in our investigations.

Let us first recall some stochastic orders. Throughout the paper, increasing means nondecreasing and decreasing means nonincreasing, respectively. All integrals and expectations are assumed to exist whenever they appear.

Definition 1.1

Let X and Y be two nonnegative random variables with density functions f and g, distribution functions F and G, survival functions $\overline{F}=1-F$ and $\overline{G}=1-G$, hazard rate functions ${r_{X}}=f/\overline{F}$ and ${r_{Y}}=g/\overline{G}$, respectively. Then, X is said to be smaller than Y in the

• (i) usual stochastic order (denoted by $X\leq _{\mathrm{st}} Y$) if $\overline{F}(x)\leq \overline{G}(x)$ for all $x\in{\mathbb{R}}_{+}$, or equivalently, $\mathbb{E}[w(X)]\leq [\geq ] \mathbb{E}[w(Y)]$ for any increasing [decreasing] function $w:{\mathbb{R}}\rightarrow{\mathbb{R}}$;

• (ii) hazard rate order (denoted by $X\leq _{\mathrm{hr}} Y$) if $\overline{G}(x)/\overline{F}(x)$ is increasing in $x\in{\mathbb{R}}_{+}$, or equivalently, ${r_{X}(x)}\geq {r_{Y}(x)}$ for all $x\in{\mathbb{R}}_{+}$;

• (iii) dispersive order (denoted by $X\leq _{\mathrm{disp}} Y$) if

  $$ F^{-1}_{X}(\beta )-F^{-1}_{X}(\alpha )\leq F^{-1}_{Y}(\beta )-F^{-1}_{Y}( \alpha )\quad \text{for}\ 0\leq \alpha < \beta \leq 1, $$

  or equivalently, if and only if

  $$ f_{Y}(F^{-1}_{Y}(F_{X}(x)))\leq f_{X}(x)\quad \text{for all } x\in{ \mathbb{R}}_{+}. $$

  (1)

It is well-known that

$$X{\le }_{\mathrm{hr}}Y⟹X{\le }_{\mathrm{st}}Y,$$

but neither reversed hazard rate order nor hazard rate order implies the other. For comprehensive discussions on stochastic orders, one may refer to [16]. One may also refer to [13].

Now, we give some preliminaries of the concept of dependence through copula function. Let $(X_{1},\ldots ,X_{n})$ be the vector of components’ lifetimes, having joint distribution F, survival function ${ \overline{\boldsymbol{F}}}$, and marginal distributions $F_{i}$, $i=1,\ldots ,n$. A function $\mathbb{C} :[0,1]^{m}\rightarrow \mathbb{R}^{+}$ is said to be a copula of $(X_{1},\ldots ,X_{n})$ if

$$ \boldsymbol{F}(x_{1},\ldots ,x_{n})=\mathbb{C}(F_{1}(x_{1}),\ldots ,F_{n}(x_{n})) ~~~~\text{for all }(x_{1},\ldots ,x_{n})\in \mathbb{R}^{+}. $$

If $F_{i}$ are continuous, then the copula $\mathbb{C}$ is unique, and it is defined as

$$ \mathbb{C}(u_{1},\ldots ,u_{n})=\boldsymbol{F}(F_{1}^{-1}(u_{1}),\ldots ,F_{n}^{-1}(u_{n}))~~~ \text{for }u_{1},\ldots ,u_{n}\in (0,1), $$

where $F_{i}^{-1}$ denotes the inverse of the distribution function of the random variable $X_{i},i=1,\ldots ,n$.

Likewise, the survival copula associated with a multivariate distribution function F is

$$ \overline{\boldsymbol{F}}(x_{1},\ldots ,x_{n})=\overline{\mathbb{C}}(F_{1}(x_{1}), \ldots ,F_{n}(x_{n})) ~~~~ \text{for all }(x_{1},\ldots ,x_{n})\in \mathbb{R}^{+}. $$

Among copulas (or survival copulas), the class of Archimedean copulas is particularly interesting. Archimedean copulas are widely used in reliability theory and actuarial mathematics because of their mathematical tractability and wide range of dependencies. For a decreasing and continuous function $\phi : [0, \infty ) \rightarrow [0,1]$ such that $\phi (0)=1$ and $\phi (\infty )=0$, where $\psi =\phi ^{-1}$ is the pseudoinverse, a copula is called Archimedean if it can be written as

$$ \mathbb{C}(u_{1}, \ldots , u_{n}) = \phi (\psi (u_{1}) +\cdots + \psi (u_{n}))~~~ \text{for all }u_{i}\in [0,1]\text{, }i=1,\ldots ,n, $$

where ϕ is usually called the generator of the Archimedean copula $\mathbb{C}$, if $(-1)^{k}\phi ^{[k]}(x)\geq 0$, for $k = 0,\ldots , n-2$ and $(-1)^{n-2}\phi ^{[n-2]}(x)$ is decreasing and convex. In the above, $\phi ^{[k]}(x)$ denotes the kth derivative of the function $\phi (x)$ with respect to x.

Majorization is one of the key tools in mathematical statistics and applied probability, which is a preordering on vectors by sorting all components in nonincreasing order. The concepts of majorization of vectors and Schur-concavity (Schur-convexity) of functions are given as follows.

Definition 1.2

Let λ, $\boldsymbol{\lambda}^{*}$ denote two n-dimensional real vectors. Let $\lambda _{(1)}\leq \lambda _{(2)}\leq \cdots \leq \lambda _{(n)}$, $\lambda ^{*}_{(1)}\leq \lambda ^{*}_{(2)}\leq \cdots \leq \lambda ^{*}_{(n)}$ be their ordered components. Then

• λ is said to be majorized by $\boldsymbol{\lambda} ^{*}$, in symbols $\boldsymbol{\lambda} \overset{m}{\preceq}\boldsymbol{\lambda} ^{*}$, if $\sum _{i=1}^{k} \lambda ^{*}_{(i)}\leq \sum _{i=1}^{k}\lambda _{(i)}$; for $k=1,2,\ldots ,n-1$, and $\sum _{i=1}^{n} \lambda _{(i)}=\sum _{i=1}^{n}\lambda ^{*}_{(i)}$;

• λ is said to be weakly submajorized by $\boldsymbol{\lambda} ^{*}$, in symbols $\boldsymbol{\lambda} \preceq _{w}\boldsymbol{\lambda} ^{*}$, if $\sum _{i=1}^{k} \lambda _{(i)}\leq \sum _{i=1}^{k}\lambda ^{*}_{(i)}$; for $k=1,2,\ldots , n$;

• λ is said to be p-larger than another vector $\boldsymbol{\lambda} ^{*}$, in symbols $\boldsymbol{\lambda} \overset{p}{\preceq}\boldsymbol{\lambda} ^{*}$, if $\prod _{i=1}^{j} \lambda ^{*}_{(i)}\leq \prod _{i=1}^{j} \lambda _{(i)}$, $j=1,\ldots ,n$.

The following lemmas show that the notion of majorization is quite useful in establishing various inequalities.

Lemma 1.3

Let $\Phi :\mathbb{R}^{n}\rightarrow \mathbb{R}$ be continuously differentiable. Necessary and sufficient conditions for Φ to be Schur-convex (concave) on $\mathbb{R}^{n}$ are: Φ is symmetric on $\mathbb{R}^{n}$ and for all $i\neq j$,

$$ (z_{i}-z_{j})\left (\frac{\partial \Phi (\boldsymbol{z})}{\partial z_{i}}- \frac{\partial \Phi (\boldsymbol{z})}{\partial z_{j}}\right )\geq (\leq )0~~~ \textit{for all }\boldsymbol{z}\in \mathbb{R}^{n}. $$

Lemma 1.4

A real-valued function $\Phi :\mathbb{R}^{n}\rightarrow \mathbb{R}$ is said to be a Schur-convex (Schur-concave) function if $\boldsymbol{\lambda} \overset{m}{\preceq}\boldsymbol{\lambda} ^{*}$ implies $\Phi (\boldsymbol{\lambda} )\leq (\geq )\Phi (\boldsymbol{\lambda} ^{*})$, for all $\boldsymbol{\lambda} ,\boldsymbol{\lambda} ^{*}\in \mathbb{R}^{n}$.

Let $X_{1},\ldots ,X_{n}$ be independent exponential random variables with $X_{i}$, $i=1,\ldots ,n$ having hazard rates $\lambda _{i} > 0$ for $i=1,\ldots ,n$. Let $Y_{1},\ldots ,Y_{n}$ be another set of independent exponential random variables with common hazard rate $\overline{\lambda}=\frac{1}{n}\sum _{i=1}^{n} \lambda _{i}^{*}$. [3] proved that $X_{n:n}\geq _{\mathrm{disp}} Y_{n:n}$.

In Sect. 2, we generalize the above result to the cases where the random variables $X_{i} ,i=1,\ldots ,n$ and the random variables $Y_{i},i=1,\ldots ,n$ are dependent and have a common Archimedean copula with a generator function ϕ satisfying a number of mild conditions. In particular, we show that when the generator function is $\phi (x)=\exp (-x)$, the results are consistent with the case where the underlying random variables are independent. In Sect. 3, we compare two parallel systems with Archimedean copula-based dependent components with a one-parameter family of the life distribution. In Sect. 4, we continue the topic discussed in Sect. 3 for series systems. In Sect. 5, we conclude the paper by describing a number of examples, some remarks, and explanations.

2 Dispersive order of parallel systems

We bring a technical lemma which will be used in the sequel.

Lemma 2.1

Let $(1-\phi (x))^{\frac{1}{d(x)}}$ be increasing in $x\geq 0$, where $d(\cdot )$ is a nonnegative function. Then, $\frac{\lambda}{d(Z(t,\lambda ))}$ is increasing in $\lambda >0$, for all $t\geq 0$, where $Z(t,\lambda )=\psi (1-e^{-\lambda t})$.

Proof

Let us write

$$\begin{aligned} \frac{\lambda}{d(Z(t,\lambda ))}&= \frac{\frac{1}{-t}\ln (e^{-\lambda t})}{d(\psi (1-e^{-\lambda t}))} \\ &= \frac{\frac{1}{-t}\ln (1-(1-e^{-\lambda t}))}{d(\psi (1-e^{-\lambda t}))} \\ &= \frac{\frac{1}{-t}\ln (1-\phi (\psi ((1-e^{-\lambda t})))}{d(\psi (1-e^{-\lambda t}))}. \end{aligned}$$

Now, since $\psi (1-e^{-\lambda t})$ is decreasing in λ, for all $t\geq 0$, thus $\frac{\lambda}{d(Z(t,\lambda ))}$ is increasing in λ, for all $t\geq 0$, if

i.e., when

The above statement is also equivalent to $(1-\phi (x))^{\frac{1}{d(x)}}$ being increasing in $x \geq 0$. The proof of lemma is complete. □

Next result compares the largest order statistics of heterogeneous dependent exponential random variables with that of homogeneous dependent exponential random variables with respect to dispersive ordering.

Theorem 2.2

Let $\boldsymbol{X}=(X_{1},\ldots ,X_{n})$ be a dependent random vector with the Archimedean copula having generator ϕ where $X_{i}$ has exponential distribution with hazard rate $\lambda _{i}$ and, further, let $\boldsymbol{Y}=(Y_{1},\ldots ,Y_{n})$ be another dependent random vector having the same Archimedean copula as X where $Y_{i}$ has exponential distribution with hazard rate λ. If there exists a nonnegative function $d(\cdot )$ satisfying

• (i) $(1-\phi (u))^{\frac{1}{d(u)}}$ is increasing (resp. decreasing) in $u\geq 0$;

• (ii) $d(u)\frac{1-\phi (u)}{\phi '(u)}$ is decreasing (resp. increasing) and also convex in $u\geq 0$,

then

$$ m(x,\boldsymbol{\lambda} )=\frac{1}{n} \sum _{i=1}^{n} \lambda _{i} \frac{d(\bar{Z}(x,\boldsymbol{\lambda} ))}{d(Z(x,\lambda _{i}))},\quad \boldsymbol{\lambda} =(\lambda _{1},\ldots ,\lambda _{n}), $$

where $Z(x,\lambda _{i})= \psi (1-e^{-\lambda _{i} x})$, $i=1,\ldots ,n$ and $\bar{Z}(x,\boldsymbol{\lambda} )=\frac{1}{n}\sum _{i=1}^{n} Z(x,\lambda _{i})$ and $x'=\arg \max _{x\geq 0} m(x,\boldsymbol{\lambda} )$ such that $\lambda >0$, then

$$m(x^{\prime },\mathit{\lambda })\le \lambda ⟹X_{n:n}{\ge }_{disp}{Y}_{n:n}.$$

Proof

Due to Definition 1.1$(i)$, it is sufficient to prove that

$$ f_{Y_{n:n}}(F^{-1}_{Y_{n:n}}(F_{X_{n:n}}(x)))\geq f_{X_{n:n}}(x). $$

(2)

The density functions of $Y_{n:n}$ and $X_{n:n}$, respectively, can be represented as

$$ f_{Y_{n:n}}(x)=n\lambda e^{-\lambda x} \frac{\phi '\left (n Z(x,\lambda )\right )}{\phi '\left (Z(x,\lambda )\right )} $$

and

$$ f_{X_{n:n}}(x)=\sum _{i=1}^{n} \frac{\lambda _{i}e^{-\lambda _{i} x}}{\phi '\left (Z(x,\lambda _{i})\right )}. \phi '\left (\sum _{i=1}^{n}U(x,\lambda _{i})\right ). $$

It is easy to calculate that for $x\in \mathbb{R}^{+}$,

$$ F^{-1}_{Y_{n:n}}(x)=-\frac{1}{\lambda}\log \left (1-\phi \left ( \frac{1}{n}\psi (x)\right )\right ). $$

Thus, the left-hand side of (2) can be written as

$$\begin{aligned} f_{Y_{n:n}}(F^{-1}_{Y_{n:n}}(F_{X_{n:n}}(x)))=n\lambda \frac{1-\phi \left (\bar{Z}(x,\boldsymbol{\lambda} )\right )}{\phi '\left (\bar{Z}(x,\boldsymbol{\lambda} \right )} \phi '\left (\sum _{i=1}^{n}U(x, \lambda _{i})\right ). \end{aligned}$$

From the assumption (ii), $d(u)\frac{1-\phi (u)}{\phi '(u)}$ is a convex function, therefore, for all $x\in \mathbb{R}^{+}$,

$$\begin{aligned} \frac{1}{n}\sum _{i=1}^{n}d(Z(x,\lambda _{i})) \frac{1-\phi \left (Z(x,\lambda _{i})\right )}{\phi '\left (Z(x,\lambda _{i})\right )} \geq d(\bar{Z}(x,\boldsymbol{\lambda} )) \frac{1-\phi \left (\bar{Z}(x,\boldsymbol{\lambda} )\right )}{\phi '\left (\bar{Z}(x,\boldsymbol{\lambda} )\right )} \end{aligned}$$

(3)

Since from assumption (ii) $(1-\phi (u))^{d(u)}$ is increasing (resp. decreasing) in $u\geq 0$ and from assumption (ii) $d(u)\frac{1-\phi (u)}{\phi '(u)}$ is decreasing (resp. increasing) and, further, since $Z(x,\lambda )$ is decreasing in λ for every $x\in \mathbb{R}^{+}$, $d(Z(x,\lambda )) \frac{1-\phi \left (Z(x,\lambda )\right )}{\phi '\left (Z(x,\lambda )\right )}$ is increasing (resp. decreasing) with respect to λ. In addition, in view of the condition (i) and by using Lemma 2.1, $\frac{\lambda}{d(Z(x,\lambda ))}$ is increasing in λ, for all $x\geq 0$. By Chebyshev’s sum inequality (see, e.g., [17]), it then follows that

$$ \begin{aligned} \frac{1}{n}\sum _{i=1}^{n} \frac{\lambda _{i}e^{-\lambda _{i} x}}{\phi '\left (\psi (1-e^{-\lambda _{i} x})\right )}&= \frac{1}{n}\sum _{i=1}^{n} \frac{\lambda _{i}}{d(Z(x,\lambda _{i}))} \frac{d(Z(x,\lambda _{i}))\left [1-\phi \left (Z(x,\lambda _{i})\right )\right ]}{\phi '\left (Z(x,\lambda _{i})\right )} \\ &\geq \frac{1}{n}\sum _{i=1}^{n} \frac{\lambda _{i}}{d(Z(x,\lambda _{i}))}\frac{1}{n}\sum _{i=1}^{n} \frac{d(Z(x,\lambda _{i}))\left [1-d\left (Z(x,\lambda _{i})\right )\right ]}{\phi '\left (Z(x,\lambda _{i})\right )} \\ &\geq \frac{1}{n}\sum _{i=1}^{n} \lambda _{i} \frac{d(\bar{Z}(x,\lambda ))}{d(Z(x,\lambda _{i}))} \frac{1-\phi \left (\bar{Z}(x,\lambda )\right )}{\phi '\left (\bar{Z}(x,\lambda )\right )} \\ &= m(x,\boldsymbol{\lambda} ) \frac{1-\phi \left (\bar{Z}(x,\lambda )\right )}{\phi '\left (\bar{Z}(x,\lambda )\right )} \\ &\geq \lambda \frac{1-\phi \left (\bar{Z}(x,\lambda )\right )}{\phi '\left (\bar{Z}(x,\lambda )\right )}, \end{aligned} $$

(4)

where the second inequality follows from equation (3) and the third from the assumption $m(x',\boldsymbol{\lambda} ) \leq \lambda$, and the fact that $\phi '$ is a negative function. As $\phi '$ is a nonpositive function, it thus holds that

$$ \begin{aligned} f_{Y_{n:n}}(F^{-1}_{Y_{n:n}}(F_{X_{n:n}}(x)))-f_{X_{n:n}}(x)& \overset{sgn}{=}\frac{1}{n}\sum _{i=1}^{n} \frac{\lambda _{i}e^{-\lambda _{i} x}}{\phi '\left (\psi (1-e^{-\lambda _{i} x})\right )}\\ &\quad - \lambda \frac{1-\phi \left (\frac{1}{n}\sum _{i=1}^{n}\psi (1-e^{-\lambda _{i} x})\right )}{\phi '\left (\frac{1}{n}\sum _{i=1}^{n}\psi (1-e^{-\lambda _{i} x})\right )} \geq 0, \end{aligned} $$

where the inequality follows from (4). Hence, the required result follows from (1). □

We want to remark that there is always a proper function d in Theorem 2.2 for which both conditions (i) and (ii) in this theorem are fulfilled. Specifically, if $d(x)=-\phi '(x)$, which is a nonnegative function, it is seen that $\frac{1-\phi (x)}{\phi '(x)}d(x)=\phi (x)-1$, which is a decreasing convex function in $x \geq 0$ and, in addition, $(1-\phi (x))^{\frac{1}{d(x)}}$ is increasing in $x\geq 0$. Below we give an example to indicate that the result of Theorem 2.2 is obtained as a conclusion of the conditions presented. This example shows that the result of Theorem 2.2 is applicable when there is no dependency between random variables.

Example 2.3

Let us suppose that $\boldsymbol{X}=(X_{1},\ldots ,X_{n})$ follows the Archimedean copula with generator $\phi (x)=\exp (-x)$ where $X_{i}\sim E(\lambda _{i})$ and let $\boldsymbol{Y}=(Y_{1},\ldots ,Y_{n})$ follow the Archimedean copula with the same generator in which $Y_{i}\sim E(\lambda )$. We choose $d(x)=-\phi '(x)$. Therefore, the conditions (i) and (ii) in Theorem 2.2 hold. In this particular case of the generator function, the random variables $X_{1},\ldots ,X_{n}$ are independent and the random variables $Y_{1},\ldots ,Y_{n}$ are also independent. In addition, we observe that

$$ m(x, \boldsymbol{\lambda} )=\frac{1}{n}\sum _{i=1}^{n} \left (\lambda _{i} \prod _{j=1,j\neq i,}^{n} (1-\exp (-\lambda _{j} x))\right ) \leq m(+ \infty ,\boldsymbol{\lambda} ) =\frac{\sum _{i=1}^{n} \lambda _{i}}{n}. $$

Therefore, if $\frac{\sum _{i=1}^{n} \lambda _{i}}{n}\leq \lambda$ then, using Theorem 2.2, $X_{n:n}\geq _{disp}Y_{n:n}$. This result has been acquired by [3] without the framework of Archimedean copulas.

It is also remarkable that in Theorem 2.2 the number $m(x',\lambda )$ could be replaced by another finite upper bound of $m(x,\lambda )$ such as $m(\boldsymbol{\lambda} )$. That is, if one demonstrates that $m(x,\boldsymbol{\lambda} ) \leq m(\boldsymbol{\lambda} )$, for all $x\geq 0$, then the condition $m(x',\boldsymbol{\lambda} ) \leq \lambda$ in Theorem 2.2 can be substituted by $m(\boldsymbol{\lambda} ) \leq \lambda$. The following example illustrates another application of Theorem 2.2 in the dependent case.

Example 2.4

Consider the Clayton copula which has generator $\phi (x)=(1+x)^{-\frac{1}{\theta}}$, $\theta >0$. We have $\psi (x)=x^{-\theta}-1$. Let us take $d(x)=-\phi '(x)$ and recall that the conditions (i) and (ii) in Theorem 2.2 are satisfied as remarked before. Therefore,

$$ \frac{d(\bar{Z}(x,\boldsymbol{\lambda} ))}{d(Z(x,\lambda _{i}))}= n^{1+ \frac{1}{\theta}}\left ( \frac{(1-\exp (-\lambda _{i} x))^{-\theta}}{\sum _{j=1}^{n} (1-\exp (-\lambda _{j} x))^{-\theta}}\right )^{1+ \frac{1}{\theta}}. $$

Let us denote by $\lambda _{(1)} \leq \cdots \leq \lambda _{(n)}$ the ordered values of $\lambda _{i}$’s, from the smallest to the biggest. Then, one obtains

$$\begin{aligned} m(x,\boldsymbol{\lambda} )&= n^{\frac{1}{\theta}}\sum _{i=1}^{n} \lambda _{i} \left ( \frac{(1-\exp (-\lambda _{i} x))^{-\theta}}{\sum _{j=1}^{n} (1-\exp (-\lambda _{j} x))^{-\theta}}\right )^{1+ \frac{1}{\theta}} \\ &=n^{\frac{1}{\theta}}\sum _{i=1}^{n} \lambda _{(i)} \left ( \frac{(1-\exp (-\lambda _{(i)} x))^{-\theta}}{\sum _{j=1}^{n} (1-\exp (-\lambda _{(j)} x))^{-\theta}}\right )^{1+ \frac{1}{\theta}}. \end{aligned}$$

Now, since for every $j=1,2,\ldots , i$, $\lambda _{(j)} \leq \lambda _{(i)}$, thus for all $j=1,2,\ldots , i$ one has

$$ \frac{\left (1-\exp (-\lambda _{(j)}x)\right )^{-\theta}}{\left (1-\exp (-\lambda _{(i)}x)\right )^{-\theta}} \geq 1, $$

and, consequently,

$$ \sum _{j=1}^{n} \frac{(1-\exp (-\lambda _{(j)}x))^{-\theta}}{(1-\exp (-\lambda _{(i)}x))^{-\theta}} \geq i. $$

Hence, one has

$$ m(x,\boldsymbol{\lambda} ) \leq \sum _{i=1}^{n} \frac{\lambda _{(i)}}{i} \left ( \frac{n}{i}\right )^{\frac{1}{\theta}}. $$

Thus, as an application of Theorem 2.2,

$$\sum _{i=1}^n\frac{{\lambda }_{(i)}}{i}{\left(\frac{n}{i}\right)}^{\frac{1}{\theta }}\le \lambda ⟹X_{n:n}{\ge }_{disp}{Y}_{n:n}$$

The following example illustrates another application of Theorem 2.2.

Example 2.5

Let us consider Gumbel copula with generator $\phi (x)=\exp (-\sqrt{x})$. In the context of Theorem 2.2, we take $d(x)=\phi (x)$. It can be observed after some routine calculation that $(1-\phi (x))^{\frac{1}{d(x)}}$ is increasing in $x>0$, and further that $d(x)\frac{1-\phi (x)}{\phi '(x)}$ is decreasing and convex in $x>0$. Denote $F_{\lambda _{i}}(x)=1-e^{-\lambda _{i} x}$. Now, we can get

$$\begin{aligned} m(x,\boldsymbol{\lambda} )&:=\frac{1}{n}\sum _{i=1}^{n} \lambda _{i} \frac{d(\bar{Z}(x, \boldsymbol{\lambda} ))}{d(Z(x,\lambda _{i}))} \\ &=\frac{1}{n}\sum _{i=1}^{n} \lambda _{i} e^{-\sqrt{\bar{Z}(x, \boldsymbol{\lambda} )}+\sqrt{Z(x,\lambda _{i})}}, \end{aligned}$$

where

$$\begin{aligned} Z(x,\lambda _{i})&:=\psi (F_{\lambda _{i}}(x))=(-\ln (F_{\lambda _{i}}(x)))^{2}, \\ d(\bar{Z}(x, \boldsymbol{\lambda} ))&=\frac{1}{n}\sum _{i=1}^{n} \psi (F_{ \lambda _{i}}(x))=\sum _{i=1}^{n} (-\ln (F_{\lambda _{i}}(x)))^{2}. \end{aligned}$$

By Lyapunov’s inequality, one obtains

$$ -\sqrt{\frac{1}{n}\sum _{i=1}^{n} (-\ln (F_{\lambda _{i}}(x)))^{2}} \leq -\frac{1}{n}\sum _{i=1}^{n} (-\ln (F_{\lambda _{i}}(x))). $$

For a fixed i, when $i=1,2,\ldots ,n$, and by assuming without loss of generality that $\lambda _{1}\leq \cdots \leq \lambda _{n}$, one thus gets

$$\begin{aligned} -\sqrt{\bar{Z}(x, \boldsymbol{\lambda} )}+\sqrt{Z(x,\lambda _{i})}&\leq - \frac{1}{n}\sum _{j=1}^{n} (-\ln (F_{\lambda _{j}}(x)))-\ln (F_{ \lambda _{i}}(x)) \\ &=\frac{1}{n}\sum _{j=1}^{n} \ln \left ( \frac{F_{\lambda _{j}}(x)}{F_{\lambda _{i}}(x)}\right ) \\ &=\frac{1}{n}\sum _{j=1}^{i} \ln \left ( \frac{F_{\lambda _{j}}(x)}{F_{\lambda _{i}}(x)}\right )+ \frac{1}{n} \sum _{j=i+1}^{n}\ln \left ( \frac{F_{\lambda _{j}}(x)}{F_{\lambda _{i}}(x)}\right ). \end{aligned}$$

Since, for $\lambda _{j} \geq \lambda _{i}$, $\ln \left (\frac{F_{\lambda _{j}}(x)}{F_{\lambda _{i}}(x)}\right )$ is decreasing in $x>0$, for every $j>i$,

$$ \ln \left (\frac{F_{\lambda _{j}}(x)}{F_{\lambda _{i}}(x)}\right ) \leq \lim _{x\rightarrow 0^{+}} \ln \left ( \frac{F_{\lambda _{j}}(x)}{F_{\lambda _{i}}(x)}\right )=\ln \Big( \frac{\lambda _{j}}{\lambda _{i}}\Big). $$

In parallel, $\lambda _{j} \leq \lambda _{i}$, $\ln \left (\frac{F_{\lambda _{j}}(x)}{F_{\lambda _{i}}(x)}\right )$ is increasing in $x>0$, thus for every $j\leq i$,

$$ \ln \left (\frac{F_{\lambda _{j}}(x)}{F_{\lambda _{i}}(x)}\right ) \leq \lim _{x\rightarrow +\infty} \ln \left ( \frac{F_{\lambda _{j}}(x)}{F_{\lambda _{i}}(x)}\right )=0. $$

Therefore,

$$\begin{aligned} m(x,\boldsymbol{\lambda} )&:= \frac{1}{n} \sum _{i=1}^{n} \lambda _{i} e^{- \sqrt{\bar{Z}(x, \boldsymbol{\lambda} )}+\sqrt{Z(x,\lambda _{i})}} \\ &\leq \frac{1}{n} \sum _{i=1}^{n} \lambda _{i} e^{\frac{1}{n} \sum _{j=i+1}^{n} \ln (\frac{\lambda _{j}}{\lambda _{i}})} \\ &=\frac{1}{n} \sum _{i=1}^{n} (\lambda _{i} ^{i}\prod _{j=i+1}^{n} \lambda _{j})^{\frac{1}{n}}. \end{aligned}$$

Hence, an application of Theorem 2.2 yields

$$\frac{1}{n}\sum _{i=1}^n{\left({\lambda }_i^i\prod _{j=i+1}^n{\lambda }_j\right)}^{\frac{1}{n}}\le \lambda ⟹X_{n:n}{\ge }_{disp}{Y}_{n:n}.$$

The next example provides another application of Theorem 2.2.

Example 2.6

Let us take $\psi (u)=(1-u)^{\theta}$, $\theta \geq 1$. In Theorem 2.2, let us take $d(x)=1$. It can be verified that $(1-\phi (x))^{\frac{1}{d(x)}}$ is increasing in $x>0$, and also $d(x)\frac{1-\phi (x)}{\phi '(x)}$ is decreasing and convex in $x>0$. Using Theorem 2.2, one gets

$$\overline{\lambda }\le \lambda ⟹X_{n:n}{\ge }_{disp}{Y}_{n:n}.$$

The following result also presents another set of conditions under which the dispersive order among the lifetimes of parallel systems with dependent exponential random variables is satisfied. The proof of it being similar to the proof of Theorem 2.2 has been omitted.

Theorem 2.7

Let $\boldsymbol{X}=(X_{1},\ldots ,X_{n})$ be a dependent random vector with the Archimedean copula having generator ϕ where $X_{i}$ has exponential distribution with hazard rate $\lambda _{i}$ and, further, let $\boldsymbol{Y}=(Y_{1},\ldots ,Y_{n})$ be another dependent random vector having the same Archimedean copula as X where $Y_{i}$ has exponential distribution with hazard rate λ. Let there exist a nonnegative function d for which

• (i) $(1-\phi (u))^{d(u)}$ is increasing (resp. decreasing) in $u\geq 0$;

• (ii) $d(u)\frac{1-\phi (u)}{\phi '(u)}$ is increasing (resp. decreasing) and also concave in $u\geq 0$.

If $x''=\arg \min _{x\geq 0} m(x,\boldsymbol{\lambda} )$ and $\lambda >0$, then

$$m(x^{″},\mathit{\lambda })\ge \lambda ⟹X_{n:n}{\le }_{disp}{Y}_{n:n}.$$

3 Usual stochastic order of parallel systems

Theorem 3.1

Let X be a dependent random vector with $X_{i}\sim F(\cdot ;\lambda _{i})$ and with the Archimedean copula having generator ϕ and let Y be another dependent random vector with $Y_{i}\sim F(\cdot ;\lambda _{i}^{*})$ and with the Archimedean copula having generator ϕ. Let

• (i) $F(\cdot ;\lambda )$ be increasing in λ;

• (ii) $F(\cdot ;\lambda )$ be log-concave in λ;

• (iii) $u\psi '(u)$ be increasing in $u\in (0,1)$.

Then, we have

$$\mathit{\lambda }\stackrel{m}{⪯}{\mathit{\lambda }}^{\ast }⟹X_{n:n}{\le }_{\mathrm{st}}{Y}_{n:n}.$$

Proof

The survival function of $X_{n:n}$ is of the form

$$ \overline{F}_{X_{n:n}}(x;\boldsymbol{\lambda} )=1-\phi \left (\sum _{i=1}^{n} \psi (F(x;\lambda _{i})\right ). $$

Thus for establishing the desired result, it is enough to show that the function $\overline{F}_{X_{n:n}}(x;\boldsymbol{\lambda} )$ is Schur-convex. Taking the derivative of $\overline{F}_{X_{n:n}}(x;\boldsymbol{\lambda} )$ with respect to $\lambda _{i}$, we have

$$ \frac{\partial \overline{F}_{X_{n:n}}(x;\boldsymbol{\lambda} )}{\partial \lambda _{i}}=- \frac{\partial{F}(x;\lambda _{i})}{\partial \lambda _{i}}\psi '(F(x, \lambda _{i}))\phi '\left (\sum _{i=1}^{n}\psi (F(x;\lambda _{i}) \right ). $$

Therefore, for $1\leq i< j\leq n$ and $\boldsymbol{\lambda} \in \mathfrak{D}_{+}=\{\boldsymbol{\lambda}:\lambda _{1}\geq \lambda _{2}\geq \cdots \geq \lambda _{n}>0\}$, we show that $\frac{\partial \overline{F}_{X_{n:n}}(x;\boldsymbol{\lambda} )}{\partial \lambda _{i}}$ is increasing in $\lambda _{i}$. Thus, we can compute that

$$ \begin{aligned} \frac{\partial \overline{F}_{X_{n:n}}(x;\boldsymbol{\lambda} )}{\partial \lambda _{i}}- \frac{\partial \overline{F}_{X_{n:n}}(x;\boldsymbol{\lambda} )}{\partial \lambda _{j}}&= \frac{\partial{F}(x;\lambda _{j})}{\partial \lambda _{j}}\psi '(F(x, \lambda _{j}))\phi '\left (\sum _{i=1}^{n}\psi (F(x;\lambda _{j}) \right ) \\ &\quad -\frac{\partial{F}(x;\lambda _{i})}{\partial \lambda _{i}} \psi '(F(x,\lambda _{i}))\phi '\left (\sum _{i=1}^{n}\psi (F(x; \lambda _{i})\right ) \\ &=\left [\frac{\partial{F}(x;\lambda _{j})}{\partial \lambda _{j}} \psi '(F(x,\lambda _{j})) - \frac{\partial{F}(x;\lambda _{i})}{\partial \lambda _{i}}\psi '(F(x, \lambda _{i}))\right ]\\ &\quad \times\phi '\left (\sum _{i=1}^{n}\psi (F(x;\lambda _{i}) \right ) \\ &=\eta _{1}\phi '\left (\sum _{i=1}^{n}\psi (F(x;\lambda _{i})\right ) \end{aligned} $$

From the fact that $\phi '$ is negative, it is enough to show that $\eta _{1}$ is negative. We have

$$ \begin{aligned} \eta _{1}&= \frac{\frac{\partial{F}(x;\lambda _{j})}{\partial \lambda _{j}}}{F(x;\lambda _{j})}F(x; \lambda _{j})\psi '(F(x,\lambda _{j})) - \frac{\frac{\partial{F}(x;\lambda _{i})}{\partial \lambda _{i}}}{F(x;\lambda _{i})}F(x; \lambda _{i})\psi '(F(x,\lambda _{i})) \\ &\leq \frac{\frac{\partial{F}(x;\lambda _{j})}{\partial \lambda _{j}}}{F(x;\lambda _{j})}F(x; \lambda _{i})\psi '(F(x,\lambda _{i})) - \frac{\frac{\partial{F}(x;\lambda _{i})}{\partial \lambda _{i}}}{F(x;\lambda _{i})}F(x; \lambda _{i})\psi '(F(x,\lambda _{i})) \\ &=\left ( \frac{\frac{\partial{F}(x;\lambda _{j})}{\partial \lambda _{j}}}{F(x;\lambda _{j})} - \frac{\frac{\partial{F}(x;\lambda _{i})}{\partial \lambda _{i}}}{F(x;\lambda _{i})} \right )F(x;\lambda _{i})\psi '(F(x,\lambda _{i})) \\ &\overset{sgn}{=} \frac{\frac{\partial{F}(x;\lambda _{i})}{\partial \lambda _{i}}}{F(x;\lambda _{i})} - \frac{\frac{\partial{F}(x;\lambda _{j})}{\partial \lambda _{j}}}{F(x;\lambda _{j})} \leq 0, \end{aligned} $$

where $\overset{sgn}{=}$ follows from the fact that $\psi '$ is a negative function. The first inequality comes from the assumption that $F(\cdot ;\lambda )$ is increasing in λ and $u\psi '(u)$ is increasing in u, and the last inequality is based on the assumption $F(\cdot ;\lambda )$ is log-concave. Then, the desired result follows by applying Lemma 1.3. For $\boldsymbol{\lambda} \in \mathfrak{I}_{+}=\{\boldsymbol{\lambda}:0<\lambda _{1}\leq \lambda _{2}\leq \cdots \leq \lambda _{n}\}$, it can be proved in a similar manner that the desired result holds. □

Example 3.2

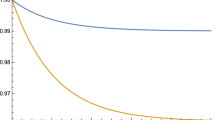
Consider the family of Lomax distributions with cdf $F(x; \lambda )=\frac{\lambda x}{1+\lambda x}$, $x\geq 0$, $\lambda >0$, denoted by $Lo(\lambda )$. Suppose that $X_{i}$ follows $Lo(\lambda _{i})$, with $\lambda _{1}=2$, $\lambda _{2}=3$, $\lambda _{3}=4$ and, further, assume that $Y_{i}$ follows $Lo(\lambda ^{\star}_{i})$ with $\lambda ^{\star}_{1}=1$, $\lambda ^{\star}_{2}=3$, $\lambda ^{\star}_{3}=5$. Contemplate the multivariate Gumbel copula having generator $\psi _{\theta}(u)=(-\ln (u))^{\theta}$, for $\theta \geq 1$. It can be verified plainly that $F(x; \lambda )$ is increasing and log-concave in λ, for all $x \geq 0$. Moreover, $u\psi '_{\theta}(u)$ is increasing in $u\in (0,1)$. Since $\boldsymbol{\lambda} \overset{m}{\preceq}\boldsymbol{\lambda} ^{*}$, using Theorem 3.1, we deduce that $X_{3:3} \leq _{st} Y_{3:3}$. Note that

$$ \bar{F}_{X_{3:3}}(x;\boldsymbol{\lambda} )= 1-\exp \bigg\{ -\left (\sum _{i=1}^{3} \ln ^{\theta}\left (\frac{1+\lambda _{i} x}{\lambda _{i} x}\right ) \right )^{\frac{1}{\theta}}\bigg\} $$

and

$$ \bar{F}_{Y_{3:3}}(x;\boldsymbol{\lambda} ^{\star})= 1-\exp \bigg\{ -\left ( \sum _{i=1}^{3} \ln ^{\theta}\left ( \frac{1+\lambda ^{\star}_{i} x}{\lambda ^{\star}_{i} x}\right ) \right )^{\frac{1}{\theta}}\bigg\} . $$

The graphs of $\bar{F}_{X_{3:3}}(x;\boldsymbol{\lambda} )$ and $\bar{F}_{Y_{3:3}}(x;\boldsymbol{\lambda} ^{\star})$ for $\theta =2$ are plotted in Fig. 1 to acknowledge the achieved conclusion. The upper curve (blue) is the graph of $\bar{F}_{Y_{3:3}}(x;\boldsymbol{\lambda} ^{\star})$ and the lower curve (red) is that of $\bar{F}_{X_{3:3}}(x;\boldsymbol{\lambda} )$.

Figure 1

Plots of survival functions of ${X_{3:3}}$ and ${Y_{3:3}}$

In the setting of Theorem 3.1, in order to see what happens if $F(\cdot ;\lambda )$ is log-convex in $\lambda >0$, a counterexample is presented below.

Counterexample 3.3

Suppose that $F(x;\lambda )=\left (1-e^{-x^{3}}\right )^{\sqrt{\lambda }}$ where $x>0$ and $\lambda >0$. Denote by $X_{1}$, $X_{2}$, and $X_{3}$ the component lifetimes of parallel system with dependent components, where $X_{i} \sim F(\cdot ;\lambda _{i})$, $i=1,2,3$ with Gumbel copula having parameter $\theta >0$. Denote by $Y_{1}$, $Y_{2}$, and $Y_{3}$ the component lifetimes of another parallel system with dependent components such that $Y_{i} \sim F(\cdot ;\lambda ^{*}_{i})$ with the same Gumbel copula as that of $X_{i}$’s. It is easy to see that $F(x;\lambda )$ is log-convex in λ, for all $x>0$. Let us choose $\boldsymbol{\lambda} =(4,5,6)$, $\boldsymbol{\lambda} ^{*}=(3,5,7)$, and $\theta =2$. Note that $\boldsymbol{\lambda} \overset{m}{\preceq}\boldsymbol{\lambda} ^{*}$. It can be numerically verified that $X_{3:3} \nleq _{st} Y_{3.3}$. Therefore, the result of Theorem 3.1 does not hold when $F(\cdot ;\lambda )$ is log-convex in λ.

Proposition 3.4

Let X be a dependent random vector with $X_{i}\sim F(\cdot ;\lambda _{i})$ and having the Archimedean copula with generator ϕ and let Y be another dependent random vector with $Y_{i}\sim F(\cdot ;\lambda _{i}^{*})$ and having the Archimedean copula with generator ϕ. If

• (i) $F(\cdot ;\lambda )$ is decreasing in λ;

• (ii) $F(\cdot ;\lambda )$ is log-concave in λ;

• (iii) $u\psi '(u)$ is decreasing in $u\in (0,1)$.

Then, we have

$$\mathit{\lambda }\stackrel{m}{⪯}{\mathit{\lambda }}^{\ast }⟹X_{n:n}{\le }_{\mathrm{st}}{Y}_{n:n}.$$

Proof

In a manner similar to the proof of Theorem 3.1, we have that

$$\begin{aligned} \frac{\partial \overline{F}_{X_{n:n}}(x;\boldsymbol{\lambda} )}{\partial \lambda _{i}}- \frac{\partial \overline{F}_{X_{n:n}}(x;\boldsymbol{\lambda} )}{\partial \lambda _{j}}= \eta _{1}\phi '\left (\sum _{i=1}^{n}\psi (F(x;\lambda _{i})\right ), \end{aligned}$$

where $\eta _{1}=\frac{\partial{F}(x;\lambda _{j})}{\partial \lambda _{j}} \psi '(F(x,\lambda _{j})) - \frac{\partial{F}(x;\lambda _{i})}{\partial \lambda _{i}}\psi '(F(x, \lambda _{i}))$. It suffices to show that $\eta _{1}\leq 0$. Indeed, $\eta _{1}$ can be rewritten as follows:

$$ \eta _{1}= \frac{\frac{\partial{F}(x;\lambda _{j})}{\partial \lambda _{j}}}{F(x;\lambda _{j})}F(x; \lambda _{j})\psi '(F(x,\lambda _{j}))- \frac{\frac{\partial{F}(x;\lambda _{i})}{\partial \lambda _{i}}}{F(x;\lambda _{i})}F(x; \lambda _{i})\psi '(F(x,\lambda _{i})). $$

From the condition that $F(\cdot ;\lambda )$ is log-concave in λ, it follows that

$$ 0\geq \frac{\frac{\partial{F}(x;\lambda _{j})}{\partial \lambda _{j}}}{F(x;\lambda _{j})} \geq \frac{\frac{\partial{F}(x;\lambda _{i})}{\partial \lambda _{i}}}{F(x;\lambda _{i})}, $$

(5)

and from the assumption that $u\psi '(u)$ is decreasing in $u\in (0,1)$, one gets

$$ 0\geq F(x;\lambda _{j})\psi '(F(x,\lambda _{j}))\geq F(x;\lambda _{i}) \psi '(F(x,\lambda _{i})). $$

(6)

By combining (5) and (6), it follows that $\eta _{1}$ is nonpositive. Hence, the desired result follows by applying Lemma 1.3. □

It is notable that there are many Archimedean copulas satisfying the condition that $u\psi '(u)$ increases or decreases in u of as required in Theorems 3.1 and 4.1. For example, if we consider the Ali–Mikhail–Haq (AMH) copula with the generator $\phi (u)=\frac{1-\theta}{e^{u}-\theta}$ for $\theta \in [-1,1)$, it follows that $\psi (u)=\ln \left (\frac{1-\theta +\theta u}{u}\right )$. It can be seen that

$$ u\psi '(u)=\frac{\theta -1}{1-\theta +\theta u}, $$

which is increasing in u for $\theta \in [0,1)$ and decreasing in u for $\theta \in [-1,0)$. For another example, consider Clayton copula with generator inverse $\psi (u)=\frac{1}{\theta}( u^{-\theta}-1)$ for $\theta \in [-1,\infty )\setminus \{0\}$. It can be seen that

$$ u\psi '(u)=-\frac{1}{u^{\theta}}, $$

which is decreasing in u for $\theta \in [-1,0)$ and increasing in u for $\theta \in [1,\infty )$.

Example 3.5

Consider the multivariate Clayton copula described by the generator $\psi _{\theta}(x)=\frac{1}{\theta}\left (\frac{1}{x^{\theta}}-1 \right )$, for $\theta >0$ such that $x\psi '_{\theta}(x)$ is increasing in $x\in (0,1)$. Suppose that $X_{i}$ and $Y_{i}$, $i=1,2,3$, are exponential random variables with density functions $f_{X_{i}}(x)=\lambda _{i}e^{-\lambda _{i}x}$, linked by an Archimedean copula with generator function $\psi _{\theta}$ defined above and scale parameters $(\lambda _{1},\lambda _{2},\lambda _{3})=(2,4,5)$ and $(\lambda ^{*}_{1},\lambda ^{*}_{2},\lambda ^{*}_{3})=(1,3,7)$, respectively. It is easy to check that the conditions in Theorem 3.1 are satisfied.

In Proposition 3.4, to realize what happens if $F(\cdot ;\lambda )$ is log-convex in $\lambda >0$, the next counterexample is useful.

Counterexample 3.6

Let us take $F(x;\lambda )=\left (\frac{x^{2}}{1+x^{2}}\right )^{\sqrt{\lambda }}$ where $x,\lambda >0$. Let $X_{1}$, $X_{2}$, and $X_{3}$ be three nonnegative dependent random variables, where $X_{i} \sim F(\cdot ;\lambda _{i})$, $i=1,2,3$ with AMH copula having parameter $\theta \in [-1,1)$. Further, let $Y_{1}$, $Y_{2}$, and $Y_{3}$ be three nonnegative dependent random variables, where $Y_{i} \sim F(\cdot ;\lambda ^{*}_{i})$ with the same AMH copula as that of $X_{i}$’s. It can be easily verified that $F(x;\lambda )$ is log-convex in λ, for all $x>0$. Suppose that $\boldsymbol{\lambda} =(0.4,1.4,2.1)$, $\boldsymbol{\lambda} ^{*}=(0.6,1.1,2.5)$, and let $\theta =-0.2$. We see that $\boldsymbol{\lambda} \preceq _{w} \boldsymbol{\lambda} ^{*}$. Now, after some calculation, we observe that $X_{3:3} \nleq _{st} Y_{3.3}$, and, consequently, Proposition 3.4 does not remain valid if $F(\cdot ;\lambda )$ is log-convex in λ.

Theorem 3.7

Let X be a dependent random vector with $X_{i}\sim F(\cdot ;\lambda _{i})$ and having the Archimedean copula with generator ϕ and let Y be another dependent random vector with $Y_{i}\sim F(\cdot ;\lambda _{i}^{*})$ and having the Archimedean copula with generator ϕ. If

• (i) $F(\cdot ;\lambda )$ is decreasing in λ;

• (ii) $F(\cdot ;\lambda )$ is log-concave in λ;

• (iii) $u\psi '(u)$ is decreasing in $u\in (0,1)$.

Then, we have

$$\mathit{\lambda }{⪯}_w{\mathit{\lambda }}^{\ast }⟹X_{n:n}{\le }_{\mathrm{st}}{Y}_{n:n}.$$

Proof

By Theorem 3.1 and since $F(\cdot ;\lambda )$ is decreasing in λ, we conclude that $\overline{F}_{X_{n:n}}(x;\boldsymbol{\lambda} )$ is decreasing in $\lambda _{i}$. For $\boldsymbol{\lambda} ,\boldsymbol{\lambda} ^{*}\in \mathfrak{D}_{+}=\{\boldsymbol{\lambda}: \lambda _{1}\geq \lambda _{2}\geq \cdots \geq \lambda _{n}>0\}$, where $\boldsymbol{\lambda} \preceq _{w}\boldsymbol{\lambda} ^{*}$, in accordance with Theorem 5.A.9 of [11], there exists some $\boldsymbol{\beta} \in \mathfrak{D}_{+}$ such that $\boldsymbol{\lambda} \preceq \boldsymbol{\beta}$ and $\boldsymbol{\beta} \overset{m}{\preceq}\boldsymbol{\lambda} ^{*}$, where $\boldsymbol{\lambda} \preceq \boldsymbol{\beta}$ means that $\lambda _{i}\leq \beta _{i}$, $i=1,\ldots ,n$. Under the assumptions $(i)$–$(iii)$ of Proposition 3.4, it follows that $\boldsymbol{\beta} \overset{m}{\preceq}\boldsymbol{\lambda} ^{*}$ implies $T_{n:n}\leq _{st}Y^{*}_{n:n}$, where $T_{n:n}$ is the lifetime of a parallel system formed from random lifetimes $\boldsymbol{T}=(T_{1},\ldots ,T_{n})$ with $T_{i}\sim F(\cdot ,\beta _{i})$ for $i=1,\ldots ,n$. Also due to the assumption that $\overline{F}_{X_{n:n}}(x;\boldsymbol{\lambda} )$ is increasing function in $\lambda _{i}$, it follows that $\boldsymbol{\lambda} \preceq \boldsymbol{\beta}$ implies $\overline{F}_{X_{n:n}}(x;\boldsymbol{\lambda} )\leq \overline{F}_{T_{n:n}}(x; \boldsymbol{\beta} )$, which in turn implies that $X_{n:n}\leq _{st}T_{n:n}$. By combining these observations, it holds that $X_{n:n}\leq _{st}X^{*}_{n:n}$. For $\boldsymbol{\lambda} \in \mathfrak{I}_{+}=\{\boldsymbol{\lambda}:0<\lambda _{1}\leq \lambda _{2}\leq \cdots \leq \lambda _{n}\}$, it can be proved in a similar manner that the desired result holds, hence the claim of the theorem. □

Example 3.8

Under the setup of Example 3.5, it is easy to check that $x\psi '_{\theta}(x)$ is decreasing in x for all $\theta \in [-1,0)$. Suppose that $X_{i}$ and $Y_{i}$, $i=1,2,3$, are exponential random variables with density functions $f_{X_{i}}(x)=\frac{1}{\lambda _{i}}e^{-\frac{1}{\lambda _{i}}x}$, linked by an Archimedean copula with generator function $\psi _{\theta}$ and scale parameters $(\lambda _{1},\lambda _{2},\lambda _{3})=(1,2,4)$ and $(\lambda ^{*}_{1},\lambda ^{*}_{2},\lambda ^{*}_{3})=(2,3,5)$, respectively. It is easy to check that $(\lambda _{1},\lambda _{2},\lambda _{3})\preceq _{w}(\lambda ^{*}_{1}, \lambda ^{*}_{2},\lambda ^{*}_{3})$ and also the conditions in Theorem 3.7 are satisfied.

In the framework of Theorem 3.7, to see what happens if $F(\cdot ;\lambda )$ is log-convex in $\lambda >0$, we give the following counterexample.

Counterexample 3.9

Consider the cumulative distribution function $F(x;\lambda )=e^{-\frac{\sqrt{\lambda }}{x}}$ where $x,\lambda >0$. We also consider $X_{1}$, $X_{2}$, and $X_{3}$ as three nonnegative dependent random variables, where $X_{i} \sim F(\cdot ;\lambda _{i})$, $i=1,2,3$ with Clayton copula having parameter $\theta >0$. Moreover, take $Y_{1}$, $Y_{2}$, and $Y_{3}$ as three nonnegative dependent random variables, where $Y_{i} \sim F(\cdot ;\lambda ^{*}_{i})$ with the same Archimedean copula as that of $X_{i}$’s. It can be seen that $F(x;\lambda )$ is log-convex in λ, for all $x>0$. Let $\boldsymbol{\lambda} =(0.4,1.4,2.1)$, $\boldsymbol{\lambda} ^{*} =(0.6,1.1,2.5)$, and $\theta =4.25$. It is seen that $\boldsymbol{\lambda} \preceq _{w} \boldsymbol{\lambda} ^{*}$. We observe that $X_{3:3} \nleq _{st} Y_{3:3}$. Hence, the result of Theorem 3.7 is not satisfied in the case when $F(\cdot ;\lambda )$ is log-convex in λ.

4 Usual stochastic order of series systems

This section develops the usual stochastic ordering of extreme order statistics in the dependent case provided that the original random variables follow a one-parameter lifetime distribution. We use the notation d.non-i.d. in place of dependent and nonidentically distributed.

Theorem 4.1

Let $\boldsymbol{X}=(X_{1},\dots ,X_{n})$ be a vector of nonnegative d.non-i.d. random variables, where $X_{i}\sim F(\cdot ;\lambda _{i})$ and the dependence structure follows the Archimedean copula with generator ϕ and let $\boldsymbol{Y}=(Y_{1},\dots ,Y_{n})$ be another vector of d.non-i.d. random variables following the Archimedean copula with generator ϕ, where $Y_{i}\sim F(\cdot ;\lambda _{i}^{*})$. Let

• (i) $\overline{F}(\cdot ;\lambda )$ be decreasing in λ;

• (ii) $\overline{F}(\cdot ;\lambda )$ be log-convex in λ;

• (iii) $u\psi '(u)$ be decreasing in $u\in (0,1)$.

Then,

$$\mathit{\lambda }\stackrel{m}{⪯}{\mathit{\lambda }}^{\ast }⟹X_{1:n}{\le }_{\mathrm{st}}{Y}_{1:n}.$$

Proof

The distribution function of $X_{1:n}$ is of the form

$$ {F}_{X_{1:n}}(x;\boldsymbol{\lambda} )=1-\phi \left (\sum _{i=1}^{n}\psi ( \overline{F}(x;\lambda _{i})\right ). $$

Thus for establishing the desired result, it is enough to show that the function ${F}_{X_{1:n}}(x;\boldsymbol{\lambda} )$ is Schur-concave. Set $1\leq i< j\leq n$ and $\boldsymbol{\lambda} \in \mathfrak{D}_{+}=\{\boldsymbol{\lambda}:\lambda _{1}\geq \lambda _{2}\geq \cdots \geq \lambda _{n}>0\}$. Taking the derivative of ${F}_{X_{1:n}}(x;\boldsymbol{\lambda} )$ with respect to $\lambda _{i}$, we have

$$ \frac{\partial{F}_{X_{1:n}}(x;\boldsymbol{\lambda} )}{\partial \lambda _{i}}=- \frac{\partial \overline{F}(x;\lambda _{i})}{\partial \lambda _{i}} \psi '(\overline{F}(x,\lambda _{i}))\phi '\left (\sum _{i=1}^{n}\psi ( \overline{F}(x;\lambda _{i})\right ). $$

Therefore, for $i\neq j$, it follows that

$$\begin{aligned} \frac{\partial{F}_{X_{1:n}}(x;\boldsymbol{\lambda} )}{\partial \lambda _{i}}- \frac{\partial{F}_{X_{1:n}}(x;\boldsymbol{\lambda} )}{\partial \lambda _{j}}&= \frac{\partial \overline{F}(x;\lambda _{j})}{\partial \lambda _{j}} \psi '(\overline{F}(x,\lambda _{j}))\phi '\left (\sum _{i=1}^{n}\psi ( \overline{F}(x;\lambda _{i})\right ) \\ &\quad - \frac{\partial \overline{F}(x;\lambda _{i})}{\partial \lambda _{i}} \psi '(\overline{F}(x,\lambda _{i}))\phi '\left (\sum _{i=1}^{n}\psi ( \overline{F}(x;\lambda _{i})\right ) \\ &= \left ( \frac{\partial \overline{F}(x;\lambda _{j})}{\partial \lambda _{j}} \psi '(\overline{F}(x,\lambda _{j}))- \frac{\partial \overline{F}(x;\lambda _{i})}{\partial \lambda _{i}} \psi '(\overline{F}(x,\lambda _{i}))\right )\\ &\quad \times\phi '\left (\sum _{i=1}^{n} \psi (\overline{F}(x;\lambda _{j})\right ) \\ &=\eta _{2}\phi '\left (\sum _{i=1}^{n}\psi (\overline{F}(x;\lambda _{j}) \right ) . \end{aligned}$$

Due to the fact that $\phi '$ is negative, it is enough to show that $\eta _{2}$ is positive. We can compute

$$ \begin{aligned} \eta _{2}&= \frac{\partial \overline{F}(x;\lambda _{j})}{\partial \lambda _{j}} \psi '(\overline{F}(x,\lambda _{j}))- \frac{\partial \overline{F}(x;\lambda _{i})}{\partial \lambda _{i}} \psi '(\overline{F}(x,\lambda _{i})) \\ &= \frac{\frac{\partial \overline{F}(x;\lambda _{j})}{\partial \lambda _{j}}}{\overline{F}(x;\lambda _{j})} \overline{F}(x;\lambda _{j})\psi '(\overline{F}(x,\lambda _{j}))- \frac{\frac{\partial \overline{F}(x;\lambda _{i})}{\partial \lambda _{i}}}{\overline{F}(x;\lambda _{i})} \overline{F}(x;\lambda _{i})\psi '(\overline{F}(x,\lambda _{i})). \end{aligned} $$

Since $\overline{F}(\cdot ;\lambda )$ is log-convex with respect to λ, we have

$$ \frac{\frac{\partial \overline{F}(x;\lambda _{j})}{\partial \lambda _{j}}}{\overline{F}(x;\lambda _{j})} \leq \frac{\frac{\partial \overline{F}(x;\lambda _{i})}{\partial \lambda _{i}}}{\overline{F}(x;\lambda _{i})} \leq 0, $$

(7)

and due to the condition that $u\psi '(u)$ is decreasing in u and the fact that $\overline{F}(x;\lambda _{i})\geq \overline{F}(x;\lambda _{j})$, we see that

$$ \overline{F}(x;\lambda _{j})\psi '(\overline{F}(x,\lambda _{j}))\leq \overline{F}(x;\lambda _{i})\psi '(\overline{F}(x,\lambda _{i}))\leq 0. $$

(8)

By combining (7) and (9), it follows that $\eta _{2}$ is nonnegative. From these observations, according to Lemma 1.3, it follows that ${F}_{X_{1:n}}$ is Schur-concave. This in turn guarantees that $\overline{F}_{X_{1:n}}$ is Schur-convex. Hence, the desired result follows by applying Lemma 1.3. For $\boldsymbol{\lambda} \in \mathfrak{I}_{+}=\{\boldsymbol{\lambda}:0<\lambda _{1}\leq \lambda _{2}\leq \cdots \leq \lambda _{n}\}$, it can be proved in a similar manner that the desired result holds. □

Example 4.2

Under the setup of Example 3.5, it is easy to check that $x\psi '_{\theta}(x)$ is decreasing in x for all $\theta \in [-1,0)$ and that the conditions in Theorem 4.1 are satisfied.

In connection with Theorem 4.1, one can ask what happens if $\bar{F}(\cdot ;\lambda )$ is log-concave in $\lambda >0$. The following counterexample clarifies the issue.

Counterexample 4.3

Consider a parametric family of distributions with survival function $\bar{F}(x;\lambda )=e^{-\lambda x^{2}}$, $x>0$, and $\lambda >0$. Assume that $X_{1}$, $X_{2}$, and $X_{3}$ are nonnegative dependent random variables, where $X_{i} \sim \bar{F}(\cdot ;\lambda _{i})$, $i=1,2,3$ with Gumbel copula having generator $\phi (x)=e^{-x^{\frac{1}{\theta }}}$, where $\theta \geq 1$. Let $Y_{1}$, $Y_{2}$, and $Y_{3}$ be nonnegative dependent random variables, where $Y_{i} \sim \bar{F}(\cdot ;\lambda ^{*}_{i})$ with the same Archimedean copula as that of $X_{i}$. It can be seen that $\bar{F}(x;\lambda )$ is log-concave in λ, for all $x>0$. Let us choose $\boldsymbol{\lambda} =(3,4,5)$, $\boldsymbol{\lambda} ^{*} =(2,4,6)$ which fulfill that $\boldsymbol{\lambda} \overset{m}{\preceq}\boldsymbol{\lambda} ^{*}$. We consider Gumbel copula with $\theta =3$. It can be seen that $X_{1:3} \nleq _{st} Y_{1:3}$. As a result, Theorem 4.1 does not remain valid in situations where $F(\cdot ;\lambda )$ is log-concave in λ.

Theorem 4.4

Let $\boldsymbol{X}=(X_{1},\dots ,X_{n})$ be a vector of d.non-i.d. random variables with $X_{i}\sim F(\cdot ;\lambda _{i})$ and having the Archimedean copula with generator ϕ and let $\boldsymbol{Y}=(Y_{1},\dots ,Y_{n})$ be another vector of d.non-i.d. random variables with $Y_{i}\sim F(\cdot ;\lambda _{i}^{*})$ and having the Archimedean copula with generator ϕ. If

• (i) $\overline{F}(\cdot ;\lambda )$ is increasing in λ;

• (ii) $\overline{F}(\cdot ;\lambda )$ is log-concave in λ;

• (iii) $u\psi '(u)$ is increasing in $u\in (0,1)$.

Then, we have

$$\mathit{\lambda }\stackrel{m}{⪯}{\mathit{\lambda }}^{\ast }⟹Y_{1:n}{\le }_{\mathrm{st}}{X}_{1:n}.$$

Proof

In a manner similar to the proof of Theorem 4.1 for establishing the desired result, it is enough to show that the function ${F}_{X_{1:n}}(x;\boldsymbol{\lambda} )$ is Schur-convex. Taking the derivative of ${F}_{X_{1:n}}(x;\boldsymbol{\lambda} )$ with respect to $\lambda _{i}$, we have

$$ \frac{\partial{F}_{X_{1:n}}(x;\boldsymbol{\lambda} )}{\partial \lambda _{i}}=- \frac{\partial \overline{F}(x;\lambda _{i})}{\partial \lambda _{i}} \psi '(\overline{F}(x,\lambda _{i}))\phi '\left (\sum _{i=1}^{n}\psi ( \overline{F}(x;\lambda _{i})\right ). $$

Therefore, for $i\neq j$, it follows that

$$ \begin{aligned} \frac{\partial{F}_{X_{1:n}}(x;\boldsymbol{\lambda} )}{\partial \lambda _{i}}- \frac{\partial{F}_{X_{1:n}}(x;\boldsymbol{\lambda} )}{\partial \lambda _{j}}&= \left ( \frac{\partial \overline{F}(x;\lambda _{j})}{\partial \lambda _{j}} \psi '(\overline{F}(x,\lambda _{j}))- \frac{\partial \overline{F}(x;\lambda _{i})}{\partial \lambda _{i}} \psi '(\overline{F}(x,\lambda _{i}))\right )\\ &\quad \times\phi '\left (\sum _{i=1}^{n} \psi (\overline{F}(x;\lambda _{j})\right ) \\ &=\eta _{2}\phi '\left (\sum _{i=1}^{n}\psi (\overline{F}(x;\lambda _{j}) \right ) . \end{aligned} $$

Since $\phi '$ is negative, it is enough to show that $\eta _{2}$ is nonpositive. We can compute

$$ \begin{aligned} \eta _{2}&= \frac{\partial \overline{F}(x;\lambda _{j})}{\partial \lambda _{j}} \psi '(\overline{F}(x,\lambda _{j}))- \frac{\partial \overline{F}(x;\lambda _{i})}{\partial \lambda _{i}} \psi '(\overline{F}(x,\lambda _{i})) \\ &\leq \left [ \frac{\frac{\partial \overline{F}(x;\lambda _{j})}{\partial \lambda _{j}}}{\overline{F}(x;\lambda _{j})} - \frac{\frac{\partial \overline{F}(x;\lambda _{i})}{\partial \lambda _{i}}}{\overline{F}(x;\lambda _{i})} \right ]\overline{F}(x;\lambda _{i})\psi '(\overline{F}(x,\lambda _{i})), \end{aligned} $$

(9)

where, using the same arguments as in proof of Theorem 4.1, the first inequality follows from the conditions that $\overline{F}(x;\lambda _{i})$ is increasing in λ and $u\psi '(u)$ is increasing in u. Since $\psi '$ is nonpositive and $\overline{F}(x;\lambda )$ is log-concave in λ, it holds that

$$ \frac{\frac{\partial \overline{F}(x;\lambda _{j})}{\partial \lambda _{j}}}{\overline{F}(x;\lambda _{j})} \geq \frac{\frac{\partial \overline{F}(x;\lambda _{i})}{\partial \lambda _{i}}}{\overline{F}(x;\lambda _{i})} \geq 0, $$

from which the right-hand side of (9) is nonpositive. Hence, the desired result follows by applying Lemma 1.3. □

In the next example, using Theorem 4.1, we present a situation where the reliability of a system with components of different ages used increases as the ages of the components become more widely separated. Recall that a nonnegative random variable X has a distribution with the $IFR$ property when the hazard rate function of X, i.e., $r_{X}(x)$, is increasing in $x\geq 0$.

Example 4.5

Denote by X the lifetime of a fresh unit that has survival function F̄. Then the lifetime of the unit at age λ as the used unit, where $\lambda > 0$ has survival function $\bar{F}(x;\lambda )=\frac{\bar{F}(x+\lambda )}{\bar{F}(\lambda )}$. Assume that $X_{i}$ is the lifetime of a used unit with age $\lambda _{i}$, and further assume that $Y_{i}$ is the lifetime of a used unit with age $\lambda ^{\star}_{i}$, where $\boldsymbol{\lambda} =(3,4,5)$ and $\boldsymbol{\lambda} ^{*} =(2,4,6)$ are two quantities of different ages. If F possesses the $IFR$ property with a concave hazard rate function, then it is easy to show that $\bar{F}(x;\lambda )$ is decreasing in λ and is also log-convex in λ for all $x \geq 0$. Consider the multivariate Gumbel copula with the generator $\psi _{\theta}(u)=(-\ln (u))^{\theta}$, for $\theta \geq 1$. It can be proved that $u\psi '_{\theta}(u)$ is increasing in $u\in (0,1)$. Thus, since $\boldsymbol{\lambda} \preceq _{m}\boldsymbol{\lambda} ^{*}$, using Theorem 4.1, one concludes that $X_{1:3}\leq _{\mathrm{st}} Y_{1:3}$. Thus, considering two series systems with used components where the component lifetimes satisfy the $IFR$ property and have a concave hazard rate function, the system comprising used components with close ages has a lower reliability compared to the system comprising used components with scattered ages in the sense of the majorization order.

In Theorem 4.4, we present a counterexample where $\bar{F}(\cdot ;\lambda )$ is log-convex in $\lambda >0$.

Counterexample 4.6

Let $\bar{F}(x;\lambda )=e^{-\sqrt{\lambda } x^{2}}$ be the underlying survival function where $\lambda >0$. Suppose that $X_{1}$, $X_{2}$, and $X_{3}$ are nonnegative dependent random variables, where $X_{i} \sim \bar{F}(\cdot ;\lambda _{i})$, $i=1,2,3$ with Gumbel copula having generator $\phi (x)=e^{-x^{\frac{1}{\theta }}}$, where $\theta \geq 1$. In addition, we assume that $Y_{1}$, $Y_{2}$, and $Y_{3}$ are nonnegative dependent random variables, where $Y_{i} \sim \bar{F}(\cdot ;\lambda ^{*}_{i})$ with the same copula function as that of $X_{i}$’s. It can be seen that $\bar{F}(x;\lambda )$ is log-convex in λ, for all $x>0$. Let us choose $\boldsymbol{\lambda} =(1,2,3)$, $\boldsymbol{\lambda} ^{*} =(0.8,2,3.2)$, and take $\theta =4.5$. It is observed that $X_{1:3} \nleq _{st} Y_{1:3}$. It can be seen that $\boldsymbol{\lambda} \overset{m}{\preceq}\boldsymbol{\lambda} ^{*}$. Therefore, the result of Theorem 4.4 does not hold in the case where $\bar{F}(\cdot ;\lambda )$ is log-convex in λ.

5 Conclusion

In this study, the usual stochastic ordering between the lifetimes of two series/parallel systems with nonidentical lifetimes of the dependent components under an Archimedean copula dependence structure was performed under certain circumstances. It was assumed that the heterogeneous components follow a one-parameter lifetime distribution for which the cdf (e.g., $F(x,\boldsymbol{\lambda} )$) or the survival function (e.g., $\bar{F}(x,\boldsymbol{\lambda} )$) must satisfy the property of being a monotone function of λ which, moreover, is log-concave (log-convex) with respect to λ. The inverse generator of the Archimedean copula should satisfy some special properties. It was shown that the majorization order and the weak submajorization order are relevant to establish the usual stochastic order between the lifetimes of the systems. Several examples were used to investigate the sufficient conditions to obtain the results. In general, the problem of ordering the lifetimes of two parallel/series systems with respect to the usual stochastic ordering shows which system is more reliable, which can be a useful investigation in the context of decision making and optimization for the assembly of components in a system. In the study conducted in this paper, the selection of components with lifetimes that follow a general distribution with one parameter whose parameters are more scattered improves the reliability of the system compared to the case in which components are selected with lifetimes that follow the same family of distributions with less variable parameters.

In a future study, we could consider nonparametric distributions instead of the general family of distributions with one parameter associated with the component lifetimes in a parallel/series system when the component lifetimes are heterogeneous and, moreover, dependent with an Archimedean copula structure. In such a situation, it is an interesting development to establish the usual stochastic ordering between the lifetimes of two parallel/series systems. In addition, another study can be conducted to investigate the ordering properties of dependent random variables having a more general dependence structure than that of an Archimedean dependence structure.