HR and RHR orderings of generalized order statistics

Abstract

In this article, we compare generalized order statistics in terms of increasing convex, mean residual life, hazard rate and reversed hazard rate orderings and establish some general results, including resolving an open problem. Some counterexamples are also provided for the cases wherein the results are not valid in general. Finally, some new applications of these results are demonstrated for sequential systems, k-record values and Pfeifer’s records.

1 Introduction

During the last two decades, several stochastic comparisons of ordered random variables have been discussed in the literature. Kamps (1995) introduced the concept of generalized order statistics (GOS) as a unified approach to several models of ordered random variables. Since then, comparisons of GOS have been discussed by numerous authors including Franco et al. (2002), Belzunce et al. (2005), Zhao and Balakrishnan (2009), Balakrishnan et al. (2012), and Alimohammadi et al. (2021). In this article, we establish some additional new results in this direction.

Let X be a nonnegative random variable with an absolutely continuous cumulative distribution function (cdf) F, survival function (sf) ${\overline{F}}=1-F$, and probability density function (pdf) f. Let $F^{-1}$ be the right continuous inverse (quantile function) of F. Let $h_X=f/{\bar{F}}$ and $\lambda _X=f/F$ denote the hazard rate (HR) and reversed hazard rate (RHR) functions of X, respectively.

The random variables $X_{(r,n,{\widetilde{m}}_n,k)}$, $r=1,2,\dots ,n$, arising from independent and identically distributed random variables, are referred to as GOS if their joint density function is given by

$$\begin{aligned}&{\mathbf {f}}({x_1},\dots ,{x_n})= k\Bigg (\prod _{j=1}^{n-1}{\gamma _{(j,n,{\widetilde{m}}_n,k)}}\Bigg ) \Bigg (\prod _{i=1}^{n-1}{[{\bar{F}}{(x_i)}]^{m_i}f(x_i)\Bigg )}{[\bar{F}{(x_n)}]^{k-1}f(x_n)}, \end{aligned}$$

for all $F^{-1}(0)<x_1\le x_2 \le \dots \le x_n <F^{-1}(1-)$, where $n \in {\mathbb {N}}$, $k>0$ and $m_1,\dots ,m_{n-1}\in {\mathbb {R}}$ are such that ${\gamma _{(i,n,{\widetilde{m}}_n,k)}}=k+n-i+\sum _{j=i}^{n-1}{m_j}>0 \text { for all } i\in \{1,\dots ,n-1\},$ and ${\widetilde{m}}_n=(m_1,\dots ,m_{n-1})$ if $n\ge 2$ (${\widetilde{m}}_n\in {\mathbb {R}}$ is arbitrary if $n=1$). Note that the parameters k and $m_i$ form the structure of this model. Indeed, special choices of them correspond to some well-known submodels. For example, if $m_1=\dots =m_{n-1}=0$ and $k=1$, or $m_1=\dots =m_{n-1}=-1$ and $k \in {\mathbb {N}}$, then GOS would reduce to ordinary order statistics and k-record values, respectively. Sequential order statistics (SOS) under proportional HR are also included in GOS. Indeed, the specific choice of distribution functions

$$\begin{aligned} F_i(x) = 1-(1-F (x))^{\alpha _i},~i=1,\dots ,n, \end{aligned}$$

(1)

with a cdf F and positive real numbers $\alpha _1,\dots ,\alpha _n$, leads to the model of GOS with parameters $k=\alpha _n$ and $m_i=(n-i+1)\alpha _i-(n-i)\alpha _{i+1}-1$. In the literature, (1) is usually referred to as the proportional HR assumption. We refer the readers to Table 1 of Kamps (1995) for complete information on various submodels.

Throughout this paper, we shall use the word increasing (decreasing) for non-decreasing (non-increasing). We say that X is smaller than Y (with pdf g, sf $\bar{G}$ and cdf G) in the

• likelihood ratio order (denoted by $X\le _{lr} Y$) if g(x)/f(x) is increasing in x;

• HR order (denoted by $X\le _{hr} Y$) if $\bar{G}(x)/\bar{F}(x)$ is increasing in x or, equivalently, $h_Y(x)\le h_X(x)$;

• RHR order (denoted by $X\le _{rh} Y$) if G(x)/F(x) is increasing in x or, equivalently, $\lambda _X(x)\le \lambda _Y(x)$;

• mean residual life order (denoted by $X\le _{mrl} Y$) if ${\bar{G}(t)}{\int _t^\infty \! \bar{F}(x)~dx}\le {\bar{F}(t)}{\int _t^\infty \! \bar{G}(x)~dx}$, $\forall t$;

• usual stochastic order (denoted by $X\le _{st} Y$) if $\bar{F}(x)\le \bar{G}(x)$;

• increasing convex order (denoted by $X\le _{icx} Y$) if $\int _t^\infty \! \bar{F}(x)~dx\le \int _t^\infty \! \bar{G}(x)~dx$, $\forall t$.

It is well-known that (cf. Shaked and Shanthikumar 2007)

$X\le _{lr} Y$	$\Rightarrow$	$X\le _{hr} Y$	$\Rightarrow$	$X\le _{mrl} Y$
$\Downarrow$		$\Downarrow$		$\Downarrow _a$                  ,
$X\le _{rh} Y$	$\Rightarrow$	$X\le _{st} Y$	$\Rightarrow$	$X\le _{icx} Y$

where implication (a) is valid when X and Y have finite means.

A study of stochastic comparisons of GOS was initiated by Franco et al. (2002). They investigated likelihood ratio, HR and usual stochastic orders under the condition that $m_1=m_2=\cdots =m_{n-1}$ for the two-sample problem in the univariate case. Then, Belzunce et al. (2005) gave these results for dispersive ordering without restriction for the two-sample problem in the multivariate case. They also obtained results for different $m_i$ and $m'_i$ with regard to the vectors $(X_{(1,n,{\widetilde{m}}_n,k)},\cdots ,X_{(n,n,{\widetilde{m}}_n,k)})$ and $(Y_{(1,n,{\widetilde{m}}'_n,k)},\cdots ,Y_{(n,n,{\widetilde{m}}'_n,k)})$. Finally, in the univariate case, Hu and Zhuang (2005) obtained these results for both one-sample and two-sample problems without the restriction $m_1=m_2=\cdots =m_{n-1}$, but for the case when $m_i=m'_i$. They also discussed RHR ordering of GOS for the one-sample problem in the univariate case. Recently, Esna-Ashari et al. (2020) and Alimohammadi et al. (2021) established the likelihood ratio and dispersive orderings, respectively, without the restriction $m_1=m_2=\cdots =m_{n-1}$ and for different $m_i$ and $m'_i$ in the univariate case. Note that the consideration of different $m_i$ and $m'_i$ would facilitate the comparison of submodels of GOS among themselves, such as among progressively Type II right censored order statistics with arbitrary censoring schemes, order statistics under multivariate imperfect repair and, in addition, more generally among different submodels, e.g., between order statistics and sequential order statistics, between record values and Pfeifer’s records, and so on. Further, it is worth mentioning that, unlike the usual and likelihood ratio orderings, the multivariate HR ordering is not known to be preserved under marginalization. So, it is meaningful to study the HR and RHR orderings of GOS for different $m_i$ and $m'_i$ in the univariate case.

Now, let us specifically consider the following two-sample problems:

($P_1$):

 $X\le _{icx} Y \Rightarrow X_{(r,n,{\widetilde{m}}_n,k)}\le _{icx} Y_{(r,n,{\widetilde{m}}_n,k)}$: Remained open;

($P_2$):

 $X\le _{st} Y \Rightarrow X_{(r,n,{\widetilde{m}}_n,k)}\le _{st} Y_{(r,n,{\widetilde{m}}_n,k)}$: Franco et al. (2002);

($P_3$):

 $X\le _{mrl} Y \Rightarrow X_{(r,n,{\widetilde{m}}_n,k)}\le _{mrl} Y_{(r,n,{\widetilde{m}}_n,k)}$: Remained open;

($P_4$):

 $X\le _{hr} Y \Rightarrow X_{(r,n,{\widetilde{m}}_n,k)}\le _{hr} Y_{(r,n,{\widetilde{m}}_n,k)}$: Belzunce et al. (2005), Hu and Zhuang (2005);

($P_5$):

 $X\le _{rh} Y \Rightarrow X_{(r,n,{\widetilde{m}}_n,k)}\le _{rh} Y_{(r,n,{\widetilde{m}}_n,k)}$: Remained open;

($P_6$):

 $X\le _{lr} Y \Rightarrow X_{(r,n,{\widetilde{m}}_n,k)}\le _{lr} Y_{(r,n,{\widetilde{m}}_n,k)}$: Belzunce et al. (2005), Esna-Ashari et al. (2020).

For the two-sample situation, we note that few results exist in the literature for increasing convex and mean residual life orders among the GOS. Also, there exists no result for the RHR ordering of GOS so far in the literature. In Sect. 2, we first give negative answers to ($P_1$) and ($P_3$) by providing Counterexamples 2.1 and 2.2, respectively. Then, we obtain the HR and RHR orderings for different parameters $m_i$ and $m'_i$ for the one-sample situation in the univariate case. We provide a proof for the open problem ($P_5$) in Theorem 2.8. Furthermore, through a new method used in the proof of this theorem, we also give a simpler proof for ($P_4$) in Theorem 2.9. In Sect. 3, we explain how these new findings provide useful results for some submodels of GOS such as sequential systems, k-record values and Pfeifer’s records. Finally, some concluding remarks are made in Sect. 4.

2 Main results

As mentioned above, in ($P_6$), if $X \le _{hr} Y$ or $X \le _{st} Y$ instead, then the results established can be weakened from the likelihood ratio order to HR and usual stochastic order of GOS, respectively. One may then ask the question whether it can be further weakened from the usual stochastic order to increasingly convex order, or, from the HR order to mean residual life order. In the following counterexamples, we show that it does not hold even in the case of ordinary order statistics, denoted by $X_{(r,n)}$.

Counterexample 2.1

Suppose

$$\begin{aligned} {\bar{F}(x)=\left\{ \begin{array}{ll} 1 &{} , x<1.1 \\ 2.1-x &{} , 1.1\le x< 2.1 \\ 0 &{} , x\ge 2.1 \\ \end{array} \right. },\hbox {and~} {\bar{G}(x)=\left\{ \begin{array}{ll} 1 &{} , x<1 \\ 1-\ln (x) &{} , 1\le x < e \\ 0 &{} , x\ge e \\ \end{array} \right. }. \end{aligned}$$

It is then easy to verify that $X \le _{icx} Y$ (but, $X \nleq _{st} Y$). Let $r=2$ and $n=5$. Then,

$$\begin{aligned}&\int _1^e \! \Big \{\bar{G}_Y{(2,5)}(x)-\bar{F}_X{(2,5)}(x)\Big \}dx\\&\qquad =\int _1^{1.1} \! \Bigg [\big \{5\left( 1-\ln \left( x\right) \right) ^4\ln \left( x\right) +\left( 1-\ln \left( x\right) \right) ^5\big \}-1\Bigg ]dx\\&\qquad \quad +\int _{1.1}^{2.1} \! \Bigg [\big \{5\left( 1-\ln \left( x\right) \right) ^4\ln \left( x\right) +\left( 1-\ln \left( x\right) \right) ^5\big \} \\&\qquad \quad -\big \{5\left( 2.1-x\right) ^4\left( x-1.1\right) +\left( 2.1-x\right) ^5\big \}\Bigg ]dx\\&\qquad \quad +\int _{2.1}^e \! \Bigg [\big \{5\left( 1-\ln \left( x\right) \right) ^4\ln \left( x\right) +\left( 1-\ln \left( x\right) \right) ^5\big \}-0\Bigg ]dx\\&\qquad \approx -0.0027-0.0142+0.0021 \ngeq 0. \end{aligned}$$

Thus, $X \le _{icx} Y$ does not imply $X_{({2,5})} \le _{icx} Y_{({2,5})}$.

Counterexample 2.2

Consider the following Weibull distributions:

$$\begin{aligned} {\bar{F}(x)=\left\{ \begin{array}{ll} 1, &{} x<0 \\ \exp \left\{ -\left( \frac{x}{b_1}\right) ^{a_1}\right\} , &{} x\ge 0 \\ \end{array} \right. },\hbox {and} {\bar{G}(x)=\left\{ \begin{array}{ll} 1, &{} x<0 \\ \exp \left\{ -\left( \frac{x}{b_2}\right) ^{a_2}\right\} , &{} x\ge 0 \\ \end{array} \right. }, \end{aligned}$$

where $a_1,b_1,a_2,b_2>0$. According to Example 2.6 of Belzunce et al. (2013), if $a_1 > a_2$ and $b_1\Gamma (1+1/{a_1})\le b_2\Gamma (1+1/{a_2})$, then we have $X \le _{mrl} Y$ (but, $X \nleq _{hr} Y$), where $\Gamma (x)$ is the complete gamma function. Let $a_1=4$, $a_2=1$ and $b_1=b_2=1$. Note that $0.9064\approx \Gamma (1.25)<\Gamma (2)=1$. For $r=2$ and $n=3$, we then have

$$\begin{aligned}&{\bar{G}_Y{(2,3)}(0.2)}{\int _{0.2}^\infty \! \bar{F}_X{(2,3)}(x)~dx}\\&\qquad = \left( 3\mathrm {e}^{-\frac{2}{5}}(1-\mathrm {e}^{-\frac{1}{5}})+\mathrm {e}^{-\frac{3}{5}}\right) \int _{0.2}^\infty \! \left\{ 3\mathrm {e}^{-2x^4}(1-\mathrm {e}^{-x^4})+\mathrm {e}^{-3x^4}\right\} ~dx\\&\qquad \approx 0.6477 \end{aligned}$$

and

$$\begin{aligned}&{\bar{F}_X{(2,3)}(0.2)}{\int _{0.2}^\infty \! \bar{G}_Y{(2,3)}(x)~dx}\\&\qquad = \left( 3\mathrm {e}^{-\frac{2}{625}}(1-\mathrm {e}^{-\frac{1}{625}})+\mathrm {e}^{-\frac{3}{625}}\right) \int _{0.2}^\infty \! \left\{ 3\mathrm {e}^{-2x}(1-\mathrm {e}^{-x})+\mathrm {e}^{-3x}\right\} ~dx\\&\qquad \approx 0.6396. \end{aligned}$$

Thus, $X \le _{mrl} Y$ does not imply $X_{({2,3})} \le _{mrl} Y_{({2,3})}$.

Remark 2.3

• (a) It is worth mentioning that Balakrishnan et al. (2012) imposed the condition of increasingly convex ordering of first GOS based on F and G (to conclude increasingly convex ordering of the r-th GOS) but not on the random variables themselves, while in Counterexample 2.1 we show that the condition on the random variables does not imply increasingly convex ordering among the order statistics (and thus among GOS);

• (b) Belzunce et al. (2013) imposed the condition on the means of first GOS based on F and G (with other conditions) to conclude mean residual life ordering of the r-th GOS. Counterexample 2.2 shows that the condition on the random variables does not imply mean residual life ordering among the order statistics and GOS.

Now, we establish some results about the HR and RHR orderings. An expression for the pdf of GOS given by Cramer et al. (2004) is

$$\begin{aligned} f_{X_{(r,n,{\widetilde{m}}_n,k)}}(x)=c_{r-1}{[\bar{F}{(x)}]^{\gamma _{(r,n,{\widetilde{m}}_n,k)}-1}}\xi _{r}(F(x))f(x),~ x\in {\mathbb {R}}_+, \end{aligned}$$

(2)

where $c_{r-1}=\prod _{i=1}^{r}\gamma _{(i,n,{\widetilde{m}}_n,k)}$, $r=1,\dots ,n$, $\gamma _{(n,n,{\widetilde{m}}_n,k)}=k$, and $\xi _{r}$ is a particular Meijer’s G-function. According to Lemma 2.1 of Alimohammadi and Alamatsaz (2011), the following recursive relation is satisfied by the $\xi _{r}$ function:

$$\begin{aligned} \xi _{1}(x)=1,~ \xi _{r}(x)=\int _0^x \! \xi _{r-1}(t)(1-t)^{m_{r-1}}dt,~0\le x \le 1,~r=2,\ldots ,n. \end{aligned}$$

(3)

Now, let ${\widetilde{m}}^\prime _{n'}=(m'_1,\ldots ,m'_{n'-1})$ and ${\check{\xi }}_r$ be as defined in (3) with parameter $m'_{i}$.

   Then, we have the following result for the HR ordering in the one-sample case.

Theorem 2.4

Let ${X_{(r,n,{\widetilde{m}}_n,k)}}$ be the GOS based on an absolutely continuous cdf F. If $k' \le k$ and $m'_i \le m_j$, for any $i\ge j$, then:

• (i) ${X_{(r,n,{\widetilde{m}}_n,k)}} \le _{hr} {X_{(r+1,n,{\widetilde{m}}'_n,k')}}$, provided $m_i \ge -1$ $\forall i$;

• (ii) ${X_{(r,n,{\widetilde{m}}_n,k)}} \le _{hr} {X_{(r,n-1,{\widetilde{m}}'_{n-1},k')}}$, provided $m_i \ge -1$ $\forall i$;

• (iii) ${X_{(r,n,{\widetilde{m}}_n,k)}} \le _{hr} {X_{(r+1,n+1,{\widetilde{m}}'_{n+1},k')}}$.

Proof

We prove Part (i) while the other two parts can be proved in an analogous manner. From (2), we have

$$\begin{aligned} \bar{F}_{X_{(r,n,{\widetilde{m}}_n,k)}}(x)=c_{r-1}{[\bar{F}{(x)}]^{\gamma _{(r,n,{\widetilde{m}}_n,k)}}}\int _0^1 \! {(1-t)^{\gamma _{(r,n,{\widetilde{m}}_n,k)}-1}}\xi _{r}(t\bar{F}{(x)}+F(x))dt, \end{aligned}$$

and so

$$\begin{aligned} h_{X_{(r,n,{\widetilde{m}}_n,k)}}(x)=h_X(x)\Bigg [\int _0^1 \! {(1-t)^{\gamma _{(r,n,{\widetilde{m}}_n,k)}-1}}\frac{\xi _{r}(t\bar{F}{(x)}+F(x))}{\xi _{r}(F{(x)})}dt\Bigg ]^{-1}. \end{aligned}$$

(4)

From (4), to prove that $h_{X_{(r,n,{\widetilde{m}}_n,k)}}(x)\ge h_{X_{(r+1,n,{\widetilde{m}}'_n,k')}}(x)$, it is sufficient to prove that

$$\begin{aligned}&{(1-t)^{\gamma _{(r,n,{\widetilde{m}}_n,k)}}}\frac{\xi _{r}(t\bar{F}{(x)}+F(x))}{\xi _{r}(F{(x)})} \\&\quad \le {(1-t)^{\gamma _{(r+1,n,{\widetilde{m}}'_n,k')}}}\frac{{\check{\xi }}_{r+1}(t\bar{F}{(x)}+F(x))}{{\check{\xi }}_{r+1}(F{(x)})}, \end{aligned}$$

for any $t\in (0,1)$. First, note that

$$\begin{aligned} {\gamma _{(r,n,{\widetilde{m}}_n,k)}}-{\gamma _{(r+1,n,{\widetilde{m}}'_n,k')}}=(k-k')+\sum _{j=r+1}^{n-1}(m_j-m'_{j})+(m_{r}+1)\ge 0 \end{aligned}$$

(5)

due to the conditions on the parameters. We then show that

$$\begin{aligned} \frac{\xi _{r}(t{\bar{F}}{(x)}+F(x))}{\xi _{r}(F{(x)})} \le \frac{{\check{\xi }}_{r+1}(t\bar{F}{(x)}+F(x))}{{\check{\xi }}_{r+1}(F{(x)})} \end{aligned}$$

(6)

by induction on r. From (3), ${\xi }_{r}(x)$ is continuous and is also increasing in x. Now, the inequality in (6) holds for $r=1$ because

$$\begin{aligned} F{(x)}\le t{\bar{F}}{(x)}+F(x), \end{aligned}$$

(7)

and for $r=1$ we have $1 \le \frac{{\check{\xi }}_{2}(t\bar{F}{(x)}+F(x))}{{\check{\xi }}_{2}(F{(x)})}$. For $r\ge 2$, we consider two cases in each of which we need an inequality similar to the one in (7) to hold.

Case 1: $t \le F(x)$. $\square$

This is because in the integral (10) below, we need $F^{-1}(\frac{F(x)-t}{1-t})$ to be defined or, equivalently, $\frac{F(x)-t}{1-t} \in (0,1)$. Let us assume that

$$\begin{aligned} \frac{\xi _{j}(t{\bar{F}}{(y)}+F(y))}{\xi _{j}(F{(x)})} \le \frac{{\check{\xi }}_{j+1}(t\bar{F}{(y)}+F(y))}{{\check{\xi }}_{j+1}(F{(x)})} \end{aligned}$$

(8)

holds for $j=2,\dots ,r-1$, and for any y such that $x \le y$, we have $F(x)\le t{\bar{F}}{(y)}+F(y)$ (since $F(x)\le F(y) \le t{\bar{F}}{(y)}+F(y)$) as needed. We then have

$$\begin{aligned}&\frac{\xi _{r}(t{\bar{F}}{(y)}+F(y))}{\xi _{r}(F{(x)})} \le \frac{{\check{\xi }}_{r+1}(t\bar{F}{(y)}+F(y))}{{\check{\xi }}_{r+1}(F{(x)})}\nonumber \\&\qquad \iff 1+\frac{\int _{F{(x)}}^{t\bar{F}{(y)}+F(y)} \! \xi _{r-1}(w_1)(1-w_1)^{m_{r-1}}dw_1}{\int _0^{F{(x)}} \! \xi _{r-1}(w_2)(1-w_2)^{m_{r-1}}dw_2}\nonumber \\&\qquad \le 1+\frac{\int _{F{(x)}}^{t{\bar{F}}{(y)}+F(y)} \! {\check{\xi }}_{r}(w_1)(1-w_1)^{m'_{r}}dw_1}{\int _0^{F{(x)}} \! {\check{\xi }}_{r}(w_2)(1-w_2)^{m'_{r}}dw_2}. \end{aligned}$$

(9)

Upon setting $w_1=t{\bar{F}}{(u)}+F(u)$ and $w_2=F{(v)}$ in (9), we get

$$\begin{aligned}&\int _{F^{-1}(\frac{F(x)-t}{1-t})}^{y}\Bigg [ \int _{0}^{x} A_1^{-1}B^{m_{r-1}} f(v)dv\Bigg ]^{-1}f(u)du\nonumber \\&\qquad \le \int _{F^{-1}(\frac{F(x)-t}{1-t})}^{y}\Bigg [\int _{0}^{x} A_2^{-1}B^{m'_{r}} f(v)dv\Bigg ]^{-1}f(u)du, \end{aligned}$$

(10)

where

$$\begin{aligned} A_1= & {} \frac{\xi _{r-1}(t{\bar{F}}{(u)}+F(u))}{\xi _{r-1}(F(v))},\\ A_2= & {} \frac{{\check{\xi }}_{r}(t{\bar{F}}{(u)}+F(u))}{{\check{\xi }}_{r}(F(v))},\\ B= & {} \frac{{\bar{F}}(v)}{{\bar{F}}{(u)(1-t)}}. \end{aligned}$$

As $F^{-1}\left( \frac{F(x)-t}{1-t}\right) \le u$ and $v \le x$, we have $F(v) \le F(x) \le (1-t)F{(u)}+t$ and so $F(v) \le t\bar{F}{(u)}+F(u)$, which is also equivalent to $\frac{{\bar{F}}(v)}{\bar{F}{(u)(1-t)}}\ge 1$. By induction, we get $A_1 \le A_2$ and according to $m'_i \le m_j$, for any $i\ge j$, we have $B^{m_{r-1}} \ge B^{m'_{r}}$. Thus, (8) holds for $j=r$. Therefore, by letting $y \rightarrow x$ in (8), we obtain (6).

Case 2: $F(x)<t$.

This is because in the integral (13) below, we need ${F^{-1}(1-\frac{F(x)-F(z)}{t})}$ to be defined. Let us assume that

$$\begin{aligned} \frac{\xi _{j}(t{\bar{F}}{(y)}+F(z))}{\xi _{j}(F{(x)})} \le \frac{{\check{\xi }}_{j+1}(t\bar{F}{(y)}+F(z))}{{\check{\xi }}_{j+1}(F{(x)})} \end{aligned}$$

(11)

holds for $j=2,\dots ,r-1$, and for any y and z such that $y \le z \le x$, we have $F(x)\le t{\bar{F}}{(y)}+F(z)$ (since $tF(y) \le F(y) \le F(z)$ implies that $0 \le F(z)-tF(y)$ and with $F(x)< t$, we have $F(x)\le t+F(z)-tF(y)$). We then have

$$\begin{aligned}&\frac{\xi _{r}(t{\bar{F}}{(y)}+F(z))}{\xi _{r}(F{(x)})} \le \frac{{\check{\xi }}_{r+1}(t\bar{F}{(y)}+F(z))}{{\check{\xi }}_{r+1}(F{(x)})}\nonumber \\&\qquad \iff 1+\frac{\int _{F{(x)}}^{t\bar{F}{(y)}+F(z)} \! \xi _{r-1}(w_1)(1-w_1)^{m_{r-1}}dw_1}{\int _0^{F{(x)}} \! \xi _{r-1}(w_2)(1-w_2)^{m_{r-1}}dw_2}\nonumber \\&\qquad \le 1+\frac{\int _{F{(x)}}^{t{\bar{F}}{(y)}+F(z)} \! {\check{\xi }}_{r}(w_1)(1-w_1)^{m'_{r}}dw_1}{\int _0^{F{(x)}} \! {\check{\xi }}_{r}(w_2)(1-w_2)^{m'_{r}}dw_2}. \end{aligned}$$

(12)

Now, upon setting $w_1=t{\bar{F}}{(u)}+F(z)$ and $w_2=F{(v)}$ in (12), we get

$$\begin{aligned}&\displaystyle \int _{y}^{F^{-1}(1-\frac{F(x)-F(z)}{t})} \! \Bigg [\int _{0}^x \! C_1^{-1}D^{m_{r-1}} f(v)dv\Bigg ]^{-1}f(u)du\nonumber \\&\displaystyle \qquad \qquad \le \int _{y}^{F^{-1}(1-\frac{F(x)-F(z)}{t})} \! \Bigg [\int _{0}^x \! C_2^{-1}D^{m'_{r}} f(v)dv\Bigg ]^{-1}f(u)du, \end{aligned}$$

(13)

where

$$\begin{aligned} C_1= & {} \frac{\xi _{r-1}(t{\bar{F}}{(u)}+F(z))}{\xi _{r-1}(F(v))},\\ C_2= & {} \frac{{\check{\xi }}_{r}(t{\bar{F}}{(u)}+F(z))}{{\check{\xi }}_{r}(F(v))},\\ D= & {} \frac{{\bar{F}}(v)}{{\bar{F}}{(z)}-t{\bar{F}}{(u)}}. \end{aligned}$$

As $u \le {F^{-1}(1-\frac{F(x)-F(z)}{t})}$ and $v \le x$, we have $F(v) \le F(x) \le t{\bar{F}}{(u)}+F(z)$ and so $F(v) \le t\bar{F}{(u)}+F(z)$, which is also equivalent to $\frac{{\bar{F}}(v)}{\bar{F}{(z)}-t{\bar{F}}{(u)}}\ge 1$. By induction, we get $C_1 \le C_2$ and according to $m'_i \le m_j$, for any $i\ge j$, we have $D^{m_{r-1}} \ge D^{m'_{r}}$. Thus, (11) holds for $j=r$. Finally, by letting $y \rightarrow z \rightarrow x$ in (11), we arrive at (6). The proof thus gets completed. $\square$

Theorem 2.5

Let ${X_{(r,n,{\widetilde{m}}_n,k)}}$ be the GOS based on an absolutely continuous cdf F. If $k' \le k$ and $m'_i \le m_j$, for any $i\ge j$, then:

• (i) ${X_{(r,n,{\widetilde{m}}_n,k)}} \le _{rh} {X_{(r+1,n,{\widetilde{m}}'_n,k')}}$, provided $m_i \ge -1$ $\forall i$;

• (ii) ${X_{(r,n,{\widetilde{m}}_n,k)}} \le _{rh} {X_{(r,n-1,{\widetilde{m}}'_{n-1},k')}}$, provided $m_i \ge -1$ $\forall i$;

• (iii) ${X_{(r,n,{\widetilde{m}}_n,k)}} \le _{rh} {X_{(r+1,n+1,{\widetilde{m}}'_{n+1},k')}}$.

Proof

Once again, we prove Part (i) while the other two parts can be proved in an analogous manner. From (2), we have

$$\begin{aligned} {F}_{X_{(r,n,{\widetilde{m}}_n,k)}}(x)=c_{r-1}F(x)\int _0^1 \! {(1-tF(x))^{\gamma _{(r,n,{\widetilde{m}}_n,k)}-1}}\xi _{r}(tF{(x)})dt, \end{aligned}$$

and so

$$\begin{aligned} \lambda _{X_{(r,n,{\widetilde{m}}_n,k)}}(x)=\lambda _X(x)\Bigg [\int _0^1 \! {\Bigg [\frac{(1-tF(x))}{\bar{F}(x)}\Bigg ]^{\gamma _{(r,n,{\widetilde{m}}_n,k)}-1}}\frac{\xi _{r}(tF(x))}{\xi _{r}(F{(x)})}dt\Bigg ]^{-1}. \end{aligned}$$

(14)

From (14), to prove that $\lambda _{X_{(r,n,{\widetilde{m}}_n,k)}}(x)\le \lambda _{X_{(r+1,n,{\widetilde{m}}'_n,k')}}(x)$, it is sufficient to prove that

$$\begin{aligned} {\Bigg [\frac{(1-tF(x))}{\bar{F}(x)}\Bigg ]^{\gamma _{(r,n,{\widetilde{m}}_n,k)}}}\frac{\xi _{r}(tF(x))}{\xi _{r}(F{(x)})} \ge {\Bigg [\frac{(1-tF(x))}{\bar{F}(x)}\Bigg ]^{\gamma _{(r+1,n,{\widetilde{m}}'_n,k')}}}\frac{{\check{\xi }}_{r+1}(tF(x))}{{\check{\xi }}_{r+1}(F{(x)})}, \end{aligned}$$

for any $t\in (0,1)$. According to (5) and $1 \le \frac{(1-tF(x))}{\bar{F}(x)}$, it is now sufficient to show that

$$\begin{aligned} \frac{\xi _{r}(tF(x))}{\xi _{r}(F{(x)})} \ge \frac{{\check{\xi }}_{r+1}(tF(x))}{{\check{\xi }}_{r+1}(F{(x)})} \end{aligned}$$

(15)

by induction on r. Clearly, (15) holds for $r=1$. For $r\ge 2$, let us assume that

$$\begin{aligned} \frac{\xi _{j}(tF(y))}{\xi _{j}(F{(z)})} \ge \frac{{\check{\xi }}_{j+1}(tF(y))}{{\check{\xi }}_{j+1}(F{(z)})} \end{aligned}$$

holds for $j=2,\dots ,r-1$, and for any y and z such that $y \le x \le z$. Then, the rest of the proof follows along the lines of Theorem 2.4, and is therefore omitted for brevity.

The following corollary is an immediate consequence of Theorems 2.4 and 2.5. $\square$

Corollary 2.6

Let ${X_{(r,n,{\widetilde{m}}_n,k)}}$ and ${X_{(r',n',{\widetilde{m}}'_{n'},k')}}$ be the GOSs based on an absolutely continuous cdf F. If $k' \le k$, $m'_i \le m_j$, for any $1\le j\le i \le \min \{n-1,n'-1\}$, and $m_i \ge -1$ $\forall i$, then ${X_{(r,n,{\widetilde{m}}_n,k)}} \le _{hr[rh]} {X_{(r',n',{\widetilde{m}}'_{n'},k')}}$, provided $r \le r'$ and $n'-r' \le n-r$.

Remark 2.7

• (a) Navarro and Burkschat (2011) obtained Part (i) of Theorem 2.4 for SOS. Then, with a different condition than these authors imposed, Torrado et al. (2012) obtained the same result. If we take $k=k'$ and $m_i=m'_i$ in Part (i) of Theorem 2.4 and the proportional HR model in (1) with $(n-i+1)\alpha _i\ge (n-i)\alpha _{i+1}$ $\forall i$ in the result of Navarro and Burkschat (2011) (or Torrado et al. 2012), then these two results coincide;

• (b) Burkschat and Torrado (2014) obtained Part (i) of Theorem 2.5 for SOS. Once again, as mentioned above, if we consider some conditions in our theorem as well as in their theorem, then these two results coincide;

• (c) Burkschat and Navarro (2018) obtained Corollary 2.6 under different conditions and also by assuming that ${\gamma _{(i,n,{\widetilde{m}}_n,k)}} \ne {\gamma _{(j,n,{\widetilde{m}}_n,k)}}$ and ${\gamma _{(i,n',{\widetilde{m}}'_{n'},k')}} \ne {\gamma _{(j,n',{\widetilde{m}}'_{n'},k')}}$ for all $i \ne j$.

We now shift our focus to the preservation of HR and RHR orderings among GOS from two distributions F and G.

Theorem 2.8

Let ${X_{(r,n,{\widetilde{m}}_n,k)}}$ and ${Y_{(r,n,{\widetilde{m}}_n,k)}}$ be the GOSs based on absolutely continuous cdfs F and G, respectively. Let $\gamma _{(r,n,{\widetilde{m}}_n,k)}\ge 1$ and $m_i \ge 0$ $\forall i$. If $X \le _{rh} Y$, then ${X_{(r,n,{\widetilde{m}}_n,k)}} \le _{rh} {Y_{(r,n,{\widetilde{m}}_n,k)}}$.

Proof

From (14) and noting that $X \le _{rh} Y \iff \lambda _X(x) \le \lambda _Y(x)$, the result gets established if

$$\begin{aligned} {\Bigg [\frac{(1-tF(x))}{\bar{F}(x)}\Bigg ]^{\gamma _{(r,n,{\widetilde{m}}_n,k)}-1}}\frac{\xi _{r}(tF(x))}{\xi _{r}(F{(x)})} \ge \! {\Bigg [\frac{(1-tG(x))}{\bar{G}(x)}\Bigg ]^{\gamma _{(r,n,{\widetilde{m}}_n,k)}-1}}\frac{\xi _{r}(tG(x))}{\xi _{r}(G{(x)})}, \end{aligned}$$

for any $t\in (0,1)$. As the function $(1-tx)/(1-x)$ is increasing in x, $\gamma _{(r,n,{\widetilde{m}}_n,k)}\ge 1$, and that $X \le _{rh} Y \Rightarrow X \le _{st} Y \iff G(x) \le F(x)$, it is sufficient to show that ${\xi _{r}(tx)}/{\xi _{r}(x)}$ is increasing in $x \in (0,1)$, which we shall do by induction on r. It is clearly valid for $r=1$. For $r\ge 2$, let us assume that ${\xi _{j}(tx)}/{\xi _{j}(x)}$ is increasing in x for $j=2,\dots ,r-1$. We then have

$$\begin{aligned} \frac{d}{dx}\left( \frac{\xi _{r}(tx)}{\xi _{r}(x)}\right) \ge 0\iff & {} t\cdot {\xi }_{r-1}(tx)(1-tx)^{m_{r-1}}\cdot \xi _{r}(x) \ge {\xi }_{r-1}(x)(1-x)^{m_{r-1}}\cdot \xi _{r}(tx)\nonumber \\\iff & {} t\cdot \frac{ {\xi }_{r-1}(tx)}{ {\xi }_{r-1}(x)}\left( \frac{1-tx}{1-x}\right) ^{m_{r-1}} \ge \frac{\xi _{r}(tx)}{\xi _{r}(x)}. \end{aligned}$$

(16)

$\square$

Let us define

$$\begin{aligned} \phi (x)=\int _{tx}^{1} \! {\xi }_{r-1}(w)(1-w)^{m_{r-1}}dw~\hbox {and}~ \chi (x)=\int _{x}^{1} \! {\xi }_{r-1}(w)(1-w)^{m_{r-1}}dw. \end{aligned}$$

Then, we have the RHS of (16) to be

$$\begin{aligned} \frac{\xi _{r}(tx)}{\xi _{r}(x)}=\frac{\int _{0}^{1} \! {\xi }_{r-1}(w)(1-w)^{m_{r-1}}dw-\int _{tx}^{1} \! {\xi }_{r-1}(w)(1-w)^{m_{r-1}}dw}{\int _{0}^{1} \! {\xi }_{r-1}(w)(1-w)^{m_{r-1}}dw-\int _{x}^{1} \! {\xi }_{r-1}(w)(1-w)^{m_{r-1}}dw}=\frac{\phi (x)-\phi (0)}{\chi (x)-\chi (0)}. \end{aligned}$$

According to Cauchy Theorem, there exists some $\vartheta \in (0,x)$ such that

$$\begin{aligned} \frac{\phi (x)-\phi (0)}{\chi (x)-\chi (0)}=\frac{\phi '(\vartheta )}{\chi '(\vartheta )}. \end{aligned}$$

Also, we have

$$\begin{aligned} \frac{\phi '(\vartheta )}{\chi '(\vartheta )}=t\cdot \frac{{\xi }_{r-1}(t\vartheta )}{{\xi }_{r-1}(\vartheta )}\left( \frac{1-t\vartheta }{1-\vartheta }\right) ^{m_{r-1}}. \end{aligned}$$

Now, as $\vartheta \le x$ and $[(1-tx)/(1-x)]^{m_{r-1}}$ is increasing in x for $m_i \ge 0$, the RHS of (16) becomes less than or equal to the LHS by induction. $\square$

Theorem 2.9

Let ${X_{(r,n,{\widetilde{m}}_n,k)}}$ and ${Y_{(r,n,{\widetilde{m}}_n,k)}}$ be the GOSs based on absolutely continuous cdfs F and G, respectively. If $X \le _{hr} Y$, then ${X_{(r,n,{\widetilde{m}}_n,k)}} \le _{hr} {Y_{(r,n,{\widetilde{m}}_n,k)}}$.

Proof

From (4) and due to the fact $X \le _{hr} Y \iff h_X(x) \ge h_Y(x)$, the result gets established if

$$\begin{aligned} \frac{\xi _{r}(t{\bar{F}}{(x)}+F(x))}{\xi _{r}(F{(x)})} \le \frac{{\xi }_{r}(t{\bar{G}}{(x)}+G(x))}{{\xi }_{r}(G{(x)})}, \end{aligned}$$

for any $t\in (0,1)$. As $X \le _{hr} Y \Rightarrow X \le _{st} Y \iff G(x) \le F(x)$, it is sufficient to show that ${\xi _{r}(t(1-x)+x)}/{\xi _{r}(x)}$ is decreasing in $x \in (0,1)$, which we shall do by induction on r. According to (3), this ratio is decreasing in x for $r=1$. For $r\ge 2$, let us assume that ${\xi _{j}(t(1-x)+x)}/{\xi _{j}(x)}$ is decreasing in x for $j=2,\dots ,r-1$. We then have

$$\begin{aligned}&\frac{d}{dx}\left( \frac{\xi _{r}(t(1-x)+x)}{\xi _{r}(x)}\right) \le 0\nonumber \\&\quad \iff (1-t)\cdot {\xi }_{r-1}(t(1-x)+x)[(1-t)(1-x)]^{m_{r-1}}\cdot \xi _{r}(x)\nonumber \\&\quad \le {\xi }_{r-1}(x)(1-x)^{m_{r-1}}\cdot \xi _{r}(t(1-x)+x)\nonumber \\&\quad \iff (1-t)^{m_{r-1}+1}\cdot \frac{ {\xi }_{r-1}(t(1-x)+x)}{ {\xi }_{r-1}(x)}\le \frac{\xi _{r}(t(1-x)+x)}{\xi _{r}(x)}. \end{aligned}$$

(17)

First, we observe that

$$\begin{aligned}&{\xi _{r}(t(1-x)+x)}={\xi _{r}(t+x(1-t))}\\&\quad =\int _{0}^{t} \! {\xi }_{r-1}(w)(1-w)^{m_{r-1}}dw+\int _{t}^{1} \! {\xi }_{r-1}(w)(1-w)^{m_{r-1}}dw\\&\quad \quad -\int _{t+x(1-t)}^{1} \! {\xi }_{r-1}(w)(1-w)^{m_{r-1}}dw\\&\quad \ge \int _{t}^{1} \! {\xi }_{r-1}(w)(1-w)^{m_{r-1}}dw-\int _{t+x(1-t)}^{1} \! {\xi }_{r-1}(w)(1-w)^{m_{r-1}}dw. \end{aligned}$$

Thus, instead of proving (17), it is sufficient to show that

$$\begin{aligned}&(1-t)^{m_{r-1}+1}\cdot \frac{ {\xi }_{r-1}(t(1-x)+x)}{ {\xi }_{r-1}(x)}\nonumber \\&\qquad \le \frac{ \int _{t}^{1} \! {\xi }_{r-1}(w)(1-w)^{m_{r-1}}dw-\int _{t+x(1-t)}^{1} \! {\xi }_{r-1}(w)(1-w)^{m_{r-1}}dw}{ \int _{0}^{1} \! {\xi }_{r-1}(w)(1-w)^{m_{r-1}}dw-\int _{x}^{1} \! {\xi }_{r-1}(w)(1-w)^{m_{r-1}}dw}. \end{aligned}$$

(18)

Let us now define $\phi (x)=\int _{t+x(1-t)}^{1} \! {\xi }_{r-1}(w)(1-w)^{m_{r-1}}dw$ and $\chi (x)=\int _{x}^{1} \! {\xi }_{r-1}(w)(1-w)^{m_{r-1}}dw$. Then, the RHS of (18) is equal to $\frac{\phi (x)-\phi (0)}{\chi (x)-\chi (0)}$. Here again, according to Cauchy Theorem, there exists some $\vartheta \in (0,x)$ such that $\frac{\phi (x)-\phi (0)}{\chi (x)-\chi (0)}=\frac{\phi '(\vartheta )}{\chi '(\vartheta )}$. Moreover, we have

$$\begin{aligned} \frac{\phi '(\vartheta )}{\chi '(\vartheta )}=(1-t)^{m_{r-1}+1}\cdot \frac{ {\xi }_{r-1}(t(1-\vartheta )+\vartheta )}{ {\xi }_{r-1}(\vartheta )}. \end{aligned}$$

Now, as $\vartheta \le x$, the required result follows by induction. $\square$

Remark 2.10

Suppose the HR function of GOS is of the form $h_X(x)\cdot \eta (x)$. Then, Cramer and Kamps (2003) showed that $\eta (x)$ is decreasing. Also, Belzunce et al. (2005) and Hu and Zhuang (2005) proved Theorem 2.9 in a different way. But, Theorem 2.9 has been established here in a direct and simpler manner.

By combining Corollary 2.6 with Theorems 2.9 and 2.8, we obtain the following corollary.

Corollary 2.11

Let ${X_{(r,n,{\widetilde{m}}_n,k)}}$ and ${Y_{(r',n',{\widetilde{m}}'_{n'},k')}}$be the GOSs based on absolutely continuous cdfs F and G. Suppose $k' \le k$, $m'_i \le m_j$, for any $1\le j\le i \le \min \{n-1,n'-1\}$, $r \le r'$ and $n'-r' \le n-r$.

• i. If $X \le _{hr} Y$, then ${X_{(r,n,{\widetilde{m}}_n,k)}} \le _{hr} {Y_{(r',n',{\widetilde{m}}'_{n'},k')}}$, provided $m_i \ge -1$ $\forall i$;

• ii. If $X \le _{rh} Y$, then ${X_{(r,n,{\widetilde{m}}_n,k)}} \le _{rh} {Y_{(r',n',{\widetilde{m}}'_{n'},k')}}$, provided $\gamma _{(i,n,{\widetilde{m}}_n,k)}\ge 1$ and $m_i \ge 0$ $\forall i$.

Remark 2.12

• (a) Belzunce et al. (2005) established a result similar to that of Part (i) for the multivariate HR ordering (which is not preserved under marginalization);

• (b) Hu and Zhuang (2005) proved the results in Theorems 2.4 and 2.5, Corollary 2.6 and Part (i) of Corollary 2.11 for the special case when $k=k'$ and $m_i=m'_i$;

• (c) Khaledi (2005) obtained Corollary 2.6 just for the HR ordering and, subsequently, Part (i) of Corollary 2.11 under different conditions on the parameters and using majorization ordering of $\gamma _i$’s. But, since the structure of GOS is based on k and $m_i$, it seems that the comparison of submodels based on k and $m_i$ is more reasonable and practical.

By comparing Theorems 2.9 and 2.8, we see that Theorem 2.9 is valid for any $m_i \in {\mathbb {R}}$, while Theorem 2.8 is valid just for $m_i \ge 0$. Indeed, Theorem 2.8 does not include the model of record values for which $m_i=-1$ $\forall i$. In the following theorem, we give the affirmative result for this model and, also more generally for the model of k-records. We then provide a counterexample to show that Theorem 2.8 is not valid for $m_i<0$ in general. For some related results regarding partial orderings and aging properties of record values, we refer the readers to Kochar (1990), Raqab and Amin (1997), and Ahmadi and Arghami (2001), for example.

Theorem 2.13

Let $X^{*}_{(1,k)},~X^{*}_{(2,k)},\dots$ and $Y^{*}_{(1,k)},~Y^{*}_{(2,k)},\dots$ be k-record values based on the sequence of i.i.d. nonnegative random variables with absolutely continuous cdfs F and G, respectively. Suppose $r=1,2,\dots$ and $k\in {\mathbb {N}}$.

• i. If $X \le _{rh} Y$, then $X^{*}_{(r,k)} \le _{rh} Y^{*}_{(r,k)}$;

• ii. If $X \le _{rh} Y$, then $X^{*}_{(r,k)} \le _{rh} Y^{*}_{(r',k')}$, provided $r\le r'$ and $k' \le k$.

Proof

• (i) The pdf of the r-th upper k-record value is given by

  $$\begin{aligned} f_{X^{*}_{(r,k)}}(x)={k^r \over (r-1)!}{[{\bar{F}}{(x)}]^{k-1}}[-\ln \bar{F}(x)]^{r-1}f(x), \quad x\in {\mathbb {R}}_+; \end{aligned}$$

  see Arnold et al. (1998). So, we have

  $$\begin{aligned} \lambda _{X^{*}_{(r,k)}}(x)=\lambda _X(x)\Bigg [\int _0^1 \! {\Bigg [\frac{(1-tF(x))}{\bar{F}(x)}\Bigg ]^{k-1}}\Bigg [\frac{-\ln (1-tF(x))}{-\ln \bar{F}(x)}\Bigg ]^{r-1}dt\Bigg ]^{-1}. \end{aligned}$$

  We observe that ${\ln (1-tx)}/{\ln (1-x)}$ is increasing in $x \in (0,1)$, for any $t \in (0,1)$. Then, the rest of the proof follows along the same lines as those in the proof of Theorem 2.8.

• (ii) It is obvious from Part (i) and Corollary 2.6. $\square$

Counterexample 2.14

Let us consider the Pareto distributions

$$\begin{aligned} {{F}(x)=\left\{ \begin{array}{ll} 0 &{} , x<1 \\ 1-x^{-2} &{} , x\ge 1 \\ \end{array} \right. },\\ \hbox {and}\, {{G}(x)=\left\{ \begin{array}{ll} 0 &{} , x<1 \\ 1-x^{-1} &{} , x\ge 1 \\ \end{array} \right. }. \end{aligned}$$

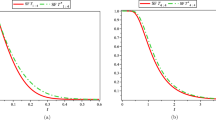
Evidently, G(x)/F(x) is increasing in x, and so $X \le _{rh} Y$. Consider $r=2$, $n=3$, $k=2$ and ${\widetilde{m}}_2=\{-1.5,-2\}$. Then, Fig. 1 shows that $\rho (x)=F_{Y_{(2,3,\{-1.5,-2\},2)}}(x) / F_{X_{(2,3,\{-1.5,-2\},2)}}(x)$ is non-increasing in x, and, therefore, ${X_{(2,3,\{-1.5,-2\},2)}} \nleq _{rh} {Y_{(2,3,\{-1.5,-2\},2)}}$.

Fig. 1

Plot of $\rho (x)$ in Counterexample 2.14

Remark 2.15

Burkschat et al. (2003) introduced a dual model, called dual generalized order statistics (DGOS), through which descendingly ordered random variables can be studied, including reversed ordered order statistics and lower k-record values. It is worth mentioning that the main results of this section hold true for DGOS in the reversed direction.

3 Results for submodels

The HR and RHR are two important measures for studying lifetime random variables in reliability theory and survival analysis. The results established in the last section facilitate the comparison of submodels of GOS among themselves and, also more generally, among different submodels. Due to the equality of $m_i$’s in order statistics and ordinary record values, we present some applications for other useful submodels.

3.1 Sequential systems

It is known that r-out-of-n systems play an important role in reliability theory and life-testing. This system consists of n components that start working simultaneously and it operates if and only if at least r components function. The lifetime of such a system is evidently the $(n-r+1)$-th order statistic in a sample of size n; for elaborate details on order statistics, we refer the readers to Arnold et al. (1992) and David and Nagaraja (2003). In practical applications, components often fail sequentially and the failure of one component may have an impact on the performance of the remaining components. For example, the breakdown of an aircraft’s engine will increase the load on the remaining engines, and consequently their lifetimes would tend to become smaller. For this reason, a more flexible model for a r-out-of-n system should take the dependence structure into consideration. For describing the ordered lifetimes of the components in such a system, SOS can be made use of. This model of ordered data allows the modelling of failure mechanism wherein, upon the failure of some component, the remaining components could have a possibly different underlying lifetime distribution. Thus, if the different lifetime distribution functions are denoted by $F_1$, $F_2$, $\dots$, then this leads to the interpretation that, after the failure of the i-th component, the HR of remaining components will change from $h_i$ to $h_{i+1}$, where $h_i = f_i /(1 - F_i)$. In the literature on SOS, it is usually assumed that there exists some common baseline HR h with $h_i=\alpha _i\cdot h$, $i = 1, 2,\dots$, for positive constants $\alpha _1$, $\alpha _2$, $\dots$ . Without changing the joint distribution in the above manner, the HR remains $\alpha _1\cdot h$ for any component working on its own. Thus, the introduction of unequal parameters $\alpha _i$ is to accommodate load sharing (Cramer and Kamps 1996, 2001). Thus, the results established here enable us to compare the HR and RHR of two sequential systems with different aging structures under the proportional HR model in (1).

Example 3.1

Consider two systems with n and $n'$ components following the SOS model described above with structure parameters $\alpha _i$ and $\alpha '_i$, when the components have two different lifetime distributions F and G, respectively. In this case, $X^{SOS}_{(r,n,{\widetilde{\alpha }})}$ and $Y^{SOS}_{(r',n',{\widetilde{\alpha }}')}$ represent the lifetime of a sequential $(n-r+1)$-out-of-n system and a sequential $(n'-r'+1)$-out-of-$n'$ system, respectively. Suppose $r \le r'$, $n'-r' \le n-r$, $\alpha '_{n'} \le \alpha _n$, $(n'-i+1)\alpha '_i-(n'-i)\alpha '_{i+1}\le (n-j+1)\alpha _j-(n-j)\alpha _{j+1}$, for any $1\le j\le i \le \min \{n-1,n'-1\}$. According to Part (i) of Corollary 2.11, if $X \le _{hr} Y$, then $X^{SOS}_{(r,n,{\widetilde{\alpha }})} \le _{hr} Y^{SOS}_{(r',n',{\widetilde{\alpha }}')}$, provided $(n-i+1)\alpha _i \ge (n-i)\alpha _{i+1}$, for any $1\le i \le n-1$.

Fig. 2

Plots of the HR functions of sequential parallel systems with ${\widetilde{\alpha }}$ (solid) and ${\widetilde{\alpha }}'$ (dashed)

We now compare the HR of some sequential systems for illustrative purpose. Let us consider the Weibull distributions

$$\begin{aligned} {\bar{F}(x)=\left\{ \begin{array}{ll} 1 &{} , x<0 \\ e^{-x^2} &{} , x\ge 0 \\ \end{array} \right. }, {\bar{G}(x)=\left\{ \begin{array}{ll} 1 &{} , x<0 \\ e^{-(\frac{x}{2})^2} &{} , x\ge 0 \\ \end{array} \right. }, \end{aligned}$$

${\widetilde{\alpha }}=\{1,1.3,2\}$ and ${\widetilde{\alpha }}'=\{1,1.25,1.7,1.9\}$. It is then not difficult to see that $X \le _{hr} Y$ and that the above conditions on the parameters are also satisfied. Now, let us consider the following systems:

System 1: a sequential 2-out-of-3 system (i.e., $r=2$ and $n=3$) with parameters ${\widetilde{\alpha }}$ in which the initial components have reliability $\bar{F}$;

System 2: a sequential 2-out-of-4 system (i.e., $r=3$ and $n=4$) with parameters ${\widetilde{\alpha }}'$ in which the initial components have reliability $\bar{F}$;

System 3: a sequential 2-out-of-4 system (i.e., $r=3$ and $n=4$) with parameters ${\widetilde{\alpha }}'$ in which the initial components have reliability $\bar{G}$.

If we denote their HR functions by $h^{SOS}_1$, $h^{SOS}_2$ and $h^{SOS}_3$, respectively, then we have

$$\begin{aligned} h^{SOS}_3(x) \le h^{SOS}_2(x) \le h^{SOS}_1(x), ~\forall x\ge 0. \end{aligned}$$

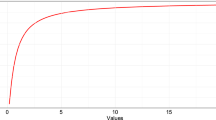
It is worth mentioning that computing the HR functions of such systems is not possible (or at least is quite complicated) in most cases. In the simpler case of two-component systems having the same initial components with standard exponential distribution, we show that if the conditions on the parameters are not satisfied, then the result does not hold. For this purpose, let us consider two sequential parallel systems (i.e., $r=r'=2$ and $n=n'=2$), ${\widetilde{\alpha }}=\{1,3\}$ and ${\widetilde{\alpha }}'=\{1,4\}$. We have

$$\begin{aligned} -2=(n'-1+1)\alpha '_1-(n'-1)\alpha '_{2}\le (n-1+1)\alpha _1-(n-1)\alpha _{2}=-1, \end{aligned}$$

but, $4=\alpha '_{2} \nleq \alpha _2=3$ and $2=(n-1+1)\alpha _1 \ngeq (n-1)\alpha _{2}=3$. Figure 2 shows that the HR function of the system with ${\widetilde{\alpha }}$ is not greater than that of the system with ${\widetilde{\alpha }}'$. Thus, $X^{SOS}_{(2,2,{\widetilde{\alpha }})} \nleq _{hr} X^{SOS}_{(2,2,{\widetilde{\alpha }}')}$.

Note that the case $\alpha _1=\dots =\alpha _n=1$ reduces to ordinary $(n-r+1)$-out-of-n systems. Moreover, we can also compare a sequential system with an ordinary one with the same component structure, i.e., in the case when $r=r'$ and $n=n'$, and with the same lifetime distribution as follows.

Example 3.2

Let $X_{(r,n)}$ represent the lifetime of an ordinary $(n-r+1)$-out-of-n system. If $\alpha _1\le \dots \le \alpha _n \le 1$ ($1\le \alpha _n\le \dots \le \alpha _1$), then $X_{(r,n)} \le _{hr} (\ge _{hr}) X^{SOS}_{(r,n,{\widetilde{\alpha }})}$.

3.2 k-record values

Record values are defined as a model of successive extremes in a sequence of i.i.d. random variables. If not the record values themselves, but second or third largest values are of special interest, then the model of k-record values will be useful, where k is some positive integer. Choosing $m_1=\cdots =m_{n-1}=-1$ and $k \in {\mathbb {N}}$, GOS can be viewed as k-record values (Kamps 1995). The result established in Part (i) of Corollary 2.11 can then be applied to compare the HR of different kand $k'$-record values. Specifically, if $X^{*}_{(r,k)}$ represents the r-th k-record value based on X, then we have $X^{*}_{(r,k)} \le _{hr} X^{*}_{(r,k')}$ for any $r\ge 1$ and $1\le k' <k$.

3.3 Pfeifer’s records

As mentioned above, record values are defined in a sequence of i.i.d. random variables. Pfeifer’s record model is based on non-identically distributed random variables in which the distribution of the underlying random variables changes after each record event. The particular choice of distribution functions $F_i(x) = 1-(1-F (x))^{\beta _i},~ i \in {\mathbb {N}},$ with a cdf F and positive real numbers $\beta _1,\beta _2,\dots$, leads to the model of GOS with parameters $k=\beta _n$ and $m_i=\beta _i-\beta _{i+1}-1$ (Kamps 1995). Then, with the results established in the last section, we can compare the HR and RHR of one or two sequences of Pfeifer’s records with different parameters $\beta _i$ and $\beta '_i$. Also, we can compare Pfeifer’s records with k-record values or with the epoch times of a nonhomogeneous Poisson process (Belzunce et al. 2003).

4 Concluding remarks

In this article, we have discussed increasing convex, mean residual life, hazard rate and reversed hazard rate orderings of ordered random variables. We have strengthened and complemented some previously known results in this regard. According to Theorems 2.8 and 2.13 and Counterexample 2.14, there remains a problem just for $-1< m_i <0$ for the reversed hazard rate ordering in the two-sample case as unsolved. According to our numerous computations, we feel this result also holds, but its resolution is left as an open problem.