1 Introduction

Mixed convection in lid-driven cavity is an important research topic in the field of fluid mechanics due to its significance in several engineering applications and various industrial devices such as heat-exchangers, air-condition refrigerators, lubrication technologies, refrigeration of electronic devices, atmospheric flows, drying technologies, solar energy storage or solar collectors, mixing, coating and drying applications including nuclear reaction systems [1,2,3,4,5]. A new type of medium with high thermal conductivity, called as nanofluid has been considered as the most potential heat transfer fluid in various fields including energy, chemical industry, construction and microelectronics [4]. On the other hand, the displacement of the lid including the doubly driven become an attractive ongoing research topic [5]. Tiwari and Das [6] examined numerically the behavior of nanofluids in a differentially heated lid-driven square cavity. In addition, Hillal and Sameh [7] simulated the steady MHD of mixed convection in a lid-driven cavity filled with nanofluid, where non-uniform heating were imposed at the vertical side walls. The authors concluded that the fluid was slowed down due to the presence of a magnetic field.

A lot of researchers consider steady wall temperature/heat flux; however, these boundary condition are rarely seen in practice. In many applied cases such as solar energy collection and cooling of electronic components, the thermally active walls may be subjected to non-uniform heating due to shading or other effects. Therefore, the study of natural or mixed convection that considers non-uniform heating is crucial. Sarris et al. [8] simulated the natural convection in an air-filled rectangular cavity subjected to sinusoidal temperature at the top wall. Basak et al. [9] performed the numerical study on laminar natural convection in an air-filled square cavity subjected to both non-uniform and uniform heating at the lower wall. Bilgen and Yedder [10] studied the natural convection with sinusoidal temperature profiles at the side walls. In addition, Sathiyamoorthy et al. [11] imposed linear temperature distributions at both side walls of a cavity. Sameh et al. [12] examined the impact of non-uniform heating on both vertical side walls. They studied MHD mixed convection in an inclined lid-driven cavity and concluded that non-uniform heating at both side walls would increase heat transfer rate. Furthermore, Sivasankaran and Pan [13] simulated the mixed convection in the (porous) square lid-driven cavity subjected to unsteady heating at both side walls. On the other hand, Sivasankaran et al. [14] studied the mixed convection in a rectangular enclosure by imposing sinusoidal temperature distribution at both vertical side walls. Moreover, as outlined in [13] and [14], the non-uniform heating at both side walls tend to give higher heat transfer rate. Sivakumar and Sivasankaran [15] simulated the mixed convection in an inclined square cavity with non-uniform temperature distributions at both side walls. They have concluded that heat transfer increases dramatically in the dominant buoyancy mode when the angle of inclination of the cavity increases if both walls have identical heating and cooling zones. Arani et al. [16] studied numerically the mixed convection in a lid-driven cavity filled with nanofluid (Cu–water) subjected to sinusoidal heating at the side walls. They have reported that while maintaining the Reynolds number, the heat transfer rate increases with respect to Richardson number. In another study, Sivasankaran et al. [17] have investigated the effect of magnetic field on the mixed convection in a square lid-driven cavity by imposing sinusoidal temperature profiles at both side walls. Oztop et al. [18] have investigated the natural convections of nanofluids (Al\(_2\)O\(_3\)–water) and, (TiO\(_2\)–water) inside an inclined enclosure by considering sinusoidal temperature profiles. Deng and Chang [19] have investigated analytically the natural convection in a rectangular cavity subjected to sinusoidal temperature distributions at the right and left sidewalls. By varying the phase or amplitude of the sinusoidal function, the heat transfer can indeed be manipulated. Sathiyamoorthy and Chamkha [20] and [21] studied the natural convection in a square cavity with linearly-heated sidewalls. Bhuvaneswari et al. [22] simulated the magneto-convection in a square cavity subjected to sinusoidal boundary temperature distributions at both vertical walls using FVM. Using the Galerkin finite-element method, Basak and Chamkha [23] conducted the heatline experiment on natural convection in a square cavity filled with nanofluids. In contrast, heatline on thermal management with conjugate natural convection in a square cavity was studied by Basak and Chamkha [24]. The vulnerability of heat function boundary conditions was examined by Biswal and Basak [25] on the invariance of Bejan heatlines for natural convection in enclosures with various wall heating. One of the key aims in performing such heat transfer studies is to improve the heat transfer rate inside an enclosure. Dipping nanoparticles, such as copper and alumina into a base fluid like water (hence nanofluid), is among the current development in accomplishing this aim. Hybrid nanofluid, which is consisting of one base fluid and more than one type of nanoparticles, has been used in many practical engineering applications (see Nield and Bejan [26], Vadasz [27], and Vafai [28]). Suresh et al. [29] conducted an experimental analysis using hybrid nanofluid (Al\(_2\)O\(_3\)–Cu–water) for heat transfer augmentation. Their experimental results showed that in the case of hybrid nanofluid, there is a 13.56% increase in Nusselt number relative to the pure fluid at Re =1730. A computational analysis of the time-dependent conjugate convective flow of hybrid nanofluids in semi-circular enclosures was conducted by Chamkha et al. [30]. Alsabery et al. [31] and [33] conducted a study of hybrid nanofluid within enclosure with a wavy wall. While, Rashad et al. [35] simulated the MHD natural convection of hybrid nanofluids in triangular cavity. Beg et al. [37] studied numerically the transient Marangoni thermo-convection flow of an Newtonian fluid in an isotropic Darcy porous rectangular semiconductor melt enclosure with buoyancy and internal heat generation effects. Venkatadri et al. [38] conducted a theoretical and numerical study of natural convection in two-dimensional laminar incompressible flow in a trapezoidal enclosure in the presence of thermal radiation and found that the local Nusselt number and velocity are increasing functions of the Rayleigh number and radiation parameter. Chandanam et al. [39] investigated laminar viscous MHD natural convection flow in a triangular shaped porous enclosure containing two hot obstacles filled with electrically conducting air. Devi et al. [40] examined numerically the buoyancy-driven flow of Casson viscoelastic fluid in a square cavity in the presence of magnetic field and found that the temperature gradient is an increasing function of the buoyancy force. Venkatadri et al. [41] investigated numerically a steady MHD convection flow of a Carreau nanofluid past a vertical plate with radiative heat flux using Buongiorno model and studied the impact of thermophoresis and Brownian motion. Venkatadri et al. [42] studied the effect of magnetic wire position on natural convection of nanofluid in square cavity. While, Venkatadri et al. [43] studied a natural convection of heat transfer in a trapezoidal enclosure at various wall temperatures at four walls with various Prandtl number using a finite-difference method.

While many research works have been conducted on studying natural and mixed convections in air-filled cavities subjected to non-uniformly heating, the convection study involving single and hybrid nanofluid in enclosures is lacking.

2 Mathematical formulation

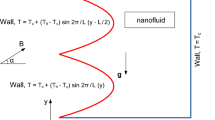
The physical model of the current research is schematically explained in Fig. 1. The problem considered in this work is the lid-driven cavity flow of an incompressible, laminar, viscous fluid with two moving horizontal walls. Both the top and bottom lids move with a uniform velocity in any indicated direction either from left to right or vice versa. Here, two-dimensional mixed convection in a rectangular lid-driven cavity filled with hybrid nanofluid (Al\(_2\)O\(_3\)–Cu–water) is considered by insulating the vertical side walls and imposing sinusoidal temperatures at horizontal walls with length (L) and height (H). The no-slip condition for all solid walls is assumed. It is also assumed that the nanoparticles are in thermal equilibrium with the base fluid. Steady convective flow is a flow in which the velocity and temperature of the fluid do not change with time. With these assumptions, the dimensional governing equations for the mixed convection, namely the continuity, momentum, and energy equations, can be expressed as follows:

$$\begin{aligned} \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y}=0 \end{aligned}$$
(1)
$$\begin{aligned} u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y}= -\frac{1}{\rho _{\text {hnf}}} \frac{\partial p}{\partial x} + \nu _{\text {hnf}} \left( \frac{\partial ^2 u}{\partial x^2} + \frac{\partial ^2 u}{\partial y^2} \right) \end{aligned}$$
(2)
$$\begin{aligned}&u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y}= -\frac{1}{\rho _{\text {hnf}}} \frac{\partial p}{\partial y} \nonumber \\&\quad + \nu _{\text {hnf}} \left( \frac{\partial ^2 v}{\partial x^2} + \frac{\partial ^2 v}{\partial y^2} \right) + \frac{(\rho \beta )_{\text {hnf}}}{\rho _{\text {hnf}}}g(T-T_c) \end{aligned}$$
(3)
$$\begin{aligned} u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y}= \alpha _{hnf} \left( \frac{\partial ^2 T}{\partial x^2} + \frac{\partial ^2 T}{\partial y^2} \right) \end{aligned}$$
(4)

subjected to the boundary conditions [7, 10, 16]

$$\begin{aligned}&\text {top wall: } u \!=\! \pm u_0, v \!=\! 0, T \!=\! T_c \!+\! A_t \sin (2\pi x/L+\gamma )\qquad \end{aligned}$$
(5)
$$\begin{aligned}&\text {bottom wall: } u \!=\! \pm u_0, v\!=\!0, T\!=\!T_c\!+\!A_b \sin (2\pi x/L)\qquad \end{aligned}$$
(6)
$$\begin{aligned}&\text {left and right walls: } u=v=0, \frac{\partial T}{\partial x}=0 \end{aligned}$$
(7)
Fig. 1
figure 1

Physical model of convection in a rectangular cavity together with the coordinate system

Full size image

Here, x and y are the Cartesian coordinates of both horizontal and vertical directions, g refers to the gravitational acceleration, \(\rho _{hnf}\) denotes the density of the hybrid nanofluid, and \(\nu _{hnf}\) refers to the kinematic viscosity of the hybrid nanofluid. The physical properties related to hybrid nanofluid are [31]:

Hybrid nanofluid density \(\rho _{\text {{hnf}}}\) given as

$$\begin{aligned} \rho _{\text {{hnf}}}&=\varphi _{\text {Cu}}\rho _{\text {Cu}} + \varphi _{\hbox {Al} _2 \hbox {O} _3}\rho _{\hbox {Al} _2 \hbox {O} _3} \nonumber \\&\quad + \left( 1- \varphi _{\hbox {Cu}} - \varphi _{\text {Al} _2 \hbox {O} _3} \right) \rho _{f} \end{aligned}$$
(8)

Hybrid nanofluid heat capacitance \(\left( \rho C_p \right) _{\text {{hnf}}}\) given is

$$\begin{aligned} \left( \rho C_p \right) _{\text {{hnf}}}&=\varphi _{\text {Cu}}\left( \rho C_p \right) _{\hbox {Cu}} + \varphi _{\text {Al} _2 \hbox {O} _3}\left( \rho C_p \right) _{\hbox {Al} _2 \hbox {O} _3} \nonumber \\&\quad + \left( 1- \varphi _{\text {Cu}} - \varphi _{\hbox {Al} _2 \hbox {O} _3} \right) \left( \rho C_p \right) _{f} \end{aligned}$$
(9)

Hybrid nanofluid buoyancy coefficient \(\left( \rho \beta \right) _{\text {{hnf}}}\) can be determined by

$$\begin{aligned} \left( \rho \beta \right) _{\text {{hnf}}}&=\varphi _{\text {Cu}}\left( \rho \beta \right) _{\hbox {Cu}} + \varphi _{\text {Al} _2 \hbox {O} _3}\left( \rho \beta \right) _{\hbox {Al} _2 \hbox {O} _3} \nonumber \\&\quad + \left( 1- \varphi _{\text {Cu}} - \varphi _{\hbox {Al} _2 \hbox {O} _3} \right) \left( \rho \beta \right) _{f} \end{aligned}$$
(10)

The dynamic viscosity ratio of nanofluids can be determined as Corcione [32]:

$$\begin{aligned} \frac{\mu _{\text {nf}}}{\mu _f}= \frac{1}{ 1-34.87{\left( {\frac{d_p}{d_f}}\right) ^{-0.3}} \varphi ^{1.03}} \end{aligned}$$
(11)

and the thermal conductivity ratio of nanofluids can be calculated as (Corcione et al. model [32]):

$$\begin{aligned} \frac{k_{\text {nf}}}{k_f}= 1+ 4.4\text {Re}_B^{0.4} \text {Pr}^{0.66}{\left( {\frac{T}{T_f}}\right) ^{10}} {\left( {\frac{k_p}{k_f}}\right) ^{0.03}} \varphi ^{0.66} \nonumber \\ \end{aligned}$$
(12)

Depending on these models, we now devise the dynamic viscosity ratio and the thermal conductivity ratio of (Al\(_2\)O\(_3\)–Cu–water) hybrid nanofluids from the particle sizes of 33 nm and 29 nm [33] in the ambient condition as follows:

$$\begin{aligned} \frac{\mu _{\text {hnf}}}{\mu _f}= \frac{1}{ 1-34.87{\left( {{d_f}}\right) ^{0.3}} \left[ \left( d_{\text {{Cu}}}\right) ^{-0.3} \left( \varphi _{\text {{Cu}}}\right) ^{1.03} + \left( d_{\text {Al}_2\text {O}_3}\right) ^{-0.3} \left( \varphi _{\text {Al}_2\text {O}_3}\right) ^{1.03} \right] } \end{aligned}$$
(13)
$$\begin{aligned} \frac{k_{\text {hnf}}}{k_f}= & {} 1+ 4.4\text {Re}_B^{0.4} \text {Pr}^{0.66}{\left( {\frac{T}{T_f}}\right) ^{10}} {\left( {{k_f}}\right) ^{-0.03}} \nonumber \\&\times \left[ \left( k_{\text {{Cu}}}\right) ^{0.03} \left( \varphi _{\text {{Cu}}}\right) ^{0.66} + \left( k_{\text {Al}_2 \text {O}_3}\right) ^{0.03} \left( \varphi _{\text {Al}_2\text {O}_3}\right) ^{0.66} \right] \nonumber \\ \end{aligned}$$
(14)

where \(\text {Re}_B\) is defined for hybrid nanofluid as

$$\begin{aligned} \text {Re}_B=\frac{\rho _f u_{\text {B}}\left( d_{\text {{Cu}}} + d_{\text {Al}_2\text {O}_3} \right) }{\mu _{f}} \end{aligned}$$
(15)
$$\begin{aligned} \text {u}_B=\frac{2k_{b}T}{\pi \mu _{f}\left( d_{\text {{Cu}}} + d_{\text {Al}_2\text {O}_3} \right) ^2} \end{aligned}$$
(16)

where \(k_b=1.380648 \times 10^{-23}\) (J/K) is the Boltzmann constant, \(l_f\) = 0.17 nm is the mean path of fluid particles, \(d_f\) is the molecular diameter of water as [32]

$$\begin{aligned} d_f=\frac{6M}{N^*\pi \rho _f} \end{aligned}$$
(17)

where M denotes the molecular mass of the working fluid, \(N^*\) is the Avogadro number, and \(\rho _f\) indicates the density of the working fluid at regular temperature (310K).

Now, the non-dimensional variables are presented as follows:

$$\begin{aligned} X&=\frac{x}{L},\quad Y=\frac{y}{L},\quad U= \frac{u}{U_{0}},\quad V=\frac{v}{U_{0}},\nonumber \\ \theta&=\frac{T-T_{c}}{T_{h}-T_{c}} =\frac{T-T_{c}}{\Delta T}, \nonumber \\ \Pr&=\frac{\nu _f}{\alpha _f},\quad P=\frac{pL^2}{\rho _f \alpha _f^2},\quad Ri=\frac{Gr}{Re^2},\nonumber \\ Gr&= \frac{g\beta \left( T_{h}-T_{c}\right) L^{3}}{\nu ^{2}}. \end{aligned}$$
(18)

Then, the non-dimensional governing equations can be written as

$$\begin{aligned} \frac{\partial U}{\partial X} + \frac{\partial V}{\partial Y}=0 \end{aligned}$$
(19)
$$\begin{aligned}&U\frac{\partial U}{\partial X} + V\frac{\partial U}{\partial Y}= \nonumber \\&\quad - \frac{\partial P}{\partial X} + \frac{1}{Re} \frac{\mu _{\text {hnf}}}{\mu _f} \frac{\rho _f}{\rho _{\text {hnf}}} \left( \frac{\partial ^2 U}{\partial X^2} + \frac{\partial ^2 U}{\partial Y^2} \right) \nonumber \\ \end{aligned}$$
(20)
$$\begin{aligned} U\frac{\partial V}{\partial X} + V\frac{\partial V}{\partial Y}= & {} - \frac{\partial P}{\partial Y} + \frac{1}{Re} \frac{\mu _{\text {hnf}}}{\mu _f} \frac{\rho _f}{\rho _{\text {hnf}}} \left( \frac{\partial ^2 V}{\partial X^2} + \frac{\partial ^2 V}{\partial Y^2} \right) \nonumber \\&+ \frac{(\rho \beta )_{\text {hnf}}}{\rho _{\text {hnf}}\beta _f} Ri\theta \nonumber \\ \end{aligned}$$
(21)
$$\begin{aligned} U\frac{\partial \theta }{\partial X} + V\frac{\partial \theta }{\partial Y}= \frac{\alpha _{\text {hnf}}}{\alpha _f}\frac{1}{Pr Re} \left( \frac{\partial ^2 \theta }{\partial X^2} + \frac{\partial ^2 \theta }{\partial Y^2} \right) \end{aligned}$$
(22)

The dimensionless boundary conditions are

Top horizontal wall:

$$\begin{aligned} \text { }&U=\lambda , V=0, \theta =\epsilon \sin (2\pi X +\gamma ) \end{aligned}$$
(23)

Bottom horizontal wall:

$$\begin{aligned} U=\lambda , V=0, \theta = \sin (2\pi X) \end{aligned}$$
(24)

Left and right walls:

$$\begin{aligned} U=V=0, \frac{\partial \theta }{\partial X}=0 \end{aligned}$$
(25)

where \(\lambda =\pm 1\) and \(\epsilon =\frac{A_t}{A_b}\).

Heat transfer in the cavity is characterized by the Nusselt number. The local Nusselt numbers along the lower and upper horizontal walls are defined as

$$\begin{aligned}&Nu_{b-{\text {hnf}}}=-\left( \displaystyle \frac{\partial \theta _w}{\partial Y}\right) _{Y=0}, \end{aligned}$$
(26)
$$\begin{aligned}&Nu_{t-{\text {hnf}}}=-\frac{k_{\text {hnf}}}{k_f}\left( \displaystyle \frac{\partial \theta _{\text {hnf}}}{\partial Y}\right) _{Y=1} \end{aligned}$$
(27)

The fluid in the enclosure gains heat upon heating half of the horizontal wall, which gives (\(Nu > 0\)). However, the fluid loses heat upon cooling half of the horizontal wall, which yields (\(Nu < 0\)). The total heat transfer rate at the cavity wall is the sum of the average Nusselt number together with the heating halves of both horizontal walls, as defined by the following average Nusselt number:

$$\begin{aligned} {\overline{Nu}}_{hnf}&=\frac{k_{\text {hnf}}}{k_f} \left[ \int _{\text {heating half}} Nu_{b-{\text {hnf}}} ~dy \right. \nonumber \\&\quad \left. + \int _{\text {heating half}} Nu_{t-{\text {hnf}}} ~dy \right] \end{aligned}$$
(28)

3 Numerical method

By employing the finite-volume method [34], the governing equations (19)–(22) are numerically solved. The convection–diffusion terms are discretized by the power-law scheme. The pressure and velocity components are coupled using the SIMPLE algorithm. Then, the tri-diagonal matrix algorithm (TDMA) technique is employed to solve iteratively the coupled set of discretized equations. The algorithm is coded using FORTRAN90. The relaxation coefficient of below 0.5 can be used for momentum and energy equations to achieve convergence. The convergence criterion is calculated using the following expression:

$$\begin{aligned} \epsilon =\frac{\sum _{j=1}^m \sum _{i=1}^n\left| \eta _{i,j}^{k+1}-\eta _{i,j}^{k}\right| }{\sum _{j=1}^m\sum _{i=1}^n\left| \eta _{i,j}^{k+1}\right| }\le 10^{-7}, \end{aligned}$$
(29)

where \(\epsilon \) represents the tolerance, m and n denote the number of grid points in the x and y directions, respectively, \(\eta \) denotes any computed field variable, and k refers to the iteration number.

4 Grid-independence test

To check the grid independence of the solution, a numerical experiment is performed with different grid resolutions. The grid independence test is performed using uniform grid in X and Y directions. The grid sizes of 100 \(\times \) 50, 120 \(\times \) 60, 140 \(\times \) 70, 160 \(\times \) 80, 180 \(\times \) 90, and 200 \(\times \) 100 with the following chosen parameters (see Table 1): Re = 100; Ri = 1; L = 2; \(\varphi \) = 0.02; Pr = 6.2 and direction of the moving walls (\(U_{\text {down}} = -1\), \(U_{\text {up}}\) = +1) are considered. Table 1 shows that the grid of 200 \(\times \) 100 is sufficiently accurate for studying the problem considered in the current work. For the purpose of data validation, the present results are compared against those reported by Sarris et al. [8] as shown in Fig. 2. It is found that both results are in good agreement.

Table 1 The average Nusselt number and the number of grids
Full size table
Fig. 2
figure 2

Streamlines (a), Sarris et al. [8] (left), present study (right), isotherms (b), Sarris et al. [8] (left), present study (right) for Ra\(_f=10^5\), \(\varphi =0\) and Pr\(_f=100\)

Full size image
Table 2 Thermo-physical properties of water, Cu, Al\(_2\)O\(_3\) nanoparticles at T = 310 K [35]
Full size table

5 Results and discussion

Numerical simulations are conducted with non-uniform heating at both horizontal walls in a rectangular cavity. The following parameters are considered: Reynolds numbers (Re = 2,10,50,100,200), amplitude ratio (\(\epsilon = \) 0, 0.3, 0.7, 1), phase deviation (\(\gamma =0, \frac{\pi }{4}, \frac{3\pi }{4}, \pi \)), Length (L) and Prandtl number (Pr = 6.2), volume fraction (\(\varphi = 0.02\)) of hybrid nanoparticles (Al\(_2\)O\(_3\)–Cu) and Richardson number (Ri = 1). The thermophysical characteristics of the basic fluid (water) and Al\(_2\)O\(_3\), Cu nanoparticles are shown in Table 2.

Fig. 3
figure 3

Stream function (left) and temperature contours (right) for non-uniformly heated up and down walls at various Reynolds number

Full size image

Figure 3 shows the effect of Reynolds number on the streamlines and isotherms due to the horizontal wall movement (the top wall moves to the right, \(\lambda _t=1\) while, the bottom wall moves to the left, \(\lambda _b=-1\)). At Reynolds number (Re = 2, 10, 50, 100, 200), a single streamline cell rotating in the clockwise direction can be seen. Obviously, the direction is synchronized to the both top and bottom lids movement. The streamlines are distributed along the whole cavity instead of being confined near the top and bottom walls. The special curve form of flow pattern can be observed clearly at the top left and bottom right corners of the cavity at high Reynolds numbers Re \(=100, 200\). This pattern formed due to the constant lids movement and can be expected obviously in Fig. 4 when various directions of the lid-driven are observed.

Fig. 4
figure 4

Stream function (left) and temperature contours (right) for non-uniformly heated up and down walls with effect of direction of the moving walls

Full size image

From streamline plot, it shows that the flow is circulated clockwise. Starting from the sinusoidal heated bottom left wall due to buoyancy effect, that is the low-density hot hybrid nanofluids rise and reach the sinusoidal heated top wall with the effects of phase deviation \(\gamma =\pi /4\) and \(\epsilon =1\). However, due to the constant movement of top lid-driven to the right with the effect of adiabatic wall on the left, the special curve form of flow pattern is formed at the corner of top left of the cavity. Later, the flow moves following the direction of the upper wall until it reaches right adiabatic wall. Here, the effect of cold bottom right wall is much more dominant compared to the heated top right upper wall. With the temperature gradient, the considered cold hybrid nanofluids becomes more high-density and moves downward along the adiabatic right vertical wall and reaches the cold bottom wall. With the effect of movement of bottom lid-driven to the left, the special curve flow pattern is formed at the bottom right corner of the cavity. This circulated motion is repeated and one form of hybrid nanofluids is rotating clockwise in the whole cavity. As Ra increases, the formation of special curve form of flow pattern of streamlines is more visible at the top left and bottom right corners of the cavity. The isotherm contours are formed clearly in the pattern of sinusoidal heating at top and bottom walls at low Reynolds number due to the significant effect of high viscous term. With the increase in Re, isothermal lines become vertical at both vertical walls due to movement of hybrid nanofluids. Isotherm rotation is improved with an increase in Re. It is worth mentioning that an increase in Re increases heat transfer rate.

Figure 4 shows the effect of direction of the moving wall on the streamlines and isotherms at Richardson number (Ri \(=1\)), Reynolds numbers (Re \(= 100\)), \(\epsilon =1\) and \(\gamma =\pi /4\). The combination of various directions of the upper and bottom lids are considered upon four cases. For Case 1, the top wall moves in the positive direction to the right, \(\lambda _t=1\), while the bottom wall moves in the negative direction to the left, \(\lambda _b=-1\). Figure 4a shows that the motion of hybrid nanofluid is characterized by a single primary vortex rotating in a clockwise direction. For Case 2, the top wall moves in the negative direction to the left, while the bottom wall moves in the positive direction to the right. Figure 4b shows that a single primary vortex is rotating counter-clockwise due to the movements of the top and bottom surfaces. Owing to this counter-clockwise rotation, the warmer fluid ascends near the right wall and arrives at the upper wall, while the cold liquid descends near the left wall. Therefore, isothermal lines with higher temperatures are observed near the right wall and isothermal lines with lower temperatures appear near the upper and left walls. The formation of streamlines and isotherm are contradicted to the Case 1. In Fig. 4 (Case 3), the upper and lower walls move in the positive direction to the right. Flow symmetry is observed which is characterized by two primary vortices of identical size. This occurs due to the movement of cavity walls thus leading to clockwise and counter-clockwise rotations (Fig. 4c). Lower fluid layers rotate counter-clockwise while upper fluid layers rotate clockwise.

Two rotations at the boundary have an almost zero velocity. Conduction is the key concept of heat flow, where laminar is the transfer and isothermal lines in this region are nearly horizontal. The warm fluid at the left wall rises and mixes with the top cold fluid. Upon mixing, the fluid descends near the left wall, thus forming a counter-clockwise rotation. Isothermal lines with higher temperatures are hence seen near the left wall. Near the top wall, the reverse process clockwise of the rotation pattern has been observed. The fluid is heated upon mixing with the warmer fluid; therefore, the fluid that rises near the left wall cools down because when it comes in contact with the cold wall, then after the fluid has moved towards the wall right and consequently the rotation has been completed. Therefore, the warmest region is near the top of the left wall. In Fig. 4d, the movement directions of the lower and upper walls are opposite to those in Fig. 4c. Therefore, the bottom-layer rotates in clockwise direction and the top-layer rotates in counter-clockwise direction.

Therefore, it is shown that the movement of the lid plays a significant role, leading to different fluid flow patterns. The fluid velocity at the center of the vortex is faster when the lids are in a different direction. Here, the special curve form of flow pattern can be observed at: Case 1: top left and bottom right; Case 2: top right and bottom left; Case 3: top left and bottom left; while, Case 4: top right and bottom right, of the corners of the cavity.

Fig. 5
figure 5

Stream function (left) and temperature contours (right)for non-uniformly heated up and down walls with effect of phase deviation

Full size image
Fig. 6
figure 6

Stream function (left) and temperature contours (right) for non-uniformly heated up and down walls with effect of amplitude ratio

Full size image
Fig. 7
figure 7

a Variation of average Nusselt number interfaces with Re for different phase deviations \(\gamma \), b variation of average Nusselt number interfaces with Re for different amplitude ratios \(\epsilon \)

Full size image
Fig. 8
figure 8

a Variation of average Nusselt number interfaces with Re for different \(\varphi \), b variation of the of average Nusselt number with \(\varphi \) for different particle types

Full size image
Fig. 9
figure 9

Variation of local Nusselt number interfaces with Y for different amplitude ratios \(\epsilon \) for Cu–Al\(_2\)O\(_3\)–water

Full size image
Fig. 10
figure 10

Variation of local Nusselt number interfaces with Y for different phase deviations \(\gamma \) for Cu–Al\(_2\)O\(_3\)–water

Full size image
Fig. 11
figure 11

Variation of local Nusselt number interfaces with Y for different Reynold numbers Re for Cu–Al\(_2\)O\(_3\)–water

Full size image

Figure 5 shows the streamlines (left) and isotherms (right) for the following parameters: Richardson number (Ri \(=1\)), Reynolds numbers (Re \(= 100\)), volume fraction (\(\varphi =0.02\)) of hybrid nanoparticles (Al\(_2\)O\(_3\)–Cu), phase deviations (\(\gamma =0, \frac{\pi }{4}, \frac{3\pi }{4}, \pi \)) and horizontal wall movement (the upper wall moves to the positive direction, while the lower wall moves to the negative direction). As shown in Fig. 3, for all the phase deviations considered, a single large vortex rotating in a clockwise direction is formed inside the cavity. The flow of the hybrid nanofluid is mainly driven by the shearing effect of the lid motion. As the Richardson number is constant, the variation of phase deviation does not affect the flow pattern significantly. The core region of the cavity is isothermal while the temperature gradient occurs near the horizontal walls with the Richardson number being constant, and the thermal boundary layers condense along the horizontal walls of the cavity. Here, the natural convection is weak, and the forced convection prevails due to the motions of top and bottom lids. Under these conditions, the high thermal conductivity of the hybrid nanofluids has little effect on the thermal field in the cavity. This has been previously observed by Arefanish and Mahmoudi [36]. It is found that the changes in phase deviation affect the velocity of the fluid. When phase deviation values are changed from 0 to \(\pi \), the core region of the cavity is isothermal while the temperature gradient occurs within a region near the horizontal walls with the Richardson number being constant, and the thermal boundary layers condense along the horizontal walls of the cavity. As heating zone is moved upward on increasing, and we conclude that the velocity of fluid is first increased and then decreased.

Figure 6 shows streamlines and isotherms for the following parameters: Richardson number (Ri \(=1\)), Reynolds numbers (Re \(= 100\)), volume fraction (\(\varphi \)=0.02) of hybrid nanoparticles (Al\(_2\)O\(_3\)–Cu), amplitude ratio (\(\epsilon =0, 0.3, 0.7, 1\)) and horizontal wall movement (the upper wall moves to the positive direction, while the lower wall moves to the negative direction). As shown in Fig. 6, for all the amplitude ratios considered, a large vortex rotating in clockwise direction is formed inside the cavity. In addition, the velocity of the fluid is increased on increasing the amplitude ratio.

The impact of varying phase deviation on the average Nusselt number along the horizontal walls at Ri \( =1\) is shown in Fig. 7a. The heat transfer rate rises with increasing Re. By raising Re, convection heat transfer is consistently increased, while the lower and higher phase deviation provides the highest average Nusselt number along the horizontal walls. Increasing the phase deviation to \(\pi \), however, creates a significant improvement in the convection heat transfer. Figure 7b illustrates the effects of varying amplitude ratio on the average Nusselt number along the horizontal walls at Ri \(=1\).When the amplitude ratio is zero, there is a strong enhancement of convective heat transfer

Figure 8a shows the effects of hybrid nanoparticle volume fractions on the average Nusselt number along the horizontal walls at Ri \(=1\). Due to the increased thermal conductivity of the nanoparticles, heat transfer rate increases with respect to nanoparticle volume fraction. As Re increases, the rate of the heat transfer increases as well. Nevertheless, raising the volume of hybrid nanoparticle fractions to 0.04 provides a significant increase in convective heat transfer. The impacts of different nanoparticles on the average Nusselt number are presented in Fig. 8b. Hybrid nanofluid provides higher heat transfer rate due to the higher thermal conductivity of hybrid nanoparticles (Al\(_2\)O\(_3\)–Cu).

Figure 9 shows the effects of amplitude ratio on the local Nusselt numbers at the top and bottom walls at Ri \(=1\). As seen, convective heat transfer is enhanced with increasing amplitude ratio. At the bottom wall, similar to the previous case, increasing the amplitude ratio from 0 to 1 causes the heating domain to move upward and the cooling domain to move downward, which causes the local Nusselt number to take a sinusoidal shape. Higher non-uniform heating (\(\epsilon =1\)) leads to strong enhancement of the local heat transfer rate. At the top horizontal wall, no change occurs for the local heat transfer rate with the absence of the amplitude ratio (\(\epsilon =0\)). However, significant enhancement of local heat transfer occurs with increasing amplitude ratio, and higher amplitude ratios (\(\epsilon =1\)) strongly enhance heat transfer, obtaining the maximum value of the local average Nusselt number.

The impacts of differing phase deviation on the local Nusselt numbers at the top and bottom horizontal walls at Ri \(=1\) are illustrated in Fig. 10. Because of different temperature profiles, the increase in convection heat transfer at the top is greater than that at the bottom horizontal wall. At the bottom wall, as phase deviation increases from 0 to \(\pi \), the heating domain tends to move upward and the cooling domain downward, which causes the local Nusselt number to take a sinusoidal shape. The temperature distribution is significantly enhanced at the top horizontal wall by changing the phase deviation, whereas higher phase deviation (\(\gamma =\pi \)) produces adverse effects on the local heat transfer rate. Thus, increasing \(\gamma \) causes the heating domain to move downward and the cooling domain to move upward.

The results of differing Re on the local Nusselt numbers at the top and bottom horizontal walls at Ri \(=1\) are shown in Fig. 11. The convective heat transfer rates at the bottom and top walls increase with respect to Re.

6 Conclusions

The current numerical study focuses on 2D steady mixed convection in a rectangular cavity filled with hybrid nanofluid subjected to sinusoidal temperature distributions at the top and bottom horizontal walls. The primary objective is to study the impact of parameters such as Reynolds number (Re), amplitude ratio (\(\epsilon \)), phase deviation (\(\gamma \)) and direction of lid motion on the fluid flow and heat transfer characteristics of hybrid nanofluid. The major findings are:

  • The increase in phase deviation greatly impacts the flow behavior and the temperature distribution inside the cavity. This is due to the difference between the sinusoidal temperature variations on the horizontal walls. Overall, as the phase deviation increases, the temperature distribution decreases except for \(\frac{3\pi }{4}\).

  • The convective heat transfer is significantly enhanced upon imposing the sinusoidal temperature profiles at both horizontal walls.

  • Because of the greater thermal conductivity of hybrid nanoparticle, the average Nusselt number increases substantially with respect to the hybrid nanoparticle volume fraction. Convective heat transfer increases with respect to phase deviation as well.

  • At the lower and upper walls, heat transfer rate increases upon increasing the Re value.

  • The velocity of fluid is increased as increasing the Richardson number and amplitude ratio. The non-uniform heating on both walls provides higher heat transfer rate than non-uniform heating of one wall.