1 Introduction

An electrically conducting fluid flow can be employed in industrial problem considering a magnetic field; therefore, Lorentz force can be applied to the fluid, and thus, the flow velocity is reduced. The study by Oreper and Szekely [1] demonstrates that the magnetic field holds back the natural convection and also the noticeable issue which regards the strength of magnetic field as one of the most vital factors for crystal formation. The transient heat transfer in a square cavity is investigated by Mohamad and Viskanta [2] where it is considered that the horizontal walls are adiabatic and the vertical walls possess different constant temperatures. Magnetohydrodynamic (MHD) flow equations are solved analytically by Garandet et al. [3]. The natural convection within rectangular cavity with a transverse magnetic field is studied numerically by Rudraiah and Barron [4] where it is supposed that one side wall is cooled and the other is heated, while the top and bottom walls are insulated. The transient MHD equations are solved by the use of control volume method by Al-Najem et al. [5], Sarris et al. [6], and Kandaswamy et al. [7]. The two-dimensional steady-state MHD flows are solved by Borghi et al. [8, 9], Verardi et al. [10,11,12], and Shadid et al. [13] using finite-difference and finite-element methods (FDM and FEM). Steady-state MHD laminar natural convection flow equations in a rectangular enclosure are solved via numerical procedures for the stream function, vorticity and temperature by Taghikhani [14, 15] and Ece et al. [16, 17].

Nanofluid heat transfer proposed by Rashidi et al. [18] is analyzed in a wavy channel under magnetic field, and so the effects of volume fraction, Reynolds number (Re), Grashof number (Gr) and Hartman number (Ha) on important issues such as heat transfer and fluid flow characteristics are assessed. The obtained results by Rashidi et al. represent that the addition of nanoparticles to the base fluid makes the Nusselt number increase, while the average Poiseuille number decreases in this case. Micropolar-nanofluid Al2O3–water-transient natural convection is considered by Bourantas and Loukopoulos [19] in an inclined rectangular cavity under a magnetic field. Authors show that increasing Rayleigh (Ra) and microrotation numbers makes convection stronger, but a magnetic field significantly suppresses those. Heat transfer and fluid flow are investigated by Heidary et al. [20] in a channel by numerical analysis, while the flow field is under magnetic field. Usage of magnetic field crosswise to fluid velocity and also applying nanoparticles in the fluid are two techniques proposed in the mentioned research to improve heat transfer in a straight duct.

The two-dimensional Fe3O4–water nanomaterial in a half-circular shaped cavity and semi-annulus enclosure, possessing sinusoidal hot wall in the case that an external magnetic field exists, are numerically addressed by Sheikholeslami et al. [21, 22], and numerical explanation is brought by the application of control volume-based finite-element method (CVFEM). It has been found that an increase in magnetic number, Ra, and nanofluid volume fraction results in enhancement of the gradient of temperature, whereas it is reduced by the increase in Lorentz forces. The MHD natural convection of CuO–water nanofluid flow and heat transfer in a circumstance that the cavity is heated from below are proposed by Sheikholeslami et al. [23], so that the governing equations are solved via lattice Boltzmann method. The results have pointed out the direct correlation of heat transfer enhancement with Ha and heat source length, while declare having reverse connection with Ra. MHD mixed convection with volumetric heat generation and an elastic wall is studied by Selimefendigil and Oztop [24] in a CuO–nanofluid-filled lid-driven cavity. The left side wall moves with a constant velocity in +y direction and has cold temperature which is assumed constant, whereas the right side wall of the cavity is kept at hot temperature and the other walls are considered to be insulated. The increase in nanofluid thermal conductivity when solid nanoparticles volume fraction increases results in better heat transfer within the cavity. Selimefendigil and Oztop [25, 26] propose numerical MHD natural and mixed convection flow in the presence of an elastic-sided, partially heated fluid-filled (and nanofluid-filled) triangular enclosure once internal heat generation exists.

The impact of a disposed magnetic field on mixed convection is investigated by Selimefendigil and Oztop [27] where an oscillating nanofluid-filled lid-driven cavity is considered. The cavity bottom wall is hot; the top wall is cold, whereas adiabatic side walls have been assumed for the cavity. The top wall has sinusoidal velocity, but the other walls have no-slip boundary conditions. Their results have indicated that the increase in the magnetic field intensity (Ha greater than 20) results in the suppression of the convection within the cavity. Selimefendigil et al. [28] also numerically studied CuO–water-filled lid-driven enclosure of MHD mixed convection with upper and lower triangular domains. The top wall moves in +x direction possessing constant speed, whereas no-slip boundary conditions are applied to the remained walls. The top wall has cold temperature, which is assumed constant, whereas the bottom wall is kept at hot temperature and the other walls are considered to be adiabatic. MHD free convection in a Cu–water-filled inclined wavy enclosure under an inclined uniform magnetic field has been proposed by Sheremet et al. [29]. The left bottom corner of the cavity is hot; the wavy wall at the top is cold, whereas the other walls of the cavity are assumed adiabatic. The variation of heat transfer rate with nanoparticles volume fraction can be illustrated, and it is shown that changes in the inclination angle of the cavity cause important variations in the fluid flow and heat transfer.

The effects of magnetic field and Joule heating on natural convection and the entropy generation within a sinusoidal heated Fe3O4–water nanofluid-filled lid-driven cavity are studied numerically by Ghaffarpasand [30]. It is demonstrated that increasing both Ha and Eckert number (Ec) leads to a decrease in the averaged Nusselt number (Nuavg) and an increase in the entropy generation. Al2O3–water nanofluid mixed convection flows have been studied, and the effect of inclination angle on the heat transfer is numerically simulated by Hussain et al. [31] in a partially heated double lid-driven inclined cavity. Two heat sources are assumed to be at the cavity bottom wall, while the other parts of the bottom wall is kept insulated. Top wall and the walls that are moving vertically are fixed at cold temperature. Hussain et al. [32] also studied the entropy generation in the same configuration in [31] under the effect of an inclined magnetic field. The transient MHD mixed convection of SWCNT–water and Au–water nanofluids inside a straight grooved channel which possesses two solid cylinders for heat generation is investigated by Job and Gunakala [33]. It has been shown that groove area and groove shape can noticeably affect the fluid flow and temperature. Alternatively, the heat transfer is superior in the case which the Au–water at low Re is studied, but at high Re, the heat transfer will be higher when the SWCNT–water is employed. Forced convection of the combination of FMWNT carbon nanotubes suspended in water in the microchannels under the influence of constant magnetic field is proposed by Karimipour et al. [34]. The slip velocity is assumed for the inlet boundary condition of the channel, while an insulated lower wall is considered and the top wall of the channel has a heat flux which is kept constant.

The mixed convection in Cu–water nanofluid-filled lid-driven cavity, which is influenced by an inclined magnetic field, is examined by Ismael et al. [35]. Slip velocity is assumed to exist along the lid horizontal walls, while the vertical wall at the left side is heated by a constant heat flux source, the right wall is cold and the other walls are thermally insulted. It has been shown that the magnetic field angle can control the convective heat transfer and the magnetic field suppression on Nusselt number (Nu) can be decreased by the increase in the magnetic field angle. Aghaei et al. [36] consider the issue which states how the flow field, entropy generation and also heat transfer in a Cu–water nanofluid-filled trapezoidal enclosure can be affected by the magnetic field. The top wall of the enclosure is kept cold and moves to the right or left direction but the bottom wall is supposed to be hot, and lastly the insulated side walls are considered. The impact of an external oriented magnetic field on the heat transfer and the entropy generation of Cu–water nanofluid flow in a heated from below open cavity is investigated by Mehrez et al. [37], and the finite-volume technique is employed to solve the governing equations. The influence of magnetic field on Fe2O3 and Fe3O4 nanofluids’ thermal conductivity and the boiling heat transfer characteristics of nanofluids are presented by Karimi et al. [38] and Naphon [39], respectively.

Although the nanofluid heat transfer enhancement in a square cavity has been considered in several papers, based on the discussion about the literature and the authors’ best knowledge, the problem that comprises MHD mixed convection in a lid-driven cavity considered to be filled by nanofluid, with two sinusoidal heat sources and also Joule heating, has not been proposed yet. Moreover, no appropriate study exists in the literature in which the stream function–velocity formulation has been applied for numerical simulation of nanofluid-filled cavity. Therefore, in this paper, the effects of magnetic field and Joule heating on the fluid flow and also heat transfer behavior in a Cu–Water nanofluid-filled lid-driven cavity are assessed. The dimensionless equations governing the stream function and also the temperature are solved via a numerical procedure which applies to the enhanced stream function–velocity method for various Reynolds numbers (Re), Hartmann numbers (Ha), Eckert numbers (Ec), magnetic field angle(α) and the solid nanoparticles volume fraction(ϕ) in MATLAB software [40]. To discretize the stream function–velocity formulation, a five-point constant coefficient second-order compact finite-difference approximation is used which keeps away the difficulties existing for the conventional stream function–vorticity and also the primitive variable formulations. Fast Poisson’s equation solver (POICALC) in MATLAB is employed to solve the equation of stream function on a rectangular grid, whereas the temperature equation is solved using the Jacobi bi-conjugate gradient-stabilized (BiCGSTAB) method [41]. The paper is arranged as follows: Section 2 designates the problem geometry and the mathematical formulations. Discretizing procedures regarding the governing equations and the solution method are proposed in Sect. 3. Grid independency check and code validation are provided in Sect. 4. Results and discussion are analyzed comprehensively in Sect. 5. Lastly, conclusion is brought in Sect. 6.

2 Mathematical Formulations

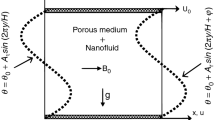
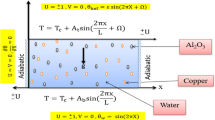
The physical configuration of the problem is shown in Fig. 1. The inclined constant magnetic field with flux density B is applied to the cavity. The left wall of the cavity is heated by two sinusoidal heat sources, and the other walls have a constant temperature T = Tc. The top horizontal wall of the cavity moves with a constant speed in + x direction, while no-slip boundary conditions are imposed on the other walls. The cavity is filled with a Cu–water nanofluid. The thermophysical properties of water and copper at the reference temperature are presented in Table 1. The nanofluid is taken to be Newtonian, incompressible and laminar, and the nanoparticles are assumed to have a uniform shape and size. Moreover, it is assumed that both the fluid phase and the nanoparticles are in thermal equilibrium state and that the slip velocity between the phases is ignored. Therefore, the nanofluid is modeled by a single-phase approach. On the other hand, the buoyancy force in the momentum equation is approximated using the Boussinesq approximation. Thus, the continuity, momentum and the energy equations in scalar forms considering the internal Joule heating effect in a two-dimensional Cartesian coordinate system are written as follows:

$$ \frac{{\partial v_{x} }}{\partial x} + \frac{{\partial v_{y} }}{\partial y} = 0 $$
(1)
$$ - \mu_{nf} \left( {\frac{{\partial^{2} v_{x} }}{{\partial x^{2} }} + \frac{{\partial^{2} v_{x} }}{{\partial y{}^{2}}}} \right) + \rho_{nf} \left( {v_{x} \frac{{\partial v_{x} }}{\partial x} + v_{y} \frac{{\partial v_{x} }}{\partial y}} \right) = - \frac{\partial p}{\partial x} - \sigma_{nf} B_{y} (v_{x} B_{y} - v_{y} B_{x} ) $$
(2)
$$ \begin{aligned} & - \mu_{nf} \left( {\frac{{\partial^{2} v_{y} }}{{\partial x^{2} }} + \frac{{\partial^{2} v_{y} }}{{\partial y^{2} }}} \right) + \rho_{nf} \left( {v_{x} \frac{{\partial v_{y} }}{\partial x} + v_{y} \frac{{\partial v_{y} }}{\partial y}} \right)\\ &\quad = - \frac{\partial p}{\partial y} + (\rho \beta )_{nf} g_{y} (T - T_{c} ) + \sigma_{nf} B_{x} (v_{x} B_{y} - v_{y} B_{x} ) \end{aligned} $$
(3)
$$ - k_{nf} \left( {\frac{{\partial {}^{2}T}}{{\partial x^{2} }} + \frac{{\partial^{2} T}}{{\partial y^{2} }}} \right) + (\rho C_{p} )_{nf} \left( {v_{x} \frac{\partial T}{\partial x} + v_{y} \frac{\partial T}{\partial y}} \right) = \sigma_{nf} (v_{x} B_{y} - v_{y} B_{x} )^{2} $$
(4)

where vx and vy are the velocities in the x and y directions, respectively. Bx and By are the magnetic flux densities in the x and y directions, respectively. p is the pressure, T is the temperature and gy is the gravitational acceleration in the y direction. ρnf, μnf, knf, Cpnf and σnf are the density, the viscosity, the thermal conductivity, the specific heat and the electrical conductivity of the nanofluid, respectively. The terms \( - \sigma_{nf} B_{y} (v_{x} B_{y} - v_{y} B_{x} ) \) and \( + \sigma_{nf} B_{x} (v_{x} B_{y} - v_{y} B_{x} ) \) appearing in Eqs. 2 and 3, respectively, represent the Lorentz force per unit volume in the x and y directions and occur due to the electrical conductivity of the fluid. The term \( \sigma_{nf} (v_{x} B_{y} - v_{y} B_{x} )^{2} \) in Eq. 4 represents the Joule heating. The effective density, specific heat, thermal expansion coefficient and the electrical conductivity of nanofluid are given by the following formulas:

$$ \rho_{nf} = (1 - \phi )\rho_{f} + \phi \rho_{s} $$
(5)
$$ (\rho C_{p} )_{nf} = (1 - \phi )(\rho C_{p} )_{f} + \phi (\rho C_{p} )_{s} $$
(6)
$$ (\rho \beta )_{nf} = (1 - \phi )(\rho \beta )_{f} + \phi (\rho \beta )_{s} - \phi (1 - \phi )(\rho_{s} - \rho_{f} )(\beta_{s} - \beta_{f} ) $$
(7)
$$ \sigma_{nf} = \left( {1 + \frac{{3(\sigma_{s} - \sigma_{f} )\phi }}{{(\sigma_{s} + 2\sigma_{f} ) - (\sigma_{s} - \sigma_{f} )\phi }}} \right)\sigma_{f} $$
(8)

where ϕ is the solid nanoparticles volume fraction and the subscripts f and s denote the base fluid and solid particle, respectively. The effective thermal conductivity of the nanofluid includes the effect of Brownian motion which has a significant effect on the effective thermal conductivity. The effect of enhanced thermal conductivity is modeled as follows [36]:

$$ k_{nf} = k_{static} + k_{\text{Brownian}} $$
(9)
$$ k_{static} = k_{f} + k_{s} \frac{{d_{f} \phi }}{{d_{s} (1 - \phi )}} $$
(10)
$$ k_{\text{Brownian}} = 36\,000k_{s} \frac{{U_{s} d_{s} }}{{k_{f} }}(\rho C_{p} )_{f} \frac{{d_{f} \phi }}{{d_{s} (1 - \phi )}} $$
(11)
$$ U_{s} = \frac{{2k_{b} T}}{{\pi \mu_{f} d_{s}^{2} }} $$
(12)
Fig. 1
figure 1

Geometry and the coordinate system

Full size image
Table 1 Thermophysical properties (Selimefendigil and Oztop [27])
Full size table

Equation 11 is for nanofluids containing spherical nanoparticles with a volume fraction between 1 % and 8 % and the base fluid can be water or ethylene glycol. Us is the Brownian motion velocity. df and ds are the water molecules and copper nanoparticles diameter (df= 2×10−10 and ds= 100 × 10−9). The effective viscosity of the nanofluids is given by Koo and Kleinstreuer [42]:

$$ \mu_{nf} = \mu_{st} + \mu_{\text{Brownian}} = \frac{{\mu_{f} }}{{(1 - \phi )^{2.5} }} + \frac{{k_{\text{Brownian}} }}{{k_{f} }} \times \frac{{\mu_{f} }}{{Pr_{f} }} $$
(13)

The boundary conditions for temperature are as follows:

$$ \left\{ {\begin{array}{*{20}c} {T(0,y) = T_{c} + (T_{h} - T_{c} ){ \sin }\left( {\frac{2\pi y}{L}} \right)} & { 0\le y \le \frac{L}{2}} \\ {T(0,y) = T_{c} + (T_{h} - T_{c} ){ \sin }\left( {\frac{{2\pi \left( {y - \frac{L}{2}} \right)}}{L}} \right)} & {\frac{L}{2} < y \le L} \\ \end{array} } \right. $$
(14)

The continuity, momentum and energy equations are expressed in the non-dimensional form using the following dimensionless parameters:

$$ \begin{aligned} X & = \frac{x}{L},\,Y = \frac{y}{L},\,V_{x} = \frac{{v_{x} }}{{u_{0} }},\,V_{y} = \frac{{v_{y} }}{{u_{0} }},\,P = \frac{p}{{\rho_{f} u_{0}^{2} }},\,\theta = \frac{{T - T_{c} }}{{T_{h} - T_{c} }} = \frac{{T - T_{c} }}{\Delta T}\\ Pr & = \frac{{(\mu C_{p} )_{f} }}{{k_{f} }},\,Gr = \frac{{\rho_{f}^{2} g_{y} \beta_{f} L^{3} \Delta T}}{{\mu_{f}^{2} }}, \\ Re & = \frac{{\rho_{f} u_{0} L}}{{\mu_{f} }},\,Ha = \left| B \right|L\sqrt {\frac{{\sigma_{f} }}{{\mu_{f} }}} ,\,Ec = \frac{{u_{0}^{2} }}{{C_{pf} \Delta T}},\,Ri = \frac{Gr}{{Re^{2} }} \\ \end{aligned} $$
(15)

where the dimensionless numbers Pr, Gr, Re, Ha, Ec and Ri are the Prandtl, Grashof, Reynolds, Hartmann, Eckert and Richardson numbers, respectively. Therefore, the dimensionless form of the governing equations can be expressed as:

$$ \frac{{\partial V_{x} }}{\partial X} + \frac{{\partial V_{y} }}{\partial Y} = 0 $$
(16)
$$ \begin{aligned} & - \frac{1}{Re}\frac{{\mu_{nf} }}{{\mu_{f} }}\left( {\frac{{\partial^{2} V_{x} }}{{\partial X^{2} }} + \frac{{\partial^{2} V_{x} }}{{\partial Y{}^{2}}}} \right) + \frac{{\rho_{nf} }}{{\rho_{f} }}\left( {V_{x} \frac{{\partial V_{x} }}{\partial X} + V_{y} \frac{{\partial V_{x} }}{\partial Y}} \right) \\ &\quad = - \frac{\partial P}{\partial X} - \frac{{\sigma_{nf} }}{{\sigma_{f} }}\frac{{Ha^{2} }}{Re}(V_{x} { \sin }^{2} \alpha - V_{y} { \sin }\alpha { \cos }\alpha ) \end{aligned} $$
(17)
$$ \begin{aligned} & - \frac{1}{Re}\frac{{\mu_{nf} }}{{\mu_{f} }}\left( {\frac{{\partial^{2} V_{y} }}{{\partial X^{2} }} + \frac{{\partial^{2} V_{y} }}{{\partial Y{}^{2}}}} \right) + \frac{{\rho_{nf} }}{{\rho_{f} }}\left( {V_{x} \frac{{\partial V_{y} }}{\partial X} + V_{y} \frac{{\partial V_{y} }}{\partial Y}} \right) \\ &\quad = - \frac{\partial P}{\partial Y} + \frac{{(\rho \beta )_{nf} }}{{(\rho \beta )_{f} }}Ri\theta + \frac{{\sigma_{nf} }}{{\sigma_{f} }}\frac{{Ha^{2} }}{Re}(V_{x} { \cos }\alpha { \sin }\alpha - V_{y} { \cos }^{2} \alpha ) \end{aligned} $$
(18)
$$ \begin{aligned} & - \frac{{k_{nf} }}{{k_{f} }}\left( {\frac{{\partial {}^{2}\theta }}{{\partial X^{2} }} + \frac{{\partial^{2} \theta }}{{\partial Y^{2} }}} \right) + \frac{{(\rho C_{p} )_{nf} }}{{(\rho C_{p} )_{f} }}Re \cdot Pr\left( {V_{x} \frac{\partial \theta }{\partial X} + V_{y} \frac{\partial \theta }{\partial Y}} \right)\\ &\quad = \frac{{\sigma_{nf} }}{{\sigma_{f} }}Ec \cdot Pr \cdot Ha^{2} (V_{x} { \sin }\alpha - V_{y} { \cos }\alpha )^{2}\end{aligned} $$
(19)

The local Nusselt number along the vertical hot wall of the cavity is calculated as

$$ Nu_{y} = - \frac{{k_{nf} }}{{k_{f} }}\left. {\frac{\partial \theta }{\partial X}} \right|_{X = 0} $$
(20)

The averaged Nusselt number is obtained after integrating the local Nusselt number along the hot wall of the cavity as

$$ Nu_{avg} = \int_{0}^{1} {Nu_{y} } dY $$
(21)

3 Solution Method

In this paper, an efficient compact finite-difference approximation (five-point constant coefficient second-order compact (5PCC-SOC) scheme) is used for the stream function formulation of the steady incompressible Navier–Stokes equations, in which the grid values of the stream function and the values of its first derivatives (velocities) are carried as the unknown variables. The stream function is defined as:

$$ V_{x} = \frac{\partial \varPsi }{\partial Y} $$
(22)
$$ V_{y} = - \frac{\partial \varPsi }{\partial X} $$
(23)

Therefore, from Eq. 16 to Eq. 18 we have the following stream function–velocity formulation:

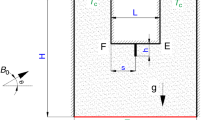
$$ \begin{aligned} & - \frac{1}{Re}\frac{{\mu_{nf} }}{{\mu_{f} }}\left( {\frac{{\partial^{4} \varPsi }}{{\partial X^{4} }} + 2\frac{{\partial^{4} \varPsi }}{{\partial X^{2} \partial Y^{2} }} + \frac{{\partial^{4} \varPsi }}{{\partial Y^{4} }}} \right) \\ &\quad = \frac{{\rho_{nf} }}{{\rho_{f} }}\left[ {V_{x} \left( {\frac{{\partial^{3} \varPsi }}{{\partial X^{3} }} + \frac{{\partial^{3} \varPsi }}{{\partial X\partial Y^{2} }}} \right) + V_{y} \left( {\frac{{\partial^{3} \varPsi }}{{\partial X^{2} \partial Y}} + \frac{{\partial^{3} \varPsi }}{{\partial Y^{3} }}} \right)} \right] + \frac{{(\rho \beta )_{nf} }}{{(\rho \beta )_{f} }}Ri\frac{\partial \theta }{\partial X} \\ & \qquad + \frac{{\sigma_{nf} }}{{\sigma_{f} }}\frac{{Ha^{2} }}{Re}\left[ {\left( {\frac{{\partial V_{x} }}{\partial Y}{ \sin }^{2} \alpha - \frac{{\partial V_{y} }}{\partial X}{ \cos }^{2} \alpha } \right) + \left( {\frac{{\partial V_{x} }}{\partial X} - \frac{{\partial V_{y} }}{\partial Y}} \right){ \cos }\alpha { \sin }\alpha } \right] \\ \end{aligned} $$
(24)

Equations 19 and 24 are solved considering the dimensionless boundary conditions \( \varPsi = 0 \) at all walls, the dimensionless form of Eq. 14 at the left side wall and \( \theta = 0 \) at the other walls. Some standard finite-difference operators at mesh point (xi, yj) (Fig. 2) are given by Tian and Yu [43]:

$$ \delta_{x}^{2} \delta_{y} \varPsi = \frac{{\varPsi_{5} + \varPsi_{6} - \varPsi_{7} - \varPsi_{8} - 2\left( {\varPsi_{2} - \varPsi_{4} } \right)}}{{2h^{3} }} $$
$$ \delta_{x} \delta_{y}^{2} \varPsi = \frac{{\varPsi_{5} - \varPsi_{6} - \varPsi_{7} + \varPsi_{8} - 2\left( {\varPsi_{1} - \varPsi_{3} } \right)}}{{2h^{3} }} $$
$$ \delta_{x}^{2} \varPsi = \frac{{\varPsi_{1} - 2\varPsi_{0} + \varPsi_{3} }}{{h^{2} }} $$
$$ \delta_{y}^{2} \varPsi = \frac{{\varPsi_{2} - 2\varPsi_{0} + \varPsi_{4} }}{{h^{2} }} $$
$$ \delta_{x} \varPsi = \frac{{\varPsi_{1} - \varPsi_{3} }}{2h} $$
$$ \delta_{y} \varPsi = \frac{{\varPsi_{2} - \varPsi_{4} }}{2h} $$
(25)

where subscript 0 refers to the point (xi, yj) in the cavity, while h is the grid spacing. We can obtain the following relations at an interior grid point (xi, yj) for a sufficiently smooth solution Ψ using the Taylor series:

$$ \delta_{x}^{2} \varPsi = \frac{{\partial^{2} \varPsi }}{{\partial X^{2} }} + \frac{{h^{2} }}{12}\frac{{\partial^{4} \varPsi }}{{\partial X^{4} }} + O(h^{4} ) $$
$$ \delta_{x} \varPsi_{x} = \frac{{\partial^{2} \varPsi }}{{\partial X^{2} }} + \frac{{h^{2} }}{6}\frac{{\partial^{4} \varPsi }}{{\partial X^{4} }} + O(h^{4} ) $$
$$ \delta_{y}^{2} \varPsi = \frac{{\partial^{2} \varPsi }}{{\partial Y^{2} }} + \frac{{h^{2} }}{12}\frac{{\partial^{4} \varPsi }}{{\partial Y^{4} }} + O(h^{4} ) $$
$$ \delta_{y} \varPsi_{y} = \frac{{\partial^{2} \varPsi }}{{\partial Y^{2} }} + \frac{{h^{2} }}{6}\frac{{\partial^{4} \varPsi }}{{\partial Y^{4} }} + O(h^{4} ) $$
$$ \frac{{\partial^{4} \varPsi }}{{\partial X^{2} \partial Y^{2} }} = \frac{{\partial^{3} \varPsi_{x} }}{{\partial X\partial Y^{2} }} = \delta_{x} \delta_{y}^{2} \varPsi_{x} + O(h^{2} ) $$
$$ \frac{{\partial^{4} \varPsi }}{{\partial X^{2} \partial Y^{2} }} = \frac{{\partial^{3} \varPsi_{y} }}{{\partial X^{2} \partial Y}} = \delta_{x}^{2} \delta_{y} \varPsi_{y} + O(h^{2} ) $$
(26)
Fig. 2
figure 2

Computational pattern

Full size image

We can obtain from (26):

$$ \frac{{\partial^{4} \varPsi }}{{\partial X^{4} }} = \frac{12}{{h^{2} }}\left( { - \delta_{x}^{2} \varPsi + \delta_{x} \varPsi_{x} } \right) + O(h^{2} ) = \frac{12}{{h^{2} }}\left( { - \delta_{x}^{2} \psi - \delta_{x} V_{y} } \right) + O(h^{2} ) $$
$$ \frac{{\partial^{4} \varPsi }}{{\partial Y^{4} }} = \frac{12}{{h^{2} }}\left( { - \delta_{y}^{2} \varPsi + \delta_{y} \varPsi_{y} } \right) + O(h^{2} ) = \frac{12}{{h^{2} }}\left( { - \delta_{y}^{2} \varPsi + \delta_{y} V_{x} } \right) + O(h^{2} ) $$
$$ \frac{{\partial^{4} \varPsi }}{{\partial X^{2} \partial Y^{2} }} = \frac{1}{2}\left( {\delta_{x} \delta_{y}^{2} \varPsi_{x} + \delta_{x}^{2} \delta_{y} \varPsi_{y} } \right) + O(h^{2} ) = \frac{1}{2}\left( { - \delta_{x} \delta_{y}^{2} V_{y} + \delta_{x}^{2} \delta_{y} V_{x} } \right) + O(h^{2} ) $$
(27)

Substituting Eq. 27 into Eq. 24 and using Eq. 25 and omitting the truncation error, we can obtain the following second-order compact finite-difference formulation:

$$ \begin{aligned} 48\varPsi_{0} - 12\mathop \sum \limits_{k = 1}^{4} \varPsi_{k} & = 6h\left( {V_{y1} - V_{y3} - V_{x2} + V_{x4} } \right) + h^{4} \left( {\delta_{x} \delta_{y}^{2} V_{y} - \delta_{x}^{2} \delta_{y} V_{x} } \right) \\ & \quad + \frac{{\mu_{f} }}{{\mu_{nf} }}\frac{{\rho_{nf} }}{{\rho_{f} }}Reh^{2} \left( {V_{y0} \mathop \sum \limits_{k = 1}^{4} V_{xk} - V_{x0} \mathop \sum \limits_{k = 1}^{4} V_{yk} } \right) \\ & \quad + \frac{{\mu_{f} }}{{\mu_{nf} }}\frac{{(\rho \beta )_{nf} }}{{(\rho \beta )_{f} }}ReRih^{4} \frac{\partial \theta }{\partial X} \\ & \quad + \frac{{\mu_{f} }}{{\mu_{nf} }}\frac{{\sigma_{nf} }}{{\sigma_{f} }}Ha^{2} h^{4} \left[ {(\delta_{y}^{2} \varPsi { \sin }^{2} \alpha + \delta_{x}^{2} \varPsi { \cos }^{2} \alpha ) + (\delta_{x} V_{x} - \delta_{y} V_{y} ){ \cos }\alpha { \sin }\alpha } \right] \\ \end{aligned} $$
(28)

The fourth-order compact approximations for Vx and Vy are given, respectively, by

$$ \frac{1}{6}V_{x2} + \frac{4}{6}V_{x0} + \frac{1}{6}V_{x4} = \frac{{\varPsi_{2} - \varPsi_{4} }}{2h} $$
(29)
$$ \frac{1}{6}V_{y1} + \frac{4}{6}V_{y0} + \frac{1}{6}V_{y3} = \frac{{\varPsi_{3} - \varPsi_{1} }}{2h} $$
(30)

The sequence of the algorithm is provided here:

  1. 1.

    Assuming the value of the velocity and the stream function fields to be zero.

  2. 2.

    Solving the discretized temperature equation, using the Jacobi BiCGSTAB method.

  3. 3.

    Solving the discretized stream function Equation (Eq. 28), using the fast Poisson’s equation solver on a rectangular grid (POICALC function) in MATLAB.

  4. 4.

    Calculating the velocity field from Eqs. 29 and 30, using the stream function field and tri-diagonal matrix solver (tridiag function) in MATLAB.

  5. 5.

    Checking the errors in the temperature and stream function fields. If the errors are below the specified tolerance, exit the loop, otherwise return to step 2. Repeat the whole procedure till a converged solution is obtained. The tolerance of the convergence criterion used for all variables is 10−5:

    $$ \left| {\frac{{\theta^{k + 1} - \theta^{k} }}{{\theta^{k + 1} }}} \right| \le 10^{ - 5} , { }\left| {\frac{{\varPsi^{k + 1} - \varPsi^{k} }}{{\varPsi^{k + 1} }}} \right| \le 10^{ - 5} $$
    (31)

4 Grid Independency Test and Validation

A grid independence test is performed for this study, with Pr = 6.837, Gr = 105, Re = 50, Ha = 50, Ec = 0, ϕ = 0 and α = 0 (angle of flux density B) in order to determine the proper grid size. The following six mesh-grid sizes are considered for the grid independence study. These mesh-grid densities are 40 × 40, 64 × 64, 80 × 80, 100 × 100, 128 × 128 and 144 × 144. The minimum stream function Ψmin of the fluid and the averaged Nusselt number Nuavg on the left hot side wall of the cavity are used as a sensitivity measures of the solution accuracy and are selected as the monitoring variables for the grid independence study. Table 2 shows the dependence of the quantities Ψmin and Nuavg on the grid size. Considering the accuracy of the numerical values, the following calculations are performed with 128 × 128 grid. The numerical code is benchmarked with a differently heated cavity problem filled with a pure fluid, which is maintained at cooled condition, by the right wall. The left wall is hot, whereas the two horizontal walls are under adiabatic conditions. The governing equations are solved on a uniform grid and Pr = 0.71. The solutions are obtained for different values of the Rayleigh number (Ra) and Ha = 0. Comparisons of some relevant flow and heat transfer parameters with the corresponding literature data using different approaches are reported in Table 3. The parameters considered are the maximum value of the horizontal velocity component (Vxmax) on the vertical mid-plane (X = 0.5) and the maximum value of the vertical velocity component (Vymax) on the horizontal mid-plane (Y = 0.5) and Nuavg values on the heated side wall (X = 0). The obtained results of the proposed code show an acceptable agreement with the others.

Table 2 Different mesh-grid densities for Pr = 6.837, Gr = 105, Re = 50, Ha = 50, Ec = 0,ϕ = 0 and α = 0
Full size table
Table 3 Comparison of the present results with those of [44,45,46,47,48] for different Ra
Full size table

Furthermore, the present solver is validated against the existing numerical results from Heidary et al. [20] and Selimefendigil et al. [28]. The comparison of the streamline contours and the isothermal lines obtained from the present code and those of Heidary et al. [20] and Selimefendigil et al. [28] for natural convection through the enclosure under a magnetic field is shown in Fig. 3 for (Ra = 7000 and Ha = 25) and (Ra = 7×105 and Ha = 100). The comparisons confirm an accurate agreement with those of the literature. Figure 3(c) shows structural uniform quadrilateral (square) mesh with grid number 128 × 128 used for the problem solution.

Fig. 3
figure 3

Streamlines and isotherms comparison of the present code with the results obtained by Heidary et al. [20] and Selimefendigil et al. [28]: (a) Ra = 7000 and Ha = 25; (b) Ra = 7×105 and Ha = 100; (c) Structural uniform square mesh with grid number 128 × 128 used for the problem solution

Full size image

When solid nanoparticles volume fraction increases, grid number must be increased (for convergence). On the other hand, when Grashof, Reynolds and Eckert numbers increase, grid number must be increased (above 64 × 64 grid). Hartmann number has little effect on the grid selection (compared to the other dimensionless numbers). For example, Tables 4 and 5 show the effects of the solid nanoparticles volume fraction (ϕ) and Hartmann number (Ha) on different mesh-grid densities and grid selection.

Table 4 Different mesh-grid densities for ϕ = 0.08
Full size table
Table 5 Different mesh-grid densities for Ha = 100
Full size table

5 Results and Discussion

The MHD convection in a Cu–water nanofluid-filled lid-driven cavity with Joule heating and in the presence of an external magnetic field is considered in this study. Parametric numerical simulations are performed in the following range of parameter values: Gr = 105; 0 ≤ Re ≤ 100; 0 ≤ Ha ≤ 100; 0 ≤ Ec ≤ 0.08; 0 ≤ ϕ ≤ 0.08 and 0 ≤ α≤135°. The fluid flow and thermal fields are analyzed through the streamlines and isotherm contours. The heat transfer within the cavity is characterized by the averaged Nusselt number.

5.1 Effect of Reynolds Number

To study the influence of the Reynolds number, it should be mentioned that it is varied between 1 ≤ Re ≤ 100, while α = 0°, Ha = 0, 0 ≤ ϕ≤0.08 and Ec = 0. Figures 4 and 5 show the effect of the Reynolds number on isotherms and the streamline contours. It can be seen from these figures that eddies become small, Ψmax decreases, and one eddy moves toward the center of the cavity by increasing the Reynolds number. As it can be observed from the isotherm plots at low Reynolds numbers (Re = 1), the contours are almost parallel. However, further increase in the Reynolds number enhances the convective cooling, the isotherm contours change significantly and become asymmetric and the dense isotherm zones become localized close to the heat source. For the value of Re = 100, the forced convection is dominant, the isotherms concentration is near to the left side wall, and the rotating vortices become smaller. Figure 5 indicates that the increase in the solid nanoparticles volume fraction to 0.08 increases the values of Ψmax and eddy also shifts toward the center of the cavity. The effect of the Reynolds number on the Nusselt number with different nanoparticles volume fraction is shown in Fig. 6. It is observed that the Nusselt number Nuavg increases by increasing the values of the solid nanoparticles volume fraction. But increasing Re from 50 to 100 plays a little role in enhancement of Nuavg at a constant nanoparticles volume fraction. On the other hand, it can be seen from Fig. 6 that constant variation of the solid nanoparticles volume fraction causes constant variation (increase) of Nuavg values.

Fig. 4
figure 4

Isotherms (left) and streamlines (right) contours at different Reynolds numbers and ϕ = 0

Full size image
Fig. 5
figure 5

Isotherms (left) and streamlines (right) contours at different Reynolds numbers and ϕ = 0.08

Full size image
Fig. 6
figure 6

Variations of Nuavg with Re and ϕ for Ha = 0, Ec = 0 and α = 0

Full size image

5.2 Effect of Hartmann Number

To study the influence of the Hartmann number, the values Ha = 25, 50, 75 and 100 are considered, while Re = 100, Ec = 0, 0 ≤ ϕ≤0.08 and α = 0. Figures 7 and 8 show the effect of the Hartmann number on the isotherms and the streamline contours. It is clear that Lorentz force will be generated perpendicularly to the direction of the applied magnetic field. Accordingly, the streamlines are weakened and a secondary vortex is created close to the center of the cavity by increasing the values of Ha. The isotherms are transmitted from a convection model to a parallel pattern upon increasing Ha due to the magnetic force effect which points out to the suppression of the convection. In addition, Fig. 7 shows that the isotherms start to move away from the top moving wall of the cavity toward the center of the cavity with the increase in the Hartmann number. The existence of the metallic nanoparticles in the base fluid improves the thermal conductivity of the nanofluid, and hence, the thermal buoyancy forces are enhanced. The effects of the Hartmann number and the volume fraction of nanoparticles on Nusselt number are shown in Fig. 9. It can be seen from Fig. 9 that variation of the Nusselt number is nonlinear against Hartmann number. The heat transfer within the cavity is decreased by increasing the values of the Hartmann number and improves conduction heat transfer and so reduces the Nuavg value. On the other hand, it can be seen that the presence of nanoparticles in the base fluid improves the heat transfer of the nanofluid within the cavity compared to the pure fluid and so increases the Nuavg value.

Fig. 7
figure 7

Isotherms (left) and streamlines (right) contours at different Ha, α = 0 and ϕ = 0

Full size image
Fig. 8
figure 8

Isotherms (left) and streamlines (right) contours at different Ha, α = 0 and ϕ = 0.08

Full size image
Fig. 9
figure 9

Variations of Nuavg with Ha for Re = 100, Ec = 0 and α = 0 at different ϕ

Full size image

5.3 Effect of Magnetic Field Orientation

To study the influence of the magnetic field angle, the values α = 45°, 90° and 135° for Ha = 100 are considered, while Re = 100, Ec = 0 and 0 ≤ ϕ ≤ 0.08. Figures 10 and 11 present the isotherms and the streamlines for various values of α. It is shown that for α = 45°, the streamlines are more clustered toward the left and the top walls of the cavity (the same direction of the magnetic field angle) and the isotherms are more clustered toward the top wall of the cavity. When the inclination angle is increased to 90, the main cluster of the streamlines is shifted to the left vertical wall and the isotherms move away from the top wall of the cavity toward the center of the cavity. Finally, for α = 135°, the main cluster of the streamlines moves toward the top wall of the cavity. On the other hand, it can be seen that increasing the magnetic field angle improves a small amount convective heat transfer across the cavity. Impacts of the magnetic field inclination angle and the volume fraction of nanoparticles on Nuavg are shown in Fig. 12. It can be observed from Fig. 12 that variation of the Nusselt number is linear against solid nanoparticles volume fraction. It is also shown that the presence of the solid nanoparticles in the base fluid increases the Nuavg value. When the inclination angle is α = 90°, we have the maximum value of the Nusselt number. On the other hand, it can be indicated that the value of Nuavg increases with α = 0, 135°, 45° and 90°, respectively, at the same volume fraction of nanoparticles.

Fig. 10
figure 10

Isotherms (left) and streamlines (right) contours at different α, Ha = 100 and ϕ = 0

Full size image
Fig. 11
figure 11

Isotherms (left) and streamlines (right) contours at different α, Ha = 100 and ϕ = 0.08

Full size image
Fig. 12
figure 12

Variations of Nuavg with ϕ for Re = 100, Ha = 100 and Ec = 0 at different α

Full size image

5.4 Effect of Eckert Number

To study the influence of the Eckert number, it should be mentioned that it is varied between 0 ≤ Ec ≤ 0.08, while Re = 100, Ha = 50, α = 0 and 0 ≤ ϕ≤0.08. Figures 13 and 14 show the effect of the Eckert number on the isotherms and the streamline contours. It can be observed that the secondary vortices are formed in the vicinity of the center of the cavity. In addition, it can also be seen that the stream function values are enhanced when the Eckert number is increased and the vortices become smaller for a pure fluid compared to a nanofluid. The isotherms start to move away from the left wall to the right wall of the cavity, and the convection is decreased by increasing the values of Ec, and therefore, Joule heating has a negative effect on the convection within the cavity. The effect of the Eckert number on the Nusselt number is shown in Fig. 15. The figure also shows that variation of the Nusselt number is linear against Eckert number. When the solid nanoparticles volume fraction is ϕ = 0.08, we have the maximum value of the Nusselt number. It can be observed that Nuavg decreases with the increase in the Eckert number due to the distortion effect of the Joule heating on the convection heat transfer currents. Furthermore, it can be seen from Fig. 15 that the differences between a pure fluid and a nanofluid are more pronounced when the Eckert number is varied. In fact, Joule heating affects the high thermal conductive solid nanoparticles in a nanofluid more than a pure fluid.

Fig. 13
figure 13

Isotherms (left) and streamlines (right) contours at different Ec, Ha = 50, α = 0 and ϕ = 0

Full size image
Fig. 14
figure 14

Isotherms (left) and streamlines (right) contours at different Ec, Ha = 50, α = 0 and ϕ = 0.08

Full size image
Fig. 15
figure 15

Variations of Nuavg with Ec for Re = 100, Ha = 50 and α = 0 at different ϕ

Full size image

6 Conclusion

This paper presents the effects of Joule heating and MHD natural convection on heat transfer and fluid flow in a Cu–water nanofluid-filled lid-driven cavity with two sinusoidal heat sources. A fast and accurate stream function–velocity method is used to solve the governing equations of the problem. To discretize the stream function–velocity formulation, a five-point constant coefficient second-order compact (5PCC-SOC) finite-difference approximation is used. The stream function equation is solved using a fast Poisson’s equation solver on a rectangular grid (POICALC function in MATLAB), and the temperature equation is solved using the Jacobi bi-conjugate gradient-stabilized (BiCGSTAB) method. The dimensionless governing equations are solved for the following parametric values: Grashof number Gr = 105, Reynolds number 0 ≤ Re ≤ 100, Hartmann number 0 ≤ Ha ≤ 100, Eckert number 0 ≤ Ec ≤ 0.08, magnetic field angle 0 ≤ α ≤ 135°and solid nanoparticles volume fraction in the nanofluid 0 ≤ ϕ ≤ 0.08. The present study leads to the following results:

  1. 1.

    The Nusselt number Nuavg is increased by increasing the values of the nanoparticles volume fraction. But increasing Re from 50 to 100 plays a little role in the enhancement of Nuavg at a constant nanoparticles volume fraction.

  2. 2.

    The heat transfer within the cavity is decreased by increasing the values of the Hartmann number, and this reduces the Nuavg value. On the other hand, it is seen that the presence of nanoparticles in the base fluid improves the heat transfer of the nanofluid within the cavity compared to the pure fluid, and this presence increases the Nuavg value.

  3. 3.

    It is found that Nuavg increases with α = 0, 135°, 45° and 90°, respectively, at the same volume fraction of nanoparticles.

  4. 4.

    The stream function values are enhanced when the Eckert number is increased and the vortices are smaller for a pure fluid compared to a nanofluid. The value of Nuavg is decreased by increasing the values of the Eckert number, and therefore, Joule heating has a negative effect on the convection within the cavity. On the other hand, Joule heating has more effect on a nanofluid with high thermal conductive nanoparticles than on a pure fluid.