1 Introduction

A good recognition gained by the non-Newtonian fluid in the hydraulic machinery helps researchers and engineers to improve the work productivity in various fields such as drive engineering, automotive, construction, agricultural, mining, petrochemical industries, and power plant construction. For instance, the usage of the non-Newtonian lubricant in the bearings maximizes its effectiveness in the process pumps. A few salt arrangements and liquid polymers are non-Newtonian liquids, as are numerous different fluids experienced in science and innovation, for example, dental creams, physiological liquids, cleansers and paints. In a non-Newtonian liquid, the connection between the shear stretch and the shear rate is by and large non-direct and can even be time subordinate. The Carreau model although simple is useful in simulating a number of polymers, Coating hydrodynamics has been an area of considerable interest, since Landau and Levich [1] have published in their pioneering work in 1942, in which an elegant formulation was developed for the thickness of the Newtonian viscous fluid films, which is deposited on a plate withdrawn vertically from a bath at a constant velocity. Lawrence and Zhou [2] have reported in their interesting investigation that the non-Newtonian polymer fluids are encountered in many modern industries, especially in the polymer coating processes. Numerous researchers have investigated the coating dynamics of different geometrical bodies (plates, cones, spheres, cylinders) with non-Newtonian liquids and have employed a range of mathematical constitutive equations. Jenekhe and Schuldt [3] have studied the coating flows of power law and Carreau fluids on spinning disks. Campanella et al. [4] have treated the dip coating of a circular cylinder in non-Newtonian power law fluids. Zevallos et al. [5] have used the finite element for simulating the forward roll coating flows for viscoelastic liquids using both Oldroyd-B and FENE-P models. However, these studies ignored the heat transfer which may be critical in certain coating systems. This remark has been confirmed by Mitsoulis [6] and Mark [7]; they have shown in their research papers that the diffusion of heat can modify the polymer properties significantly.

For portraying the non-Newtonian stream conduct, Navier–Stokes conditions are insufficient. We require some physical models to fill this hole, for example, the Cross and Ellis display, the Carreau show, the Casson demonstrate, and so on. Non-Newtonian liquids are extremely useful in glass blowing, optimal design, paper creation, consistent throwing, and so on. The use of physical states of non-Newtonian liquid streams is directly trying for researchers, mathematicians and physicists, in viable and in addition hypothetical examinations. The explanation for this is these liquids are exceptionally perplexing in nature and there is no specific constitutive condition for speaking to all stream properties of non-Newtonian liquids. In Carreau liquids, the thickness is lessened with rising shear stretch rates. This model has discovered some fame in building reenactments. Hashim and Masood [8] scrutinized the multiple solutions for the Carreau fluid flow over a shrinking cylinder. The influence of the magnetic field on the stagnation-point flow and heat transfer of Carreau fluid over a convectively heated surface has been theoretically reviewed by Khan et al. [9]. By keeping this into view, the researchers of [10,11,12,13,14] analyzed the non-Newtonian fluid flow properties by considering the various flow geometries and different physical effects. Wall slip in thermal polymer processing was considered by Liu and Gehde [15] in which slip was shown to significantly modify temperature distribution in polymers. Hatzikiriakos and Mitsoulis [16] presented closed form solutions and finite element computations for wall slip effects on pressure drop of power law fluids in tapered dies. Many studies of both momentum (hydrodynamic or velocity) slip and thermal slip on transport phenomena have also been reported. Amanulla et al. [17, 18] have used the MATLAB software to compute the influence of momentum and thermal jump convective conditions on two-dimensional viscoelastic boundary layers in nanofluid flows over a sphere. Sparrow et al. [19] presented the first significant analysis of laminar slip-flow heat transfer for tubes with uniform heat flux, observing that momentum slip acts to improve heat transfer whereas thermal slip (or temperature jump) reduces heat transfer.

Among the interesting viscoelastic model in non-Newtonian fluid mechanics we find the Carreau fluid model, which is degenerated to a Newtonian fluid at a very high wall shear stress. This model approximates reasonably well the rheological behavior of a wide range of industrial liquids including biotechnological detergents, physiological suspensions, foams, geological material, cosmetics and syrups. Many researchers have explored a range of industrial and biological flow problems using the Carreau model. Khellaf and Lauriat [20] investigated the Carreau fluid flow and heat transfer between two concentric cylinders. Khan et al. [21] analyzed the MHD non-Newtonian Carreau fluid flow over a convective surface with non-linear radiative heat transfer effects. Raju and Sandeep [22] examined the heat and mass transfer in Falkner–Skan Carreau fluid flow past an isothermal wedge. MHD stagnation-point flow of Carreau fluid over a shrinking sheet is studied theoretically by Akbar et al. [23]. The steady radiative MHD free convection flow of a Carreau fluid from a shrinking sheet with magnetic field, thermal and concentration slip has been investigated by Reddy and Sandeep [24]. Furthermore, this model utilizes time derivatives rather than converted derivatives, which facilitates numerical solutions in boundary value problems.

The previous studies invariably assumed the classical boundary conditions. However, the slip effects have shown to be important in numerous polymeric transport processes including the production stage of polymers from the raw materials. Black [25] has reported that the slip effect on the wall must be taken into account during converting high molecular weight products into specific products. Consequently, many researchers, primarily in chemical engineering, have studied experimentally and numerically the influence of wall slip on polymer dynamics. The important works in this regard include Wang et al. [26] who considered low density polyethylene liquids, Piau et al. [27] who addressed polymer extrudates, Piau and Kissi [28] who quantified macroscopic wall slip in polymer melts, Lim and Schowalter [29] who studied boundary slip in polybutadiene flows and Hatzikiriakos and Kalogerakis [30] who studied molten polymer wall slip. The wall slip in thermal polymer processing was considered by Liu and Gehde [15], in which the slip was shown to significantly modify temperature distribution in polymers. Hatzikiriakos and Mitsoulis [16] have presented closed form solutions and finite element computations for wall slip effects on pressure drop of power law fluids in tapered dies. Many studies of the effects of both the momentum slip (i.e., velocity slip) and the thermal slip on transport phenomena have also been reported. Sparrow et al. [31] have presented the first significant analysis of laminar slip-flow heat transfer for tubes with uniform heat flux. They have observed that the momentum slip acts to improve the heat transfer, whereas the thermal slip (i.e., temperature jump) reduces the heat transfer. Ali and Khan [32] studied exact solution of MHD free convection slip flow and heat transfer over a porous plate in the presence of heat flux. Aziz et al. [33] examined the slip effect on boundary layer flow of power law fluid including heat transfer over a porous flat sheet embedded in a porous medium. Ellahi et al. [34] work on hall and ion slip on MHD peristaltic flow of an elastic viscous fluid from a rectangular duct. Recently, the researchers [35,36,37,38,39,40] discussed the non-Newtonian fluid flow of vertical surfaces with velocity and temperature jump boundary conditions. In these studies, they found very interesting solutions as the momentum slip and thermal slip parameter has tendency to control the skin friction and local Nusselt number profiles and also the non-Newtonian fluids are regulating the temperature profiles of the flow.

All the above studies have focused on the flow over a plane, over a parabolic leading edge parabolic or in many other regions. In this work, we investigate numerically the two-dimensional MHD Carreau fluid flow over a sphere in the presence of velocity and thermal slip effects, using the Keller-Box numerical method. The impact of different parameters on the fluid flow, thermal fields, skin friction and rate of heat transfer is shown graphically. The results are presented in tabular form to discuss the wall friction and the reduced local Nusselt number.

2 Formulation of the problem

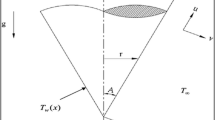
Consider the steady laminar boundary layer flow of two-dimensional incompressible Carreau fluid over an isothermal spherical body of fixed radius \(\, a\), in the presence of a uniform radial magnetic field \({\mathbf{\rm B}}_{{\mathbf{0}}}\). In this investigation, the induced magnetic field, the Hall effect and the viscous and Joule dissipation terms are assumed to be negligible, so that the surface temperature of the sphere \(\, T_{w}\) is taken greater than the ambient temperature of the fluid \(\, T_{\infty }\). (e.g., heated sphere). The physical model considered is illustrated in Fig. 1.

Fig. 1
figure 1

Magnetohydrodynamic non-Newtonian heat transfer from a sphere

Full size image

Following Akbar et al. [10, 23], Molla et al. [41] and Haque et al. [42], the differential equations governing the present problem are given as follows:

$$\nabla \cdot {\mathbf{V}} = 0$$
(1)
$$\rho \left[ {\frac{{\partial {\mathbf{V}}}}{\partial t} + \left( {{\mathbf{V}} \cdot \nabla } \right){\mathbf{V}}} \right] = - \, \nabla P + \nabla \cdot \, {\bar{{\varvec{\tau}}}} + \rho \, {\mathbf{g}} + \sigma \left( {{\mathbf{V}} \times {\mathbf{B}}_{{\mathbf{0}}} } \right) \times {\mathbf{B}}_{{\mathbf{0}}}$$
(2)
$$\rho c \left[ {\frac{\partial T}{\partial t} + \left( {{\mathbf{V}} \cdot \nabla } \right) \, T} \right] = - \nabla \cdot {\mathbf{q}}$$
(3)

Here, V is the velocity vector, \({\bar{\varvec{\tau }}}\) is the extra stress tensor, q is the heat flux vector, where \({\mathbf{V}} = \left( { \, U,V} \right)\) and \({\mathbf{q}} = - k\nabla T\).

In the case where the infinite shear rate viscosity \(\mu_{\infty }\) of this kind of non-Newtonian fluids is neglected \(\left( {\text{i} .e.,\mu_{\infty } \approx 0} \right)\), the extra stress tensor \(\bar{\tau}\) is defined as:

$${\bar{\varvec{\tau }}} = \mu_{0} \,\left( {1 + (\varGamma \dot{\gamma })^{2} } \right)^{{\frac{(n - 1)}{2}}} \left( {{\bar{\mathbf{L}}} + {\bar{\mathbf{L}}}^{T} } \right)$$
(4)

Here \(\mu_{0}\) is the zero shear rate viscosity, \(\varGamma\) is the time constant, \(n\) is the power law index, \(\dot{\gamma }\) is the shear rate and \(\prod\) is the second invariant strain rate tensor \(\left( {\text{i} .e.,\;\prod = \text{trace}\left[ {\left( {{\bar{\mathbf{L}}} + {\bar{\mathbf{L}}}^{\text{T} } } \right)^{2} } \right]} \right)\), where \({\bar{\mathbf{L}}} = \nabla {\text{ V}}\) and \(\dot{\gamma } = \,\sqrt {\frac{1}{2}\prod }\).

We consider in the constitutive Eq. (4) the case for which \(\, \varGamma \dot{\gamma } \ll 1\), so we can write:

$${\bar{\tau}} = \mu_{0} \,\left( {1 + \frac{(n - 1)}{2}(\varGamma \dot{\gamma })^{2} } \right)\left( {{\bar{\text{L}}} + {\bar{\text{L}}}^{{ \, \text{T} }} } \right)$$
(5)

Under the Boussinesq and boundary layer approximations, the simplified steady governing equations are expressed as follows:

$$\frac{\partial (Ur)}{\partial x} + \frac{\partial (Vr)}{\partial y} = 0$$
(6)
$$U\frac{\partial U}{\partial x} + V\frac{\partial U}{\partial y} = g\beta_{{}} (T - T_{\infty } )\sin \left( {\frac{x}{a}} \right) - \frac{{\sigma B_{0}^{2} }}{\rho }U + \nu \frac{{\partial^{2} U}}{{\partial y^{2} }} + \nu \frac{{3(n - 1) \, \varGamma^{2} }}{2}\left( {\frac{\partial U}{\partial y}} \right)^{2} \frac{{\partial^{2} U}}{{\partial y^{2} }}$$
(7)
$$U\frac{\partial T}{\partial x} + V\frac{\partial T}{\partial y}\, = \alpha \frac{{\partial^{2} T}}{{\partial y^{2} }}$$
(8)

Rewriting Eqs. (6)–(8) in terms of the stream function \(\, \psi\) \(\left( {{\text{ i}} . {\text{e}} . , { }Ur = {{\partial (r\psi )} \mathord{\left/ {\vphantom {{\partial (r\psi )} \partial }} \right. \kern-0pt} \partial }y{\text{ and }}Vr = {{ - \, \partial (r\psi )} \mathord{\left/ {\vphantom {{ - \, \partial (r\psi )} \partial }} \right. \kern-0pt} \partial }x} \right)\), \(r = a\sin \left( {{\raise0.7ex\hbox{$x$} \!\mathord{\left/ {\vphantom {x a}}\right.\kern-0pt} \!\lower0.7ex\hbox{$a$}}} \right)\) is the radial distance from the symmetrical axis to the surface of the sphere and the temperature T.

Considering the case of presence of velocity slip and temperature jump conditions at the cylindrical exterior wall, we can write the boundary conditions imposed to the system of Eqs. (8) and (9) as follows:

$$\begin{aligned} & u = N_{0} \frac{\partial u}{\partial y},\,\,v = 0,\, \, \,T = T_{w} + K_{0} \frac{\partial T}{\partial y}\quad {\text{at}}\;y = 0 \\ & & & \quad \quad u \to 0, \, \,v \to 0,\, \, T \to T_{\infty } \quad {\text{as}}\;y \to \infty \\ \end{aligned}$$
(9)

The parameters \(N_{0}\) and \(K_{0}\) used in the boundary conditions (6) represent the thermal jump and momentum slip factors, respectively. For recovering the no-slip case, one can take \(N_{0} = K_{0} = 0\).

In order to write the governing equations and the boundary conditions in dimensionless form, the following non-dimensional quantities are introduced:

$$\,\xi = \frac{x}{a},\;\eta = \frac{y}{a} \, Gr^{1/4} ,\;f(\xi ,\eta )\, = \frac{\psi }{{\nu \, \xi \, Gr^{1/4} }},\;\theta (\xi ,\eta ) = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }}$$
(10)

By applying the non-similar transformations of Eq. (12) on the system of Eqs. (9)–(11), we obtain:

$$\begin{aligned} & f^{\prime\prime\prime}(\eta ) + (1 + \xi \cot \xi )ff^{\prime\prime}(\eta ) + \frac{3(n - 1) \, We}{2}\left( {f^{\prime\prime}(\eta )} \right)^{2} f^{\prime\prime\prime}(\eta ) - \left( {f(\eta )} \right) \\ & \quad + \frac{\sin \left( \xi \right)}{\xi }\theta - Mf(\eta ) = \xi \left( {f^{\prime}(\eta )\frac{{\partial f^{\prime}(\eta )}}{\partial \xi } - f^{\prime\prime}(\eta )\frac{\partial f}{\partial \xi }} \right) \\ \end{aligned}$$
(11)
$$Pr^{ - 1} \theta^{\prime\prime}(\eta ) + (1 + \xi \cot \xi )f\theta^{\prime}(\eta ) = \xi \left( {f^{\prime}(\eta )\frac{\partial \theta }{\partial \xi } - \theta^{\prime}(\eta )\frac{\partial f}{\partial \xi }} \right)$$
(12)
$$\begin{aligned} & f = 0,\,\,\,\,\,f^{\prime}(\eta ) = S_{f} f^{\prime\prime}(\eta ),\,\,\,\,\,\theta = 1 + S_{T} \theta^{\prime}(\eta ){\text{ at }}\eta = 0\,\,\,\,\,\, \\ & \quad \quad f^{\prime} \to 0,\,\,\,\,\,\,\theta \to 0\quad {\text{as}}\;\eta \to \infty \\ \end{aligned}$$
(13)

The skin friction coefficient \(C_{f}\) and the local Nusselt number \(Nu_{x}\) can be found using the following expressions:

$$Gr^{ - 3/4} {\text{ C}}_{f} = \xi \, f^{\prime \prime } (\xi ,0) \, \left( {1 + \frac{(n - 1) \, We}{2} \, f^{\prime \prime 2} (\xi ,0)} \right)$$
(14)
$$Gr^{ - 1/4} \, Nu_{x} = - \theta^{\prime}(\xi ,0)$$
(15)

3 Computational solution with Keller-Box implicit method

The coupled boundary layer equations in a \(\left( {\xi ,\eta } \right)\) coordinate system remain strongly nonlinear. An efficient implicit finite difference method, called the Keller-Box scheme, is therefore used as numerical technic to solve the boundary value problem defined by Eqs. (11) and (12) with the boundary conditions (13). This technique has been described succinctly in Cebeci and Bradshaw [43] and Keller [44]. It has been used recently in polymeric flow dynamics by Amanulla et al. [35,36,37,38, 48] for viscoelastic models and Rao et al. [45,46,47] for non-Newtonian fluids. Very few of these papers, however, have provided guidance for researchers as to customization of the Keller-Box scheme to heat transfer problems. We have included the full details for discretizing the present problem with this procedure, so that the implementation of Keller’s scheme involves the following steps:

  1. (a)

    Reduction of the Nth order corresponding to the system of partial differential equations to a set of N first order equations.

  2. (b)

    Discretization of the obtained first-order equations with finite difference schemes.

  3. (c)

    Quasilinearization of the nonlinear Keller algebraic equations.

  4. (d)

    Solve the system of linear Keller algebraic equations using an efficient block tridiagonal elimination procedure.

Considering the following change of variables:

$$f^{\prime} = u$$
(16)
$$u' = v$$
(17)
$$\theta^{\prime} = t$$
(18)

Equations (11) and (12) can be reduced to the following form:

$$v^{\prime} + (1 + \xi \cot \xi )f_{{}} v + \frac{3(n - 1) \, We}{2}v_{{}} v^{\prime} - u^{2} + \,\frac{\sin \left( \xi \right)}{\xi }s - M_{{}} u = \xi \, \left( {u\frac{\partial u}{\partial \xi } - v\frac{\partial f}{\partial \xi }} \right)$$
(19)
$$Pr^{ - 1}_{{}} t^{\prime} + (1 + \xi \cot \xi )f_{{}} t = \xi \, \left( {u\frac{\partial s}{\partial \xi } - t\frac{\partial f}{\partial \xi }} \right)$$
(20)

Here, the primes denote differentiation with respect to \(\, \eta\) and \(\, \theta = s\).

In terms of the dependent variables, the boundary conditions (13) become:

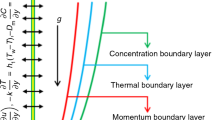
$$\begin{aligned} f = 0 \, ,\;f^{\prime} = S_{f} f^{\prime\prime}(0),\;\theta = 1 + S_{T} \theta^{\prime}(0)\quad {\text{at}}\;\eta = 0 \hfill \\ \quad \quad f^{\prime} \to 0,\;\theta \to 0\;\;\quad {\text{as}}\;\eta \to \infty \hfill \\ \end{aligned}$$
(21)

A two-dimensional computational mesh is imposed on the \(\xi { - }\eta\) plane as shown in Fig. 2. The stepping process is defined by:

Fig. 2
figure 2

Keller-Box element and boundary layer mesh

Full size image
$$\eta_{{^{0} }} = 0 \, ,\,\,\,\,\eta_{{^{j} }} = \eta_{{^{j - 1} }} + h_{j} \, ,\,\,\,\,\,1 \le j \le J \, ,\,\,\,\,\,\,\eta_{J} \equiv \eta_{\infty }$$
(22)
$$\xi^{0} = 0 \, ,\,\,\,\,\,\,\xi^{n} = \xi^{n - 1} + k_{n} \, ,\,\,\,\,\,1 \le n \le N$$
(23)

Here, \(k_{n}\) and \(h_{j}\) denote the step distances in the \(\, \xi\) and \(\, \eta\) directions, respectively.

If \(g_{j}^{n}\) denotes the value of any variable at \(\left( {\eta_{j} ,\xi^{n} } \right)\), then the variable and derivative terms appeared in Eqs. (19) and (20) at \(\left( {\eta_{j - 1/2} ,\xi^{n - 1/2} } \right)\) are replaced by:

$$g_{j - 1/2}^{n - 1/2} = \frac{1}{4}\left( {g_{j}^{n} + g_{j - 1}^{n} + g_{j}^{n - 1} + g_{j - 1}^{n - 1} } \right)$$
(24)
$$\left( {\frac{\partial g}{\partial \eta }} \right)_{j - 1/2}^{n - 1/2} = \frac{1}{{2h_{j} }}\left( {g_{j}^{n} - g_{j - 1}^{n} + g_{j}^{n - 1} - g_{j - 1}^{n - 1} } \right)$$
(25)
$$\left( {\frac{\partial g}{\partial \xi }} \right)_{j - 1/2}^{n - 1/2} = \frac{1}{{2k^{n} }}\left( {g_{j}^{n} - g_{j - 1}^{n} + g_{j}^{n - 1} - g_{j - 1}^{n - 1} } \right)$$
(26)

The finite difference approximations at the mid-point \(\left( {\eta_{j - 1/2} ,\xi^{n} } \right)\) for the variables \(\, u\), \(v\) and \(t\) are given as:

$$h_{j}^{ - 1} \left( {f_{j}^{n} - f_{j - 1}^{n} } \right) = u_{j - 1/2}^{n}$$
(27)
$$h_{j}^{ - 1} \left( {u_{j}^{n} - u_{j - 1}^{n} } \right) = v_{j - 1/2}^{n}$$
(28)
$$h_{j}^{ - 1} \left( {s_{j}^{n} - s_{j - 1}^{n} } \right) = t_{j - 1/2}^{n}$$
(29)

Hence, the appropriate discretized form of Eqs. (19) and (20) are written as follows:

$$\begin{aligned} & \left( {v_{j} - v_{j - 1} } \right)\,\, + (1 + \alpha + \xi \cot \xi )\,\frac{{h_{j} }}{4}\left( {f_{j} + f_{j - 1} } \right)\left( {v_{j} + v_{j - 1} } \right)\, - \,\frac{{\left( {1 + \alpha } \right)h_{j} }}{4}\left( {u_{j} + u_{j - 1} } \right)^{2} \, + \frac{{3(n - 1)_{{}} We}}{4}\left[ {\left( {v_{j} } \right)^{2} - \left( {v_{j - 1} } \right)^{2} } \right] \\ & \quad + \,\,\frac{{Ah_{j} }}{2}\left( {s_{j} + s_{j - 1} } \right)\, - \,\,\frac{{Mh_{j} }}{2}\left( {u_{j} + u_{j - 1} } \right)\, - \,\,\frac{{\alpha h_{j} }}{2}f_{j - 1/2}^{n - 1} \left( {v_{j} + v_{j - 1} } \right)\, + \,\,\frac{{\alpha h_{j} }}{2}v_{j - 1/2}^{n - 1} \left( {f_{j} + f_{j - 1} } \right)\,\,\, = \,\,\left[ {R_{1} } \right]_{j - 1/2}^{n - 1} \, \\ \end{aligned}$$
(30)
$$\begin{aligned} & Pr^{ - 1} \left( {t_{j} - t_{j - 1} } \right) + \left( {1 + \alpha + \xi \cot \xi } \right)\frac{{h_{j} }}{4}\left[ {\left( {f_{j} + f_{j - 1} } \right)\left( {t_{j} + t_{j - 1} } \right)} \right] - \frac{{\alpha h_{j} }}{4}\left[ {\left( {u_{j} + u_{j - 1} } \right)\left( {s_{j} + s_{j - 1} } \right)} \right] + \frac{{\alpha h_{j} }}{2}s_{j - 1/2}^{n - 1} \left( {u_{j} + u_{j - 1} } \right) \\ & \quad - \frac{{\alpha h_{j} }}{2}u_{j - 1/2}^{n - 1} \left( {s_{j} + s_{j - 1} } \right) - \frac{{\alpha h_{j} }}{2}f_{j - 1/2}^{n - 1} \left( {t_{j} + t_{j - 1} } \right)\, + \,\,\frac{{\alpha h_{j} }}{2}t_{j - 1/2}^{n - 1} \left( {f_{j} + f_{j - 1} } \right)\,\, = \,\,\left[ {R_{2} } \right]_{j - 1/2}^{n - 1} \\ \end{aligned}$$
(31)

Here, the following abbreviations are used:

$$\alpha = \frac{{\xi^{n - 1/2} }}{{k_{n} }}{ , }A = \frac{{\sin \left( {\xi^{n - 1/2} } \right)}}{{\xi^{n - 1/2} }}$$
(32)
$$\begin{aligned} & \frac{{ - \left[ {R_{1} } \right]_{j - 1/2}^{n - 1} }}{{h_{j} }} = \left( {\frac{{v_{j}^{{}} - v_{j - 1}^{{}} }}{{h_{j} }}} \right) + \left( {1 - \alpha + \xi \cot \xi } \right)_{{}} \left( {f_{j - 1/2}^{{}} \, v_{j - 1/2}^{{}} } \right) + \frac{3(n - 1) \, We}{2}\left( {v_{j - 1}^{{}} \, v_{j - 1/2}^{'} } \right) + \left( {1 - \alpha } \right)_{{}} \left( {u_{j - 1/2} } \right)^{2} \\ & \quad + A_{{}} s_{j - 1/2}^{{}} - M_{{}} u_{j - 1/2} \\ \end{aligned}$$
(33)
$$\frac{{ - \left[ {R_{2} } \right]_{j - 1/2}^{n - 1} }}{{h_{j} }} = Pr^{ - 1} \left( {\frac{{t_{j}^{{}} - t_{j - 1}^{{}} }}{{h_{j} }}} \right) + \left( {1 - \alpha + \xi \cot \xi } \right)_{{}} \left( {f_{j - 1/2}^{{}} \, t_{j - 1/2}^{{}} } \right) + \alpha_{{}} \left( {u_{j - 1/2}^{{}} \, s_{j - 1/2}^{{}} } \right)$$
(34)

The system of Eqs. (30) and (31) is solved subject to the following boundary conditions:

$$f_{0}^{n} = u_{0}^{n} = 0 \, ,\, \, \,\theta_{0}^{n} = 1 \, ,\, \, \,\,u_{J}^{n} = 0 \, ,\, \, \,v_{J}^{n} = 0 \, ,\, \, \,\,\theta_{J}^{n} = 0$$
(35)

The emerging nonlinear system of algebraic equations is linearized by means of Newton’s method and then solved by the block elimination procedure. The accuracy of computations is influenced by the number of mesh points in both directions. After experimenting with various grid sizes in the \(\eta\) direction a larger number of mesh points are selected whereas in the \(\xi\) direction significantly less mesh points are utilized. The numerical value of \(\eta_{\hbox{max} }\) has been set at 10, and this defines a sufficiently large value at which the prescribed boundary conditions are satisfied, whereas the limited value \(\xi_{\hbox{max} }\) is set at 3 for this flow domain. Mesh independence is therefore achieved in the present computations. The present problem is solved using the Keller-Box finite difference scheme with the help of software MATLAB.

Assuming that \(\, f_{j - 1}^{n - 1}\), \(u_{j - 1}^{n - 1}\), \(v_{j - 1}^{n - 1}\), \(s_{j - 1}^{n - 1}\) and \(t_{j - 1}^{n - 1}\) are known for \(1 \le j \le J\), the discretized Eqs. (29)–(33) constitute a system of \(5 \, J + 5\) equations, which is composed by the \(5 \, J + 5\) unknowns \(\, f_{j}^{n}\), \(u_{j}^{n}\), \(v_{j}^{n}\), \(s_{j}^{n}\) and \(t_{j}^{n}\),where \(0 \le j \le J\). The resulting nonlinear system of algebraic equations is linearized by means of Newton’s method, and then solved in a very efficient manner by using the Keller-Box method, which has been explained more clearly by Cebeci and Bradshaw [43], taking the initial interaction with a given set of converged solutions at \(\xi = \xi^{n}\). To initiate the process with \(\xi = 0\), we first prescribe a set of guess profiles for the functions \(\, f\), \(u\), \(v\), \(s\) and \(t\) which are unconditionally convergent. These profiles are then employed in the Keller-Box scheme with second-order accuracy to compute the correct solution step by step along the boundary layer. For a given \(\xi\) the iterative procedure is stopped to give the final velocity and temperature distributions when the difference in computing of these functions in the next procedure become less than \(\, 10^{ - 5}\), i.e., \(\left| {\delta f^{i} } \right| \le 10^{ - 5}\), where the superscript \(\, i\) denotes the number of iterations. For laminar flows, the rate of convergence of the solutions for Eqs. (29)–(33) is quadratic provided the initial estimate to the desired solution is reasonably close to the final solution. Calculations are performed with four different \(\Delta \eta\) spacing showing that the rate of convergence of the solutions is quadratic in all cases for these initial profiles with typical iterations. The fact that Newton’s method is used to linearize the nonlinear algebraic equations and that with proper initial guess \(\xi^{n}\) usually obtained from a solution at \(\, \xi^{n - 1}\), the rate of convergence of the solutions should be quadratic, it can be used to test the code for possible programming errors and to aid in the choice of the spacing \(\Delta \xi\) in the downstream direction. To study the effect of the spacing \(\Delta \xi \,\) on the rate of convergence of solutions, calculations were performed in the range \(0 \le \xi \le 0.4 \,\) with uniform spacing \(\, \Delta \xi\) corresponding to 0.08, 0.04, 0.02 and 0.01. Except for the results obtained with \(\Delta \xi = 0.08\), the rate of convergence of the solutions was essentially quadratic at each \(\xi\) station. In most laminar boundary layer flows, a step size from 0.02 to 0.04 is sufficient to provide accurate and comparable results. In fact in the present problem, we can even go up to \(\Delta \xi = 0.1\) and still get accurate and comparable results. This particular value of \(\Delta \xi = 0.1\) has also been used successfully by Molla et al. [41]. A uniform grid across the boundary is quite satisfactory for most laminar flow calculations, especially in laminar boundary layer. However, the Keller-Box method is unique in which various spacing in both \(\eta\) and \(\xi\) directions can be used.

4 Numerical results and interpretation

In order to verify the accuracy of the Keller-box method solutions, computations are benchmarked with earlier results reported by Molla et al. [41] and Haque et al. [42], via the values of the skin friction and heat transfer coefficients \(C_{f} \,\) and \(Nu_{x}\) of a Newtonian fluid \(\, \left( {{\text{i}} . {\text{e}} . ,\;We = 0} \right)\), respectively, for various values of the parameter \(\, \xi\), in the case where \(Pr\, = 1,S_{f} = 0,S_{T} = 0\,{\text{and}}\,M = 0\).

The results of this comparison are summarized in Table 1. Very close correlation is achieved between the Keller-Box computational results and the solutions of Molla et al. [41] and Haque et al. [42]. Hence, the Keller-Box numerical code used in this investigation leads to quite accurate numerical results. In order to give the truthfulness and reliability to the numerical method used in this investigation, we present in Tables 2, 3, 4 and 5 the numerical values of the quantities \(\, f^{\prime\prime}(\xi ,0)\) and \(\, - \theta^{'} (\xi ,0)\), which are obtained after many computational tests, for various values of the parameters \(\, S_{f} \,\), \(\, S_{T} \,\), \(\xi\), \(\, We\,\), \(\, M\,\) and \(Pr\).

Table 1 Comparison of \(Nu\,\) with the existing works of Molla et al. [32] and Haque et al. [33], in the case where \(Pr\, = 0.7\) and \(We = S_{f} = S_{T} = \,M = 0\)
Full size table
Table 2 Impact of \(\, S_{f}\), \(S_{T}\) and \(\xi\) on \(\, f^{\prime\prime}(\xi ,0)\), in the case where \(Pr\, = 7\), \(We = 0.3\) and \(\, M = 1\)
Full size table
Table 3 Impact of \(\, S_{f}\), \(S_{T}\) and \(\xi\) on \(\, - \theta^{\prime}(\xi ,0)\), in the case where \(Pr\, = 7\), \(We = 0.3\) and \(M = 1\)
Full size table
Table 4 Impact of \(\, We\), \(M\) and \(Pr\) on \(\, f^{\prime\prime}(\xi ,0)\), in the case where \(S_{f} = 0.5\), \(S_{T} = \,1\) and \(\xi = 1\)
Full size table
Table 5 Impact of \(\, We\), \(M\) and \(Pr\) on \(\, - \theta^{\prime}(\xi ,0)\), in the case where \(S_{f} = 0.5\), \(S_{T} = \,1\) and \(\xi = 1\)
Full size table

The effects of major controlling parameters on the profiles of the functions \(\, f^{'} (\xi ,\eta )\), \(\,\theta (\xi ,\eta )\), \(Gr^{ - 3/4} {\text{ C}}_{f}\) and \(\, Gr^{ - 1/4} \, Nu\) are analyzed graphically through the curves plotted in Figs. 3, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12. It is shown from Eq. (12) that there is a direct relation between the function \(\, f^{'} (\xi ,\eta )\) and the dimensionless velocity of the Carreau fluid. Hence, these figures allow to analyze the distributions of the dimensionless velocity, temperature, skin friction coefficient and local Nusselt number.

Fig. 3
figure 3

Effect of the Weissenberg number \(We\,\) on a the velocity and b temperature profiles, when n = 0.1, Pr = 7, M = 1, Sf = 0.5, ST = 1 and ξ = 1

Full size image
Fig. 4
figure 4

Effect of the Magnetic parameter M on a the velocity and b temperature profiles, when n = 0.1, We = 0.3, Pr = 7, Sf = 0.5, ST = 1 and ξ = 1

Full size image
Fig. 5
figure 5

Effect of the velocity slip parameter Sf on a the velocity and b temperature profiles, when n = 0.1, We = 0.3, Pr = 7, M = 1, ST = 1 and ξ = 1

Full size image
Fig. 6
figure 6

Effect of the thermal jump parameter ST on a the velocity and b temperature profiles, when n = 0.1, We = 0.3, Pr = 7, M = 1, Sf = 0.5 and ξ = 1

Full size image
Fig. 7
figure 7

Effect of the Prandtl number Pr on a the velocity and b temperature profiles, when n = 0.1, We = 0.3, M = 1, Sf = 0.5, ST = 1 and ξ = 1

Full size image
Fig. 8
figure 8

Effect of the power law index parameter n on a the velocity and b temperature profiles, when We = 0.3, Pr = 7, Sf = 0.5, ST = 1 and ξ = 1

Full size image
Fig. 9
figure 9

Effect of steam-wise coordinate ξ on a the velocity and b temperature profiles, when n = 0.1, We = 0.3, Pr = 7, M = 1, Sf = 0.5 and ST = 1

Full size image
Fig. 10
figure 10

Effect of the Magnetic parameter M on a the skin friction and b Nusselt number profiles, when n = 0.1, We = 0.3, Pr = 7, Sf = 0.5 and ST = 1

Full size image
Fig. 11
figure 11

Effect of the velocity slip parameter Sf on a the skin friction and b Nusselt number profiles, when n = 0.1, We = 0.3, Pr = 7, M = 1 and ST = 1

Full size image
Fig. 12
figure 12

Effect of the thermal jump parameter ST on a the skin friction and b Nusselt number profiles, when n = 0.1, We = 0.3, Pr = 7, M = 1 and Sf = 0.5

Full size image

Figures 3, 4, 5, 6, 7, 8 and 9 exhibit the velocity and temperature distributions \(\left( {{\text{i}} . {\text{e}} . , { }f^{'} (\xi ,\eta ){\text{ and }}\,\theta (\xi ,\eta )} \right)\) for various thermo-physical parameters, namely the Carreau fluid parameter (i.e., Weissenberg number)\(\, We\,\), the magnetic body force parameter \(\, M\,\), the velocity slip parameter \(\, S_{f} \,\), the thermal slip parameter \(\, S_{T} \,\), the Prandtl number \(Pr\), the power law index \(\, n\,\) and the steam-wise coordinate \(\xi\).

Figures 10, 11 and 12 depict the effects of the parameters \(\, M\,\), \(S_{f} \,\) and \(S_{T} \,\) on the variation of both the skin friction coefficient and local Nusselt number \(\left( {\text{i} .e., \, Gr^{ - 3/4} {\text{ C}}_{f} {\text{ and }}Gr^{ - 1/4} \, Nu} \right)\) with the steam-wise coordinate \(\xi\) for such a Carreau electro-conductive fluid, which is characterized by \(\, n\, = 0.1\), \(\, We\, = 0.3\) and \(Pr = 7\)

Figure 3 illustrates the influence of the Weissenberg number \(\,We\) on the velocity and temperature distributions. It is shown from Fig. 3a that the dimensionless velocity component is considerably reduced with the increase in the value of the parameter \(\, We\). This result can be explained by the increase in the relaxation time of the polymer fluid, which creates a resistance to the fluid flow. The Weissenberg number \(\, We\) introduces a kind of nonlinearity to the system. Furthermore, it is noted that the Weissenberg number \(\, We\) is arised in connection with some higher order derivatives in the momentum boundary layer equation, especially in the mixed derivative \(\, We\,\left( {{{\partial^{2} f} \mathord{\left/ {\vphantom {{\partial^{2} f} {\partial \eta^{2} }}} \right. \kern-0pt} {\partial \eta^{2} }}} \right)^{2} \left( {{{\partial^{3} f} \mathord{\left/ {\vphantom {{\partial^{3} f} {\partial \eta^{3} }}} \right. \kern-0pt} {\partial \eta^{3} }}} \right)\). From Fig. 3b, it is quite clear that an increase in the Weissenberg number \(\, We\) enhances somewhat the temperature throughout the boundary layer regime.

Figure 4 is plotted to highlight the effect of the magnetic parameter \(\, M\) on the velocity and temperature distributions. From Fig. 4a, it is observed that the velocity profile decreases with the rise in the values of the magnetic parameter \(\, M\). The presence of a magnetic field in an electrically conducting fluid introduces a drag-like force known as Lorentz force, which acts against the flow, in the case where the magnetic field is applied vertically across the fluid flow. Hence, the magnetic resistive forces allow to slow down the fluid velocity. Moreover, it is found from Fig. 4b that the temperature is increased with the increase in the values of the magnetic parameter \(\, M\). As a result, the momentum boundary layer thickness is reduced and the temperature throughout the boundary layer increases slightly with the increase in the magnetic parameter \(\, M\). It is worth mentioning here that the resistance caused by the presence of the external magnetic field will produce the heat in the system and increase the thermal boundary layer thickness.

Figure 5 exhibits the influence of the effect of the velocity slip parameter Sf on the velocity and temperature distributions. It is seen from Fig. 5a that the flow is markedly accelerated in the vicinity of the sphere surface with the increase in the velocity slip parameter \(\, S_{f} \,\). The velocity profiles plotted in Fig. 5a show the presence of peaks from some distance of the wall. These peaks are taken high values and shifted closer to the sphere wall, when the value of the velocity slip parameter Sf is increased. Thereafter, the momentum slip induces a notable acceleration in the flow near to the sphere surface and decreases the momentum boundary layer thickness. On the contrary, it is observed that the momentum slip retards the fluid motion near and at the infinity boundary condition. Moreover, dragging of the fluid adjacent to the sphere surface is partially transmitted into the fluid, which induces a deceleration near the wall. However, this observation is eliminated and reversed further from the sphere surface. From Fig. 5b, it is found that the temperature profiles decay monotonically from a maximum at the sphere surface to the free stream, so that these profiles is converged at a large value of transverse coordinate \(\, \eta\) to the zero value, again showing that a sufficiently large infinity boundary condition has been taken into account during the numerical computations. With greater momentum slip, the temperature in the boundary layer is substantially decreased, and hence the thermal boundary layer thickness is dropped appreciably with the increase in the velocity slip parameter \(\, S_{f} \,\). Therefore, the regime is hottest when the momentum slip is absent \(\left( {\text{i} .e., \, S_{f} = 0} \right)\,\) and coolest with a strong hydrodynamic wall slip.

Figure 6 shows the influence of the thermal slip parameter \(\, S_{T} \,\) on the velocity and temperature distributions. From Fig. 6a, b, it is clearly noticed that both the velocity and the temperature are consistently decreased with the increase in the thermal slip parameter \(\, S_{T} \,\) in the vicinity of the sphere surface, so that the temperature becomes strongly depressed at the sphere surface. Hence, an increase in the value of the thermal jump parameter \(\, S_{T} \,\) allows to decelerate the flow and cool the boundary layer. It is also found that the momentum and thermal boundary layer thicknesses arise slightly when the thermal slip parameter \(\, S_{T} \,\) is increased. Physically, an increase in the thermal slip parameter \(\, S_{T} \,\) renders the fluid flow within the boundary layer progressively less sensitive to the heating effects at the sphere surface, so that a decreased quantity of thermal energy is transferred from the hot surface to the fluid, producing a fall in the temperature throughout the boundary layer. These results have important implications in the thermal polymer enrobing, since the thermal slip modifies the heat transferred to the polymer material, which in turn alters characteristics of the final product.

Figure 7 represents the velocity and temperature profiles for various values of the Prandtl number \(Pr\).From Fig. 7a, b, it is found that an increase in the Prandtl number \(Pr\) decreases both the polymer flow velocity and the temperature throughout the boundary layer. Physically, the Prandtl number \(Pr\) represents the ratio of the viscosity to the thermal diffusivity. Hence, the rise in the values of the Prandtl number \(Pr\) will cause a large increase in the fluid viscosity, so that the fluid becomes extremely thick, and hence moves so slowly. The most prominent variation in the velocity and temperature distributions arises at intermediate distances from the sphere surface. Furthermore, it is quite clear that the momentum and thermal boundary layers are thinner at large values of the Prandtl number \(\, Pr\) compared with the case where the values of the Prandtl number \(\, Pr\) are taken smaller. This fact is due to the inverse relation between the Prandtl number \(\, Pr\) and the thermal diffusivity. So, an increase in the Prandtl number \(\, Pr\) prevents spreading a large amount of heat within the boundary layer.

Figure 8 depicts the impact of the power law index parameter \(n\,\) on the velocity and temperature distributions for distinct values of the magnetic parameter \(\, M\). In the presence or absence of an external magnetic field, it is observed from Fig. 8a that there is an opposite behavior of the power law index parameter \(n\,\) toward the fluid velocity, so that for higher values of the power law index parameter \(n\,\), the fluid velocity decreases and the thickness of the boundary layer becomes thinner. This result can be explained by the augmentation in the apparent viscosity of the Carreau fluid. Therefore, the fluid flow becomes more resistive, and hence the temperature distribution and the thermal boundary layer thickness are increased as shown in Fig. 8b.

Figure 9 is plotted to examine the impact of the stream-wise coordinate \(\, \xi\) on the velocity and temperature distributions. From Fig. 9a, it is quite clear that the velocity of the fluid flow is reduced in the vicinity of the sphere surface, when we move away from the lower stagnation point \(\, \left( {\xi ,\eta } \right) = \left( {0,0} \right)\). It is also observed that the momentum boundary layer thickness is increased marginally with the stream-wise coordinate \(\, \xi\). Conversely, it is shown in Fig. 9b that there is an enhancement in both the temperature distribution along the boundary layer and the thermal boundary layer thickness.

The variation of on the engineering quantities \(Gr^{ - 3/4} {\text{ C}}_{f}\) and \(Gr^{ - 1/4} \, Nu\) of a Carreau fluid versus the stream-wise coordinate \(\, \xi\) for various values of the magnetic parameter \(\, M\,\), the velocity slip parameter \(\, S_{f} \,\) and the thermal slip parameter \(\, S_{T} \,\) are presented graphically in Figs. 10, 11 and 12 and summarized numerically in Table 6, in the case where \(\, n\, = 0.1\), \(\, We\, = 0.3\) and \(Pr = 7\). From these figures, it is seen that for extensive values of the parameters \(\, M\,\), \(\, S_{f} \,\) and \(\, S_{T} \,\) there is a significant depletion in the local shear stress at the sphere surface. Hence, the presence of an external magnetic source with the momentum and thermal slip conditions allow to minimize the effect of the resulting viscous friction forces at the sphere surface. Furthermore, it is noticed that the local heat transfer rate is reduced when the parameters \(\, M\,\) and \(\, S_{T} \,\) is increased. It is also found that the local heat transfer rate can be enhanced when the parameter \(\, S_{f} \,\) is increased.

Table 6 Numerical values of the quantities \(Gr^{ - 3/4} \, C_{f}\) and \(\, Gr^{ - 1/4} \, Nu\) for various values of \(\, M\), \(S_{f}\) and \(\, S_{T}\), in the case where \(We\, = 0.3\) \(n\, = 0.1\) and \(\, Pr\, = \,7\)
Full size table

5 Conclusions

A mathematical model has been developed for the buoyancy driven MHD boundary layer flow of a Carreau fluid over a sphere. The transformed conservation equations have been solved with prescribed boundary conditions using the finite difference implicit Keller-Box method, which has a second-order accuracy. Excellent convergence and stability characteristics are demonstrated by the Keller-Box scheme, which is capable of solving very strongly nonlinear rheological problems.

The present simulations have shown that:

  1. 1.

    An increase in either the Carreau viscoelastic fluid parameter \(\, We\,\), the magnetic parameter \(\, M\), the thermal slip parameter \(\, S_{T} \,\), the Prandtl number \(Pr\), the power law index \(\, n\,\) or the steam-wise coordinate \(\, \xi\) allows to decrease the fluid velocity near the sphere surface.

  2. 2.

    The presence of the velocity slip condition \(\, S_{f} \,\) allows to increase the fluid velocity near the sphere surface.

  3. 3.

    An increase in either the Carreau viscoelastic fluid parameter \(\, We\,\), the magnetic parameter \(\, M\), the power law index \(\, n\,\) or the steam-wise coordinate \(\, \xi\) allows to improve the temperature throughout the boundary layer.

  4. 4.

    The temperature distribution throughout the boundary layer can be reduced by the increase in either the velocity slip parameter \(\, S_{f}\), the thermal slip parameter \(\, S_{T} \,\) or the Prandtl number \(Pr\).

  5. 5.

    The effect of viscous friction at the sphere surface can be minimized by increasing the values of the magnetic parameter \(\, M\), the velocity slip parameter \(\, S_{f}\) and the thermal slip parameter \(\, S_{T}\).

  6. 6.

    The local heat transfer rate is enhanced with the increase in the velocity slip parameter \(\, S_{f}\), while an inverse result is observed when the parameters \(\, M\,\) and \(\, S_{T} \,\) are increased.