Finite-size effects, demographic noise, and ecosystem dynamics

Abstract

Strong positive feedback is considered a necessary condition to observe abrupt shifts in ecosystems. A few previous studies have shown that demographic noise—arising from the probabilistic and discrete nature of birth and death processes in finite systems—makes the transitions gradual. In this paper, we investigate the impact of demographic noise on finite ecological systems. We use a simple cellular automaton model with births and deaths influenced by positive feedback processes. We present our methods in a tutorial like format. Using the approach of van Kampen’s system-size expansion, we derive a stochastic differential equation that describes how local probabilistic rules scale to stochastic population dynamics in finite systems. We illustrate that as a consequence of enhanced demographic noise, finite-sized ecological systems can show an ‘effective abrupt transition’ even with weak positive interactions. Numerical simulations of our spatially explicit model confirm this analytical expectation. Thus, we predict that small-sized populations and ecosystems, in response to environmental drivers, are prone to abrupt collapse while larger systems—with the same microscopic interactions—show a smooth response.

1 Introduction

Several ecosystems exhibit alternative stable states [1,2,3,4]. For example, in semi-arid ecosystems, a vegetated state and a bare (or low-vegetation) state can co-exist at similar values of mean annual precipitation. Similarly, lakes can exist in turbid or clear states for the same nutrient loading rates. Such systems with bistable (or multiple stable) states can abruptly shift from one state to another when they cross a threshold value of the external driver. These systems also show hysteresis, i.e. the reverse transition occurs at a driver value different from the conditions that caused the initial transition [1, 2]. Therefore, restoration is often difficult and sometimes even impossible. To explain this phenomenon, strong positive feedback within ecosystems is often invoked as a necessary condition [5,6,7,8]. Here, we illustrate how demographic noise arising in finite systems can give rise to a bimodal distribution of ecosystem states—even without strong positive interactions.

Organisms display positive interactions which enhance (or reduce) each other’s fecundity (mortality). Many analytical and numerical simulation models incorporate ecosystem specific positive interactions [5, 8,9,10,11,12,13,14,15]. For example, in semi-arid ecosystems, plants increase local infiltration of surface water and reduce evapotranspiration: the chance of germination and growth of a plant in the vicinity of another plant is higher than that of plant in a bare region. Such positive density dependence on the growth rates—also called Allee effect—is an important factor in maintaining multiple stable states and in driving abrupt transitions between these states [5,6,7,8].

Besides positive interactions, stochasticity also plays an important role in determining ecosystem dynamics and stability. Broadly, stochasticity is of two types: environmental (extrinsic) stochasticity arising from random fluctuations in the environmental drivers and demographic (intrinsic) stochasticity arising from probabilistic and discrete nature of birth and death of individuals in finite systems. We now understand that environmental stochasticity can alter resilience and induce shifts between bistable systems [3, 16,17,18,19]. The effect of demographic stochasticity on the resilience of ecosystems has received less attention [18, 20,21,22,23,24]. For example, demographic noise may smoothen out abrupt transitions [21, 22]. In contrast, some studies make an opposite prediction too, i.e. demographic noise promotes alternative stable states [24] and abrupt transitions [20]. Although demographic noise is now relatively well studied in a number of ecological contexts [25,26,27,28,29,30], the precise role of finite population size on ecosystem dynamics is not much explored. Furthermore, few studies show how local interactions scale to demographic noise or disentangle the effects of spatial interactions from demographic stochasticity on the stability and resilience of ecosystems (but see [20, 31,32,33]).

In this paper, we use a simple model of vegetation dynamics to explore how finite system size affects ecosystem dynamics; we refer to the finite size description as mesoscopic dynamics. The manuscript is organised as follows, with an effort to make it pedagogical and accessible to anyone familiar with the basics of stochastic processes. In Sect. 2, we present a minimal, cellular automaton model which incorporates local processes of birth and death and positive feedback interactions among individuals [8, 34, 35]. We then present van Kampen’s system-size expansion method in Sect. 3 which yields a mesoscopic model, i.e. a stochastic differential equation governing the system dynamics while accounting for finite-size stochastic effects. Using this method, we are able to relate microscopic interaction rules to the structure of demographic noise at mesoscopic scales. In Sect. 4, we show the results of the model in the deterministic mean-field (i.e. infinite size) limit. In Sects. 5 and 6, using analytical calculations and numerical simulations, we show that strong demographic stochasticity caused by finite system size can give rise to a bimodal distribution of densities, even with relatively weak positive interactions. Finally, we discuss various implications.

2 A minimal individual-based model for ecosystem transitions

Our model is based on a statistical-physics inspired cellular-automaton model of tricritical directed percolation [34] that has been adopted in ecological contexts [4, 8, 35]. A two dimensional space is divided into $L\times L = N$ discrete sites. Each site can take one of the two states: empty (denoted by 0) or occupied (by an organism; denoted by 1). We update these states at discrete time steps using probabilistic rules of birth and death, described below (see Fig. 1 for a schematic of the update rules of the model).

Fig. 1

Schematic of the model update rules. Left panel shows the baseline reproduction process as implemented when the neighbouring site of a focal plant is empty. Right panel shows the positive feedback process which is implemented when the neighbouring site of a focal plant is occupied. (This schematic adapted with modification from Fig. 1 in the Supporting Information for [8])

2.1 Baseline reproduction

During each discrete time step, a site is selected randomly, henceforth called the focal site. If the focal site is empty, we make no update and choose another site randomly. However, if the focal site is occupied by an organism, one of its four nearest neighbours is selected at random. This neighbour may be occupied or empty. If it is empty, we implement the baseline reproduction rule: the focal plant reproduces with a probability p and establishes a new plant at the neighbouring empty site (resulting in a transition represented as 10 $\rightarrow$ 11). In addition, the focal plant may die with a probability d (represented as 10 $\rightarrow$ 00).

The baseline birth probability p of the plants (or more generally an organism) per unit time can be thought of as a parameter representative of external factors like precipitation; we also refer to p as the environmental driver and a reduction in p as increased environmental stress. We interpret d as the density-independent death rate; this is in contrast to the previous models where the death rate was assumed to be $1-p$ [4, 8, 34, 35].

2.2 Positive feedback

If the neighbouring site of the focal site is occupied, we implement the positive feedback rule: we randomly pick one of the six neighbours of the pair as the third site. If the third site is empty a plant germinates there with a probability q (represented as 110 $\rightarrow$ 111) or the focal plant dies with a probability d (represented as 11 $\rightarrow$ 01); the latter rule is implemented only if there is no germination at the third site. The positive feedback (i.e. $q>0$) has two effects: (1) it enhances the birth rate of the plants, (2) it reduces the death rate of the focal plant when its neighbouring sites are occupied.

Therefore, a discrete step update may involve (i) nothing if the focal site is empty, (ii) a basic reproduction rule if the chosen pair is 10, leading to one of the four outcomes shown in the left panel of Fig. 1 or (iii) a positive feedback rule if the chosen pair is 11, leading to one of the two outcomes shown in the right panel of Fig. 1. One time unit completes after $L^2$ discrete updates such that all the cells are selected, on average, once for an update.

This model relates to the contact process, a well known spatial stochastic process studied in the context of infectious disease spread and population dynamics [36, 37]. Unlike the contact process, we assume that reproduction by the focal plant and its death are not mutually exclusive. We model birth and death as independent processes and both can happen in the same discrete time step, corresponding to the update $10 \rightarrow 01$ which occurs with a probability pd. Likewise, there is a finite chance of neither of these events occurring, corresponding to the update $10 \rightarrow 10$ with a probability $(1-p)(1-d)$. Therefore, the update rules of our model do not converge to the discrete formulation of the contact process by setting $q=0$ and $d=1-p.$

However, we stress that $10 \rightarrow 10$ and $10 \rightarrow 01$ transitions have no effect on the macroscopic density of plants on the landscape. See Sect. 3 and Appendix A. Hence, in the mean-field limit, our model with $q=0$ and $d=1-p$ is equivalent to the contact process. Likewise, these transitions do not affect the doublet densities either; therefore, the pair-approximation for the contact process and our model with $q=0$ and $d=1-p$ are identical (see Appendix B).

3 Mesoscopic dynamics: coarse-grained population level model with demographic noise

Mean-field approximation of stochastic cellular-automaton models is constructed in the macroscopic limit ($N \rightarrow \infty$); thus, apart from spatial interactions, it fails to account for the stochasticity arising from finite system sizes. We use van Kampen’s system-size expansion method to address this limitation [25, 38, 39]. We note that our model exhibits an absorbing state at zero density, i.e. when all cells are unoccupied. See [40, 41] for improvements over van Kampen’s system size expansion in describing the dynamics of a system close to an absorbing boundary.

We further remark that the dynamics of the cellular-automaton can be described by a state variable n which is the the absolute number of occupied sites on the lattice, and hence $n \in [0, N]$. Here N is the size of the system, i.e. the number of sites on the lattice. We define density as $\rho = n/N$ and hence can take discrete values in the range 0 and 1, separated by 1/N. Below, we consider an approximation to obtain the mesoscopic dynamics of the density under the assumption that it can be approximated as a continuous variable $\rho$.

3.1 Deriving the mesoscopic model with system-size expansion

We wish to describe the dynamics of a scalar variable $\rho$, representing the proportion of occupied cells or density of the landscape. Assuming that in a finite system of size N the stochastic update rules are ‘birth’ or ‘death’ like events, which may change $\rho$ to $\rho +\frac{1}{N}$ or $\rho -\frac{1}{N}$, the master equation to describe the temporal evolution of the probability distribution of $\rho$ at time t [42, 43], denoted by $P(\rho ,t)$ is

$$\begin{aligned} \frac{\partial P(\rho ,t)}{\partial t}= & {} \sum _{\rho ' \ne \rho } [T(\rho |\rho ')P(\rho ',t) - T(\rho '|\rho )P(\rho ,t)] \nonumber \\= & {} T\left( \rho |\rho +\frac{1}{N}\right) P\left( \rho +\frac{1}{N},t\right) \nonumber \\&+ T \left( \rho |\rho -\frac{1}{N}\right) P\left( \rho -\frac{1}{N},t\right) \nonumber \\&- T\left( \rho +\frac{1}{N}|\rho \right) P(\rho ,t) \nonumber \\&- T \left( \rho -\frac{1}{N}|\rho \right) P(\rho ,t), \end{aligned}$$

(1)

where $T(\rho |\rho ')$ is the transition rate from the state $\rho '$ to state $\rho$, which in turn depends on the stochastic update rules of the model.

To simplify the above master equation, we follow [28, 39] and define the step operators $\epsilon ^+$ and $\epsilon ^-$ that have the following effect on a continuously differentiable single variable function $h(\rho )$

$$\begin{aligned} \epsilon ^+ h(\rho ) = h\left( \rho +\frac{1}{N}\right) \quad \epsilon ^- h(\rho ) = h\left( \rho -\frac{1}{N}\right) . \end{aligned}$$

For brevity, we denote the transition rates that correspond to birth and death as $T^+$ and $T^-$, respectively,

$$\begin{aligned} T^+(\rho )= & {} T \left( \rho +\frac{1}{N}|\rho \right) \\ T^-(\rho )= & {} T\left( \rho -\frac{1}{N}|\rho \right) . \end{aligned}$$

Using these operators and the abbreviated notation for transition rates, we rewrite the master equation (1) as

$$\begin{aligned} \frac{\partial P(\rho ,t)}{\partial t}= & {} (\epsilon ^- - 1) T^+(\rho ) P(\rho ,t) \nonumber \\&+ (\epsilon ^+ - 1) T^-(\rho ) P(\rho ,t). \end{aligned}$$

(2)

Assuming large N, the step operators are approximated with a second-order Taylor series:

$$\begin{aligned} \epsilon ^{\pm } h(\rho ) \approx \left[ 1 \pm \frac{1}{N} \frac{\partial }{\partial \rho } + \frac{1}{2N^2} \frac{\partial ^2}{\partial \rho ^2} \right] h(\rho ). \end{aligned}$$

(3)

Substituting Eq. (3) in Eq. (2), distributing terms and rearranging, we have

$$\begin{aligned} \begin{aligned} \frac{\partial P(\rho ,t)}{\partial t}&\approx - \frac{1}{N} \frac{\partial }{\partial \rho } \left[ \left( T^+(\rho ) - T^-(\rho )\right) P(\rho ,t) \right] \\&\quad + \frac{1}{2N^2} \frac{\partial ^2}{\partial \rho ^2} \left[ \left( T^+(\rho ) + T^-(\rho )\right) P(\rho ,t) \right] . \end{aligned} \end{aligned}$$

To ease the notation, we make the following substitutions

$$\begin{aligned} f(\rho ) = T^+(\rho ) - T^-(\rho ) \quad g(\rho ) = \sqrt{T^+(\rho ) + T^-(\rho )}.\quad \end{aligned}$$

(4)

Next, we rescale time as $t=Nt'$ and drop the prime to obtain

$$\begin{aligned} \frac{\partial P(\rho ,t)}{\partial t} = - \frac{\partial }{\partial \rho } \left[ f(\rho ) P(\rho ,t) \right] + \frac{1}{2N} \frac{\partial ^2}{\partial \rho ^2} \left[ g(\rho )^{2}P(\rho ,t) \right] .\nonumber \\ \end{aligned}$$

(5)

This is the Fokker–Plank equation (FPE). For a given stochastic process, FPE describes the time evolution of the state variable’s probability distribution $P(\rho ,t)$. The function $f(\rho )$ and $g(\rho )^{2}$ are called the drift and diffusion coefficient, respectively. If we wish to analyse individual trajectories, we must construct a stochastic differential equation (SDE) for the state variable. For a given stochastic process, the SDE and FPE are closely related [42, 43]. The Ito sense SDE corresponding to the the FPE (5) is given by [42, 43]

$$\begin{aligned} \frac{{\text {d}}\rho }{{\text {d}}t} = f(\rho ) + \frac{1}{\sqrt{N}}g(\rho ) \eta (t), \end{aligned}$$

(6)

where $\eta (t)$ is a Gaussian white noise with $\left< \eta (t) \right> = 0$ and $\left<\eta (t)\eta (t') \right> = \delta (t-t').$ Equation (6) together with Eq. (4) constitute the mesoscopic description of the microscopic stochastic model. The stochastic term in this description has two features: First, the noise is multiplicative, i.e. the strength of noise depends on the current value of the state variable $\rho$. Second, the strength depends inversely on the system size N.

3.2 Mesoscopic dynamics (SDE) of our model

For a well-mixed system, specifying the transition rates is a straightforward application of the law of mass action: the rate of reaction is proportional to the concentration of the reacting species. Applying the approximation of well-mixed system to our model, we obtain the following transition rates:

$$\begin{aligned} T^+(\rho )= & {} T\left( \rho + \frac{1}{N}|\rho \right) = \rho (1-\rho )p + \rho ^{2}(1-\rho )q, \end{aligned}$$

(7)

$$\begin{aligned} T^-(\rho )= & {} T\left( \rho - \frac{1}{N}|\rho \right) = \rho (1-\rho )d + \rho ^{2}(1-q)d. \end{aligned}$$

(8)

In Eq. (7) we have used the fact that the density can change from $\rho$ to $\rho + \frac{1}{N}$ in two ways: $01 \rightarrow 11$ with a probability p or $011 \rightarrow 111$ with a probability q. Similarly, in Eq. (8) the density can change from $\rho$ to $\rho -\frac{1}{N}$ in two ways: $10 \rightarrow 00$ with a probability d or $11 \rightarrow 01$ with a probability $(1-q)d$. See Appendix 1 for further detailed steps on well-mixed or mean-field approximation.

We emphasise that reactions $01 \rightarrow 01$ and $01 \rightarrow 10$ have no effect on $\rho$, hence they do not appear in the master equation.

Substituting Eqs. (7) and (8) in Eq. (6), we obtain the mesoscopic SDE for our model, interpreted in an Ito sense,

$$\begin{aligned} \frac{{\text {d}}\rho }{{\text {d}}t}= & {} (p-d)\rho - (p-q-qd)\rho ^{2} - q\rho ^{3} \nonumber \\&+ \frac{1}{\sqrt{N}} \sqrt{(p+d)\rho -(p-q+qd)\rho ^{2} -q\rho ^{3}} \, \eta (t),\qquad \end{aligned}$$

(9)

where $\eta (t)$ is a Gaussian white noise with zero mean and a unit variance.

The mesoscopic SDE (9) has two terms: The first term is the deterministic part and is same as the mean-field approximation (see Appendix 1). The second term is the stochastic part, where the strength of noise depends on the state of the system ($\rho$) and is inversely related to the system size N. Therefore, via Eq. (9) we are able to capture the defining feature of demographic noise—discrete and probabilistic nature of birth and death in finite systems.

3.3 Solving the Fokker–Planck equation

In the above derivation, we have assumed that the drift and diffusion coefficients are not time dependent. In such a case, we can in principle obtain the steady-state probability distribution function $P_{\text {s}}(\rho )$—if it exists—by setting $\frac{\partial P_{\text {s}}(\rho ,t)}{\partial t} = 0$ in Eq. (5) and invoking appropriate boundary conditions. If we have natural boundaries at the edges of the interval of our interest (i.e the variable is restricted to this interval), we can then solve the resulting ordinary differential equation under the no current condition at the boundary. This yields

$$\begin{aligned} P_{\text {s}}(\rho ) = {\mathcal {N}}{\exp \left( - \, \frac{2}{\sigma ^2} U(\rho )\right) }, \end{aligned}$$

(10)

where $U(\rho )$ is referred to as effective potential and is given by [43, 44]

$$\begin{aligned} U(\rho ) = - \int _{\rho _0}^{\rho } \frac{f(\rho ') - \sigma ^2 g(\rho ') g'(\rho ')}{g(\rho ')^2} {\text {d}}\rho ', \end{aligned}$$

(11)

where $\rho _0$ is an arbitrary point in the domain on which we wish to study the stochastic process. ${\mathcal {N}}$ is a normalization constant.

Bifurcation diagrams that show the steady states of the system are typically described for mean-field deterministic systems (but see [16]). When we have a stochastic process, we can only speak in terms of most probable/least probable states of the steady-state, assuming a steady-state exists for the system. Following [44], we find the most probable/least probable states via extrema of $P_{\text {s}}(\rho )$. If an extremum is a mode of $P_{\text {s}}$, it corresponds to a most likely state which can be considered equivalent to a stable state subject to perturbations. On the other hand, if an extremum is a minimum of $P_{\text {s}}$, it may be interpreted as an unstable state from which the system is kicked out, so to speak, by stochasticity.

However, the model we have presented here and the associated mesoscopic SDE describe a stochastic process that has an absorbing boundary at $\rho =0$, i.e once the system reaches this boundary, it cannot reflect back into the region from which it arrived. The other boundary is at $\rho =1$, which is a reflecting boundary. Technically, for such systems, a steady-state normalisable probability density function does not exist. However, we can still use this function to gain insight into the dynamics of the system sufficiently far from the singularity at $\rho =0$; we will denote the non-trivial solution of the FPE for our model as $F(\rho )$ in all subsequent invocations.

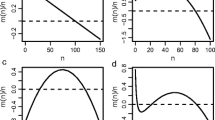
In this spirit, we plot the extrema of $F_{\text {s}}$ as a function of p, for different values of N (Fig. 3). The modes are shown (each with a different color) as solid lines while the minimum is shown as a red dashed line.

4 Mean-field approximation shows that positive feedback promotes alternative stable states in infinitely large systems

Fig. 2

Mean-field model shows continuous transition (A) or abrupt transition (B), depending on the value of the positive feedback parameter q. Black, blue and red curves show the three equilibrium densities. Solid lines are the stable states and dotted lines are the unstable states. For low values of positive feedback ($q<q_t$), the system shifts from a vegetated state to a bare state ($\rho =0$) continuously at $p_c=d$. For strong positive feedback ($q>q_t$), two stable states exist for a range of parameter value: $p_{c2}-p_{c1}$. When p is reduced below a threshold ($p_{c_1} = d-\frac{(p_{c_1}-q-qd)^2}{4q}$, hence lower than d), the system shifts from a vegetated state to bare state abruptly. The reverse transition occurs at the $p_{c_2}=d$ (C) shows the stability diagram of the mean-field model for all values of p and q. Solid line shows the critical thresholds ($p_{c1}$) below which only bare state is stable. Black dot represents the tri-critical point at which the nature of transition changes from continuous to abrupt. The region between the solid line and the dotted line has two states. Here, d is kept fixed as 0.3

Considering the macroscopic limit, i.e. $N \rightarrow \infty$, the stochastic differential equation converges to an ordinary (deterministic) differential equation given by

$$\begin{aligned} \frac{{\text {d}}\rho }{{\text {d}}t} = (p-d)\rho - (p-q-qd)\rho ^2 - q\rho ^3. \end{aligned}$$

(12)

The equilibria and associated stability of the mean-field model is found by setting ${\text {d}}\rho /{\text {d}}t = 0$ and performing linear stability analysis [45] on the resulting steady states (see Appendix A). One of the equilibria is a bare state $\rho *=0$. The bare state is stable when $p<d$ and unstable for $p>d$. In other words, when the baseline birth rate p exceeds a critical threshold of $p_c=d$, the system in bare state undergoes a transition to a vegetated state ($\rho ^*>0$).

The nature of the transition as a function of p, however, depends on the value of the positive feedback parameter q. The transition from a bare state to a vegetated state, as a function of p, is a continuous transition for $0 \le q<\frac{d}{1+d}$, i.e. low values of q. In other words, for ecosystems with weak positive interactions, the transition from a vegetated to a bare state with deteriorating environmental conditions is gradual (Fig. 2A).

For systems with strong positive feedback, specifically $q >q_t = \frac{d}{1+d}$, the transition between bare state and the vegetated state is a discontinuous function of p (Fig. 2B). Here, for a range of driver values $p_{c_1}<p<p_{c_2}$, where $p_{c_1}=d-\frac{(p_{c_1}-q-qd)^2}{4q}$ and $p_{c_2}=d$, we find three equilibria; a stable bare state (solid black line in Fig. 2B), an unstable intermediate vegetated state (dotted red line in Fig. 2B) and a stable large vegetated state (solid blue line in Fig. 2B). The value of parameter p at which the stable and unstable vegetated states meet and cease to exist, denoted $p_{c1}$, is referred to as a saddle-node bifurcation.

If a system is in the vegetated state and the driver value reduces below the critical threshold of $p_{c1}$ ($<d$), the system collapses from a vegetated state to the bare state. Likewise, when the driver increases above the threshold $p_{c2}=d$, a system in bare state undergoes an abrupt transition to a vegetated state. These transitions are also referred to as abrupt regime shifts, catastrophic shifts, tipping points or critical transitions [2, 46]. We also note that the system exhibits hysteresis; i.e. the two abrupt transitions occur at different threshold values of p. Furthermore, depending on the initial condition, the system may reach either the bare state or the vegetated state.

The threshold value of positive feedback at which the type of transition changes from smooth to abrupt ($q=\frac{d}{1+d}$) is called the tri-critical point. The region of bistability, i.e. the range $p_{c_1}$ to $p_{c_2}$, increases with the strength of positive feedback q.

Figure 2C summarises the mean-field predictions of our model, as a function of environmental driver (baseline birthrate p) and positive feedback parameter (q). It shows that vegetated systems with strong positive feedback can survive in harsher environmental conditions (i.e. for lower values of p than the critical threshold of continuous transitions; note that $p_{c1}<d$). However, systems with strong positive feedback are also prone to collapse as a function of changing environmental conditions. In other words, large positive feedback among individuals promotes bistability in ecosystems. These mean-field approximation results and interpretations of our model are consistent with the literature on spatial ecosystem models with positive feedback [7, 9, 47, 48], which often incorporate models of ecosystems with many more parameters (but see [4, 8]).

5 Demographic noise can lead to a bimodal distribution of densities even with weak positive feedback

To investigate the effects of demographic noise in finite systems, we solve for $F_{{\text {s}}}(\rho )$ (see Sect. 3.3) for the case of our model where $q=0$. We use $F_{{\text {s}}}(\rho )$ instead of $P_{{\text {s}}}(\rho )$ to emphasize that $F_{{\text {s}}}(\rho )$ is a non-normalizable function. In the FPE,

$$\begin{aligned} \frac{\partial F(\rho ,t)}{\partial t}= & {} - \frac{\partial }{\partial \rho } \left[ \left( (p-d)\rho -p\rho ^2\right) F(\rho ) \right] \nonumber \\&+ \frac{1}{2N} \frac{\partial ^2}{\partial \rho ^2} \left[ \left( (p+d)\rho -p\rho ^2\right) F(\rho ) \right] \qquad \end{aligned}$$

(13)

the strength of demographic noise is proportional to $\frac{1}{\sqrt{N}}$. In the mean-field limit of the $q=0$ case, the escape time [43] from both the active phase (stable, when $p>d$) and the absorbing phase (stable, when $p<d$) is infinite, i.e. they are asymptotically stable in the respective ranges.

Fig. 3

The vegetated state and the bare state can coexist via a bimodal distribution of densities in finite systems. For finite N, the trivial steady-state solution of the FPE is a delta-function at $\rho =0$ for all values of p (solid black line in A and B). When we consider the non-trivial solution $F_{{\text {s}}}$ (see text) of the FPE, a non-zero mode—denoting a vegetated state (solid blue lines in A and B)—appears when the baseline birth probability p is greater than a threshold value. This mode co-exists with the divergence at $\rho =0$; they are separated by a minimum denoted with a red-dashed line. In the $N\rightarrow \infty$ limit (C), steady-state density shows a continuous transition, which is consistent with the transcritical bifurcation that can be obtained from a linear stability analysis of the mean-field model. Here, $d=0.3$ and $q=0$

However, when N is finite, we find the following: (i) the threshold value of p at which the vegetated state (the non-zero mode of $F_{{\text {s}}}(\rho )$) ceases to exist is larger than the mean-field threshold (i.e $p_{\text {c}}(N)>d$), and (ii) the absorbing phase is asymptotically stable for the entire range of p.

This has the following implications: (1) a finite system has a non-zero probability of collapse from a vegetated state to the bare state, and (2) for a given value of p and d that sustain a non-zero mode for $F_{{\text {s}}}$, the probability of collapse from the vegetated to the bare state is higher for a smaller system.

Therefore, due to finite-size effects that manifest via enhanced demographic noise, we predict small systems exhibit a bimodal distribution of densities and an abrupt collapse of the system from the non-zero density to a bare state.

We caution that we have not demonstrated that this abrupt collapse is equivalent to a first order phase transition. However, we demonstrate that the bimodal distribution of density leads to an ‘effectively discontinuous transition’.

6 Numerical simulations show similar effects of demographic noise

Fig. 4

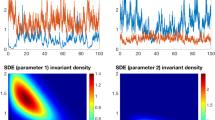
Numerical simulations of the spatially-explicit individual-based model confirm bimodality for finite-size systems. A L=16 (or $N=16 \times 16$). Region between $p=0.45$ to $p=0.5$ shows bi-modality. Furthermore, a range of densities with zero-probability of occurrence is evident between the non-zero mode and the mode at zero. B L=128 (or $N=128 \times 128$). There is no sign of bi-modality and the transition from $\rho ^{*}=0$ to $\rho ^{*}>0$ is much smoother. C, D, E and F show phase diagram constructed from numerical simulations for different system sizes in two dimensions

To verify if we observe these effects in spatially explicit systems that are finite, we conducted numerical simulations of our cellular automaton model using the stochastic update rules described in Sect. 2. We display the results in Fig. 4 for many system sizes $N=L \times L$. For all parameter values (except for $p>0.65$ in $L=512$, where we simulated 10,000 time steps), we run the simulation for 1 million time steps. We chose four system sizes: $16 \times 16, 32 \times 32$, $128 \times 128$ and $512 \times 512$ for the purpose of illustration in Fig. 4. For the system size $16 \times 16$ (i.e. $L=16$), for each value of p we construct a normalized frequency distribution of density based on 10,000 independent realizations (Fig. 4A). For $L=128$ (hence, $N=128 \times 128$), due to computational constraints, we calculate frequency distribution based on 100 realisations only (Fig. 4B). We then plot the average density for $L = 16$ (Fig. 4C), 32 (Fig. 4D), 128 (Fig. 4E), 512 (Fig. 4F) based respectively on 10,000, 2000, 100 and 100 realisations as follows: for each p, the upper arm was constructed by culling the realizations that fell into the absorbing phase ($\rho =0$) and calculating the mean of the densities of the remaining realisations. The lower arm $(\rho =0)$ was plotted if at least one realization with $\rho =0$ was reported. This method gives a well defined bimodal region for each L.

Our numerical simulations confirm the qualitative predictions of the analytical results based on system-size approximation: (1) small systems exhibit bimodal frequency distribution of density (Fig. 4A, C, D), (2) the vegetated state abruptly ceases to exist when p is less than a threshold value (Fig. 4C–E); this threshold value is larger for smaller system sizes, (3) the region of bimodality reduces with increasing system size (Fig. 4C–D).

We observe a sizeable range of p in which the absorbing phase is never reached, even in systems as small as $L=16.$ Although this may be attributed to finite runtime of our simulations, it is nevertheless a plausible feature of real ecological systems when the time to reach a steady state is large. For large systems, the transition from vegetated to bare state is much less abrupt, and for $L=512$, becomes continuous for all practical purposes (Fig. 4B, F).

7 Discussion

In this study, we used a spatially explicit individual-based model to investigate the role of demographic stochasticity in ecological transitions. Using analytical methods and numerical simulations, we showed that finite-size effects on demographic noise can result in a bimodal distribution of densities, thus potentially causing stochasticity-driven abrupt transitions, even with weak positive feedback mechanisms.

Our conclusions are broadly consistent with the results in the ecology literature, which has extensively looked at the role of stochasticity in population extinctions. Specifically, these studies conclude that demographic stochasticity can induce Allee-like effects, in which populations smaller than a threshold size are likely to go to extinction [20, 32, 33]. However, these studies write a continuum description for the system. In contrast, using the system-size expansion, we show how the local microscopic update rules scale to mesoscopic dynamics of the population. This allowed us to explicitly capture the effect of finite system size in the stochastic term. Our derivations show that the stochastic term is multiplicative, depending on both the state variable density ($\rho$) and the system size (N); this is of the form $\frac{1}{\sqrt{N}}\sqrt{\rho + {\mathcal {O}}(\rho ^2)}$. However, most previous studies include density effects via a $\sqrt{\rho }$ term alone [21, 49,50,51,52] and do not consider the effect of system size.

The variance of the white noise process driving the mesoscopic dynamics is proportional to 1/N, the smallest possible increment/decrease in density in a finite system of size N. Decreasing N increases the relative role of stochasticity in determining trajectories by reducing the range and increasing step-size of the stochastic process associated with n (the absolute number of individuals). Finiteness brings the vegetated state closer to the absorbing boundary at $\rho =0$. Trajectories that are closer to the absorbing boundary lead to a higher probability of a collapse to a bare state. Thus, apart from finite system-size, considering the effect of boundary conditions on the dynamics of the system is important.

Environmental noise is another form of stochasticity important for determining ecosystem dynamics. Several studies have shown that large environmental noise can induce abrupt transitions in ecosystems before it reaches the critical threshold [3, 16, 53, 54]. However, in some cases [50], environmental fluctuations can change the stability landscape and induce resilience. The combined effect of demographic noise and environmental noise needs to be carefully investigated to obtain insights for the management of ecosystems [55].

Abrupt transitions in our model must not be confused with a first-order phase transition occurring at a critical point. In the physics literature, phase transitions are defined at the thermodynamic limit while our focus here is on finite systems. We think that explicitly accounting for finite system sizes is important for gaining insights into ecological applications, for no ecological system is infinitely large. Furthermore, habitat fragmentation is likely to lead to many patches of small sizes where finite-size induced demographic noise can not be ignored. By virtue of having their dynamics restricted closer to an absorbing state (bare state in our model), these systems are prone to an abrupt collapse. In the absence of early mitigation, restoration would in principle have to ensure a non-negligible re-establishment seeding and a significant improvement of environmental conditions, to ensure that the system is pushed back into a growth dominated regime.

A plethora of recent studies have investigated the possibility of forecasting abrupt transitions, using the idea of early warning signals [17, 23, 46, 56,57,58,59,60,61,62,63]. Can similar early warning signals be constructed for systems with demographic noise? Investigating this and other related questions is a possible future direction.

Appendices

Appendix A: Mean-field approximation

To write the mean-field equation for the dynamics of the model, we assume infinite size and no spatial structure in the ecosystem, meaning each site in the system is equally likely to be occupied. The probability of any site being occupied is same as the global occupancy. Therefore, the transition rates in this model are as follows. Transition rate for a site to change from 1 to 0 :

$$\begin{aligned} \omega (1 \rightarrow 0) = d (1-\rho ) + (1-q){\text {d}}\rho \end{aligned}$$

(Here d is the death rate, not the symbol for a differential). Similarly, transition rate from 0 to 1:

$$\begin{aligned} \omega (0 \rightarrow 1) = p \rho + q\rho ^2. \end{aligned}$$

Probability of finding a site in occupied(1) state : $P(1)=\rho$ and probability of finding a site in state in empty(0) site: $P(0)=(1-\rho )$

The master equation can then be written as:

$$\begin{aligned} \frac{{\text {d}}P(1)}{{\text {d}}t} = \omega (0 \rightarrow 1)P(0) - \omega (1 \rightarrow 0) P(1). \end{aligned}$$

Substituting the above transition rates,

$$\begin{aligned} \frac{{\text {d}}\rho }{{\text {d}}t}= f(\rho ) = (p-d)\rho - (p-q-qd)\rho ^2 - q\rho ^3. \end{aligned}$$

(14)

For simplicity, the above equation can be written in terms of a, b and c as:

$$\begin{aligned} f(\rho ) = a\rho - b\rho ^2 - c\rho ^3, \end{aligned}$$

(15)

where $a=p-d$, $b=p-q-qd$ and $c=q$. At equilibrium, $\frac{{\text {d}}\rho }{{\text {d}}t}=0$. This gives the following equilibria:

$$\begin{aligned} \rho \text {*}=0 , \rho \text {*} = -\frac{b}{2c}+\root \of {\frac{b^2}{4c^2} + \frac{a}{c}}\text { and } \rho \text {*} = -\frac{b}{2c}-\root \of {\frac{b^2}{4c^2} + \frac{a}{c}}. \end{aligned}$$

We call these solutions as $\rho _0$ , $\rho _A$ and $\rho _B$ respectively. For the above equilibria to be stable, $f'(\rho \text {*})<0$.

From (15), we get:

$$\begin{aligned} f'(\rho )= & {} a\rho - b \rho ^{2} -c \rho ^{3}\nonumber \\ f'(\rho )|_{\rho _0}= & {} a \nonumber \\ f'(\rho )|_{\rho _A}= & {} -2a - \frac{b^2}{2c} + b \root \of {\frac{a}{c}+ \frac{b^2}{4c^2}} \nonumber \\ f'(\rho )|_{\rho _B}= & {} -2a - \frac{b^2}{2c} - b \root \of {\frac{a}{c}+ \frac{b^2}{4c^2}}. \end{aligned}$$

(16)

In this analyses, we consider $c>0$ because $c=q$ in our model which is a probability. From the above three equilibrium densities, only real and positive solutions are realistic. Therefore, we will reject the negative solutions. For the non-zero solutions to be real, $a>-\frac{b^2}{4c}$

1.1 Case 1: $b>0$

In this parameter region, given $a>-\frac{b^2}{4c}$, $\rho _B$ is always negative. Therefore, the mean-field equation has only two solutions $\rho _0$, which is stable for $a<0$ and $\rho _A$, which is stable for $a>0$. At $a=0$, $\rho _A = 0$ and it increases monotonically after that. The mean-field system undergoes a continuous transition (also called second-order transition or trans-critical bifurcation) at a critical point $a=0$ for all values of $b>0$.

1.2 Case 2: $b<0$

In this parameter regime, $\rho _0$ is stable for $a<0$ and unstable for $a>0$. $\rho _B$ is real and positive only when $\frac{-b^2}{4c}< a < 0$ and it is unstable in this regime. $\rho _A$ is stable for $a \ge \frac{-b^2}{4c}$. At $a = \frac{-b^2}{4c}$, $\rho _A = \frac{|b|}{2c}$. The mean-field system shows a saddle-node bifurcation at the point $(a,\rho ^*) = (\frac{-b^2}{4c}, \frac{|b|}{2c})$. The transition from an active phase (vegetated state) to absorbing phase (bare state) is discontinuous.

In the mean-field approximation, our model undergoes a continuous transition when $b>0$ and a discontinuous transition when $b<0$. The system has a tri-critical point at $a=0, b=0$ where the nature of transition changes from continuous to discontinuous. Now, translating it back to our system (Eq. 14) with parameters p, q and d,the tri-critical point occurs at $p_t=d$ and $q_t=\frac{d}{1+d}$. For $q<q_t$, continuous phase transition occurs at $p_c=d$. However, the critical point ($p_{c_1}$) decreases as a function of q when $q>q_t$. Therefore, in discontinuous regime, the vegetated state can sustain harsher conditions represented by low values of p when strength of positive feedback among plants is high. However, when the external conditions pass a threshold, the system collapses abruptly to the bare state.

Appendix B: Pair approximation

In the mean-field approximation, we assumed that each site on the lattice has equal probability of being occupied by a plant and that there are no spatial fluctuations in the system. We now incorporate the local spatial effects in the master equation. We assume that the probability of occupancy of a site depends on the state of its nearest neighbours. Therefore, we introduce conditional probability $q_{i|j}$ defined as probability that a site is in state i given its nearest neighbour is in state j. In this approximation we have singlet density $\rho _1$ (same as mean-field approximation) and an additional doublet density ($\rho _{ij}$) defined as the probability of a site being in state i and its neighbour being in state j. The pair ij has the following properties in this approximation.

$$\begin{aligned} \rho _{ij} = \rho _{ji} \quad \rho _{ij} = \rho _i~q_{j|i} \quad q_{j|i} = 1- q_{i|i}. \end{aligned}$$

(17)

Note that i and j can be 0 or 1. For singlet density ($\rho _1$), the master equation can be written as:

$$\begin{aligned} \frac{{\text {d}}\rho _1}{{\text {d}}t} = \omega (0 \rightarrow 1)\rho _0 - \omega (1 \rightarrow 0) \rho _1. \end{aligned}$$

(18)

The transition rates $\omega (0 \rightarrow 1)$ and $\omega (1 \rightarrow 0)$ are defined as follows:

$$\begin{aligned}&\omega (0 \rightarrow 1)= p~q_{1|0} + q~q_{1|0}~q_{1|1} \nonumber \\&\quad \text {and} \quad \quad \omega (1 \rightarrow 0) = d~q_{0|1} - (1-q)~d~q_{1|1}. \end{aligned}$$

(19)

Here p is the baseline birth probability, q is the positive feedback parameter and d is the death probability. Substituting Eq. (19) in Eq. (18) and using the fact that $\rho _{ij} = \rho _{ji}$ and $\rho _{ij} = \rho _i~q_{j|i}$ (Eq. 17) we obtain the following form for the master equation

$$\begin{aligned} \frac{{\text {d}}\rho _1}{{\text {d}}t} = \left\{ p~q_{0|1} + q~q_{1|1}~q_{0|1} - d~q_{0|1} - (1-q)~d~q_{1|1} \right\} \rho _1.\nonumber \\ \end{aligned}$$

(20)

Similarly, for the doublet density ($\rho _{11}$), the master equation can be written as

$$\begin{aligned} \frac{{\text {d}}\rho _{11}}{{\text {d}}t}= & {} \omega (10 \rightarrow 11)\rho _{10} + \omega (01 \rightarrow 11)\rho _{01} \nonumber \\&- \omega (11 \rightarrow 01)\rho _{11} - \omega (11 \rightarrow 10)\rho _{11}\nonumber \\= & {} 2 \lbrace \omega (10 \rightarrow 11)\rho _{10}\rbrace - 2 \lbrace \omega (11 \rightarrow 10)\rho _{11}\rbrace . \end{aligned}$$

(21)

The transition rate $\omega (10 \rightarrow 11)$ is defined as

$$\begin{aligned} \omega (10 \rightarrow 11)= & {} \frac{1}{z}~p + \frac{z-1}{z}~p~q_{1|0}\nonumber \\&+ \frac{1}{z}~q~q_{1|1} + \frac{z-1}{z}~q~q_{1|0}~q_{1|1}. \end{aligned}$$

(22)

Here z is the number of nearest neighbours. The first term represents the rate of the event in which the 1 in the pair 10 reproduces at 0 with probability p. The second term represents the rate of the event in which a neighbour of 0 in the pair 10 other than the 1 in the pair is also 1 (we call such neighbours as non-pair neighbours; this occurs with probability $q_{1|0}$) and it reproduces at 0 with probability p. The next two terms represent the growth rate due to positive feedback. The third term represents the event in which a non-pair neighbour of the 1 in 10 is also occupied (this occurs with probability $q_{1|1}$) and a birth occurs with enhanced probability q at 0 of the pair. The last term represents the event in which a non-pair neighbour of the 0 in 10 is occupied (this occurs with probability $q_{1|0}$) and its next neighbour is also occupied (this occurs with probability $q_{1|1}$) and a birth occurs at the 0 of the pair with enhanced probability q.

Similarly, we define the transition rate $\omega (11 \rightarrow 10)$ as

$$\begin{aligned} \omega (11 \rightarrow 10)= & {} \frac{1}{z}(1-q)~d \nonumber \\&+ \frac{z-1}{z}(1-q)~d~q_{1|1} + \frac{z-1}{z}d~q_{0|1}.\qquad \end{aligned}$$

(23)

The first term represents the rate of the event in which a 1 in the pair 11 dies with a diminished probability $(1-q)d$ due to the facilitative interaction with the other 1 of the pair. The second term represents the rate of the event in which a non-pair neighbour of 1 in the pair 11 (which we call focal to distinguish it from the other 1 of the pair) is occupied (this occurs with probability $q_{1|1}$) and the focal 1 dies with a diminished probability $(1-q)d$ due to the facilitative interaction with this non-pair neighbour. The third term represents the rate of the event in which a non-pair neighbour of the focal 1, is 0 (this occurs with probability $q_{0|1}$) and the focal 1 dies with probability d.

Fig. 5

Bifurcation diagram obtained by pair approximation analysis. A and B show the continuous and discontinuous transitions at $q<q_t$ and $q>q_t$ respectively. C is the full phase diagram as a function of q and p.The black dot represents the tri-critical point $q=q_t$ at which the nature of transition changes from continuous to discontinuous. The region between solid and dotted black lines is the bistable region

Substituting Eqs. (22) and (23) in Eq. (21), the master equation for the doublet density takes the following form

$$\begin{aligned} \frac{{\text {d}}\rho _{11}}{{\text {d}}t}= & {} 2 \left\{ \lbrace \frac{1}{z} p +\frac{z-1}{z} p~q_{1|0} \right. \nonumber \\&\left. + \frac{1}{z} q~q_{1|1} + \frac{z-1}{z} q~q_{1|0}~q_{1|1} \rbrace \rho _{10} \right\} \nonumber \\&-2\left\{ \lbrace \frac{1}{z}(1-q)~d + \frac{z-1}{z}(1-q)~d~q_{1|1} \right. \nonumber \\&\left. + \frac{z-1}{z}d~q_{0|1}\rbrace \rho _{11} \right\} . \end{aligned}$$

(24)

We are interested in two dimensional landscapes modelled by a square lattice. We use a von-Newmann neighbourhood $(z=4)$ in all our analyses. Note that using the properties in Eq. (17), we may write $\rho _{10}=(q_{0|1}/q_{1|1})\rho _{11}.$ Further, we may write $q_{1|1}=1-q_{0|1}.$ Substituting these in Eqs. (20) and (24) we obtain

$$\begin{aligned} \frac{{\text {d}}\rho _1}{{\text {d}}t}= & {} M_1 \rho _1 \\ \frac{{\text {d}}\rho _{11}}{{\text {d}}t}= & {} M_{11} \rho _{11} \end{aligned}$$

$M_{1}$ and $M_{11}$ are defined as follows

$$\begin{aligned} M_1= & {} p~q_{0|1} + q~(1-q_{0|1})~q_{0|1} \nonumber \\&- d~q_{0|1} - (1-q)d~(1-q_{0|1}) \end{aligned}$$

(25)

$$\begin{aligned} M_{11}= & {} 2 \left( ~\frac{1}{4}~p~\frac{q_{0|1}}{(1-q_{0|1})} + \frac{3}{4} p~q_{1|0}~\frac{q_{0|1}}{(1-q_{0|1})}\right. \nonumber \\&\left. + \frac{1}{4} q~q_{0|1} +\frac{3}{4} q~q_{1|0}~q_{0|1} \right) \nonumber \\&- 2 \left( ~\frac{1}{4}(1-q)~d + \frac{3}{4} (1-q)~d~(1-q_{0|1})\right. \nonumber \\&\left. + \frac{3}{4} q_{0|1}~d ~\right) \end{aligned}$$

(26)

$\rho _1 = 0$ and $\rho _{11}=0$ give the trivial equilibria. In addition, $M_1 = 0$ and $M_{11}= 0$ provide other equilibria of the system. To ease the notation, we substitute $q_{0|1}=\mathbf{a}$ in Eq. (25), set $M_{1}=0$ and simplify to obtain a quadratic equation in $\mathbf{a}$

$$\begin{aligned} q \mathbf{a^2} - \left[ p + q(1-d) \right] \mathbf{a} + d(1-q) = 0. \end{aligned}$$

(27)

Assuming $q \ne 0$, the two solutions $\mathbf{a_+}$ and $\mathbf{a_-}$ are:

$$\begin{aligned} \mathbf{a_+}= & {} \frac{p + q(1-d) + \sqrt{ \left[ p+q(1-d)\right] ^2 - 4q(1-q)d }}{2q},\qquad \end{aligned}$$

(28)

$$\begin{aligned} \mathbf{a_-}= & {} \frac{p + q(1-d) - \sqrt{ \left[ p+q(1-d)\right] ^2 - 4q(1-q)d }}{2q}.\qquad \end{aligned}$$

(29)

Now, we substitute $q_{0|1}=\mathbf{a}$ and $q_{1|0} = \mathbf{b}$ in Eq. (26), set $M_{11}=0$ and simplify to obtain a solution for $\mathbf{b}$ assuming $3 {\mathbf {a}} [p + q(1- {\mathbf {a}})] \ne 0$

$$\begin{aligned} {\mathbf {b}} = \frac{ (1-{\mathbf {a}})\lbrace {(1-q)d\left[ 1+3(1-{\mathbf {a}})\right] + {\mathbf {a}}\left( 3d-q\right) \rbrace } - p{\mathbf {a}}}{3 {\mathbf {a}} [p + q(1- {\mathbf {a}})]}.\nonumber \\ \end{aligned}$$

(30)

Density ($\rho _1$) can be calculated from $q_{0|1}$ and $q_{1|0}$ as following

$$\begin{aligned} \rho _1= & {} \frac{\rho _{10}}{q_{0|1}} = \frac{\rho _{01}}{q_{0|1}} = \frac{\rho _0~q_{1|0}}{q_{0|1}} \nonumber \\ \rho _1~q_{0|1}= & {} (1-\rho _1)~q_{1|0} \nonumber \\ \rho _1= & {} \frac{q_{1|0}}{q_{0|1}+q_{1|0}} = \frac{\mathbf{b}}{\mathbf{a}+\mathbf {b}}. \end{aligned}$$

(31)

Therefore, the steady-state density can be calculated from Eq. (31) where a and b can be obtained from Eqs. (28), (29) and (30).

1.1 Case 1: No positive feedback ($q=0$)

The master equation for the singlet and doublet density reduces to the contact process when $q=0$ [64]. We know that the contact process model undergoes a continuous phase transition [65], where density of active cells (vegetation density in our case) decreases to zero continuously. Therefore, at the critical point ($p_c$), the density ($\rho _1$) goes to zero. Substituting $q=0$ and $p=p_{{\text {c}}}$ in Eq. (27)

$$\begin{aligned} -p_{\text {c}} \mathbf{a} + d = 0 \implies \mathbf{a} = \frac{d}{p_{\text {c}}}. \end{aligned}$$

Because $\rho _1 = 0$ at $p=p_{{\text {c}}}$, Eq. (31) implies $\mathbf{b} = 0.$ Substituting $q=0$, $p=p_{{\text {c}}}$, ${\mathbf {a}}=d/p_{{\text {c}}}$ and ${\mathbf {b}}=0$ in Eq. (30), assuming $d \ne 0$ and simplifying we get

$$\begin{aligned} p_{{\text {c}}} = \frac{4}{3}d. \end{aligned}$$

(32)

Thus, given that the contact process exhibits a continuous phase transition, the pair approximation predicts a critical point $p_{\text {c}}=\frac{4d}{3}.$ This result is consistent with the results of [64].

1.2 Case 2: With positive feedback ($q>0$)

Now, we investigate the role of positive feedback on phase transition in our model. For $q>0$, ${\mathbf {a}}$ will have two solutions given by Eqs. (28) and (29). Therefore, substituting these in Eq. (30) to obtain ${\mathbf {b}}$ and then substituting ${\mathbf {a}}$ and ${\mathbf {b}}$ in Eq. (31), vegetation density will have two non-zero values for some values of p and d. From mean-field approximation, we know that one of these solutions is stable and the other is unstable. The region in parameter space where these two solutions (one stable and one unstable) coexist and are positive will show the discontinuous transition. Indeed for a fixed $d=0.3$, the system shows continuous transition for low values of q and discontinuous transition for high values of q.

We define the critical point $p=p_{{\text {c}}}$ as the point where vegetation density drops to zero. At the critical point for discontinuous transition, two non-zero solutions of $\rho _1$ (one stable and one unstable) meet. This occurs where determinant in Eq. (28) or Eq. (29) vanishes.

$$\begin{aligned} \left[ p_{\text {c}} +q(1-d)\right] ^2 - 4q(1-q)d = 0. \end{aligned}$$

Since $p_c, q$ and d are non-negative, we have

$$\begin{aligned} p_c = \sqrt{4q(1-q)d} - (1-d)q. \end{aligned}$$

At the tri-critical point ($q=q_t$), the transition changes from continuous to discontinuous (see 5). Therefore, at this point, the critical density (defined as the density at which transition occurs) is zero. Substituting these values in Eq. (30) for $d=0.3$, we get, $(p_t,q_t)=(0.27,0.36)$.

In the continuous transition regime ($q<q_t$), unlike the mean-field approximation, critical point decreases as a function of q. This shows that in our model, positive feedback in the systems with local spatial interactions helps the system sustain its vegetated state in harsh conditions which are represented as low values of p. Note that we did not perform stability analysis for this model. However, it is reasonable to assume that the stability of the equilibria will remain the same as the mean-field model. The bifurcation diagram obtained by the pair approximation is shown in Fig. 5. It is qualitatively same as the output of mean-field model. However, it is clear that the vegetated state is sustained for harsher conditions because there is a reduction in the area of the bare state region. The region of bistability is also reduced in this approximation. Therefore, it can be concluded that local spatial interactions increase the resilience of the system as compared to well-mixed system. This effect of local spatial interactions is the opposite of the effect of the demographic noise as shown in Fig. 3. The real system with both the local interactions and finite-size can show the dynamics resulting from the interplay between these two effects.