A new chaotic system with different equilibria and attractors

Abstract

This paper presents an interesting four-dimensional chaotic system with different equilibria and attractors. The proposed system has three quadratic nonlinearities and has no equilibrium, three equilibria and infinite equilibria for different regions of system parameters. As the values of parameters change, the system performs stable, periodic and chaotic states. Also it has period-doubling bifurcation which leads to chaos and has Hopf bifurcation which makes the system loses stability. Moreover, the system generates hidden chaotic attractor when it has no equilibria and generates coexisting chaotic attractors for different initial values. The electronic circuit implementation of the system is given to illustrate the corresponding dynamical properties of the system.

1 Introduction

Chaos refers to an interesting physical phenomenon featured by highly sensitivity to initial conditions. There is a popular belief that it has a wide range of engineering applications, including image encryption, secure communication, weather forecast, path planning, etc. [1,2,3,4]. In the last few decades, a large number of important achievements in chaos research have emerged attribute to the discovery of famous Lorenz attractor [5]. Pecora and Carrol proposed the concept of chaos synchronization which is the basis of chaotic secure communication [6]. Chen et al. established a simple and rigorous control method for chaotification [7].

Fig. 1

Bifurcation diagram and LEs of system (1) versus the parameter $a \in [5,10]$

Fig. 2

Hidden periodic and chaotic attractors of system (1): a $a=5$; b $a=7$; c $a=8$; d $a=10$

Fig. 3

Bifurcation diagrams and LEs of system (1) versus the parameter $a \in [7,12]$ from initial values (1, 1, 1, 1) (red color), $( - 1, - 1,1, - 1)$ (blue color)

A dynamical system with chaotic solution is usually called chaotic system. One commonly used method to judge the chaotic system is the Lyapunov exponent spectrum. It suggests that a bounded system with positive largest Lyapunov exponent is chaotic. Basically so many chaotic systems have been discovered in recent years [8,9,10,11,12]. The equilibrium usually plays an important influence on the dynamical properties of chaotic system. Some chaotic systems were created and classified by considering their equilibria. Sprott et al. proposed a class of chaotic systems with only one unstable node and an attracting torus inspiring the coexistence of chaos and limit cycle [13]. Jafari et al. produced seventeen no-equilibrium chaotic flows with hidden attractors whose basins of attraction are far away the neighborhoods of equilibria [14]. Yu et al. constructed multi-wing chaotic attractors from Lorenz-type systems by configuring multiple 2-index saddle foci [15]. Lai found an interesting chaotic system with infinite equilibria, that can generate infinite coexisting chaotic attractors from different initial conditions [16]. Wang and Chen created a novel chaotic system with any number of symmetric equilibria and ring attractor [17]. Molaie et al. presented twenty-three chaotic flows with only one stable equilibrium [18]. Mezatio et al. proposed six-dimensional system with hyperchaos and coexisting infinite hidden attractors [19]. Pham et al. presented the dynamical analysis and circuit realization of no-equilibrium system with hidden chaos and boostable variable [20]. Nazarimehr et al. investigated the circuit design and entropy of three-dimensional chaotic flow with one unstable equilibrium and symmetric coexisting attractors [21]. Tuna et al. considered the complex dynamics, FPGA realization and random number generator analysis of hyperjerk multiscroll oscillators with megastability [22]. Singh et al. proposed a new class of four-dimensional hyperchaotic and chaotic systems with surfaces of equilibria and coexisting attractors [23]. Recently, the studies of hidden attractors and coexisting attractors have attracted a lot of attention. The no-equilibrium system is found to be able to generate hidden attractors, and the system with multiple equilibria is easy to produce coexisting attractors. Thereby some chaotic systems with hidden attractors or coexisting attractors were established by focusing on the study of their equilibria [24,25,26].

In all known chaotic systems, there are few examples of chaotic systems which have both hidden attractors and coexisting attractors. So this paper will construct a new chaotic system whose equilibria are determined by the parameters. The proposed system has the following features: (i) it generates from an existing three-dimensional chaotic system by simple linear feedback control; (ii) it is a dissipative system with three quadratic nonlinearities; (iii) it has no equilibrium, three equilibria, infinite equilibrium for different values of parameters; (iv) it has hidden attractors and coexisting attractors; (v) it performs period-doubling bifurcation and Hopf bifurcation. Dynamical behaviors and circuit implementation of the system will be given.

2 The new system

The new system studied in this paper is given by the following fourth-order ordinary differential equations:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {\dot{x} = - ay + yz + m}\\ {\dot{y} = - x + y - w}\\ {\dot{z} = - bz + {x^2} + c{y^2}}\\ {\dot{w} = py - kw,} \end{array}} \right. \end{aligned}$$

(1)

where x, y, z, w denote the state variables, a, b, c, p, k, m are real numbers. It is easy to verify that system (1) is dissipative since its divergence is $\nabla V = \partial \dot{x}/\partial x + \partial \dot{y}/\partial y + \partial \dot{z}/\partial z + \partial \dot{w}/\partial w = 1 - b - k < 0$ for $b + k > 1$. It suggests that the orbits of system (1) will be tend to an attractor of zero measure with the time increases infinity. By assuming $\dot{x} = \dot{y} = \dot{z} = \dot{w} = 0$ and $a>0$, $b>0$, $c>0$, we obtain the equilibria of system (1) as follows.

• (i) For $p \ne 0, k = 0, m \ne 0$, system (1) has no equilibrium. All the attractors in system (1) are hidden attractors.

• (ii) For $p \ne 0,k \ne 0,m = 0$, system (1) has three equilibria O(0, 0, 0, 0), ${S_{1,2}}( \pm (k - p)q/k, \pm q,a, \pm pq/k)$, where $q = k\sqrt{ab} /\sqrt{{{(k - p)}^2} + c{k^2}}$. The eigenvalue $\lambda$ of equilibrium O meets the characteristic equation $(\lambda + b)[{\lambda ^3} + (k - 1){\lambda ^2} + (p - a - k)\lambda - ak] = 0$. We can easily verify that this equation has at least one root with positive real part. Thereby the equilibrium O is unstable. The eigenvalue $\mu$ of equilibria ${S_{1,2}}$ meets the following characteristic equation:

  $$\begin{aligned} {\mu ^4} + {s_1}{\mu ^3} + {s_2}{\mu ^2} + {s_3}\mu + {s_4} = 0, \end{aligned}$$

  (2)

  where ${s_1} = b + k - 1$, ${s_2} = bk + p - b - k - 2r{q^2}$, ${s_3} = bp - bk + 2c{q^2} - 2r{q^2}(k - 1)$, ${s_4} = 2(ck + rk - pr){q^2}, r = (k - p)/k$. The Routh–Hurwitz stability criterion suggests that all the roots of Eq. (2) are in the left half of the complex plane if and only if ${s_i} > 0(i = 1,2,3,4)$, ${s_1}{s_2} > {s_3}$, ${s_1}{s_2}{s_3} > s_3^2 + s_1^2{s_4}$. Accordingly the equilibria ${S_{1,2}}$ are stable as long as these conditions are satisfied.

• (iii) For $p \ne 0,k = 0,m = 0$, system (1) has infinite equilibria which can be described by the set $\Omega = \{ (\tilde{x},\tilde{y},\tilde{z},\tilde{w})\left| {\tilde{y} = 0,\tilde{z} = {{\tilde{x}}^2}/b,\tilde{w} = - \tilde{x},\tilde{x} \in R\} } \right.$. The eigenvalues of these equilibria satisfy the characteristic equation $\lambda (\lambda + b)({\lambda ^2} - \lambda + p + a - \tilde{z}) = 0$. Thus, we can conclude that all these equilibria are unstable.

Fig. 4

Different attractors of system (1): a $a=8$; b $a=9$; c $a=10$; d $a=10.5$; e $a=11$

Fig. 5

Bifurcation diagram and LEs of system (1) versus the parameter $b \in [8,16]$

3 Dynamical analysis

The dynamical properties of system (1) are presented in this section by numerical methods. The dynamical evolution with respect to system parameters are studied using the bifurcation diagrams and Lyapunov exponents (LEs). Simulation results show that system (1) will perform different attractors for different values of parameters. What is particularly surprising is that system (1) has hidden attractors and coexisting attractors.

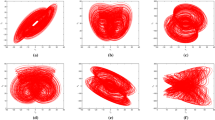
Let $b=8$, $c=4$, $p=1$, $k=0$, $m=5$, then system (1) has no equilibrium and all its attractors are hidden attractors. Figure 1 presents the bifurcation diagram and LEs of system (1) with respect to the parameter $a \in [5,10]$. It shows that system (1) produces chaos via period-doubling bifurcation with the increase of a. Figure 2 gives the phase portraits of its hidden periodic and chaotic attractors for parameter values $a=5,7,8,10$ which can also illustrate the existence of period-doubling bifurcation.

Fig. 6

The phase projection on $x-z$, time series of z and Poincaré maps on plane $y=0$ of system (1) with $b=12$

Fig. 7

Bifurcation diagrams and LEs of system (1) versus the parameter $p \in [8,16]$

Fix $b=8$, $c=4$, $p=4$, $k=4$, $m=0$, and vary the parameter $a \in [7,12]$, then we can generate the bifurcation diagrams and LEs of system (1) from initial values $x_ + ^0 = (1,1,1,1)$ (red color), $x_ - ^0 = ( - 1, - 1,1, - 1)$ (blue color) to show the appearance of its coexisting attractors, as illustrated in Fig. 3. The overlapping red and blue color branches in Fig. 3a imply that system (1) yields the same attractor for these two initial values, while the separated branches imply the generation of different attractors. Figure 3a also shows the process of period-doubling bifurcation of system (1). With the increase of a, system (1) experiences single periodic state $\rightarrow$ double periodic states $\rightarrow$ double chaotic states $\rightarrow$ single chaotic state, which can be illustrated by plotting the phase portraits of system (1) for $a=8,9,10,10.5,11$ as shown in Fig. 4.

Fig. 8

Different attractors of system (1): a $p=3$; b $p=4$; c $p=5$; d $p=6$; e $p=7$

Let $a=10$, $c=4$, $p=5$, $k=0$, $m=0$, then we can generate the bifurcation diagrams and LEs of system (1) versus the parameter $b \in [8,16]$ from initial value $x_ + ^0 = (1,1,1,1)$, as illustrated in Fig. 5. It is clear that system (1) is chaotic in the large area of $b \in [8,16]$. The chaotic attractor of system (1) with $b=12$ are given in Fig. 6. The LEs are numerically computed as $L{E_1} = 0.4365$, $L{E_2} = 0.0000$, $L{E_2} = - 0.1771$, $L{E_2} = - 11.2594$. Accordingly, the Lyapunov dimension is ${D_{LE}} = 3.0382$ which is fractional.

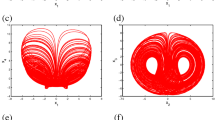
Fix $a=10$, $b=8$, $c=4$, $k=4$, $m=0$, then we can plot the bifurcation diagrams and LEs of system (1) versus $p \in [2,8]$ as shown in Fig. 7, where the red and blue color branches in Fig. 7a are, respectively, generated from initial values $x_ + ^0 = (1,1,1,1)$, $x_ - ^0 = ( - 1, - 1,1, - 1)$. Figure 7 gives three observations of system (1) with the variation of p: (i) it performs chaotic, periodic and stable states; (ii) it has period-doubling bifurcation and Hopf bifurcation; (iii) it coexists different attractors in phase space. Figure 8 shows different states of system (1): (i) single chaos with $p=3$ in Fig. 8a; (ii) double limit cycles with $p=4,5$ in Fig. 8b, c; (iii) single limit cycle with $p=6$ in Fig. 8d; (iv) double stable states with $p=7$ in Fig. 8e. When $p=7$, system (1) has two stable equilibria ${S_{1,2}}( \mp {{36}}{{.9231,}} \pm {{49}}{{.2308}},10, \pm {{86}}{{.1538)}}$ with the eigenvalues ${\lambda _{1,2}} = - 1.3165 \pm 60.1188i,{\lambda _{3,4}} = - {{4}}{{.1835}} \pm {{2}}{{.6387i}}$, and Fig. 8e presents that system (1) has double stable states for $p=7$.

Fig. 9

The circuit diagram of system (1)

4 Circuit design

The circuit implementation of chaotic systems is of important practical significance. It can turn the chaotic signals into reality by transforming the theoretical mathematical model of chaotic system into circuit model, and prove the existence of chaos and other dynamical behaviors of the system via hardware device. An important prerequisite for all chaotic signals to be applied is that they can be realized in practice. So the circuit implementation of chaos is an indispensable research content in chaos research. This section presents the circuit implementation of system (1) for realizing its chaotic attractor and coexisting attractors.

Fig. 10

Chaotic attractor of system (1) from the oscilloscope for $a=10$, $b=8$, $c=4$, $p=1$, $k=0$, $m=5$

Fig. 11

Coexisting chaotic attractors of system (1) from the oscilloscope for $a=10.5$, $b = 8$, $c = 4$, $p = 4$, $k = 4$, $m = 0$

The circuit contains four output channels which correspond to variables x, y, z, w of system (1), and we can observe the phase portraits from the oscilloscope connected with output channels. According to the mathematical model of system (1), we can design the corresponding circuit as shown in Fig. 9, where $S_1$, $S_2$, $S_3$, $S_4$ are switches and $U_1$, $U_2$, $U_3$, $U_4$ are integrators. The values of capacitors are fixed as $C_1 = C_2 = C_3 = C_4 = 10\mathrm{{nF}}$. To realize the hidden chaotic attractor of system (1) for $a=10$, $b=8$, $c=4$, $p=1$, $k=0$, $m=5$ shown in Fig. 1d and the coexisting chaotic attractors of system (1) for $a=10.5$, $b = 8$, $c = 4$, $p = 4$, $k = 4$, $m = 0$ shown in Fig. 4d, we fix the values of elements of Fig. 9 as follows:

$$\begin{aligned} \begin{array}{l} {R_{1a}} = 50\;\mathrm{{k\Omega ,}}{R_{1b}} = 47.619\;\mathrm{{k\Omega ,}}{R_2} = 50\;\mathrm{{k\Omega ,}}\\ {R_3} = 12.5\;\mathrm{{k\Omega ,}}{R_4} = 5\mathrm{{k\Omega }}, {R_5} = 50\;\mathrm{{k\Omega }}, {R_6} = 50\;\mathrm{{k\Omega }},\\ {R_7} = 6.25\;\mathrm{{k\Omega }},{R_8} = 20\;\mathrm{{k\Omega }},{R_9} = 500\;\mathrm{{k\Omega }}, {R_{10a}} = 50\;\mathrm{{k\Omega ,}}\\ {R_{10b}} = 12.5\;\mathrm{{k\Omega ,}}{R_{11}} = 12.5\;\mathrm{{k\Omega ,}}\\ {R_{12}} = {R_{13}} = 10\;\mathrm{{k\Omega ,}}V = 0.5\;\mathrm{{V}}. \end{array} \end{aligned}$$

Switching the $S_1$ to ‘a’, $S_2$ to ‘c’, $S_3$ to ‘e’, and breaking the $S_4$, we can observe the corresponding hidden chaotic attractors from the oscilloscope, as shown in Fig. 10. Switching the $S_1$ to ‘b’, $S_2$ to ‘d’, $S_3$ to ‘f’, and closing the $S_4$, we can observe the corresponding coexisting chaotic attractors from the oscilloscope, as shown in Fig. 11, which has good accordance with the Fig. 4d. Also, we can verify other dynamical behaviors of system (1) by fixing other values of circuit elements.

5 Conclusions

A new dissipative chaotic system was studied in this paper. The system has no equilibrium, three equilibria and infinite equilibria for different values of parameters. The stabilities of the equilibria were discussed. The dynamical behaviors (including the hidden attractors, coexisting attractors, period-doubling bifurcation, etc.) were numerically investigated. Interestingly, the system has hidden chaotic attractors when it has no equilibrium and has a pair of symmetric point, or periodic, or chaotic attractors for different initial values. Finally, the circuit implementation gave a good observation on the physically existence of the system. There are many important research issues on chaotic systems with hidden attractors and coexisting attractors still need to be investigated, including the formation mechanism analysis of hidden attractors and coexisting attractors, the unified methods for constructing hidden attractors and coexisting attractors, the new technologies for control hidden attractors and coexisting attractors, the actual engineering applications of hidden attractors and coexisting attractors, etc. On the one hand, we can continue to consider the applications of chaotic systems with hidden attractors and coexisting attractors in some traditional application areas of chaos. On the other hand, we can explore the new applications of hidden attractors and coexisting attractors of chaotic systems. There is some evidence that chaotic systems with coexisting attractors have better flexibility and plasticity in engineering application. In the future, more valuable research results will be achieved.