A Three-Dimensional Chaotic System with Square Equilibrium and No-Equilibrium

Abstract

Recently, Leonov and Kuznetsov have introduced a new definition “hidden attractor”. Systems with hidden attractors, especially chaotic systems, have attracted significant attention. Some examples of such systems are systems with a line equilibrium, systems without equilibrium or systems with stable equilibria etc. In some interesting new research, systems in which equilibrium points are located on different special curves are reported. This chapter introduces a three-dimensional autonomous system with a square-shaped equilibrium and without equilibrium points. Therefore, such system belongs to a class of systems with hidden attractors. The fundamental dynamics properties of such system are studied through phase portraits, Poincaré map, bifurcation diagram, and Lyapunov exponents. Anti-synchronization scheme for our systems is proposed and confirmed by the Lyapunov stability. Moreover, an electronic circuit is implemented to show the feasibility of the mathematical model. Finally, we introduce the fractional order form of such system.

1 Introduction

Chaos theory, chaotic systems, and chaos-based applications have been studied in last decades [5,6,7,8, 18, 19, 54, 71, 76, 106]. A significant amount of new chaotic systems has been introduced and discovered such as Lorenz [54], Rössler system [66], Arneodo system [4], Chen system [18], Lü system [55], Vaidyanathan system [83], time-delay systems [11], nonlinear finance system [78], four-scroll chaotic system [2].

Chaotic systems, that are highly sensitive to initial conditions, were applied in different areas. A new four-scroll chaotic system was used to design a random number generator [2]. Tang et al. implemented image encryption using chaotic coupled map lattices with time-varying delays [79]. Reconfiguration chaotic logic gates based on novel chaotic circuit were discovered in [12]. Chenaghlu et al. introduced a novel keyed parallel hashing scheme based on a new chaotic system [20]. Kajbaf et al. proposed fast synchronization of non-identical chaotic modulation-based secure systems using a modified sliding mode controller [38]. A new hybrid algorithm based on chaotic maps for solving systems of nonlinear equations was presented in [44]. Tacha et al. studied analysis, adaptive control and circuit simulation of a novel nonlinear finance system [78]. Performance improvement of chaotic encryption via energy and frequency location criteria was studied in [70]. Orlando investigated a discrete mathematical model for chaotic dynamics in economics [58].

Recent developments include systems with hidden attractors which are important in engineering applications [34, 35, 48, 61, 85, 110, 112]. Especially, chaotic systems with hidden attractors such as chaotic systems without any equilibrium points, chaotic systems with infinitely many equilibrium points and chaotic systems with stable equilibria have been introduced [34, 35, 43, 56, 99]. Finding new chaotic systems with different families of hidden attractors should be studied further.

In this chapter, we introduce a novel three-dimensional (3D) chaotic system. Especially the new system displays both hidden chaotic attractor with square equilibrium and hidden chaotic attractor without equilibrium. This chapter is organized as follows. The related works are reported in the next section. Section 3 presents the theoretical model of the new system. Dynamics and properties of the new system are investigated in Sect. 4 while the adaptive anti-synchronization scheme for such new system is proposed in Sect. 5. Section 6 presents circuital implementation of the theoretical model. Moreover, fractional-order form of the new no-equilibrium system is described in Sect. 7. Finally, conclusions are drawn in Sect. 8.

2 Related Work

Recently, Leonov and Kuznetsov have proposed a new approach to classify nonlinear systems. They considered dynamical systems with self-excited attractors and dynamical systems with hidden attractors [46, 48, 50, 51]. A self-excited attractor has a basin of attraction that is excited from unstable equilibria. Therefore, self-excited attractors can be localized numerically by using the standard computational procedure. In contrast, hidden attractor cannot be found by using a numerical method in which a trajectory started from a point on the unstable manifold in the neighbourhood of an unstable equilibrium [34, 48]. “Hidden attractor” is important both in nonlinear theory and practical problems [45, 50, 60, 63, 69]. Thus various researches relating hidden attractors have been introduced [16, 36, 68, 73].

Hidden attractors have discovered in a smooth Chua’s system [52], in mathematical model of drilling system [49], in a relay system with hysteresis [112], in nonlinear control systems [47], in Van der Pol-Duffing oscillators [16], in a simple four-dimensional system [105], in an impulsive Goodwin oscillator with time delay [111] or in a multilevel DC/DC converter [110]. In addition, hidden chaotic attractors are observed in 3-D chaotic autonomous system with only one stable equilibrium [43], in elementary quadratic chaotic flows with no equilibria [35], in simple chaotic flows with a line equilibrium [34], in a 4-D Rikitake dynamo system [97], in 5-D hyperchaotic Rikitake dynamo system [95], in a 5-D Sprott B system [57], in a chaotic system with an exponential nonlinear term [62] or in a system with memristive devices [10].

It is interesting that chaotic systems with an infinite number of equilibrium points or without equilibrium belong to a class of dynamical systems with “hidden attractor” [35]. A few three-dimensional chaotic systems with infinite equilibria and without equilibrium have been reported. Jafari and Sprott found chaotic flows with a line equilibrium [34]. New class of chaotic systems with circular equilibrium was presented in [26]. Gotthans et al. introduced a 3-D chaotic system with a square equilibrium in [27]. By applying a tiny perturbation into the Sprott D system, Wei obtained a new system with no equilibria [101]. Wang and Chen proposed a no-equilibrium system when constructing a chaotic system with any number of equilibria [100]. Especially, Jafari et al. found a gallery of chaotic flows with no equilibria [35]. However, investigation of new systems which can display both hidden chaotic attractors with infinite equilibria and hidden chaotic attractors without equilibrium is still an attractive research direction.

3 Model of the No-Equilibrium System

Gotthans et al. proposed an interesting three-dimensional chaotic system with a square equilibrium [27]. Gotthans’s system is given by

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x} = z\\ \dot{y} = - z\left( {ay + b\left| y \right| } \right) - x\left| z \right| \\ \dot{z} = \left| x \right| + \left| y \right| - 1, \end{array} \right. \end{aligned}$$

(1)

where x, y, z are state variables, while a, b are two positive parameters. System (1) is the simplest system with a square equilibrium and chaotic behavior. Moreover it is an example of a system with hidden attractor [27].

In this work, we study a new 3-D system based on system (1):

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x} = z\\ \dot{y} = - z\left( {ay + b\left| y \right| } \right) - x\left| z \right| - c\\ \dot{z} = \left| x \right| + \left| y \right| - 1, \end{array} \right. \end{aligned}$$

(2)

in which x, y, z are state variables and a, b, c are three positive parameters. Dynamics and properties of new nonlinear system (2) are studied in the next section.

4 Dynamics and Properties of the Proposed System

The equilibrium points of system (2) are found by solving $\dot{x} = 0$, $\dot{y} = 0$, and $\dot{z} = 0$. Therefore, we have

$$\begin{aligned} z = 0, \end{aligned}$$

(3)

$$\begin{aligned} - z\left( {ay + b\left| y \right| } \right) - x\left| z \right| - c = 0, \end{aligned}$$

(4)

$$\begin{aligned} \left| x \right| + \left| y \right| - 1 = 0, \end{aligned}$$

(5)

From (3), (4), we have $z=0$ and

$$\begin{aligned} c = 0. \end{aligned}$$

(6)

Therefore system (2) has an infinite number of equilibrium points when $c=0$. Moreover equilibrium points are located on a square (5). This case has been studied in [27], so we do not discuss about it. We focus on the case for $c \ne 0$. Obviously, Eq. (6) is inconsistent when $c \ne 0$. On the other word, there is no real equilibrium in system (2). Interestingly, system (2) belongs to a newly introduced class of systems with hidden attractors because its basin of attractor does not contain neighbourhoods of equilibria [48, 50].

We consider the new system (2) for the selected parameters $a=5$, $b=3$, $c=0.02$ and the initial conditions are

$$\begin{aligned} \left( {x\left( 0 \right) ,y\left( 0 \right) ,z\left( 0 \right) } \right) = \left( {0,0.0,0} \right) . \end{aligned}$$

(7)

Lyapunov exponents, which measure the exponential rates of the divergence and convergence of nearby trajectories in the phase space of the chaotic system [72, 76], are calculated by using the algorithm in [104]. As a result, the Lyapunov exponents of the system (2) are

$$\begin{aligned} {\lambda _1} = 0.1386,{\lambda _2} = 0,{\lambda _3} = -1.1731. \end{aligned}$$

(8)

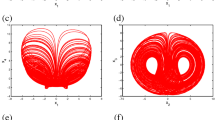
The 2-D and 3-D projections of the chaotic attractors without equilibrium in this case are illustrated in Figs. 1, 2, 3 and 4.

Fig. 1

2-D projection of system (2) in the (x, y)-plane, for $a=5$, $b=3$, $c=0.02$

Fig. 2

2-D projection of system (2) in the (x, z)-plane, for $a=5$, $b=3$, $c=0.02$

It has been known that the Kaplan–Yorke fractional dimension, which presents the complexity of attractor [23], is given by

$$\begin{aligned} {D_{KY}} = j + \frac{1}{{\left| {{\lambda _{j + 1}}} \right| }}\sum \limits _{i = 1}^j {{\lambda _i}}, \end{aligned}$$

(9)

where j is the largest integer satisfying $\sum \limits _{i = 1}^j {{\lambda _i} \ge 0}$ and $\sum \limits _{i = 1}^{j + 1} {{\lambda _i} < 0}$. Thus, the calculated fractional dimension of no-equilibrium system (2) when $a=5$, $b=3$, $c=0.02$ is

$$\begin{aligned} {D_{KY}} = 2 + \frac{{{\lambda _1} + {\lambda _2} }}{{\left| {{\lambda _3}} \right| }} = 2.1181. \end{aligned}$$

(10)

Equation (10) indicates a strange attractor. In addition, as seen in Fig. 5, the Poincaré map of system (2) in the (x, y)-plane also illustrates the strange of attractor.

Fig. 3

2-D projection of system (2) in the (y, z)-plane, for $a=5$, $b=3$, $c=0.02$

Fig. 4

3-D projection of system (2) in the (x, y, z)-space, for $a=5$, $b=3$, $c=0.02$

Fig. 5

Poincaré map of system (2) in the (x, y)-plane, for $a=5$, $b=3$, $c=0.02$

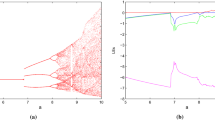
The bifurcation diagram provides a useful tool in nonlinear science. It gives the change of system’s dynamical behavior. In more details, Fig. 6 presents the bifurcation diagram of the variable y versus the parameter c. The system’s complexity has also been verified by the corresponding diagram of largest Lyapunov exponents versus the parameter c (see Fig. 7). In the regions where the value of the largest Lyapunov exponent is equal to zero the system is in a periodic state, while in the regions where the largest Lyapunov exponent has a positive value the system is in a chaotic state. As seen in Fig. 6, there is a reverse period doubling to chaos when increasing the value of parameter c from 0 to 0.15. When $c < 0.057$ a more complex behavior is emerged. For example, system exhibits chaotic behavior for $c < 0.039$. When $c > 0.057$ the system remains always in periodic states. For instant, system presents periodic behavior for $c = 0.1$ (see Fig. 8).

Fig. 6

Bifurcation diagram of system (2) when changing c for $a = 5$, $b = 3$

Fig. 7

Largest Lyapunov exponent of system (2) when varying c for $a = 5$, $b = 3$

Fig. 8

Limit cycle of system (2) for $a = 5$, $b = 3$, and $c = 0.1$

5 Adaptive Anti-synchronization of the Proposed System

Synchronization of nonlinear systems has been discovered extensively in literature because of its vital practical applications [13, 17, 22, 24, 39, 40, 59, 63, 74, 84, 86, 87, 94, 109]. Results about synchronization of various systems are reported such as synchronized states in a ring of mutually coupled self-sustained nonlinear electrical oscillators [103], ragged synchronizability of coupled oscillators [75], various synchronization phenomena in bidirectionally coupled double-scroll circuits [98], observer for synchronization of chaotic systems with application to secure data transmission was studied in [1], or shape synchronization control [33]. Futhermore different kind of synchronizations have been investigated, for example lag synchronization [65], frequency synchronization [3], projective-anticipating synchronization [31], anti-synchronization [82], adaptive synchronization [88,89,90,91, 93, 96], hybrid chaos synchronization [40], generalized projective synchronization [92], fuzzy synchronization [14, 15] or fast synchronization [38] etc. Interestingly, anti-synchronization has received significant attention [32, 42, 82, 108]. Anti-synchronization indicates the relationship between two oscillating systems that have the same absolute values at all times, but opposite signs [32, 42, 108].

In this section, the adaptive anti-synchronization of identical proposed systems with three unknown parameters is proposed. The newly introduced system (2) is considered as the master system:

$$\begin{aligned} \left\{ \begin{array}{l} {{\dot{x}}_1} = {z_1} \\ {{\dot{y}}_1} = - a{y_1}{z_1} - b\left| {y_1} \right| {z_1} - {x_1}\left| {z_1} \right| - c \\ {{\dot{z}}_1} = \left| {x_1} \right| + \left| {y_1} \right| - 1, \\ \end{array} \right. \end{aligned}$$

(11)

in which $x_1$, $y_1$, $z_1$ are state variables. The slave system is considered as the controlled system and its dynamics is described by:

$$\begin{aligned} \left\{ \begin{array}{l} {{\dot{x}}_2} = {z_2} + u_x \\ {{\dot{y}}_2} = - a{y_2}{z_2} - b\left| {y_2} \right| {z_2} - {x_2}\left| {z_2} \right| - c + u_y \\ {{\dot{z}}_2} = \left| {x_2} \right| + \left| {y_2} \right| - 1 + u_z, \\ \end{array} \right. \end{aligned}$$

(12)

where $x_2$, $y_2$, $z_2$ are the states of the slave system. Here the adaptive controls are $u_x$, $u_y$, and $u_z$. These controls will be designed for the anti-synchronization of the master and slave systems. We used A(t), B(t) and C(t) in order to estimate unknown parameters a, b and c.

The anti-synchronization error between systems (11) and (12) is given by the following relation

$$\begin{aligned} \left\{ \begin{array}{l} {e_x} = {x_1} + {x_2} \\ {e_y} = {y_1} + {y_2} \\ {e_z} = {z_1} + {z_2}. \\ \end{array} \right. \end{aligned}$$

(13)

As a result, the anti-synchronization error dynamics is described by

$$\begin{aligned} \left\{ \begin{array}{l} {{\dot{e}}_x} = {e_z} + {u_x} \\ {{\dot{e}}_y} = - a\left( {{y_1}{z_1} + {y_2}{z_2}} \right) - b\left( {\left| {y_1} \right| {z_1} + \left| {y_2} \right| {z_2}} \right) -\left( {{x_1}\left| {z_1} \right| + {x_2}\left| {z_2} \right| } \right) -2c + {u_y} \\ {{\dot{e}}_z} = \left| {x_1} \right| +\left| {x_2} \right| + \left| {y_1} \right| + \left| {y_2} \right| - 2 + {u_z}. \\ \end{array} \right. \end{aligned}$$

(14)

Our aim is to construct the appropriate controllers $u_x$, $u_y$, $u_z$ to stabilize system (14). Therefore, we propose the following controllers for system (14):

$$\begin{aligned} \left\{ \begin{array}{l} {u_x} = -{e_z} - {k_x}{e_x} \\ {u_y} = A(t) \left( {{y_1}{z_1} + {y_2}{z_2}} \right) + B(t) \left( {\left| {y_1} \right| {z_1} + \left| {y_2} \right| {z_2}} \right) + \left( {{x_1}\left| {z_1} \right| + {x_2}\left| {z_2} \right| } \right) \\ \,\quad \quad \; +2C(t) - {k_y}{e_y} \\ {u_z} = -\left| {x_1} \right| -\left| {x_2} \right| - \left| {y_1} \right| - \left| {y_2} \right| + 2 - {k_z}{e_z}. \\ \end{array} \right. \end{aligned}$$

(15)

in which $k_x$, $k_y$, $k_z$ are positive gain constants for each controllers and the estimate values for unknown system parameters are A(t), B(t), and C(t). The update laws for the unknown parameters are determined as

$$\begin{aligned} \left\{ \begin{array}{l} \dot{A} = - {e_y} \left( {{y_1}{z_1} + {y_2}{z_2}} \right) \\ \dot{B} = - {e_y} \left( {\left| {y_1} \right| {z_1} + \left| {y_2} \right| {z_2}} \right) \\ \dot{C} = - 2{e_y}. \\ \end{array} \right. \end{aligned}$$

(16)

Then, the main result of this section will be introduced and proved.

Theorem 5.1

If the adaptive controller (15) and the updating laws of parameter (16) are chosen, the anti-sychronization between the master system (11) and the slave system (12) is achieved.

Proof

It is noting that the parameter estimation errors $e_a(t)$, $e_b(t)$ and $e_c(t)$ are given as

$$\begin{aligned} \left\{ \begin{array}{l} {e_a}\left( t \right) = a - A\left( t \right) \\ {e_b}\left( t \right) = b - B\left( t \right) \\ {e_c}\left( t \right) = c - C\left( t \right) . \\ \end{array} \right. \end{aligned}$$

(17)

Differentiating (17) with respect to t, we have

$$\begin{aligned} \left\{ \begin{array}{l} {{\dot{e}}_a}\left( t \right) = - \dot{A}\left( t \right) \\ {{\dot{e}}_b}\left( t \right) = - \dot{B}\left( t \right) \\ {{\dot{e}}_c}\left( t \right) = - \dot{C}\left( t \right) . \\ \end{array} \right. \end{aligned}$$

(18)

Substituting adaptive control law (15) into (14), the closed-loop error dynamics is defined as

$$\begin{aligned} \left\{ \begin{array}{l} {{\dot{e}}_x} = - {k_x}{e_x} \\ {{\dot{e}}_y} = -\left( {a - A\left( t \right) } \right) \left( {{y_1}{z_1} + {y_2}{z_2}} \right) \\ \,\quad \quad \; -\left( {b - B\left( t \right) } \right) \left( {\left| {y_1} \right| {z_1} + \left| {y_2} \right| {z_2}} \right) - 2\left( {c - C\left( t \right) } \right) - {k_y}{e_y} \\ {{\dot{e}}_z} = - {k_z}{e_z} \\ \end{array} \right. \end{aligned}$$

(19)

Then substituting (17) into (19), we have

$$\begin{aligned} \left\{ \begin{array}{l} {{\dot{e}}_x} = - {k_x}{e_x} \\ {{\dot{e}}_y} = -{e_a}\left( t \right) \left( {{y_1}{z_1} + {y_2}{z_2}} \right) - {e_b}\left( t \right) \left( {\left| {y_1} \right| {z_1} + \left| {y_2} \right| {z_2}} \right) - 2{e_c}\left( t \right) - {k_y}{e_y} \\ {{\dot{e}}_z} = -{k_z}{e_z}. \\ \end{array} \right. \end{aligned}$$

(20)

We consider the Lyapunov function given as

$$\begin{aligned} \begin{array}{l} V\left( t \right) = V\left( {{e_x},{e_y},{e_z},{e_a},{e_b},e_c} \right) \\ \,\quad \quad = \frac{1}{2}\left( {e_x^2 + e_y^2 + e_z^2 + e_a^2 + e_b^2 + e_c^2} \right) . \\ \end{array} \end{aligned}$$

(21)

The Lyapunov function (21) is clearly definite positive.

Taking time derivative of (21) along the trajectories of (13) and (17) we have

$$\begin{aligned} \dot{V}\left( t \right) = {e_x}{\dot{e}_x} + {e_y}{\dot{e}_y} + {e_z}{\dot{e}_z} + {e_a}{\dot{e}_a} + {e_b}{\dot{e}_b} + {e_c}{\dot{e}_c}. \end{aligned}$$

(22)

From (18), (20), and (22) we get

$$\begin{aligned} \begin{array}{l} \dot{V}\left( t \right) = - {k_x}e_x^2 - {k_y}e_y^2 - {k_z}e_z^2 - {e_a}\left[ {{e_y} \left( {{y_1}{z_1} + {y_2}{z_2}} \right) + \dot{A}} \right] \\ \,\,\,\quad \quad \;\;\; - {e_b}\left[ {{e_y}\left( {\left| {y_1} \right| {z_1} + \left| {y_2} \right| {z_2}} \right) + \dot{B}} \right] - {e_c}\left( {2{e_y} + \dot{C}}\right) . \\ \end{array} \end{aligned}$$

(23)

Then by applying the parameter update law (16), Eq. (23) become

$$\begin{aligned} \dot{V}\left( t \right) = - {k_x}e_x^2 - {k_y}e_y^2 - {k_z}e_z^2. \end{aligned}$$

(24)

Obviously, the time-derivative of the Lyapunov function V is negative semi-definite. According to Barbalat’s lemma in the Lyapunov stability theory [41, 67], it follows that ${e_x}\left( t \right) \rightarrow 0$, ${e_y}\left( t \right) \rightarrow 0$, and ${e_z}\left( t \right) \rightarrow 0$, exponentially when $t \rightarrow 0$. That is, anti-synchronization between master and slave system exponentially. This completes the proof. $\square$

A numerical example is presented to illustrate the effectiveness of our proposed anti-synchronization scheme. The parameters of the no-equilibrium systems are selected as $a=5$, $b=3$, $c=0.02$ and the positive gain constant as $k=6$. The initial conditions of the master system (11) and the slave system (12) have been chosen as ${x_1}\left( 0 \right) = 0$, ${y_1}\left( 0 \right) = 0$, ${z_1}\left( 0 \right) = 0$, and ${x_2}\left( 0 \right) = 0.5$, ${y_2}\left( 0 \right) = 1$, ${z_2}\left( 0 \right) = 0.9$, respectively. We assumed that the initial values of the parameter estimates are $A\left( 0 \right) = 10$, $B\left( 0 \right) = 2$, and $C\left( 0 \right) = 0$.

It is easy to see that when adaptive control law (15) and the update law for the parameter estimates (16) are applied, the anti-synchronization of the master (11) and slave system (12) occurred as illustrated in Figs. 9, 10 and 11. Time series of master states are denoted as blue solid lines while corresponding slave states are plotted as red dash-dot lines in such figures. Moreover, the time-history of the anti-synchronization errors $e_{x}$, $e_{y}$, and $e_{z}$ is reported in Fig. 12. The anti-synchronization errors converge to the zero. Therefore the chaos anti-synchronization between the no-equilibrium systems is realized.

Fig. 9

Anti-synchronization of the states $x_1(t)$ and $x_2(t)$

Fig. 10

Anti-synchronization of the states $y_1(t)$ and $y_2(t)$

Fig. 11

Anti-synchronization of the states $z_1(t)$ and $z_2(t)$

Fig. 12

Time series of the anti-synchronization errors $e_{x}$, $e_{y}$, and $e_{z}$

6 Electronic Circuit of the Proposed System

Implementation of theoretical chaotic model by electronic circuits is an approach to confirm the feasibility of the theoretical one [2, 64, 78, 97]. In this section, we choose integrator synthesis to synthesize a circuit from the differential equations in system (2) as shown in Fig. 13.

As seen in Fig. 13, there are only some basic blocks such as integrators, summing amplifiers, multipliers or absolute value blocks. These blocks have been realized easily by electronic components (resistors, capacitors, operational amplifiers, analog multipliers). As a result, the circuit have been implemented in PSpice as illustrated in Fig. 14. Signals in the circuit are measured at the outputs of inverting integrators. Figures 15, 16, 17 present the obtained PSpice results. The designed circuit emulates well the theoretical model.

Fig. 13

Block schematic to synthesize the circuit of system (2)

Fig. 14

Observation of the electronic circuit implemented by using PSpice

Fig. 15

PSpice phase portrait of the circuit in $-V(-x) - V(y)$ plane

Fig. 16

PSpice phase portrait of the circuit in $-V(-x) - V(z)$ plane

Fig. 17

PSpice phase portrait of the circuit in $V(y) - V(z)$ plane

7 Fractional Order Form of the No-Equilibrium System

As have been known that practical models such as heat conduction, electrode-electrolyte polarization, electronic capacitors, dielectric polarization, viso-elastic systems are more adequately described by the fractional-order different equations [9, 30, 37, 77, 81, 102]. Adams-Bashforth-Mounlton numerical algorithm is often used to investigate fractional-order differential equations [21, 25, 80]. Here we present this algorithm briefly.

We consider the fractional-order differential equation as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{{{d^q}x\left( t \right) }}{{d{t^q}}} = f\left( {t,x\left( t \right) } \right) ,&{}\quad 0 \le t \le T,\\ {x^{\left( i \right) }}\left( 0 \right) = x_0^{\left( i \right) }&{}\quad i = 0,1,...,m - 1, \end{array} \right. \end{aligned}$$

(25)

where $m - 1 < q \le m \in {Z^ + }$. Equation (25) is equivalent to the following Volterra integral equation:

$$\begin{aligned} x\left( t \right) = \sum \limits _{i = 0}^{m - 1} {\frac{{{t^i}}}{{i!}}x_0^{\left( i \right) } + \frac{1}{{\varGamma \left( q \right) }}} \int \limits _0^t {{{\left( {t - \tau } \right) }^{q - 1}}f\left( {\tau ,x\left( \tau \right) } \right) d\tau ,} \end{aligned}$$

(26)

in which the Gamma function $\varGamma \left( . \right)$ is defined as

$$\begin{aligned} \varGamma \left( q \right) = \int \limits _0^\infty {{e^{ - t}}{t^{q - 1}}dt} . \end{aligned}$$

(27)

We set $h = \frac{T}{N}$, $N \in {Z^ + }$, and ${t_n} = nh\;\;\left( {n = 0,1,...,N} \right)$. So we can discrete Eq. (26) as follows

$$\begin{aligned} \begin{array}{l} {x_h}\left( {{t_{n + 1}}} \right) = \sum \limits _{i = 0}^{m - 1} {\frac{{t_{n + 1}^i}}{{i!}}} x_0^{\left( i \right) } + \frac{{{h^q}}}{{\varGamma \left( {q + 2} \right) }}f\left( {{t_{n + 1}},x_h^p\left( {{t_{n + 1}}} \right) } \right) \\ \quad \quad \quad \;\;\; + \frac{{{h^q}}}{{\varGamma \left( {q + 2} \right) }}\sum \limits _{j = 0}^n {{a_{j,n + 1}}f\left( {{t_j},{x_h}\left( {{t_j}} \right) } \right) } , \end{array} \end{aligned}$$

(28)

where

$$\begin{aligned} {a_{j,n + 1}} = \left\{ \begin{array}{lll} {n^{q + 1}} - \left( {n - q} \right) {\left( {n + 1} \right) ^q},&{} \mathrm{{if}}\;j = 0,\\ {\left( {n - j + 2} \right) ^{q + 1}} + {\left( {n - j} \right) ^{q + 1}}&{}\\ - 2{\left( {n - j + 1} \right) ^{q + 1}},&{} \mathrm{{if}}\;1 \le j \le n,\\ 1,&{} \mathrm{{if}}\;j = n + 1. \end{array} \right. \end{aligned}$$

(29)

It is noting that the predicted value $x_h^p\left( {{t_{n + 1}}} \right)$ is calculated as

$$\begin{aligned} x_h^p\left( {{t_{n + 1}}} \right) = \sum \limits _{i = 0}^{m - 1} {\frac{{t_{n + 1}^i}}{{i!}}} x_0^{\left( i \right) } + \frac{1}{{\varGamma \left( q \right) }}\sum \limits _{j = 0}^n {{b_{j,n + 1}}f\left( {{t_j},{x_h}\left( {{t_j}} \right) } \right) } , \end{aligned}$$

(30)

in which

$$\begin{aligned} {b_{j,n + 1}} = \frac{{{h^q}}}{q}\left( {{{\left( {n + 1 - j} \right) }^q} - {{\left( {n - j} \right) }^q}} \right) ,\quad 0 \le j \le n. \end{aligned}$$

(31)

Here the estimation error e in the method is given by

$$\begin{aligned} e = \max \left| {x\left( {{t_j}} \right) - {x_h}\left( {{t_j}} \right) } \right| = O\left( {{h^p}} \right) \quad \left( {j = 0,1,...,N} \right) , \end{aligned}$$

(32)

with $p = \min \left( {2,1 + q} \right)$.

Existence of chaos in fractional-order systems are investigated [28, 29, 53, 107]. In this section, we consider the fractional-order from of the no-equilibrium system which is described as

$$\begin{aligned} \left\{ \begin{array}{l} \frac{{{d^q}x\left( t \right) }}{{d{t^q}}} = z\\ \frac{{{d^q}y\left( t \right) }}{{d{t^q}}} = - z\left( {ay + b\left| y \right| } \right) - x\left| z \right| - c\\ \frac{{{d^q}z\left( t \right) }}{{d{t^q}}} = \left| x \right| + \left| y \right| - 1, \end{array} \right. \end{aligned}$$

(33)

where a, b, c are three positive parameters and $c \ne 0$ for the commensurate order $0< q \le 1$. Fractional-order system (33) has been studied by applying Adams-Bashforth-Mounlton numerical algorithm [21, 25, 80]. It is interesting that chaos exists in fractional-order system (33). Figures 18, 19, 20 display chaotic attractors generated from fractional-order system (33) for the commensurate order $q=0.999$, the parameters $a = 5$, $b = 3$, $c = 0.02$ and the initial conditions

$$\begin{aligned} \left( {x\left( 0 \right) ,y\left( 0 \right) ,z\left( 0 \right) } \right) = \left( {0,0,0} \right) . \end{aligned}$$

(34)

However, when decreasing the value of the commensurate order i.e. $q=0.995$, fractional-order system (33) generates limit cycles as illustrated in Fig. 21.

Fig. 18

2-D projection of the fractional-order system (33) in the (x, y)-plane

Fig. 19

2-D projection of the fractional-order system (33) in the (x, z)-plane

Fig. 20

2-D projection of the fractional-order system (33) in the (y, z)-plane

Fig. 21

3-D projection of the fractional-order system (33) in the (x, y, z)-space for the commensurate order $q=0.995$, the parameters $a = 5$, $b = 3$, $c = 0.02$, and the initial conditions $\left( {x\left( 0 \right) , y\left( 0 \right) , z\left( 0 \right) } \right) = \left( {0,0,0} \right)$

8 Conclusion

A new three-dimensional autonomous system is proposed in this chapter. This system can exhibit chaotic attractors with square equilibrium and without equilibrium. As a result, such system is considered as a system with “hidden attractor”. Fundamental dynamical properties of the introduced system are investigated through calculating equilibrium points, phase portraits of chaotic attractors, Poincaré map, bifurcation diagram, largest Lyapunov exponents and Kaplan-Yorke dimension. Moreover, synchronization and electronic implementation of our novel system are discussed and verified by numerical examples. This work is not only to present a new system with hidden attractors but also to extend the knowledge about systems with different families of hidden attractors. Other chaotic systems with different families of hidden attractors will be presented in our next researches. In addition, further studies about potential applications of such system in secure communications and cryptography will be done in our future works.