1 Introduction

In 1963, Lorenz, a meteorologist, brought to light that deterministic system can show sensitive dependence on initial conditions [1]. This behaviour is termed as chaos. One positive Lyapunov exponent in a dynamical system is an indicator of chaos in that system. Over the years, researchers have thoroughly examined many chaotic systems and made significant contributions to it. In quantum plasma, chaotic phenomena have been vigorously studied using various techniques in many hydrodynamical models [2, 3]. Recently, it was observed that some of the chaotic system simultaneously show different numerical solutions for a fixed parametric set and separate initial values. This behaviour is termed as multistability or coexistence of trajectories and occurs as a result of the system’s high sensitivity to initial condition. Arecchi et al. [4] were the first to experimentally report multistable chaotic systems in a laser model of Q-switched gas. Since then, coexisting chaotic systems were extensively reported by various authors. A new type of three-dimensional system displaying coexisting chaotic phenomenon was put forward by Natiq et al. [5]. Numerous authors have studied chaotic [6] and hyperchaotic [7] multistable behaviour in a four-dimensional system.

Coexisting features or multistability in plasmas were investigated in plasma diodes [8] and experimentally observed in discharge plasmas [9]. In the field of classical plasma, multistability behaviours in novel lunar wake plasma, solar wind plasma and electron-ion plasma were reported by Yan et al. [10], Prasad et al. [11] and Abdikian et al. [12] respectively. Yan et al. [10] reported multistable behaviour in a lunar wake plasma consisting of electron-beams. In the field of quantum plasma, multistability features were reported in electron-ion plasma [3] and pair-ion quantum plasma [13].

Lyapunov exponent (LE) quantifies the rate of convergence or separation of infinitesimally nearby trajectories [14] and was named after a Russian mathematician, physicist and mechanician, Aleksandr Lyapunov. There are as many LEs as the number of dimensions of a system. A positive value of largest Lyapunov exponent (LLE) means that different states of a system that are initially arbitrarily close, will become macroscopically separated after sufficiently long times [15]. This implies that the system is highly sensitive on initial states. Hence, a positive LLE is taken as a signature of chaos. Since many natural systems show nonlinear dynamics, LE has diverse applications. On one hand, it is used to detect seizures [16] and unilateral laryngeal paralysis [17] in the medical field while on the other hand, it is used in predicting the Earth’s atmosphere [18]. One of the most popular methods to compute LEs is by using Wolf’s algorithm [19]. Recently, De Witte et al. [20] analyzed bifurcation of limit cycles by computing LEs.

Fundamentally, the ion-acoustic wave is a low frequency wave in plasma physics, wherein the driving force required to maintain the wave is supplied by ions and restoring forces is supplied by the pressure of inertialess electrons. Substantial amount of research on localized electrostatic disturbances in laboratory, space, and astrophysical plasmas mainly focus on ion-acoustic waves. Haas et al. [21] investigated two-component quantum hydrodynamic (QHD) model and identified a nondimensional parameter H, proportional to quantum diffraction effects. They showed that their system supported linear waves that resembled the classical ion-acoustic waves in the limit of small H. Since then, a large number of authors [22,23,24,25,26,27,28] were encouraged to study linear and nonlinear properties of quantum ion-acoustic waves (QIAWs). Recently, El-Labany et al. [27] investigated the propagation of QIAWs in a strongly coupled plasma that consisted of trapped electrons and ions.

Researchers are strongly emphasizing on the nonlinear propagation of waves in a plasma comprising of ion/electron beams. The presence of electron/ion beams in a plasma may bring about significant change in its nonlinear dynamical features. A few works related to ion beams have been reported in the field of quantum plasma. Elkamash et al. [29] proposed an ultra-dense electron-ion QHD model containing ion beams and reported the existence of three kinds of waves, viz, Langmuir mode, ion-beam driven mode and ion-acoustic mode. Recently, Paul et al. [30] studied nonlinear propagation of QIAWs in a three-component quantum plasma consisting of ion beams and reported that ion beam had a significant impact on formation of solitary waves.

Investigation of nonlinear waves in plasmas by employing the concept of nonlinear dynamical systems is gaining immense popularity. In the field of quantum plasmas, Samanta et al. [31] applied the bifurcation theory of planar dynamical system to investigate nonlinear features for the first time. Chaotic and quasiperiodic phenomena without introduction of external force were studied by Sahu et al. [32] in a pair-ion quantum plasma. Very few works [3, 13] have been reported for dynamics of chaotic and coexisting features in quantum plasmas. Coexisting features of small-amplitude QIAWs were reported in electron-ion quantum plasma [3] under the framework of nonlinear Schrodinger equation, while coexisting features and chaotic phenomenon for arbitrary amplitude QIAWs were reported in pair-ion quantum plasma [13]. But there is no work regarding the dynamics of chaotic and coexisting features in ion-beam quantum plasma. The main motivation of this work is to investigate chaotic phenomena and to establish multistability in an ion-beam quantum plasma.

The manuscript is arranged as follows: in Sect. 2, governing equations are presented. In Sect. 3, a four dimensional dynamical system is proposed and stability analysis of equilibrium points are briefly discussed. Chaotic features for ion-acoustic waves are discussed in Sect. 4. In Sect. 5, coexisting features for ion-acoustic waves are shown. Conclusion is given in Sect. 6.

2 Governing equations

We consider an ion-beam quantum plasma that consists of positive beam ions, positive ions and electrons. Here, electrons are assumed to be inertialess as the low-frequency ion-acoustic phase velocity is lesser than that of electron Fermi velocity and greater than that of beam ion and positive ion Fermi velocities. The plasma particles are assumed to act as a one-dimensional Fermi gas at zero-temperature. Hence the pressure law is:

$$\begin{aligned} p_j=\frac{m_jV^2_{Fj}}{3n^2_{j0}}n_j^3, \end{aligned}$$

where index \(j= e, i\) and b for electrons, positive ions and positive beam ions respectively. Here \(m_j\) denotes mass, \(V_{Fj}\) denotes Fermi speed, \(n_j\) denotes number density and \(n_{j0}\) denotes equilibrium number density.

The normalized governing equations [30] are as follows:

$$\begin{aligned}&0=\frac{\partial \phi }{\partial x}-n_e\frac{\partial n_e}{\partial x}-\frac{H^2}{6}\frac{\partial }{\partial x} \bigg (\frac{\partial ^2 \sqrt{n}_e/\partial x^2}{\sqrt{n}_e}\bigg ), \end{aligned}$$
(1)
$$\begin{aligned}&\frac{\partial n_{i}}{\partial t}+\frac{\partial (n_{i}u_{i})}{\partial x}=0, \end{aligned}$$
(2)
$$\begin{aligned}&\bigg (\frac{\partial }{\partial t}+u_{i}\frac{\partial }{\partial x}\bigg )u_{i}=-\frac{\partial \phi }{\partial x}-\sigma _i n_i\frac{\partial n_i}{\partial x}, \end{aligned}$$
(3)
$$\begin{aligned}&\frac{\partial n_{b}}{\partial t}+\frac{\partial (n_{b}u_{b})}{\partial x}=0, \end{aligned}$$
(4)
$$\begin{aligned}&\bigg (\frac{\partial }{\partial t}+u_{b}\frac{\partial }{\partial x}\bigg )u_{b}=-\mu \frac{\partial \phi }{\partial x}-\mu \sigma _b n_b\frac{\partial n_b}{\partial x}, \end{aligned}$$
(5)
$$\begin{aligned}&\frac{\partial ^2 \phi }{\partial x^2}= \chi n_e-n_i-(\chi -1)n_b, \end{aligned}$$
(6)

where space variable x, time variable t, electrostatic potential \(\phi \), number density \(n_j\) and velocity \(u_j\) are normalised by \(V_{Fi}/\omega _{pi},~1/\omega _{pi},~2K_BT_{Fj}/e,~n_0\) and \(V_{Fe}\) respectively. Here quantum diffraction parameter is denoted by H, where \(H=\hbar \omega _{pe}/2k_BT_{Fe}\). The ratio between unperturbed number density of electrons and ions is denoted by \(\chi \), i.e. \(\chi =n_{e0}/n_{i0}\). The mass ratio between positive ions and beam ions is denoted by \(\mu \), i.e. \(\mu =m_i/m_b\), while the Fermi temperature ratio between positive ions (beam ions) and electrons is denoted by \(\sigma _{i,b}\), i.e. \(\sigma _{i,b}=T_{Fi,b}/T_{Fe}\).

In case of one-dimensional, strong degeneracy limit, the pre-factor of Bohm potential for low frequency ion-acoustic wave is \(-1/3\) [33, 34], which has been used in Eq. (1).

3 Dynamical system and stability analysis

To study arbitrary amplitude QIAWs, we consider the transformation \(\xi =x-Mt\), where M is the Mach number. Employing the transformation in Eqs. (1)–(6) and considering \(n_e=A^2\), we get the following system of ODEs:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{dx_1}{d\xi }=x_2,\\ \displaystyle \frac{dx_2}{d\xi }=\chi x_3^2+P_1+P_2x_1+P_3x_1^2+P_4x_1^3+P_5x_1^4,\\ \displaystyle \frac{dx_3}{d\xi }=x_4,\\ \displaystyle \frac{dx_4}{d\xi }=\frac{6x_3}{H^2}\bigg (x_1-\frac{x_3^4}{2}+\frac{\chi ^2}{2}\bigg ), \end{array} \right. \end{aligned}$$
(7)

where \(a=M+\sqrt{\sigma _i},\) \(b=M-\sqrt{\sigma _i},\) \(c=M+\sqrt{\mu \sigma _b}(\chi -1),\) \(d=M-\sqrt{\mu \sigma _b}(\chi -1),\)

\(P_1=-\frac{1}{2\sqrt{\sigma _i}}(a-b)-\frac{1}{2\sqrt{\mu \sigma _b}}(c-d),\) \(P_2=-\frac{1}{2\sqrt{\sigma _i}}\bigg (-\frac{1}{a}+\frac{1}{b}\bigg )-\frac{1}{2\sqrt{\mu \sigma _b}}\bigg (-\frac{1}{c}+\frac{1}{d}\bigg ),\)

\(P_3=-\frac{1}{2\sqrt{\sigma _i}}\bigg (-\frac{1}{2a^3}+\frac{1}{2b^3}\bigg )-\frac{1}{2\sqrt{\mu \sigma _b}}\bigg (-\frac{1}{2c^3}+\frac{1}{2d^3}\bigg ),\) \(P_4=-\frac{1}{2\sqrt{\sigma _i}}\bigg (-\frac{1}{2a^5}+\frac{1}{2b^5}\bigg )-\frac{1}{2\sqrt{\mu \sigma _b}}\bigg (-\frac{1}{2c^5}+\frac{1}{2d^5}\bigg ),\) and \(P_5=-\frac{1}{2\sqrt{\sigma _i}}\bigg (-\frac{5}{8a^7}+\frac{5}{8b^7}\bigg )-\frac{1}{2\sqrt{\mu \sigma _b}}\bigg (-\frac{5}{8c^7}+\frac{5}{8d^7}\bigg ).\)

Here, we have assumed \(\phi =x_1\), \(\frac{d\phi }{d\xi }=x_2\), \(A=x_3\) and \(\frac{dA}{d\xi }=x_4\).

Let \(\overrightarrow{F}=\bigg (x_2,~\chi x_3^2+P_1+P_2x_1+P_3x_1^2+P_4x_1^3+P_5x_1^4,~x_4,~\frac{6x_3}{H^2}\bigg (x_1-\frac{x_3^4}{2}+\frac{\chi ^2}{2}\bigg )\bigg )\) and \(\overrightarrow{\nabla }=\bigg (\frac{\partial }{\partial x_1}, \frac{\partial }{\partial x_2}, \frac{\partial }{\partial x_3}, \frac{\partial }{\partial x_4}\bigg )\). Then vector field divergence of \(\overrightarrow{F}\) is:

$$\begin{aligned} \overrightarrow{\nabla } .\overrightarrow{F}=\frac{\partial \dot{x_1}}{\partial x_1}+\frac{\partial \dot{x_2}}{\partial x_2}+\frac{\partial \dot{x_3}}{\partial x_3}+\frac{\partial \dot{x_4}}{\partial x_4}=0. \end{aligned}$$
(8)

Therefore we can conclude that the dynamical system is conservative which is further supported by zero sum of Lyapunov exponents given in Fig. 2a and b.

The equilibrium points of the conservative dynamical system (CDS) (7) are calculated by solving the following equations:

$$\begin{aligned} \left\{ \begin{array}{ll} x_2=0,\\ \chi x_3^2+P_1+P_2x_1+P_3x_1^2+P_4x_1^3+P_5x_1^4=0,\\ x_4=0,\\ \displaystyle \frac{6x_3}{H^2}\bigg (x_1-\frac{x_3^4}{2}+\frac{\chi ^2}{2}\bigg )=0, \end{array} \right. \end{aligned}$$
(9)

The equilibrium point \(E(x_1^*,~x_2^*,~x_3^*,~x_4^*)\) of the system (7) can be obtained in the following way:

Case I:

When we consider \(x_3=0\), equilibrium points are of the form \(E(x_1^*,~x_2^*,~x_3^*,~x_4^*)\), where \(x_2^*=0,~x_3^*=0,~x_4^*=0\) and \(x_1^*\) is a root of the equation given below:

$$\begin{aligned} P_1+P_2x_1+P_3x_1^2+P_4x_1^3+P_5x_1^4=0. \end{aligned}$$
(10)

which is obviously a biquadratic equation of \(x_1\) with \(P_5 \ne 0\). Using Ferrari’s method, we obtain a solution of Eq. (10) having the form

$$\begin{aligned} x_1=\frac{-g \pm \sqrt{g^2-8h}}{4}, \end{aligned}$$

where \(g=\frac{P_4}{P_5} \pm \sqrt{\frac{P_4^2}{P_5^2}-\frac{4P_3}{P_5}+4y_1},\) \(h=y_1\pm \sqrt{y_1^2-\frac{4P_1}{P_5}}\)

and \(y_1\) is a real root of the cubic equation

$$\begin{aligned} y^3-\frac{P_3}{P_5}y^2+\bigg (\frac{P_4P_2}{P_5^2}-\frac{4P_1}{P_5}\bigg )y+\bigg (\frac{4P_3P_1}{P_5^2}-\frac{P_4^2P_1}{P_5^3}-\frac{P_2^2}{P_5^2}\bigg )=0. \end{aligned}$$

Therefore, in this case equilibrium points of the system (7) are of the form \(\bigg (\frac{-g \pm \sqrt{g^2-8h}}{4},0,0,0\bigg )\).

Case II:

When \(\bigg (x_1-\frac{x_3^4}{2}+\frac{\chi ^2}{2}\bigg )=0\), equilibrium points are of the form \(E(x_1^*,~x_2^*,~x_3^*,~x_4^*)\), where \(x_2^*=0,~x_4^*=0\), \(x_1^*=\frac{x_3^{*4}}{2}-\frac{\chi ^2}{2}\) and \(x_3^*\) is a root of the equation given below:

$$\begin{aligned}&\chi x_3^2 +P_1+P_2\bigg (\frac{x_3^4}{2}-\frac{\chi ^2}{2}\bigg )+P_3\bigg (\frac{x_3^4}{2}-\frac{\chi ^2}{2}\bigg )^2\nonumber \\&+P_4\bigg (\frac{x_3^4}{2}-\frac{\chi ^2}{2}\bigg )^3+P_5\bigg (\frac{x_3^4}{2}-\frac{\chi ^2}{2}\bigg )^4=0. \end{aligned}$$
(11)

This equation in \(x_3\) can be numerically solved using Matlab or Mathematica for a distinct set of values.

The CDS (7) has no equilibrium point if Eq. (9) has no real solution. On the other hand, if Eq. (9) has (have) real solution(s) then the CDS (7) has (have) equilibrium point(s). The stability of equilibrium point depends on the nature of eigenvalues of the Jacobian matrix \(J_E\).

After linearising system (7) at equilibrium point \(E(x_1^*,~x_2^*,~x_3^*,~x_4^*)\), the Jacobian matrix \(J_E\) can be written as:

$$\begin{aligned} J_{E}=\begin{pmatrix} 0 &{} 1 &{} 0 &{} 0 \\ P_2+2P_3x_1^*+3P_4x_1^{*2}+4P_5x_1^{*3} &{} 0 &{} 2\chi x_3^* &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \\ \frac{6x_3^*}{H^2} &{} 0 &{} \frac{6}{H^2}\bigg (x_1^*+\frac{\chi ^2}{2}\bigg )-\frac{15x_3^{*4}}{H^2} &{} 0 \\ \end{pmatrix}. \end{aligned}$$

One can obtain eigenvalues of the CDS (7) at \(E(x_1^*,~x_2^*,~x_3^*,~x_4^*)\)by solving the following equation:

$$\begin{aligned} det(\lambda I-J_E)=0. \end{aligned}$$
(12)

The characteristic equation is given by:

$$\begin{aligned} \lambda ^4+M_1\lambda ^3+M_2\lambda ^2+M_3\lambda +M_4=0, \end{aligned}$$
(13)

where

$$\begin{aligned} \left\{ \begin{array}{ll} M_1=0,\\ M_2=\frac{15x_3^{*4}}{H^2}+\frac{6}{H^2}\bigg (x_1^*+\frac{\chi ^2}{2}\bigg )-P_2-2P_3x_1^*-3P_4x_1^{*2}-4P_5x_1^{*3},\\ M_3=0,\\ M_4=-\bigg (P_2+2P_3x_1^*+3P_4x_1^{*2}+4P_5x_1^{*3}\bigg )\\ \qquad \bigg (\frac{15x_3^{*4}}{H^2}-\frac{6}{H^2}\bigg (x_1^*+\frac{\chi ^2}{2}\bigg )\bigg )-\frac{12\chi x_3^{*2}}{H^2}. \end{array} \right. \end{aligned}$$

The equilibrium point \(E(x_1^*,~x_2^*,~x_3^*,~x_4^*)\) is stable if all the solutions of Eq. (13) have negative real parts for a given equilibrium point or else it is unstable. For the plasma system (7), it is not possible to find a relation for the stability of the fixed points. We have discussed stability (stable/unstable) of the fixed point based on suitable values of the physical parameters in Sect. 4.

4 Chaotic features of quantum ion-acoustic flow

A situation where the solutions (or trajectories) of a set of ODEs do not converge to a periodic or a stationary function but continue to show irregular and unpredictable phenomenon is described by the term chaos. It is a long term aperiodic behaviour in a deterministic system and shows sensitive dependence on initial condition [14].

Case I: Effect of quantum diffraction parameter H

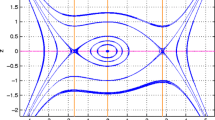
We set parameter values of system (7) fixed at \(\sigma _i=0.08,~\sigma _b=0.1,~\mu =1,~\chi =1.3,~M=3\) and show the effect of quantum diffraction parameter H by plotting different phase orientations of chaotic trajectories for ion-acoustic waves. Initial value is taken as \((5,~ -0.2,~ -1.5,~ 0.3)\). Figure 1a–c depict phase orientations of the chaotic orbits for ion-acoustic waves when \(H=5.5,~H=6.92\) and \(H=9.4\) respectively. The system (7) has four equilibrium points for all values of H: \((6.37846,~0,~-1.94959,~0),~(6.37846,~0,~1.94959,~0),~(-0.523958,~0,~-0.895155,~0)\) and \((-0.523958,~0,~0.895155,~0)\). Stabilities of these four equilibrium points are discussed below for three cases viz. \(H=5.5,~H=6.92\) and \(H=9.4\):

  1. 1.

    When H=5.5: Eigenvalues corresponding to equilibrium points \((6.37846,~0,~-1.94959,~0)\) and (6.37846,  0,  1.94959,  0) are \(\lambda _{1,2}=\pm 1.11622i\) and \(\lambda _{3,4}=\pm 2.48356 i\), while eigenvalues corresponding to equilibrium points \(~(-0.523958,~0,~-0.895155,~0)\) and \((-0.523958,~0,~0.895155,~0)\) are \(\lambda _1=-0.69253,~\lambda _2=0.69253\) and \(\lambda _{3,4}=\pm 0.904137i\). We can clearly see that some eigenvalues corresponding to each of the four equilibrium points do not have negative real parts. Hence we can say that equilibrium points corresponding to \(H=5.5\) are unstable.

  2. 2.

    When H=6.92: For \(H=6.92\), eigenvalues corresponding to equilibrium points \((6.37846,~0,~-1.94959,~0)\) and (6.37846,  0,  1.94959,  0) are \(\lambda _{1,2}=\pm 1.08459i\) and \(\lambda _{3,4}=\pm 2.03149i\), while eigenvalues corresponding to equilibrium points \(~(-0.523958,~0,~-0.895155,~0)\) and \((-0.523958,~0,~0.895155,~0)\) are \(\lambda _1=-0.624796\), \(\lambda _2=0.624796\) and \(\lambda _{3,4}=\pm 0.796509i\). In this case also we can see that some eigenvalues corresponding to each of the four equilibrium points do not have negative real parts. Therefore it is obvious that equilibrium points corresponding to \(H=5.5\) are unstable.

  3. 3.

    When H=9.4: Here, eigenvalues corresponding to equilibrium points \(~(-0.523958,~0,~-0.895155,~0)\) and \((-0.523958,~0,~0.895155,~0)\) are \(\lambda _{1,2}=\pm 0.679197i,~\lambda _3=0.539401\) and \(\lambda _{3.4}=-0.539401\). With arguments same as in the above cases it becomes evident that equilibrium points corresponding to \(H=9.4\) are also unstable. It is interesting to note that the system (7) shows chaotic phenomenon without the introduction of any external force.

Lyaunov exponent (LE) quantifies the exponential rate of divergence or convergence of nearby trajectories of a dynamical system [14]. A positive value of LE signifies that the nearby trajectories of that system move apart from each other in every iteration. Therefore, that system is said to be chaotic when it possesses one positive value of LE. By setting parameters fixed at \(\sigma _i=0.08,~\sigma _b=0.1,~\mu =1,~\chi =1.3,~M=3\) and \(H \in [5,10]\), Fig. 2a shows the graph of LEs of the system (7) w.r.t. quantum diffraction parameter H for the initial value \((5,~ -0.2,~ -1.5,~ 0.3)\). Clearly, we can see one positive LE (\(\mathrm{LE}_1>0\)) throughout the range of H which confirms chaotic behaviour of the three trajectories for ion-acoustic waves shown in Fig. 1a–c. Further, the sum of all Lyapunov exponents \(\sum _{i=1}^{4} {\mathrm{LE}_i}=0\), with \(\mathrm{LE}_1=-\mathrm{LE}_4\) and \(\mathrm{LE}_2=-\mathrm{LE}_3\), clearly indicating conservative behaviour of the dynamical system (7).

Fig. 1
figure 1

Phase spaces of chaotic trajectories of the system (7) for a \(H=5.5\), b \(H=6.92\), c \(H=9.4\) with \(M=3\) and d \(M=2.5001\), e \(M=3\), f \(M=3.2\) with \(H=7\) while other values of parameters are fixed at \(\sigma _i=0.08,~\sigma _b=0.1,~\mu =1,~\chi =1.3\) and for the initial value \((5,~ -0.2,~ -1.5,~ 0.3).\)

Full size image
Fig. 2
figure 2

a LEs with respect to quantum diffraction parameter H with \(M=3\) and b LEs with respect to Mach number M with \(H=7\) for the initial value \((5,~ -0.2,~ -1.5,~ 0.3)\) with other values of the parameters fixed at \(\sigma _i=0.08,~\sigma _b=0.1,~\mu =1,~\chi =1.3\)

Full size image

Case II: Effect of Mach number M

We set parameter values fixed at \(\sigma _i=0.08,~\sigma _b=0.1,~\mu =1,~\chi =1.3,~H=7\) and show effect of Mach number M by plotting phase spaces of chaotic trajectories for ion-acoustic waves. In this case also we take the initial value \((5,~ -0.2,~ -1.5,~ 0.3)\). Figure 1d–f display phase spaces of the chaotic orbits for ion-acoustic waves when \(M=2.5001, ~M=3\) and \(M=3.2\) respectively. Equilibrium points and their stabilities for the cases \(M=2.5001, ~M=3\) and \(M=3.2\) are discussed below:

  1. 1.

    When M=2.5001: The system (7) has four equilibrium points when \(M=2.5001\): \((3.98165,~0,~-1.7662661,~0),~(3.98165,~0,~1.7662661,~0),~(-0.536106,~0,~-0.886563,~0)\) and \((-0.536106,~0,~0.886563,~0)\). Eigenvalues at equilibrium points \((3.98165,~0,~-1.7662661,~0)\) and \((3.98165,~0,~1.7662661,~0)\) are \(\lambda _{1,2}=\pm 1.05324i\) and \(\lambda _{3,4}=\pm 5.7028 \), while eigenvalues at equilibrium points \((-0.536106,~0,~-0.886563,~0)\) and \((-0.536106,~0,~0.886563,~0)\) are \(\lambda _1=-1.00334,~\lambda _2=1.00334\) and \(\lambda _{3,4}=\pm 1.77861 i\). In this case we can see that some eigenvalues corresponding to each of the four equilibrium points do not have negative real parts which clearly indicates that equilibrium points corresponding to \(M=2.5001\) are unstable.

  2. 2.

    When M=3: The CDS (7) has four equilibrium points for \(M=3\): \((6.37846,~0,~-1.94959,~0),~(6.37846,~0,~1.94959,~0),~(-0.523958,~0,~-0.895155,~0)\) and \((-0.523958,~0,~0.895155,~0)\). Eigenvalues corresponding to equilibrium points \((6.37846,~0,~-1.94959,~0)\) and (6.37846,  0,  1.94959,  0) are \(\lambda _{1,2}=\pm 1.08242i\) and \(\lambda _{3,4}=\pm 2.01231i\), while eigenvalues corresponding to equilibrium points \(~(-0.523958,~0,~-0.895155,~0)\) and \((-0.523958,~0,~0.895155,~0)\) are \(\lambda _1=-0.621482\), \(\lambda _2=0.621482\) and \(\lambda _{3,4}=\pm 0.791605i\). Like in the previous case we can see that not all eigenvalues corresponding to each of the four equilibrium points have negative real parts which makes it obvious that equilibrium points corresponding to \(M=3\) are unstable.

  3. 3.

    When M=3.2: The system (7) has four equilibrium points for \(M=3.2\): \((7.52127,~0,~-2.02251,~0)\), \((7.52127,~0,~2.02251,~0),~(-0.520469,~0,~-0.8975766,~0)\) and \((-0.520469,~0,~0.8975766,~0)\). Eigenvalues corresponding to equilibrium points \((7.52127,~0,~-2.02251,~0)\) and \((7.52127,~0,~2.02251,~0)\) are \(\lambda _{1,2}=\pm 1.123821i\) and \(\lambda _{3,4}=7.4797i\), while eigenvalues corresponding to equilibrium points \(~(-0.520469,~0,~-0.8975766,~0)\) and \((-0.520469,~0,~0.8975766,~0)\) are \(\lambda _1=-1.01022,~\lambda _2=1.01022\) and \(\lambda _{3,4}=\pm 1.80361i\). Equilibrium points corresponding to \(M=3.2\) are unstable just like in the previous cases. Its is noteworthy that the system (7) shows chaotic behaviour without the introduction of any external force.

Keeping other values of parameters fixed at \(\sigma _i=0.08,~\sigma _b=0.1,~\mu =1,~\chi =1.3,~H=7\) and \(M \in [2.45,3.5]\), Fig. 2b shows the graph of LEs of the system (7) versus Mach number M for the initial value \((5,~ -0.2,~ -1.5,~ 0.3)\). Clearly, we can see \(\mathrm{LE}_1>0\) throughout the range of M therefore validating chaotic behaviour of the three trajectories for ion-acoustic waves shown in Fig. 1d–f. Additionally, we can see that the sum of all \(\mathrm{LE}_is\) is zero, i.e. \(\sum _{i=1}^{4} {\mathrm{LE}_i}=0\), as \(\mathrm{LE}_1=-\mathrm{LE}_4\) and \(\mathrm{LE}_2=-\mathrm{LE}_3\), evidently displaying conservative nature of the dynamical system (7).

5 Coexisting features of quantum ion-acoustic flow

Multistability basically means coexistence of various solutions of a dynamical system for a predefined set of parameters and separate initial conditions. The solution crucially depends on the initial states. To investigate coexisting features for ion-acoustic waves, we set the parameter values fixed at \(\sigma _i=0.08,~\sigma _b=0.1,~\mu =1,~\chi =1.3,~H=7\) and \(M=3\) and the phase spaces of the system (7) for separate initial values are shown in Fig. 3. This coexisting phase spaces are drawn for a particular set of parameter values and different initial states. Here, a trajectory of one colour corresponds to an initial state. Clearly, Fig. 3 depicts coexistence of multiple chaotic trajectories for ion-acoustic waves initiated by \((5,~-0.2,~-1.5,~0.46)\) (red), \((5,~-0.2,~-1.59,~0.46)\) (blue), \((5,~-0.2,~-1.5,~0.3)\) (cyan), \((5,~-0.2,~-2,~0.1)\) (green) and \((5,~-0.2,~-1.65,~0.1)\) (magenta). The system (7) is seen to achieve multistability behaviour for ion-acoustic waves without the introduction of any external force.

If the LLE is positive, it clearly ascertains chaos in that dynamical system. Figure 4a and c display variation of LLEs w.r.t. quantum diffraction parameter (H) and Mach number M, respectively. The set of other parameters are kept same as Fig. 3. The colours of LLEs correspond to the same coloured initial states shown in Fig. 3. From Fig. 4a and c, it can be observed that the values of all LLEs initiated by these five initial states are greater than zero for all \(H \in [6,8]\) and \(M \in [2.55,3.5]\). Hence, we can say that the trajectories for ion-acoustic waves shown in Fig. 3 initiated by these initial values are indeed chaotic in nature.

Initial values for multistability can be chosen by drawing basins of attraction. However, one can draw the basins of attraction for all possible choice of the initial values. Further, it is possible to obtain all possible multistability behaviours in a system using basins of attraction. Therefore, basins of attraction is drawn to chose initial values and to validate multistability. Basins of attraction for our dynamical system are four dimensional regions but we will plot cross-section in two-dimension. To compute cross section of basins of attraction for multistability behaviour, we keep \(x_1\) and \(x_2\) as fixed (\(x_1=5,~x_2=-0.2\)) and we obtain all possible values of \(x_3\) and \(x_4\) for the different qualitative features at different initial condition values keeping fixed values of physical parameters. In Fig. 4b, we present cross section of the basins of attraction of the CDS (7) on \(x_3-x_4\) plane with \(x_1=5\) and \(x_2=-0.2\) where the system is seen to exhibit multiple chaotic trajectories (red, blue, cyan, green and magenta). Figure 5a–e show bifurcation diagrams w.r.t. H initiated by initial states \((5,~-0.2,~-1.5,~0.46)\), \((5,~-0.2,~-1.59,~0.46)\), \((5,~-0.2,~-1.5,~0.3)\), \((5,~-0.2,~-2,~0.1)\) and \((5,~-0.2,~-1.65,~0.1)\), respectively, with \(\sigma _i=0.08,~\sigma _b=0.1,~\mu =1,~\chi =1.3\) and \(M=3\). Different types of chaotic features for different initial states can be observed at \(H=7\).

Fig. 3
figure 3

Coexistence of chaotic trajectories for ion-acoustic waves with different initial values: \((5,~-0.2,~-1.5,~0.46)\) (red), \((5,~-0.2,~-1.59,~0.46)\) (blue), \((5,~-0.2,~-1.5,~0.3)\) (cyan), \((5,~-0.2,~-2,~0.1)\) (green) and \((5,~-0.2,~-1.65,~0.1)\) (magenta) with parameter values fixed at \(\sigma _i=0.08,~\sigma _b=0.1,~\mu =1,~\chi =1.3,~H=7\) and \(M=3\) in a \(x_1-x_4\) plane, b \(x_2-x_3\) plane and c \(x_3-x_4\) plane

Full size image
Fig. 4
figure 4

a Spectrums of LLEs with respect to H for \(M=3\), b cross section of basins of attraction in \(x_3-x_4\) plane with \(x_1=5\) and \(x_2=-0.2\) where green, blue, magenta, cyan and red colours represent chaotic trajectories of the system (7) with \(M=3\) and \(H=7\), and c spectrums of LLEs with respect to M for \(H=7\). The other parameter values are taken as \(\sigma _i=0.08,~\sigma _b=0.1,~\mu =1\) and \(~\chi =1.3\). In a and c LLEs are initiated by \((5,~-0.2,~-1.5,~0.46)\) (red), \((5,~-0.2,~-1.59,~0.46)\) (blue), \((5,~-0.2,~-1.5,~0.3)\) (cyan), \((5,~-0.2,~-2,~0.1)\) (green) and \((5,~-0.2,~-1.65,~0.1)\) (magenta)

Full size image
Fig. 5
figure 5

Bifurcation diagram w.r.t. H for initial states a \((5,~-0.2,~-1.5,~0.46)\), b \((5,~-0.2,~-1.59,~0.46)\), c \((5,~-0.2,~-1.5,~0.3)\), d \((5,~-0.2,~-2,~0.1)\) and e \((5,~-0.2,~-1.65,~0.1)\) with \(\sigma _i=0.08,~\sigma _b=0.1,~\mu =1,~\chi =1.3\) and \(M=3\)

Full size image
Fig. 6
figure 6

a–c Phase space showing coexistence of chaotic trajectory initiated by \((8.5,~0,~-1.94959,~0)\) (magenta), quasiperiodic trajectories initiated by \((5,~0,~-1.94959,~0)\) (cyan), \((5.38,~0,~-1.94959,~0)\) (red) and \((5.65,~0,~-1.94959,~0)\) (green) and multiperiodic trajectories initiated by \((6,~0,~-1.94959,~0)\) (blue) and \((6.5,~-0.1,~-1.94959,~0)\) (yellow) for ion-acoustic waves with values of parameters fixed at \(\sigma _i=0.08,~\sigma _b=0.1,~\mu =1,~\chi =1.3,~H=9\) and \(M=3\), d–f enlarged view of multiperiodic trajectories initiated by \((6,~0,~-1.94959,~0)\) (blue) and \((6.5,~-0.1,~-1.94959,~0)\) (yellow)

Full size image
Fig. 7
figure 7

a Spectrums of LLEs w.r.t. H with \(M=3\), b cross-section of basins of attraction for \(x_3=-1.94959\) and \(x_4=0\), where system (7) shows chaotic trajectories (blue and cyan), quasiperiodic trajectories (red and green) and periodic trajectory (yellow) with \(H=9\) and \(M=3\), and c spectrums of LLEs w.r.t. M with \(H=9\). The other parameters are taken as \(\sigma _i=0.08,~\sigma _b=0.1,~\mu =1\) and \(~\chi =1.3\). In a and c LLEs are initiated by \((8.5,~0,~-1.94959,~0)\) (magenta), \((5,~0,~-1.94959,~0)\) (cyan), \((5.38,~0,~-1.94959,~0)\) (red), \((5.65,~0,~-1.94959,~0)\) (green), \((6,~0,~-1.94959,~0)\) (blue) and \((6.5,~-0.1,~-1.94959,~0)\) (yellow)

Full size image
Fig. 8
figure 8

Coexistence of two types of chaotic trajectories initiated by \((7.52, - 1.5, - 1.95, 0)\) (blue) and \((6, 0, - 1.95, 0)\) (cyan), two types of quasiperiodic trajectories initiated by \((6.5, 0, - 1.95, 0)\) (red) and \((7, 0, - 1.95, 0)\) (green) and periodic trajectory initiated by \((7.52, 0, - 1.95, 0)\) (yellow) for ion-acoustic waves with values of parameters fixed at \(\sigma _i=0.08, \sigma _b=0.1, \mu =1, \chi =1.3, H=7\) and \(M=3.2\) in a \(x_1-x_4\) plane, b \(x_2-x_3\) plane and c \(x_3-x_4\) plane

Full size image
Fig. 9
figure 9

a Spectrums of LLEs w.r.t. H for \(M=3.2\), b cross-section of basins of attraction with \(x_3 = - 1.95\) and \(x_4 = 0\), where system exhibits chaotic trajectories (blue and cyan), quasiperiodic trajectories (red and green) and periodic trajectory (yellow) with \(H = 7\) and \(M = 3.2\) and c spectrums of LLEs w.r.t. M for \(H=7\). The other parameter values are taken as \(\sigma _i=0.08,\sigma _b=0.1,\mu =1\) and \(\chi =1.3\). In Fig. 7a and c LLEs are initiated by \((7.52, - 1.5, - 1.95, 0)\) (blue) and \((6, 0, - 1.95, 0)\) (cyan), \((6.5, 0, - 1.95, 0)\) (red), \((7, 0, - 1.95, 0)\) (green) and \((7.52, 0, - 1.95, 0)\) (yellow)

Full size image
Fig. 10
figure 10

Bifurcation diagrams with respect to quantum diffraction parameter H initiated by initial values a \((8.5,~0, -1.94959,~0)\), b \((5, 0, -1.94959, 0)\), c \((5.38, 0, -1.94959, 0)\), d \((5.65, 0, -1.94959, 0)\), e \((6, 0, -1.94959, 0)\) and f \((6.5, -0.1, -1.94959, 0)\) with \(\sigma _i=0.08, \sigma _b=0.1, \mu =1, \chi =1.3\) and \(M=3\)

Full size image
Fig. 11
figure 11

Bifurcation diagrams w.r.t. quantum diffraction parameter H initiated by initial values a \((7.52,~-1.5,~-1.95,~0)\), b \((6,~0,~-1.95,~0)\), c \((6.5,~0,~-1.95,~0)\), d \((7,~0,~-1.95,~0)\) and e \((7.52,~0,~-1.95,~0)\) with \(\sigma _i=0.08,~\sigma _b=0.1,~\mu =1,~\chi =1.3\) and \(M=3.2\)

Full size image

Coexistence of a chaotic, quasiperiodic and multiperiodic trajectories for ion-acoustic waves is displayed in Fig. 6. For this purpose, we have fixed values of parameters at \(\sigma _i=0.08,~\sigma _b=0.1,~\mu =1,~\chi =1.3,~H=9\) and \(M=3\). Here, chaotic trajectory is initiated by \((8.5,~0,~-1.94959,~0)\) (magenta), quasiperiodic trajectories are initiated by \((5,~0,~-1.94959,~0)\) (cyan), \((5.38,~0,~-1.94959,~0)\) (red) and \((5.65,~0,~-1.94959,~0)\) (green) and multiperiodic trajectories are initiated by \((6,~0,~-1.94959,~0)\) (blue) and \((6.5,~-0.1,~-1.94959,~0)\) (yellow). Coexisting phase spaces in \(x_1-x_4,~x_2-x_3\) and \(x_3-x_4\) planes for the six initial values mentioned above are shown in Fig. 6a–c respectively. The multiperiodic trajectories (initiated by \((6,~0,~-1.94959,~0)\) (blue) and \((6.5,~-0.1,~-1.94959,~0)\) (yellow)) are inconspicuous in the phase spaces Fig. 6a–c, so we have shown them separately in Fig. 6d–f.

In Fig. 7a, we show variation of LLEs wr.t. quantum diffraction parameter H for other parameter values same as Fig. 6. Each colour of LLE correspond to respective coloured initial state displayed in Fig. 6. Vividly, one can observe that the LLE initiated by \((8.5,~0,~-1.94959,~0)\) (magenta) is positive throughout \(H\in [5,10]\). This clearly supports random irregular nature of the trajectory initiated by the same initial value displayed in phase spaces (Fig. 6). On the other hand, LLE initiated by \((5,~0,~-1.94959,~0)\) (cyan) attains positive value when \(H\in [5,8.92]\) and zero value when \(H\in (8.92,10]\). Hence, the system shows chaotic phenomenon when \(H\in [5,8.92]\) and non chaotic phenomenon when \(H\in (8.92,10]\) for this initial state. Similarly, LLE initiated by \((5.38,~0,~-1.94959,~0)\) (red) attains positive values when \(H\in [5,5.83)\), \(H\in (6.12,6.18)\) and \(H\in (6.4,6.79)\) and zero in other regions of H. For this initial state also, the system shows both chaotic and non chaotic phenomenon. Finally, LLEs initiated by \((5.65,~0,~-1.94959,~0)\) (green), \((6.5,~-0.1,~-1.94959,~0)\) (yellow) and \((6,~0,~-1.94959,~0)\) (blue) coincides with one another and have zero value throughout \(H\in [5,10]\) indicating non-chaotic phenomena for \(H\in [5,10]\).

Figure 7b depicts cross section of basins of attraction for chaotic trajectory (magenta), quasiperiodic trajectory (cyan, red and green) and multiperiodic trajectories (yellow and blue) for the CDS (7) with \(x_3=-1.94959\) and \(x_4=0\). Values of parameters are kept same as Fig. 6. In Fig. 7c, we present spectrums of LLEs wr.t. Mach number M for values of other parameters same as Fig. 6. At \(M=3\), one can clearly observe a positive LLE (magenta), while other LLEs (cyan, red, green, blue and yellow) have zero values. Therefore, one can deduce that the magenta trajectory shown in Fig. 6 shows chaotic phenomenon, while other trajectories (cyan, red, green, blue and yellow) show non chaotic phenomena.

In Fig. 10, we display six bifurcation diagrams w.r.t. quantum diffraction parameter H for parameters same as Fig. 6. Initial states for Fig. 10a–f are, respectively, \((8.5,~0,~-1.94959,~0)\), \((5,~0,~-1.94959,~0)\), \((5.38,~0,~-1.94959,~0)\), \((5.65,~0,~-1.94959,~0)\), \((6,~0,~-1.94959,~0)\) and \((6.5,~-0.1,~-1.94959,~0)\). Here, Fig. 10a–e show chaotic and non chaotic regions throughout the range of H, while Fig. 10f shows only chaotic regions for all values of H.

By setting parameters fixed at \(\sigma _i=0.08,~\sigma _b=0.1,~\mu =1,~\chi =1.3,~H=7\) and \(M=3.2\), we vary only the initial values. Two types of aperiodic and irregular trajectories for ion-acoustic waves are observed at initial states \((7.52,~-1.5,~-1.95,~0)\) (blue) and \((6,~0,~-1.95,~0)\) (cyan). Again, two kinds of irregular periodic orbits for ion-acoustic waves are perceived at initial values \((6.5,~0,~-1.95,~0)\) (red) and \((7,~0,~-1.95,~0)\) (green) and a closed single-periodic orbit for ion-acoustic waves is observed at initial state \((7.52,~0,~-1.95,~0)\) (yellow). It is remarkable to note that chaotic, quasiperiodic and periodic trajectories coexist for a fixed parameter set and separate initial values and their coexistence is depicted in Fig. 8.

Spectrums of LLEs w.r.t. H are presented in Fig. 9a for values of other parameters same as Fig. 8. Two LLEs initiated by \((7.52,~-1.5,~-1.95,~0)\) (blue) and \((6,~0,~-1.95,~0)\) (cyan) in Fig. 9a are clearly positive while other LLEs for initial values \((6.5,~0,~-1.95,~0)\) (red), \((7,~0,~-1.95,~0)\) (green) and \((7.52,~0,~-1.95,~0)\) (yellow) are almost zero and overlapping with each other for \(H\in [6,8]\). Variation of LLEs w.r.t. M is presented in Fig. 9c for values of other parameters same as Fig. 8. At \(M=3.2\), LLEs initiated by \((7.52,~-1.5,~-1.95,~0)\) (blue) and \((6,~0,~-1.95,~0)\) (cyan) are positive, while LLEs initiated by \((6.5,~0,~-1.95,~0)\) (red), \((7,~0,~-1.95,~0)\) (green) and \((7.52,~0,~-1.95,~0)\) (yellow) have zero value. This proves that trajectories for ion-acoustic waves initiated by \((7.52,~-1.5,~-1.95,~0)\) (blue) and \((6,~0,~-1.95,~0)\) (cyan) (phase spaces shown in Fig. 8) are indeed chaotic in nature while other trajectories are non chaotic.

For parameter values same as Fig. 8, cross section of basins of attraction of the CDS (7) is given in Fig. 9b with \(x_3=-1.95\) and \(x_4=0\) and the system (7) is seen to exhibit chaotic trajectories (blue and cyan), quasiperiodic trajectories (red and green) and periodic trajectory (yellow). Bifurcation diagram w.r.t. diffraction parameter H for the same parameter set as Fig. 10 initiated by \((7.52,~-1.5,~-1.95,~0)\), \((6,~0,~-1.95,~0)\), \((6.5,~0,~-1.95,~0)\), \((7,~0,~-1.95,~0)\) and \((7.52,~0,~-1.95,~0)\) are given in Fig. 11a–e, respectively. We can observe that the dynamics of ion-acoustic waves remain chaotic throughout in Fig. 11a and non chaotic throughout \(H\in [6,8]\) in Fig. 11e. On the other hand, Fig. 11b–d clearly show that the dynamics of quantum ion-acoustic waves fluctuates from chaotic to non chaotic and back to chaotic state throughout the range of H.

6 Conclusion

Arbitrary amplitude quantum ion-acoustic wave flow has been analyzed for a dense quantum plasma containing positive beam ions, positive ions and electrons in the framework of four-dimensional conservative dynamical system. The conservative nature of the system has been confirmed by zero divergence of vector field and zero sum of LEs. We have examined effects of quantum diffraction parameter H and Mach number M on chaotic features for ion-acoustic waves in an ion-beam quantum plasma. Qualitatively different phase spaces of chaotic trajectories for ion-acoustic waves have been observed for each case indicating significant impact of H and M. Equilibrium points calculated for each parameter set have been found to be unstable. Aperiodic and irregular nature of trajectories in phase spaces have been supported by a positive Lyapunov exponent in the graphs of LEs. We have shown coexistence of multiple chaotic trajectories for one parameter set, chaotic, quasiperiodic and multiperiodic trajectories for second parameter set and chaotic, quasiperiodic and periodic trajectories for third parameter set for ion-acoustic waves in our plasma system. Phase spaces, graphs of maximum Lyapunov exponents, basins of attraction and bifurcation diagrams have supported the coexisting features for ion-acoustic waves. It has been observed that electrostatic potential of our quantum plasma system is sensitive to initial conditions and qualitatively different features: periodic, multiperiodic, quasiperiodic and chaotic were seen at different initial conditions with fixed values of physical parameters. The results are suitable for comprehending the beam-plasma interaction and analyzing dynamics of coexisting features for ion-acoustic waves in extreme astrophysical plasmas, such as, neutron stars.