1 Introduction

Non-Newtonian liquids are encountered in many technological applications including polymer processing, biotechnology, lubrication of aerospace and automotive vehicles and nuclear thermo-hydraulics [1]. Such fluids may be delineated broadly into three classes, namely “rate type”, “differential type” and “integral type”. The Oldroyd-B fluid model belongs to the “rate type” of model and is a generalization of the upper-convected Maxwell model. Rate models provide features not possible in the differential [2] or integral-type models, and these include stress relaxation, material retardation, nonlinear creep and normal stress differences in simple shear flows. However, further modification is required to simulate shear thinning/shear thickening effects. Although the original Oldroyd-B model is in fact a three-dimensional rate-type models satisfying frame indifference, in modern fluid dynamics it has evolved into one of the simplest constitutive fluid models available for modelling viscoelastic flows under general flow conditions. In recent years, this model has stimulated renewed interest as it quite accurately captures the shear-stress–strain characteristics of many working fluids encountered in the nuclear, petroleum and materials processing industries. Tan et al. [3] investigated Oldroyd-B fluid transport in porous media with a modified Darcy law, employing a Fourier sine transformation. Further studies of Oldroyd-B fluids include transient hydrodynamics in a helical pipe [4], inclined channel slurry flows [5], bifurcating heat transfer in permeable media [6] and flat plate accelerating flows [7].

The above studies ignored electrically conducting properties of the fluid. However, many working fluids are doped with salts or carry electrical charges. To simulate this behaviour the preferred approach is magnetohydrodynamics (MHD). MHD is important in modern nuclear engineering systems since via the imposition of a magnetic field it is possible to successfully control the heat transfer rates in ducts, channels, etc. MHD features in lithium blanket systems [8], nuclear coolant pumping [9] and tokamak liquid metal systems [10]. Experimental studies of such flows are very challenging. Numerical and mathematical modelling has therefore emerged as a major complimentary area of study. In flow simulations important parameters which characterize MHD flows include the Hartmann number (used for the Lorentzian body force effect), Chandrasekhar number (the square of the Hartmann number and a popular parameter also for magnetic convection), Batchelor number (important when magnetic induction arises), and the magnetic Prandtl number (relative influence of momentum diffusion rate and magnetic diffusion rate). Han et al. [11] employed a finite-volume technique to study the heat transfer in hydromagnetic rectangular ducts flow. Khan et al. [12] used a Laplace transform technique to derive closed-form solutions for oscillatory magneto-convection in an Oldroyd-B fluid. Zheng et al. [13] utilized Fox H-functions and the discrete Laplace transform to analyse hydromagnetic Oldroyd-B slip flow. These studies all confirmed a substantial modification in velocity field or thermal field with magnetic field imposition.

Stagnation point flows constitute yet another important family of flows in which boundary layer theory [14] may be applied. Such flows are characterized by viscous (or inviscid) fluids impinging on solid surfaces and manifest in a vanishing of the local velocity and an associated peak in stagnation pressure. They arise in many areas of chemical engineering (food stuff processing), coating of components in the polymer industry, aircraft wing aerodynamics, duct flows in nuclear reactors and spray cooling of metallic components. In nuclear and chemical engineering the solid surface may also be distensible, i.e. may contract or extend. Chiam [15] studied the stagnation flow of Newtonian viscous fluid over linearly stretching wall. Ishak et al. [16] computed incompressible Newtonian flow solutions on an upright permeable stretched surface with non-isothermal conditions using Keller’s box finite difference. Mixed convection heat transfer in stagnation flows is also of some interest in engineering systems. Buoyancy forces are generated when temperature differences becomes significant. These forces amend the hydrodynamic stream and temperature fields which interact differently in the presence of buoyancy. These forces may be in the or opposite to the flow direction and may therefore increase or decrease heat transfer especially at boundaries. Many such studies have been communicated for non-Newtonian fluids with and without magnetic field effects. Gupta et al. [17] used variational finite element code to analyse magnetized stagnation flow of micropolar fluid from an extending sheet with wall transpiration. Uddin et al. [18] used Maple quadrature to compute the stagnation flow of nanofluid containing gyrotactic micro-organisms with anisotropic hydrodynamic and thermal slip effects. Le Blanc and Malone [19] computed with finite elements the velocity, pressure and stress fields in steady flow in a planar stagnation die using the Maxwell viscoelastic model. Parks [20] presented extensive simulations of Oldroyd-B viscoelastic fluid stagnation flows in polystyrene melts. Further rheological stagnation flows have been investigated by Sadeghy et al. [21] for Maxwell fluids and Renardy [22] for Oldroyd-B fluids. In this latter study, an exact solution (quadratic velocity profile) was obtained for the axisymmetric case whereas for the planar case, the velocity was shown to be quadratic close to the stagnation point, whereas it followed an exponential growth further away. These studies were confined to the orthogonal impinging flow scenario (flow field is at right angles to the solid surface). However, a more general family of stagnation point flows is known as the non-orthogonal flows where the oncoming flow field impinges obliquely to the solid surface. Orthogonal flows are therefore a special case of non-orthogonal flows. In recent years, non-orthogonal stagnation point flows have attracted some attention as they generalize the models used by engineers to include all possible angles of impingement of industrial flows on solid surfaces. The classical normal stagnation flow (sometimes known as Hiemenz flow) can be extended to consider non-orthogonal stagnation flow by supplementing the inviscid stream function with a constant vorticity. Studies of non-orthogonal stagnation flow for two-dimensional problems also provide a very good benchmark for generalization to three-dimensional computational fluid dynamics with commercial software e.g. ANSYS FLUENT, ADINA-F. Javed et al. [23] studied oblique MHD flow over an oscillating sheet with Keller’s box method by formulating the stream function in terms of both Hiemenz and tangential components. They observed that magnetic field assists in trans-locating the oblique stagnation point. Mahapatra et al. [24] identified both conventional and inverted boundary layer structures in oblique stagnation point Newtonian flow. Labropulu et al. [25] used the Bellman-Kalaba quasi-linearization method to compute non-orthogonal stagnation point flow and convective heat transfer towards a stretching surface in a second-order Reiner–Rivlin viscoelastic fluid. Newtonian oblique stagnation point flows with heat transfer were addressed by Wu et al. [26] and Yian et al. [27]. Li et al. [28] reported on Weissenberg number effects in non-orthogonal stagnation flow and heat transfer in second-order Reiner–Rivlin viscoelastic fluids, also supplementing the orthogonal flow with shear flow. Zheng and Phan-Tien [29] presented a seminal study of non-orthogonal stagnation flow of an Oldroyd-B fluid in channel using a finite difference numerical method with a parameter continuation method.

The classical approach to modelling heat transfer in viscous flows has been the Fourier thermal conduction equation [30]. This approach, however, diminishes heat conservation formulation to parabolic energy equation which displays that medium under scrutiny goes through an initial disturbance. To tackle this difficulty, Cattaneo [31] presented relaxation time term in Fourier’s law of heat conduction which results in the physically realistic finite-speed heat conduction. Following further modifications, a modern form of the non-Fourier model which has emerged and been embraced in computational studies is the Cattaneo–Christov heat flux model. Several recent studies have utilized this non-Fourier heat flux model in thermal convection flows via the inclusion of a thermal relaxation term. Akbar et al. [32] used fourth-order Runge–Kutta shooting quadrature to compute the hydromagnetic flow of nanofluids from a stretching surface with the Cattaneo–Christov heat flux model noting that heat transfer rates are substantially altered with non-Fourier thermal relaxation effects. Further studies include Bhatti et al. [33] who simulated the multi-mode heat transfer in electrically conducting viscoelastic boundary layer flow from an extending sheet with thermal relaxation effects.

In numerous industrial systems, chemical reactions are known to take place. These include corrosive effects in nuclear heat transfer, polymer radical manipulation, catalytic conversion and distillation processes. They require mass, i.e. species diffusion. There are two major classifications of chemical reactions, namely homogeneous and heterogeneous. Chemical changes occurring with liquids or gases depend on the type of interactions of these chemical substances. Homogeneous reactions occur in one phase only whereas heterogeneous reactions occur in two or more phases. The majority of analytical studies in the literature dwell on complex purely heterogeneous chemical reactions, for example in catalysis. The major applications of homogeneous–heterogeneous reactions are ammonia, transition of metal and metal oxides (including nuclear corrosive environments), Friedel processes, hydrogen, silica, alumina and catalytic ceramics. Chaudhary and Merkin [34] used asymptotic expansions to study homogeneous–heterogeneous chemical reaction effects in stagnation boundary layer flows by considering isothermal autocatalytic processes for homogeneous reactions and first-order kinetics for the heterogeneous reactions. Khan et al. [35] presented numerical results for the influence of homogeneous–heterogeneous reactions in viscoelastic flow. Kameswaran et al. [36] analysed homogeneous–heterogeneous chemical reaction effects in silver-water and copper–water nanofluid flows, considering both cases of diffusion coefficients of reactants and autocatalytic behaviour. Shaw et al. [37] also explored equal diffusive reactant and autocatalyst for a steady micropolar fluid model on a porous shrinking/stretching sheet. Rana et al. [38] studied oblique viscoplastic slip flow with homogeneous–heterogeneous reactions. Magnetohydrodynamic flows of reactive fluids have also received significant attention. Soundalgekar and Gupta [39] presented analytical solutions for hydrodynamic dispersion in a magnetohydrodynamic channel flow with homogeneous and heterogeneous reactions. These studies all verified the marked influence of chemical reaction in multi-physical Newtonian and non-Newtonian heat and mass transfer. In the present article we develop a mathematical model for magnetohydrodynamic chemically reacting oblique stagnation point flow, heat and mass transfer from a stretching sheet to an Oldroyd-B viscoelastic fluid. The non-Fourier Cattaneo–Christov heat flux model is utilized and both homogeneous–heterogeneous reactions are examined in the species (concentration) conservation equation. Numerical quadrature solutions are obtained for the normalized ordinary differential boundary value problem. An extensive parametric study is conducted to evaluate heat, momentum and concentration characteristics. Validation with the Adomian decomposition method is included. To the best knowledge of the authors the present study has never been reported before and is relevant to certain nuclear and materials processing operations.

2 Physico-chemical magnetohydrodynamic viscoelastic transport model

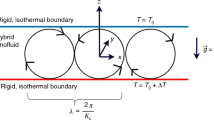
Consider the steady, two-dimensional oblique stagnation flow and mixed convection heat and mass transfer in a reactive electrically conducting Oldroyd-B elastic-viscous fluid from a stretching sheet. The viscoelastic fluid is doped with a species which undergoes both homogeneous and heterogeneous chemical reactions. The Cattaneo–Christov heat flux model is used in the heat (energy) conservation equation to simulate thermal relaxation effects. Two Equal but oppositely forces are applied in both directions along \( x_{1} \)-axis. (See Fig. 1.) A magnetic field of constant strength is applied transverse to plane of the sheet. The governing conservation equations for mass, momentum, energy and species may be formulated as follows [40]

Fig. 1
figure 1

Physical model

Full size image
$$ \bar{\nabla }.\bar{\varvec{V}} = 0, $$
(1)
$$ \rho \left[ {\frac{{\partial \bar{\varvec{V}}}}{\partial t} + \left( {\bar{\varvec{V}}.\bar{\nabla }} \right)\bar{\varvec{V}}} \right] = \bar{\varvec{V}}.\bar{\varvec{T}} + \varvec{J} \times \varvec{B}, $$
(2)
$$ \bar{\nabla } \times \varvec{B} =\varvec{\mu}_{\varvec{e}} \varvec{ J}, $$
(3)
$$ \bar{\nabla } \times \varvec{E} = - \frac{{\partial \varvec{B}}}{{\partial \varvec{t}}}\varvec{ }, $$
(4)
$$ \bar{\nabla }.\varvec{B} = 0, $$
(5)
$$ \varvec{J} = \sigma \left( {E + V \times \varvec{B}} \right), $$
(6)

The constitutive equation for Oldroyd-B fluid is:

$$ \varvec{T} = - p\varvec{I} + \varvec{S}, $$
(7)
$$ \varvec{S} + \lambda_{1} \left( {\frac{{\varvec{DS}}}{{\varvec{Dt}}} - \varvec{LS} - \varvec{SL}^{\varvec{T}} } \right) = \mu \left[ {A_{1} + \lambda_{2} \left( {\frac{{\varvec{D}A_{1} }}{{\varvec{Dt}}} - \varvec{L}A_{1} - A_{1} \varvec{L}^{\varvec{T}} } \right)} \right], $$
(8)
$$ \varvec{L} = grad \varvec{V},\varvec{ }A_{1} = L + L^{T} , $$
(9)

Here the upper-convected time derivative, \( \frac{D}{Dt}, \) in a Cartesian coordinate system can be defined as:

$$ \frac{\varvec{D}}{{\varvec{Dt}}} = \frac{\partial }{{\partial \varvec{t}}} + \varvec{V}.\nabla - \varvec{L} - \varvec{L}^{\varvec{T}} . $$
(10)

For this problem velocity vector and stress tensor is defined as:

$$ \varvec{V} = (\varvec{u}_{1} ,\varvec{u}_{2} )^{\varvec{T}} , $$
(11)
$$ S = \left( {\begin{array}{*{20}c} {S_{xx} } & {S_{xy} } \\ {S_{yx} } & {S_{yy} } \\ \end{array} } \right), $$
(12)

Navier–stokes equations become then:

$$ \bar{u}_{1} \frac{{\partial \bar{u}_{1} }}{{\partial \bar{x}_{1} }} + \bar{u}_{2} \frac{{\partial \bar{u}_{1} }}{{\partial \bar{x}_{2} }} + \frac{1}{\rho }\frac{{\partial \bar{p}}}{{\partial \bar{x}_{1} }} + \lambda_{1} \left( {\bar{u}_{1}^{2} \frac{{\partial^{2} \bar{u}_{1} }}{{\partial \bar{x}_{1}^{2} }} + \bar{u}_{2}^{2} \frac{{\partial^{2} \bar{u}_{1} }}{{\partial \bar{x}_{2}^{2} }} + 2\bar{u}_{1} \bar{u}_{2} \frac{{\partial^{2} \bar{u}_{1} }}{{\partial \bar{x}_{1} \partial \bar{x}_{2} }}} \right) = \nu \left[ {\frac{{\partial^{2} \bar{u}_{1} }}{{\partial \bar{x}_{1}^{2} }} + \frac{{\partial^{2} \bar{u}_{1} }}{{\partial \bar{x}_{2}^{2} }} + \lambda_{2} \left( {\bar{u}_{1} \frac{{\partial^{3} \bar{u}_{1} }}{{\partial \bar{x}_{1}^{3} }} + \bar{u}_{1} \frac{{\partial^{3} \bar{u}_{1} }}{{\partial \bar{x}_{1} \partial \bar{x}_{2}^{2} }} + \bar{u}_{2} \frac{{\partial^{3} \bar{u}_{1} }}{{\partial \bar{x}_{2}^{3} }} + \bar{u}_{2} \frac{{\partial^{3} \bar{u}_{1} }}{{\partial \bar{x}_{2} \partial \bar{x}_{1}^{2} }} - \frac{{\partial \bar{u}_{1} }}{{\partial \bar{x}_{1} }}\frac{{\partial^{2} \bar{u}_{1} }}{{\partial \bar{x}_{1}^{2} }} - \frac{{\partial \bar{u}_{1} }}{{\partial \bar{x}_{1} }}\frac{{\partial^{2} \bar{u}_{1} }}{{\partial \bar{x}_{2}^{2} }} - \frac{{\partial \bar{u}_{1} }}{{\partial \bar{x}_{2} }}\frac{{\partial^{2} \bar{u}_{2} }}{{\partial \bar{x}_{1}^{2} }} - \frac{{\partial \bar{u}_{1} }}{{\partial \bar{x}_{2} }}\frac{{\partial^{2} \bar{u}_{2} }}{{\partial \bar{x}_{2}^{2} }}} \right)} \right] - \frac{{\sigma B_{0}^{2} }}{\rho }\left( {\bar{u}_{1} + \lambda_{1} \bar{u}_{2} \frac{{\partial \bar{u}_{1} }}{{\partial \bar{x}_{2} }}} \right) + g_{1} \beta \{ \left( {\bar{T} - T_{\infty } } \right) + \lambda_{1} \left( {\bar{u}_{1} \frac{{\partial \bar{T}}}{{\partial \bar{x}_{1} }} + \bar{u}_{2} \frac{{\partial \bar{T}}}{{\partial \bar{x}_{2} }} - \frac{{\partial \bar{u}_{1} }}{{\partial \bar{x}_{1} }}\left( {\bar{T} - T_{\infty } } \right)} \right) $$
(13)
$$ \bar{u}_{1} \frac{{\partial \bar{u}_{2} }}{{\partial \bar{x}_{1} }} + \bar{u}_{2} \frac{{\partial \bar{u}_{2} }}{{\partial \bar{x}_{2} }} + \frac{1}{\rho }\frac{{\partial \bar{p}}}{{\partial \bar{x}_{2} }} + \lambda_{1} \left( {\bar{u}_{1}^{2} \frac{{\partial^{2} \bar{u}_{2} }}{{\partial \bar{x}_{1}^{2} }} + \bar{u}_{2}^{2} \frac{{\partial^{2} \bar{u}_{2} }}{{\partial \bar{x}_{2}^{2} }} + 2\bar{u}_{1} \bar{u}_{2} \frac{{\partial^{2} \bar{u}_{2} }}{{\partial \bar{x}_{1} \partial \bar{x}_{2} }}} \right) = \nu \left[ {\frac{{\partial^{2} \bar{u}_{2} }}{{\partial \bar{x}_{1}^{2} }} + \frac{{\partial^{2} \bar{u}_{2} }}{{\partial \bar{x}_{2}^{2} }} + \lambda_{2} \left\{ {\bar{u}_{1} \frac{{\partial^{3} \bar{u}_{2} }}{{\partial \bar{x}_{1}^{3} }} + \bar{u}_{1} \frac{{\partial^{3} \bar{u}_{2} }}{{\partial \bar{x}_{1} \partial \bar{x}_{2}^{2} }} + \bar{u}_{2} \frac{{\partial^{3} \bar{u}_{2} }}{{\partial \bar{x}_{2}^{3} }} + \bar{u}_{2} \frac{{\partial^{3} \bar{u}_{2} }}{{\partial \bar{x}_{2} \partial \bar{x}_{1}^{2} }} - \frac{{\partial \bar{u}_{2} }}{{\partial \bar{x}_{1} }}\frac{{\partial^{2} \bar{u}_{1} }}{{\partial \bar{x}_{1}^{2} }} - \frac{{\partial \bar{u}_{2} }}{{\partial \bar{x}_{1} }}\frac{{\partial^{2} \bar{u}_{1} }}{{\partial \bar{x}_{2}^{2} }} - \frac{{\partial \bar{u}_{2} }}{{\partial \bar{x}_{2} }}\frac{{\partial^{2} \bar{u}_{2} }}{{\partial \bar{x}_{1}^{2} }} - \frac{{\partial \bar{u}_{2} }}{{\partial \bar{x}_{2} }}\frac{{\partial^{2} \bar{u}_{2} }}{{\partial \bar{x}_{2}^{2} }}} \right\}} \right] $$
(14)
$$ \rho C_{p} \left( {\bar{u}_{1} \frac{{\partial \bar{T}}}{{\partial \bar{x}_{1} }} + \bar{u}_{2} \frac{{\partial \bar{T}}}{{\partial \bar{x}_{2} }}} \right) = - \bar{\nabla }.\bar{\varvec{q}} $$
(15)
$$ \bar{u}_{1} \frac{{\partial \bar{c}_{1} }}{{\partial \bar{x}_{1} }} + \bar{u}_{2} \frac{{\partial \bar{c}_{1} }}{{\partial \bar{x}_{2} }} = D_{A} \frac{{\partial^{2} \bar{c}_{1} }}{{\partial \bar{x}_{2}^{2} }} - k_{c} \bar{c}_{1} \bar{c}_{2}^{2} $$
(16)
$$ \bar{u}_{1} \frac{{\partial \bar{c}_{2} }}{{\partial \bar{x}_{1} }} + \bar{u}_{2} \frac{{\partial \bar{c}_{2} }}{{\partial \bar{x}_{2} }} = D_{B} \frac{{\partial^{2} \bar{c}_{2} }}{{\partial \bar{x}_{2}^{2} }} + k_{c} \bar{c}_{1} \bar{c}_{2}^{2} $$
(17)

Here \( \bar{\varvec{V}} \) having \( \bar{u}_{1} \) and \( \bar{u}_{2} \) as the \( \bar{x}_{1} - \) and \( \bar{x}_{2} - \) velocity components, respectively, \( \nu \) is effective kinematic viscosity, \( \bar{p} \) is pressure, \( \rho \) is s density, the term \( \varvec{J} \times \varvec{B} \) is ponder motive force of the fluid because of electric current, \( \varvec{J} \) is current density of fluid and \( \varvec{B} \) is the magnetic flux. \( \varvec{\mu}_{\varvec{e}} \) is constant known as magnetic permeability, E is electric field and \( \sigma \) is electric conductivity, \( p\varvec{I} \) is spherical part of stress tensor and \( \varvec{S} \) is extra stress tensor, \( \bar{T} \) is temperature of the fluid, \( \lambda_{1} \) is relaxation time, \( \lambda_{2} \) is retardation time, \( \alpha \) is thermal diffusivity, \( T_{\infty } \) is ambient fluid temperature, \( \bar{c}_{1} \) and \( \bar{c}_{2} \) are absorption coefficients of the organic classes \( A \) and \( B \), \( k_{c} \) and \( k_{s} \) are the rate factors, assuming the same reaction progressions, \( D_{A} \) and \( D_{B} \) are dispersion quantities, \( a,b.c \) are constants, \( \bar{q}, \) the heat flux satisfying the non-Fourier theory [41]:

$$ \bar{\varvec{q}} + \lambda_{2} \frac{{\partial \bar{\varvec{q}}}}{{\partial \bar{t}}} + \lambda_{2} \left( {\bar{\nabla }.\bar{V}} \right)\bar{\varvec{q}} + \lambda_{2} \bar{V}.\bar{\nabla }\bar{\varvec{q}} - \lambda_{2} \bar{\varvec{q}}.\bar{\nabla }\bar{V} + k\bar{\nabla }\bar{T} = 0, $$
(18)

In Eq. (7) \( \lambda_{2} \) is thermal retardation time and \( k \), denotes the viscoelastic fluid thermal conductivity. Eliminating \( \bar{q} \) from Eqs. (15) and (18) yields:

$$ \bar{u}_{1} \frac{{\partial \bar{T}}}{{\partial \bar{x}_{1} }} + \bar{u}_{2} \frac{{\partial \bar{T}}}{{\partial \bar{x}_{2} }} = \frac{k}{{\rho C_{p} }}\frac{{\partial^{2} \bar{T}}}{{\partial \bar{x}_{2}^{2} }} - \lambda_{2} \left( {\bar{u}_{1}^{2} \frac{{\partial^{2} \bar{T}}}{{\partial \bar{x}_{1}^{2} }} + \bar{u}_{2}^{2} \frac{{\partial^{2} \bar{T}}}{{\partial \bar{x}_{2}^{2} }}} \right) + 2\bar{u}_{1} \bar{u}_{2} \frac{{\partial^{2} \bar{T}}}{{\partial \bar{x}_{1} \partial \bar{x}_{2} }} + \left( {\bar{u}_{1} \frac{{\partial \bar{u}_{1} }}{{\partial \bar{x}_{1} }} + \bar{u}_{2} \frac{{\partial \bar{u}_{1} }}{{\partial \bar{x}_{2} }}} \right)\frac{{\partial \bar{T}}}{{\partial \bar{x}_{1} }} + \left( {\bar{u}_{1} \frac{{\partial \bar{u}_{2} }}{{\partial \bar{x}_{1} }} + \bar{u}_{2} \frac{{\partial \bar{u}_{2} }}{{\partial \bar{x}_{2} }}} \right)\frac{{\partial \bar{T}}}{{\partial \bar{x}_{2} }} $$
(19)

The prescribed boundary conditions at the wall (sheet) and free stream are:

$$ \left. {\begin{array}{*{20}l} {\bar{u}_{1} = c\bar{x}_{1} , \bar{u}_{2} = 0, - k\frac{{\partial \bar{T}}}{{\partial \bar{x}_{2} }} = h\left( {T_{f} - \bar{T}} \right),} \hfill \\ {D_{A} \frac{{\partial \bar{c}_{1} }}{{\partial \bar{x}_{2} }} = k_{s} \bar{c}_{1} , D_{B} \frac{{\partial \bar{c}_{2} }}{{\partial \bar{x}_{2} }} = - k_{s} \bar{c}_{1} ,} \hfill \\ \end{array} } \right\}{\text{at}}\quad \bar{x}_{2} = 0, $$
(20)
$$ \bar{u}_{1} = a\bar{x}_{1} + b\bar{x}_{2} , \bar{T} = T_{\infty } , \bar{c}_{1} \to c_{0} , \bar{c}_{2} \to 0, {\text{as}}\,\bar{x}_{2} \to \infty . $$
(21)

Introducing similarity transformations following Nadeem et al. [42]:

$$ \left. {\begin{array}{*{20}c} {x_{1} = \bar{x}_{1} \sqrt {\frac{c}{\nu }} ,x_{2} = \bar{x}_{2} \sqrt {\frac{c}{\nu }} ,u_{1} = \bar{u}_{1} \frac{1}{{\sqrt {\nu c} }} ,u_{2} = \bar{u}_{2} \frac{1}{{\sqrt {\nu c} }}} \\ {p = \frac{{\bar{p}}}{\mu c}, T = \frac{{\bar{T} - T_{\infty } }}{{T_{f} - T_{\infty } }} , \bar{c}_{1} = c_{0} j\left( {x_{2} } \right),\bar{c}_{2} = c_{0} s\left( {x_{2} } \right)} \\ \end{array} } \right\} $$
(22)

Invoking Eq. (22), into Eqs. (13–21) yields the following dimensionless equations:

$$ \frac{{\partial u_{1} }}{{\partial x_{1} }} + \frac{{\partial u_{2} }}{{\partial x_{2} }} = 0, $$
(23)
$$ u_{1} \frac{{\partial u_{1} }}{{\partial x_{1} }} + u_{2} \frac{{\partial u_{2} }}{{\partial x_{2} }} + \beta_{1} \left\{ {u_{1}^{2} \frac{{\partial^{2} u_{1} }}{{\partial x_{1}^{2} }} + u_{2}^{2} \frac{{\partial^{2} u_{1} }}{{\partial x_{2}^{2} }} + 2u_{1} u_{2} \frac{{\partial^{2} u_{1} }}{{\partial x_{1} \partial x_{2} }}} \right\} = - \frac{\partial p}{{\partial x_{1} }} + \frac{{\partial^{2} u_{1} }}{{\partial x_{1}^{2} }} + \frac{{\partial^{2} u_{1} }}{{\partial x_{2}^{2} }} + \beta_{2} \left\{ {u_{1} \frac{{\partial^{3} u_{1} }}{{\partial x_{1}^{3} }} + u_{1} \frac{{\partial^{3} u_{1} }}{{\partial x_{1} \partial x_{2}^{2} }} + u_{2} \frac{{\partial^{3} u_{1} }}{{\partial x_{2} \partial x_{1}^{2} }} + u_{2} \frac{{\partial^{3} u_{1} }}{{\partial x_{2}^{3} }}{-}\frac{{\partial u_{1} }}{{\partial x_{1} }}\frac{{\partial^{2} u_{1} }}{{\partial x_{1}^{2} }} - \frac{{\partial u_{1} }}{{\partial x_{1} }}\frac{{\partial^{2} u_{1} }}{{\partial x_{2}^{2} }} - \frac{{\partial u_{1} }}{{\partial x_{2} }}\frac{{\partial^{2} u_{2} }}{{\partial x_{1}^{2} }} - \frac{{\partial u_{1} }}{{\partial x_{2} }}\frac{{\partial^{2} u_{2} }}{{\partial x_{2}^{2} }}} \right\}{-}{\text{M}}\left( {u_{1} + \beta_{1} u_{2} \frac{{\partial u_{1} }}{{\partial x_{1} }}} \right) + \lambda \left[ {{\text{T}} + \beta_{1} \left\{ {u_{1} \frac{\partial T}{{\partial x_{1} }} + u_{2} \frac{\partial T}{{\partial x_{2} }} - T\frac{{\partial u_{1} }}{{\partial x_{1} }}} \right\}} \right], $$
(24)
$$ u_{1} \frac{{\partial u_{2} }}{{\partial x_{1} }} + u_{2} \frac{{\partial u_{2} }}{{\partial x_{2} }} + \beta_{1} \left\{ {u_{1}^{2} \frac{{\partial^{2} u_{2} }}{{\partial x_{1}^{2} }} + u_{2}^{2} \frac{{\partial^{2} u_{2} }}{{\partial x_{2}^{2} }} + 2u_{1} u_{2} \frac{{\partial^{2} u_{2} }}{{\partial x_{1} \partial x_{2} }}} \right\} = - \frac{\partial p}{{\partial x_{2} }} + \frac{{\partial^{2} u_{2} }}{{\partial x_{1}^{2} }} + \frac{{\partial^{2} u_{2} }}{{\partial x_{2}^{2} }} + \beta_{2} \left\{ {u_{1} \frac{{\partial^{3} u_{2} }}{{\partial x_{1}^{3} }} + u_{1} \frac{{\partial^{3} u_{2} }}{{\partial x_{1} \partial x_{2}^{2} }} + u_{2} \frac{{\partial^{3} u_{2} }}{{\partial x_{2} \partial x_{1}^{2} }} + u_{2} \frac{{\partial^{3} u_{2} }}{{\partial x_{2}^{3} }}{-}\frac{{\partial u_{2} }}{{\partial x_{1} }}\frac{{\partial^{2} u_{1} }}{{\partial x_{1}^{2} }} - \frac{{\partial u_{2} }}{{\partial x_{1} }}\frac{{\partial^{2} u_{1} }}{{\partial x_{2}^{2} }} - \frac{{\partial u_{2} }}{{\partial x_{2} }}\frac{{\partial^{2} u_{2} }}{{\partial x_{1}^{2} }} - \frac{{\partial u_{2} }}{{\partial x_{2} }}\frac{{\partial^{2} u_{2} }}{{\partial x_{2}^{2} }}} \right\}, $$
(25)
$$ u_{1} \frac{\partial T}{{\partial x_{1} }} + u_{2} \frac{\partial T}{{\partial x_{2} }} = \frac{1}{{P_{r} }}\frac{{\partial^{2} T}}{{\partial x_{2}^{2} }} - \beta_{2} \left\{ {u_{1}^{2} \frac{{\partial^{2} T}}{{\partial x_{1}^{2} }} + u_{2}^{2} \frac{{\partial^{2} T}}{{\partial x_{2}^{2} }} + 2u_{1} u_{2} \frac{{\partial^{2} T}}{{\partial x_{1} \partial x_{2} }} + \left( {u_{1} \frac{{\partial u_{1} }}{{\partial x_{1} }} + u_{2} \frac{{\partial u_{1} }}{{\partial x_{2} }}} \right)\frac{\partial T}{{\partial x_{1} }} + \left( {u_{1} \frac{{\partial u_{2} }}{{\partial x_{1} }} + u_{2} \frac{{\partial u_{2} }}{{\partial x_{2} }}} \right)\frac{\partial T}{{\partial x_{2} }}} \right\}, $$
(26)
$$ u_{2} \frac{\partial j}{{\partial x_{2} }}\left( {x_{2} } \right) = \frac{1}{Sc}\frac{{\partial^{2} j}}{{\partial x_{2}^{2} }}\left( {x_{2} } \right) - k_{1} j\left( {x_{2} } \right)s^{2} \left( {x_{2} } \right), $$
(27)
$$ u_{2} \frac{\partial s}{{\partial x_{2} }}\left( {x_{2} } \right) = \frac{\delta }{Sc}\frac{{\partial^{2} s}}{{\partial x_{2}^{2} }}\left( {x_{2} } \right) + k_{1} j\left( {x_{2} } \right)s^{2} (x_{2} ), $$
(28)

The normalized boundary conditions take the form:

$$ \left. {\begin{array}{*{20}l} {u_{1} = x_{1} , u_{2} = 0, \frac{\partial T}{{\partial x_{2} }} = - Bi\left( {1 - T} \right),} \hfill \\ {D_{A} \frac{\partial j}{{\partial x_{2} }}\left( {x_{2} } \right) = k_{s} \sqrt {\frac{\nu }{c}} j\left( {x_{2} } \right), D_{B} \frac{\partial s}{{\partial x_{2} }}\left( {x_{2} } \right) = - k_{s} \sqrt {\frac{\nu }{c}} j\left( {x_{2} } \right),} \hfill \\ \end{array} } \right\}{\text{at}}\,x_{2} = 0, $$
(29)
$$ u_{1} = \frac{a}{c}x_{1} + \gamma_{1} x_{2} , T = 0, j\left( {x_{2} } \right) \to 1, s\left( {x_{2} } \right) \to 0, at x_{2} \to \infty . $$
(30)

Here \( \beta_{1} = \lambda_{1} c \) and \( \beta_{2} = \lambda_{2} c \) are the relaxation and retardation Deborah numbers, \( \frac{{\sigma B_{0}^{2} }}{\rho c} = M \) is magnetic field parameter, \( Pr = \frac{\nu }{\alpha } \) is Prandtl number, \( \lambda = \frac{{g_{1} \beta \left( {T_{f} - T_{\infty } } \right)}}{{c\sqrt {\nu c} }} \) is mixed convection parameter, \( Bi = - \frac{h}{k}\sqrt {\frac{\nu }{c}} \) is Biot number,\( Sc = \frac{\nu }{{D_{B} }}\,{\text{is}}\,{\text{Schmidt}}\,{\text{number}}, \frac{a}{c} \) is stretching ratio and \( \gamma_{1} = \frac{b}{c} \) is obliqueness parameter.

Defining the stream function as:

$$ u_{1} = \frac{\partial \zeta }{{\partial x_{2} }},u_{2} = - \frac{\partial \zeta }{{\partial x_{1} }}. $$
(31)

Redefining the stream function [42]:

$$ \zeta = x_{1} f\left( {x_{2} } \right) + g\left( {x_{2} } \right), T\left( {x_{1} ,x_{2} } \right) = \theta \left( {x_{2} } \right). $$
(32)

Using Eq. (31), (see Appendix) and then Eq. (32), we have set of equations

$$ f^{\prime \prime \prime } + ff^{\prime \prime } - \left( {f^{\prime } } \right)^{2} + \beta_{1} \left( {2ff^{\prime } f^{\prime \prime } - f^{2} f^{\prime \prime \prime } } \right) + \beta_{2} \left( {f^{\prime \prime 2} - ff^{\prime \prime \prime \prime } } \right) + M\left( {\beta_{1} ff^{\prime \prime } - f^{\prime } } \right) + B_{1} = 0 $$
(33)
$$ g^{\prime \prime \prime } - f^{\prime } g^{\prime } + fg^{\prime \prime } + \beta_{1} \left( {2fg^{\prime } f^{\prime \prime } - f^{2} g^{\prime \prime \prime } } \right) + \beta_{2} \left( { - f^{\prime } g^{\prime \prime \prime } + f^{\prime \prime } g^{\prime \prime } - fg^{\prime \prime \prime \prime } + f^{\prime \prime \prime } g^{\prime } } \right) + M\left( {\beta_{1} fg^{\prime \prime } - g^{\prime } } \right) + \lambda \left\{ {\theta - \beta_{1} \left( {f\theta^{\prime } - f^{\prime } \theta } \right)} \right\} + B_{2} = 0, $$
(34)
$$ \theta^{\prime \prime } + \Pr \left[ {f\theta^{\prime } - \beta_{2} \left\{ {f^{2} \theta^{\prime \prime } + ff^{\prime } \theta^{\prime } } \right\}} \right] = 0. $$
(35)

Assuming the dispersion constant of organic class reactants \( A \) and \( B \) are of similar extent, using the following constraint \( D_{A} = D_{B} \Rightarrow \delta = 1, \) leads to:

$$ j\left( {x_{2} } \right) + s\left( {x_{2} } \right) = 1 $$
(36)
$$ j^{\prime \prime } \left( {x_{2} } \right) + Sc\left[ {f\left( {x_{2} } \right)j^{\prime } \left( {x_{2} } \right) - k_{1} j\left( {x_{2} } \right)\left\{ {1 - j^{2} \left( {x_{2} } \right)} \right\}} \right] = 0, $$
(37)

The transformed “similarity” boundary conditions (see “Appendix”) assume the form:

$$ f = 0,f^{\prime } = 1, g^{\prime } = 0 , \theta^{\prime } = - Bi\left( {1 - \theta \left( 0 \right)} \right), j^{\prime } = k_{2} j\left( 0 \right),\quad {\text{at}}\,x_{2} = 0, $$
(38)
$$ f^{\prime } = \frac{a}{c}, g^{\prime } \left( {x_{2} } \right) \to \gamma_{1} x_{2} , \theta = 0,j \to 1,\quad {\text{at}}\,x_{2} \to \infty . $$
(39)

Using asymptotic condition (39) in Eqs. (33) and (34), we get:

$$ B_{1} = \left( {\frac{a}{c}} \right)^{2} + M\frac{a}{c}, B_{2} = - \gamma_{1} \left[ {A + M\left\{ {x_{2} - K_{1} \left( {\frac{a}{c}x_{2} + A} \right)} \right\}} \right], $$
(40)

Here \( A \) is a boundary layer constant.

Introducing:

$$ g^{\prime } \left( {x_{2} } \right) = \gamma_{1} h\left( {x_{2} } \right). $$
(41)

Using Eqs. (40) and (41) in Eqs. (33) and (34), we have:

$$ f^{\prime \prime \prime } + ff^{\prime \prime } - \left( {f^{\prime } } \right)^{2} + \beta_{1} \left( {2ff^{\prime } f^{\prime \prime } - f^{2} f^{\prime \prime \prime } } \right) + \beta_{2} \left( {f^{\prime \prime 2} - ff^{\prime \prime \prime \prime } } \right) + M\left( {\beta_{1} ff^{\prime \prime } - f^{\prime } } \right) + \left( {a/c} \right)^{2} + M\frac{a}{c} = 0 $$
(42)
$$ h^{\prime \prime } - f^{\prime } h + fh^{\prime } + \beta_{1} \left( {2fhf^{\prime \prime } - f^{2} h^{\prime \prime } } \right) + \beta_{2} \left( {f^{\prime \prime \prime } h + f^{\prime \prime } h^{\prime } - f^{\prime } h^{\prime \prime } - fh^{\prime \prime \prime } } \right) + M\left( {\beta_{1} fh^{\prime } - h} \right) + \frac{\lambda }{{\gamma_{1} }}\left\{ {\theta - \beta_{1} \left( {f\theta^{\prime } - f^{\prime } \theta } \right)} \right\} - \left\{ {A\left( {1 + M\beta_{1} } \right) + x_{2} M \left( {\beta_{1} \frac{a}{c} - 1} \right)} \right\}, $$
(43)
$$ \theta^{\prime \prime } + \Pr \left\{ {f\theta^{\prime } - \beta_{2} \left( {f^{2} \theta^{\prime \prime } + ff^{\prime } \theta^{\prime } } \right)} \right\} = 0. $$
(44)
$$ j^{\prime \prime } + Sc\left\{ {fj^{\prime } - k_{1} j\left( {1 - j^{2} } \right)} \right\} = 0. $$
(45)

The associated boundary conditions emerge as:

$$ \left. {\begin{array}{*{20}l} {f = h = 0,f^{\prime } = 1 ,\theta^{\prime } = - Bi\left( {1 - \theta \left( 0 \right)} \right),j^{\prime } = k_{2} j\left( 0 \right), \,{\text{at}}\,x_{2} = 0,} \hfill \\ {f^{\prime } = \gamma_{1} , h^{\prime } = 1, \theta = 0, j \to 1,\,{\text{as}}\, x_{2} \to \infty .} \hfill \\ \end{array} } \right\} $$
(46)

Here \( \left( \right)^{\prime } \) denotes ordinary derivative with respect to \( x_{2} . \)

Important engineering design quantities are the local heat and mass flux, which in dimensional and non-dimensional form are defined, respectively, as:

$$ q_{w} = - k\left( {\frac{\partial T}{\partial y}} \right)_{y = 0} , $$
(47)
$$ z_{w} = \left( {\frac{\partial j}{\partial y}} \right)_{y = 0} , $$
(48)

and

$$ q_{w} = - \theta^{\prime } \left( 0 \right), $$
(49)
$$ z_{w} = - j^{\prime } \left( 0 \right). $$
(50)

3 Computational solutions of boundary value problem

Analytical solutions of non-dimensional nonlinear coupled ordinary differential equation system defined by Eqs. (42–45) with boundary conditions (46) are challenging. A computational methodology is therefore elected in which numerical quadrature is implemented (i.e. a shooting algorithm) together with the popular and robust Runge–Kutta–Fehlberg method. This approach can easily handle multi-order ordinary differential boundary value problems and has been implemented via different symbolic codes in many studies including reactive mixed double-diffusive convection, magnetohydrodynamic slip flow [43], contracting/expanding nanopolymer sheet flows, free convection autocatalytic reactive magnetic flows [44] and gyrotactic bioconvection nanofluid pumping. By making use of the following substitutions in Eqs. (42–46), we have:

$$ \left. \begin{aligned} \left( {\begin{array}{*{20}c} f \\ {f^{\prime } } \\ {f^{\prime \prime } } \\ {f^{\prime \prime \prime } } \\ {f^{\prime \prime \prime \prime } } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {y_{1} } \\ {y_{1}^{\prime } = y_{2} } \\ {y_{2}^{\prime } = y_{3} } \\ {y_{3}^{\prime } = y_{4} } \\ {y_{4}^{\prime } = y_{5} } \\ \end{array} } \right), \left( {\begin{array}{*{20}c} h \\ {h^{\prime } } \\ {h^{\prime \prime } } \\ {h^{\prime \prime \prime } } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {y_{6} } \\ {y^{\prime}_{6} = y_{7} } \\ {y^{\prime}_{7} = y_{8} } \\ {y_{8}^{'} = y_{9} } \\ \end{array} } \right), \hfill \\ \left( {\begin{array}{*{20}c} \theta \\ {\theta^{\prime } } \\ {\theta^{\prime \prime } } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {y_{10} } \\ {y_{10}^{\prime } = y_{11} } \\ {y_{11}^{\prime } = y_{12} } \\ \end{array} } \right), \left( {\begin{array}{*{20}c} j \\ {j^{\prime } } \\ {j^{\prime \prime } } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {y_{13} } \\ {y_{13}^{\prime } = y_{14} } \\ {y_{14}^{\prime } = y_{15} } \\ \end{array} } \right), \hfill \\ \end{aligned} \right\} $$
(51)
$$ y_{1} y_{4}^{\prime } = \frac{1}{{\beta_{2} }}\left[ {\begin{array}{*{20}c} {y_{4} + y_{1} y_{3} - y_{2}^{2} + \beta_{1} \left\{ {2y_{1} y_{2} y_{3} - y_{4} y_{1}^{2} } \right\}} \\ { - M\left( { - y_{2} + \beta_{1} y_{1} y_{3} } \right) - \left( {\frac{a}{c}} \right)^{2} - M\frac{a}{c}} \\ \end{array} } \right] + y_{3}^{2} , $$
(52)
$$ y_{1} y_{8}^{\prime } = \frac{1}{{\beta_{2} }}\left[ {y_{8} + y_{1} y_{7} - y_{2} y_{6} + \beta_{1} \left\{ {2y_{1} y_{3} y_{6} - y_{8} y_{1}^{2} } \right\} - M\left( {\beta_{1} y_{1} y_{7} - y_{6} } \right) - \frac{\lambda }{{\gamma_{1} }}\left\{ {\theta - \beta_{1} \left( {y_{1} \theta^{\prime } - y_{2} \theta } \right)} \right\} + A\left( {1 + M\beta_{1} } \right) + x_{2} M\left( {\beta_{1} \gamma_{1} - 1} \right)} \right] + y_{4} y_{6} + y_{3} y_{7} - y_{2} y_{8} , $$
(53)
$$ y_{11}^{\prime } = - Pr\left[ { y_{1} y_{11} - \beta_{2} \left\{ {y_{1}^{2} y_{12} + y_{1} y_{2} y_{11} } \right\}} \right], $$
(54)
$$ y_{15}^{\prime } = - {\text{Sc }}\left\{ {y_{1} y_{14} - k_{1} y_{13} \left( {1 - y_{13}^{2} } \right)} \right\}, $$
(55)
$$ y_{1} \left( 0 \right) = 0, y_{3} \left( 0 \right) = 0, y_{4} \left( 0 \right) = \alpha_{1} , $$
(56)
$$ y_{6} \left( 0 \right) = 0, y_{8} \left( 0 \right) = \alpha_{2} , $$
(57)
$$ y_{8} \left( 0 \right) = \alpha_{3} , $$
(58)
$$ y_{11} \left( 0 \right) = \alpha_{4} ,\quad y_{13} \left( 0 \right) = \alpha_{5} , $$
(59)

Here \( \alpha_{i} , 1 \le i \le 5 \) are shooting parameters. A tolerance level of \( 10^{ - 5} \) is considered in all calculations. Note that for all computations the variable y is used instead of \( x_{2 } . \)

4 Validation with Adomian decomposition method (ADM)

Since the present model is novel there are no existing solutions in the literature with which validation of the general model can be conducted. We therefore use an alternative approach and validate the solutions with an alternative numerical method known as Adomian decomposition method (ADM). Equations (42–45) with boundary conditions (46) are therefore resolved with ADM and selected comparison is visualized in Fig. 2. Introduced by Adomian [45], this approach employs very precise polynomial expansions to achieve faster convergence compared with other methods. ADM has been exploited recently in numerous sophisticated fluid dynamics problems. The reader is referred to Kezzar and Sar [46] and Ebaid et al. [47] who studied nanofluids, Bég et al. [48] who applied ADM to bio-magneto-rheological lubrication flows and Aaboubi et al. [49] for electrochemical species diffusion flows. An advantage of ADM is that it gives analytical approximations to an extensive class of nonlinear equations without linearization, perturbed solution or discretization. ADM sets up an infinite series solution for unidentified functions and exploits recursive relations. Applying standard procedure of Adomian Decomposition Method (ADM), inverse operators are formulated. The unknown dependent flow variable functions arising in the momentum, energy, species conservation equations i.e. normal velocity \( f\left( y \right) \), tangential velocity \( h\left( y \right) \), temperature \( \theta \left( y \right) \) and concentration, \( j \left( y \right) \), can be conveyed as infinite series’ of the form:

Fig. 2
figure 2

Variation of normal velocity \( f^{\prime } \left( y \right) \) with relaxation Deborah number \( \beta_{1} \)

Full size image
$$ f\left( y \right) = \sum\limits_{m = 0}^{\infty } {f_{m} } ,h\left( y \right) = \sum\limits_{m = 0}^{\infty } {h_{m} } ,\theta \left( y \right) = \sum\limits_{m = 0}^{\infty } {\theta_{m} } ,j\left( y \right) = \sum\limits_{m = 0}^{\infty } {j_{m} } $$
(60)

These expansions are introduced into Eqs. (42–46) and the resulting linear and nonlinear terms are decomposed by an infinite series of polynomials. Boundary conditions (46) are also adapted. The resulting solutions are lengthy algebraic relations and omitted for brevity. The numerical evaluation is executed in MATLAB symbolic software. Figure 2 shows the comparison of the ADM and quadrature solutions for the case β1 = 0.05. Evidently very close agreement is achieved for the normal velocity component velocity \( f^{\prime } \left( y \right). \) Figure 2 further shows that with increasing relaxation Deborah number, \( \beta_{1} \), there is a sustained decrease in normal velocity component throughout the boundary layer. The flow is therefore decelerated and momentum boundary layer also decreases.

The Oldroyd-B model is in fact a quasilinear rheological rate model. It is equivalent to the convected Jeffery model. Although often in simulations a single Deborah number is deployed which represents the ratio of relaxation to retardation times, in the present work we employ two distinct Deborah numbers, β1 and β2 which, respectively, are known as the relaxation Deborah number (a function of \( \lambda_{1} \) i.e. relaxation time) and the retardation Deborah number (a function of \( \lambda_{2} \) i.e. retardation time). Rheological fluids exhibits distinctive time scaled memory a feature known as relaxation time. At zero deformation rates such materials ease through their relaxation time which is their constitutive property. Similarly, under nonlinear deformation of rheological fluids, considerable tension cultivates in the streamlines due to large relaxation time which leads to nonzero normal stresses. The larger the relaxation time the greater the tension and the associated tensile stresses cause a deceleration in the fluid i.e. reduction in momentum (hydrodynamic) boundary layer thickness, as shown in Fig. 2. In the current work, we have constrained the value of \( \lambda_{2} \), i.e. retardation time as 0.2 which implies that the timescale of fluid movement is low which is appropriate for working fluids in nuclear reactors, industrial heat transfer processes, etc. Retardation time is also in rheology. When retardation times are high the behaviour corresponds more to high-density polymers where elastic forces dominate the viscous forces and therefore this is not relevant to the present discussion. Many investigations have confirmed that relaxation time has a much more prominent role in viscoelastic fluids whereas retardation time is generally more dominant in viscoelastic solids [50]. Further validation with ADM is also included for Figs. 3, 4, 5 i.e. for tangential velocity, temperature and concentration fields and again very close correlation is achieved. It is also noteworthy that in each of these and the figures plotted there is a very smooth behaviour of profiles in free stream indicating that an effectively large infinity boundary condition is prescribed in both numerical quadrature and the ADM codes. Confidence in the shooting quadrature method is therefore justifiably high.

Fig. 3
figure 3

Variation of tangential velocity \( h^{\prime } \left( y \right) \) with relaxation Deborah number \( \beta_{1} \)

Full size image

5 Computational results and discussion

Broad calculations have been conducted with shooting quadrature technique and are visualized in Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12 for the primitive variables (i.e. normal velocity, tangential velocity, temperature and concentration) and in Table 1 for derivative functions (local heat flux and local mass flux). We note that for brevity we constrain the values of certain geometric parameters i.e. \( \frac{a}{c} \) (stretching ratio) fixed at 0.1 and \( \gamma_{1} = \frac{b}{c} \) (obliqueness parameter) is fixed at 0.5 as is thermal relaxation parameter (γ).

Fig. 4
figure 4

Variation of tangential velocity \( h^{\prime } \left( y \right) \) with mixed convection parameter \( \lambda \)

Full size image
Fig. 5
figure 5

Variation of tangential velocity \( h^{\prime } \left( y \right) \) with Biot number, Bi

Full size image
Fig. 6
figure 6

Variation of temperature \( \theta \left( y \right) \) with relaxation Deborah number \( \beta_{1} \)

Full size image
Fig. 7
figure 7

Variation of temperature \( \theta \left( y \right) \) with Prandtl number \( Pr \)

Full size image
Fig. 8
figure 8

Variation of concentration j(y) with relaxation Deborah number \( \beta_{1} \)

Full size image
Fig. 9
figure 9

Variation of concentration \( j\left( y \right) \) with magnetic body force parameter, M

Full size image
Fig. 10
figure 10

Variation of concentration \( j\left( y \right) \) with Schmidt number, \( Sc \)

Full size image
Fig. 11
figure 11

Variation of concentration \( j\left( y \right) \) with homogeneous chemical reaction, \( k_{1} \)

Full size image
Fig. 12
figure 12

Variation of concentration \( j\left( y \right) \) with heterogeneous chemical reaction, \( k_{2} \)

Full size image
Table 1 Variation in local heat flux \( - \theta^{\prime } \left( 0 \right) \) and mass flux \( j^{\prime } \left( 0 \right) \) when \( \beta_{1} = 0.1, \beta_{2} = 0.1, \lambda = 0.2, \frac{a}{c} = 0.1, \gamma_{1} = 0.5, \Pr = 0.1, Bi = 0.1. \)
Full size table

Figures 3, 4 and 5 illustrate the behaviour of tangential velocity \( h^{\prime } \left( y \right), \) with variation in, respectively, relaxation Deborah number \( \beta_{1} \), mixed convection parameter, \( \lambda \), and finally Biot number, Bi. Tangential velocity \( h^{\prime } \left( y \right) \) increases with greater relaxation Deborah number \( \beta_{1} \) close to the wall but further from the wall it decreases. As noted earlier, relaxation time incorporates elastic as well as viscous properties of material. Higher Deborah number materials acts as rheological fluid while for smaller Deborah number, it works as a Newtonian fluid. The destruction in momentum in the normal direction (reduced normal velocity component) is compensated with a generation in tangential momentum. The higher Deborah number therefore only decelerates the normal velocity field component but acts to accelerate the tangential field. Figure 4 shows that with increasing mixed convection parameter \( \lambda \), tangential velocity \( h^{\prime } \left( y \right) \) declines close to surface whereas away from the surface it is accelerated. \( \lambda = \frac{{g_{1} \beta \left( {T_{f} - T_{\infty } } \right)}}{{c\sqrt {\nu c} }} \) and embodies comparative involvement of thermal buoyancy force to viscous hydrodynamic force. When this parameter is increased the flow is energized with buoyancy and the viscous effect is reduced. However, owing to the dominance of viscosity in boundary layer, the net effect is to inhibit tangential flow near the sheet and to enhance it further from the wall towards the edge of the boundary layer. Figure 5 specifies that with increasing Biot number \( Bi \) the tangential component of velocity \( h^{\prime } \left( y \right) \), is reduced near the wall whereas it is elevated further from the wall. Magnitudes of Biot number less than 0.1 infer that heat conduction within body is much quicker than heat convection away from surface, and temperature gradients are insignificant inside. This range is therefore ignored in our study (Biot number lesser than 0.1 corresponds to “thermally thin” scenarios). We consider exclusively cases wherein the Biot number is much larger than 0.1 and this relates to “thermally thick” regimes. All values of Biot number are associated with thermally thick behaviour. The Biot number is directly proportional to convection heat transfer coefficient at surface and inversely proportional to thermal conductivity, with other parameters fixed (\( Bi = - \frac{h}{k}\sqrt {\frac{\nu }{c}} \)). Higher thermal conductivities imply a lower Biot number and vice versa. The modification in thermal regime at the wall exerts an indirect influence on the tangential component of velocity. Increasing Biot number boosts the temperature near the wall which decreases momentum diffusion here and depresses the tangential velocity near wall. This effect is though reversed further towards the free stream where wall conduction effects are negated.

Figures 6 and 7 illustrate the response in temperature profile \( \theta \left( y \right) \) with relaxation Deborah numbers \( \beta_{1} \) and Prandtl number \( Pr. \) From Fig. 6 it is evident that temperature is elevated with increasing Deborah number \( \beta_{1} \). The increase in viscous effects associated with larger relaxation Deborah number serves to reduce momentum diffusion and to enhance thermal diffusion, for fixed Prandtl number. This manifests in heating in the boundary layer and increasing thermal boundary layer thickness. With increasing Prandtl number \( Pr, \) the tangential velocity \( h^{\prime } \left( y \right) \), declines near the surface whereas it is accelerated further from the surface, as observed in Fig. 7. This is so as smaller Prandtl number fluids are vastly conductive and their thermal diffusivity decreases with increasing values of Prandtl number. This stifles thermal diffusion and enhances momentum diffusion leading to flow acceleration further from the wall. Figures 8, 9, 10, 11 and 12 visualize the evolution in species concentration profile \( j\left( y \right) \) with various parameters. Figure 8 shows that concentration magnitude is reduced by increasing relaxation Deborah number \( \beta_{1} \). The increased viscous effect associated with greater relaxation Deborah number implies a reduction in momentum diffusion rate. Via coupling with the concentration field the latter is therefore also adversely affected and this results in a decrease in concentration boundary layer thickness. Figure 9 shows that similarly an increase in magnetic body force parameter, \( M = \frac{{\sigma B_{0}^{2} }}{\rho c}, \) also depresses concentration profile \( j\left( y \right). \) The inhibiting effect of Lorentzian magnetohydrodynamic drag associated with magnetic parameter serves to retard the flow. This decreases momentum diffusion in the boundary layer and again via coupling with the concentration field also indirectly opposes species diffusion. Concentration boundary layer thickness is also therefore depleted with greater magnetic field applied transverse to the wall. Asymptotically smooth convergence of all concentration plots is also achieved in the free stream confirming again the imposition of a sufficiently large infinity boundary condition in the computations. Figure 10 demonstrates that for an increment in Schmidt number \( Sc \), there is a considerable enhancement in concentration magnitudes and therefore boosts the concentration boundary layer thickness. Schmidt number is chosen between 0.1 and 0.5 and these correspond to communal diffusing chemical species which including (hydrogen, Sc ~ 0.1), (helium, Sc ~ 0.2), (water vapour, Sc ~ 0.4–0.8). Schmidt is ratio of momentum to species diffusivity. Small values of Sc lead to enhanced chemical molecular diffusivity. Sc also represents relative thickness of velocity boundary layer to concentration (solutal) boundary layer. Larger Sc fluids have lower mass diffusion characteristics. Evidently Sc modifies significantly the concentration distribution throughout the regime. Figures 11 and 12 show that concentration profile \( j\left( y \right) \) declines with intensification in strength of either homogeneous or heterogeneous reactions i.e. increase in either \( k_{1} \) and \( k_{2} . \) Owing to consumption of the reactive species, the concentration magnitudes are suppressed rapidly as \( k_{1} \) and \( k_{2} \) increase. Thus the diffusion rates can be tremendously altered by destructive first-order homogeneous or heterogeneous chemical reactions which both serve to thin the concentration boundary layer thickness.

Table 1 depicts the response in local heat and mass flux \( - \theta^{\prime } \left( 0 \right), j^{\prime } \left( 0 \right) \) with a variation in homogeneous or heterogeneous reactions \( k_{1} \) and \( k_{2} , \) magnetic field parameter \( M \), and Schmidt number \( Sc \). In this table, it is found that with elevating homogeneous reactions \( k_{1} \), there is no tangible change in heat flux \( - \theta^{\prime } \left( 0 \right), \) since the homogeneous reactions do not affect heat transfer rates but do impact on the mass transfer rate. Local mass flux \( j^{\prime } \left( 0 \right) \) decreases with increasing homogeneous reaction, \( k_{1} \). Also it shows that the heat flux is not noticeably modified with heterogeneous reaction parameter, \( k_{2} , \) whereas there is a considerable elevation in local mass flux. It is mentioned that with greater magnetic field parameter, M, both heat and mass flux \( - \theta^{\prime } \left( 0 \right), j^{\prime } \left( 0 \right) \) are suppressed. It also demonstrates that with elevation in the Schmidt number \( Sc \), heat flux \( - \theta^{\prime } \left( 0 \right) \) is not altered whereas there is a substantial accentuation in mass flux \( j^{\prime } \left( 0 \right) \).

6 Concluding remarks

Motivated by simulating rheological transport phenomena in nuclear reactor thermos-hydraulics near-wall regimes, a mathematical study has been conducted for time-independent hydromagnetic mixed convective heat and mass transfer in Oldroyd-B viscoelastic electrically conducting fluid non-orthogonal (oblique) stagnation flow impinging on a stretching sheet under homogeneous–heterogeneous chemical reaction effects. Non-Fourier Cattaneo–Christov heat flux model is being utilized in the model. The non-dimensional governing boundary layer equations along with viable boundary conditions are solved expending shooting algorithm. Validation has been performed with the Adomian decomposition method (ADM). Important deductions from the present simulation may be summarized as follows:

  1. 1.

    Momentum boundary layer thickness declines whereas thermal boundary layer thickness upsurges with cumulative relaxation Deborah number and magnetic body force parameter.

  2. 2.

    Concentration of chemical species increases with elevating Schmidt number whereas it is depleted with increasing strength of homogeneous- heterogeneous reactions.

  3. 3.

    Normal and tangential velocity components are influenced differently with increasing relaxation Deborah number.

  4. 4.

    With increasing Prandtl number the tangential velocity component is accelerated further from the wall whereas it is decelerated near the wall.

  5. 5.

    Increasing Biot number decelerates tangential velocity near the wall whereas it induces the opposite effect further from the wall towards the free stream.

  6. 6.

    Local heat flux is stifled with increasing magnetic field parameter \( M \).

  7. 7.

    Local mass flux is reduced with increasing homogeneous reaction parameter and also with greater magnetic field parameter whereas it is elevated with increasing heterogeneous reaction parameter and Schmidt number.

An important implication of the current work is that the complex rheology, reactive and other effects have a significant impact on the fluid dynamics of the stagnation flow. The multi-physics is therefore important in more realistic simulations for nuclear reactor transport phenomena. It is envisaged that inclusion of these complex phenomena (non-Fourier, rheological, magnetic etc.) associated with real fluids in nuclear engineering should not be neglected. The current simulations have considered a no-slip wall condition for velocity. Future studies will investigate both isotropic and anisotropic hydrodynamic slip and furthermore may explore thermal and solutal slip also.