1 Introduction

In the pursuit of high confinement mode in fusion devices, the use of high-power auxiliary heating, such as neutral beam injection (NBI) and electron cyclotron resonance heating (ECRH), is common [1,2,3]. However, these external agents can introduce energetic particles (EPs), leading to instability [4,5,6,7,8]. These EP-driven instabilities remove impurities from the core and reduce heating efficiency by causing a significant loss of EPs [9,10,11,12]. Therefore, investigating of energetic particle modes (EPMs) driven by EPs is crucial for understanding their properties and improving plasma confinement.

In the fusion device, the steady-state operating scenario characterized by reversed magnetic shear is generally regarded as an advanced operation mode [2, 3, 6,7,8]. A hollow current distribution is induced by an off-axis current drive, such as neutral beam current drive, resulting in the safety factor q > 1 and magnetic shear s < 0 [2, 3]. In this configuration, tearing and kink modes are usually stable because the lower-order rational surfaces of q = 1 and q = 2 are avoided [13, 14]. However, many circulating EPs generated by the tangential injection of NBI may still drive fishbone-like or non-resonant modes at q > 1 or q = 2 [15,16,17,18,19]. These high-frequency instabilities are typically excited more easily and lead to rapid loss of EPs, significantly reducing plasma confinement. In recent decades, this issue has received extensive attention in related research [20,21,22,23,24,25]. The linear dispersion relation of the m/n = 1 mode for a reversed magnetic shear configuration has been theoretically described in references [19, 20], where m and n represent poloidal and toroidal mode numbers, respectively. Helander et al. have also investigated the fishbone-like modes with m/n = 1/1 [18], assuming a fixed mode structure. However, the value of EP-beta significantly influences the mode structure. Specifically, when value of EP-beta is large, the singularity of the mode structure is disrupted, such that the top-hat structure hypothesis does not apply as expected. Moreover, while most theoretical studies have concentrated on instabilities driven by trapped EPs, less attention has been given to circulating EPs. Recent experimental observations have revealed that circulating particles can trigger a fishbone-like mode instability. Therefore, further study is necessary to understand the influence of the EPM instability of m/n = 2/1 excited by the circulating EPs in a reversed shear configuration.

In this study, the excitation of EPM by energetic ions under a reversed shear configuration with m/n = 2/1 was simulated by solving the eigenvalue equation, which preserves the self-consistent variation of the mode structure. The rest of this paper is organized as follows. Section 2 presents the eigenvalue equations including magnetohydrodynamic (MHD) and EPs; In Sect. 3, the effects of EP parameters and the coupling strength of rational surfaces on the growth rate and frequency of EPM are discussed through numerical analysis of the eigenvalue equation. Finally, Sect. 4 presents the conclusions.

2 Model and basic equations

The eigenmode equation of EP-driven instabilities with arbitrary m/n is presented in this section. The linear momentum equation in fluid approximation can be expressed as [10, 26]

$${\rho }_{m}\frac{{\partial }^{2}}{\partial {t}^{2}}{\varvec{\xi}}=-\frac{1}{c}\left(\delta {\varvec{j}}\times {\varvec{B}}+{\varvec{j}}\times \delta {\varvec{B}}\right)-\nabla \delta {p}_{c},$$
(1)

where \({\rho }_{m}={n}_{0}{m}_{i}\) is the mass density with mass \({m}_{i}\) and density \({n}_{0}\) of background ions, t is the time, the radial displacement vector \({\varvec{\xi}}={\varvec{\xi}}\left(r\right)\mathit{exp}\left[i\left(m\theta +{k}_{z}-\omega t\right)\right]\) with \({k}_{z}=-n/R\), R is the major radius, \(\theta \) is poloidal angle, \(\omega ={\omega }_{r}+i\gamma \) is the frequency with \({\omega }_{r}\) and \(\gamma \) being mode frequency and growth rate, c is the speed of light, \(\delta {\varvec{j}}\) is the perturbed current density, \({\varvec{B}}\) is the magnetic field, \({\varvec{j}}\) is the current density, \(\delta {\varvec{B}}\) is the perturbed magnetic field, \(\delta {p}_{c}\) is the perturbed plasma pressure. The equation of state can be approximately expressed as a linear relationship, given by \(\delta {p}_{c}=-\Gamma p\nabla \cdot{\varvec{\xi}}-{\varvec{\xi}}\cdot \nabla p\), where the plasma is incompressible \(\nabla \cdot{\varvec{\xi}}=0\), \(\Gamma \) is the adiabatic index, \(p\) is the equilibrium plasma pressure. The perturbed kinetic energy’s inertia term takes the form of [10]

$$\delta K=\frac{\pi {B}_{0}^{2}}{2R}\frac{-\left(1+\Delta \right){\omega }^{2}}{{\omega }_{A}^{2}}{\int }_{0}^{a}d r{\left|{\varvec{\xi}}\right|}^{2},$$
(2)

where the plasma inertia enhancement factor for the collisionless regime \(\Delta \approx \left[ {\left( {1.2/\varepsilon_{1}^{1/2} } \right) + \left( {0.4/\varepsilon_{1}^{1/2} } \right) + 0.5} \right]q^{2}\) with \(\varepsilon_{1} \equiv {{r_{s} } \mathord{\left/ {\vphantom {{r_{s} } R}} \right. \kern-0pt} R}\) and \({r}_{s}\) being the radial location of the singular layer [27], \({\omega }_{A}\) is the Alfvén frequency, \(a\) is the minor radius. For the energy equation, including the EP effect,

$$\delta K+\delta {W}_{MHD}+\delta {W}_{K}=0,$$
(3)

where \(\delta {W}_{MHD}\) and \(\delta {W}_{K}\) are contributions of MHD and EPs on the perturbed potential energy, respectively. Due to the focus of this paper on EPM instability driven by EPs and its primary discussion of the dynamic effects caused by these particles, the contribution of fluid term to perturbation potential energy is disregarded. According to Betti et al. theory, the potential energy of circulating EPs can be expressed as follows [15,16,17]:s

$$ \begin{aligned} \delta W_{K} = & \frac{{2\pi ^{2} R_{0} m_{h} q_{s}^{2} }}{{\omega _{c} r_{{\min ^{2} }} \xi _{0}^{2} B_{0}^{2} \left( {\left| {s_{1} } \right| + \left| {s_{2} } \right|} \right)^{2} }}\sum\limits_{\sigma } {\int {v^{3} } } dv\int d P_{\phi } \\ & \quad \times \int d \Lambda \tau _{b} \frac{{\partial F_{h} }}{{\partial E}}\frac{{\omega - n\omega _{{*h}} }}{{\omega - k\left\| v \right\|}} \times \left| {\left\langle {\left( {\frac{{v_{ \bot }^{2} }}{2} + v_{{||}}^{2} } \right)\xi \cdot \kappa e^{{ - i\left( {\omega - k\left\| v \right\|} \right)t}} } \right\rangle } \right|^{2} \\ \end{aligned} $$
(4)

where \({\omega }_{c}\) is the cyclotron frequency, \({m}_{h}\) is the fast ion mass, the fast ion kinetic energy \(E={m}_{h}{v}^{2}/2\), \(\Lambda \equiv \mu {B}_{0}/E\) with \(\mu \) being the magnetic moment, \(v\) is the velocity of energetic ions, \({\omega }_{*h}={(\partial {F}_{h}/\partial {P}_{\phi })(\partial {F}_{h}/\partial E)}^{-1}\) is the energetic ions diamagnetic frequency, \({F}_{h}\) is the mean-field distribution function of energetic ions, \({P}_{\phi }\) is the toroidal angular momentum with\({P}_{\phi }={m}_{h}{v}_{\parallel }R+(e/c)\psi \), \({\tau }_{b}\) is the transit time of particles, \(\langle ...\rangle \) means the particle orbital average, \({\varvec{\kappa}}={B}^{-2}{\nabla }_{\perp }({B}^{2}/2+4\pi p)\) is curvature of magnetic field lines,\(\sigma ={v}_{\parallel }/\left|{v}_{\parallel }\right|\), \({v}_{\parallel }\) and \({v}_{\perp }\) are the velocity of a EP along and perpendicular to the magnetic field, respectively. Applying variational and asymptotic matching to Eq. (3), we can obtain the eigenvalue equation for the m/n ≥ 1 mode [13,14,15]:

$$ \begin{aligned} & \frac{d}{dr}\left\{ {\left[ {\frac{{\left( {1 + \Delta } \right)}}{{m^{2} }}\frac{{\omega^{2} }}{{\omega_{A}^{2} }} - \left( {\frac{1}{q} - \frac{n}{m}} \right)^{2} } \right]r^{3} \frac{d\xi }{{dr}}} \right\} - r\left( {m^{2} - 1} \right)\left[ {\frac{{\left( {1 + \Delta } \right)}}{{m^{2} }}\frac{{\omega^{2} }}{{\omega_{A}^{2} }} - \left( {\frac{1}{q} - \frac{n}{m}} \right)^{2} } \right]\xi \\ & - r^{2} \frac{d\beta }{{dr}}\left( {1 - \frac{1}{{q^{2} }}} \right)\xi - C_{m + 1} \left( {\frac{{r_{1} }}{{r_{2} }}} \right)^{{\left( {m + 1} \right)}} A\mathop \int \limits_{{r_{1} }}^{{r_{2} }} A\left( {\frac{r}{{r_{1} }}} \right)^{{\left( {m + 1} \right)}} \xi dr - C_{m - 1} \left( {\frac{{r_{1} }}{{r_{2} }}} \right)^{{\left( {m - 1} \right)}} A\mathop \int \limits_{{r_{1} }}^{{r_{2} }} A\left( {\frac{r}{{r_{1} }}} \right)^{{\left( { - m + 1} \right)}} \xi dr \\ & - r\left\{ {\mathop \sum \limits_{i = 1,2} \frac{1}{3}\left( {\frac{{R_{0} }}{{r_{si} }}} \right) \times \frac{{q_{s}^{2} }}{{\left( {\left| {s_{1} } \right| + \left| {s_{2} } \right|} \right)^{2} }}\left[ { - \frac{{\Delta r_{b} }}{\left| s \right|}\frac{{d\beta_{E} }}{dr}} \right]_{{r_{si} }} F\left( {\frac{\omega }{{\omega_{si} }}} \right)} \right\}\xi^{*} = 0, \\ \end{aligned} $$
(5)

where \(F\left(x\right)=\frac{1}{\pi }\left\{10x-8{x}^{\frac{3}{2}}\left[{tan}^{-1}\frac{1}{\sqrt{x}}+{tanh}^{-1}\frac{1}{\sqrt{x}}\right]+(1+3{x}^{2})ln\frac{1+x}{x-1}\right\}\),

$$ \begin{gathered} C_{m + 1} = \frac{{ - n^{2} \left( {m + 1} \right)\left( {2 + m + b_{m + 1} } \right)\left( {2 + m + c_{m + 1} } \right)}}{{2m^{2} \left[ {\left( {m - b_{m + 1} } \right)\left( {2 + m + c_{m + 1} } \right) - \left( {m - c_{m + 1} } \right)\left( {2 + m + b_{m + 1} } \right)} \right]}}, \hfill \\ C_{m - 1} = \frac{{ - n^{2} \left( {m - 1} \right)\left( {2 - m + b_{m - 1} } \right)\left( {2 - m + c_{m - 1} } \right)}}{{2m^{2} \left[ {\left( {m + b_{m - 1} } \right)\left( {2 - m + c_{m - 1} } \right) - \left( {m + c_{m - 1} } \right)\left( {2 - m + b_{m - 1} } \right)} \right]}}, \hfill \\ \end{gathered} $$

with \({b}_{m\pm 1}=\frac{{r}_{1}}{{\xi }_{1}^{\left(m\pm 1\right)}({r}_{1})}\frac{d{\xi }_{1}^{\left(m\pm 1\right)}}{dr}\left({r}_{1}-\right)\) and \({c}_{m\pm 1}=\frac{{r}_{2}}{{\xi }_{1}^{\left(m\pm 1\right)}({r}_{2})}\frac{d{\xi }_{1}^{\left(m\pm 1\right)}}{dr}\left({r}_{2}+\right)\), \({r}_{s1}\) and \({r}_{s2}\) are the radial position of two rational surfaces, \({s}_{1}\) and \({s}_{2}\) represent the magnetic shear on the two rational surfaces. \({\omega }_{si}=\left|{s}_{i}\right|{v}_{\parallel }^{2}/({\omega }_{c}{R}_{0}{r}_{si})\). \(\Delta {r}_{b}\) is the orbit width of EPs. \(A=-{\beta }{\prime}R{q}^{2}\) with \({\beta }{\prime}\equiv d\beta /dr\). The background plasma beta has a form of \(\beta =8\pi p/{B}_{0}^{2}\). \({\beta }_{E}\) is the EP beta. [17].

3 Numerical results

In this section, the eigenvalue equation Eq. (5) is solved using the shooting method. The safety factor distribution used in the calculation is specified for the reversed shear configuration.

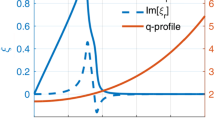
$$q={q}_{min}+\left({q}_{1}-{q}_{min}\right)\times {\left(r-{r}_{min}\right)}^{\lambda }$$
(6)

where \({q}_{1}=7.0\), \({r}_{min}=0.45\), and \(\lambda =2\). Moreover, \({q}_{min}\) is the minimum value of q with the radial position \({r}_{min}\). The two rational surfaces with q = 2 are located at \({r}_{\text{1,2}}={r}_{min}\pm \sqrt{\frac{{q}_{s}-{q}_{min}}{{q}_{1}-{q}_{min}}}\). Figure 1a shows the safety factor q-profile, where case 1 and case 2 represent the weak and strong coupling scenarios, corresponding to \({q}_{min}=1.8\) and \({q}_{min}=1.95\), respectively. For parameters similar to those of the ASDEX Upgrade [6, 28, 29], the major radius \(R=1.6m\), the minor radius \(a=0.5m\), the magnetic field \(B\approx 1.0T\), the plasma density \({n}_{i}\approx 5.31\times {10}^{19}{m}^{-3}\), and the Alfvén frequency \({\omega }_{A}\approx 2.99\times {10}^{6}{s}^{-1}\). The plasma beta profile was chosen according to the following equation. \(\beta \left(r\right)={\beta }_{0}\left[{1-(r/a)}^{2}\right]\) with \({\beta }_{0}\) being the pressure value at the axis. Additionally, the distribution of beta of EPs was as per the following formulation. \({\beta }_{E}\left(r\right)={\beta }_{h}{e}^{-{(\frac{r}{\sigma })}^{4}}\), where \({\beta }_{h}\) is the EP beta at the magnetic axis and \(\sigma \) is the radial width of the beam distribution. In this work, \(\sigma =0.6\) and \({\beta }_{0}=0.01\).

Fig. 1
figure 1

a The q-profiles for cases 1 and 2; b the mode frequency and growth rate as a function of \({\beta }_{h}\)

Full size image

When the distance between rational surfaces is sufficiently large, decoupling the two rational surfaces causes the mode to degenerate into two single tearing modes [30,31,32]. Conversely, when distance between rational surfaces is sufficiently small, mode coupling intensifies and forms a characteristic top-hat mode structure [30]. Usually, EPs stabilize tearing mode instability, but a sufficient number of EPs can drive new instabilities [33, 34]. Here, we examine case 1 and case 2 separately, corresponding to the weak and strong mode coupling scenarios, respectively. The growth rate of the instability exhibits an almost linear dependency on \({\beta }_{h}\), which represents the ratio of the pressure of the EPs to the magnetic pressure, in Fig. 1b. For the case of small \({\beta }_{h}\) values, the mode remains stable in case 1. However, in case 2, the mode has a significantly high growth rate and a low threshold \({\beta }_{h,c}\) value.

In general, for EPM, the precession drift of EPs results in a mode frequency \(\omega >0\) to intersect with the Alfvén continuum spectrum, causing a shift in resonance location as per the following relation. \({k}_{\parallel }=(\frac{m}{q}-n)/R\ne 0\) [35,36,37,38,39,40]. This leads to the appearance of a double-step mode structure near the rational surface [38,39,40,41]. Figure 2a shows that an increase in \({\beta }_{h}\) can disrupt the singularity of the rational surface and significantly broaden the mode structure due to the finite mode frequency. The Alfvén continuum spectrum is depicted in Fig. 2b. The position of the intersection between the mode frequency and the Alfvén continuum spectrum satisfies the following relation. \(2/q-1=\pm {\omega }_{r}/{\omega }_{A}\). In case of positive shear with \(q=1+2r\) and \({\omega }_{r}/{\omega }_{A}\ll 1\), two resonant layers are expected near the rational surface with a spacing approximately equal to \({\Delta r}_{s}\approx 2{\omega }_{r}/{\omega }_{A}\).

Fig. 2
figure 2

a Normalized radial displacement of the mode for case 1, where the real and dashed lines represent the real and imaginary parts of the displacement. b the Alfvén continuum spectrum and mode frequency (dashed line), where the red, green, and blue lines correspond to m = 2,3,4 (the same below), respectively, \({\beta }_{h}=0.008\). c Normalized radial displacement of the mode for case 2. d the Alfvén continuum spectrum and mode frequency (dashed lines) for case 2, \({\beta }_{h}=0.02\%\)

Full size image

In Fig. 2(c), the mode is marginally stable when \({\beta }_{h}\sim 0.0002\). As \({\beta }_{h}\) increases, the resonant layer broadens, and the mode frequency increases. Meanwhile, the mode structure begin to interact and couple each, similar to the behavior of a 2/1 mode with a single rational surface [19]. Figure 2d shows the mode frequency corresponding to the threshold of instability, where \({\beta }_{h}=0.02\%\). The maximum value of the m = 2 branch of the Alfvén continuum spectrum is estimated as follows. \(\frac{{\omega }_{max}}{{\omega }_{A}}=\frac{2}{qmin}-1\sim 0.0256\) at r = rmin. Since the Alfvén continuum damping is minimized for \({\omega }_{r}{\gtrsim \omega }_{max}\) and \({\beta }_{h}>0.01\), the growth rate of the instability increases. Finally, the peak of mode structure is located at r = rmin. This result is similar to a reversed shear Alfvén eigenmode [38].

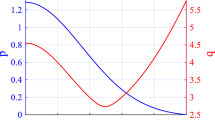
Since the distance \(\Delta r\) between the two resonant surfaces, \(=2\sqrt{\frac{{q}_{s}-{q}_{min}}{{q}_{1}-{q}_{min}}}\), directly affects the coupling strength of the mode, it alters the frequency and growth rate of the mode [22]. In this study, we considered a range of values for the distance \(\Delta r\) between the two resonant surfaces, where\(0.2\lesssim \Delta r\lesssim 0.4\), with \({q}_{min}\) ranging from 1.8 to 1.95. Figure 3 shows that due to enhanced mode coupling, the growth rate almost linearly increases with\({q}_{min}\). The frequency of the mode approaches the transit frequency of circulating EPs, which is represented as follows.\({\omega }_{t}{/\omega }_{A}\sim 0.01\sim {\omega }_{r}/{\omega }_{A}\). This frequency range is also comparable to the results observed in cases with positive magnetic shear [42,43,44,45]. It should be noted that when\({q}_{min}>m/n\), an Alfvén continuum spectrum \({\omega }_{min}>0\) exists at an r = rmin. In this scenario, mode conversion into a non-resonant mode with\({\omega }_{r}{<\omega }_{min}\), can be driven by the circulating EPs. However, in Betti’s model, the finite magnetic shear at the rational surface (\(\left|{s}_{1}\right|,\left|{s}_{2}\right|\ne 0\)) is required. Therefore, the theoretical model used here is not suitable for non-resonant modes where \(q\gtrsim m/n\) [19, 21].

Fig. 3
figure 3

The mode frequency and growth rate as a function of \({q}_{min}\)

Full size image

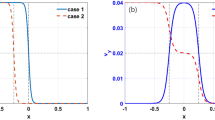
Figure 4(a) shows that the top-hat structure gradually degenerates due to the enhanced coupling between the rational surface and the influence of EPs. It is especially evident near the outer rational surface, where the singularity at the resonance layer almost completely disappears. When the resonant layers merge ultimately, a 2/1 global mode structure with \(Im(\xi )\) exhibiting a single peak value emerges. It is worth noting that although the frequency of the mode remains almost constant in Fig. 4b–e, the maximum value of the m = 2 branch of the Alfvén continuum spectrum decreases significantly. In the strong coupling cases of \({q}_{min}=1.98\) and \({\omega }_{r}{/\omega }_{A}{\left(\sim 0.02\right)>\omega }_{max}{/\omega }_{A}(\approx 0.01)\). Hence, under the reversed magnetic shear configuration, the mode properties are more sensitive to \({q}_{min}\), which can lead to some mode transitions, such as between EPM and Alfvén eigenmodes. This sensitivity could provide a theoretical explanation for early experimental results [6,7,8].

Fig. 4
figure 4

a Normalized radial displacement of the mode for \({q}_{min}=\text{1.8,1.85,1.9,1.98}\), where the solid line represents the real part of the displacement and the dashed line represents the imaginary part of the displacement; b–e Alfvén continuum spectrum and mode frequency (dashed lines) for \({q}_{min}=\text{1.8,1.85,1.9,1.98}\), respectively

Full size image

Moreover, off-axis external heating could also cause a radial shift of the mode [2, 3]. The effect of \({r}_{min}\) on the EPM also shown in Fig. 5a–b, where \({q}_{min}=1.98\) is fixed. It can be observed that when the rational surface moves outward, the growth rate and frequency of instability decrease rapidly until the mode becomes completely stable. When the rational surface is close to the boundary, the growth rate \(\gamma <{\omega }_{r}\). However, in the core region with \({r}_{min}<0.3\), the growth rate \(\gamma \gtrsim {\omega }_{r}\), indicating a potential change in the nature of the mode.

Fig. 5
figure 5

a The q-profiles for \({r}_{min}=\text{0.15,0.3,0.5}\); b The mode frequency and growth rate as a function of \({r}_{min}\) and \({\beta }_{h}=0.0005\)

Full size image

Figure 6 demonstrates that a pronounced singularity occurs in the resonance layer near the boundary when the mode is marginal unstable. Within the region \({r<r}_{1}\), there is a transition in the real part of the mode structure from \(\xi \sim {r}^{m}\) to \(\xi \sim {r}^{m-1}\). Simultaneously, the imaginary part of the mode structure becomes negative, like the feature of EP-driven interchange modes [46, 47]. As can be seen from Fig. 6b–d, the frequency of the mode increases significantly as the unstable resonance region moves inward. When the mode is close enough to the core, it may no longer exhibit the characteristics of an m/n = 2/1 EPM, but may transforms into an instability like the reversed shear Alfvén eigenmode (\({\omega }_{r}{\gtrsim \omega }_{max}\)) as shown in Fig. 6b. This result suggests another possibility for mode conversion. When \({r}_{min}\) decreases due to factors like off-axis external heating, the type of instability may also change along with variation in mode frequencies [48, 49].

Fig. 6
figure 6

a Normalized radial displacement of the mode for different \({r}_{min}\); b–d the Alfvén continuum spectrum and mode frequency (dashed lines) for case 2 with \({r}_{min}=0.15, 0.3, 0.5\), respectively

Full size image

4 Conclusions

In this paper, we derived the eigenvalue equation for the m/n = 2/1 energetic particle mode driven by the circulating EPs and solved it using the shooting method. The main conclusions are as follows:

  1. 1.

    we observed a global double top-hat mode structure of EPMs driven by circulating EPs reminiscent of double kink modes for weak mode coupling. In contrast, strong mode coupling results in the merging of modes into a global instability characterized by a single peaking mode structure at the resonant surface. It highlights the substantial impact of mode coupling on the growth rate of the mode.

  2. 2.

    As \({q}_{min}\) increase, the mode frequency also increases. It occurs because the damping of the continuous Alfvén spectrum is minimized near \({\omega }_{r}\sim {\omega }_{max}\), and the spatial distribution of the mode resembles that of reversed shear Alfvén eigenmodes.

  3. 3.

    The radial position \({r}_{min}\) can also influence the mode frequency and growth rate. As the unstable resonance region moves inward, the frequency increases significantly. Particularly when the mode approaches the core, its structure resembles that of an interchange-like mode structure.

In this study, the small orbit radius approximation was employed, where \(\left|{s}_{1}\right|\text{ and} \left|{s}_{2}\right|\ne 0\). However, in cases of strong mode coupling, where \(\left|{s}_{1}\right|,\left|{s}_{2}\right|\sim 0\) at \({q}_{min}\sim m/n\), or for non-resonant modes with \(q\gtrsim m/n\), it will be necessary to develop a new theoretical model in the future [50,51,52].