Nonlinear simulations of energetic particle modes in tokamak plasmas with reversed magnetic shear

Abstract

Effects of energetic particles (EPs) on m/n = 3/1 magnetohydrodynamic (MHD) instabilities have been investigated via hybrid simulations for reversed magnetic shear configurations. The simulation results shown that a global instability, energetic particle modes (EPMs), can be excited by the strong energetic particle drive with the frequency lying into the Alfvén continuum. In the linear growth stage, EPs not only induce radial broadening of mode structures but also enhance toroidal mode coupling when EP beta is large enough. In the nonlinear saturation stage, the good flux surfaces are still kept over the entire plasma area in a long time evolution of EPMs. To clarify nonlinear saturation of the mode, effects of the energetic particle beta values, the width of the particle distribution, the beam energy and the initial pitch angle on the saturation amplitude of the EPMs are discussed in detail. Furthermore, MHD nonlinearity is found to reduce the saturation level of the EPM compared to linear MHD case, while the high-n harmonics have less impact.

1 Introduction

Multiple current layers are commonly discovered in various situations, such as the Earth’s magnetotail, the coronal helmet streamers in solar corona and fusion plasma devices [1,2,3,4]. Reversed magnetic shear configuration is a very attractive discharge configuration for the steady-state operation in advanced tokamaks [3, 4], because it is able to stabilize pressure driven ballooning modes and improve the plasma confinement, multiple current layers in the reversed magnetic shear can however cause a fast growing magnetohydrodynamic (MHD) instability, double tearing modes (DTMs) [5,6,7,8,9,10,11,12,13,14,15].

In previous works, the linear behavior of DTMs is investigated within the framework of MHDs. If the separation of the rational surfaces is sufficiently small, the growth rate is scaled as a function of plasma resistivity with $\gamma \sim \eta^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}}$ [5]. When the separation is large enough, the scaling of modes makes a transition to $\gamma \sim \eta^{{{3 \mathord{\left/ {\vphantom {3 5}} \right. \kern-0pt} 5}}}$ and the mode structure becomes a form of standard tearing modes, but DTMs induce the enhancement of radial transports. Since its significant importance is not only on the fusion plasma but also space plasmas, in the last three decades, the basic characteristics of the DTMs have been studied widely. There are lots of researches on how to suppress double tearing modes, e.g. the equilibrium shear flow generated by the external neutral beam injection (NBI) has a stabilizing effect on the double tearing instability [8, 9]. In fact, the NBI not only drive the plasma flow but also produce the energetic particles (EPs) [16, 17]. It has been demonstrated analytically that EPs have a stabilizing effect on the DTM [18] with appropriate energetic particle beta $\beta_{h}$. Furthermore, energetic particle mode (EPM) can be excited owing to resonance between bulk plasma and trapped energetic particles when $\beta_{h}$ is larger than a critical value [18,19,20]. So far, the investigation of EPMs has been limited to the theoretical analysis and linear simulation [21, 22]. The role of nonlinear evolution of EPMs has not been considered in the reversed magnetic shear configuration.

In this paper, we concentrate on energetic particle induced EPMs for reversed magnetic shear, the linear and nonlinear behavior of the mode are investigated and compared with DTMs by the hybrid simulations in toroidal geometries. Effects of the energetic particle beta values, the width of the particle distribution, the beam energy and the initial pitch angle on the mode are also discussed. And MHD nonlinearity is also carried out, which compares to linear MHD cases. The simulation model used in the CLT-K code is given in Sect. 2, numerical results and summary are presented in Sect. 3 and 4, respectively.

2 Model and equations

The CLT-K code is a hybrid initial value code that solves both the full resistive MHD and drift kinetic equations in a cylindrical coordinate system $(R,\phi ,Z)$ [23,24,25,26],

$$\frac{\partial \rho }{{\partial t}} = - \nabla \cdot (\rho v) + \nabla \cdot \left[ {D\nabla (\rho - \rho_{0} )} \right],$$

(1)

$$\frac{\partial p}{{\partial t}} = - {\varvec{v}} \cdot \nabla p - \Gamma p\nabla \cdot {\varvec{v}} + \nabla \cdot \left[ {\kappa \nabla (p - p_{0} )} \right],$$

(2)

$$\frac{{\partial {\varvec{v}}}}{\partial t} = - {\varvec{v}} \cdot \nabla {\varvec{v}} + \left[ {({\varvec{J}} - {\varvec{J}}_{h} ) \times {\varvec{B}} - \nabla p} \right]/\rho + \nabla \cdot \left[ {\nu \nabla ({\varvec{v}} - {\varvec{v}}_{0} )} \right],$$

(3)

$$\frac{{\partial {\varvec{B}}}}{\partial t} = - \nabla \times {\varvec{E}},$$

(4)

$${\varvec{E}} = - {\varvec{v}} \times {\varvec{B}} + \eta ({\varvec{J}} - {\varvec{J}}_{0} ),$$

(5)

$${\varvec{J}} = \frac{1}{{\mu_{0} }}\nabla \times {\varvec{B}},$$

(6)

where $\rho$, $p$, ${\varvec{v}}$, ${\varvec{B}}$, ${\varvec{E}}$ and ${\varvec{J}}$ are the plasma density, the plasma pressure, the velocity, the magnetic field, the electric field and the current density, respectively. The subscript of “0” represents equilibrium variables and $\Gamma$ is the ratio of specific heat of the plasma. Equations (1)–(6) are solved by the finite difference method in the $R$ and $Z$ directions, while in the $\phi$ direction either a finite difference or pseudo-spectrum method is used. According to the current coupling formalism of the hybrid kinetic-MHD model [27], there is an additional contribution from EP current ${\varvec{J}}_{{\text{h}}}$ in the momentum equation, where the subscript “$h$” stands for EPs. The approximation of this model is under the condition that the density of fast particle is much less than the bulk plasma density, i.e. $n_{h} \ll n_{b}$. The energetic particle current density ${\varvec{J}}_{{\text{h}}}$ has a form of

$${\varvec{J}}_{h} = {\varvec{J}}_{GC} + {\varvec{J}}_{MAG} + {\varvec{J}}_{POL}$$

(7)

where ${\varvec{J}}_{GC}$ is the guiding center current associated with the guiding center drift velocity, ${\varvec{J}}_{MAG}$ is the magnetization current and ${\varvec{J}}_{POL}$ is the polarization current, respectively. The detail of the current density of EPs can be written as [24]

$$\begin{aligned} \user2{J}_{h} & = \left[ {\frac{m}{B}\left( {NV_{\parallel } \nabla \times \user2{v}_{E} + \frac{{n_{h} }}{2}\user2{b} \times \nabla |\user2{v}_{E} |^{2} + NV_{\parallel } \user2{b} \times \frac{{\partial \user2{b}}}{{\partial t}}} \right)} \right. \\ & \quad \left. { + Z_{h} eNV_{\parallel } \user2{b} + \frac{1}{B}p_{{h\parallel }} \nabla \times \user2{b} + \frac{1}{B}\user2{b} \times \nabla p_{{h \bot }} } \right] \\ & \quad + \left[ { - \frac{1}{B}P_{{h \bot }} \nabla \times \user2{b}} \right] + \left[ {\frac{{n_{h} m}}{B}\user2{b} \times \frac{{\partial \user2{v}_{E} }}{{\partial t}}} \right] \\ \end{aligned}$$

(8)

In the time advance, the 4-th order Runge–Kutta scheme is adopted. For TFTR-like equilibrium [3], in this work, the major and minor radiuses are $R_{0} = 2.60\;{\text{m}}$ and $a = 0.94\;{\text{m}}$, respectively. The toroidal field is set to be $4.2T$, the electron density $n_{e} \sim 1.0 \times 10^{20} {\text{m}}^{ - 3}$, and electron temperature $T{}_{e} \sim 4\;{\text{keV}}$. The plasma resistivity and viscosity are $\eta \sim 1 \times 10^{{ - 5}}$ and $\nu \sim 1 \times 10^{{ - 6}}$, respectively. A slowing-down distribution is employed for EPs, and is given by:

$$f_{0} = \frac{{c_{f} }}{{(v^{3} + v_{c}^{3} )}} \times \left( {1 + \frac{{erf(v_{0} - v)}}{\Delta v}} \right)\exp \left( { - \frac{\left\langle \psi \right\rangle }{{c_{1} \cdot \Delta \psi }}} \right)\exp \left( { - \left( {\frac{{\Lambda - \Lambda_{0} }}{\Delta \Lambda }} \right)^{2} } \right)$$

(9)

where $v_{c}$ is the critical velocity, $v_{0}$ is the injection velocity, $v_{c} = 0.58v_{0}$, $c_{1} = 0.37$, $\Lambda = \mu B_{0} /E$ is pitch angle, $\Lambda_{0} = 0.9$, $\Delta \Lambda = 0.1$. As there are two $q = 3$ resonant surfaces, the $m/n = 3/1$ DTM is the most unstable mode in the system. The plasma density $\rho = 1$ is assumed in the simulation for simplification. Also, the resistivity is chosen to be constant in the present paper. The equilibrium is obtained from the NOVA code [28]. The grids used in the simulations are $128 \times 16 \times 128$ in $(R,\phi ,Z)$ directions, the number of EPs is $5 \times 10^{6}$.

In order to study the effect of energetic particles on the nonlinear evolution of the EPMs by CLT-K, we employ an equilibrium without flows and the function of the safety factor is [13]

$$q(r) = q_{0} + q_{c} \left\{ {1 + \left( {\frac{r}{{r_{0} }}} \right)^{{2\lambda }} } \right\}^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}} \left[ {1 + A \cdot \exp \left\{ { - \left( {\frac{{r - r_{d} }}{\delta }} \right)^{2} } \right\}} \right],$$

(10)

where $q_{c} = 1.2$ is the safety factor at the magnetic axis, constant values of $q_{0} = 0.95$,$\lambda = 10$, $r_{0} = 0.5$, $\delta = 0.39$, $r_{d} = 0$, and $A = 2$. This set of parameters give the minimum value of $q$ is $q_{\min } = 2.733$, $r_{s1} = 0.397$, $r_{s2} = 0.598$, $\Delta r_{s} = r_{s1} - r_{s2}$, here, $r_{s1}$ and $r_{s2}$ are the locations of $q = 3$ rational surface, respectively. This profile is similar that in the Ref. [13]. The safety factor profile q and plasma pressure profile p are shown in Fig. 1.

Fig. 1

The profiles of safety factor (q) and plasma pressure (p)

3 Simulation results

The growth rates as a function of the energetic particle beta $\beta_{h}$ are shown in Fig. 2. In the low $\beta_{h}$ $\left( {\beta_{h} < 0.6{\text{\% }}} \right)$ cases, the growth rate of DTMs decreases with increasing $\beta_{h}$. This indicates that EPs have a stabilizing effect on DTM, which is similar to the result of resistive tearing modes [29,30,31,32,33]. When $\beta_{h}$ is larger than the threshold value ($\sim 0.6{\text{\% }}$), the growth rate increases with increasing $\beta_{h}$, meanwhile, the mode frequency increases rapidly as shown in Fig. 2. Then a new mode could be driven by EPs, the mode structure should be different from that of DTMs.

Fig. 2

The growth rate $\gamma$ and mode frequency $\omega$ against $\beta_{h}$

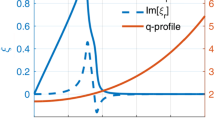
In order to examine the type of modes in the high $\beta_{h}$, we show the Alfvén continuum spectrum (black solid line) of the toroidal mode number n = 1 in Fig. 3, which is calculated by the NOVA code. Here, it can be found that the mode with its normalized frequency $\omega = 0.046$ marked by the red cross line lies in the Alfvén continuum and the location of the largest mode amplitude of radial perturbed velocity $v_{r}$ with $\beta_{{\text{h}}} = 0.01$ is almost at $r\sim 0.43$, which is consistent with that in Fig. 4 (d). The primary harmonic m/n = 3/1 is maximized at the peak location, and the location of the unstable mode is defined by the region where the intensity of the cosine part of the m/n = 3/1 harmonic of radial velocity $v_{r}$ is larger than 90% of the peak value. We can find that the unstable EPM is excited by the strong energetic particle drive with lying into the Alfvén continuum.

Fig. 3

Alfvén continuum spectra of the toroidal mode number n = 1. The mode frequency and the radial location of the unstable modes for $\beta_{{\text{h}}} = 0.01$(red line). The peaking locations are marked by the cross

Fig. 4

The mode structure with different $\beta_{{\text{h}}}$. a $\beta_{{\text{h}}} = 0$ b $\beta_{{\text{h}}} = 0.004$ c $\beta_{{\text{h}}} = 0.008$ d $\beta_{{\text{h}}} = 0.01$

To show the mode structure changed by EPs, we plot the radial perturbed velocity normalized by Alfvén velocity in Fig. 4. In theory, the radial displacement of DTMs, $\xi$, is usually assumed to be a “top-hat” shape as similar to Fig. 4(a) and Fig. 4(b) due to the singularity of $d\xi /dr$ near dual 3/1 rational surfaces [5]. In the presence of strong EPs, however, the mode structure is modified near the rational surfaces. A possible reason is that the finite mode frequency changes the local resonance condition. For $\beta_{{\text{h}}} = 0.008$ and $\beta_{{\text{h}}} = 0.01$, the EPMs driven by energetic particles are different from the DTMs with a wider mode structure relaxed with increasing $\beta_{{\text{h}}}$. When $\beta_{{\text{h}}}$ is large enough, high-m modes can be driven, such as $m = 4$ and 5, and lead to an enhancement of the mode coupling.

Poincaré plot can be used to describe the nonlinear evolution of magnetic islands and show a mode coupling directly. As we can see in Fig. 5, due to the strong nonlinear mode coupling, the outer rational surfaces of $m/n = 3/1$ DTM push inward, and the position of the inner rational surfaces gradually expand outward, which undergoes an overlap of dual 3/1 rational surfaces. As a comparison, when the value of energetic particle beta is high, $\beta_{{\text{h}}} = 0.01$, the width of magnetic island is reduced, the field randomization is improved clearly in nonlinear phase and good magnetic flux surfaces are kept well for a long time in the nonlinear stage. It means that the EPMs appear like an ideal MHD mode rather than a resistive mode. The related discussions for the double kink mode/EPM are reported in the previous papers [21, 34, 35].

Fig. 5

(Top) Poincaré plot of magnetic field lines for $m/n = 3/1$ DTM with $v = 1 \times 10^{ - 6}$, $\eta = 1 \times 10^{{{ - }5}}$, $\beta_{{\text{h}}} = 0$, and (bottom) Poincaré plot of magnetic field lines for $m/n = 3/1$ EPM with $v = 1 \times 10^{ - 6}$, $\eta = 1 \times 10^{{{ - }5}}$, $\beta_{{\text{h}}} = 0.01$

In order to further clarify the type of mode with the high energetic particle beta, we perform nonlinear simulations of the toroidal perturbed electric field $E_{\phi }$ and show the time evolution of mode frequency for $\beta_{h} = 0.01$ in Fig. 6. It is interesting to note that frequency is basically constant and $\omega_{r} \sim 0.046$ normalized by Alfvén frequency. Thus, this mode is typical EPMs with an almost constant resonant frequency [16].

Fig. 6

Time evolution of frequency spectrum of the toroidal electric field for $\beta_{{\text{h}}} = 0.01$

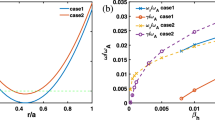
In Fig. 7, the comparison of the toroidal perturbed electric field excitation is shown for different energetic particle beta values, $\beta_{{\text{h}}} = 0.008$, $\beta_{{\text{h}}} = 0.01$, $\beta_{{\text{h}}} = 0.012$ and $\beta_{{\text{h}}} = 0.014$. Figure 7a shows the nonlinear evolution of the m/n = 3/1 harmonics of toroidal perturbed electric field $E_{\phi }$ for different $\beta_{{\text{h}}}$ measured at the EPM peak location $r\sim 0.43$. It is found that the nonlinear saturation amplitude of EPM increases when the energetic particle-driving is large enough to overcome the stabilizing of field line bending and Alfvén continuum damping in the regime $r\sim 0.43$. And it is interesting that the largest nonlinear amplitude and energetic particle beta value are basically linear growth relationships, which is shown in Fig. 7b.

Fig. 7

The toroidal electric field evolution and the saturation amplitude of $E_{\phi }$ using the cosine part of m/n = 3/1 harmonics with different $\beta_{{\text{h}}}$

The reversed magnetic shear configuration is in general produced by the external driving sources, such as NBI, LHCD et al. [36,37,38,39]. Therefore, it is also necessary to know the beam width effect on the EPMs. In Fig. 8, we consider the radial beam width effect on the nonlinear saturation amplitude of $E_{\phi }$ for $\beta_{{\text{h}}} = 0.01$. The comparison is made for different $c_{1}$, the width of the beam distribution, and the results show that for the beam-like narrow energetic particle distribution, $c_{1} = 0.148$, the nonlinear saturation amplitude of EPM largely depends on the energetic particle driving. As the energetic particle distribution profile gets flattened sufficiently, the difference for the results of $c_{1} = 0.148$ and $c_{1} = 0.37$ is significant as shown in Fig. 8(a), indicating a weak dependence on the energetic particle driving in the wide distribution regime.

Fig. 8

The toroidal electric field evolution and the saturation amplitude of $E_{\phi }$ using the cosine part of m/n = 3/1 harmonics with different $c_{1}$

The linear effect of the beam energy on the EPM has been studied extensively. In Fig. 9, the nonlinear saturation amplitude of the m/n = 3/1 mode as a function of the beam injection velocity $v_{0}$ is shown for $\beta_{{\text{h}}} = 0.01$. We found that in the regime of small $v_{0}$$(v_{0} = 1.2,1.3)$, the mode is excited as one gap mode, since the precession frequency $(\omega_{r} \sim {0}{\text{.03965}},0.0424)$ is near the minimum local Alfvén frequency $\omega_{A\min }$ $(\omega_{A\min } \sim 0.0422)$ where the continuum damping has a minimum. However, once in the regime of large $v_{0}$$(v_{0} = 1.4 - 1.9)$, the mode is excited as an EPM, the mode frequency above the $\omega_{A\min }$, and the enhanced Alfvén continuum damping due to $v_{0}$ increasing is effective to suppress nonlinear saturation amplitude of EPMs. As is shown in Fig. 9b, when $v_{0}$ is large enough than the threshold value ($v_{0} > 1.3v_{A}$), the largest amplitude variation of the bursts is significantly reduced as beam injection velocity $v_{0}$ increases.

Fig. 9

The toroidal electric field evolution and the saturation amplitude of $E_{\phi }$ using the cosine part of m/n = 3/1 harmonics with different $v_{0}$

In order to clarify the role of initial pitch angle $\Lambda_{0}$, in Fig. 10, the comparison of the nonlinear evolution of the EPMs is made for different initial pitch angles, $\Lambda_{0} = 0.5$, $\Lambda_{0} = 0.6$, $\Lambda_{0} = 0.7$, $\Lambda_{0} = 0.8$, $\Lambda_{0} = 0.9$ and $\Lambda_{0} = 1.0$. It is found that the saturation amplitude of the perturbed toroidal electric field $E_{\phi }$ changes between $1.3 \times 10^{{{ - }4}} \sim 2.0 \times 10^{{{ - }4}}$, while the pitch angles have a little effect on nonlinear saturation amplitude of EPMs. For cases where the initial pitch angle is lower than $\Lambda_{0} = 0.5$, the new mode is excited (not shown here), the mode structure of which differs from the EPM here.

Fig. 10

The toroidal electric field evolution and the saturation amplitude of $E_{\phi }$ using the cosine part of m/n = 3/1 harmonics with different $\Lambda_{0}$

The evolution of the m/n = 3/1 harmonics of the toroidal perturbed electric field $E_{\phi }$ is compared in Fig. 11 for the linear MHD simulation and the nonlinear MHD simulation, simultaneously the normalized frequency and growth rate are $\omega_{r} \sim 0.046$,$\gamma \sim {0}{\text{.022}}$ for $\beta_{h} = 0.01$. A significant reduction in the saturation level can be seen for the nonlinear MHD run here. The MHD nonlinearity effects reduce the EPM saturation level by ~ 40% of the linear case when it reaches $E_{\phi } \sim 1.4 \times 10^{{{ - }4}}$. Then the saturation mechanism is dominated by the particle nonlinear dynamics, i.e. the particle trapping by the EP mode causes the saturation. For cases where the instability growth is lower, the MHD nonlinearity does not play any important role.

Fig. 11

Comparison of toroidal electric field evolution for the linear-MHD and the nonlinear MHD runs using the cosine part of m/n = 3/1 harmonics at $r\sim 0.43$ for $\beta_{{\text{h}}} = 0.01$

In the time evolution of the EPM, the nonlinear terms in the MHD equations generate the fluctuations with toroidal mode numbers multiples of n (n = 0, 1, 2, 3, 4, 5, …). It is interesting to investigate which toroidal mode number is important for the EPM saturation level reduction. We conducted three types of nonlinear MHD simulations in Fig. 12. In the first type, only the n = 0–1 modes are retained while the high-n (n = 2–7) modes are removed artificially. In the second type, the n = 0–4 modes are retained while the high-n (n = 5–7) modes are removed artificially. In the last type, all toroidal modes (n = 0–7) are retained. With our spatial resolution in the toroidal direction, the maximal toroidal mode number n = 7 is chosen, the mode numbers in the multiple mode simulation is n = 0, 1, 2,…,7. We can see that coupling between n = 0 and n = 1 dominates the saturation level of the EPM, while high-n harmonics have weak effect on the mode.

Fig. 12

Comparison of toroidal electric field evolution for cosine part of m/n = 3/1 harmonics at $r\sim 0.43$ for $\beta_{{\text{h}}} = 0.01$ with the nonlinear MHD runs a with only $n = 0 - 1$ retained, b with $n = 0 - 4$ retained and c with $n = 0 - 7$ retained

4 Conclusions

In this paper, we have studied the effect of energetic particles on the m/n = 3/1 MHD instabilities by the CLT-K code for tokamak plasmas. The roles of the energetic particles on the linear and nonlinear behavior of the EPM have been discussed in detail. The main results are as follows:

• 1. In the low $\beta_{h}$ cases, suppression of DTMs by EPs has been found by the simulations. When the value of $\beta_{h}$ is larger than a threshold, the energetic particle mode is excited with a higher mode frequency.

• 2. Compared to the DTMs, for the linear modes, high EPs not only induce radial broadening of the mode but also enhanced the toroidal mode coupling; for the nonlinear modes, the magnetic field lines overlap of the EPMs is significantly reduced and the magnetic flux surfaces keep well in the nonlinear saturation.

• 3. With the particle radial flattening, the nonlinear saturation amplitude of the EPMs is reduced as a result of energetic particle driving reduction. Meanwhile, the nonlinear saturation amplitude of the EPMs can be decreased by strong Alfvén continuum damping as the beam injection velocity $v_{0}$ increasing than a threshold. And the pitch angles have a little effect on the nonlinear saturation amplitude of the EPMs when $\Lambda_{0}$ is large enough than the threshold value.

• 4. Nonlinear simulation shows that MHD nonlinearity reduces the saturation level of the EPM. Then the saturation mechanism is dominated by the particle nonlinear dynamics, i.e. the particle trapped by the EP mode causes the saturation. And the high-n harmonics have little important effect on the EPM.

In brief, we found the EPs have a critical effect on the magnetohydrodynamic instabilities with reversed shear profile. The results will be useful for the qualitative understanding of the linear and nonlinear behavior of EPMs in experiments. More realistic simulations with respect to the experimental conditions should be carried out in the future for quantitative comparison with the experiments.