Free Vibrational Characteristics of Sandwich Cylindrical Shells Containing a Zero Poisson's Ratio Cellular Core

Abstract

Purpose

Cellular configurations with ZPR more suitable for cylindrical sandwich shell in which the structure needs undergo pure cylindrical bending. To date, research in the vibration response of cylindrical sandwich shell is still a challenging task. This article proposes one method for free vibration analysis of sandwich cylindrical shells consisting of elastic-isotropic skin and a zero Poisson's ratio cellular core was proposed.

Method

The free vibration characteristics of the sandwich cylindrical shells has been studied using classical thin shell theory. Theoretical models of the effective mechanical performances of the cellular core are established by homogenization methods. The accuracies of theoretical predictions are validated by the finite element method and comparing with others from some available literatures.

Results and Conclusions

Based on the theoretical predictions, the influences on effective mechanical performances of the cellular core and natural frequencies of the sandwich cylindrical shell caused by geometric parameters are evaluated in detail. These geometrical parameters provide different contributions to the effective mechanical properties and dynamic response, which can lead to separate designs for improving their dynamic characteristics.

Introduction

As an advanced material and structure, the cellular structure has shown great potential for automotive, aerospace, and marine applications due to its outstanding properties, including high strength-to-weight ratio and specific stiffness, as well as good structural stability and energy absorption [1,2,3]. Shell structures are one of the most important structures in engineering applications. Sandwich cylindrical shells with cellular core not only remain the characteristics of cellular structure but also embody the special geometry, resulting in sandwich cylindrical shells have been shown great potential in a wide range of gas and fluid storage tanks, solar cell shells, flexible pipe, etc. [4, 5]. These structures are always suffering from dynamic loads at their service. Therefore, vibration characteristics analysis of sandwich cylindrical shells with cellular core has become extremely important.

Cellular structures are generally considered homogeneous orthotropic materials by predicting their equivalent properties, regardless of the complexity of the internal structures [6]. Up to now, researchers have been working extensively on the various calculated methods of effective elastic properties of cellular structures, among the common methods are energy [7, 8] and homogenization methods [9, 10]. Gibson explores the effective mechanical properties of hexagonal honeycomb based on the energy method [11]. However, Gibson's model showed some errors in the theoretical results due to the neglect of the axial deformation and shear deformation, resulting that some research focusing on the revision of Gibson's theory [12]. In addition, traditional hexagonal honeycombs with positive Poisson's ratio (PPR) can no longer keep up with the growing demand for capricious practical applications. Numerous novel structures have been developed and applied with the characteristic of negative Poisson's ratio (NPR) [13, 14], zero Poisson's ratio (ZPR) [15, 16], and tailorable Poisson's ratio [17] in recent years. However, when subjected to pure bending, the NPR cellular structures exhibit a saddle-like curvature, while the PPR cellular structures exhibit a dome-like curvature [18], which makes the processing of sandwich cylindrical shells with cellular core considerably more complicated and precludes their application on some special occasions. Zero Poisson's ratio (ZPR) feature can preclude a significant increase of effective stiffness in the horizontal direction by limiting the contraction (or bulging) in the vertical direction [19, 20].

Up to now, there are three typical theories to predict the vibrational behavior of composite cylindrical plates/shells: (1) the classical laminate plates/shells theory (CLPT/CLST), (2) the First-order shear deformation theory (FSDT), and (3) the High-order shear deformation theory (HSDT). Reissner modified the CLPT and proposed the FSDT by considering the effect of shear deformation [21]. Reddy developed an HSDT of laminated composite plates [22]. Wang et al. [23] derived the nonlinear equations for laminated composite structures. Duc et al. [24] discussed the nonlinear response of functionally graded (FG) cylindrical shells based on the Donnell classical shell theory by applying the Galerkin's method. Qin et al. [25] utilized the FSDT to present the free vibration of rotating FG carbon nanotube-reinforced composite cylindrical shells. Pang et al. [26] extracted the displacement functions of combined composite laminated cylindrical and spherical shells using the FSDT. Eipakchi et al. [27] studied the vibrational behavior of an auxetic composite cylindrical shell based on the CLST and Hamilton's principle.

As is reviewed from the published literatures, many researchers have been working extensively on the equivalent mechanical performances of cellular core and vibration issues of composite structures. However, a limited number of research articles are available to study the vibration behavior of sandwich cylindrical shells with ZPR honeycomb core. No saddle-like or dome-like curvature could be found for structure exhibiting ZPR under out-of-plane bending, which makes ZPR cellular configurations more suitable for cylindrical sandwich shell in which the structure needs undergo pure cylindrical bending. Therefore, it is more advantageous in terms of structural stability compared to other honeycomb structures and is more suitable to be incorporated in the design of piping structures.

Summarizing, the originality of the present paper lies in exploring the free flexural vibration characteristics of sandwich cylindrical shells containing a ZPR cellular core in the light of equivalent single-layer theory. The main contents are as follows: First, the effective mechanical performances of the ZPR cellular core are deduced in detail. Second, the Hamilton principle and CLST are utilized to establish the governing equations and mathematical model. Thirdly, FEM and some available literature results are introduced to prove the feasibility and correctness of the current method. Last, parametric analysis shows the influences of structural parameters on the mechanical performances of the cellular core and the free vibrational behavior of sandwich cylindrical shells.

Formulations

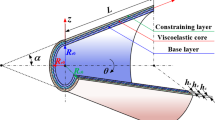
Figure 1 shows the schematic sketch and the coordinate system of the sandwich cylindrical shell containing the ZPR cellular core layer, where the radius of middle surface is R, the thickness is h, and the length is L. The cylindrical shell is composed of three layers, the inner layer and outer layer are elastic and isotropic materials with equal thickness, and the middle layer is a cellular structure with a thickness of h₀. In addition, an orthogonal coordinate system (z, x, and θ) is fixed at the middle surface. The deformations of the point at the shell's middle surface are denoted U_x, U_θ, and U_z, in the x, θ, and z directions, respectively. A coordinate (z_k, k = 1,2,3,4) is defined for each layer as shown in Fig. 1, in which $Z_{1} = \frac{h}{2}$, $Z_{2} = \frac{{h_{0} }}{2}$, $Z_{3} = - \frac{{h_{0} }}{2}$, and $Z_{4} = - \frac{h}{2}$.

Fig. 1

Schematic sketch and the coordinate system of the sandwich cylindrical shell

Effective Mechanical Performances of Cellular Core Layer with ZPR

When analyzing the vibrational behavior of the sandwich cylindrical shell containing the ZPR cellular core, we first need to predict the effective mechanical performances of the ZPR cellular core. There are several assumptions made for the theoretical analysis:

• (1) The formulation is based on the Euler–Bernoulli beam theory;

• (2) All the joints of the cellular walls are considered to be rigid.

Figure 2 illustrates the schematic diagram of the ZPR cellular, where φ is internal angles, l represents the length of diagonal walls, 2αl represents the length of vertical walls, and t = βl represents the thickness of sloping walls. Here, α and β represent the aspect and cell wall thickness ratios, respectively.

Fig. 2

Geometrical parameters of the ZPR cellular core

Unit cell structure is selected and illustrated in Fig. 3(a). The first step for the unit cell model is a simplification, as shown in Fig. 3(b), which transforms the model into a quarter model owing to the biaxial symmetry. After simplification, a fixed boundary is set to the left end of the model, while the right is set with a concentrated force F and a moment M. On the one hand, the deformation of the ZPR cellular structure is driven mainly by the sloping walls' bending deformation when honeycombs withstand a load along direction-x [28]. On the other hand, the vertical wall length along direction-x is smaller than that of the sloping walls. Therefore, the tensile deformation of the vertical walls is ignored, only the bending and tensile deformation of the sloping walls are considered.

Fig. 3

Schematic illustration of unit cell model used to calculate the elastic modulus in direction-x: a tensile stress along direction-x; b simplified model

According to the equilibrium equations [29], it can be concluded that the vertical force is zero, and the moment M is:

$$ M = \frac{1}{2}Fl\sin \varphi $$

(1)

The strain energy U of a cantilever beam subjected to bending moment $M\left( x \right)$ and axial load $F_{N} \left( x \right)$ can be expressed as:

$$ U = \int_{0}^{l} {\frac{{M^{2} \left( x \right)}}{2EI}} dx + \int_{0}^{l} {\frac{{F_{N}^{2} \left( x \right)}}{2EA}} dx $$

(2)

where E, I, and A are the elastic modulus, inertia moment, and cross-sectional area, respectively.

In this paper, it is assumed that the bending moment in the anti-clockwise direction is positive. By now, the bending moment is:

$$ M\left( x \right) = \left( {\frac{1}{2}l - x} \right)F\sin \varphi $$

(3)

And the axial load is:

$$ F_{N} (x) = F\cos \varphi $$

(4)

Combining Eqs. (2), (3), and (4), it can be concluded that the strain energy U is:

$$ U = \frac{{F^{2} l^{3} \sin^{2} \varphi }}{{24E_{s}^{c} I}} + \frac{{F^{2} l\cos^{2} \varphi }}{{2E_{s}^{c} A}} $$

(5)

where $E_{s}^{c}$ is the elastic modulus of raw materials.

According to Castigliano's second theorem [30], when the elastic system is enduring static load, the displacement δ_i of the point of force action can be calculated by the partial derivative of the strain energy U for any applied force F_i:

$$ \delta_{i} = \frac{\partial U}{{\partial F_{i} }} $$

(6)

Combining Eqs. (5) and (6), it can be concluded that horizontal displacement of the point of force action is:

$$ \delta_{x} = \frac{{Fl^{3} \sin^{2} \varphi }}{{12E_{s}^{c} I}} + \frac{{Fl\cos^{2} \varphi }}{{E_{s}^{c} A}} $$

(7)

According to the homogenization theory [31], the equivalent tensile modulus in direction-x can be deduced:

$$ \sigma_{x} = \frac{F}{{\alpha lh_{0} }} $$

(8)

$$ \varepsilon_{x} = \frac{{\delta_{x} }}{l\cos \varphi } $$

(9)

$$ E_{x} = \frac{{\sigma_{x} }}{{\varepsilon_{x} }} $$

(10)

where $\sigma_{x}$ and $\varepsilon_{x}$ are the equivalent stress and strain in direction-x, respectively.

Substituting Eqs. (7), (8) (9) into Eq. (10), it can be concluded that the equivalent elastic modulus in direction-x can be expressed as:

$$ E_{x} = E_{s}^{c} \frac{{\beta^{3} \cos \varphi }}{{\alpha (\sin^{2} \varphi + \beta^{2} \cos^{2} \varphi )}} $$

(11)

Similarly, Fig. 4 shows the schematic illustration of the unit cell model used to calculate the elastic modulus in direction-θ.

Fig. 4

Schematic illustration of unit cell model used to calculate the elastic modulus in direction-θ: a tensile stress along direction-θ; b simplified model

In this case, the strain energy U is:

$$ U = \frac{{F^{2} \alpha l}}{{E_{s}^{c} A}} $$

(12)

Then, displacement in direction-θ of the point of force action is:

$$ \delta_{\theta } = \frac{2F\alpha }{{E_{s}^{c} \beta h_{0} }} $$

(13)

According to the homogenization theory, the equivalent tensile modulus along direction-x can be deduced:

$$ \sigma_{\theta } = \frac{F}{{h_{0} l\cos \varphi }} $$

(14)

$$ \varepsilon_{\theta } = \frac{{\delta_{\theta } }}{2\alpha l} $$

(15)

$$ E_{\theta } = \frac{{\sigma_{\theta } }}{{\varepsilon_{\theta } }} $$

(16)

where ${\sigma }_{\theta }$ and ${\varepsilon }_{\theta }$ are the equivalent stress and strain in direction-θ, respectively

Substituting Eqs. (13), (14), (15) into Eq. (16), it can be concluded that the equivalent tensile modulus along direction-θ can be expressed as:

$$ E_{\theta } = E_{s}^{c} \frac{\beta }{\cos \varphi } $$

(17)

The rotation of the joints in the structure is assumed to be zero owing to the structural symmetry. According to the above assumptions, it is considered that the deformations of sloping walls and vertical walls have relative independence, resulting that the strain along direction-x being zero when the cellular structure suffers a tensile loading along the direction-θ. Likewise, the above consideration also applies to the deformation of cellular structure along direction-x. Therefore, both values of the Poisson's ratio μ_θx and μ_xθ are considered to be zero.

The relative density of the ZPR cellular core is

$$ \rho = \rho^{c} \frac{{\left( {2 + \alpha } \right)\beta }}{2\alpha \cos \varphi } $$

(18)

where $\rho^{c}$ is the density of raw materials.

Vibrational Behavior of the Cylindrical Shell

Governing Equations

The assumptions generally employed in Sect. ''Vibrational Behavior of the Cylindrical Shell" are:

• (1) The sandwich cylindrical shells are thin shells, and the shell thickness is less than 10% of the shell radius.

• (2) No external load is borne to the sandwich cylindrical shell.

• (3) Compared with the radius of the sandwich cylindrical shell, its deformations are small. The cross-section of the sandwich cylindrical shell remains perpendicular to the middle surface after deformation.

• (4) Rotary inertia and shear deformation are neglected.

• (5) The outer and inner layers are bonded perfectly to the middle layer.

Duo to axisymmetry, arbitrary particle displacement of the cylinder caused by bending, based on the CLST [32] is:

$$ \left\{ \begin{gathered} U_{x} (x,z,t) = u(x,t) - z\frac{\partial w(x,t)}{{\partial x}} \hfill \\ U_{\theta } (x,z,t) = 0 \hfill \\ U_{z} (x,z,t) = w(x,t) \hfill \\ \end{gathered} \right. $$

(19)

According to the linear kinematic relations [33], strain–displacement relations are:

$$ \left\{ \begin{gathered} \varepsilon_{x} = \frac{{\partial U_{x} }}{\partial x} = \frac{\partial u}{{\partial x}} - z\frac{{\partial^{2} w}}{{\partial x^{2} }} \hfill \\ \varepsilon_{\theta } = \frac{{U_{z} }}{r} = \frac{w}{R + z} \hfill \\ \end{gathered} \right. $$

(20)

Based on Hooke's law [34], the stress–strain relations of the thin sandwich cylindrical shell are as the following:

$$ \left\{ \begin{gathered} \sigma_{x} \hfill \\ \sigma_{\theta } \hfill \\ \end{gathered} \right\} = \left( {\begin{array}{*{20}c} {Q_{11}^{(k)} } & {Q_{12}^{(k)} } \\ {Q_{21}^{(k)} } & {Q_{22}^{(k)} } \\ \end{array} } \right)\left\{ \begin{gathered} \varepsilon_{x} \hfill \\ \varepsilon_{\theta } \hfill \\ \end{gathered} \right\},k = 1,2,3 $$

(21)

where $Q_{ij}^{(k)} \left( {i,j = 1,2} \right)$ are elastic constants and given as

$$ \left\{ \begin{gathered} Q_{11}^{(k)} = E_{x}^{(k)} /\left( {1 - \mu_{x\theta }^{(k)} \mu_{\theta x}^{(k)} } \right) \hfill \\ Q_{12}^{(k)} = E_{\theta }^{(k)} \mu_{x\theta }^{(k)} /\left( {1 - \mu_{x\theta }^{(k)} \mu_{\theta x}^{(k)} } \right) \hfill \\ Q_{21}^{(k)} = E_{x}^{(k)} \mu_{\theta x}^{(k)} /\left( {1 - \mu_{x\theta }^{(k)} \mu_{\theta x}^{(k)} } \right) \hfill \\ Q_{22}^{(k)} = E_{\theta }^{(k)} /\left( {1 - \mu_{x\theta }^{(k)} \mu_{\theta x}^{(k)} } \right) \hfill \\ \end{gathered} \right.,k = 1,2,3 $$

(22)

where $E_{x}^{(k)}$ and $E_{\theta }^{(k)}$ are effective elastic modulus of the inner, outer, and core layer. $\mu_{\theta x}^{(k)}$ and $\mu_{x\theta }^{(k)}$ are the Poisson's ratios. k = 1, 2, and 3 stand for the inner, core, and outer layers, respectively.

For simplicity, it is assumed that the inner and outer layers have the same material performances with elastic modulus$E$, density ${\rho }^{t}$, and Poisson's ratio$\mu$. Therefore, we obtain:

$$ \left\{ \begin{gathered} E_{x}^{(1)} = E_{x}^{(3)} = E_{\theta }^{(1)} = E_{\theta }^{(3)} = E \hfill \\ \mu_{x\theta }^{(1)} = \mu_{x\theta }^{(3)} = \mu_{\theta x}^{(1)} = \mu_{\theta x}^{(3)} = \mu \hfill \\ \rho^{(1)} = \rho^{(3)} = \rho^{t} \hfill \\ \end{gathered} \right. $$

(23)

The equivalent material performances of the ZPR cellular, including elastic modulus, density, and Poisson's ratios, are obtained in Sect. "Effective Mechanical Performances of Cellular Core Layer with ZPR":

$$ \left\{ \begin{gathered} E_{x}^{(2)} = E_{s}^{c} \frac{{\beta^{3} \cos \varphi }}{{\alpha (\sin^{2} \varphi + \beta^{2} \cos^{2} \varphi )}} \hfill \\ E_{\theta }^{(2)} = E_{s}^{c} \frac{\beta }{2\cos \varphi } \hfill \\ \mu_{x\theta }^{(2)} = \mu_{\theta x}^{(2)} = 0 \hfill \\ \rho^{\left( 2 \right)} = \rho^{c} \frac{{\left( {2 + \alpha } \right)\beta }}{2\alpha \cos \varphi } \hfill \\ \end{gathered} \right. $$

(24)

The kinetic energy T, strain energy U and the external work W, are given as:

$$ \left\{ \begin{gathered} T = \frac{1}{2}\left\{ {\mathop {\mathop \sum \nolimits }\limits_{k = 1}^{3} \left[ {\mathop \int \nolimits_{0}^{t} \mathop \int \nolimits_{{z_{k} }}^{{z_{k + 1} }} \mathop \int \nolimits_{0}^{l} \mathop \int \nolimits_{0}^{2\pi } \rho^{(k)} \left( {\left( {\frac{{\partial U_{x} }}{\partial t}} \right)^{2} + \left( {\frac{{\partial U_{z} }}{\partial t}} \right)^{2} } \right)(R + z)d\theta dxdzdt} \right]} \right\} \hfill \\ U = \frac{1}{2}\left\{ {\mathop {\mathop \sum \nolimits }\limits_{k = 1}^{3} \left[ {\mathop \int \nolimits_{0}^{t} \mathop \int \nolimits_{{z_{k} }}^{{z_{k + 1} }} \mathop \int \nolimits_{0}^{l} \mathop \int \nolimits_{0}^{2\pi } \left( {\sigma_{x}^{(k)} \varepsilon_{x}^{(k)} + \sigma_{\theta }^{(k)} \varepsilon_{\theta }^{(k)} } \right)(R + z)d\theta dxdzdt} \right]} \right\} \hfill \\ W = 0 \hfill \\ \end{gathered} \right. $$

(25)

The governing equations of the sandwich cylindrical shell containing the ZPR cellular core are based on deduction from Hamilton's principle [35]:

$$ \left\{ \begin{gathered} R\frac{{\partial N_{x} }}{\partial x} - C_{2} \frac{{\partial^{2} u}}{{\partial t^{2} }} - \frac{{C_{3} }}{2}\frac{{\partial^{3} w}}{{\partial x\partial t^{2} }} = 0 \hfill \\ C_{1} \frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }} - C_{2} \frac{{\partial^{2} w}}{{\partial t^{2} }} + \frac{{C_{3} }}{2}\frac{{\partial^{3} u}}{{\partial x\partial t^{2} }} + R\frac{{\partial^{2} M_{x} }}{{\partial x^{2} }} - N_{\theta } = 0 \hfill \\ \end{gathered} \right. $$

(26)

where

$$ \left\{ \begin{gathered} N_{x} = \mathop {\mathop \sum \nolimits }\limits_{k = 1}^{3} \mathop \smallint \nolimits_{{z_{k} }}^{{{\text{z}}_{k + 1} }} \sigma_{x}^{(k)} \frac{R + z}{R}{\text{d}}z \hfill \\ M_{x} = \mathop {\mathop \sum \nolimits }\limits_{k = 1}^{3} \mathop \smallint \nolimits_{{z_{k} }}^{{{\text{z}}_{k + 1} }} \sigma_{x}^{(k)} \frac{R + z}{R}z{\text{d}}z \hfill \\ N_{\theta } = \mathop {\mathop \sum \nolimits }\limits_{k = 1}^{3} \mathop \smallint \nolimits_{{z_{k - 1} }}^{{z_{k} }} \sigma_{\theta }^{(k)} dz \hfill \\ C_{1} = \frac{1}{12}\rho^{t} R(h^{3} - h_{0}^{3} ) + \frac{1}{12}\rho^{(2)} Rh_{0}^{3} \hfill \\ C_{2} = \left[ {\rho^{t} (h - h_{0} ) + \rho^{(2)} h_{0} } \right]R \hfill \\ C_{3} = - \frac{1}{6}\rho^{(2)} h_{0}^{3} - \frac{1}{6}\rho^{t} \left( {h^{3} - h_{0}^{3} } \right) \hfill \\ \end{gathered} \right. $$

(27)

Then, the governing equations rewrite as follows:

$$ \left\{ \begin{gathered} A_{11} \frac{{\partial^{3} w}}{{\partial x^{3} }} - A_{12} \frac{{\partial^{2} u}}{{\partial x^{2} }} - A_{13} \frac{\partial w}{{\partial x}} - \frac{{C_{3} }}{2}\frac{{\partial^{3} w}}{{\partial x\partial t^{2} }} - C_{2} \frac{{\partial^{2} u}}{{\partial t^{2} }} = 0 \hfill \\ C_{1} \frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }}{ + }A_{21} \frac{{\partial^{4} w}}{{\partial x^{4} }} - C_{2} \frac{{\partial^{2} w}}{{\partial t^{2} }} + \frac{{C_{3} }}{2}\frac{{\partial^{3} u}}{{\partial x\partial t^{2} }} - A_{22} \frac{{\partial^{3} u}}{{\partial x^{3} }} + A_{23} \frac{\partial u}{{\partial x}} + A_{24} w = 0 \hfill \\ \end{gathered} \right. $$

(28)

where

$$ \left\{ \begin{gathered} A_{11} = A_{22} = \frac{{E\left( {h^{3} - h_{0}^{3} } \right)}}{{12\left( {\mu^{2} - 1} \right)}} - \frac{{E_{x}^{(2)} h_{0}^{3} }}{12} \hfill \\ A_{12} = \frac{{ER(h - h_{0} )}}{{\mu^{2} - 1}} - E_{x}^{(2)} Rh_{0} \hfill \\ A_{13} = A_{23} = \frac{E\mu }{{\left( {\mu^{2} - 1} \right)}}\left( {h - h_{0} } \right) \hfill \\ A_{21} = \frac{{ER(h^{3} - h_{0}^{3} )}}{{12\left( {\mu^{2} - 1} \right)}} - \frac{{E_{x}^{(2)} Rh_{0}^{3} }}{12} \hfill \\ A_{24} = \frac{1}{12}\frac{E}{{\mu^{2} - 1}}\left( {h^{3} - h_{0}^{3} } \right)\frac{1}{{R^{3} }} - \frac{1}{12}E_{\theta }^{(2)} h_{0}^{3} \frac{1}{{R^{3} }} + \frac{E}{{\mu^{2} - 1}}\left( {h - h_{0} } \right)\frac{1}{R} - E_{\theta }^{(2)} h_{0} \frac{1}{R} \hfill \\ \end{gathered} \right. $$

(29)

According to Hamilton's principle, the boundary conditions are also given as:

$$ \left\{ \begin{gathered} - \left. {2R\left( {N_{x} \delta u} \right)} \right|_{x = 0}^{x = L} = 0 \Rightarrow N_{x} = 0 \, OR \, u = 0 \, at \, x = 0,L \hfill \\ \left. {\left( { - 2C_{1} \frac{{\partial^{3} w}}{{\partial x\partial t^{2} }} - C_{3} \frac{{\partial^{2} u}}{{\partial t^{2} }} - 2R\frac{{\partial M_{x} }}{\partial x}} \right)\delta w} \right|_{x = 0}^{x = L} = 0 \Rightarrow - 2C_{1} \frac{{\partial^{3} w}}{{\partial x\partial t^{2} }} - C_{3} \frac{{\partial^{2} u}}{{\partial t^{2} }} - 2R\frac{{\partial M_{x} }}{\partial x} = 0 \, OR \, w = 0 \, at \, x = 0,L \hfill \\ \left. {\left( {2RM_{x} \delta \left( {\frac{\partial w}{{\partial x}}} \right)} \right)} \right|_{x = 0}^{x = L} = 0 \Rightarrow M_{x} = 0 \, OR \, \frac{\partial w}{{\partial x}} = 0 \, at \, x = 0,L \hfill \\ \end{gathered} \right. $$

(30)

Boundary conditions may be written as:

$$ w = N_{x} = M_{x} = 0 $$

(31a)

simply supported boundary (SS)

$$ u = w = \frac{\partial w}{{\partial x}} = 0 $$

(31b)

clamped supported boundary (C)

$$ N_{x} = M_{x} = - 2C_{1} \frac{{\partial^{3} w}}{{\partial x\partial t^{2} }} - C_{3} \frac{{\partial^{2} u}}{{\partial t^{2} }} - 2R\frac{{\partial M_{x} }}{\partial x} = 0 $$

(31c)

free boundary (F)

Natural Frequency

For a cylindrical shell with different boundaries, as shown in Fig. 1, one can assume the solution forms of the field of spatial displacement as [36]:

$$ \left\{ \begin{gathered} u = A\frac{\partial \phi (x)}{{\partial x}}\sin \; (\omega t) \hfill \\ w = B\phi (x)\sin \; (\omega t) \hfill \\ \end{gathered} \right. $$

(32)

where A and B are two unknown coefficients, and ω denotes the angular frequency.

By substituting Eqs. (32) into Eqs. (31a, 31b, 31c), boundary conditions then become:

$$ \left\{ \begin{gathered} \phi (x) = \frac{{\partial^{2} \phi (x)}}{{\partial x^{2} }} = 0,\left( {SS} \right) \hfill \\ \phi (x) = \frac{\partial \phi (x)}{{\partial x}} = 0,\left( C \right) \hfill \\ \frac{{\partial^{2} \phi (x)}}{{\partial x^{2} }} = \frac{{\partial^{3} \phi (x)}}{{\partial x^{3} }} = 0,\left( F \right) \hfill \\ \end{gathered} \right. $$

(33)

The axial modal function $\phi (x)$ is defined as [37]:

$$ \phi (x) = \alpha_{1} \cosh \left( {\frac{\eta x}{L}} \right) + \alpha_{2} \cos \left( {\frac{\eta x}{L}} \right) - \lambda_{{\text{m}}} \left( {\alpha_{3} \sinh \left( {\frac{\eta x}{L}} \right) + \alpha_{4} \sin \left( {\frac{\eta x}{L}} \right)} \right) $$

(34)

where $\alpha_{i}$ (i = 1,2,3,4) values 0 or ± 1 are determined for each boundary condition. η is a natural number of axial waves. $\lambda_{{\text{m}}}$ is a coefficient dependent on η. Table 1 shows the value of $\alpha_{i}$, η and $\lambda_{{\text{m}}}$ for different boundary conditions.

Table 1 Value of α_i, η and $\lambda_{{\text{m}}}$ for different boundary conditions [37]

Substituting Eqs. (32), (33), and (34) into (28) results in a set of governing eigenvalue equations:

$$ \left( {\begin{array}{*{20}c} {L_{11} } & {L_{12} } \\ {L_{21} } & {L_{22} } \\ \end{array} } \right)\left( \begin{gathered} A \hfill \\ B \hfill \\ \end{gathered} \right) = \left( \begin{gathered} 0 \hfill \\ 0 \hfill \\ \end{gathered} \right) $$

(35)

where

$$ \left\{ \begin{gathered} L_{11} = C_{2} \frac{\partial \phi }{{\partial x}}\omega^{2} - A_{12} \frac{{\partial^{3} \phi }}{{\partial x^{3} }} \hfill \\ L_{12} = A_{11} \frac{{\partial^{3} \phi }}{{\partial x^{3} }} - A_{13} \frac{\partial \phi }{{\partial x}} + \frac{{C_{3} }}{2}\frac{\partial \phi }{{\partial x}}\omega^{2} \hfill \\ L_{21} = A_{23} \frac{{\partial^{2} \phi }}{{\partial x^{2} }} - \frac{{C_{3} }}{2}\frac{{\partial^{2} \phi }}{{\partial x^{2} }}\omega^{2} - A_{22} \frac{{\partial^{4} \phi }}{{\partial x^{4} }} \hfill \\ L_{22} = A_{21} \frac{{\partial^{4} \phi }}{{\partial x^{4} }} - C_{1} \frac{{\partial^{2} \phi }}{{\partial x^{2} }}\omega^{2} + C_{2} \phi \omega^{2} + A_{24} \phi \hfill \\ \end{gathered} \right. $$

(36)

To obtain the angular frequencies of the sandwich cylindrical shell, we solve the equation $\left| {L_{ij} } \right| = 0$. Then the following polynomial can be factorized into:

$$ \lambda_{1} \omega^{4} + \lambda_{2} \omega^{2} + \lambda_{3} = 0 $$

(37)

where, λ_i (_i = 1, 2, 3) are constants. By solving Eq. (37), one can obtain two angular frequencies in the axial and radial directions. This investigation considers only the smallest angular frequency.

Numerical Simulation

In order to verify the calculation results in the above theories, numerical simulation with a commercial FE software ABAQUS (version 6.14) is carried out. Unit cell with a 2-node linear element B21 is used to analyze the effective mechanical performances of the ZPR cellular core, as shown in Fig. 5. The tensile of the honeycomb under a linear static loading was developed by imposing concentrated force P along direction-x and direction-θ. The boundary conditions are listed in Table 2. The effective stress $\sigma_{FEM}$ is calculated by $\sigma_{FEM} = \frac{P}{{\alpha lh_{0} }}$, The effective strain $\varepsilon_{FEM}$ is calculated by $\sigma_{FEM} = \frac{P}{{\alpha lh_{0} }}$ and $\varepsilon_{FEM} = \frac{{U_{i} }}{2l\cos \varphi }(i = 1,2)$, where $U_{1}$ and $U_{2}$ are the displacement along direction-x and direction-θ, respectively. The modulus along direction-x and direction-θ were then obtained as the ratios between the effective stresses and strains. Table 3 itemizes the corresponding material performances of the cellular core in FEM. The relative percentage error is given as:

$$ Error(\% ) = \frac{{\left| {\omega_{theoretical} - \omega_{FEM} } \right|}}{{\omega_{theoretical} }} \times 100\% $$

(38)

where $\omega_{theoretical}$ and $\omega_{FEM}$ are the theoretical and simulation results, respectively.

Fig. 5

The 2D geometric model for the simulation of the mechanical properties of cellular core

Table 2 Boundary conditions on FE models to calculate the mechanical properties of cellular core

Table 3 Material performances of cellular core in FEM

Figure 6 shows the theoretical and FE results of equivalent mechanical performances of the cellular core under different internal angles. One can see that the theoretical predictions of the elastic modulus of the cellular core are consistent with the simulation results both in direction-x and direction-θ. The mean relative percentage error of the elastic modulus in direction-x is 1.98%, while in direction-θ is 0.01%. The main reason is that the deformations of the vertical cellular walls are ignored in predicting the elastic moduli in direction-x. The simulation results, it should be noted, are somewhat below the theoretical ones, contributing to the difference between the simulation model and the theoretical model [38]. In fact, the beam model applied to the Finite element simulation is the Timoshenko beam, while to theoretical analysis is the Euler–Bernoulli beam. In addition, with the increase of the internal angle, the elastic moduli in direction-x decrease, while the elastic moduli in direction-θ grow.

Fig. 6

Theoretical and simulation results of effective mechanical properties of cellular core: a effective elastic modulus in direction-x, b effective elastic modulus in direction-θ

To evaluate the accuracy of natural frequencies in the current method, Table 4 lists the natural frequencies of the isotropic elastic cylindrical shell under the SS-SS boundary calculated by the current method, FEM, experiment [39], and four shell theories [40]: (1) Soedel (SST), (2) Flügge (FST), (3) Morley-Koiter (MKST) and (4) Donnell (DST), where Exact and APP. denote exact and approximate solutions, respectively. If we chose h₀ = 0, the vibration characteristics of the sandwich cylindrical shell would turn into the vibration characteristics of an isotropic cylindrical shell. In this case, the geometry dimensions and material properties are chosen as E = 68.2GPa, ρ = 2700 kg/m³, and v = 0.33. L = 1.7272 m, R = 0.0762 m, and h = 0.00147 m. In addition, unlike FEM analysis of effective mechanical properties, a 3D model with 8-node linear brick C3D8R is employed to calculate the natural frequencies of the elastic and isotropic cylindrical shell, as shown in Fig. 7. The boundary conditions are listed in Table 5, where u_i and UR_i are displacements in x, θ, and z directions and related rotations, respectively.

Table 4 Natural frequencies of the isotropic elastic cylindrical shell under SS-SS boundary

Fig. 7

3D model for the simulation of the natural frequencies

Table 5 Boundary conditions on FE models to calculate the natural frequencies

Figure 8 shows the errors for natural frequencies of the SS-SS shell obtained by experiment, Soedel, Flügge, Morley-Koiter, Donnell, and FEM relative to those obtained by the current method. It can be seen that some discrepancies are made between the natural frequencies obtained by the present method and DST (Exact). Except for DST (Exact) and MKST (Exact), the error values of the natural frequencies of the SS-SS shell are less than 5%. Uncertainties affecting the results among those theories are due to the various assumptions made about the form of small terms and the order of terms that are retained in the analysis [41, 42]. Generally, the DST is the simplest of these theories. The FST is felt to be the most accurate. The various shell theories sometimes predict significantly different results [43]. However, over broad ranges of parameters of engineering importance, these theories yield similar results [44]. In addition, as shown in Table 4, the theoretical result of natural frequency in the current method is higher than the FEM and FST owing to the neglect of rotary inertia and shear deformation.

Fig. 8

Error for the natural frequencies of the SS-SS shell

Results and Discussion

The structural parameter analysis is evaluated in this section. Since the validity of theoretical predictions is confirmed in FEM and some available literature results in Sect. "Numerical simulation", all the results are theoretical values according to Table 6 except those mentioned in this section.

Table 6 Geometry dimensions and material properties of sandwich cylindrical shells

Effective Mechanical Properties of ZPR Cellular Core Layer

Figure 9 describes the effects of α and β on the relative density of cellular core versus internal angle φ. The plot illustrates that an increased internal angle φ leads to an increase in the relative density of the cellular core when other parameters are given fixed values. In addition, geometric parameters, including α and β, provide opposite contributions to the relative density. In other words, a decrease of α and/or an increase of β will increase the cellular core's relative density when φ keeps constant. Indeed, the increase of φ can decrease the equivalent area of the cellular core, resulting in an increase in the relative density. While the equivalent area increases with decrease of α.

Fig. 9

Effect of a α and b β on the relative density of cellular core versus internal angle φ

Figure 10 illustrates the effects of α and β on the elastic modulus along direction-x of cellular core versus φ. It is clear that the elastic modulus in direction-x decreases with increasing φ value for fixed α and β values, which is similar to Fig. 6(a). An increase of φ value leads to the increase of the bending of the cell wall along direction-x. Consequently, φ value is increased, resulting in a decreased elastic modulus in direction-x. From Fig. 10(a), it can be seen that the elastic modulus in direction-x decreases with the increase of α values when other parameters are given fixed values owing to the increased cross-sectional area induced by the parameters α. In addition, Fig. 10(b) indicates that β increases, the elastic modulus in direction-x increases when other parameters are given fixed values. In the unit cell, increasing value of φ and decreasing value of β tend to increase the bending deformation along the direction-x, resulting in larger effective strains and lower equivalent elastic modulus. The decreasing value of α leads to smaller sectional area normal to loading direction, leading to large equivalent stress and elastic modulus in direction-x.

Fig. 10

Effect of a α and b β on the elastic modulus in direction-x of cellular core versus φ

Figure 11 illustrates the effects of α and β on the elastic modulus along the direction-θ of the cellular core versus φ. The elastic modulus in direction-θ increases with the increase of φ value for fixed α and β values, which is similar to Fig. 6(b). An increasing internal angle φ decreases a cross-section perpendicular to the loading direction, leading to larger equivalent stress and elastic modulus. As shown in Fig. 11(a), the α value variations do not affect the elastic modulus in direction-θ when other parameters remain constant. According to the above analysis in Sect. 2.1, the deformations of diagonal and vertical walls have relative independence. No deformation occurs in sloping walls when the cellular structure suffers a tensile loading along the direction-θ. Therefore, the variations of α value are irrelevant to the elastic modulus in direction-θ. In addition, Fig. 11(b) indicates that an increase of β value leads to an increasing elastic modulus in direction-θ when other parameters remain constant owing to the increasing cross-section of vertical walls.

Fig. 11

Effect of a α and b β on the elastic modulus along direction-θ of cellular core versus φ

Natural Frequencies of Sandwich Cylindrical Shell

Figure 12 shows the effects of α on natural frequencies of the shell containing ZPR cellular core versus φ under different boundaries, where β = 0.1, R = 0.2 m, h₀/h = 0.8, L/R = 5, R/h = 20. The detailed values of natural frequency in Fig. 12 are listed in Table 7. It can be concluded that the natural frequencies of this system decrease with the increase of φ value for SS-SS, SS-F, and SS-C boundary conditions. In addition, an increase of α results in decline in natural frequencies.

Fig. 12

Natural frequencies of the shell versus internal angles φ, for different α (β = 0.1, R = 0.2 m, h₀/h = 0.8, L/R = 5, R/h = 20)

Table 7 Effects of α on natural frequencies of the shell containing ZPR cellular core versus φ under different boundaries (β = 0.1, R = 0.2 m, h₀/h = 0.8, L/R = 5, R/h = 20)

Figure 13 exhibits the effects of β on natural frequencies of the shell containing ZPR cellular core versus φ under different boundaries, where α = 2, R = 0.2 m, h₀/h = 0.8, L/R = 5, R/h = 20. Natural frequencies of this system increase with the increase of β value. The detailed values of natural frequency in Fig. 13 are listed in Table 8. From the mechanical properties of the cellular core obtained in Sect. "Effective Mechanical properties of ZPR Cellular Core Layer", we can conclude that an increasing internal angle φ leads to an increase in the relative density, resulting in lower natural frequencies. Likewise, the intricate trend of natural frequencies induced by α and β can be expounded by the mechanical properties of the cellular core. As shown in Fig. 9, an increase of α and/or a decrease of β will increase the overall mass, resulting in the natural frequencies decreasing.

Fig. 13

Natural frequencies of the shell versus internal angles φ, for different β (α = 2, R = 0.2 m, h₀/h = 0.8, L/R = 5, R/h = 20)

Table 8 Effects of β on natural frequencies of the shell containing ZPR cellular core versus φ under different boundaries (α = 2, R = 0.2 m, h₀/h = 0.8, L/R = 5, R/h = 20)

Figure 14 shows the effects of radius-to-thickness ratio R/h on natural frequencies of the shell versus containing ZPR cellular core core-thickness ratio h₀/h under different boundaries, where α = 2, β = 0.1, φ = 30°, h = 0.01 m, L/R = 5. The detailed values of natural frequency in Fig. 14 are listed in Table 9. Results show that as R/h increases, the natural frequencies decrease. Moreover, the natural frequencies decrease with the increase of h₀/h. That is, the density of elastic and isotropic materials is less than that of this system's cellular core. When the shell thickness h is given a definite value, an increase in core thickness h₀ leads to the reduction of the inner and outer layer thickness. In other words, the increased h₀ will increase the shell's overall mass, resulting in the natural frequencies decreasing. In addition, the increased h₀ can weaken the core layer's enhancement effect on the sandwich shell's global bending rigidity, leading to the decline of the global bending rigidity of the sandwich shell. At this point, the enhancement effect of the core layer as the upper and lower panel spacing on the overall bending stiffness of the sandwich shell is weakened, resulting in the reduction of the overall bending stiffness of the sandwich shell.

Fig. 14

Natural frequencies of the shell versus h₀/h for different R/h (α = 2, β = 0.1, φ = 30°, h = 0.01 m, L/R = 5)

Table 9 Effects of R/h on natural frequencies of the shell containing ZPR cellular core versus h₀/h under different boundaries (α = 2, β = 0.1, φ = 30°, h = 0.01 m, L/R = 5)

Figure 15 shows the influences of length-to-radius ratio L/R on natural frequencies of the shell containing ZPR cellular core versus R/h under different boundary conditions, where α = 2, β = 0.1, φ = 30°, h = 0.01 m, h₀/h = 0.8. The detailed values of natural frequency in Fig. 15 are listed in Table 10. Those diagrams illustrate the natural frequencies decrease with the increase of the L/R, which is very similar to what was reported by Li et al. [45]. This intuitively correct because the stiffness decreases with the increases in length.

Fig.15

Natural frequencies of the shell versus R/h for different L/R (α = 2, β = 0.1, φ = 30°, h = 0.01 m, h₀/h = 0.8)

Table 10 Effects of L/R on natural frequencies of the shell containing ZPR cellular core versus R/h under different boundaries (α = 2, β = 0.1, φ = 30°, h = 0.01 m, h₀/h = 0.8)

Conclusions

This work investigates the effective mechanical properties of a ZPR cellular core and the vibrational behavior of sandwich cylindrical shells with the ZPR cellular core. Homogenization methods are used to analyze the effective mechanical properties of the cellular core. The CLST and Hamilton principles are employed to form the equilibrium equations to determine the vibrational behavior of the sandwich cylindrical shells. The small discrepancies between the theoretical predictions and the FEM results prove the analytical models are accurate for engineers to quickly select geometric parameters in designing a desired structure. The following conclusions are drawn from this study:

• (1) These structural geometric parameters contribute to the effective mechanical performances of the ZPR cellular core, including the relative density and the effective modulus. For example, an increased α and/or a decreased β will lead to the relative density of the cellular core increasing, and the elastic modulus in direction-x of the cellular core decreases with the increase of α while increases with the increase of β.

• (2) The effective mechanical performances of the cellular core and geometric parameters of the shell can influence the natural frequencies of the sandwich cylindrical shell under different boundaries driven by changing overall mass and bending rigidity of the sandwich shell. For example, an increase of α and/or a decrease in β leads to an increase in relative density, resulting in larger natural frequencies. The increase of core thickness h₀ leads to the natural frequencies decrease owing to the weakened overall bending rigidity of the sandwich shell.