Modeling the dynamics of mixed immunotherapy and chemotherapy for the treatment of immunogenic tumor

Abstract

We investigate a mathematical model that delineates the nonlinear dynamics of tumor-immune interplay by considering the roles of immunotherapy and chemotherapy. The proposed model explores a system of coupled nonlinear ordinary differential equations (ODEs), involving tumor cells, cytotoxic T-lymphocytes (CD8+T cells), macrophages, dendritic cells, regulatory T-cells (Tregs), IL-10, TGF-$\beta$, IL-12, IFN-$\gamma$ and the concentration of chemotherapeutic drug. We use optimal control theory to understand the dynamics under what conditions the immune system can eradicate tumor cells. The control problem is solved with an objective functional that minimizes the tumor cell population and maximizes the immune components. The basic properties of optimal control theory are established through the boundedness of solutions for each state variable. Our optimal control theory is characterized by coupling the state variables with costates. Additionally, our study investigates the uniqueness property of the optimal control problem within a small time window. Subsequently, we explored the methods employed to estimate the system parameters. Finally, we demonstrate numerically that the optimal control strategy minimizes the burden of tumor cells and maximizes immune cell populations under different scenarios. Moreover, we provide corresponding biological implications.

1 Introduction

Tumors arise from the abnormal proliferation and differentiation of cells in our body. Many benign tumors are under the effective control of the immune system, and hence, they do not affect patients’ life. However, some malignant tumors (such as lymphoma, meningioma, melanoma, mesothelioma, epithelial cancer, and so on) pose a serious threat to human life and can significantly impact patients’ quality of life [1, 2]. As per report by the World Health Organization (WHO) [3], cancer is the second largest cause of death globally, estimated to account for around 1 crore deaths in 2020. Nowadays, the most significant and demanding questions in oncology are how the immune system prevents cancer growth and evolution [1, 4]. The interaction between tumor and the immune system is a complicated process. So far, the underlying mechanisms are still not fully understood and have been the focus of research in many disciplines including medicine and mathematics. Mathematical modeling has been proven to be an effective tool for understanding the interaction and providing guidelines on controlling the growth of tumor [1, 2, 5, 6].

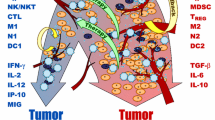
Our immune system is also a very complicated network composed of many cells, signals and proteins that defend our body against tumor cells and foreign invaders or pathogens. Different kinds of B-cells, T-cells (CD8+T cells or CD4+T cells), macrophages, natural killer cells (NK cells), antigen-presenting dendritic cells (such as dendritic cells, macrophages and Langerhans cells) and cytokines (immuno-stimulatory) are primary components of our immune system. Macrophages, CD8+T cells and NK cells are generally considered as effector cells. They can either destroy the tumor cell population or inhibit their proliferation. Meanwhile, tumor cells can in turn neutralize immune-effector cells, leading to a competitive relationship among these two types of cells [7]. On the other hand, in the presence of a tumor, it can promote the production of effector cells by releasing tumor antigens. In other words, the tumor can promote the growth of effector cells to some extent. Thus, there is an interaction between the tumor and the immune system analogous to the predator–prey relationship, with tumor cells as prey and effector cells as predators. [8]. As a result, models on the tumor-immune system dynamics typically incorporate these relationships of competition and predation. To simplify the mechanism underlying tumor-immune interactions and facilitate mathematical analysis, some dynamical models with effector cells and tumor cells only are proposed [6, 9].

In the context of the described research paper on tumor-immune interactions, the mathematical model likely incorporates hypotheses and assumptions regarding the relationships between cytokines and various immune and tumor cells. Cytokines are known to play roles in stimulating or inhibiting the activities of immune cells. The hypotheses could suggest that particular cytokines boost the functionality of cytotoxic T-lymphocytes (CD8+T cells) and macrophages playing a critical role in antitumor responses. Some cytokines such as TGF-$\beta$ and IL-10 are often associated with immunosuppressive effects. Hypotheses may include the idea that these cytokines contribute to regulatory T-cell (Treg) function and suppression of immune responses against tumor cells. The model might hypothesize specific interactions between different cell types such as the activation of dendritic cells leading to the activation of CD8+T cells or the inhibition of immune responses by Tregs. Hypotheses may consider the temporal dynamics of cytokine production and cell responses. For instance, the model might assume that certain cytokines are produced rapidly in response to tumor presence, influencing the immune response over time.

Despite medical improvements, many challenges remain in the prognosis and treatment of malignant tumors. The most effective treatments for cancer patients are chemotherapy, surgery, hormone therapy, radiation therapy and so on [10]. The primary method of treatment is used to determine the appropriate position, nature and stage of cancer. Immunotherapy stimulates our immune system against cancer cell population to eliminate them. This type of treatment is effective in promoting an immune response and obstructing the growth of the cancer cell population [11]. Chemotherapy has many harmful side effects, which can result in the patient becoming susceptible to infections, and it also reduces the immune system’s ability to fight against the cancer cell population. Therefore, an optimal control problem is used in the cancer growth model with chemotherapy to minimize the total drug dosage [5].

There are many research articles that focus on the tumor-immune interaction model [1, 2, 4, 6, 12,13,14], but few researchers have applied optimal control theory to eliminate/eradicate the tumor cell population [5, 10, 11, 15,16,17,18,19]. G.W. Swan [20] studied a mathematical model for tumor-immune interplays with cancer immunotherapy by applying optimal control problem. In this paper, the author incorporated both experimental and clinical data to analyze the tumor cell population. In [21], the authors applied an optimal control strategy to develop an optimal control technique for chemotherapeutic drugs. They applied chemotherapy to study the qualitative behavior of three different cell-kill models. In each case, the authors aimed to minimize both the drug dosage and the tumor cell burden. Fister and Donnelly [22] introduced optimal control theory to better understand under what circumstances the tumor cells could be eradicated. They demonstrated that tumor cells exhibit a cyclic nature during therapy and established the existence of bang-bang control in two linear optimal control problems. Burden et al. [10] applied optimal control theory to a mathematical model involving the interaction between tumor cell populations, immune components and the immuno-stimulatory cytokine IL-2, as originally explored by Kirschner and Panetta [2]. In their approach to treating cancer cells, the authors derived an optimal treatment technique involving the external injection of adoptive cellular immunotherapy (ACI). de Pillis et al. [5] analyzed a mathematical model of the interaction between tumor cells and immune cells and they introduced chemotherapy to minimize the tumor cell burden. The authors established the existence property of optimal control problem and solved both the linear and quadratic controls. An interesting thing in this paper is that graphical region on which the singular control is optimal. Khajanchi and Ghosh [11] implemented an optimal control strategy in nonlinear dynamics of tumor-immune interaction system, which was described by Kuznestov et al. [6]. A glioma-immune interaction system, incorporating the immune-therapeutic drug T11 target structure (T11TS), was explored in the research paper by Khajanchi et al. [23]. In this study, the authors introduced an optimal control strategy into their mathematical model to minimize the glioma burden and maximize the immune cells (CD8+T cells and macrophages).

In this paper, we have constructed a mathematical model of nine nonlinear ordinary differential equations (ODEs) that captured different types of cell population and cytokines (immuno-stimulatory and immunosuppressive). By applying the quasi-steady-state approximations [24] to the concentrations of cytokines, our mathematical model reduces to a system of four nonlinear coupled ODEs, describing tumor cells, cytotoxic T-lymphocytes (CD8+T cells), macrophages and dendritic cells. Next, we incorporate immunotherapeutic and chemotherapeutic drugs into our system. We utilize the optimal control theory in our model to understand the dynamics and determine the conditions under which tumors can be eradicated. We also conduct a stability analysis of both the tumor-free singular point and the interior singular point. To study the control theory, we construct an objective function for minimizing the tumor cell burden and maximizing the immune cells. The main aim of this paper is to provide a better treatment policy to eliminate the tumor cell population or at least to improve the patient’s quality of life.

The remaining portion of the research paper is described as follows. We describe the mathematical system with biological justification in Sect. 2. In Sect. 3, we investigate the stability analysis around biologically feasible singular points of the given system. We define the control problem in our stated model in Sect. 4. Section 5 describes the existence of the control problem. We use Pontryagin’s Maximum Principle [25] to analyze the characteristics of the optimal control problem in Sect. 6. In Sect. 7, we study the uniqueness property of the optimality system, in which the state variables are coupled with adjoint or costate system. In Sect. 8, we have estimated the values of some parameters. Section 9 deals with extensive numerical simulations for our optimal control problem. Finally, our research paper ends with a brief conclusion.

2 Deterministic model

In this section, we studied a mathematical model for nine coupled system of ordinary differential equations (ODEs) that take into account the role of various cells and cytokines, namely tumor cells (T(t)), cytotoxic T-lymphocytes (L(t)), macrophages (M(t)), dendritic cells (D(t)), Tregs ($T_{g}(t)$), IL-10 $(I_{10}(t))$, TGF-$\beta$ $(T_{\beta }(t))$, IL-12 $(I_{12}(t))$ and IFN-$\gamma$ $(I_{\gamma }(t))$. The mathematical model is given by the following system of ODEs:

$$\begin{aligned} \frac{\textrm{d}T}{\textrm{d}t}=\, & {} r_{T}T (1-b_{T}T) - \frac{(\alpha _{T}^{'}M+\gamma _{T}^{'}L)T}{g_{T}^{'}+I_{10}}, \nonumber \\ \frac{\textrm{d}L}{\textrm{d}t}=\,& {} \frac{\alpha _{l}^{'}I_{12}}{g_{l}^{'}+T_{g}} - \delta _{l}L, \nonumber \\ \frac{\textrm{d}M}{\textrm{d}t}=\,& {} s_{m} + \frac{\alpha _{m}^{'}I_{\gamma }}{(g_{m}^{'}+I_{\gamma })}\cdot \frac{1}{(g_{m1}^{'}+T_{\beta })} - \gamma _{m}MT- \delta _{m}M, \nonumber \\ \frac{\textrm{d}D}{\textrm{d}t}=\,& {} s_{d} + \frac{\alpha _{d}T}{g_{d}+T} - \delta _{d}D, \nonumber \\ \frac{dT_{g}}{\textrm{d}t}=\,& {} \alpha _{g}L - \delta _{g}T_{g}, \nonumber \\ \frac{dI_{10}}{\textrm{d}t}=\,& {} \alpha _{10}M - \delta _{10}I_{10}, \nonumber \\ \frac{dT_{\beta }}{\textrm{d}t}=\,& {} s_{\beta } + \alpha _{\beta }T - \delta _{\beta }T_{\beta }, \nonumber \\ \frac{dI_{12}}{\textrm{d}t}=\,& {} \alpha _{12}D - \delta _{12}I_{12}, \nonumber \\ \frac{dI_{\gamma }}{\textrm{d}t}=\,& {} \alpha _{\gamma }L - \delta _{\gamma }I_{\gamma }. \end{aligned}$$

(1)

• The initial Eq. in (1) characterizes the tumor cell density at any given time t. The first term $r_{T}T (1-b_{T}T)$ delineates the logistic growth of tumor cells in the absence of any immune response [26]. Here, $r_{T}$ denotes the intrinsic growth rate and the maximum carrying capacity for tumor cells is $\frac{1}{b_{T}}$. The second term accounts for the removal of tumor cells due to interactions with macrophages [4] and CD8+T cells [6], each exhibiting elimination rates $\alpha _{T}^{'}$ and $\gamma _{T}^{'}$, respectively. The term $g_{T}^{'}$ represents the half-saturation constant, where $\frac{1}{g_{T}^{'}+I_{10}}$ acts as a primary immunosuppressive factor influencing both macrophages and CD8+T cells.

• The second Eq. in (1) characterizes the density of CD8+T cells, with the first term illustrating the activation of CD8+T cells at a rate $\alpha _{l}^{'}$. This activation is contingent upon the presence of CD4+T cells, which are enhanced by the cytokine IL-12 [27]. Simultaneously, the activation of CD8+T cells is suppressed by the influence of regulatory T-cells [28] at suppressive rate $g_{l}^{'}$. The intrinsic mortality rate of CD8+T cells is denoted by $\delta _{l}$.

• The third Eq. in (1) characterizes the density of macrophages. The term $s_{m}$ represents the constant source rate of macrophages [29]. The recruitment rate of macrophages ($\alpha _{m}^{'}$) is influenced by the direct presence of IFN-$\gamma$ [4, 29]. Additionally, $g_{m}^{'}$ signifies the half-saturation constant. Meanwhile, the term $\frac{1}{g_{m1}^{'}+T_{\beta }}$ acts as an immunosuppressive factor for macrophages, where $g_{m1}^{'}$ is the half-saturation constant. The third term outlines the inactivation of macrophages due to interactions with tumor cells at the rate $\gamma _{m}$ [4] and $\delta _{m}$ represents the natural death rate of macrophages.

• The fourth equation in (1) details the density of antigen-presenting dendritic cells. The term $s_{d}$ signifies the constant source rate of dendritic cells [30]. The coefficient $\alpha _{d}$ represents the activation rate of dendritic cells triggered by the direct presence of tumor cells, with $g_{d}$ serving as the half-saturation constant following Michaelis-Menten kinetics [31]. The death rate of dendritic cells is denoted by $\delta _{d}$.

• The fifth equation in (1) elucidates the dynamics of regulatory T-cells (Tregs). Regulatory T-cells are generated from activated CD8+T cells [32] with an activation term $\alpha _{g}$, while the natural degradation rate of Tregs is denoted by $\delta _{g}$.

• The sixth equation in the model (1) depicts the density of the anti-inflammatory cytokine IL-10. IL-10 is activated by macrophages [29] with an activation rate $\alpha _{10}$, and $\delta _{10}$ represents the decay rate of IL-10.

• The seventh equation in the model (1) describes the concentration of TGF-$\beta$. The term $s_{\beta }$ denotes the constant source rate of TGF-$\beta$ [4]. The second term represents the source term, directly proportional to the size of the tumor cells, with $\alpha _{\beta }$ indicating the release rate per tumor cell [33]. The final term accounts for the decay of the immunosuppressive cytokine TGF-$\beta$ at a constant rate of $\delta _{\beta }$.

• The eighth equation in the model (1) articulates the density of IL-12. IL-12 is activated by dendritic cells, with $\alpha _{12}$ representing the release rate per single antigen-specific dendritic cell [27]. The degradation rate of IL-12 is denoted by $\delta _{12}$.

• The final equation in the system (1) describes the dynamics of IFN-$\gamma$. We postulate that IFN-$\gamma$ is generated by CD8+T cells [4, 33] with a production rate $\alpha _{\gamma }$. The last term accounts for the degradation of IFN-$\gamma$ at a constant rate of $\delta _{\gamma }$.

To better understand the interactive dynamics of tumor-immune competitive system, we simplify our model system by utilizing the quasi-steady-state approximations [24] for the concentrations of cytokines. Based on the hypothesis, the cytokine equations, that is, from fifth to nine equations of (1) lead to

$$\begin{aligned} T_{g}=\,& {} \frac{\alpha _{g}}{\delta _{g}}L,~I_{10}=\frac{\alpha _{10}}{\delta _{10}}M,~T_{\beta } =\frac{s_{\beta }}{\delta _{\beta }}+\frac{\alpha _{\beta }}{\delta _{\beta }}T, \\ I_{12}=\,& {} \frac{\alpha _{12}}{\delta _{12}}D,~I_{\gamma }=\frac{\alpha _{\gamma }}{\delta _{\gamma }}L. \end{aligned}$$

After substituting these cytokine expressions into the first to fourth equations of (1), we obtain the following four ordinary differential equations for the tumor-immune interactive dynamics

$$\begin{aligned} \frac{\textrm{d}T}{\textrm{d}t}=\,& {} r_{T}T (1-b_{T}T) - \frac{(\alpha _{T}M+\gamma _{T}L)T}{g_{T}+M}, \nonumber \\ \frac{\textrm{d}L}{\textrm{d}t}=\,& {} \frac{\alpha _{l}D}{g_{l}+L} - \delta _{l}L, \nonumber \\ \frac{\textrm{d}M}{\textrm{d}t}=\,& {} s_{m} + \frac{\alpha _{m}L}{(g_{m}+L)}\cdot \frac{1}{(g_{m1}+T)} - \gamma _{m}MT- \delta _{m}M, \nonumber \\ \frac{\textrm{d}D}{\textrm{d}t}=\,& {} s_{d} + \frac{\alpha _{d}T}{g_{d}+T} - \delta _{d}D, \end{aligned}$$

(2)

where

$$\begin{aligned} \alpha _{T}=\,& {} \frac{\delta _{10}}{\alpha _{10}}\alpha _{T}^{'},~~~\gamma _{T}=\frac{\delta _{10}}{\alpha _{10}}\gamma _{T}^{'}, ~~~~g_{T}=\frac{\delta _{10}}{\alpha _{10}}g_{T}^{'},~~~\alpha _{l} =\,\frac{\delta _{g}}{\alpha _{g}}\frac{\alpha _{12}}{\delta _{12}}\alpha _{l}^{'}, \\ g_{l}=\,& {} \frac{\delta _{g}}{\alpha _{g}}g_{l}^{'}, ~~~\alpha _{m}=\,\frac{\delta _{\beta }}{\alpha _{\beta }}\alpha _{m}^{'},~~~g_{m}=\frac{\delta _{\gamma }}{\alpha _{\gamma }}g_{m}^{'}, ~~~g_{m1}=\frac{\delta _{\beta }}{\alpha _{\beta }}g_{m1}^{'}+\frac{s_{\beta }}{\alpha _{\beta }}. \end{aligned}$$

Fig. 1

This schematic diagram illustrates the interaction among tumor cells, immune cells and cytokines. Activation is denoted by blue sharp arrows, while deactivation is represented by red dashed block arrows

By employing the role of chemotherapeutic drug and introduce the optimal control theory, we obtain the following system of ODEs (Fig. 1):

$$\begin{aligned} \begin{array}{llll} \frac{\textrm{d}T}{\textrm{d}t} &{}=&{} r_{T}T (1-b_{T}T) - \frac{(\alpha _{T}M+\gamma _{T}L)T}{g_{T}+M}-k_{T}(1-e^{-\eta _{T}C})T, \\ \frac{\textrm{d}L}{\textrm{d}t} &{}=&{} \frac{\alpha _{l}D}{g_{l}+L} - \delta _{l}L + u_{2}(t)-k_{l}(1-e^{-\eta _{l}C})L, \\ \frac{\textrm{d}M}{\textrm{d}t} &{}=&{} s_{m} + \frac{\alpha _{m}L}{(g_{m}+L)}\cdot \frac{1}{(g_{m1}+T)} - \gamma _{m}M T- \delta _{m}M + u_{3}(t)-k_{m}(1-e^{-\eta _{m}C})M, \\ \frac{\textrm{d}D}{\textrm{d}t} &{}=&{} s_{d}u_{4}(t) + \frac{\alpha _{d}T}{g_{d}+T} - \delta _{d}D - k_{d}(1-e^{-\eta _{d}C})D, \\ \frac{dC}{\textrm{d}t} &{}=&{} -\gamma C + v_{c}(t), \end{array} \end{aligned}$$

(3)

with the following initial values:

$$\begin{aligned} T(0)= & {} T_{0} \ge 0,~~~ L(0) = L_{0}> 0,~~~ M(0) = M_{0}> 0,~~~ D(0) = D_{0}> 0,~~~C(0) = C_{0} > 0. \end{aligned}$$

(4)

Here,

• the term $r_{T}T (1-b_{T}T)$ represents the logistic growth of tumor cell population without any immune response, where $r_{T}$ is intrinsic growth rate and $\frac{1}{b_{T}}$ is carrying capacity of tumor cells.

• The function $\frac{(\alpha _{T}M+\gamma _{T}L)T}{g_{T}+M}$ is the clearance term of tumor cells due to macrophages and CD8+T cells with clearance rate $\alpha _{T}$ and $\gamma _{T}$, respectively. Here, $g_{T}$ is the Michaelis-Menten term and the term $\frac{1}{g_{T}+M}$ represents the major immunosuppressive factor for both macrophages and CD8+T cells.

• Last term of the first equation of system (3) represents the tumor death induced by chemotherapy, where $k_{T}$ is the rate of chemotherapy induced tumor death, and $\eta _{T}$ is the chemotherapy efficacy coefficient.

• First term of the second equation of system (3) is the activation term of CD8+T cells. It signifies that the presence of dendritic cells contributes positively to the activation of CD8+T cells. As the population of dendritic cells increases, it enhances the activation of CD8+T cells. $\alpha _{l}$ is the activation rate, determining how fast CD8+T cells are activated in response to the presence of dendritic cells. The term $\frac{1}{g_{l}+L}$ is the Michaelis-Menten term. In the context of this equation, it represents the saturation effect of CD8+T cell activation. $g_{l}$ is the half-saturation constant, representing the level of CD8+T cells at which activation is half-maximal. In summary, the term $\frac{\alpha _{l}D}{g_{l}+L}$ captures the influence of dendritic cells on the activation of CD8+T cells, incorporating both positive activation effects and saturation dynamics.

• The natural death rate of CD8+T cells is $\delta _{l}$.

• $u_{2}(t)$ serves as the control parameter regulating the CD8+T cell population. This parameter plays a pivotal role in implementing an immunotherapeutic strategy aimed at enhancing the immune response. It represents a crucial factor in the design and execution of immunotherapy. In this approach, the introduction of antigen-specific cytotoxic immune cells empowers the body’s immune system to more effectively target and eliminate cancer cells.

• $k_{l}(1-e^{-\eta _{l}C})L$ is the CD8+T cells death induced by chemotherapy, where $k_{l}$ is the rate of chemotherapy induced CD8+T cell death, and $\eta _{l}$ is the chemotherapy efficacy coefficient.

• $s_{m}$ is the constant source rate of macrophages. The function $\frac{\alpha _{m}L}{(g_{m}+L)}\cdot \frac{1}{(g_{m1}+T)}$ is activation term of macrophages. $\alpha _{m}$ is the activation rate of macrophages due to the presence of CD8+T cells, where $g_{m}$ is the half-saturation constant in Michaelis-Menten dynamics. $\frac{1}{(g_{m1}+T)}$ is the immunosuppressive factor of macrophages, and $g_{m1}$ is the suppressive parameter.

• $\gamma _{m}$ represents the loss of macrophages due to interaction of tumor cells.

• Natural death rate of macrophages is $\delta _{m}$.

• $u_{3}(t)$ acts as a control parameter for macrophages, regulating various aspects of macrophage behavior and function within the immune system. It plays a crucial role in directing the body’s immune response to cancer cells. The function of $u_{3}(t)$ can vary depending on the specific biological context and the particular immune responses under consideration.

• $k_{m}(1-e^{-\eta _{m}C})M$ is the macrophages death induced by chemotherapy, where $k_{m}$ is the rate of chemotherapy induced macrophages death and $\eta _{m}$ is the chemotherapy efficacy coefficient.

• The variable $u_4(t)$ represents a control input or a control function that can be applied to modulate or regulate the constant source rate of dendritic cells, $s_d$. This implies that the production or supply of dendritic cells can be influenced externally. This control input could be in the form of a signal, treatment, medication or any other intervention aimed at enhancing the immune response against tumor cells. Dendritic cells play a crucial role in presenting antigens to activate the immune response. The introduction of $u_{4}$ as a control parameter allows for the modeling of scenarios, where the production of dendritic cells can be strategically increased or decreased. This may represent the impact of external factors such as the administration of drugs or cytokines that influence dendritic cell production. Dendritic cells are central to initiating and regulating immune responses. Modulating their production rate could reflect efforts to the immune system’s activity, possibly to avoid excessive inflammation or to enhance the recognition of tumor antigens.

• The coefficient $\alpha _{d}$ incorporates the activation rate of dendritic cells due to the direct presence of tumor cells, where $g_{d}$ is the half-saturation constant following Michaelis-Menten term.

• The loss of dendritic cells is given by $\delta _{d}$.

• Last term of the fourth equation of (3) represents the decay of dendritic cells induced chemotherapy. $\eta _{d}$ is the chemotherapy efficacy coefficient and $k_{d}$ is the rate of chemotherapy induced dendritic cells decay.

• Chemotherapy decays at a rate is proportional to its concentration $\gamma$ [16].

• $v_c(t)$ is a dynamic control parameter that regulates the administration of chemotherapeutic drugs in a tumor-immune interaction system. It is an important component of personalized cancer treatment strategies, aiming to strike a balance between effectively targeting the tumor and minimizing harm to healthy tissues while considering the individual characteristics of patient and the tumor’s behavior over time.

• The chemotherapy interacts each of the cell T, L, M and D through a term of the form $K_{Y}(1-e^{-\eta _{Y}C})Y$ [17]. This term indicates the fractional killing rate of the drug.

3 Dynamical overview

In this section, we shall study the stability analysis around the biologically feasible steady states to understand the dynamics of our control system (3). To do this, we assumed that $u_{2}(t)=u_{2},~u_{3}(t)=u_{3},~u_{4}(t)=u_{4},~v_{c}(t)=v_{c}$, where $u_{2},~u_{3},~u_{4}$ and $v_{c}$ are all constants. The system has the following two steady states:

(i) Tumor-free singular point is $E^{0} (0,L^{0},M^{0},D^{0},C^{0})$, where

$$\begin{aligned} M^{0}= & {} \frac{1}{\delta _{m}+k_{m}\big (1-e^{-\frac{\eta _{m}v_{c}}{\gamma }} \big )}\Big [s_{m}+u_{3}+\frac{\alpha _{m}L^{0}}{g_{m1}(g_{m}+L^{0})} \Big ], \\ D^{0}= & {} \frac{s_{d}u_{4}}{\delta _{d}+k_{d}\big (1-e^{-\frac{\eta _{d}v_{c}}{\gamma }} \big )}, \\ C^{0}= & {} \frac{v_{c}}{\gamma }, \end{aligned}$$

and $L^{0}$ is defined in following quadratic form:

$$\begin{aligned} n_{1}(L^{0})^{2}+n_{2}L^{0}+n_{3} = 0, \end{aligned}$$

(5)

with

$$\begin{aligned} n_{1}=\, & {} \delta _{l}+k_{l}\big (1-e^{-\frac{\eta _{l}v_{c}}{\gamma }}\big ), \\ n_{2}=\, & {} n_{1}g_{l}-u_{2}, \\ n_{3}=\, & {} -(u_{2}g_{l}+\alpha _{l}D^{0}). \end{aligned}$$

Since $n_{3} < 0$, then, above second degree Eq. (5) has a unique positive root is given by

$$\begin{aligned} L^{0}=\, & {} \frac{-n_{2}+\sqrt{n_{2}^{2}-4n_{1}n_{3}}}{2n_{1}}. \end{aligned}$$

To know the dynamical nature around the singular point E(T,  L,  M,  D,  C), first, we calculate the Jacobian matrix $J_{E}$ is derived as

$$\begin{aligned} J_{E}=\, & {} \left( \begin{array}{ccccc} a_{11} &{} a_{12} &{} a_{13} &{} 0 &{} a_{15}\\ 0 &{} a_{22} &{} 0 &{} a_{24} &{} a_{25} \\ a_{31} &{} a_{32} &{} a_{33} &{} 0 &{} a_{35} \\ a_{41} &{} 0 &{} 0 &{} a_{44} &{} a_{45} \\ 0 &{} 0 &{} 0 &{} 0 &{} a_{55}\\ \end{array} \right) , \end{aligned}$$

where

$$\begin{aligned} a_{11}=\, & {} r_{T}-2r_{T}b_{T}T-\frac{(\alpha _{T}M+\gamma _{T}L)}{g_{T}+M}-k_{T}\big (1-e^{-\eta _{T}C}\big ),\\ a_{12}=\, & {} -\frac{\gamma _{T}T}{g_{T}+M},\\ a_{13}=\, & {} -\frac{(g_{T}\alpha _{T}-\gamma _{T}L)T}{(g_{T}+M)^{2}},\\ a_{15}=\, & {} -\eta _{T}k_{T}Te^{-\eta _{T}C}, \\ a_{22}=\, & {} -\frac{\alpha _{l}D}{(g_{l}+L)^{2}}-\delta _{l}-k_{l}\big (1-e^{-\eta _{l}C}\big ),\\ a_{24}=\, & {} \frac{\alpha _{l}}{g_{l}+L},\\ a_{25}=\, & {} -\eta _{l}k_{l}Le^{-\eta _{l}C}, \\ a_{31}=\, & {} -\frac{\alpha _{m}L}{(g_{m}+L)(g_{m1}+T)^{2}}-\gamma _{m}M,\\ a_{32}=\, & {} \frac{\alpha _{m}g_{m}}{(g_{m}+L)^{2}(g_{m1}+T)},\\ a_{33}=\, & {} -\gamma _{m}T-\delta _{m}-k_{m}\big (1-e^{-\eta _{m}C}\big ),\\ a_{35}=\, & {} -\eta _{m}k_{m}Me^{-\eta _{m}C}, \\ a_{41}=\, & {} \frac{g_{d}\alpha _{d}}{(g_{d}+T)^{2}},\\ a_{44}=\, & {} -\delta _{d}-k_{d}\big (1-e^{-\eta _{d}C}\big ), \\ a_{45}=\, & {} -\eta _{d}k_{d}De^{-\eta _{d}C}, \\ a_{55}=\, & {} -\gamma . \end{aligned}$$

At the tumor-free singular point $E^{0}$, the Jacobian matrix $J_{E^{0}}$ has the following eigenvalues

$$\begin{aligned} \begin{array}{llll} e_{1}^{0} &{}=&{} r_{T}-\frac{\alpha _{T}M^{0}+\gamma _{T}L^{0}}{g_{T}+M^{0}}-k_{T}\big (1-e^{-\frac{\eta _{T}v_{c}}{\gamma }}\big ), \\ e_{2}^{0} &{}=&{} - \frac{\alpha _{l}D^{0}}{(g_{l}+L^{0})^{2}} - \delta _{l} -k_{l}\big (1-e^{-\frac{\eta _{l}v_{c}}{\gamma }}\big ), \\ e_{3}^{0} &{}=&{} -\delta _{m}-k_{m}\big (1-e^{-\frac{\eta _{m}v_{c}}{\gamma }}\big ), \\ e_{4}^{0} &{}=&{} -\delta _{d}-k_{d}\big (1-e^{-\frac{\eta _{d}v_{c}}{\gamma }}\big ), \\ e_{5}^{0} &{}=&{} -\gamma . \end{array} \end{aligned}$$

All the eigenvalues are negative if $e_{1}^{0} < 0$. Therefore, the tumor-free singular point $E^{0}$ is locally asymptotically stable (LAS) if

$$\begin{aligned} r_{T}< & {} \frac{\alpha _{T}M^{0}+\gamma _{T}L^{0}}{g_{T}+M^{0}}+k_{T}\big (1-e^{-\frac{\eta _{T}v_{c}}{\gamma }}\big ). \end{aligned}$$

(ii) Let us assume the interior singular point to be $E^{1}(T^{1},~L^{1},~M^{1},~D^{1},~C^{1})$. To determine this interior singular point, we analyze the conditions $\frac{\textrm{d}T}{\textrm{d}t}=\frac{\textrm{d}L}{\textrm{d}t}=\frac{\textrm{d}M}{\textrm{d}t}=\frac{\textrm{d}D}{\textrm{d}t}=\frac{dC}{\textrm{d}t}=0$. Subsequently, we can express the values of $T^{1},~ L^{1},~ M^{1}, ~D^{1}$ and $C^{1}$ as follows

$$\begin{aligned} C^{1}=\, & {} \frac{v_{c}}{\gamma },~ D^{1} =\, \frac{s_{d}u_{4}(g_{d}+T^{1})+\alpha _{d}T^{1}}{(g_{d}+T^{1})[\delta _{d}+k_{d}(1-e^{\frac{-\eta _{d}v_{c}}{\gamma }})]},~ M^{1} =\, \frac{\gamma _{T}L^{1}+k_{T}g_{T}(1-e^{\frac{-\eta _{T}v_{c}}{\gamma }})-g_{T}r_{T}(1-b_{T}T^{1})}{r_{T} (1-b_{T}T^{1})-\alpha _{T}-k_{T}(1-e^{\frac{-\eta _{T}v_{c}}{\gamma }})},\\ L^{1}=\, & {} \frac{u_{2}-\delta _{l}g_{l}-g_{l}k_{l}(1-e^{\frac{-\eta _{l}v_{c}}{\gamma }})+\sqrt{[\delta _{l}g_{l} -u_{2}+g_{l}k_{l}(1-e^{\frac{-\eta _{l}v_{c}}{\gamma }})]^{2}+4(\alpha _{l}D^{1}+u_{2}g_{l})[\delta _{l} +k_{l}(1-e^{\frac{-\eta _{l}v_{c}}{\gamma }})]}}{2[\delta _{l}+k_{l}(1-e^{\frac{-\eta _{l}v_{c}}{\gamma }})]},\\ \end{aligned}$$

and

$$\begin{aligned} s_{m} + \frac{\alpha _{m}L^{1}}{(g_{m}+L^{1})(g_{m1}+T^{1})}+u_{3}=\, & {} [\gamma _{m}T^{1}+\delta _{m}+k_{m}(1-e^{\frac{-\eta _{m}v_{c}}{\gamma }})]M^{1}. \end{aligned}$$

Obtaining the explicit form of the interior singular point $E^{1}$ analytically from the provided expressions poses a significant challenge. As a result, we determine the singular point through numerical simulation. To evaluate the stability of interior equilibrium point $E^{1}$, we proceed by calculating the variational matrix around the interior equilibrium point $E^{1}$, is defined below

$$\begin{aligned} J(E^{1}) =\, [j_{ij}]=\, & {} \left[ \begin{array}{ccccccc} j_{11} &{} j_{12} &{} j_{13} &{} 0 &{} j_{15} \\ 0 &{} j_{22} &{} 0 &{} j_{24} &{} j_{25} \\ j_{31} &{} j_{32} &{} j_{33} &{} 0 &{} j_{35} \\ j_{41} &{} 0 &{} 0 &{} j_{44} &{} j_{45} \\ 0 &{} 0 &{} 0 &{} 0 &{} j_{55} \\ \end{array} \right] , \end{aligned}$$

where

$$\begin{aligned} j_{11}=\, & {} r_{T}-2r_{T}b_{T}T^{1}-\frac{(\alpha _{T}M^{1}+\gamma _{T}L^{1})}{g_{T}+M^{1}}-k_{T} (1-e^{\frac{-\eta _{T}v_{c}}{\gamma }}), \\ j_{12}=\, & {} -\frac{\gamma _{T}T^{1}}{g_{T}+M^{1}}, \\ j_{13}=\, & {} -\frac{(g_{T}\alpha _{T}-\gamma _{T}L^{1})T^{1}}{(g_{T}+M^{1})^{2}}, \\ j_{15}=\, & {} -\eta _{T}k_{T}T^{1}e^{\frac{-\eta _{T}v_{c}}{\gamma }}, \\ j_{22}=\, & {} -\frac{\alpha _{l}D^{1}}{(g_{l}+L^{1})^{2}}-\delta _{l}-k_{l}(1-e^{\frac{-\eta _{l}v_{c}}{\gamma }}), \\ j_{24}=\, & {} \frac{\alpha _{l}}{g_{l}+L^{1}}, \\ j_{25}=\, & {} -\eta _{l}k_{l}L^{1}e^{\frac{-\eta _{l}v_{c}}{\gamma }}, \\ j_{31}=\, & {} -\frac{\alpha _{m}L^{1}}{(g_{m}+L^{1})(g_{m1}+T^{1})^{2}}-\gamma _{m}M^{1}, \\ j_{32}=\, & {} \frac{\alpha _{m}g_{m}}{(g_{m}+L^{1})^{2}(g_{m1}+T^{1})}, \\ j_{33}=\, & {} -\gamma _{m}T^{1}-\delta _{m}-k_{m}(1-e^{\frac{-\eta _{m}v_{c}}{\gamma }}), \\ j_{35}=\, & {} -\eta _{m}k_{m}M^{1}e^{\frac{-\eta _{m}v_{c}}{\gamma }}, \\ j_{41}=\, & {} \frac{g_{d}\alpha _{d}}{(g_{d}+T^{1})^{2}}, \\ j_{44}=\, & {} -\delta _{d}-k_{d}(1-e^{\frac{-\eta _{d}v_{c}}{\gamma }}), \\ j_{45}=\, & {} -\eta _{d}k_{d}D^{1}e^{\frac{-\eta _{d}v_{c}}{\gamma }}, \\ j_{55}= & {} -\gamma . \end{aligned}$$

The characteristic equation at the interior singular point $E^{1}(T^{1},~L^{1},~M^{1},~D^{1},~C^{1})$ is

$$\begin{aligned} \phi ^{5} + B_{1}\phi ^{4} + B_{2}\phi ^{3} + B_{3}\phi ^{2} + B_{4}\phi + B_{5} = 0, \end{aligned}$$

where

$$\begin{aligned} B_{1}= & {} -\sum \limits _{i=1}^{5} j_{ii}, B_{2} = \sum \limits _{i,j=1}^{5} j_{ii}j_{jj}-\sum \limits _{i,j=1}^{5} j_{ij}j_{ji}, B_{3} = \sum \limits _{i,j,k=1}^{5} j_{ij}j_{ji}j_{kk}-\sum \limits _{i,j,k=1}^{5} j_{ii}j_{jj}j_{kk}-\sum \limits _{i,j,k=1}^{5} j_{ij}j_{jk}j_{ki}, \\ B_{4}= & {} \sum \limits _{i,j,k,l=1}^{5} j_{ii}j_{jj}j_{kk}j_{ll}+\sum \limits _{i,j,k,l=1}^{5} j_{ij}j_{ji}j_{ki}j_{ll}-\sum \limits _{i,j,k,l=1}^{5} j_{ij}j_{ji}j_{kl}j_{lk}-\sum \limits _{i,j,k,l=1}^{5} j_{ij}j_{ji}j_{kk}j_{ll}-\sum \limits _{i,j,k,l=1}^{5} j_{ij}j_{jk}j_{kl}j_{li}, \\ B_{5}= & {} -det(J(E^{1})). \end{aligned}$$

For all of the expressions mentioned above, it holds that $i \ne j \ne k \ne l$. According to the Routh-Hurwitz condition, all roots of the characteristic equation have negative or negative real parts if $B_{1}> 0,~B_{5}> 0,~B_{1}B_{2} - B_{3}> 0,~(B_{1}B_{2} - B_{3})B_{3} - B_{1}(B_{1}B_{4}-B_{5}) > 0$ and $(B_{1}B_{2}-B_{3})(B_{3}B_{4}-B_{2}B_{5})+(B_{1}B_{4}-B_{5})(B_{5}-B_{1}B_{4}) > 0$. If the eigenvalues have negative real parts, then, the interior singular point is considered stable.

4 Optimal control problem

This section describes the control problem in our model (3) to minimize the tumor cell population and maximize the immune components. Thus, we assume our control set $\mathbb {U}$ as follows

$$\begin{aligned} \mathbb {U}=\{u_{2}(t),~u_{3}(t)~,u_{4}(t),~v_{c}(t) ~\text {are piecewise continuous}:~ 0 \le u_{2}(t),~u_{3}(t)~,u_{4}(t),~v_{c}(t), ~\forall ~ t \in [0,t_{f}]\}. \end{aligned}$$

We would like to maximize the immune components (CD8+T cells and macrophages) to eliminate the tumor cell population. Therefore, we define the following objective functional

$$\begin{aligned} J(u_{2},~u_{3}~,u_{4},~v_{c})=\int _{0}^{t_{f}} [T(t)+\frac{1}{2}\epsilon _{2}u_{2}^{2}+\frac{1}{2}\epsilon _{3}u_{3}^{2}+\frac{1}{2} \epsilon _{4}u_{4}^{2}+\frac{1}{2}\epsilon _{c}v_{c}^{2}] dt, \end{aligned}$$

(6)

where $\epsilon _{2},~\epsilon _{3},~\epsilon _{4}$ and $\epsilon _{c}$ are constants. We must have to show that J is concave and its minimum value can be obtained. We suggest the objective functional J is a function of u, then, our main aim is to characterize the optimal control $u^{*}(t)=(u^{*}_{2}(t),~u^{*}_{3}(t)~,u^{*}_{4}(t),~v^{*}_{c}(t))$ in such a way that

$$\begin{aligned} J(u^{*})=\max \limits _{0 \le u}\{J(u_{2},~u_{3}~,u_{4},~v_{c})\}. \end{aligned}$$

5 Existence of optimal control

In this section, we shall prove the existence property of optimal control for the given system with the control set $\mathbb {U}$ due to the method described by Fleming & Rishel [18]. For this, we need to show that in a finite time interval, the solution of each state equations of the system is bounded. Thus, we calculate the upper bounds (super-solutions) of T, L, M, D and C for the system (3). The first equation of (3) can be written as

$$\begin{aligned} \frac{\textrm{d}T}{\textrm{d}t}\le & {} r_{T}T(1-b_{T}T), \end{aligned}$$

which implies that

$$\begin{aligned} T\le & {} \frac{m_{1}\frac{1}{b_{T}}}{m_{1}+e^{-r_{T}t}},~~~~~ m_{1}\text { being an arbitrary constant.} \end{aligned}$$

Then, we have

$$\begin{aligned} \limsup \limits _{t\rightarrow \infty } T(t)\le & {} \frac{1}{b_{T}} = T_{\max } ~(\text {say}). \end{aligned}$$

Third equation for the system (3) can be written as

$$\begin{aligned} \frac{\textrm{d}M}{\textrm{d}t}= & {} s_{m} + \frac{\alpha _{m}}{g_{m1}+T} - \frac{\alpha _{m}g_{m}}{(g_{m}+L)(g_{m1}+T)} - \gamma _{m}MT- \delta _{m}M +u_{3}-k_{m}(1-e^{-\eta _{m}C})M \\\le & {} s_{m}+\frac{\alpha _{m}}{g_{m1}} -\delta _{m}M +u_{3}, \end{aligned}$$

which implies that

$$\begin{aligned} \frac{\textrm{d}M}{\textrm{d}t}+ \delta _{m}M\le & {} \frac{(s_{m}+u_{3})g_{m1}+\alpha _{m}}{g_{m1}}. \end{aligned}$$

After solving above inequality, we have

$$\begin{aligned} M\le & {} \frac{(s_{m}+u_{3})g_{m1}+\alpha _{m}}{g_{m1}\delta _{m}} + m_{3}e^{-\delta _{m}t},~~~~~ m_{3}\text { being an arbitrary constant.} \end{aligned}$$

For $t>0$, we get

$$\begin{aligned} \limsup \limits _{t\rightarrow \infty } M(t)\le & {} \frac{(s_{m}+u_{3})g_{m1}+\alpha _{m}}{g_{m1}\delta _{m}} = M_{\max } ~(\text {say}). \end{aligned}$$

Now, from the fourth equation of (3), we have

$$\begin{aligned} \frac{\textrm{d}D}{\textrm{d}t}= & {} (s_{d}u_{4}+\alpha _{d})-\frac{\alpha _{d}g_{d}}{g_{d}+T}-\delta _{d}D, \end{aligned}$$

which leads to

$$\begin{aligned} \frac{\textrm{d}D}{\textrm{d}t} + \delta _{d}D\le & {} (s_{d}u_{4}+\alpha _{d}). \end{aligned}$$

For $t>0$, we get

$$\begin{aligned} \limsup \limits _{t\rightarrow \infty } D(t)\le & {} \frac{s_{d}u_{4}+\alpha _{d}}{\delta _{d}} = D_{\max } ~(\text {say}). \end{aligned}$$

By using the upper bound of D(t), we get the following inequality

$$\begin{aligned} \frac{\textrm{d}L}{\textrm{d}t}\le & {} \frac{\alpha _{l}D_{\max }}{g_{l}+L} - \delta _{l} L + u_{2} \\ \frac{\textrm{d}L}{\textrm{d}t}+ \delta _{l}L\le & {} \frac{\alpha _{l}D_{\max }}{g_{l}} + u_{2}. \end{aligned}$$

Solving the above inequality for $t>0$, we have

$$\begin{aligned} \limsup \limits _{t\rightarrow \infty } L(t)\le & {} \frac{\alpha _{l}D_{\max }+u_{2}g_{l}}{g_{l}\delta _{l}} = L_{\max } ~(\text {say}). \end{aligned}$$

Again, the last equation of (3) implies that

$$\begin{aligned} \frac{dC}{\textrm{d}t}\le & {} v_{c}. \end{aligned}$$

If $C_{\max }$ be an upper bound of solution of C then $C_{\max } = v_{c}t + m_{5}$, ($m_{5}$ being an arbitrary constant). By using the bounds of $T_{\max },~L_{\max },~M_{\max },~D_{\max },~C_{\max }$, we have a set of upper bound solutions for the system (3). By denoting these notations $\overline{T},~\overline{L},~\overline{M},~\overline{D}$ and $\overline{C}$, we have

$$\begin{aligned} \begin{array}{llll} \frac{d\overline{T}}{\textrm{d}t} &{}=&{} r_{T}\overline{T}, \\ \frac{d\overline{L}}{\textrm{d}t} &{}=&{} \alpha _{l}\overline{D}+u_{2}, \\ \frac{d\overline{M}}{\textrm{d}t} &{}=&{} s_{m}+\alpha _{m}\overline{L}+u_{3}, \\ \frac{d\overline{D}}{\textrm{d}t} &{}=&{} s_{d}u_{4}+\alpha _{d}\overline{T}, \\ \frac{d\overline{C}}{\textrm{d}t} &{}=&{} v_{c}, \end{array} \end{aligned}$$

(7)

are bounded in a finite time interval. The above system can be written as

$$\begin{aligned} \left( \begin{array}{ccccc} \overline{T} \\ \overline{L} \\ \overline{M} \\ \overline{D} \\ \overline{C} \end{array} \right) '= & {} \left( \begin{array}{ccccc} r_{T} &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} \alpha _{l} &{} 0 \\ 0 &{} \alpha _{m} &{} 0 &{} 0 &{} 0 \\ \alpha _{d} &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{array} \right) \left( \begin{array}{ccccc} \overline{T} \\ \overline{L} \\ \overline{M} \\ \overline{D} \\ \overline{C} \end{array} \right) + \left( \begin{array}{ccccc} 0 \\ u_{2} \\ s_{m}+u_{3} \\ s_{d}u_{4} \\ v_{c} \end{array} \right) . \end{aligned}$$

We found a linear system with bounded coefficients, then the super-solutions $\overline{T},~\overline{L},~\overline{M},~\overline{D},~\overline{C}$ are uniformly bounded. Now, we use the boundedness of solutions of each state variables for established the existence of an optimal control.

Theorem 1

For the given optimal control problem and the objective functional $J(u_{2},~u_{3}~,u_{4},~v_{c})=\int _{0}^{t_{f}} [T(t)+\frac{1}{2}\epsilon _{2}u_{2}^{2}+\frac{1}{2}\epsilon _{3}u_{3}^{2} +\frac{1}{2}\epsilon _{4}u_{4}^{2}+\frac{1}{2}\epsilon _{c}v_{c}^{2}] dt$, with the control set

$$\begin{aligned} \mathbb {U}=\{u_{2}(t),~u_{3}(t),~u_{4}(t),~v_{c}(t) ~\text {are piecewise continuous}:~ \le u_{2}(t),~u_{3}(t),~u_{4}(t),~v_{c}(t), ~\forall ~ t \in [0,t_{f}]\}, \end{aligned}$$

subject to state equations with initial solutions $T(0)=T_{0},~L(0)=L_{0},~M(0)=M_{0},~D(0)=D_{0},~C(0)=C_{0}$, there exists an optimal control $u^{*}(t) \in \mathbb {U}$, which minimizes $J(u^{*})$, that is,

$$\begin{aligned} J(u^{*})=\max \limits _{0 \le u}\{J(u_{2},~u_{3},~u_{4},~v_{c})\}, \end{aligned}$$

given by the following conditions are satisfied:

• (1) The admissible control set $\mathbb {U}$, the optimal control u(t) with initial solutions along with each of the given state variables are non-empty.

• (2) The admissible optimal control set $\mathbb {U}$ is closed and convex.

• (3) By adding the sum of bounded control, right hand side of given system (3) is continuous and bounded above and state equation can be expressed as a linear function of u with coefficients depend on sufficient time interval and the state variables.

• (4) The integrand of objective functional J(u) is concave on $\mathbb {U}$ and bounded by $c_{1}+c_{2}|u_{2}|^{2}+c_{3}|u_{3}|^{2}+c_{4}|u_{4}|^{2}+c_{c}|v_{c}|^{2}$.

Proof

Due to the theory developed by Fleming and Rishel [18], we prove the above theorem.

• (1) An optimal control set $\mathbb {U}$ is continuous and the coefficients of given model are bounded. Also, in the finite time interval, solutions of the given system are bounded.

• (2) By definition, $\mathbb {U}$ is closed and convex.

• (3) The right hand side of given optimal control system is continuous. Let $\sigma (t,X)$ be the right hand side of (3) excluding terms of $u_{2},~u_{3},~u_{4},~v_{c}$. Then,

  $$\begin{aligned} H(t,X,u_{2},u_{3},u_{4},~v_{c})= & {} \sigma (t,X)+\left( \begin{array}{ccccc} 0 \\ u_{2} \\ u_{3} \\ s_{d} u_{4} \\ v_{c} \end{array} \right) , \end{aligned}$$

  where $X=[T(t),~L(t),~M(t),~D(t),~C(t)]^{T}$. Considering the upper bounds of solutions, we get

  $$\begin{aligned} |H(t,X,u_{2},u_{3},u_{4},~v_{c})|\le & {} \left| \left( \begin{array}{ccccc} r_{T} &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} \alpha _{l} &{} 0 \\ 0 &{} \alpha _{m} &{} 0 &{} 0 &{} 0 \\ \alpha _{d} &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{array} \right) \left( \begin{array}{ccccc} T \\ L \\ M \\ D \\ C \end{array} \right) \right| + \left| \begin{array}{ccccc} 0 \\ u_{2} \\ u_{3} \\ s_{d} u_{4} \\ v_{c} \end{array} \right| \\\le & {} H_{1}(|X|+|u|), \end{aligned}$$

  with $H_{1}$ depends on the coefficients of the system.

• (4) It can be noted that in $\mathbb {U}$, the integrand of J(u) is concave. Also, $T(t)+\frac{1}{2}\epsilon _{2}u_{2}^{2}+\frac{1}{2}\epsilon _{3}u_{3}^{2} +\frac{1}{2}\epsilon _{4}u_{4}^{2}+\frac{1}{2}\epsilon _{c}v_{c}^{2} \le c_{1}+c_{2}|u_{2}|^{2}+c_{3}|u_{3}|^{2}+c_{4}|u_{4}|^{2}+c_{c}|v_{c}|^{2}$, where $c_{1}$ is the upper bound of T(t) and depends on T(t),  L(t),  M(t),  D(t),  C(t) and $c_{c}=\frac{\epsilon _{c}}{2}, ~c_{i}=\frac{\epsilon _{i}}{2}$ for $i =$ 2, 3, 4.

  Hence, all conditions of the theorem are proved.$\hfill\square$

6 Characterization of optimal control

We use the theory of calculus of variation for prove the necessary conditions of given optimal control problem. To determine the characterization of optimal control, we employ the Pontryagin’s Maximum Principle [25]. To perform the necessary conditions, at first, we define the Hamiltonian as

$$\begin{aligned} \mathbb {H}&= {} T(t)+\frac{1}{2}\epsilon _{c}(v_{c}(t))^{2}+\frac{1}{2}\epsilon _{2}(u_{2}(t))^{2} +\frac{1}{2}\epsilon _{3}(u_{3}(t))^{2}+\frac{1}{2}\epsilon _{4}(u_{4}(t))^{2} + A_{1} \Big [r_{T}T (1-b_{T}T) - \frac{(\alpha _{T}M+\gamma _{T}L)T}{g_{T}+M} \\&\quad- {} k_{T}(1-e^{-\eta _{T}C})T\Big ] + A_{2}\Big [\frac{\alpha _{l}D}{g_{l}+L} - \delta _{l}L + u_{2}(t)-k_{l}(1-e^{-\eta _{l}C})L\Big ] +A_{3}\Big [s_{m} + \frac{\alpha _{m}L}{(g_{m}+L)}\cdot \frac{1}{(g_{m1}+T)} \\&\quad- {} \gamma _{m}M T- \delta _{m}M + u_{3}(t)-k_{m}(1-e^{-\eta _{m}C})M \Big ] + A_{4}\Big [s_{d}u_{4}(t) + \frac{\alpha _{d}T}{g_{d}+T} - \delta _{d}D - k_{d}(1-e^{-\eta _{d}C})D\Big ] \\&\quad+ {} A_{5} [-\gamma C + v_{c}(t)]. \end{aligned}$$

Since the controls $u_{2}(t),~u_{3}(t),~u_{4}(t)$ and $v_{c}(t)$ are bounded, we define the Lagrangian as

$$\begin{aligned} \mathbb {L}&= {} \mathbb {H} + Q_{1}(t)v_{c}(t)-Q_{2}(t)(1-v_{c}(t))+ Q_{3}(t)u_{2}(t)-Q_{4}(t)(1-u_{2}(t))+ Q_{5}(t)u_{3}(t)-Q_{6}(t)(1-u_{3}(t)) \\&\quad+ {} Q_{7}(t)u_{4}(t)-Q_{8}(t)(1-u_{4}(t)), \end{aligned}$$

where $A_{i}(t)~(i=1,2,3,4,5)$ are adjoint variables and the penalty multipliers $Q_{i}(t) \ge 0$ satisfy the equations

$$\begin{aligned} Q_{1}(t)v_{c}(t)= & {} 0, \\ Q_{2}(t)(1-v_{c}(t))= & {} 0, \end{aligned}$$

at the optimal control $v_{c}^{*}(t)$;

$$\begin{aligned} Q_{3}(t)u_{2}(t)= & {} 0, \\ Q_{4}(t)(1-u_{2}(t))= & {} 0, \end{aligned}$$

at the optimal control $u_{2}^{*}(t)$;

$$\begin{aligned} Q_{5}(t)u_{3}(t)= & {} 0, \\ Q_{6}(t)(1-u_{3}(t))= & {} 0, \end{aligned}$$

at the optimal control $u_{3}^{*}(t)$ and

$$\begin{aligned} Q_{7}(t)u_{4}(t)= & {} 0, \\ Q_{8}(t)(1-u_{4}(t))= & {} 0, \end{aligned}$$

at the optimal control $u_{4}^{*}(t)$.

Theorem 2

For the control $u^{*}$ with corresponding solutions of state variables at interior steady state $E^{1}(T^{1},~L^{1},~M^{1},~D^{1},~C^{1})$ that minimizes the objective functional J(u), there exists costates $A_{i}(t)$; ($i =$ 1–5) satisfying the following equations

$$\begin{aligned} \begin{array}{llllllllll} A_{1}^{'} &{}=&{} -\Big [1+A_{1}\Big \{r_{T}(1-2b_{T}T)-\frac{\alpha _{T}M+\gamma _{T}L}{g_{T}+M}-k_{T}(1-e^{-\eta _{T}C}) \Big \}-A_{3}\Big \{\frac{\alpha _{m}L}{(g_{m}+L)\cdot (g_{m1}+T)^{2}}+\gamma _{m}M \Big \} \\ &&\quad{}+{} A_{4}\frac{\alpha _{d}g_{d}}{(g_{d}+T)^{2}} \Big ], \\ A_{2}^{'} &{}=&{} -\Big [-A_{1}\frac{\gamma _{T}T}{g_{T}+M} -A_{2} \Big \{\frac{\alpha _{l}D}{(g_{l}+L)^{2}}+\delta _{l}+k_{l}(1-e^{-\eta _{l}C}) \Big \} + A_{3}\frac{\alpha _{m}g_{m}}{(g_{m}+L)^{2}(g_{m1}+T)} \Big ], \\ A_{3}^{'} &{}=&{} -\Big [-A_{1}\frac{(\alpha _{T}g_{T}-\gamma _{T}L)T}{(g_{T}+M)^{2}} -A_{3}(\gamma _{m}T+\delta _{m}+k_{m}(1-e^{-\eta _{m}C})) \Big ], \\ A_{4}^{'} &{}=&{} -\Big [A_{2}\frac{\alpha _{l}}{g_{l}+L}-A_{4}(\delta _{d}+k_{d}(1-e^{-\eta _{d}C}) \Big ], \\ A_{5}^{'} &{}=&{} A_{1}\eta _{T}k_{T}Te^{-\eta _{T}C}+A_{2}\eta _{l}k_{l}L e^{-\eta _{l}C}+A_{3}\eta _{m}k_{m}Me^{-\eta _{m}C}+A_{4}\eta _{d}k_{d}De^{-\eta _{d}C}+A_{5} \gamma , \end{array} \end{aligned}$$

(8)

where $A_{i}(t_{f})=0$; (i = 1–5) known as transversality terminal conditions. Also, $v_{c}^{*},~u_{2}^{*},~u_{3}^{*},~u_{4}^{*}$ are represented by

$$\begin{aligned} v_{c}^{*}= & {} \min \Big (1,\Big (\frac{-A_{5}}{\epsilon _{c}} \Big )^{+}\Big ), \\ u_{2}^{*}= & {} \min \Big (1,\Big (\frac{-A_{2}}{\epsilon _{2}} \Big )^{+}\Big ), \\ u_{3}^{*}= & {} \min \Big (1,\Big (\frac{-A_{3}}{\epsilon _{3}} \Big )^{+}\Big ), \\ u_{4}^{*}= & {} \min \Big (1,\Big (\frac{-A_{4}s_{d}}{\epsilon _{4}} \Big )^{+}\Big ). \end{aligned}$$

Proof

We use Pontryagin’s Maximum Principle [25], to obtain the costates and transversality conditions. By differentiating Lagrangian $\mathbb {L}$ with reference to given state equations, we get $A^{'}_{1}=-\frac{\partial \mathbb {L}}{\partial T},~A^{'}_{2}=-\frac{\partial \mathbb {L}}{\partial L},~A^{'}_{3}=-\frac{\partial \mathbb {L}}{\partial M},~A^{'}_{4}=-\frac{\partial \mathbb {L}}{\partial D},~A^{'}_{5}=-\frac{\partial \mathbb {L}}{\partial C}$. To obtain the optimal controls of $v_{c}^{*},~u_{2}^{*},~u_{3}^{*},~u_{4}^{*}$, we set $\frac{\partial \mathbb {L}}{\partial v_{c}} = \frac{\partial \mathbb {L}}{\partial u_{2}} = \frac{\partial \mathbb {L}}{\partial u_{3}} = \frac{\partial \mathbb {L}}{\partial u_{4}} = 0$. Then, we have

$$\begin{aligned} \epsilon _{c}v_{c}+A_{5}+Q_{1}(t)+Q_{2}(t)= & {} 0, \\ \epsilon _{2}u_{2}+A_{2}+Q_{3}(t)+Q_{4}(t)= & {} 0, \\ \epsilon _{3}u_{3}+A_{3}+Q_{5}(t)+Q_{6}(t)= & {} 0, \\ \epsilon _{4}u_{4}+A_{4}s_{d}+Q_{7}(t)+Q_{8}(t)= & {} 0. \end{aligned}$$

By using standard optimality condition, we have

$$\begin{aligned} v_{c}^{*}= & {} \min \Big (1,\Big (\frac{-A_{5}}{\epsilon _{c}} \Big )^{+}\Big ), \\ u_{2}^{*}= & {} \min \Big (1,\Big (\frac{-A_{2}}{\epsilon _{2}} \Big )^{+}\Big ), \\ u_{3}^{*}= & {} \min \Big (1,\Big (\frac{-A_{3}}{\epsilon _{3}} \Big )^{+}\Big ), \\ u_{4}^{*}= & {} \min \Big (1,\Big (\frac{-A_{4}s_{d}}{\epsilon _{4}} \Big )^{+}\Big ), \end{aligned}$$

where the notation is

$$\begin{aligned} s^{+}= & {} \left\{ \begin{array}{cccc} &{}s,&{}~\text {if}~&{} s \ge 0 \\ &{}0,&{}~\text {if}~&{} s < 0. \end{array} \right. \end{aligned}$$

Hence, the proof. $\hfill\square$

After getting the explicit expression of the optimal controls $u_{2}^{*},~u_{3}^{*},~u_{4}^{*},~v_{c}^{*}$, the adjoint or costate equations coupled with the state system including transversality conditions, we obtain optimality system as follows

$$\begin{aligned} \begin{array}{llllllllll} \frac{\textrm{d}T}{\textrm{d}t} &{}=&{} r_{T}T (1-b_{T}T) - \frac{(\alpha _{T}M+\gamma _{T}L)T}{g_{T}+M}-k_{T}(1-e^{-\eta _{T}C})T, \\ \frac{\textrm{d}L}{\textrm{d}t} &{}=&{} \frac{\alpha _{l}D}{g_{l}+L} - \delta _{l}L + \min \Big (1,\Big (\frac{-A_{2}}{\epsilon _{2}} \Big )^{+}\Big ) - k_{l}(1-e^{-\eta _{l}C})L, \\ \frac{\textrm{d}M}{\textrm{d}t} &{}=&{} s_{m} + \frac{\alpha _{m}L}{(g_{m}+L)}\cdot \frac{1}{(g_{m1}+T)} - \gamma _{m}M T- \delta _{m}M + \min \Big (1,\Big (\frac{-A_{3}}{\epsilon _{3}} \Big )^{+}\Big ) - k_{m}(1-e^{-\eta _{m}C})M, \\ \frac{\textrm{d}D}{\textrm{d}t} &{}=&{} s_{d}\Big (\min \Big (1,\Big (\frac{-A_{4}s_{d}}{\epsilon _{4}} \Big )^{+}\Big ) \Big ) + \frac{\alpha _{d}T}{g_{d}+T} - \delta _{d}D - k_{d}(1-e^{-\eta _{d}C})D, \\ \frac{dC}{\textrm{d}t} &{}=&{} -\gamma C + \min \Big (1,\Big (\frac{-A_{5}}{\epsilon _{c}} \Big )^{+}\Big ), \\ A_{1}^{'} &{}=&{} -\Big [1+A_{1}\Big \{r_{T}(1-2b_{T}T)-\frac{\alpha _{T}M+\gamma _{T}L}{g_{T}+M}-k_{T}(1-e^{-\eta _{T}C}) \Big \}-A_{3}\Big \{\frac{\alpha _{m}L}{(g_{m}+L)\cdot (g_{m1}+T)^{2}}+\gamma _{m}M \Big \}\\ &&\quad{}+{} A_{4}\frac{\alpha _{d}g_{d}}{(g_{d}+T)^{2}} \Big ], \\ A_{2}^{'} &{}=&{} -\Big [-A_{1}\frac{\gamma _{T}T}{g_{T}+M} -A_{2} \Big \{\frac{\alpha _{l}D}{(g_{l}+L)^{2}}+\delta _{l}+k_{l}(1-e^{-\eta _{l}C}) \Big \} + A_{3}\frac{\alpha _{m}g_{m}}{(g_{m}+L)^{2}(g_{m1}+T)} \Big ], \\ A_{3}^{'} &{}=&{} -\Big [-A_{1}\frac{(\alpha _{T}g_{T}-\gamma _{T}L)T}{(g_{T}+M)^{2}} -A_{3}(\gamma _{m}T+\delta _{m}+k_{m}(1-e^{-\eta _{m}C})) \Big ], \\ A_{4}^{'} &{}=&{} -\Big [A_{2}\frac{\alpha _{l}}{g_{l}+L}-A_{4}(\delta _{d}+k_{d}(1-e^{-\eta _{d}C})) \Big ], \\ A_{5}^{'} &{}=&{} A_{1}\eta _{T}k_{T}Te^{-\eta _{T}C}+A_{2}\eta _{l}k_{l}Le^{-\eta _{l}C}+A_{3} \eta _{m}k_{m}Me^{-\eta _{m}C}+A_{4}\eta _{d}k_{d}De^{-\eta _{d}C}+A_{5} \gamma , \end{array} \end{aligned}$$

(9)

where $T(0)=T_{0},~L(0)=L_{0},~M(0)=M_{0},~D(0)=D_{0},~C(0)=C_{0}$ and $A_{i}(t_{f})=0$ for $i =$ 1–5.

7 Uniqueness of optimal control

By the boundedness property of the given optimal control system, the state equations and adjoint or costate equations both have bounded coefficients. For the small time interval, we shall prove the uniqueness of solution of the optimal system (3).

Theorem 3

The solution of the optimal control system is unique for sufficient small time interval $t_{f}$.

Proof

Let us consider $(T,~L,~M,~D,C,~A_{1},~A_{2},~A_{3},~A_{4},~A_{5})$ and $(\overline{T}, ~\overline{L}, ~\overline{M}, ~\overline{D},~\overline{C},~ {\overline{A}}_{1},~ {\overline{A}}_{2}, ~{\overline{A}}_{3},~ {\overline{A}}_{4},~{\overline{A}}_{5})$ are two distinct solutions of the optimal system. Suppose, $\lambda >0$ be such that $T=e^{\lambda t}p_{1},~ L=e^{\lambda t}p_{2}, ~M=e^{\lambda t}p_{3}, ~D=e^{\lambda t}p_{4},~C=e^{\lambda t}p_{5} ~A_{1}=e^{-\lambda t}q_{1}, ~ A_{2}=e^{-\lambda t}q_{2}, ~A_{3}=e^{-\lambda t}q_{3},~ A_{4}=e^{-\lambda t}q_{4},~ A_{5}=e^{-\lambda t}q_{5}, ~\overline{T}=e^{\lambda t}{\overline{p}}_{1}, ~ \overline{L}=e^{\lambda t}{\overline{p}}_{2},~ \overline{M}=e^{\lambda t}{\overline{p}}_{3}, ~\overline{D}=e^{\lambda t}{\overline{p}}_{4}, ~\overline{C}=e^{\lambda t}{\overline{p}}_{5},~ {\overline{A}}_{1}=e^{-\lambda t}{\overline{q}}_{1}, ~{\overline{A}}_{2}=e^{-\lambda t}{\overline{q}}_{2}, ~{\overline{A}}_{3}=e^{-\lambda t}{\overline{q}}_{3},~ {\overline{A}}_{4}=e^{-\lambda t}{\overline{q}}_{4},~ {\overline{A}}_{5}=e^{-\lambda t}{\overline{q}}_{5}$.

Also, we consider

$$\begin{aligned} v_{c}^{*}(t) = \min \Big (1,\Big (\frac{-e^{-\lambda t}q_{5}}{\epsilon _{c}} \Big )^{+}\Big )&,&\overline{v}_{c}^{*}(t) = \min \Big (1,\Big (\frac{-e^{-\lambda t}\overline{q}_{5}}{\epsilon _{c}} \Big )^{+}\Big ); \\ u_{2}^{*}(t) = \min \Big (1,\Big (\frac{-e^{-\lambda t}q_{2}}{\epsilon _{2}} \Big )^{+}\Big )&,&\overline{u}_{2}^{*}(t) = \min \Big (1,\Big (\frac{-e^{-\lambda t}\overline{q}_{2}}{\epsilon _{2}} \Big )^{+}\Big ); \\ u_{3}^{*}(t) = \min \Big (1,\Big (\frac{-e^{-\lambda t}q_{3}}{\epsilon _{3}} \Big )^{+}\Big )&,&\overline{u}_{3}^{*}(t) = \min \Big (1,\Big (\frac{-e^{-\lambda t}\overline{q}_{3}}{\epsilon _{3}} \Big )^{+}\Big ); \\ u_{4}^{*}(t) = \min \Big (1,\Big (\frac{-e^{-\lambda t}q_{4}s_{d}}{\epsilon _{4}} \Big )^{+}\Big )&,&\overline{u}_{4}^{*}(t) = \min \Big (1,\Big (\frac{-e^{-\lambda t}\overline{q}_{4}s_{d}}{\epsilon _{4}} \Big )^{+}\Big ). \end{aligned}$$

We use $T=e^{\lambda t}p_{1}$ in first equation of the optimality system (9); then, the state equation leads to

$$\begin{aligned} \dot{p_{1}}+(\lambda -r_{T})p_{1}= & {} -r_{T}b_{T}e^{\lambda t}p_{1}^{2}-\frac{\alpha _{T}p_{1}p_{3}e^{\lambda t}}{g_{T}+e^{\lambda t} p_{3}}-\frac{\gamma _{T}p_{1}p_{2}e^{\lambda t}}{g_{T}+e^{\lambda t} p_{3}}-k_{T}p_{1}(1-e^{-\eta _{T}p_{5}e^{\lambda t}}), \end{aligned}$$

with $\dot{p} \equiv \frac{dp}{\textrm{d}t}$. Similarly, after putting $A_{1}=e^{-\lambda t}q_{1}$ in sixth equation of (9), we have

$$\begin{aligned} -\dot{q_{1}}+\lambda q_{1} &= {} e^{\lambda t} + q_{1}\Big \{r_{T}(1-2b_{T}e^{\lambda t} p_{1})-\frac{(\alpha _{T}p_{3}+\gamma _{T}p_{2})e^{\lambda t}}{g_{T}+e^{\lambda t}p_{3}} - k_{T}(1-e^{-\eta _{T}p_{5}e^{\lambda t}} \Big \} \\&\quad- {} e^{\lambda t}q_{3} \Big \{\frac{\alpha _{m}p_{2}}{(g_{m}+e^{\lambda t}p_{2})(g_{m1}+e^{\lambda t}p_{1})^{2}}+\gamma _{m}p_{3} \Big \} + \frac{q_{4}\alpha _{d}g_{d}}{(g_{d}+e^{\lambda t}p_{1})^{2}} \Big ]. \end{aligned}$$

At first, the equations of T and $\overline{T}$, L and $\overline{L}$, M and $\overline{M}$, D and $\overline{D}$, C and $\overline{C}$, $A_{1}$ and ${\overline{A}}_{1}$, $A_{2}$ and ${\overline{A}}_{2}$, $A_{3}$ and ${\overline{A}}_{3}$, $A_{4}$ and ${\overline{A}}_{4}$, $A_{5}$ and ${\overline{A}}_{5}$ are subtracted. The resulting equations are multiplied by a suitable difference of functions and integrated from 0 to $t_{f}$. After that, we add all 10 integral equations and estimates to find the uniqueness of the optimality system. As for example, some integrals are listed as

$$\begin{aligned} \frac{1}{2}(p_{1}-{\overline{p}}_{1})^{2}(t_{f})+ & {} (\lambda -r_{T}+k_{T})\int _{0}^{t_{f}} (p_{1}-{\overline{p}}_{1})^{2} dt \le r_{T}b_{T}\int _{0}^{t_{f}} e^{\lambda t}(p_{1}+{\overline{p}}_{1})(p_{1}-{\overline{p}}_{1})^{2} \textrm{d}t \\+ & {} \alpha _{T} \int _{0}^{t_{f}}e^{\lambda t}(p_{1}-{\overline{p}}_{1}) \Big [\frac{g_{T}(p_{1}p_{3}-{\overline{p}}_{1}{\overline{p}}_{3})+e^{\lambda t}p_{3}{\overline{p}}_{3}(p_{1}-{\overline{p}}_{1})}{(g_{T}+e^{\lambda t}p_{3})(g_{T}+e^{\lambda t}{\overline{p}}_{3})} \Big ]dt \\+ & {} \gamma _{T} \int _{0}^{t_{f}}e^{\lambda t}(p_{1}-{\overline{p}}_{1}) \Big [\frac{g_{T}(p_{1}p_{2}-{\overline{p}}_{1}{\overline{p}}_{2})+e^{\lambda t}(p_{1}p_{2}{\overline{p}}_{3}-{\overline{p}}_{1}{\overline{p}}_{2}p_{3})}{(g_{T}+e^{\lambda t}p_{3})(g_{T}+e^{\lambda t}{\overline{p}}_{3})} \Big ]dt\\+ & {} k_{T} \int _{0}^{t_{f}} e^{-\eta _{T}p_{5}e^{\lambda t}}(p_{1}-{\overline{p}}_{1})^{2} dt. \end{aligned}$$

Now, we shall obtain the bounds on the right hand sides of the integral equations. Since $p_{i},~\overline{p}_{i} \ge 0$ ($i =$ 1–5), we estimate

$$\begin{aligned} (g_{T}+e^{\lambda t}p_{3})\ge & {} g_{T}, \\ (g_{T}+e^{\lambda t}\overline{p}_{3})\ge & {} g_{T}. \end{aligned}$$

Then, we obtain

$$\begin{aligned} \frac{1}{2}(p_{1}-{\overline{p}}_{1})^{2}(t_{f})+(\lambda -r_{T}+k_{T})\int _{0} ^{t_{f}}(p_{1}-{\overline{p}}_{1})^{2} dt\le & {} 2\mu _{1}r_{T}b_{T} \int _{0}^{t_{f}}e^{\lambda t}(p_{1}-{\overline{p}}_{1})^{2}\textrm{d}t\\+ & {} \frac{\alpha _{T} }{g_{T}} \int _{0}^{t_{f}}e^{\lambda t}(p_{1}-{\overline{p}}_{1})(p_{1}p_{3}-\overline{p}_{1}\overline{p}_{3}) dt \\+ & {} \frac{\alpha _{T}\mu ^{2}_{3}}{g_{T}^{2}} \int _{0}^{t_{f}}e^{2 \lambda t}(p_{1}-{\overline{p}}_{1})^{2}\textrm{d}t \\+ & {} \frac{\gamma _{T} }{g_{T}} \int _{0}^{t_{f}}e^{\lambda t}(p_{1}-{\overline{p}}_{1})(p_{1}p_{2}-\overline{p}_{1}\overline{p}_{2}) dt \\+ & {} \frac{\gamma _{T} }{g_{T}^{2}} \int _{0}^{t_{f}} e^{2 \lambda t}(p_{1}p_{2}{\overline{p}}_{3}-{\overline{p}}_{1}{\overline{p}}_{2}p_{3})(p_{1}-\overline{p}_{1}) dt\\+ & {} k_{T} \int _{0}^{t_{f}} e^{-\eta _{T}p_{5}e^{\lambda t}}(p_{1}-{\overline{p}}_{1})^{2} dt, \end{aligned}$$

where $\mu _{1},~\mu _{2},~\mu _{3},~\mu _{4}$ and $\mu _{5}$ are upper bounds of $p_{1},~p_{2},~p_{3},~p_{4}$ and $p_{5}$, respectively. Now, we shall analyze the term $\int _{0}^{t_{f}} (p_{1}p_{2}{\overline{p}}_{3}-{\overline{p}}_{1}{\overline{p}}_{2}p_{3})(p_{1}-\overline{p}_{1}) dt$ explicitly. To evaluate this estimate, we apply the Cauchy-Schwarz inequality to separate linear terms from quadratic terms. It can be observed that

$$\begin{aligned} (p_{1}p_{2}{\overline{p}}_{3}-{\overline{p}}_{1}{\overline{p}}_{2}p_{3})= & {} (p_{1}p_{2}-\overline{p}_{1}\overline{p}_{2})\overline{p}_{3}-\overline{p}_{1} \overline{p}_{2}(p_{3}-\overline{p}_{3}), \end{aligned}$$

and we get

$$\begin{aligned} \int _{0}^{t_{f}} (p_{1}p_{2}{\overline{p}}_{3}-{\overline{p}}_{1}{\overline{p}}_{2}p_{3})(p_{1}-\overline{p}_{1}) dt\le & {} \int ^{t_{f}}_{0} \overline{p}_{3} (p_{1}-{\overline{p}}_{1})(p_{1}p_{2}-\overline{p}_{1}\overline{p}_{2}) dt + \int ^{t_{f}}_{0} \overline{p}_{1}\overline{p}_{2}(p_{1}-\overline{p}_{1})(p_{3}-\overline{p}_{3}) dt \\\le & {} \mu _{3} \int ^{t_{f}}_{0} (p_{1}-{\overline{p}}_{1})(p_{1}p_{2}-\overline{p}_{1}\overline{p}_{2}) dt + \mu _{1}\mu _{2}\int ^{t_{f}}_{0} (p_{1}-\overline{p}_{1})(p_{3}-\overline{p}_{3})\textrm{d}t \\\le & {} \frac{\mu _{1}\mu _{2}}{2} \int ^{t_{f}}_{0} (p_{3}-{\overline{p}}_{3})^{2}\textrm{d}t+ \frac{\mu _{1}\mu _{3}}{2} \int ^{t_{f}}_{0} (p_{2}-{\overline{p}}_{2})^{2}\textrm{d}t \\+ & {} \frac{\mu _{1}\mu _{2}+2\mu _{2}\mu _{3}+\mu _{1}\mu _{3}}{2} \int ^{t_{f}}_{0} (p_{1}-{\overline{p}}_{1})^{2} dt. \end{aligned}$$

Again, we can write that

$$\begin{aligned} \frac{1}{2}(q_{1}-{\overline{q}}_{1})^{2}(t_{f})+(\lambda -r_{T}+k_{T}) \int _{0}^{t_{f}}(q_{1}-{\overline{q}}_{1})^{2} dt\le & {} \int ^{t_{f}}_{0} 2 r_{T}b_{T} e^{\lambda t} (p_{1}q_{1}-\overline{p}_{1}\overline{q}_{1})(q_{1}-\overline{q}_{1})dt \\+ & {} \int ^{t_{f}}_{0} \alpha _{T}e^{\lambda t} \Big \{\frac{p_{3}q_{1}}{g_{T}+e^{\lambda t}p_{3}}-\frac{\overline{p}_{3}\overline{q}_{1}}{g_{T}+e^{\lambda t}\overline{p}_{3}} \Big \} (q_{1}-\overline{q}_{1})\textrm{d}t\\+ & {} \int ^{t_{f}}_{0} \gamma _{T}e^{\lambda t} \Big \{\frac{p_{2}q_{1}}{g_{T}+e^{\lambda t}p_{3}}-\frac{\overline{p}_{2}\overline{q}_{1}}{g_{T}+e^{\lambda t}\overline{p}_{3}} \Big \} (q_{1}-\overline{q}_{1})\textrm{d}t\\+ & {} \int ^{t_{f}}_{0} \alpha _{m}e^{\lambda t} \Big \{\frac{p_{2}q_{3}}{(g_{m}+e^{\lambda t}p_{2})(g_{m1}+e^{\lambda t}p_{1})^{2}} \\- & {} \frac{\overline{p}_{2}\overline{q}_{3}}{(g_{m}+e^{\lambda t}\overline{p}_{2})(g_{m1}+e^{\lambda t}\overline{p}_{1})^{2}} \Big \} (q_{1}-\overline{q}_{1})\textrm{d}t\\+ & {} \int ^{t_{f}}_{0} \gamma _{m}e^{\lambda t}(p_{3}q_{3}-\overline{p}_{3}\overline{q}_{3})(q_{1}-\overline{q}_{1}) dt \\+ & {} \int ^{t_{f}}_{0} \alpha _{d}g_{d} \Big \{\frac{q_{4}}{(g_{d}+e^{\lambda t}p_{1})^{2}}-\frac{\overline{q}_{4}}{(g_{d}+e^{\lambda t}\overline{p}_{1})^{2}} \Big \} (q_{1}-\overline{q}_{1})\textrm{d}t\\+ & {} k_{T} \int _{0}^{t_{f}} e^{-\eta _{T}p_{5}e^{\lambda t}}(q_{1}-{\overline{q}}_{1})^{2} dt. \end{aligned}$$

It is to be noted that

$$\begin{aligned} \int ^{t_{f}}_{0} \alpha _{T}e^{\lambda t} \Big \{\frac{p_{3}q_{1}}{g_{T}+e^{\lambda t}p_{3}}-\frac{\overline{p}_{3}\overline{q}_{1}}{g_{T}+e^{\lambda t}\overline{p}_{3}} \Big \} (q_{1}-\overline{q}_{1})\textrm{d}t\le & {} \frac{\alpha _{T}}{g_{T}} \int ^{t_{f}}_{0} e^{\lambda t}(p_{3}q_{1}-\overline{p}_{3}\overline{q}_{1})(q_{1}-\overline{q}_{1}) dt \\+ & {} \frac{\alpha _{T}}{g_{T}^{2}} \int ^{t_{f}}_{0}e^{2 \lambda t} p_{3}\overline{p}_{3} (q_{1}-\overline{q}_{1})^{2} dt. \end{aligned}$$

Again, we have

$$\begin{aligned} \int ^{t_{f}}_{0} \alpha _{m}e^{\lambda t} \Big \{\frac{p_{2}q_{3}}{(g_{m}+e^{\lambda t}p_{2})(g_{m1}+e^{\lambda t}p_{1})^{2}}- & {} \frac{\overline{p}_{2}\overline{q}_{3}}{(g_{m}+e^{\lambda t}\overline{p}_{2})(g_{m1}+e^{\lambda t}\overline{p}_{1})^{2}} \Big \} (q_{1}-\overline{q}_{1})\textrm{d}t \\\le & {} \frac{\alpha _{m}}{g_{m}g_{m1}^{2}} \int _{0}^{t_{f}} e^{\lambda t}(p_{2}q_{3}-\overline{p}_{2}\overline{q}_{3})(q_{1}-\overline{q}_{1}) dt \\+ & {} \frac{2 \alpha _{m}}{g_{m}g_{m1}^{3}} \int _{0}^{t_{f}}e^{2 \lambda t} (p_{2}q_{3}\overline{p}_{1}-\overline{p}_{2}\overline{q}_{3}p_{1})(q_{1}-\overline{q}_{1}) dt \\+ & {} \frac{\alpha _{m}}{g_{m}g_{m1}^{4}} \int _{0}^{t_{f}}e^{3 \lambda t} (p_{2}q_{3}\overline{p}_{1}^{2}-\overline{p}_{2}\overline{q}_{3}p_{1}^{2})(q_{1}-\overline{q}_{1}) dt \\+ & {} \frac{\alpha _{m}}{g_{m}^{2}g_{m1}^{2}} \int _{0}^{t_{f}} e^{2 \lambda t}(p_{2}q_{3}\overline{p}_{2}-\overline{p}_{2}\overline{q}_{3}p_{2})(q_{1}-\overline{q}_{1}) dt \\+ & {} \frac{2 \alpha _{m}}{g_{m}^{2}g_{m1}^{3}} \int _{0}^{t_{f}} e^{3 \lambda t} (p_{2}q_{3}\overline{p}_{1}\overline{p}_{2}-\overline{p}_{2}\overline{q}_{3}p_{1}p_{2})(q_{1}-\overline{q}_{1}) dt \\+ & {} \frac{\alpha _{m}}{g_{m}^{2}g_{m1}^{4}} \int _{0}^{t_{f}} e^{4 \lambda t} (p_{2}q_{3}\overline{p}_{1}^{2}\overline{p}_{2}-\overline{p}_{2} \overline{q}_{3}p_{1}^{2}p_{2})(q_{1}-\overline{q}_{1}) dt. \end{aligned}$$

To obtain the specific expression, we consider

$$\begin{aligned} \int _{0}^{t_{f}} (p_{2}q_{3}\overline{p}_{1}^{2}\overline{p}_{2}-\overline{p}_{2} \overline{q}_{3}p_{1}^{2}p_{2})(q_{1}-\overline{q}_{1}) dt\le & {} \int _{0}^{t_{f}} \overline{p}_{1}^{2}\overline{p}_{2}(p_{2}q_{3}-\overline{p}_{2} \overline{q}_{3})(q_{1}-\overline{q}_{1}) dt \\+ & {} \int _{0}^{t_{f}} \overline{p}_{2}\overline{q}_{3}(p_{1}^{2}p_{2}-\overline{p}_{1}^{2}\overline{p}_{2})(q_{1}-\overline{q}_{1}) dt \\\le & {} \mu _{1}\mu _{2}^{2}\nu _{3}\int _{0}^{t_{f}}(p_{1}-\overline{p}_{1})^{2}dt + \mu ^{2}_{1}\mu _{2}\nu _{3}\int _{0}^{t_{f}}(p_{2}-\overline{p}_{2})^{2} dt \\+ & {} \frac{2\mu ^{2}_{1}\mu _{2}\nu _{3}+\mu ^{2}_{1}\mu _{2}^{2}+2\mu _{1}\mu _{2}^{2} \nu _{3}}{2}\int _{0}^{t_{f}}(q_{1}-\overline{q}_{1})^{2} dt\\+ & {} \frac{\mu _{1}^{2}\mu _{2}^{2}}{2} \int _{0}^{t_{f}} (q_{3}-\overline{q}_{3})^{2}dt,\\ \end{aligned}$$

where $\nu _{i}$ are the upper bounds of $q_{i}$ ($i =$ 1–5), respectively. We add all the integrals of $(p_{i}-\overline{p}_{i})$ (for $i =$ 1–5) and $(q_{j}-\overline{q}_{j})$ (for $j =$ 1–5) for proving uniqueness of optimal control system. Since maximum fraction of killing rate by chemotherapeutic drug is 1, then $|e^{-\eta _{T}p_{5}e^{\lambda t}}| < 1$. Thus, we have the following inequality:

$$\begin{aligned} \frac{1}{2} (p_{1}-\overline{p}_{1})^{2}(t_{f})+ & {} \frac{1}{2} (p_{2}-\overline{p}_{2})^{2}(t_{f})+\frac{1}{2} (p_{3}-\overline{p}_{3})^{2}(t_{f})+\frac{1}{2} (p_{4}-\overline{p}_{4})^{2}(t_{f})+\frac{1}{2} (p_{5}-\overline{p}_{5})^{2}(t_{f})\\+ & {} \frac{1}{2} (q_{1}-\overline{q}_{1})^{2}(t_{f})+\frac{1}{2} (q_{2}-\overline{q}_{2})^{2}(t_{f}) + \frac{1}{2} (q_{3}-\overline{q}_{3})^{2}(t_{f})+\frac{1}{2} (q_{4}-\overline{q}_{4})^{2}(t_{f})\\+ & {} \frac{1}{2} (q_{5}-\overline{q}_{5})^{2}(t_{f}) + (\lambda -r_{T}+k_{T})\int ^{t_{f}}_{0}(p_{1}-\overline{p}_{1})^{2} dt + (\lambda +\delta _{l}+k_{l})\int ^{t_{f}}_{0}(p_{2}-\overline{p}_{2})^{2} dt\\+ & {} (\lambda +\delta _{m}+k_{m})\int ^{t_{f}}_{0}(p_{3}-\overline{p}_{3})^{2} dt + (\lambda +\delta _{d}+k_{d})\int ^{t_{f}}_{0}(p_{4}-\overline{p}_{4})^{2} dt \\+ & {} (\lambda +\gamma )\int ^{t_{f}}_{0}(p_{5}-\overline{p}_{5})^{2} dt + (\lambda -r_{T}+k_{T})\int ^{t_{f}}_{0}(q_{1}-\overline{q}_{1})^{2} dt \\+ & {} (\lambda +\delta _{l}+k_{l})\int ^{t_{f}}_{0}(q_{2}-\overline{q}_{2})^{2} dt + (\lambda +\delta _{m}+k_{m})\int ^{t_{f}}_{0}(q_{3}-\overline{q}_{3})^{2} dt\\+ & {} (\lambda +\delta _{d}+k_{d})\int ^{t_{f}}_{0}(q_{4}-\overline{q}_{4})^{2} dt + (\lambda +\gamma )\int ^{t_{f}}_{0}(q_{5}-\overline{q}_{5})^{2} dt \\\le & {} \overline{C}_{1}e^{4 \lambda t} \int _{0}^{t_{f}}[(p_{1}-\overline{p}_{1})^{2}+(p_{2}-\overline{p}_{2})^{2}+(p_{3} -\overline{p}_{3})^{2}+(p_{4}-\overline{p}_{4})^{2}+(p_{5}-\overline{p}_{5})^{2}\\+ & {} (q_{1} -\overline{q}_{1})^{2} + (q_{2}-\overline{q}_{2})^{2}+(q_{3}-\overline{q}_{3})^{2}+(q_{4} -\overline{q}_{4})^{2}+(q_{5}-\overline{q}_{5})^{2}] dt. \end{aligned}$$

We use the nonnegativity of the variables at the initial and final time and simplifying; then, the above inequality is reduced to the following expression:

$$\begin{aligned} (\lambda -\overline{C}_{2}-\overline{C}_{1}e^{4 \lambda t})\int _{0}^{t_{f}}[(p_{1}-\overline{p}_{1})^{2}+ & {} (p_{2}-\overline{p}_{2})^{2}+(p_{3}-\overline{p}_{3})^{2}+(p_{4}-\overline{p}_{4})^{2} +(p_{5}-\overline{p}_{5})^{2}+(q_{1}-\overline{q}_{1})^{2} \\+ & {} (q_{2}-\overline{q}_{2})^{2} + (q_{3}-\overline{q}_{3})^{2}+(q_{4}-\overline{q}_{4})^{2}+(q_{5}-\overline{q}_{5})^{2}] dt \le 0; \end{aligned}$$

where $\overline{C}_{1},~\overline{C}_{2}$ depend on the coefficients and their bounds of the state variables. If we choose that $\lambda > \overline{C}_{2}+\overline{C}_{1}$, then we have $\lambda -\overline{C}_{2}-\overline{C}_{1}e^{4 \lambda t} > 0$. Since logarithm is increasing function, thus $t_{f} < \frac{1}{4 \lambda } \ln \big (\frac{\lambda -\overline{C}_{2}}{\overline{C}_{1}} \big )$, then $p_{i}=\overline{p}_{i}$ (for $i =$ 1–5) and $q_{j}=\overline{q}_{j}$ (for $j =$ 1–5). Therefore, in the small time interval, the solution of (9) is unique.

From the mathematical perspective, we can assert that the uniqueness of the solution of the control system satisfied for a sufficiently small time interval, where the state system has initial solutions and the adjoint or costate system has the final time conditions. The given optimal controls $u_{2}^{*},~u^{*}_{3},~u^{*}_{4}$ and $v^{*}_{c}$ are characterized in terms of the unique solution of the optimal system. $\hfill\square$

8 Parameter estimation

The system parameters have a significant impact on the behavior and analysis of the mathematical model. In this section, we will discuss how we estimated certain parameters of our system (1) based on information available in the existing literature. Our approach to parameter estimation is outlined below.

Degradation rate of CD8+T cells, denoted as $\delta _{l}$: The estimated half-life of CD8+T cells, denoted as L, is approximately 3.9 days according to the findings in [34]. We can determine the death rate $\delta _{l}$ of CD8+T cells using the following equation

$$\begin{aligned} \frac{1}{2} L(0)= & {} L(0) e^{(-\delta _{l} t_{1/2}^{L})}. \end{aligned}$$

This equation yields the value of $\delta _{l}$ as

$$\begin{aligned} \delta _{l}&= {} \frac{\ln 2}{3.9}~\text {day}^{-1} \\&\approx {} 0.178~\text {day}^{-1}. \end{aligned}$$

Degradation rate of macrophages, denoted as $\delta _{m}$: The value of $\delta _{m}$ can be calculated using the data provided by Wacker et al. [35], who observed a half-life of 12.4 days for macrophages. This can be expressed as

$$\begin{aligned} \delta _{m}&= {} \frac{\ln 2}{12.4~\text {day}} \\&\approx {} 0.056~\text {day}^{-1}. \end{aligned}$$

Death rate of dendritic cell, denoted as $\delta _{d}$: The half-life of dendritic cells is reported to range from 3 to 4 days according to Holt et al. [36]. For our calculations, we assume a median half-life of 4 days. As a result, the death rate $\delta _{d}$ can be calculated as follows

$$\begin{aligned} \delta _{d}&= {} \frac{\ln 2}{4~\text {day}} \\&\approx {} 0.17~\text {day}^{-1}. \end{aligned}$$

Activation rate of dendritic cells, denoted as $\alpha _{d}$: The parameter representing the half-saturation constant for tumor cells is denoted as $g_{d}$. This can be expressed as

$$\begin{aligned} \frac{T}{g_{d} + T} = \frac{1}{2}. \end{aligned}$$

Based on the findings by Coventry et al. [37], where the density of dendritic cells in breast cancer patients is noted as $D = 4\times 10^{-4}$ cells and by considering the steady state of the fourth equation in (1), we can derive the equation

$$\begin{aligned} \alpha _{d}\frac{T}{g_{d}+T} = \delta _{d}D, \end{aligned}$$

which can be rearranged to calculate the value of $\alpha _{d}$ as

$$\begin{aligned} \alpha _{d} = 1.36\times 10^{-4}~\text {cell}/\text {day}. \end{aligned}$$

Constant source rate of dendritic cells, denoted as $s_{d}$: Constant source rate $s_{d}$ is influenced by the presence of tumor cells. In a healthy person, the presence of tumor cells results in the absence of dendritic cell production. Therefore, at a steady state, we can express this relation as

$$\begin{aligned} s_{d}&= {} \delta _{d}D \\&= {} 0.68\times 10^{-4}~\text {cell}/\text {day}. \end{aligned}$$

Natural degradation rate of Tregs, denoted as $\delta _{g}$: As reported by Q. Tang [38], the half-life of regulatory T-cells is 32 h, which is approximately equivalent to 1.3 days. Therefore, we can calculate the death rate $\delta _{g}$ as follows

$$\begin{aligned} \delta _{g}&= {} \frac{\ln 2}{1.3}~\text {day}^{-1} \\&\approx {} 0.53~\text {day}^{-1}. \end{aligned}$$

Activation rate of Tregs, denoted as $\alpha _{g}$: According to Q. Tang [38], the estimated average count of circulating regulatory T-cells in an adult human is approximately $0.25 \times 10^{9}~pg\cdot ml^{-1}$. Additionally, we assume that the density of CD8+T cells is $2\times 10^{7}$ cells/ml. By considering the steady state of the fifth equation in (1), we derive the equation following as

$$\begin{aligned} \alpha _{g}L - \delta _{g}T_{g}= & {} 0, \end{aligned}$$

which implies that

$$\begin{aligned} \alpha _{g}= & {} \frac{\delta _{g}T_{g}}{L}. \end{aligned}$$

Substituting the known values, we have

$$\begin{aligned} \alpha _{g}= & {} \frac{0.53 \times 0.25 \times 10^{9} (\text {day}^{-1}.\text {pg}.\text {ml}^{-1})}{2 \times 10^{7}(\text {cell}.\text {ml}^{-1})}. \end{aligned}$$

This simplifies to

$$\begin{aligned} \alpha _{g}= & {} 6.62~\text {pg}.\text {day}^{-1}.\text {cell}^{-1}. \end{aligned}$$

Degradation rate of interleukin-10, denoted as $\delta _{10}$: The half-life of interleukin-10, denoted as $I_{10}$, is reported to be 4.5 h according to Huhn et al. [39], which is approximately equivalent to 0.1875 days. Therefore, we can calculate the degradation rate $\delta _{10}$ as follows

$$\begin{aligned} \delta _{10}&= {} \frac{\ln 2}{0.1875}~\text {day}^{-1} \\&\approx {} 3.696~\text {day}^{-1}. \end{aligned}$$

Activation rate of interleukin-10, denoted as $\alpha _{10}$: Toossi et al. [40] found that $10^6$ alveolar macrophages produce, in vitro, 3,200 pg/mL of interleukin-10 ($I_{10}$). Utilizing the steady-state equation from the sixth equation in (1), we can write that

$$\begin{aligned} \alpha _{10}M - \delta _{10}I_{10}= & {} 0, \end{aligned}$$

which implies

$$\begin{aligned} \alpha _{10}= & {} \frac{3.696~ \times 3200}{10^{6}}~(\text {day}^{-1}.\text {pg}.\text {ml}^{-1})/ (\text {cell}.\text {ml}^{-1}). \end{aligned}$$

Simplifying this expression, we find

$$\begin{aligned} {\alpha _{10}}= & {} {0.01182~\text {pg}.\text {day}^{-1}.\text {cell}^{-1}}. \end{aligned}$$

Death rate of TGF-$\beta$,denoted as $\delta _{\beta }$: We assume that estimated median half-life of TGF-$\beta$ is approximately 20 h, equivalent to 0.83 days. Consequently, the death rate of TGF-$\beta$ can be calculated as follows

$$\begin{aligned} \delta _{\beta }= & {} \frac{\ln 2}{0.83}~\text {day}^{-1} ~~~\approx 0.832~\text {day}^{-1}. \end{aligned}$$

Source rate of TGF-$\beta$, denoted as $s_{\beta }$: Peterson et al. [41] reported a TGF-$\beta$ $(T_{\beta })$ density of 609 pg/ml. It is observed that in a healthy person the concentration of TGF-$\beta$ is 10 times less than a cancer patient. Assuming a cerebral spinal fluid volume of 150 ml, in the absence of cancer-induced TGF-$\beta$ production, we can observe at steady state that

$$\begin{aligned} s_{\beta }= & {} \delta _{\beta }T_{\beta } \\= & {} 0.832~\text {day}^{-1} \times 150~\text {ml} \times 60.9~\text {pg}\cdot \text {ml}^{-1} \\= & {} 7.6\times 10^{3}~\text {pg}\cdot \text {day}^{-1}. \end{aligned}$$

Release rate of TGF-$\beta$ by tumor cells, denoted as $\alpha _{\beta }$: The average concentration of the immunosuppressive cytokine TGF-$\beta$ ($T_{\beta }$) is determined to be $609~\text {pg}/ \text {ml} \times 150~\text {ml} = 91350~\text {pg}$ based on the findings by Peterson et al. [41], which relates to high-grade glioblastoma patients. Utilizing the seventh equation from the system (1) at an equilibrium state, we can derive that

$$\begin{aligned} \alpha _{\beta }= & {} \frac{\delta _{\beta }T_{\beta } - s_{\beta }}{T} \\= & {} \frac{91350~\text {pg} \times 0.832~\text {day}^{-1}- 7.6\times 10^{3}~\text {pg}\cdot \text {day}^{-1}}{10^{6}~\text {cell}} \\= & {} 0.0684~\text {pg}.\text {day}^{-1}.\text {cell}^{-1}. \end{aligned}$$

Degradation rate of interleukin-12, denoted as $\delta _{12}$: The half-life of interleukin-12 $(I_{12})$ is reported to be 30 h, equivalent to 1.25 days, as documented in the study by Carreno et al. [42]. Therefore, the degradation rate of interleukin-12 $(I_{12})$ can be calculated as follows

$$\begin{aligned} \delta _{12}= & {} \frac{0.693}{1.25~\text {day}} \\\approx & {} 0.55~\text {day}^{-1}. \end{aligned}$$

Release rate of IL-12 by dendritic cells, denoted as $\alpha _{12}$: In the case of a breast cancer patient, the concentration of interleukin-12 in the blood serum is measured at $1.5 \times 10^{-10}$ pg/ml, as indicated by Derin et al. [43]. Additionally, the concentration of dendritic cells stands at $4 \times 10^{-4}$ cell/ml, based on the findings of Coventry et al. [37]. Thus, at the steady state of the eighth equation of (1), we can deduce that

$$\begin{aligned} \alpha _{12}= & {} \frac{\delta _{12}I_{12}}{D} \\= & {} \frac{1.5 \times 10^{-10}~\text {pg}\cdot \text {ml}^{-1}\times 0.55~\text {day}^{-1}}{4 \times 10^{-4}~\text {cell}\cdot \text {ml}^{-1}} \\= & {} 2.06\times 10^{-7}\text {pg}.\text {day}^{-1}.\text {cell}^{-1}. \end{aligned}$$

Decay rate of IFN-$\gamma$, denoted as $\delta _{\gamma }$: The median half-life of IFN-$\gamma$ is determined to be 6.8 h, which is approximately equivalent to 0.283 days, as reported by Turner et al. [44]. Consequently, the decay rate of IFN-$\gamma$ can be calculated as follows

$$\begin{aligned} \delta _{\gamma }= & {} \frac{\ln 2}{0.283}~\text {day}^{-1} \\\approx & {} 2.45~\text {day}^{-1}. \end{aligned}$$

Production rate of IFN-$\gamma$ by CD8+T cells, denoted as $\alpha _{\gamma }$: In a specific experimental study, Kim et al. [45] reported that CD8+T cells produce 200 pg/ml of IFN-$\gamma$. Based on this data, we assume that the concentration of CD8+ T cells is $2 \times 10^{7}$ cell/ml. Therefore, by utilizing the steady state of the ninth equation in (1), we can determine

$$\begin{aligned} \alpha _{\gamma }= & {} \frac{\delta _{\gamma }I_{\gamma }}{L} \\= & {} \frac{200~\text {pg}\cdot \text {ml}^{-1}\times 2.45~\text {day}^{-1}}{2\times 10^{7}\text {cell}\cdot \text {ml}^{-1}}\\= & {} 2.45\times 10^{-5}~\text {pg}.\text {day}^{-1}.\text {cell}^{-1}. \end{aligned}$$

Table 1 provides a summary of all the model parameters.

9 Numerical results

This section provides a detailed description of extensive numerical illustrations aimed at validating our theoretical analysis, covering aspects such as stability and the implementation of various treatment strategies. We generated numerical plots of our optimal control model using MATLAB, selecting appropriate parameters value, which can be found in Table 1. To assess the impact of these treatment strategies, we conducted a comparative analysis, contrasting the numerical illustrations with and without the application of treatment strategies for the proposed control model (3).

9.1 Numerical results without treatment strategy

In this subsection, we study numerical behavior of (3) without implementation treatment strategy. In view of this, at first, we check the existence of biologically feasible singular point(s) in absence of any control (that is, $u_{2}=u_{3}=u_{4}=v_{c}=0$). We calculate the tumor-free steady state $E^{0}$ (0, 0, 9678.57, 0, 0), and the corresponding eigenvalues are $-0.9,~-0.865109,~-0.178,~-0.17,~-0.056$. Since all the eigenvalues are negative, then we can say that tumor-free singular point $E^{0}$ is locally asymptotically stable. It is quite difficult to find the explicit form of interior singular point $E^1(T^1,~L^1,~M^1,~D^1,~C^1)$. So, we calculate interior singular point by numerically using the parameters value given in Table 1. There are two types of tumor-presence singular point. One is low tumor-presence singular point, and another is high tumor-presence singular point. From the parameters in Table 1, the low tumor-presence steady state $E^{l}$ is $(0.179273,~1.05623\times 10^{-17},~3886.15,~1.43419\times 10^{-10},~0)$ and the corresponding eigenvalues are $-0.9,~-0.300816,~-0.178,~-0.17, ~0.161346$, which shows that low tumor-presence singular point $E^{l}$ is unstable in nature. On the other hand, high tumor-presence steady state $E^{h}$ is $(800000,~2.61855\times 10^-11,~0.00145511,~0.0003555,~0)$ and the corresponding eigenvalues are $-372480,~-0.9,~-0.5822,~-0.178,~-0.17$. Since all of the eigenvalues are negative, then we can say that high tumor-presence steady state $E^{h}$ is asymptotically stable.

Table 1 The parameter values employed for simulating the tumor-immune interaction model are as follows

9.2 Numerical results with treatment strategy

In this subsection, we will explore our proposed model with the application of various treatment strategies. We have introduced four distinct treatment strategies, specifically $u_2(t)$, $u_3(t)$, $u_4(t)$ and $v_c(t)$, designed to target and eliminate the tumor cell population. Our approach involves conducting numerical simulations for the state variables using the Runge–Kutta forward method and solving the equations for the adjoint or costate variables using the Runge–Kutta backward method. To perform the numerical illustrations, we consider the initial values $T(0)=0.01,~L(0)=0.2\times 10^{-7},~M(0)=3000,~D(0)=0.0002$ and time window 200 days with taking parameters value are specified in Table 1. To better know the treatment techniques, we consider the following control strategies.

Strategy I: Implementation of only one treatment strategy.

Strategy II: Implementation of two different treatment strategies.

Strategy III: Implementation of three different treatment strategies.

Strategy IV: Implementation of four different treatment strategies.

Figure  2 illustrates the impact of tumor cells, CD8+T cells, macrophages and dendritic cells in the presence of a single treatment strategy, denoted as $(u_{2}(t),~u_{3}(t), ~u_4(t), ~v_{c}(t))$, as well as in the absence of any treatment strategy (that is, $u_{2}(t)=u_{3}(t)=u_4(t)=v_{c}(t)=0)$. In Fig. 2, the red curve represents the state variables without any optimal control strategy, while the black curve describes the state variables with only one treatment strategy, specifically $u_{2}(t)=0.8$. The blue, green and magenta curves correspond to each of the state variables when $u_{3}(t)=0.8$, $u_{4}(t)=0.8$ and $v_{c}(t)=0.8$, respectively. From the time series plot (see Fig. 2), it is evident that without application of any control strategy in our proposed model, the reduction in tumor cells takes more time than when a single control strategy is employed. Additionally, we observe that effector cells initially increase but decrease as time progresses. The utilization of a single control strategy proves to be more effective than administering no control at all.

Fig. 2

The figure shows that the comparison of the state variables without introduction of treatment strategy and with the implementation of single control

Figure 3 illustrates the impact of various state variables under the influence of two optimal control strategies. These strategies are denoted as follows: $u_{2}(t),~v_{c}(t)$; $u_{3}(t),~v_{c}(t)$; $u_{4}(t),~v_{c}(t)$; $u_{2}(t),~u_{3}(t)$; $u_{3}(t),~u_{4}(t)$; $u_{2}(t),~u_{4}(t)$; and a scenario without any control strategy. In this visualization, the red curve represents the state variables when no control strategy is employed, while the black curve signifies the state variables when two control strategies are implemented, specifically $u_{2}(t)=v_{c}(t)=0.8$. The blue curve illustrates the state variables with the application of two control strategies, namely $u_{3}(t)=v_{c}(t)=0.8$. The green curve indicates the state variables when two different controls are utilized, that is, $u_{4}(t)=v_{c}(t)=0.8$. The magenta curve represents the state variables under the influence of two control strategies, where $u_{2}(t)=u_{3}(t)=0.8$. The crayon curve depicts the state variables with two treatment strategies, specifically $u_{3}(t)=u_{4}(t)=0.8$. Finally, the maroon curve explores the state variables with two treatment strategies, where $u_{2}(t)=u_{4}(t)=0.8$. Analyzing the time series plot shown in Fig. 3, it becomes obvious that when employing two different optimal control strategies, the tumor cells rapidly reach their equilibrium point. Meanwhile, the immune components initially experience an increase but eventually saturate over time. Consequently, We can conclude that employing two control strategies is more effective compared to a scenario with no treatment strategies.

Fig. 3

The figure describes that the comparison of the state variables without implementation of any treatment strategy and with the application of two treatment strategies

The figure describes that the comparison of the state variables without implementation of any treatment strategy and with the application of two treatment strategies

The time series plot in Fig. 4 illustrates the roles of tumor cells, CD8+T cells, macrophages and dendritic cells in the presence of three control strategies: $u_{2}(t),~u_{3}(t),~v_{c}(t)$; $u_{3}(t),~u_{4}(t),~v_{c}(t)$; $u_{2}(t),~u_{3}(t),~u_{4}(t)$ and without the introduction of any control strategy. The red curve represents the state variables without any control strategy, while the black curve depicts the state variables under three different treatment strategies, specifically $u_{2}(t)=u_{3}(t)=v_{c}(t)=0.8$. The blue curve shows the state variables under three distinct control strategies, where $u_{3}(t)=u_{4}(t)=v_{c}(t)=0.8$. Finally, the green curve illustrates the state variables when three control strategies are introduced, with $u_{2}(t)=u_{3}(t)=u_{4}(t)=0.8$. Figure 4 clearly demonstrates that employing a combination of three control strategies proves more effective when compared to the scenario with no treatment strategy.

Fig. 4

The figure indicates that the comparison of the state variables without introduction of any treatment strategy and with the application of three diferent control strategies

The time series plot in Fig. 5 depicts the application of four different control strategies alongside the scenario without any control strategy for the state variables. To visualize these four treatment strategies, we set the control variables as follows: $u_{2}(t)=u_{3}(t)=u_{4}(t)=v_{c}(t)=0.8$. From the time series plot in Fig. 5, it is evident that implementing four different treatment strategies is more effective than using no treatment strategy, a single treatment strategy (Fig. 2), two different treatment strategies (Fig. 3) or three different treatment strategies (Fig. 4). Additionally, in Fig. 5, it is noticeable that tumor cells are rapidly eliminated and immune components are maximized upon the implementation of these four distinct control strategies.

Fig. 5

The figure shows that the comparison of the state variables without implementation of any treatment strategy and with the implementation four diferent treatment strategies

To visualize the dynamics of the adjoint or costate variables $A_{1},~A_{2},~A_{3}$ and $A_{4}$ with the implementation of four different control strategies, we have drawn Fig. 6. To do this, we consider the values of the control variables as follows: $u_{2}(t)=u_{3}(t)=u_{4}(t)=v_{c}(t)=0.8$. The plot clearly illustrates that the costate variables are directly linked to changes in the values of the Lagrangian. The time derivatives of the costate variables are negative with respect to the corresponding partial derivatives of the Lagrangian.

Fig. 6

The figure shows that the nature of the adjoint or costate variables with the implementation of four diferent treatment strategies

To visualize the dynamic behavior of the controls, we plot the control parameters in the Fig. 7. The plot of the four graphs represents the optimal control functions with the implementation of four control strategies, namely $u_{2}(t)=u_{3}(t)=u_{4}(t)=v_{c}(t)=0.8$. From the Fig. 7, it can be noticed that control values decreased and eventually reach 0. The control parameters vanish before 40 days due to the fact that our adjoint or costate variables vanish.

Fig. 7

The figure shows the optimal controls as a function of time corresponding to the implementation of the single control $u_{2}(t),~u_{3}(t),~u_{4}(t)$ and $v_{c}(t)$

The model is closely tied to the study of optimal control strategies within the context of tumor cell dynamics and the immune response. It explores into various control approaches, including the manipulation of tumor cell levels and key immune components (such as CD8+T cells, macrophages and dendritic cells), all with the aim of achieving specific biological outcomes. Our immune system, with its pivotal role in identifying and eliminating abnormal cells, including cancer cells, stands as a critical factor. Investigating how these control strategies impact the immune response can provide valuable insights into fortifying the body’s inherent defenses against cancer. The significance of control parameters like $u_{2}(t),~u_{3}(t),~u_{4}(t)$ and $v_{c}(t)$ cannot be overstated, as they are intricately linked to immune components such as CD8+T cells, macrophages, dendritic cells and chemotherapeutic drugs. Their relevance lies in their potential to augment the immune response against cancer cells, thereby potentially enhancing the body’s capacity to identify and eliminate cancer cells. Through comparisons of the efficacy of diverse control strategies (ranging from single to four treatments) in reducing tumor cell proliferation and maximizing the immune response, this model serves as a valuable tool for identifying the most promising avenues in cancer treatment. The control parameters represent the capacity to deploy multiple treatment strategies either individually or in combination. Moreover, the adaptability of these control parameters allows for a personalized approach to cancer treatment. Their biological significance is underscored by the ability of treatment strategies to individual patients, accounting for unique tumor characteristics and immune system profiles. Each of these parameters exerts a distinct influence on the dynamics of tumor cells and the immune response. Their biological significance lies in their potential to preserve precise control over tumor growth, ultimately suppressing the proliferation of cancer cells and potentially leading to tumor regression or even elimination.

10 Conclusion

Nowadays, it is very important and challenging question in immunology and oncology research is to understand how the immune system influences tumor progression and development. This study explores the dynamic behavior of a nonlinear tumor-immune interaction model using the theory of optimal control. Various scenarios for implementing different treatment strategies to eliminate the tumor cell population are considered. Here, we construct a mathematical model of nine nonlinear coupled ordinary differential equations (ODEs) by introducing different cells and cytokines, namely tumor cells, cytotoxic T-lymphocytes (CD8+T cells), macrophages, dendritic cells, tregs, IL-10, TGF-$\beta$, IL-12 and IFN-$\gamma$. Next, we simplify the proposed model into a system of four ODEs, which represent tumor cells, CD8+T cells, macrophages and dendritic cells, using the quasi-steady-state approximations method [24].

In this paper, we analyzed a mathematical model for tumor-immune interaction with treatment strategies. Our goal is to provide an improved treatment strategy by eliminating the tumor cell population using both chemotherapeutic and immunotherapeutic drugs. To do this, we introduce four control parameters, namely $u_{2}(t),~u_{3}(t),~u_{4}(t)$ and $v_{c}(t)$. To minimize the tumor cells and maximize the immune cells, we define an objective functional $J(u^{*})$. We prove the existence of control by applying the boundedness of super-solutions of the system. Additionally, we determine the characterization of the control by employing Pontryagin’s Maximum Principle. We calculate the variation of the Lagrangian function to delineate the maximization of our optimal controls $u_{2}^{*}(t),~u_{3}^{*}(t),~u_{4}^{*}(t)$ and $v_{c}^{*}(t)$. Finally, we establish the uniqueness of the solution for the given optimal control system holds for a sufficient small time interval $t_{f}$. Next, we estimated value of several parameters for our system (1) based on existing literature.

We conducted a numerical study of our control system (3) under various conditions, including scenarios without a control strategy, with a single treatment strategy, with two treatment strategies, with three treatment strategies and with four treatment strategies. In Fig. 2, we observed that a single control strategy proves more efficient than having no treatment strategy. Similarly, in Fig. 3, the implementation of two treatment strategies led to a rapid attainment of equilibrium in the tumor cell population compared to using a single treatment strategy or having no treatment strategy. Furthermore, the combination of three and four treatment strategies yielded remarkable results in minimizing the tumor cell burden, eventually leading to its complete elimination. This is demonstrated in Figs 4 and 5, respectively. Simultaneously, the immune components, including CD8+T cells, macrophages and dendritic cells, reached their maximum levels, as shown in Figs 4 and 5. In summary, our results indicate that the utilization of different treatment strategies, including one, two, three or four control strategies, is effective for rapidly reducing the tumor burden compared to scenarios without any treatment strategy. Additionally, this approach maximizes the presence of immune components, such as CD8+T cells, macrophages and dendritic cells, surpassing the results achieved by the alternative control strategies.

The innovative method we employ to understand and manage tumor-immune interactions is what sets our research apart. By systematically evaluating multiple treatment strategies and optimizing their effectiveness, we have provided a comprehensive framework for addressing a complex and pressing challenge in immunology and oncology. Our findings are not only underscore the significance of having structured control strategies but also highlights the potential of combining multiple treatment strategies to achieve unprecedented results in tumor elimination. This novel perspective not only contributes to the theoretical foundations of the field but also holds great promise for practical applications in cancer treatment.

We expect that the outcomes from our mathematical model will prove valuable to future researchers engaged in the study of tumor-immune interaction systems, particularly those applying optimal control theory. This study can offer significant assistance to researchers seeking to implement optimal control theory in various areas of research. Furthermore, we aspire to contribute to the improvement of cancer patient treatment by presenting a mathematical model that incorporates tumor cells and the immune system, potentially offering a more effective approach for the management of cancer patients.