Modeling Tumor–Immune Dynamics

Abstract

Mathematical models of tumor–immune interactions provide an analytical framework in which to address specific questions regarding tumor–immune dynamics and tumor treatment options. We present a mathematical model, in the form of a system of ordinary differential equations (ODEs), that governs cancer growth on a cell population level. In addition to a cancer cell population, the model includes a population of Natural Killer (NK) and CD8⁺ T immune cells. Our goal is to understand the dynamics of immune-mediated tumor rejection, in addition to exploring results of applying combination immune, vaccine and chemotherapy treatments. We characterize the ODE system dynamics by locating equilibrium points, determining stability properties, performing a bifurcation analysis, and identifying basins of attraction. These system characteristics are useful, not only for gaining a broad understanding of the specific system dynamics, but also for helping to guide the development of combination therapies. Additionally, a parameter sensitivity analysis suggests that the model can predict which patients may respond positively to treatment. Numerical simulations of mixed chemo-immuno and vaccine therapy using both mouse and human parameters are presented. Simulations of tumor growth using different levels of immune stimulating ligands, effector cells, and tumor challenge, are able to reproduce data from published studies. We illustrate situations for which neither chemotherapy nor immunotherapy alone are sufficient to control tumor growth, but in combination the therapies are able to eliminate the entire tumor.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

There are many unanswered and important questions as to how the immune system interacts with a growing tumor, and which components of the immune system play significant roles in responding to immunotherapy. For example, does the varying strength of an individual’s immune response play a significant role in affecting tumor growth during treatment, and if so, is it possible to predict which individuals will respond well, and which will not? Mathematical models provide an analytical framework in which to address such questions, and these models can be used both descriptively and predictively. It is important to develop models of tumor growth that include a representation of an immune response. The ultimate goal is to create models that can reflect a system’s response to emerging biological therapies, such as vaccine therapy. Mathematical modeling of tumor growth and treatment has been approached by a number of researchers using a variety of models over the past decades. (For overviews, see for example [4, 9, 27, 55, 68].)

The Importance of the Immune System and Immunotherapy Immunotherapies are quickly becoming an important component in the multi-pronged approaches being developed to treat certain forms of cancer. The goal of immunotherapy is to strengthen the body’s own natural ability to combat cancer by enhancing the effectiveness of the immune system. The importance of the immune system in fighting cancer has been verified in the laboratory as well as with clinical experiments. See, for example, [28, 52, 53, 57, 69]. Additionally, it is known that those with weakened immune systems, such as those suffering from AIDS, are more likely to contract certain rare forms of cancer. This phenomenon can be interpreted as providing further evidence that the role played by the immune response in battling cancer is critical. See, for example, [12, 38].

The clear importance of the immune system in controlling cancer growth, both clinically and mathematically, indicates that models incorporating tumor growth and treatment would do well to include an immune system component. Once this component is in place, it is then possible to model how various immunotherapies may affect the system, either singly or in combination with one another. Recent clinical data have shown there is potential benefit in harnessing the power of the immune system in combination with traditional chemotherapy. For example, in Wheeler et al. [72], it is demonstrated that vaccine therapy in combination with chemotherapy more effectively extends patient survival times than either chemotherapy or vaccine therapy alone.

Immunotherapy The clinical evidence for the potential of immune system control of certain malignancies has motivated new research into the development of immunotherapies and vaccine therapies for cancers. Some examples are described in [5, 11, 25, 59, 65, 72]. Immunotherapy falls into three main categories: immune response modifiers, monoclonal antibodies, and vaccines (see, for example, [64]). The first category contains substances that affect the immune response, such as interleukins (including IL-2), interferons, tumor necrosis factors (TNF), colony-stimulating factors (CSF), and B-cell growth factors. In the next category, monoclonal antibodies are currently being developed to target specific cancer antigens. These monoclonals can distinguish between normal and cancer cells, and they can then be used to diagnose cancer, as well as to treat tumors by “guiding” anticancer drugs toward the malignant cells (see, e.g., [34, 48, 62]). In the third category are vaccines, which are generally used therapeutically, and are created from tumor cells. These work by helping the immune system to recognize and attack specific cancer cells. In this work, we implement treatment from the first category in the form of mathematical terms that represent IL-2 and tumor infiltrating lymphocyte (TIL) injections, and additionally incorporate treatment from the third category: new mathematical forms that distinguish between specific and nonspecific immune responses, allowing for the incorporation of a vaccine component into the model. Although monoclonal antibody treatments are considered promising, they are currently not considered in this work.

Cancer Vaccines There are fundamental differences between the use and effects of antiviral vaccines and anticancer vaccines. While many vaccines for infectious diseases are preventative, cancer vaccines are designed to be used therapeutically, treating the disease after it has begun, and preventing the disease from recurring. Cancer vaccines are still considered to be highly experimental as compared with other forms of cancer immunotherapy, but in early clinical trials are showing increasing promise in their ability to improve the immune response to certain forms of cancer (see, e.g., [64, 72]).

Since cancer vaccines and antiviral vaccines differ in their application, mathematical models of these vaccines should exhibit different dynamics. The goal of this chapter is to build on existing models of tumor growth, incorporating an immune system response and expanding these models to include the effect of anti-tumor vaccination and immunotherapies in conjunction with chemotherapies. In another work, the authors will extend this model into a larger framework that incorporates spatial and geometric components.

The outline of this chapter is as follows. In Sect. 2 we describe four cell population growth models that are commonly used to represent cancer growth, and outline a parameter fitting approach that can extract growth parameters from laboratory data. In Sect. 3, we discuss growth and interaction dynamics governing an immune response to tumor, assuming a single population representing effector-killer cells of the immune system. In Sect. 4 we further expand our description of the immune response to include both the innate and the specific responses, and in Sect. 5, we formulate the mathematical forms that govern the different dynamics of the innate and specific immune responses. In Sect. 6, we construct a three population mathematical model that describes the interactions of a tumor cell population with both the innate and specific immune cell populations. We also carry out a parameter sensitivity analysis, as well as a bifurcation analysis of the system. In Sect. 7, we build upon our three population model to allow for simulation of treatments. Treatment modalities include both cytotoxic chemotherapy and immune-stimulating therapies. We present numerical simulations that represent both mouse and human scenarios, using parameters extracted from published literature. Finally, in Sect. 8, we provide a discussion and summary of this work.

2 Growth Models

An important step in building a tumor–immune model is to capture the dynamics of tumor cell population growth alone, before considering growth-limiting interference from, for example, immune cells or from competition by normal cells for nutrients and space. There is, so far, no universal consensus as to which fundamental growth models best reflect tumor cell growth. Among the most commonly used models, however, are exponential growth (and its generalization, power law growth), logistic growth, Von Bertalanffy growth, and Gompertz growth. The forms of these growth laws are in Table 1. All but von Bertalanffy growth require two parameter values be determined. The Von Bertalanffy model requires three parameter values.

Table 1 Commonly used cell population growth laws

The choice of growth law depends, among other things, on the cancer cell type, whether the cancer is early or late stage, and the location of the tumor. In the case of tumor stage, consider, for example, a comparison of exponential and logistic growth models. As can be seen in Fig. 1, in which we compare exponential to logistic growth, if the tumor is small (early stage), there is no significant distinction between the two growth models. The distinction becomes apparent, however, in the later stages. As opposed to exponential growth, logistic growth is self-limiting. Even though there are no external growth-limiting factors, a self-limiting growth model, such as a logistic model, accounts for self-competition within the tumor cell population for resources like space and nutrients. An exponential growth model is reasonable to use for early stage growth, but a self-limiting growth model is often more appropriate for later stage growth. Therefore, even in the absence of tumor growth data, a modeler can consider tumor size and make a qualitative decision about whether to the model should reflect self-limiting growth.

Fig. 1

Exponential versus logistic versus growth. In early stage growth, cycle zero through about cycle 6, both models are similar, and appear to overlap. After cycle 6, the two graphs begin to diverge, and by cycle 14, the growth curves have diverged significantly. By cycle 15, the logistic growth curve has leveled off, but the exponential growth curve continues to increase

Ideally, a modeler will be able to acquire some tumor growth data, and should use the model that provides the best fit to those data. The process of fitting a model to the data also yields the appropriate model parameters. There are a number of approaches to data fitting that are possible. One approach to fitting a model to data is numerical, and makes use of packaged computational routines. In Matlab [70], for example, the simplest way to fit a curve to a data set is to plot the data points and make use of Matlab’s Basic Fitting tool from the pull-down menu of the figure window. However, the choice of curves that can be fit to the data is limited to splines and polynomials. If we want to determine how well the solutions to our growth laws of interest could fit a data set, our numerical approach requires a different approach. The steps in the process are as follows.

• 1. Choose a tumor growth data set. Many tumor growth data sets are given in units of approximate volume, surface area, cross sectional area, or relative volume. Since the growth laws we are considering represent numbers or concentrations of cells, then if the data are not already given in cell counts, convert the measures to approximate cell counts. A useful conversion metric assumes that there are generally between 1. 0 × 10⁶ cellls/mm³ and 2. 0 × 10⁶ cells/mm³, [51]. Suppose we have n data points. Let us call the time-data pairs (t _i , d _i ), where $i = 1,\cdots \,,n.$

• 2. Assume the tumor cell population, T(t), obeys a particular growth law, which in our case will be chosen from Table 1.

• 3. Solve for T(t _i ), that is, determine the model’s predicted population values at the same time points, t _i , as are used in the data set. For relatively simple ODE laws, like the ones in Table 1, it is actually possible to find explicit solution formulas. Solutions to the four growth law ODEs are given in Table 2. However, it is also acceptable to solve these ODEs numerically. There are many options for how to do this in Matlab. For example, Matlab’s ode45 routine uses an adaptive fourth and fifth order Runge–Kutta scheme, and the numerical solutions are highly accurate in most cases. Many ODEs are not easily solved analytically, but are fairly straightforward to solve numerically. Thus, a numerical approach is generally more universally applicable.

• 4. Choose a metric, or distance. If you are working in Matlab, you can write a function in an m-file that Matlab can minimize. The function should return the sum of the squares of the distances of the solution (analytic or numerical) to the data points. Suppose we are fitting the logistic curve. Then the distance D depends on the two parameters a and b, and is given by

  $$\displaystyle{D(a,b) =\sum _{ i=1}^{n}(T_{ (a,b)}(t_{i}) - d_{i})^{2}}$$

  where T _(a, b)(t _i ) is the chosen model output at time point t _i using parameters a and b. The input to the distance function includes a vector of the unknown parameters [ ab ], in addition to the known values of the data points {(t _i , d _i )}, and the solution to the ODE, T(t). In some cases, the uncertainty in the data should be taken into account when defining the distance function. For example, in many cases the data at later time points have more variability, since small differences in initial conditions can grow over time. We have often found it fruitful to use a weighted distance function, where the distance to each data point is normalized by the standard error at that time point.

• 5. Call a function minimization routine to minimize the distance function D(a, b). Here, again, there is a variety of possible approaches. Routines that look for function minima can be classified broadly as either “local” or “global” search algorithms. A “local” minimization routine will attempt to move closer to the function minimum with every step. In our case, this is done by ensuring that the distance function D(a, b) can only decrease or stay the same with every iteration of the search, but D(a, b) will never be allowed to increase. The result is that if we start our search near to a local function minimum, the local algorithm will converge fairly rapidly to that close minimum point, even if there is a “better” minimum point somewhere else in the function. Global search algorithms, on the other hand, try to broaden the search for the “best” (or “global”) minimum by occasionally allowing the distance function to increase before decreasing it again. One can think of this temporary increase in D(a, b) as the search function allowing us to climb a hill that will move us to a different, deeper, valley, in which a better minimum can be found. Local algorithms that can search for a function’s minimum include Newton’s method, the Conjugate Gradients method, and the Nelder–Mead Simplex algorithm. These approaches depend on choosing initial guesses for the values of the parameters a and b, and the accuracy of the initial guess affects the outcome of the minimization. Matlab has a built-in routine fminsearch that minimizes an input function using the Nelder–Mead algorithm. Matlab also has the routine lsqnonlin, that specifically solves nonlinear least squares problems. As opposed to local algorithms, global parameter estimation algorithms are able to test a broader range of parameters, and are therefore less likely to get “stuck” in a local minimum, but they also may not yield values as accurate as local methods can. Global approaches include algorithms such as simulated annealing [37], and Markov Chain Monte Carlo [32, 67]. Whether a local or global approach is employed, this step will return values for the model parameters (a and b in the case of logistic growth), as well as the distance measure that indicates how good the model fit is (the smaller the distance, the better the fit).

Table 2 Solutions to the four commonly used cell population growth laws

As an example, we took a published tumor growth data set from Diefenbach et al. [24], and fit each of the four growth curves to the data. This example can also be found in [19, 20]. Combining Matlab’s ode45 adaptive Runge–Kutta ODE solver to get predicted solutions for T(t) with fminsearch to find the parameter values that minimized the distance between the data points and the model prediction, yielded the fits seen in Fig. 2. The data we show are from Diefenbach[24] experiments in which groups of immuno-compromised mice were challenged with increasing levels of B16-BL6 (a melanoma cell line). Data set 1 represents the mean tumor cell count in five mice over 33 days after an initial inoculation with 10⁴ melanoma cells. Data set 2 tracks over 23 days the mean tumor growth data in five mice after an inoculation of 10⁵ cells, and Data set 3 tracks the mean growth in five mice after an inoculation of 10⁶ melanoma cells, also over 23 days. With each growth curve, we also plot the “residual:” the distance between each data point and the predicted value given by the growth curve. The best fits are those with the smallest residuals. We can see from Fig. 2 that the smallest residuals and thus the best fits appear to come from the logistic model and the von Bertalanffy model. However, the principle of “parameter parsimony” says that the model with the fewest parameters that still yields a good fit is preferable. Therefore, we should choose to use the logistic model over the von Bertalanffy model, since the logistic model requires fitting one less parameter.

Fig. 2

A comparison of four growth laws. Data from [24], which describes three different mouse experiments (marked as “Data set 1,” “Data set 2,” and “Data set 3,” respectively), are used to fit four different growth laws. Data set 1 represents the mean tumor growth values in a group of five mice after an initial challenge of 10⁴ melanoma cells. Data set 2 shows growth after a challenge with 10⁵ melanoma cells, and Data set 3 shows growth after a challenge with 10⁶ cells. The solution to each growth model is shown in solid curves, while the data points are shown by filled squares. In each case, the parameters of the models are chosen to minimize the least squares distance from the model’s predicted values to the data. Residuals showing the difference between the predicted values and the data are shown as bars below the graphs in each case. Note that the first data set has more time points than the other two, so that the last three residuals are due to differences coming only from the first data set. The two models shown in the left column, the power law and the Gompertz models, have larger residuals than do the two models depicted on the right, the logistic and the von Bertalanffy models. Since the logistic model uses fewer parameters than does von Bertalanffy, we consider logistic growth to yield the best fit to these data

The interested reader can find in [66] a larger catalog of fits of these four growth laws to ten separate tumor cell types: bladder cancer, breast cancer, colon cancer, head and neck squamous cell carcinoma, hepatocellular carcinoma, lung cancer, melanoma, ovarian cancer, pancreatic cancer, and renal cell carcinoma. In that work, tumor growth information for each cell line came from collecting published peer-reviewed data from at least five separate sources. Similar to the results of [35], the authors found that the power growth law often yielded a good fit in the sense of minimizing the residual.

3 Competition Models: Adding the Immune System

An individual’s immune system is created to help defend the body from invading pathogens such as bacteria, fungi, viruses, parasites, and in some cases, cells in the body that have become cancerous. The immune system is made up of a wide variety of cells with different functions, ranging from antigen uptake and presentation to killing of infected or mutated cells. The immune cells are created in the bone marrow and can be found in the blood and tissue of an individual. The immune cells in the blood are commonly known as the “white blood cells,” and the average human body makes about 10⁹ new white blood cells each day.

The immune response to the presence of a foreign substance is a complex cascade of events, including self-regulating feedback loops. Although there is much we have learned about the dynamics of the immune response, there is still much we do not fully understand. Details about some of the known complex workings of the immune system can be found in [54].

One goal of the immune response is to attack and destroy harmful cells. Immune cells with the ability to kill are called effector cells. In this section we introduce effector cells into the model of tumor growth. In the simplest realization, we use a competition model consisting of a system of two differential equations: one equation describing the growth of the tumor population, and one equation describing the growth of the effector cell population.

Early tumor–immune models used the “predator–prey” relationship developed by Lotka in 1910, and then used by Kolmogorov and subsequently by Volterra in 1925 to describe the fate of fish populations in the Adriatic [1, 43, 71]. In the context of tumor growth, effector cells play the role of the predators, and tumor cells are the prey. Let T denote the population of tumor cells, and E the population of effector cells. The classical predator–prey relationship assumes:

• 1. the prey will grow in the absence of the predator;

• 2. interactions between predator and prey are harmful to the prey but beneficial to the predator;

• 3. the predators will die in the absence of prey;

• 4. the number of interactions between predators and prey is proportional to the product of the two populations.

If we describe the growth of the tumor population using a logistic function, these assumptions yield the following system of differential equations.

Simplest predator–prey model of tumor (prey) and effector–immune (predator) interactions:

$$\displaystyle\begin{array}{rcl} \mbox{ Tumor:} \ \ \ \frac{dT} {dt} & =& rT(1 - bT) - c_{1}TE{}\end{array}$$

(1)

$$\displaystyle\begin{array}{rcl} \mathit{Effector:\quad }\frac{dE} {dt} & =& -dE + c_{2}TE\ {}\end{array}$$

(2)

where c ₁, c ₂, d and r are constants.

The interaction terms in Eqs. (1)–(2) have a “mass-action” form, reflecting Assumption 4, that the total number of encounters between predators and prey are proportional to the product of the two populations. This follows from a well-mixed condition, i.e. we assume that each predator is equally likely to encounter each prey. The discerning reader might note that this will not be the case in the context of the immune response to solid tumors in vivo, since immune cells won’t have equal access to all of the tumor cells. We discuss this further in Sect. 5.

Another problem with this simple model is that Assumptions 2 and 3 are not biologically realistic in the context of tumor–immune interactions. Effector cells can kill tumor cells in one of two ways: by damaging the tumor cell’s membrane using a protein called perforin, or by initiating apoptosis (programmed cell death) via another protein called FasL. Since effector cells produce these proteins in a limited amount, each interaction decreases their ability to kill in the future. We therefore introduce a negative inactivation term into Eq. (2). Counteracting this negative effect is the fact that the presence of the tumor cells stimulates the production of new immune cells, and the recruitment of these immune cells to the site of the tumor However, there is some limit to the rate at which the body can produce these cells. We therefore introduce a positive rate-limiting recruitment term in the Effector cell equation shown in Fig. 3.

Effector immune cells are present in the body even in the absence of a specific threat. This “standing army” of cells is created in the bone marrow, and distributes itself in the tissues, blood and organs in search of harmful cells. We therefore include in the simple effector–tumor model a constant source rate of effector cells, σ, noting that in reality this rate will change with the overall condition of the host, as well in response to complex regulatory signals from the immune system. Putting these terms together gives a two-population model of the tumor–immune response:

Fig. 3

Saturating recruitment term. This type of term occurs frequently in biological and physical models where rates cannot be infinite

Two-population model of tumor and effector–immune interactions:

$$\displaystyle\begin{array}{rcl} \mbox{ Tumor:}\frac{dT} {dt} & =& rT(1 - bT) - c_{1}TE{}\end{array}$$

(3)

$$\displaystyle\begin{array}{rcl} \mbox{ Effector:}\ \ \ \frac{dE} {dt} & =& \sigma + \frac{\rho T} {s + T} - c_{2}TE - dE\ {}\end{array}$$

(4)

where c ₁, c ₂, d, σ, ρ, s and r are constants.

This two-population model has been useful in describing observed behavior that was mysterious to clinicians. For example, in the work of Kuznetsov et al. [45, 46], in which the nonlinear dynamics of immunogenic tumors are examined, this tumor–effector model is shown to exhibit oscillatory growth patterns in tumors, as well as dormancy and “creeping through”: when the tumor stays very small for a relatively long period of time, and subsequently grows to be dangerously large (Fig. 4). This model also demonstrates that two simulated patients could begin with almost identical characteristics (IC1 and IC2 in Fig. 4), but one has a progressive disease (IC2) while the immune response of the other patient is able to keep the tumor relatively small (IC1). Note that, in this case, it is only the initial number of immune cells that makes the difference, and that the results are non-intuitive: a slightly lower initial immune response (IC1) results in a smaller tumor. This non-intuitive behavior can be understood by knowing the geometry of the phase space of the dynamical system: a separatrix, the stable manifold of the unstable, saddle equilibrium separates the basins of attraction of the two stable equilibria. Initial conditions close to the basin boundaries, but on opposite sides of the separatrix, give rise to trajectories with drastically different long-term behavior.

In this and other mathematical models, the cyclical behavior of the tumor is directly attributable to the interaction of the tumor with the immune system. In [16], the authors also use a single effector population to represent the immune response, and are able to demonstrate the critical role this effector response plays in the process of tumor elimination, even when chemotherapy treatments are given. We discuss models with treatments in Sect. 7.

Fig. 4

Simulations of the two-population model (Eqs. 3–4) showing sensitivity to initial conditions and the “creeping through” effect. The separatrix or stable manifold of the saddle equilibrium is shown as a dashed line in the left panel. Two simulations are shown: one with initial conditions E(0) = 6. 5558 (labeled “IC 1” in red) and one with E(0) = 6. 8777 (labeled “IC 2” in blue). Both simulations have initial tumor values at T(0) = 126. 6807. Left panel The two trajectories are shown in the sate space: in both trajectories, the tumor values initially get very small and remain there for a while. The first trajectory (IC1) is in the basin of attraction of the low tumor equilibrium, and it spirals towards it. The second trajectory (IC2) is in the basin of attraction of the large tumor equilibrium, which it approaches quickly after the initial “dormant” period. Note the logarithmic scale in the left panel. Right panel The same two trajectories are shown over time. Only the tumor populations are plotted in the right panel. Units are 10⁶ cells. The parameter values used in these simulations are $a = 1.636,b = 0.002,d = 0.3743,s = 20.19,c_{1} = 1,c_{2} = 0.00311,\rho = 1.131$ and σ = 0. 06

4 The Innate and Adaptive Immune Response

As we build a mathematical model, our goal is to keep the model as simple as possible while still addressing the question of interest. If the model is found to be too simple, we then add complexity in steps. The simple model given in Eqs. (3) and (4) assumes that the response of the immune system can be represented by a single “effector” cell population. This simplification of the immune system works well when modeling clinically observed tumor–immune behaviors such as tumor dormancy, oscillations in tumor size, and spontaneous tumor regression.

This simplified single-population representation of the immune system is obviously not sufficient, however, to address questions specific to the roles different components of the immune response play in the evolution of a tumor. The next question we will address, as we continue to build and refine our model, is driven by the results of a set of experiments by Diefenbach et al. In these experiments, mouse tumor cell lines are modified to express higher levels of immune stimulating NKG2D ligands, and the responses of both the “innate” and “specific” components of the immune system are observed.

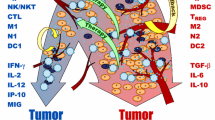
Immune cells called NK “Natural Killer” cells, are part of the innate, or non-specific, immune response. Killer T “Thymus” cells are part of the specific, or adaptive, immune response, and are activated differently from NK cells. The Killer T cells are also referred to as CTL “Cytotoxic T Lymphocyte” cells, or CD8⁺ T cells (which distinguishes them from CD4⁺ T helper cells). Both NK cells and Killer T cells come from a common lymphoid progenitor, and once activated, are both called “effector” cells. We next briefly discuss the differences between the innate and specific responses and discuss their behaviors in very general terms before introducing the model in Sect. 6 that includes these as separate populations.

The innate immune response, which includes NK cells, is an early defense against pathogens. The NK cells patrol the body, searching for and killing cells that they do not recognize as “self” cells (belonging to the body). NK cells are large granular lymphocytes which do not express markers of either T or B-cell lineage. NK cells recognize and destroy tumor cells, among others, independent of prior exposure. Natural killer cells are thought to play a key role in preventing the development of clinical cancer by killing abnormal cells before they multiply and grow. One way NK cells recognize that a potential target cell is a “self” cell is when the target cell presents self antigens through MHC class I receptors on its surface. When an NK cell comes in contact with a potential target cell, kill-activating receptors attach to common glycoproteins on the potential target cell, and the NK cell is primed to kill. However, if the target cell is expressing self antigens in the MHC-I receptor, when the NK cell binds to the MHC-I-self-antigen complex, the kill signal is interrupted and neutralized, and the potential target cell remains unharmed. In the case that the target cell is not expressing a self antigen in the MHC-I receptor, the activated NK cell will continue in kill mode, releasing perforin and granzymes, leading to the destruction of the target cell. The NK cell will also continue in kill mode if the target cell is simply not expressing MHC-I receptors on its surface. Downregulated MHC-I receptor expression means that the NK cell cannot bind to that receptor, and there therefore is nothing to inhibit the NK cell’s kill signal. In some cancer cells, MHC-I receptors are down-regulated on the cell surface, and are therefore susceptible to NK cell attack. In a sense, when a potential target cell expresses the self-antigen-MHC-I receptor complex, this can be thought of as the cell knowing the “secret handshake,” which allows it to escape NK cell patrols unharmed.

Killer T cells are unlike NK cells in that they must first be primed to recognize a particular antigen, and in the case of cancer, to recognize a tumor-specific antigen. The killer T cells, which carry the CD3⁺ marker, are morphologically small lymphocytes in the peripheral blood. They develop in the thymus and mediate the immune system’s response to infected or malignant cells. These CD3⁺CD8⁺ T cells (or just “CD8⁺” T cells) are a critical subpopulation of T-lymphocytes that can be cytotoxic to tumor cells provided previous sensitization has occurred. CD8⁺ T cells are able to kill tumor cells through recognition of the tumor-specific antigen presented on MHC-I receptors on the surface of the tumor cell. The tumor-antigen specific T cell binds to the MHC-I-tumor-antigen complex. Once bound, the CD8⁺ T cell is triggered to release perforin and granzymes, leading to the destruction of the target tumor cell. The CD8⁺ T cell can be thought of as a “police dog trained in scent discrimination”—it first has to be taught what its target is, and only then, can it seek out that specific target.

In summary, both NK cells and CTL cells must come in contact with target tumor cells in order to be able to kill them. The NK cells need no priming, are constantly on patrol, and kill tumor cells when they do not recognized them as “self.” The CTL cells, on the other hand, must first be primed to recognize antigen specific to the tumor cells, and only then will be able to destroy the target tumor cells.

5 Estimating Kill Rates from Data: The de Pillis–Radunskaya Law

In this section we explore how the differences between the innate and adaptive immune response manifest themselves in a mathematical model of tumor–immune interactions. In particular, we want to look more closely at the “kill rate” term given as c ₁ TE in Eq. (3). If we divide this term by the number of tumor cells, T, we get the “fractional cell kill rate”, which in this simplest mass-action setting is proportional to the number of effector cells. In the context of predator–prey dynamics, the mass-action form is not always appropriate, and the ecological literature discusses alternative forms, (see [2] and the references therein). As we mentioned in Sect. 3, a mass-action kill rate assumes that all immune cells are equally likely to interact with any tumor cell: it assumes spatial homogeneity. In reality, however, this is not necessarily the case. In the case of the adaptive immune response, CTLs are recruited to the tumor site by the presence of specific chemicals—not all tumor cells will be equally accessible to this type of attack. A mass-action form of cell kill also precludes “resource sharing”: the notion that the number of predators per prey affects the probability of a kill, and hence the benefit to the predator. Resource-sharing suggests that the fractional cell kill will be a function of the ratio of predator to prey.

To determine the fractional cell kill dynamics, data from chromium release assays published in [24, 26] were used. Chromium release assays determine the ability of CD8⁺ T cells to lyse target cells expressing specific ligands. The assays in both [24, 26] were standard 4 h ⁵¹Cr release assays. Standard techniques exist for collecting, storing, and co-culturing patients’ immune cells with tumor cells, a procedure which can be implemented before the onset of treatment, or anytime thereafter. The lytic activity of these cells can then be analyzed with the assay (see, e.g., approaches referenced in [26]).

We rewrite Eq. (3) in the general form:

$$\displaystyle{ \frac{dT} {dt} = rT(1 - bT) - g(E,T)T. }$$

(5)

The function g(E, T) is the fractional cell kill rate, sometimes called the “functional response”. In order to determine which fractional cell kill term best fit the data, we performed data fitting experiments with two different functional responses: one that depends only on the number of effector cells, and the other that depends on the ratio of effector to tumor cells.

$$\displaystyle\begin{array}{rcl} \mbox{ Power Form}\quad g(E,T)& =& cE^{\lambda };{}\end{array}$$

(6)

$$\displaystyle\begin{array}{rcl} \mbox{ Rational Form}\quad g(E,T)& =& d \frac{(E/T)^{\lambda }} {s + (E/T)^{\lambda }}.{}\end{array}$$

(7)

We note that the Power Form has fewer parameters than the Rational Form. Therefore, if we get good fits using both the Power Form and the Rational Form, we should select the Power Form, following the Principle of Parsimony.

Fig. 5

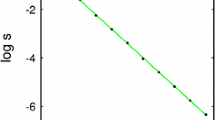
Comparison of mathematical cell lysis laws. Top row NK-Cell Lysis. The top graph shows model predictions smooth curves) plotted with experimental data (squares and circles) from [24] on RMA cells. The shallow curve predicts lysis percentages for the control cells, while the steep curve predicts lysis percentages for the ligand-transduced cells. Center and bottom row CD8⁺ T-Tumor Cell Lysis. The second row of graphs plots experimental data points (circles and squares) taken from [24] against model cell lysis predictions (solid lines). The center graphs show the power law prediction and the rational law prediction against lysis data for tumor cells whose primary and secondary challenges were with control-transduced tumor cells (RMA cells). The bottom row shows the same comparison for tumor cells whose primary and secondary challenges were with ligand-transduced cells (RMA cells transduced with Rae1β ligand)

Using cell lysis data from [24], we employed an iterative process to find the parameters c and λ in the Power Form that minimized the distance between the data points and the predicted percent lysis curves generated by the model over a range of c and λ values. For each [c, λ] pair, a prediction was made by solving a system of differential equations up to time T _final  = 4 h, with initial values from the effector:target ratio data in [24]. When using data from assays using only NK cells, the Power Form provided a good fit, with the best-fit exponent begin λ ≈ 1. Since a good mathematical model will be one in which the desired behaviors of the system are captured using the simplest mathematics possible, we chose to keep the mass-action form, $g(E,T) = -cE$, to describe the effect of the NK cells on tumor cells. In fact, the optimal value of c determined using our algorithm reproduced the lysis rate data extremely well (see Fig. 5, top row).

However, when fitting for parameters c and λ for the CD8⁺ T cell kill term, we found that the power form produced growth curves for T that were not particularly good fits to the data provided in [24]. Instead, we found that we could produce curves that better fit the data by allowing this term to have the rational form given in Eq. (7), for which we also had to determine parameter s. In (7), the exponent λ represents how the lysis rate depends on the effector:target ratio, the parameter s affects the steepness of the curve, and parameter d gives the maximum lysis rate.

We note that the additional parameter in Eq. (7) gives three degrees of freedom, so that a better fit to the data should be expected using the rational form. However, since the observations in [24] give five data points for each cell-type considered, the closeness of fit to the data supports the idea that the form of this term is correct. In particular, both in vitro and in vivo experiments indicate that percent lysis appears to be a function of the ratio of CD8⁺ T cells to tumor cells, explaining the dependence on the ratio (E∕T). Furthermore, the data indicate that the percent of cells lysed never exceeds a maximum, a saturation effect that is reflected by the rational form given in Eq. (7).

This saturation effect highlights the fact that the NK cells and CD8⁺ T cells are interacting with tumor cells in a qualitatively different way, since there is no saturation level for the NK cell competition term. It may be that the NK cell-kill rate could achieve saturation as well in theory, but in practice this does not occur. On the other hand, it may be that the antigen-specific T-cells follow this curve to saturation because they are targeting a specific tumor type, and are therefore more effective in terms of cell–cell interactions.

For conciseness, we will represent the rational form for the fractional cell kill rate with the letter D, and refer to the fact that cell lysis rates by activated CD8⁺ T-cells agree with this form as the de Pillis–Radunskaya Law.

Fig. 6

Model validation using human data from [26]. Presented here is a comparison between the power form and the rational form in describing human (CD8⁺) T-tumor lysis, as was done in Fig. 5 for mouse data. In each graph, two separate simulations are plotted along with data from two different patients who experienced regression of melanoma after receiving TIL treatment. The data show results of cytotoxicity assays with TILs taken 7 days after cell transfer. The model predictions are represented by the smooth curves, while the experimental data are represented by squares for patient nine and triangles for patient 10. Note, once again, that the rational form for predicting (CD8⁺) T-tumor lysis rates as a function of the effector:target ratio (as depicted in the lower graph) provides a much better fit to the experimental data than does the power form (as depicted in the top graph)

The de Pillis–Radunskaya Law:

For tumor-specific effector cells such as CD8⁺ T-cells, the fractional kill rate is given by:

$$\displaystyle{ g(E,T) = D = d \frac{(E/T)^{\lambda }} {s + (E/T)^{\lambda }} = d \frac{E^{\lambda }} {sT^{\lambda } + E^{\lambda }} }$$

(8)

The ratio-dependent form for the fractional cell kill term is mainly phenomenological, in the sense that it models observable outcomes, not direct underlying mechanisms. It is not immediately clear what the individual components of this term represent biologically. The use of phenomenological dynamics in modeling biological processes is quite common and can serve to provide predictive capabilities in the model. Such descriptive (as opposed to explanatory) dynamics are frequently used as a foundation on which to build models of tumor development. For example, see the comparison of several phenomenological tumor growth models presented in [7], p. 239. Perhaps future investigations may elucidate the the underlying mechanisms that give rise to the rational form of the fractional cell kill rate in the context of tumor–immune interactions.

5.1 Validation of the de Pillis–Radunskaya Law with Human Data

In order to validate the fundamental model dynamics with respect to the new rational form of the tumor-specific cell lysis term, we performed another comparison of the power form versus rational form predictions, this time using human (CD8⁺) T-tumor lysis data from [26]. Figure 6 shows the results of this comparison. The top graph shows the power–law predictions plotted against (CD8⁺) T-tumor lysis data for two separate patients. It is clear that the power–law prediction does not fit the data particularly well. On the other hand, the bottom graph shows the prediction using our newly introduced rational law. In this case, the model can predict cell lysis quite accurately, even when applied to this human data set.

For this particular set of data, effector cells are fairly efficient at lysing tumor cells, with a maximum lysis rate around 60 %. Note that, as with the ligand-transduced mouse data, the difference between the power form and the rational form fractional cell kill rates is quite pronounced, once again indicating that the rational form is particularly well suited to simulating cases in which effector cell lysis rates are relatively strong.

It is necessary in each case to find the parameters which will describe the particular type of tumor–immune interaction under study. The two data sets pictured here underline a feature inherent in the modeling process: there is a wide variety of cell behavior between any two different patients. Care must therefore be taken in making sweeping statements regarding specific responses to treatments, and any quantitative information must be interpreted as one possibility, and not as a firm predictor in any given case. However, a large set of simulations, along with some analysis of the sensitivity of the model to parameter fluctuations can certainly provide a general picture of possible behaviors under certain conditions. Further comparisons may lead to new insights in the nature of the differences between different tumor types, as well as different immuno-therapeutic protocols.

Fig. 7

The bars show the residuals (errors) for the same two data sets shown in Fig. 5 (CD8⁺ T cell lysis of control-transduced and ligand-transduced tumor cells). The height of each bar shows the value predicted by the power and rational laws, minus the experimental data values at each effector:target ratio point. The difference between the power law and rational law models is most pronounced in the ligand-transduced case, in which the effector cells are far more efficient at lysing tumor cells

6 Three Population Model: Tumor, NK, CTL

In this section, we introduce the three population tumor–immune model developed in [23]. Most of the material in this chapter can also be found in [23]. This mathematical model of tumor–immune interactions sheds light on the differing roles of the Natural Killer (NK) and CD8⁺ T cells in suppressing various tumor cell lines in mice and humans. The model is driven by the results of experiments carried out by Diefenbach et al. [24], in which mice were challenged with tumor cells that were modified to be more recognizable by NK cells and CD8⁺ T cells. The responses of these two branches of the immune system to the tumor challenge were observed both separately and in conjunction with each other. After developing the model, using the methods outlined in Sect. 5 to fit the parameters both to the murine (mouse) data from [24], and also to human data provided in Dudley et al. [26]. In the human study, subjects with metastatic melanoma were treated with highly selected tumor-reactive T cells, and results were observed. Both the mouse and the human studies provide experimental information about tumor growth rates and effector to tumor cell kill (or lysis) rates. We use the model to explore the dynamics of tumor rejection, the specific role of the NK and CD8⁺ T cells, and the development of protective immunity to subsequent tumor rechallenge.

6.1 Model Development

The specific biological assumptions we took into account when developing our model equations are based on both accepted knowledge of immune system function and conclusions stated in [24, 26]. The assumptions include:

• 1. A tumor grows logistically in the absence of an immune response. This is one accepted growth model for tumors [7], and is also based on fittings of the data in [24].

• 2. Both NK and CD8⁺ T cells are capable of killing tumor cells. (See, for example, [24, 31, 40].)

• 3. Both NK and CD8⁺ T cells respond to tumor cells by expanding and increasing cytolytic activity. (See, for example, [41, 58].) Note that the level of effector cell “effectiveness” depends on both the number of cells present, as well as the individual cell’s cytotoxicity. In the model, we do not separate the measures of high-effectiveness per cell from an increase in cell population, but measure the combined overall increase in effectiveness in response to tumor.

• 4. NK cells are normally present in the body, even when no tumor cells are present, since they are part of the innate immune response. See, for example, [63].

• 5. As part of the specific immune response, active tumor-specific CD8⁺ T cells are only present in large numbers when tumor cells are present. (See, for example, [42, 63])

• 6. NK and CD8⁺ T cells become inactive after some number of encounters with tumor cells. (See, for example, [44].)

In the equations, we denote the three cell populations by:

• T(t), tumor cell population at time t

• N(t), total level of natural killer cell effectiveness at time t

• L(t), total level of tumor specific CD8⁺ T cell effectiveness at time t

6.2 Model Equations

Using the list of assumptions from above, we describe the system as three coupled differential equations, where each equation gives the rate of change of the particular cell population in terms of growth and death, cell–cell kill, cell recruitment, and cell inactivation. In particular:

• Rate of change of tumor cell population = (Growth and death rate)− (Cell–cell kill rate)

• Rate of change of active effector cell populations = (Growth and death rate) + (Recruitment rate)− (Inactivation rate)

The mathematical forms of the growth and death terms for tumor and immune cell populations will reflect Assumptions (1), (4) and (5). Assumption (2) is reflected in the cell–cell kill term, Assumption (3) gives rise to the effector cell recruitment terms, and Assumption (6) is incorporated through the effector inactivation terms.

Immune recruitment terms are generally assumed to be of a Michaelis–Menten form, (see, e.g., [46] in which Michaelis–Menten dynamics are derived for immune cell recruitment by cancer cells). See, for example, Eq. (4). These dynamics are commonly used in mathematical tumor models that include an immune component, since they allow for a saturation effect (see, e.g., [42]). In the case of the CD8⁺ T cells, in addition to being recruited by interactions with T-cell processed tumor cells through a Michaelis–Menten dynamic, additional CD8⁺ T cells are stimulated by the interaction of NK cells with tumor cells. This NK stimulation is represented by the rNT term in Eq. (11). The term rNT, representing a fraction of the number of interactions between NK cells and tumor cells, is the vehicle through which we model the fact that the specific immune response of the CD8⁺ T cells is activated only after the activation of the earlier response of innate immunity.

Substituting specific mathematical forms for each of the growth, death, recruitment, and inactivation terms yields the following system of equations:

Three-dimensional model:

$$\displaystyle\begin{array}{rcl} \frac{dT} {dt} & =& aT(1 - bT) - cNT - DT{}\end{array}$$

(9)

$$\displaystyle\begin{array}{rcl} \frac{dN} {dt} & =& \sigma -fN + \frac{gT^{2}} {h + T^{2}}N - pNT{}\end{array}$$

(10)

$$\displaystyle\begin{array}{rcl} \frac{dL} {dt} & =& -mL + \frac{jD^{2}} {k + D^{2}}L - qLT + rNT{}\end{array}$$

(11)

where

$$\displaystyle{ D = d \frac{\left (\frac{L} {T}\right )^{\lambda }} {s + \left (\frac{L} {T}\right )^{\lambda }} }$$

(12)

From [24] we were able to get data on the growth curves in the absence of an immune response, which allowed us to estimate parameters a and b. These model parameters were estimated from the data in [24] by minimizing the least-squares distance from the simulated values to the data. Data measuring the percent of IFN-γ producing immune cells as a function of ligand expression allowed us roughly to estimate immune recruitment rates stimulated both by ligand-transduced and control-transduced tumor cells. Other parameters, such as the background source rate for NK cells (σ) and death rates for immune cells (f and m), were taken from the literature, e.g. [46, 73]. Although some of these parameters are rough estimates, and may deviate from other specific data, the model as a whole qualitatively describes the observed data both in the mouse and in the human experiments.

Table 3 provides a detailed listing of the parameters in this model, along with their units, descriptions, numerical values for the simulations, and reference sources from which these values were taken. Detailed development of all terms, except for the new fractional cell kill term D which was descried in Sect. 5, can be found in [16].

6.3 Simulating Immunotherapy: Enhancing Ligand Expression

The three-dimensional model can be used to simulate the effect of enhancing ligand expression on tumor cells by allowing the relevant parameters to depend on the tumor cell type. The relevant parameters in this model are c and d, the effectiveness of the immune cells, along with g and j, the recruitment parameters.

Figure 5 (top) plots the effector:target lysis data from [24] for NK cells, along with our simulated model curves. The ligand transduced tumor cells are lysed at a higher rate by NK cells than those that are control transduced. The two values of NK-lysis parameter c estimated from the two sets of data accurately reproduce the effects of this ligand transduction.

In the bottom two rows of Fig. 5, effector:target lysis data and simulations for the CD8⁺ T cells are presented. For our experiments, four CD8⁺ T cell lysis parameters were determined through fitting to the four ligand transduction data sets of [24], and these are all able to capture the different experimental outcomes. For brevity, only the two cases representing priming and rechallenge with control-transduced cells and priming and rechallenge with ligand-transduced cells are presented in Fig. 5. Figure 5 shows the experimental data against the mathematical model prediction using the best-fit parameter values for both the power form and the new rational form of the competition term. Note that in Fig. 5 (center row) in which we compare fits to data for non-ligand transduced cells, although the difference between the fit achieved by the traditional power kill law and by the new rational kill law is not clearly visible, the numerical difference in the error term is present. This can be seen in Fig. 7. Here, we plot the numerical errors between the predictions and the data, allowing a comparison between the goodness-of-fit of the power form and rational form of the competition term. In the bottom row of Fig. 5, the superiority of the fit achieved by the rational kill law over the power kill law is visible and striking. Similarly, the numerical error bars of the right panel of Fig. 7, reflect the much smaller error achieved by the rational kill law. It appears that it is critical to employ the rational law to fit ligand transduced cell data, whereas the use of either the rational or the power law for non-ligand transduced data will give us an acceptable fit. This may indicate that the more effective the immune cells are at lysing their target cells, the more they follow a rational law dynamic.

The simulations show what this model would predict under three different experimental scenarios similar to those reported in [24]. These simulations explain some of the reported experimental observations (see [24], Figs. 2 and 3, pp. 167–168). Ligand transduced cells stimulate the immune response sufficiently to control tumor growth (Fig. 8, top right), while control-transduced tumor cells escape immune defenses (Fig. 8, top left). In the top left panel of Fig. 8, the immune system is rechallenged at day 10 after priming with control-transduced cells, and the tumor escapes surveillance. In the top right panel of Fig. 8, the immune system is again rechallenged at day 10 with control-transduced cells, but the primary challenge was with ligand-transduced cells. This simulation shows that the tumor is controlled, indicating the development of immunity. Changing ligand levels on the cells requires changes to the model parameters d, λ, and s (all the parameters involved in the rational T cell kill term D), as well as c (strength of NK cell kill), g (NK cell recruitment rate), and j (CD8⁺ T cell recruitment rate). Numerical values for these parameters with varying ligand levels are provided in Table 3.

Simulations generated by a validated mathematical model can be used to detect thresholds for immune efficacy. In Fig. 8 (bottom row), we reproduce with a computational solution of our mathematical model the qualitative results of three sets of experiments that were presented in Fig. 2, p. 167 of [24]. For the experiments in [24], groups of mice were challenged with either 10⁴, 10⁵ or 10⁶ ligand-transduced tumor cells, then tumor establishment was tracked. For our in silico simulations, we also challenge the mathematical system with these three levels of tumor cells. Figure 8 (bottom left) shows simulated tumor cell growth over time in response to these three initial levels of tumor burden in the absence of CD8⁺ T cell activity, reflecting the experiments in which the mice were depleted of CD8⁺ T cells. This simulation represents a system lacking a strong antigen-specific immune response. The system can control a small tumor, but tumor challenges of 10⁵ cells or more escape the immune system’s control.

Figure 8 (bottom center) shows simulated tumor growth outcomes for the same three experiments done in the absence of NK cells, reflecting the experiments with mice depleted of NK cells. The system is now able to control initial tumor burdens of up to 10⁵ cells, but a larger challenge of 10⁶ cells escapes immunosurveillance.

Figure 8 (bottom right) shows simulated results with both NK and CD8⁺ T cells active, reflecting the experiments on mice with intact immune systems. With both the NK cells and the CD8⁺ T cells working together, initial tumor burdens of up to 10⁶ cells are controlled.

Fig. 8

Simulations of (tumor cell)–(NK cell)–(T cell) mutual interactions over time. Top left System evolution with control-transduced primary inoculation. Ineffective response by NK cells and CD8⁺ T cells to non-ligand transduced challenge. Top right System evolution with ligand-transduced primary inoculation. Effective response by NK and CD8⁺ T cells to non-ligand transduced challenge following priming with ligand-transduced cells. Both systems are rechallenged with control-transduced cells after 10 days. Bottom row The simulations presented in these graphs are based on data provided in [24]. In each of the three cases tumor growth is plotted over time starting with three different initial tumor challenges: 10⁴, 10⁵, and 10⁶ cells. In the plots, cell populations are converted to mean surface values. Bottom left Simulation of Tumor–NK interactions in a system with CD8⁺ T cells depleted. The simulation shows that in the absence of CD8⁺ T cells, only a tumor inoculation of up to 10⁴ cells is suppressed, whereas larger challenges escape immunosurveillance. Bottom center Simulation of Tumor-(CD8⁺ T cell) interactions in a system with NK cells depleted. The simulation shows that in the absence of NK cells, tumor inoculations of up to 10⁵ cells are suppressed, whereas a larger challenge of 10⁶ cells escapes immunosurveillance. Bottom right Simulation of Tumor-(CD8⁺) T–NK interactions in a system with all immune components intact. Note that the maximum mean tumor surface area achieved in this plot is only 6 mm², as compared with 300 mm² in the previous two plots. Tumor populations of this small size are not clearly visible in the data plots provided in [24], Fig. 2, p. 167. The simulation shows that when both NK cells and CD8⁺ T cells are present, tumor inoculations of up to 10⁶ cells are suppressed

6.4 Sensitivity Analysis

In order to discover which components of the model contribute most significantly to determining final tumor size, we performed a sensitivity analysis. Model sensitivity was assessed by measuring the effect of small parameter changes on the final volume of the tumor as represented by a simulation of the system’s evolution over 25 days. Since ultimately we are interested in predicting a patient’s response to immunotherapy treatment, we used human data for the sensitivity study. In particular, the parameter set from patient 9, available in [26], and for whom lysis data are plotted with squares in Fig. 6, was used as the base point. Each parameter was perturbed from its estimated value by 1%, and the corresponding percent change in final tumor volume was calculated.

The results of this parameter sensitivity analysis for the mathematical model are shown in Fig. 9. The system in this case is found to be most sensitive to the exponent in the CD8⁺ T lysis term, λ, as well as to the tumor growth parameter a. This suggests that, in addition to the aggressiveness of the tumor, as represented by growth parameter a, even very small changes in the cytolytic effectiveness of tumor-specific T cells, as represented by shifts in the value of λ, can affect clinical outcome. This would indicate that any treatment which might enhance this effectiveness should aggressively be pursued. By contrast, the size of the tumor after 25 days is not very sensitive to the NK cell competition parameter, c. According to this model, then, the cytolytic activity of the NK cell population alone is not a determining factor in the eventual size of the tumor, and should be considered in conjunction with CD8⁺ cell activity.

6.5 Bifurcation Analysis

In addition to a parameter sensitivity analysis of the type described in Sect. 6.4, we can gain a better understanding of the overall dynamics of the system, by performing a bifurcation analysis of the system. This type of analysis gives us a global view of the system, identifying the regions in parameter space that correspond to a “health” or “diseased” state. Furthermore, if specific parameters have been identified as being critical to the progression of the disease, or if a particular treatment affects one set of parameters, a bifurcation analysis can pinpoint values of these parameters that serve as thresholds beyond which the patient’s system enters the basin of attraction of a “healthy” stable fixed point. These bifurcation points could become the goal of therapy design. We will illustrate this idea with some specific parameter sets, guided in part by the those parameters identified as “sensitive” in Sect. 6.4.

Fig. 9

This analysis shows that the tumor size is most sensitive to the CD8⁺ T cell kill parameter, λ, as well as to the tumor growth rate parameter a

Before performing the bifurcation analysis, we add a bit more realism to the model. This model expansion is motivated by our goal of exploring the effect of different treatment strategies on the progression of the tumor, which we will pursue in Sect. 7. The expanded model will reflect two additional assumptions:

• 1. Circulating lymphocyte levels can be used as a measure of patient health (see, e.g., [33, 50, 56]). The source of the NK cell population can be represented as a fraction of the circulating lymphocyte population, a simplification meant to represent the complex cascade of biological events that leads to NK cell stimulation (see, e.g., [10]).

• 2. NK cells, circulating lymphocytes and tumor cells are components of the process of stimulation and elimination of activated effector cells, a model simplification meant to reflect the self-regulatory nature of the immune system (see, e.g., [26, 31, 39]).

Assumption (1) leads to the introduction of a new state variable, C, representing the population of circulating lymphocytes, or white blood cells. These circulating lymphocytes are assumed to be replenished at a constant rate, and die off at a constant rate, unaffected by the presence of the tumor. The constant source term for the NK-cells is replaced by a source term proportional to C(t). Assumption (2) leads to a additional positive and negative terms in the CD8⁺, or L(t) equation. With these modifications, the expanded model is:

Four-dimensional model:

$$\displaystyle\begin{array}{rcl} \frac{dT} {dt} & =& aT(1 - bT) - cNT - DT{}\end{array}$$

(13)

$$\displaystyle\begin{array}{rcl} \frac{dN} {dt} & =& eC - fN + g \frac{T^{2}} {h + T^{2}}N - pNT{}\end{array}$$

(14)

$$\displaystyle\begin{array}{rcl} \frac{dL} {dt} & =& -mL + j \frac{D^{2}T^{2}} {k + D^{2}T^{2}}L - qLT + (r_{1}N + r_{2}C)T - uNL^{2}{}\end{array}$$

(15)

$$\displaystyle\begin{array}{rcl} \frac{dC} {dt} & =& \alpha -\beta C{}\end{array}$$

(16)

where D is the de Pillis–Radunskaya Law, given in Eq. (12).

6.5.1 Finding Equilibria

The first step in understanding the long-term behavior of the tumor–immune system is to identify the equilibria, and to determine their stability. Equilibria are found by setting the right-hand side of Eqs. (13)–(15) to zero. We first note that Eq. (16) decouples from (13)–(15), so that, at equilibrium we have $C_{E} =\alpha /\beta$.

Equation (13) has one zero at the “tumor-free” equilibrium at T _E  = 0, and possibly several nonzero tumor equilibria. Setting T = 0 in (14) and (15) yields one non-negative tumor-free equilibrium in four-dimensions:

$$\displaystyle{E_{0} = (T_{E},N_{E},L_{E},C_{E}) = (0, \frac{e\alpha } {\beta f},0, \frac{\alpha } {\beta }).}$$

In the case where T _E ≠ 0, the equilibria are again determined by finding the simultaneous solutions of Eqs. (13)–(16), but the values of the nonzero tumor equilibrium points must be found numerically.

Fig. 10

The nonzero equilibria are the intersections of the graphs of the functions L(T) obtained by finding the equations of the null-surfaces. There is only one nonzero positive equilibrium for the estimated parameter set

In particular, setting Eq. (14) to zero and solving for N yields

$$\displaystyle{ N_{E} = \frac{eC_{E}(h + T^{2})} {fh + (f - g)T^{2} + phT + pT^{3}} }$$

(17)

Similarly, requiring that Eq.(13) equal zero (where T ≠ 0) gives

$$\displaystyle{ D_{E} = a - abT - cN_{E} }$$

(18)

Using this expression in Eq. (12) gives an expression for the equilibrium value of L in terms of T:

$$\displaystyle{ L_{E1} = \left ( \frac{D_{E}sT^{\lambda }} {d - D_{E}}\right )^{1/\lambda }, }$$

(19)

Finally, setting Eq. (15) to zero gives

$$\displaystyle{ L^{2}(uN_{ E}) + \left (m - \frac{jD_{E}^{2}T^{2}} {k + D_{E}^{2}T^{2}} + qT\right )L - (r_{1}N_{E} + r_{2}C_{E})T = 0, }$$

(20)

which is quadratic in L. Equation (20) has two solutions for each value of T, which we shall denote L _E2(T) and L _E3(T). Equilibrium points of the system are found by determining the T-values at which the graphs of L _E2(T) and L _E3(T) intersect the graph of L _E1(T). These T values can then be used to find the equilibrium values of N and L using Eqs. (17) and (19).

Observe that there could be multiple nonzero values of T that simultaneously satisfy Eqs. (19) and (20). However, these solutions could be negative or complex-valued. For example, using the estimated set of mouse parameters given in Table 5, we find two solutions, only one of which is biologically relevant (see Fig. 10). As a system parameter is changed, other nonzero equilibria can appear (see Fig. 11), or negative equilibria can become positive, and therefore biologically feasible.

6.5.2 Stability of Equilibria

A system will move towards an equilibrium point if that point is stable, so the next step in the analysis of the long-term dynamics of the system is to investigate the stability of all equilibria. The effect of the stability of the tumor-free equilibrium on the progression of the disease is illustrated in the lower graph of Fig. 11, dashed line. For this set of parameter values, the tumor-free equilibrium is unstable, while the high-tumor equilibrium is stable. The stability of the high-tumor equilibrium implies that, in the absence of treatment, the system will inevitably return to the high-tumor state, i.e., the tumor will escape immune surveillance unless every single tumor cell is killed. Thus, in a case such as ours for which there are only two equilibria, if the tumor-free equilibrium is unstable, then in order to realistically effect a cure, any treatment must not only reduce the tumor burden, but it must also change the parameters of the system itself. The role of immunotherapy, therefore, might be interpreted in this context as a treatment which changes system parameters by, for example, permanently raising the cytolytic potential of the natural killer cells [the parameter “c” in Eq. (13)]. We note that if the system were one that admitted a very small but stable tumor, then another “healthy” state might be one for which it is possible to maintain the system at this low tumor level.

The stability of an equilibrium is typically determined by linearizing the system about the calculated values, and by determining the stability of the linearized system by explicitly solving it. (See any textbook on differential equations, for example, [6].) However, the term D in Eq. (13) poses a problem since it is not differentiable at the tumor-free equilibrium $E_{0} = (0, \frac{e\alpha } {\beta f},0, \frac{\alpha } {\beta })$, so we cannot use this technique to determine the stability of the tumor-free state.

However, we can make some relevant observations without linearizing. Suppose T is positive. We see that $\frac{dT} {dt}$ is negative if

$$\displaystyle{a(1 - bT) - cN - D < 0 \Leftrightarrow cN > a(1 - bT) - D}$$

If we assume that N is near its value at the tumor-free equilibrium: $N_{E} = \frac{e\alpha } {f\beta }$, then we get a sufficient condition for stability. Suppose N > 0. 5N _E then:

$$\displaystyle{c > \frac{2a} {N_{E}} \Rightarrow cN > c(.5N_{E}) > a > a(1 - bT) - D.}$$

Thus, if c is sufficiently large relative to the intrinsic growth rate of the tumor cells, a small tumor can be controlled by the innate immune response: the tumor population will decrease towards zero, and the tumor-free equilibrium is stable.

Similarly, suppose we assume a small tumor population: $T < \frac{1} {b} \times 10^{-3}$ (for typical values of the intrinsic carrying capacity, b, this corresponds to a tumor of fewer than 10⁵ cells, below the level of detection). Noting that $D = \frac{dL^{\lambda }} {sT^{\lambda } + L^{\lambda }} < d$, we get a condition for instability.

$$\displaystyle\begin{array}{rcl} c < \frac{.999a - d} {N} & \Rightarrow & a(1 - bT) > 0.999a > cN + d > cN + D {}\\ & \Rightarrow & \frac{dT} {dt} = T\left (a(1 - bT) - cN - D\right ) > 0 {}\\ \end{array}$$

Thus, for small enough values of c, the tumor will escape immune surveillance and the disease will progress. Note that we must have d < 0. 999 a in order for there to be a positive value of c that satisfies the first inequality above. This makes sense, since a small value of d corresponds to a low kill-rate by the CD8⁺ T cells, reflecting a less effective immune response.

By simulating the four-dimensional model with initial values close to the tumor-free equilibrium and with gradually increasing values of c, we can estimate the critical value of c, the bifurcation point, at which the tumor-free equilibrium becomes unstable. Figure 11 shows that the bifurcation point is at approximately $c_{crit} = 4.86 \times 10^{-10}\mbox{ cell}^{-1}\mbox{ day}^{-1}$, somewhat smaller than the base value of 7. 13 × 10⁻¹⁰ shown in Table 5. For this bifurcation diagram, the parameter d is set to 0. 9a ≈ 0. 39. All other parameters are those given in Table 5. Similar observations and experiments can be made with other key parameters, such as the parameter d, the maximum kill rate by CD8⁺ cells. See [15] for other examples.

At nonzero equilibrium points, a linear stability analysis can be performed since the right-hand sides of all of the differential equations are differentiable away from $T = 0,L = 0$. As an illustrative example, we show the results of this analysis as we vary the NK-cell kill rate parameter, c, from zero to a relatively large value. For very small values of c, the tumor-free equilibrium is unstable, and there is a stable, high-tumor equilibrium. This corresponds to a system with a very weak innate immune response to the tumor, and one tumor cell will reproduce, initiating the development of a large tumor. As the parameter c increases, the tumor-free equilibrium becomes stable, and a small number of tumor cells can be controlled by the immune system. The system returns to the tumor-free equilibrium, even in the absence of any treatment (Fig. 11, bottom panel).

When the tumor-free equilibrium becomes stable, a nonzero, unstable equilibrium appears, separating the two stable equilibria. The system is now bi-stable, and the goal of treatment should be to get the system into the basin of attraction of the zero-tumor equilibrium. At c ≈ 1. 45 × 10⁻⁵, the nonzero equilibria disappear in a saddle-node bifurcation. For larger values of c the system has only the stable zero-tumor equilibrium, and the disease will not progress.

Fig. 11

(Top) Bifurcation diagram showing the effect of varying the NK-kill rate, c. As c increases from zero, the tumor-free equilibrium becomes stable in a transcritical bifurcation at c _trans  ≈ 4. 86 × 10⁻¹⁰, and an unstable, nonzero equilibrium appears. In this regime the system is bi-stable. At c _sad  ≈ 3. 0 × 10⁻⁵ the high, stable equilibrium and the unstable equilibrium coalesce and disappear in a saddle-node bifurcation. (Bottom) Two solutions of the system showing tumor growth over time for two values of c, one below the transcritical bifurcation, and one above. For the smaller value of c, the small initial tumor consisting of 10 cells grows to the high tumor equilibrium, while for the larger value of c, the immune system is able to drive the tumor back to the tumor-free equilibrium. In both panels, other parameters are from Table 5, except for d, which is set to 0.3877. Initial values for the lower panel are: $(10, \frac{e\alpha } {f\beta },0, \frac{\alpha } {\beta })$

Similar analyses can be performed using any of the system parameters in order to determine conditions for the appearance or disappearance of equilibria and to determine equilibrium stability. See [15] for a bifurcation analysis of the adaptive response parameter, j.

Two bifurcations are evident in the diagram in Fig. 11. The first is a transcritical bifurcation, where the negative equilibrium becomes positive, and the zero-tumor equilibrium changes its stability. (This bifurcation occurs at values that are too small to distinguish on the diagram). Before the bifurcation, the zero-tumor equilibrium is strictly unstable: even one tumor cell will result in the system moving toward the high-tumor equilibrium. After the bifurcation, the immune system is able to control small initial tumor populations. Initial tumor populations which are controlled are said to be in the basin of attraction of the zero-tumor equilibrium. On the other hand, those which escape immune surveillance, leading the system toward the high-tumor equilibrium, are said to be in the basin of attraction of the high-tumor equilibrium. These basins are shown in Fig. 12. Note that since the state-space of the system is actually four-dimensional, what is depicted in Fig. 12 is the projection of the basins onto the Tumor-NK plane, where the values of L and C are kept at their zero-equilibrium values. Figure 12 illustrates the consequences of bi-stability, the co-existence of two, stable fixed points. If the tumor is initially very small, the tumor will be controlled by the level of immune response represented by this parameter set. However, if the tumor somehow grows larger than this threshold, perhaps due to a temporarily weakened immune system or environmental factors, then the tumor will grow to a dangerous size, even in the renewed presence of an adequate immune response. Figure 12 shows two scenarios, where the system starts in identical states, except that in one case (the dashed red line in the lower panel), the initial tumor has exactly one additional cell. This tiny change in initial values results in a drastically different outcome for the patient. The location of the basin boundary is therefore crucial in determining the outcome of the disease. In the case of a patient who has undergone chemotherapy which reduces both tumor and immune cell levels, if these levels place the system above the basin boundary then even an undetectable tumor will regrow. However, if the patient is given immunotherapy subsequent to chemotherapy, thereby pushing NK levels to the right of the basin boundary, the system will evolve toward the stable zero-tumor equilibrium, and the tumor will not regrow. This hypothetical scenario emphasizes the potential importance of combination therapy.

7 Model Extension to Simulate Chemotherapy and Immunotherapy

The next step in model development is to add terms that reflect treatment therapies. Therefore, in addition to the list of assumptions about tumor and immune system evolution given in Sects. 6.1 and 6.5, we add assumptions used in the development of therapeutic terms: Full model development and analysis details can be found in [15].

• The fraction of the tumor population killed by chemotherapy depends on the amount of drug in the system. The fraction killed has a maximum less than one, since only tumor cells in certain stages of development can be killed by chemotherapy [60].

• A fraction of NK cells, CD8⁺ T cells, and circulating lymphocytes are also killed by chemotherapy, according to a similar fractional kill curve [29].

Fig. 12

(Top) Basins of attraction of the zero-tumor and high-tumor equilibria in the bi-stable regime. Two orbits are shown that start near the basin boundary, with initial populations differing by only one tumor cell. (Bottom) Solution curves showing the evolution of the tumor population over time for the two orbits shown in the upper graph with initial values near the basin boundary. The two initial conditions are: T ₁(0) = 2. 8817259 × 10⁷ (solid blue line) and T ₂(0) = 2. 8815260 × 10⁷. Other initial values are $N(0) = 8.201 \times 10^{4},L(0) = 0,C(0) = 1.0083 \times 10^{7}$. Parameters used in these simulations: $c = 1.0 \times 10^{05},d = 0.387702$. Other parameters are those listed in Table 5

Our model, when extended to include treatment terms, not only tracks cell populations: tumor cells (T) and immune cells (circulating lymphocytes: C, NK cells: N, and cytotoxic CD8⁺ T-cells: L), but in addition will track the total number of circulating lymphocytes (or total white blood cell count in the blood stream), C(t), a chemotherapy drug blood concentration M(t) and an immunotherapy drug blood concentration I(t). In our examples, the chemotherapy term represents a non-targeted cytotoxic medication such as doxorubicin, and the immunotherapy term represents an interleukin such as IL-2.

Since broadly cytotoxic chemotherapy is damaging to all cells in the system, we include a chemotherapy drug kill term in each of the cell population equations. We use a saturation term $1 - e^{-M}$ to represent the chemotherapy fractional cell kill, noting that the effectiveness of chemotherapy is bounded: At relatively low concentrations of drug, the kill rate is nearly linear, while at higher drug concentrations, the kill rate plateaus. The mathematical term we use reflects the dose–response curves suggested by the literature [29]. We then subtract the term $K_{\phi }(1 - e^{-}M)\phi,$ from each the four cell population equations, where ϕ = T, N, L, C.

For immunotherapy treatment, we allow for CD8⁺ T activation by interleukin-2 (IL-2) immunotherapy. This “drug” is actually a naturally occurring cytokine in the human body, and its effect on the immune system’s efficacy is described mathematically with a Michaelis–Menten interaction term in the equation for L. The presence of IL-2 stimulates the production of CD8⁺ T cells, and the cascade of effects requires that we modify certain terms in the equations for T, N and L, in addition to including new treatment term equations. Details of those modifications can be found in [15]. The extended system of equations becomes:

Model with chemotherapy and immunotherapy:

$$\displaystyle\begin{array}{rcl} \frac{dT} {dt} & =& aT(1 - bT) - cNT - DT - K_{T}(1 - e^{-M})T{}\end{array}$$

(21)

$$\displaystyle\begin{array}{rcl} \frac{dN} {dt} & =& eC - fN + g \frac{T^{2}} {h + T^{2}}N - pNT - K_{N}(1 - e^{-M})N{}\end{array}$$

(22)

$$\displaystyle\begin{array}{rcl} \frac{dL} {dt} & =& -mL + j \frac{D^{2}T^{2}} {k + D^{2}T^{2}}L - qLT + (r_{1}N + r_{2}C)T \\ & & \,-uNL^{2} - K_{ L}(1 - e^{-M})L + \frac{p_{I}LI} {g_{I} + I} + v_{L}(t){}\end{array}$$

(23)

$$\displaystyle\begin{array}{rcl} \frac{dC} {dt} & =& \alpha -\beta C - K_{C}(1 - e^{-M})C{}\end{array}$$

(24)

$$\displaystyle\begin{array}{rcl} \frac{dM} {dt} & =& -\gamma M + v_{M}(t){}\end{array}$$

(25)

$$\displaystyle\begin{array}{rcl} \frac{dI} {dt} & =& -\mu _{I}I + v_{I}(t){}\end{array}$$

(26)

$$\displaystyle\begin{array}{rcl} D& =& d \frac{(L/T)^{\lambda }} {s + (L/T)^{\lambda }}{}\end{array}$$

(27)

7.1 Tumor Growth Response to Treatments: Mouse Data

For the following set of numerical experiments, our model parameter values are determined using published data both from murine experimental studies [24] and from human clinical trials [26]. When necessary, we also use previous model parameters that have been fitted to experimental curves [17, 18, 22, 46]. Tables 5 and 6 provide a full listing of all of the parameters with their units and descriptions. Full descriptions of parameter derivation for the following set of experiments can be found in [15].

The first simulation we run represents an in silico mouse that has an immune response and has been challenged with a tumor, but no treatments are administered. Simulation results are shown in Fig. 13, top left. The parameter set and initial conditions yield a scenario representing an in silico mouse in which the immune system is not strong enough to stop tumor growth. The tumor reaches carrying capacity, and we assume the mouse dies under this extreme tumor burden. The initial conditions for this situation are chosen to be a tumor of size 10⁶ cells, a circulating lymphocyte population of 1. 1 × 10⁷, a natural killer cell population of 5 × 10⁴, and a population of 100 CD8⁺ T cells. With the set of parameters in Table 5, the outcome of the simulation is sensitive to the initial conditions chosen. This set of initial conditions is meant to reflect a laboratory mouse experiment, in which an initial tumor challenge of 10⁶ cells is directly implanted into the mouse, and then the progression of the tumor is observed.

The next two simulations employ either chemotherapy or immuotherapy treatments. The chemotherapy treatment approach involves administering seven pulsed doses of chemotherapy, each dose represented by setting v _M (t) = 1 in Eq. (25) for 1 day, and given in a 14 day cycle. The immunotherapy treatment approach involves injecting 8 × 10⁸ highly activated CD8⁺ T cells from day 7 to day 8. This CD8⁺ injection is meant to represent the TIL treatments used for certain patients (see, for example, [26]).

For an initial tumor challenge of 10⁶ cells, the tumor survives despite either method of intervention. These experiments are pictured in Fig. 13, top right and bottom left.

There are also cases in which chemotherapy alone or immunotherapy alone can be effective in killing a tumor that the immune system could not kill on its own. These experimental results are not pictured here. However, the range of initial conditions for which mono-therapies are effective is relatively small in comparison to the greater effectiveness of combination treatments. This result is consistent with experimental investigations (see, for example, [49]). The next simulation represents an in silico mouse treated with both chemotherapy and immunotherapy. The chemotherapy and immunotherapy treatments given as mono-therapies above are now given simultaneously, and initial population sizes are set to the same values as in the previous experiments. Results are displayed in the bottom right image in Fig. 13.

In these simulations, combination therapy is clearly more effective in controlling tumor growth than is either individual of treatment alone. The synergistic effect of combination treatment that we observe reflects the outcomes of some laboratory studies (see, e.g., [49, 72]). In vivo, these treatments do cause undesirable side effects, some of which are due to the damage caused to the immune cells. With this model, the circulating lymphocyte level can be used as a proxy to indicate at least whether the immune health of the mouse has been damaged too much during treatment, and dosing can be modified accordingly.

Fig. 13

Mouse data. Top left No treatment. Immune system without intervention where the tumor reaches carrying capacity and the mouse “dies”. Top right Chemotherapy. The immune system response to high tumor with chemotherapy administered for 1 day in a 14 day cycle. Bottom left Immunotherapy. Immune system response to high tumor with the administration of immunotherapy from days 7 to 8. Bottom right Combination therapy. Chemotherapy and immunotherapy as previously described given simultaneously effectively control of the tumor. Parameters for all simulations are provided in Table 5

7.2 Tumor Growth Response to Treatments: Human Data

We next run model simulations using parameters taken from experimental results of two patients—“Patient 9” and “Patient 10”—from a study by Rosenberg et al. on metastatic melanoma [26]. Model parameters for both Patients 9 and 10 are summarized in Table 6.

We first look at the “human” system without treatment. In the simulations using human parameters, we set an initial tumor burden of 10⁶ cells. This experiment represents a situation in which the immune system has not become activated against the tumor cell population until the population has reached 10⁶ cells, a size which in many cases is still considered to be below the threshold of clinical detectability in a human. For this tumor, immune system strength is very important in determining whether or not the body can eliminate a tumor in the absence of treatment interventions. Simulations show that an immune system with initial values of 1 × 10⁵ natural killer cells, 1 × 10² CD8⁺ T cells, and 6 × 10¹⁰ circulating lymphocytes can be considered “healthy,” and is, in fact, sufficient to control the growth of a 10⁶ tumor challenge (images not shown). However, when the immune system is weakened, a tumor of the same 10⁶ size grows to a dangerous level in the absence of treatment interventions. A “weakened” immune system in this case has initially values set to 1 × 10³ NK cells, 10 CD8⁺ T cells, and 6 × 10⁸ circulating lymphocytes. We note that if we challenge even the “healthy” immune system with 10⁷ tumor cells (an order of magnitude larger than the 10⁶ challenge), even the healthy immune system is unable to control the tumor. This indicates that the earlier the immune system can be activated against a growing tumor, the better. We will also use the 10⁷ size challenge to test the results of treatment interventions.

Simulations of treatments show similar outcomes to the mouse experiments: We can easily find scenarios in which chemotherapy alone or immunotherapy alone is not sufficiently effective in controlling tumor growth when initial tumor size is 10⁷ cells, but in combination the therapies can successfully eliminate a tumor. We do not include all the experiments here. The reader can refer to [15] in which a larger range of simulations is presented. Here we will focus on experiments that highlight how certain treatment scenarios can differ from patient to patient, and how outcomes will be affected if a patient’s immune system is compromised. Measuring certain patient-specific immune response parameters can be important in helping to predict whether an individual will respond well to treatments.

As a proxy representing a patient’s immunological health we use the number of circulating lymphocytes in the body, and do not allow the circulating lymphocytes to drop below a threshold for which the risk of infection may be too high. In our experiments, we chose that threshold to be on the order of 10⁸ cells. This amount reflects a fraction of approximate normal white blood cell levels in an adult human (see, e.g., [63]).

Simulation results for combination treatment on Patient 9 are shown in Fig. 14, left. The combination treatment is able to eliminate a tumor of initial size 10⁷ cells, a tumor cell count that is likely to be clinically detectable. The chemotherapy regimen is given in 9 pulsed doses total, with dose strength v _M (t) = 5, and doses given once every 10 days. Initial immune strength is 1 × 10³ NK cells, 10 CD8⁺ T cells, and 6 × 10⁸ circulating lymphocytes. Immunotherapy consists of a TIL injection followed by short doses of IL-2. This mirrors the treatment that was given to Patients 9 and 10 in Rosenberg’s experiments [26], the difference being that the patients in the clinical trial were first administered immuno-depleting chemotherapy before the administration of TIL therapy. IL-2 and chemotherapy concentrations are shown in Fig. 14, right. The combination treatment given is simply a superposition of these separate chemotherapy and immunotherapy regimens. We note that, when administered separately as monotherapies, the chemotherapy treatment alone or the immunotherapy treatment alone is unsuccessful in controlling tumor.

We next run these treatment simulations using the patient specific parameters extracted from the Rosenberg et al. study [26] for Patient 10. We use the same initial conditions for the state of the immune system and the initial tumor challenge. However, several of the immune response parameters for Patient 10 (such as d and λ) differ from those of Patient 9, causing Patient 10’s CTL response to tumor cell growth to be slower. As opposed to the positive response to the combination treatment approach for Patient 9 (see Fig. 14), the parameter set for Patient 10 allows continued growth of the tumor, as seen in in Fig. 15, top left. If we wish to control the tumor, we must modify the treatment. One approach is to administer additional immunotherapy in the form of more IL-2 doses. This expansion in treatment does lead to tumor death in silico, as shown in Fig. 15, top right. It is interesting to note that in this case, tumor behavior seems to reflect tumor dormancy followed by relapse. The tumor appears to have completely died out by day 22. However, around day 79, the tumor begins to re-emerge. Without the additional IL-2 treatment given at day 80, the tumor would regrow. In order to see longer term outcomes, we ran the simulation for 2,000 days, and the tumor did re-emerge, but at levels generally considered below detectability thresholds. The tumor subsequently died out again and did not reappear. See Fig. 15, bottom left. These results indicate that the tumor population has been drawn into the stable zero tumor equilibrium at this point. Such a case in the clinic would likely be viewed as a successful case of complete remission.

Clearly, the immune system’s tumor handling capacity and response to treatment is patient specific. This is not surprising, since the combination therapy administered to thirteen patients in the Rosenberg et al. study [26] gave rise to objective clinical responses in only 6 of the 13 patients.

8 Discussion

The first model presented in this chapter incorporates tumor–immune interactions and highlights the qualitative difference in kill rates between the innate immune response (the effect of the NK cells) and the adaptive response (the effect of the CD8⁺ cells). The model, with its two different functional forms for the kill rates, provides a good fit with experimental data resulting from priming and rechallenge with different combinations of tumor cell types. The fact that two different functional forms are needed to describe the interactions between tumor cells and the two branches of the immune system suggests that laboratory experiments might be designed to illuminate the mechanisms behind the different cell interaction dynamics. Lessons might also be learned by looking at examples in ecology in which predator–prey kill rates can obey either a rational law or a power law [2]. We hypothesize that the more effective the immune cell is at killing, the more closely it follows a rational law dynamic, as given in Eq. (8).

Fig. 14

Human data, Patient 9. Combining the separately unsuccessful therapies for a 10⁷ size tumor succeeds in eliminating the tumor. Left A 10⁷ cell tumor is successfully eliminated by combining nine 1-day chemotherapy doses of strength v _M (t) = 5 every 10 days, with a boost of TILs and IL-2. 10⁹ TILs are administered from day 7 through 8. IL-2 is administered in 6 pulses from day 8 to day 11 at concentration v _I (t) = 5 × 10⁵ per pulse. Initial conditions are: 10⁷ Tumor cells, 1 × 10³ NK cells, 10 CD8⁺ T cells, 6 × 10⁸ circulating lymphocytes. Patient 9 parameters for these simulations are in Table 6. Right Drug concentrations for IL-2 and chemotherapy

The experimental and simulated results that were presented in this chapter, along with the parameter sensitivity analysis, highlight the importance of CD8⁺ T cell activation on the time course of the disease. Model results appear to indicate that in order to promote tumor regression, it may be necessary (although perhaps not sufficient) to focus on increasing CD8⁺ T cell activity. In fact, we propose that there may be a direct positive correlation between the patient-specific efficacy of the CD8⁺ T cell response as measured by cytotoxicity assays, and the likelihood of a patient responding favorably to certain immunotherapy treatments.

Fig. 15

Human data, Patient 10. Top left Combination therapy fails to eliminate the 10⁷ cell tumor in Patient 10 with more slowly responding immune system, and initial immune strength of 10³ NK cells, 10 CD8⁺ T cells, and 6 × 10⁸ circulating lymphocytes. 10⁹ TILs are administered from days 7 through 8. IL-2 is administered in 6 pulses from day 8 to day 11 at concentration v _I (t) = 5 × 10⁶ per pulse. Top right Combination therapy kills the 10⁷ cell tumor in Patient 10. Treatment is identical to that in the top left panel, with the exception that additional pulses of IL-2 are administered from days 8 through 13, 20 through 25 and 80 through 90. Bottom left The same effective combination therapy as given in the top right panel and as shown in the bottom right panel, but viewed over 2,000 days. Tumor is eventually eliminated. Bottom right Concentrations for IL-2 and chemotherapy implemented in the simulations shown in the top right and bottom left panels. Patient 10 parameters are provided in Table 6

In the final sections of the chapter, we extended the first model to include immuno-modulating therapies. With this extended model, we could test treatment strategies that used immunotherapies and cancer vaccines in conjunction with chemotherapy.

Through an analysis of the system of equations in the absence of chemotherapy or immunotherapy, we determined the equilibrium points of the system along with the criteria for stability. In some parameter ranges, the system exhibited bi-stability, where two stable equilibria co-exist. One of these stable equilibria represents a disease-free state with no tumor cells, and the other represents an unhealthy state where the tumor grows to a significant size. In this bistable situation, a treatment that moves the system into the basin of attraction of the stable tumor-free equilibrium by, for example, reducing the tumor population (through surgery or radiation) and/or by increasing the number of immune cells (through adoptive cell transfer) could lead to a “cured” state. Once the system has moved across the boundary into the zero-tumor basin of attraction, small tumors that arise can be controlled by the immune response—as long as the system parameters do not change too much.

In other parameter regimes, the tumor-free equilibrium is unstable, and therefore it is not sufficient merely to reduce the tumor size. In this case of an unstable tumor-free equilibrium, even a few tumor cells will be able to escape the immune surveillance. A successful treatment must be able to change the system parameters in order to force this equilibrium to become stable. We note that in [30], a similar conclusion is reached through a different modeling approach: in this case, too, it is shown that unless system parameters are altered in some way, cytotoxic drugs alone are often not sufficient to control even a very small tumor.

As can be seen in Figs. 14 and 15, simulations using parameter sets from two different patients [26] show that treatment efficacy depends strongly on patient-specific parameter values. Assays exist that allow for measurement of some of the significant patient specific parameters used. For example, through chromium release assays one can measure patient specific immune-tumor lysis rates, while tumor cell reproduction rates can also be observed and measured in the laboratory. Changes in these measurable parameters clearly affect system outcomes. Although not all system parameters are yet measurable, those that are help to provide a good start in designing customized treatment protocols for individuals.

The development of combination immunotherapy–chemotherapy protocols for treating certain forms of cancer is a promising strategy in cancer treatment research. In some preliminary clinical studies, immunotherapy has been found to be most effective when administered in conjunction with chemotherapy [49], and this qualitative result has been borne out in our mathematical simulations, as shown in Figs. 14 and 15. In this chapter, combination treatments included vaccine therapy, activated anticancer-cell transfer (TIL injections), and activation-protein injections (IL-2 injections) together with chemotherapy. Mathematical models of other forms of immunotherapy and combination chemo-immunotherapy (such as dendritic cell treatments, regulatory T cell suppression, and targeted monoclonal antibody therapies) can be found in the works of, for example, [13, 14, 21]. The mathematical models presented in this chapter can be used as a springboard for further study and development of patient-specific cancer treatment protocols.

9 Appendix: Nomenclature and Parameter Values

Here we list all of the parameters used in the model, their meaning and their estimated values. Tables 3 and 4 are fits to the three-dimensional model, while Tables 5 and 6 are fits to the four-dimensional model. Tables 3 and 5 are used in the experiments run to simulate the mouse experiments from [24]. Tables 4 and 6 apply to the human data from [26]. For detailed derivations, see [15, 23].

Table 3 Estimated parameter values: based on mouse experiments provided in [24]

Table 4 Estimated parameter values: patient specific parameters used based on data in [26] and other sources

Table 5 Estimated mouse parameter values

Table 6 Estimated human parameter values