1 Introduction

Studied here, we focus on the Eq. (3) in reference [1], which is a mesoscale ocean model that takes into account complete Coriolis parameters, other factors such as dissipation, topography, adiabatic heating are not considered. In this document, the mass conservation equation and the momentum equation can be written as follows:

$$\left\{ {\begin{array}{*{20}l} {\frac{\partial \alpha }{{\partial t}} + \alpha \frac{\partial \alpha }{{\partial x}} + \beta \frac{\partial \alpha }{{\partial y}} + \gamma \frac{\partial \alpha }{{\partial z}} = - \frac{1}{{d_{0} }}\frac{\partial p}{{\partial x}} + f\beta - f^{\prime}\gamma ,} \hfill \\ {\frac{\partial \beta }{{\partial t}} + \alpha \frac{\partial \beta }{{\partial x}} + \beta \frac{\partial \beta }{{\partial y}} + \gamma \frac{\partial \beta }{{\partial z}} = - \frac{1}{{d_{0} }}\frac{\partial p}{{\partial y}} - f\alpha ,} \hfill \\ {\frac{\partial \gamma }{{\partial t}} + \alpha \frac{\partial \gamma }{{\partial x}} + \beta \frac{\partial \gamma }{{\partial y}} + \gamma \frac{\partial \gamma }{{\partial z}} = - \frac{1}{{d_{0} }}\frac{\partial p}{{\partial z}} + g\frac{\psi }{{\psi_{0} }} + f^{\prime}\alpha ,} \hfill \\ {\frac{\partial \psi }{{\partial t}} + \alpha \frac{\partial \psi }{{\partial x}} + \beta \frac{\partial \psi }{{\partial y}} + \gamma \frac{{{\text{d}}\psi_{0} }}{{{\text{d}}z}} = 0,} \hfill \\ {\frac{{\partial (d_{0} \alpha )}}{\partial x} + \frac{{\partial (d_{0} \beta )}}{\partial y} + \frac{{\partial (d_{0} \gamma )}}{\partial z} = 0,} \hfill \\ \end{array} } \right.$$
(1)

where \(x\) is the zonal coordinate, and \(\alpha\) is the zonal velocity; \(y\) is the meridional coordinate, and \(\beta\) is the meridional velocity; \(z\) is the vertical coordinate, and \(\gamma\) is the vertical velocity. In the whole ambient flow field, \(d_{0}\) represents density and \(\psi_{0}\) represents potential temperature, respectively, they are functions of \(z\), and the temperature stratification is expressed as \(\frac{{{\text{d}}\psi_{0} }}{{{\text{d}}z}}\). \(\psi\) represents the perturbation of temperature. The symbol \(f\), \(f^{\prime}\), respectively, denote the vertical component and horizontal component. The physical meanings of other symbols are in the literature [1]. An extended KdV equation is gained as model to evolve equatorial near-inertial waves via perturbation expansions and the multiple scale method, as follows:

$$C\frac{\partial A}{{\partial T}} + C_{1} \frac{\partial A}{{\partial \xi }} + C_{2} A\frac{\partial A}{{\partial \xi }} + C_{3} \frac{{\partial^{3} A}}{{\partial \xi^{3} }} = 0.$$
(2)

where \(C = - \iint\limits_{y,z} {\frac{{\tilde{q}_{0}^{*} }}{{\overline{v}_{x} - c}}}\left( {L_{3} (\tilde{t}_{0} ) + L_{4} (\tilde{v}_{x0} )} \right){\text{d}}y{\text{d}}z,\)

$$C_{1} = \gamma \iint\limits_{y,z} {\frac{{\tilde{q}_{0}^{*} }}{{\overline{v}_{x} - c}}}L_{2} (\tilde{v}_{x0} )){\text{d}}y{\text{d}}z,$$
$$\begin{aligned} C_{2} &= - \iint\limits_{y,z} {\frac{{\tilde{q}_{0}^{*} }}{{\overline{v}_{x} - c}}}\left\{ {L_{3} \left[ {\frac{1}{{d_{s} }}\left( {\tilde{v}_{x0} \tilde{t}_{0} + \tilde{v}_{y0} \frac{{\partial \tilde{t}_{0} }}{\partial y}} \right)} \right] + L_{4} \left[ {\frac{1}{{d_{s} }}\left( {\tilde{v}^{2}_{x0} + \tilde{v}_{y0} \frac{{\partial \tilde{v}_{x0} }}{\partial y} + \tilde{v}_{z0} \frac{{\partial \tilde{v}_{x0} }}{\partial z}} \right)} \right]} \right\}{\text{d}}y{\text{d}}z,\\ \;C_{3} &= - \iint\limits_{y,z} {\frac{{\tilde{q}_{0}^{*} }}{{\overline{v}_{x} - c}}}L_{1} \left[ {(\overline{v}_{x} - c)\tilde{v}_{y0} } \right]{\text{d}}y{\text{d}}z.\end{aligned}$$

Equation (2) can be reduced to:

$$\frac{\partial F}{{\partial T}} + a_{1} F\frac{\partial F}{{\partial \xi }} + a_{2} \frac{{\partial^{3} F}}{{\partial \xi^{3} }} + a_{3} \frac{\partial F}{{\partial \xi }} = 0.$$
(3)

where \(a_{1} = \frac{{C_{2} }}{C}\), \(a_{2} = \frac{{C_{3} }}{C}\), \(a_{3} = \frac{{C_{1} }}{C}\). One key coefficient \(a_{3}\) represents the horizontal component of Coriolis parameters, \(a_{3}\) took effect by controlling the velocity feature of the near-inertial waves. In the reference [1], the Eq. (3) was solved by applying Jacobian elliptic function expansions; periodic and soliton solutions are obtained. Apparently, we need more meaningful exact solutions which are not available; the horizontal Coriolis parameter effects on solitons, breathers, rogue wave and interactions have not discussed.

Actually, exact solutions of nonlinear equations have an important role in many fields, like mechanics [2], plasma physics [3, 4], optics [5], acoustics [6], thermodynamics [7]. Many researchers have studied on the exact solutions of the nonlinear equations, counting in solitons [8,9,10,11], breathers [12,13,14,15,16,17,18,19], and rouge [20,21,22]. Breathers are local wave solutions with period, non-mediocre properties caused by collision reaction of breathers, so breathers are often used to explain the modulation instability and the generation of rouge waves [23]. Rouge solution is one of rational function solution with local characteristics of space–time; it shows up in a short period, large amplitude, extremely destructive. It suddenly appears and disappears, and the crest is extremely steep, posing a great threat to ships in the sea [24]. Many researchers also focus on interaction solutions between soliton and other solutions [25,26,27,28,29]. To explain some physical phenomena further, we need to construct interaction solutions among nonlinear waves.

There have many ways to get the exact solutions of nonlinear extended equations, for instance, the Hirota bilinear method [30,31,32,33,34,35], inverse scattering transformation [36,37,38], symbolic computation approach [39,40,41], Lie group method [42,43,44], Darboux transformation [45,46,47], Bäcklund transformation [48,49,50], and so on. The Hirota bilinear transformation uses small parameter perturbation method, and the solution of a series expansion is substituted into the bilinear equation, then compare the coefficients of the parameters in the equation to the same power, so we can get the specific expressions of the one-soliton, muti-solitons of the original equation, and the general expressions for the N-soliton can be obtained by mathematical induction. The Hirota bilinear transformation uses bilinear derivatives as a tool, and this tool has one on one relationship to the equation that is being solved. It is easy to calculate and has solved a large number of nonlinear partial differential equations effectively [51].

This paper mainly studied following points: Firstly, Hirota bilinear equation of the extended equation is obtained. Secondly, the N-soliton solutions are gained by using small parameter perturbation, breather, rogue wave, and interaction between one-soliton and one-breather, interaction between two-soliton and one-rogue that are found by using the symbolic calculation method; the solution images are given with the help of Mathematica software. Lastly, it can be found that the Rossby waves rotate clockwise with the Coriolis parameter \(a_{3}\) increasing. when the wave is periodic, the period decreases with the increasing of the horizontal Coriolis parameters \(a_{3}\). When studying the interaction, we found that a change in \(a_{3}\) does not cause a change in the moment of the interaction.

2 The Hirota bilinear form

Under the following variable transformation:

$$u = 2(\ln F)_{\xi \xi } .$$
(4)

where \(u = u(\xi ,T)\), \(F = F(\xi ,T)\), and \(a_{1} = 6a_{2}\).

Substituting (4) into (3), the Eq. (3) is transformed into the below Hirota bilinear form:

$$(D_{\xi } D_{T} + a_{2} D_{\xi }^{4} + a_{3} D_{\xi }^{2} )F \cdot F = 0.$$
(5)

Then, there:

$$\begin{aligned} & D_{\xi } D_{T} F \cdot F = 2(F_{\xi T} F - F_{\xi } F_{T} ), \\ & D_{\xi }^{4} F \cdot F = 2(F_{\xi \xi \xi \xi } F - 4F_{\xi } F_{\xi \xi \xi } + 3F_{\xi \xi }^{2} ), \\ & D_{\xi }^{2} F \cdot F = 2(F_{\xi \xi } F - F_{\xi }^{2} ). \\ \end{aligned}$$
(6)

3 The soliton solutions

Next, we follow the steps of the Hirota bilinear method to get the N-soliton solution of Eq. (3), substituting (6) into (5), we get:

$$(F_{\xi T} F - F_{\xi } F_{T} ) + a_{2} (F_{\xi \xi \xi \xi } F - 4F_{\xi } F_{\xi \xi \xi } + 3F_{\xi \xi }^{2} ) + a_{3} (F_{\xi \xi } F - F_{\xi }^{2} ) = 0.$$
(7)

Using bilinear form and small parameter perturbation method suppose:

$$F = 1 + \varepsilon F_{1} + \varepsilon^{2} F_{2} + \varepsilon^{3} F_{3} + \varepsilon^{4} F_{4} \cdot \cdot \cdot .$$
(8)

substituting (8) into (7) and compare the coefficients of the same power of \(\varepsilon\) to obtain a system of linear differential equations:

$$\varepsilon : \, \left( {\partial \xi \partial T + a_{2} \partial^{4} \xi + a_{3} \partial^{2} \xi } \right)F_{1} = 0,$$
(9.1)
$$\varepsilon^{2} :2\left( {\partial \xi \partial T + a_{2} \partial^{4} \xi + a_{3} \partial^{2} \xi } \right)F_{2} = - \left( {D_{\xi } D_{T} + a_{2} D_{\xi }^{4} + a_{3} D_{\xi }^{2} } \right)F_{1} \cdot F_{1} ,$$
(9.2)
$$\varepsilon^{3} :2\left( {\partial \xi \partial T + a_{2} \partial^{4} \xi + a_{3} \partial^{2} \xi } \right)F_{3} = - 2\left( {D_{\xi } D_{T} + a_{2} D_{\xi }^{4} + a_{3} D_{\xi }^{2} } \right)F_{1} \cdot F_{2} ,$$
(9.3)
$$\varepsilon^{4} :2\left( {\partial \xi \partial T + a_{2} \partial^{4} \xi + a_{3} \partial^{2} \xi } \right)F_{4} = - \left( {D_{\xi } D_{T} + a_{2} D_{\xi }^{4} + a_{3} D_{\xi }^{2} } \right)\left( {2F_{1} \cdot F_{3} + F_{2} \cdot F_{2} } \right),$$
(9.4)

3.1 The one-soliton solution

To solve one-soliton, we suppose:

$$F = 1 + \varepsilon F_{1} ,F_{1} = {\text{e}}^{{\theta_{1} }} ,\theta_{1} = \lambda_{1} \xi + \omega_{1} T + \theta_{1}^{0} .$$
(10)

With \(\lambda_{1} ,\omega_{1}\) and \(\theta_{1}^{0}\) are arbitrary constants.

Then

$$F = 1 + \varepsilon {\text{e}}^{{\lambda_{1} \xi + \omega_{1} T + \theta_{1}^{0} }} .$$
(11)

Substituting (10) into (9.1), we can obtain the following equation:

$$\lambda_{1} \omega_{1} + a_{2} \lambda_{1}^{4} + a_{3} \lambda_{1}^{2} = 0.$$
(12)

We can get:

$$\omega_{1} = - (a_{2} \lambda_{1}^{3} + a_{3} \lambda_{1} ).$$
(13)

Let \(\varepsilon = 1\) lead to:

$$F = 1 + {\text{e}}^{{\lambda_{1} \xi - (a_{2} \gamma_{1}^{3} + a_{3} \gamma_{1} )T + \theta_{1}^{0} }} .$$
(14)

and we can get one-soliton solution:

$$u = 2\left[ {\ln \left( {1 + {\text{e}}^{{\lambda_{1} \xi - (a_{2} \gamma_{1}^{3} + a_{3} \gamma_{1} )T + \theta_{1}^{0} }} } \right)} \right]{}_{\xi \xi }.$$
(15)

3.2 The two-soliton solution

To solve two-soliton, we suppose:

$$F = 1 + \varepsilon F_{1} + \varepsilon^{2} F_{2} ,F_{1} = {\text{e}}^{{\theta_{1} }} + {\text{e}}^{{\theta_{2} }} ,F_{2} = {\text{e}}^{{\theta_{1} + \theta_{2} + A_{12} }} .$$
(16)

where \(\theta_{i} = \lambda_{i} \xi + \omega_{i} T + \theta_{i}^{0} \, (i = 1,2)\) with \(\lambda_{i} ,\omega_{i}\),and \(\theta_{i}^{0}\) are arbitrary constants.Then,

$$F = 1 + \varepsilon \left( {{\text{e}}^{{\lambda_{1} \xi + \omega_{1} T + \theta_{1}^{0} }} + {\text{e}}^{{\lambda_{2} \xi + \omega_{2} T + \theta_{2}^{0} }} } \right) + \varepsilon^{2} {\text{e}}^{{\lambda_{1} \xi + \omega_{1} T + \theta_{1}^{0} + \lambda_{2} \xi + \omega_{2} T + \theta_{2}^{0} + A_{12} }} .$$
(17)

substituting (16) into (9.1), we can obtain the following equation:

$$\left( {\lambda_{1} \omega_{1} {\text{e}}^{{\theta_{1} }} + \lambda_{2} \omega_{2} {\text{e}}^{{\theta_{2} }} } \right) + a_{2} \left( {\lambda_{1}^{4} {\text{e}}^{{\theta_{1} }} + \lambda_{2}^{4} {\text{e}}^{{\theta_{2} }} } \right) + a_{3} \left( {\lambda_{1}^{2} {\text{e}}^{{\theta_{1} }} + \lambda_{2}^{2} {\text{e}}^{{\theta_{2} }} } \right) = 0.$$
(18)

we can get:

$$\omega_{i} = - (a_{2} \lambda_{i}^{3} + a_{3} \lambda_{i} ) \, (i = 1,2).$$
(19)

substituting (16) into (9.2),\({\text{e}}^{{A_{12} }}\) can be calculated by using Mathematica:

$${\text{e}}^{{A_{12} }} = - \frac{{(\lambda_{1} - \lambda_{2} )((\omega_{1} - \omega_{2} ) + a_{2} (\lambda_{1} - \lambda_{2} )^{3} + a_{3} (\lambda_{1} - \lambda_{2} ))}}{{(\lambda_{1} + \lambda_{2} )((\omega_{1} + \omega_{2} ) + a_{2} (\lambda_{1} + \lambda_{2} )^{3} + a_{3} (\lambda_{1} + \lambda_{2} ))}}$$
(20)

let \(\varepsilon = 1\) lead to:

$$F = 1 + {\text{e}}^{{\theta_{1} }} + {\text{e}}^{{\theta_{2} }} - \frac{{(\lambda_{1} - \lambda_{2} )((\omega_{1} - \omega_{2} ) + a_{2} (\lambda_{1} - \lambda_{2} )^{3} + a_{3} (\lambda_{1} - \lambda_{2} ))}}{{(\lambda_{1} + \lambda_{2} )((\omega_{1} + \omega_{2} ) + a_{2} (\lambda_{1} + \lambda_{2} )^{3} + a_{3} (\lambda_{1} + \lambda_{2} ))}}{\text{e}}^{{\theta_{1} + \theta_{2} }} .$$
(21)

where \(\omega_{i}\) satisfies (19). Substituting (21) into (4), we can get two-soliton:

$$u = 2\left[ {\ln \left( {1 + {\text{e}}^{{\theta_{1} }} + {\text{e}}^{{\theta_{2} }} {\text{ + e}}^{{\theta_{1} + \theta_{2} + A_{12} }} } \right)} \right]_{\xi \xi } .$$
(22)

where \(\theta_{i} = \lambda_{i} \xi + \omega_{i} T + \theta_{i}^{0} \, (i = 1,2)\), \(\omega_{i} = - (a_{2} \lambda_{i}^{3} + a_{3} \lambda_{i} ) \, (i = 1,2)\) and

$${\text{e}}^{{A_{12} }} = - \frac{{(\lambda_{1} - \lambda_{2} )((\omega_{1} - \omega_{2} ) + a_{2} (\lambda_{1} - \lambda_{2} )^{3} + a_{3} (\lambda_{1} - \lambda_{2} ))}}{{(\lambda_{1} + \lambda_{2} )((\omega_{1} + \omega_{2} ) + a_{2} (\lambda_{1} + \lambda_{2} )^{3} + a_{3} (\lambda_{1} + \lambda_{2} ))}}.$$

3.3 The three-soliton solution

To solve three-soliton, we suppose:

$$F = 1 + \varepsilon F_{1} + \varepsilon^{2} F_{2} + \varepsilon^{3} F_{3} ,$$
(23)
$$F_{1} = {\text{e}}^{{\theta_{1} }} + {\text{e}}^{{\theta_{2} }} + {\text{e}}^{{\theta_{3} }} ,$$
(24)
$$F_{2} = {\text{e}}^{{\theta_{1} + \theta_{2} + A_{12} }} + {\text{e}}^{{\theta_{1} + \theta_{3} + A_{13} }} + {\text{e}}^{{\theta_{2} + \theta_{3} + A_{23} }} ,$$
(25)
$$F_{3} = {\text{e}}^{{\theta_{1} + \theta_{2} + \theta_{3} + A_{123} }} .$$
(26)

where \(\theta_{i} = \lambda_{i} \xi + \omega_{i} T + \theta_{i}^{0} \, (i = 1,2,3).\) Substituting (24) into (9.1), we can obtain:

$$\omega_{i} = - (a_{2} \lambda_{i}^{3} + a_{3} \lambda_{i} ) \, (i = 1,2,3).$$
(27)

substituting (24) and (25) into (9.2), \({\text{e}}^{{A_{ij} }}\) can be calculated by using Mathematica:

$${\text{e}}^{{A_{ij} }} = - \frac{{(\lambda_{i} - \lambda_{j} )((\omega_{i} - \omega_{j} ) + a_{2} (\lambda_{i} - \lambda_{j} )^{3} + a_{3} (\lambda_{i} - \lambda_{j} ))}}{{(\lambda_{i} + \lambda_{j} )((\omega_{i} + \omega_{j} ) + a_{2} (\lambda_{i} + \lambda_{j} )^{3} + a_{3} (\lambda_{i} + \lambda_{j} ))}} \, (i = 1,2,3,i < j).$$
(28)

substituting (24), (25) and (26) into (9.3), \(F_{3}\) can be calculated by using Mathematica:

$$F_{3} = {\text{e}}^{{\theta_{1} + \theta_{2} + \theta_{3} + A_{123} }} .$$
(29)

where \({\text{e}}^{{A_{123} }} = {\text{e}}^{{A_{12} }} {\text{e}}^{{A_{13} }} {\text{e}}^{{A_{23} }}\), let \(\varepsilon = 1\) lead to

$$F = 1 + {\text{e}}^{{\theta_{1} }} + {\text{e}}^{{\theta_{2} }} {\text{ + e}}^{{\theta_{3} }} {\text{ + e}}^{{\theta_{1} + \theta_{2} + A_{12} }} + {\text{e}}^{{\theta_{1} + \theta_{3} + A_{13} }} + {\text{e}}^{{\theta_{2} + \theta_{3} + A_{23} }} + {\text{e}}^{{\theta_{1} + \theta_{2} + \theta_{3} + A_{123} }} .$$
(30)

substituting (30) into (4), we can get three-soliton solution:

$$u = 2[\ln F]_{\xi \xi } .$$
(31)

where \(F\) satisfies formula (30). Substituting (24), (25) and (26) into (9.4), we can obtain \(F_{4} = 0\), so the three-soliton solution must exist, and the N-soliton solution must exist.

3.4 The N-soliton solution

The same can be obtained the N-soliton. The function \(F\) has the below formula:

$$F = \sum\limits_{\mu = 0,1} {{\text{e}}^{{\sum\limits_{i = 1}^{N} {\mu_{i} \theta_{i} } + \sum\limits_{1 \le i < j}^{{}} {\mu_{i} \mu_{j} A_{ij} } }} } .$$
(32)

where \(\theta_{i} = \lambda_{i} \xi + \omega_{i} T + \theta_{i}^{0} \, (i = 1,2,3 \cdots N)\), \(\omega_{i}\) satisfies (27) \((i = 1,2,3 \cdots N)\) and \({\text{e}}^{{A_{ij} }}\) satisfies (28) \((i = 1,2,3 \cdots N,1 \le i < j)\), with \(\lambda_{i}\),and \(\theta_{i}^{0}\) are arbitrary constants. \(\sum {\mu = 0,1}\) covers the sum of all possible combinations of \(\theta_{i} ,\theta_{j} = 0,1 \, i,j = 1,2,3 \cdots N\). Putting (32) into (4), we can get N-soliton solution:

$$u = 2\left[ {\ln \left( {\sum\limits_{\mu = 0,1} {{\text{e}}^{{\sum\limits_{i = 1}^{N} {\mu_{i} \theta_{i} } + \sum\limits_{1 \le i < j}^{{}} {\mu_{i} \mu_{j} A_{ij} } }} } } \right)} \right]_{\xi \xi } .$$
(33)

where \(\theta_{i} = \lambda_{i} \xi + \omega_{i} T + \theta_{i}^{0} { (}i = 1,2,3 \cdots N)\),\(\omega_{i}\) satisfies (27) \((i = 1,2,3 \cdots N)\) and \({\text{e}}^{{A_{ij} }}\) satisfies (28) \((i = 1,2,3 \cdots N,1 \le i < j)\).

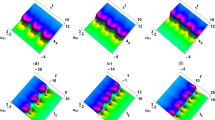
The Fig. 1 By choosing proper parameters for (15), the dynamic diagrams of one-soliton can be described: \(\lambda_{1} = 1/2,a_{2} = 1,\) (a1) \(a_{3} = 1/8\); (a2) \(a_{3} = 1\); (a3) \(a_{3} = 2\). From Figures (a1), (a2) and (a3), the same values of \(\lambda_{1}\) and \(a_{2}\), along with \(a_{3}\) increasing, the direction of wave propagation changes clockwise. Not only that, from the Figure (a4), the wave width of one-soliton solutions decreases, and the wave propagation frequency accelerates with the Coriolis parameter \(a_{3}\) increasing, but Rossby waves amplitude does not change. From Figures (a5) illustrate, one-soliton has general traveling wave properties.

Fig. 1
figure 1

One-soliton solutions of Eq. (3). Up row: 3D graphs of one-soliton solutions with \(\lambda_{1} = 1/2,a_{2} = 1\) (a1) \(a_{3} = 1/8\); (a2) \(a_{3} = 1\); (a3) \(a_{3} = 2\). Down row: The left one is the visual diagram of \(a_{3}\) transformation. The right one is the propagation of solitons overtime with \(a_{3} = 1\)

Full size image

The Fig. 2 By choosing proper parameters for (22), the dynamic diagrams of two-soliton can be described: \(\lambda_{1} = 1,\lambda_{2} = 3/2,a_{2} = 1,\) (a6) \(a_{3} = - 2\); (a7)\(a_{3} = - 1\); (a8) \(a_{3} = 7/6\). From (a6), (a7) and (a8), the same values of \(\lambda_{1} ,\lambda_{2}\) and \(a_{2}\), along with \(a_{3}\) increasing, the direction of wave propagation changes clockwise; at same time, the angle gradually decreases. we can clearly see that the two solitons are bright, and the collisions are elastic. Their speeds and shapes keep no change after collision; two solitons get phase shifts after the interactions, and as \(a_{3}\) changes, the position of the interaction between solitons does not change. From (a9), (a10) and (a11), different values \(a_{3}\) leads to the big change of density when the two waves collide. From Figures (a12), when \(a_{3} = - 1\), we can see that the shape and amplitude of the waves change with the changing of \(T\). The two solitons take interaction completely when \(T = 0\), the amplitude goes down, which reflects the energy dissipation caused by the interaction of the two solitons. When \(T = - 5\) and \(T = 5\), there are two axisymmetric graphs. From Figure (a13), when \(\xi = 0\), the shapes of the waves are very similar, the wave width decreases, and the wave propagation frequency accelerates along \(a_{3}\) increasing; Rossby waves amplitude does not change. From Figure (a14), when \(T = 1\), the wave keeps its shape and shifts to the left along \(a_{3}\) changing.

Fig. 2
figure 2

Two-soliton solutions of Eq. (3). First row: 3D graphs of two-soliton solutions with \(\lambda_{1} = 1,\lambda_{2} = 3/2,a_{2} = 1\), (a6) \(a_{3} = - 2\); (a7) \(a_{3} = - 1\); (a8) \(a_{3} = 7/6\). Second row is the contour plots. Third row: 2D graphs of two-soliton solutions

Full size image

In Fig. 3, by choosing proper parameters for (31), the dynamic diagrams of three-soliton can be described: \(\lambda_{1} = 2,\lambda_{2} = 3,\)\(\lambda_{3} = 3/2,\) \(a_{2} = 1,\) (a15) \(a_{3} = - 4\); (a16)\(a_{3} = - 2\); (a17) \(a_{3} = 1\). From (a15), (a16) and (a17), the same values of \(\lambda_{1} ,\lambda_{2} ,\lambda_{3}\) and \(a_{2}\), along with \(a_{3}\) increasing, the direction of wave propagation changes clockwise; at same time, the intersection angle of the three waves changes. we can see that the three solutions are bright solitons, and the collisions are elastic. Their speeds and shapes keep no change after collision; three solitons have phase shifts after the interactions, and as \(a_{3}\) changes, the position of the interaction between solitons does not change. From (a18), (a19) and (a20), different values of the horizontal Coriolis parameter \(a_{3}\) lead to the large change of contour density when the three waves collide. From Figures (a21), when \(a_{3} = - 2\), we can see that the shape and amplitude of the waves change with the changing of \(T\). The three solitons take interaction completely when \(T = 0\), amplitude of waves reaches the maximum value, which reflects the energy accumulation caused by the interaction of the three solitons. From Figure (a22), when \(\xi = 0\), the shapes of the waves are very similar, the wave width decreases, and the wave propagation frequency accelerates along \(a_{3}\) increasing; Rossby waves amplitude does not change. From Figure (a23), when \(T = 1\), the wave keeps its shape and shifts to the left along \(a_{3}\) changing.

Fig. 3
figure 3

Three-soliton solutions of Eq. (3). First row: 3D graphs of three-soliton solutions with \(\lambda_{1} = 2,\lambda_{2} = 3,\lambda_{3} = 3/2,a_{2} = 1\), (a15) \(a_{3} = - 4\);(a16) \(a_{3} = - 2\);(a17) \(a_{3} = 1\). The second row is the corresponding contour plots. Third row: 2D graphs of three-soliton solutions

Full size image

4 The one-breather wave solution

Supporting by the symbolic computation approach, the one-breather wave solution of Eq. (3) is gained, suppose:

$$f = {\text{e}}^{{ - \theta_{1} }} + c_{2} {\text{e}}^{{\theta_{1} }} + c_{1} \cos \theta_{2} ,$$
(34)

where \(\theta_{1} = \lambda_{1} (\xi - w_{1} T),\theta_{2} = \lambda_{2} (\xi + w_{2} T)\), where \(\lambda_{1} ,w_{1} ,\lambda_{2} ,w_{2}\) are real constant.

Substituting (34) into (7) and setting the coefficients of \(e^{{\theta_{1} }} \cos \theta_{2} ,e^{{ - \theta_{1} }} \cos \theta_{2} ,\).

\({\text{e}}^{{\theta_{1} }} \sin \theta_{2} ,\) \(e^{{ - \theta_{1} }} \sin \theta_{2}\) and constant term equal to zero, we get equation group as below:

$$\left\{ {\begin{array}{*{20}c} {c_{2} \lambda_{1}^{2} (a_{3} - w_{1} + 4a_{2} \lambda_{1}^{2} ) = 0,} \\ { - c_{1} \lambda_{1}^{2} (w_{1} + w_{2} + 4a_{2} \lambda_{1}^{2} ) = 0,} \\ { - c_{1} c_{2} \lambda_{1}^{2} (w_{1} + w_{2} + 4a_{2} \lambda_{1}^{2} ) = 0,} \\ {c_{1} \lambda_{1}^{2} ( - 2a_{3} + w_{1} - w_{2} ) = 0,} \\ {c_{1} c_{2} \lambda_{1}^{2} (2a_{3} - w_{1} + w_{2} ) = 0.} \\ \end{array} } \right.$$
(35)

We select one of the solutions to continue analysis:

$$w_{1} = a_{3} ,w_{2} = - a_{3} ,a_{2} = 0.$$
(36)

Substituting (34) (36) into (4), the one-breather wave solution is obtained:

$$\begin{gathered} u = 2\left( {\frac{{\lambda _{1}^{2} {\text{e}}^{{ - \lambda _{1} (\xi - a_{3} T)}} + c_{2} \lambda _{1}^{2} {\text{e}}^{{\lambda _{1} (\xi - a_{3} T)}} - c_{1} \lambda _{2}^{2} \cos \left[ {\lambda _{2} \left( {\xi - a_{3} T} \right)} \right]}}{{{\text{e}}^{{ - \lambda _{1} (\xi - a_{3} T)}} + c_{2} {\text{e}}^{{\lambda _{1} (\xi - a_{3} T)}} + c_{1} \cos [\lambda _{2} (\xi - a_{3} T)]}}} \right. \hfill \\ \quad \quad - \frac{{\left( { - \lambda _{1}^{{}} {\text{e}}^{{ - \lambda _{1} (\xi - a_{3} T)}} + c_{2} \lambda _{1}^{{}} {\text{e}}^{{\lambda _{1} (\xi - a_{3} T)}} - c_{1} \lambda _{2}^{{}} \sin \left[ {\lambda _{2} (\xi - a_{3} T)} \right]} \right)^{2} }}{{\left( {{\text{e}}^{{ - \lambda _{1} (\xi - a_{3} T)}} + c_{2} {\text{e}}^{{\lambda _{1} (\xi - a_{3} T)}} + c_{1} \cos \left[ {\lambda _{2} (\xi - a_{3} T)} \right]} \right)^{2} }} \hfill \\ \end{gathered}$$
(37)

In Fig. 4, by choosing proper parameters for Eq. (37), the dynamic diagrams of one-breather can be described: \(\lambda_{1} = \lambda_{2} = 1/10,c_{1} = - c_{2} = 2,\)(d1)\(a_{3} = 3\); (d2)\(a_{3} = 4\); (d3)\(a_{3} = 5\). From Figures (d1), (d2) and (d3), the same values of \(\lambda_{1} ,\lambda_{2} ,c_{1} ,c_{2}\) and \(a_{2}\), along with \(a_{3}\) increasing, the wave propagation direction changes clockwise and the period of the wave decreases. Figure (d4) is density plot of one-breather solution. From graph (d5), when \(a_{3} = 4\), as \(T\) increasing, the wave keeps the same shape and moves parallel to the right. From graph (d6), when \(T = 3\), as the horizontal Coriolis parameter \(a_{3}\) increasing, the wave keeps the same shape and moves parallel to the right.

Fig. 4
figure 4

One-breather of Eq. (3). The 3D graphs with \(\lambda_{1} = \lambda_{2} = 1/10,c_{1} = - c_{2} = 2,\)(d1)\(a_{3} = 3\);(d2)\(a_{3} = 4\);(d3)\(a_{3} = 5\). (d4) and (d5) are the density plots and the 2D graph with \(a_{3} = 4\); (d6) is the 2D graph with \(T = 3.\)

Full size image

5 The interactions of one-soliton and one-breather

Supporting by the symbolic computation approach, the interactions of one-soliton and one-breather of Eq. (3) are gained, suppose:

$$f = \cosh \theta_{1} + \cos \theta_{2} + {\text{e}}^{{\theta_{3} }} + 1,$$
(38)

where \(\theta_{1} = \lambda_{1} (\xi - w_{1} T),\theta_{2} = \lambda_{1} (\xi + w_{2} T),\theta_{3} = \lambda_{2} (\xi + w_{3} T)\), \(\lambda_{1} ,w_{1} ,\lambda_{2} ,w_{2} ,\) \(w_{3}\) are real constant. Substituting (38) into (7) and setting the coefficients of \({\text{e}}^{{\theta_{3} }} \cos \theta_{2} ,{\text{e}}^{{\theta_{3} }} \cosh \theta_{1} ,\cos \theta_{2} \cosh \theta_{1} ,{\text{e}}^{{\theta_{3} }} \sin \theta_{2} ,{\text{e}}^{{\theta_{3} }} \sinh \theta_{1} ,\sin \theta_{2} \sinh \theta_{1}\) equal to zero, this results in a group of six equations:

$$\left\{ {\begin{array}{*{20}l} { - a_{3} \lambda_{1}^{2} - w_{2} \lambda_{1}^{2} + a_{2} \lambda_{1}^{4} + a_{3} \lambda_{3}^{2} + w_{3} \lambda_{3}^{2} - 6a_{2} \lambda_{1}^{2} \lambda_{3}^{2} + a_{2} \lambda_{3}^{4} = 0,} \hfill \\ {a_{3} \lambda_{1}^{2} - w_{1} \lambda_{1}^{2} + a_{2} \lambda_{1}^{4} + a_{3} \lambda_{3}^{2} + w_{3} \lambda_{3}^{2} + 6a_{2} \lambda_{1}^{2} \lambda_{3}^{2} + a_{2} \lambda_{3}^{4} = 0,} \hfill \\ {\lambda_{1}^{2} \left( {w_{1} + w_{2} + 4a_{2} \lambda_{1}^{2} } \right) = 0,} \hfill \\ {\lambda_{1} \lambda_{3} \left( {2a_{3} + w_{2} + w_{3} - 4a_{2} \lambda_{1}^{2} + 4a_{2} \lambda_{3}^{2} } \right) = 0,} \hfill \\ \begin{gathered} \lambda_{1} \lambda_{3} \left( { - 2a_{3} + w_{1} - w_{3} - 4a_{2} \lambda_{1}^{2} + 4a_{2} \lambda_{3}^{2} } \right) = 0, \hfill \\ \lambda_{1}^{2} (2a_{3} - w_{1} + w_{2} ) = 0. \hfill \\ \end{gathered} \hfill \\ \end{array} } \right..$$
(39)

We select one of the solutions to continue analysis:

$$w_{1} = a_{3} + a_{2} \lambda_{1}^{2} + 3a_{2} \lambda_{3}^{2} ,$$
$$w_{2} = \frac{{ - a_{3} \lambda_{1}^{2} + a_{2} \lambda_{1}^{4} - a_{3} \lambda_{3}^{2} + w_{1} \lambda_{3}^{2} - 10a_{2} \lambda_{1}^{2} \lambda_{3}^{2} - 3a_{2} \lambda_{3}^{4} }}{{\lambda_{1}^{2} }},$$
$$w_{3} = - 2a_{3} + w_{1} - 4a_{2} \lambda_{1}^{2} - 4a_{2} \lambda_{3}^{2} .$$
(40)

Substituting (38) (40) into (4), the interaction of one-soliton and one-breather is obtained:

$$\begin{gathered} u = 2\left( {\frac{{\lambda _{3}^{2}{\text{e}}^{{ \lambda _{3} (\xi + w_{3} T )}} -\lambda _{1}^{2}{\text {cos}}\left [ \lambda _{1}(\xi + w_{2} T ) \right ] +\lambda _{1}^{2}{\text {cos}}h\left [ \lambda _{1}(\xi - w_{1} T ) \right ] }}{{{\text{1+e}}^{{\lambda _{3} (\xi + w_{3} T )}} +{\text {cos}}\left [ \lambda _{1}(\xi + w_{2} T ) \right ] +{\text {cos}}h\left [ \lambda _{1}(\xi - w_{1} T ) \right ] }}} \right. \hfill \\ \quad \quad \left. { - \frac{{( \lambda _{3}{\text{e}}^{{ \lambda _{3} (\xi + w_{3} T )}} -\lambda _{1}{\text {sin}}\left [ \lambda _{1}(\xi + w_{2} T ) \right ] +\lambda _{1}{\text {sin}}h\left [ \lambda _{1}(\xi - w_{1} T ) \right ] ) ^{2} }}{{{(\text{1+e}}^{{\lambda _{3} (\xi + w_{3} T )}} +{\text {cos}}\left [ \lambda _{1}(\xi + w_{2} T ) \right ] +{\text {cos}}h\left [ \lambda _{1}(\xi - w_{1} T ) \right ] )^{2} }}} \right). \hfill \\ \end{gathered}$$
(41)

where \(w_{1} ,w_{2} ,w_{3}\) satisfy (40).

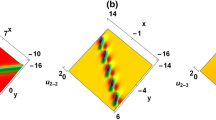
In Fig. 5, by choosing proper parameters for (41), the dynamic diagrams of the interactions of one-soliton and one-breather can be described: \(\lambda_{1} = 2,\lambda_{3} = 1,a_{2} = 1,\)(f1)\(a_{3} = - 7\); (f2)\(a_{3} = - 6\); (f3)\(a_{3} = - 5\). From (f1)–(f3), the same values of \(\lambda_{1} ,\lambda_{3}\) and \(a_{2}\), along with \(a_{3}\) increasing, the wave propagation direction changes clockwise and the shape of both waves’ changes. At same time, the angle between the two waves decreases, and the period decreases. The collision of two waves is inelastic, and they collide and merge into a wave, eventually forming a Y-type wave. From density Figures (f4) (f5) and (f6), we can clearly see the interaction of the two waves and notice that the moment of interaction of the two waves does not change with the changing of \(a_{3}\). From 2D Figures (f7) and (f8), as \(a_{3}\) increases, the waves keep the same shape and move parallel to the right; along \(T\) increasing, the shape and amplitude of wave changes.

Fig. 5
figure 5

The interaction solutions of one-soliton and one-breather of Eq. (3). 3D graphs with \(\lambda _{1} = 2,\lambda _{3} = 1,a_{2} = 1,\) (f1) \(a_{3} = - 7\);(f2)\(a_{3} = - 6\);(f3)\(a_{3} = - 5\). (f4) (f5) (f6) are density plots. (f7) (f8) are 2D plots.

Full size image

6 The one-rogue wave solution

Supporting by the symbolic computation approach, the one-rogue wave solution of Eq. (3) is gained, suppose:

$$F = (d_{1} \xi + b_{1} T + c_{1} )^{2} + (d_{2} \xi + b_{2} T + c_{2} )^{2} + c_{0} ,\;c_{0} > 0.$$
(42)

where \(d_{1} ,d_{2} ,b_{1} ,b_{2} ,c_{0} ,c_{1} ,c_{2}\) are real constant. Substituting (42) into (7), we assign coefficients \(T,T^{2} ,\xi ,\xi^{2} ,\xi T\) be equal to zero, and this results in a group of six equations:

$$\left\{ \begin{aligned} & b_{1} \left( {d_{1} (c_{0} - c_{1}^{2} + c_{2}^{2} ) - 2c_{1} c_{2} d_{2} } \right) + b_{2} \left( { - 2c_{1} c_{2} d_{1} + d_{2} (c_{0} + c_{1}^{2} - c_{2}^{2} )} \right) + a_{3} (d_{1}^{2} (c_{0} - c_{1}^{2} + c_{2}^{2} ) \\ & \quad \quad - 4c_{1} c_{2} d_{1} d_{2} + d_{2}^{2} (c_{0} + c_{1}^{2} - c_{2}^{2} )) + 6a_{2} (d_{1}^{2} + d_{2}^{2} )^{2} = 0, \\ & \quad \quad - 4\left( {b_{1}^{2} \left( {c_{1} d_{1} + c_{2} d_{2} } \right) + b_{2} \left( {b_{2} c_{1} d_{1} - a_{3} c_{2} d_{1}^{2} + b_{2} c_{2} d_{2} + 2a_{3} c_{1} d_{1} d_{2} + a_{3} c_{2} d_{2}^{2} } \right)} \right. \\ & \quad \quad + \left. {a_{3} b_{1} \left( {2c_{2} d_{1} d_{2} + c_{1} \left( {d_{1}^{2} - d_{2}^{2} } \right)} \right)} \right) = 0, \\ & \quad \quad b_{1}^{3} d_{1} + b_{1} b_{2} d_{1} \left( {b_{2} + 4a_{3} d_{2} } \right) + b_{1}^{2} \left( {b_{2} d_{2} + a_{3} \left( {d_{1}^{2} - d_{2}^{2} } \right)} \right) + b_{2}^{2} \left( {b_{2}d_{2} + a_{3}\left( { - d_{1}^{2} + d_{2}^{2} } \right)} \right) = 0, \\ & \quad \quad \left( {b_{1} c_{1} + b_{2} c_{2} + a_{3} c_{1} d_{1} + a_{3} c_{2} d_{2} } \right)\left( {d_{1}^{2} + d_{2}^{2} } \right) = 0, \\ & \quad \quad \left( {d_{1}^{2} + d_{2}^{2} } \right)\left( {b_{1}^{2} + a_{3} b_{1} d_{1} + b_{2} \left( {b_{2} + a_{3} d_{2} } \right)} \right) = 0, \\ & \quad \quad \left( {d_{1}^{2} + d_{2}^{2} } \right)\left( {b_{1} d_{1} + b_{2} d_{2} + a_{3} \left( {d_{1}^{2} + d_{2}^{2} } \right)} \right) = 0. \\ \end{aligned}\right.$$
(43)

We select one of the solutions to continue analysis:

$$b_{1} = - a_{3} d_{1} ,$$
$$b_{2} = \frac{1}{2}\left( { - a_{3} d_{2} + \sqrt { - 4b_{1}^{2} - 4a_{3} b_{1} d_{1} + a_{3}^{2} d_{2}^{2} } } \right),$$
$$c_{0} = \frac{{ - 6a_{2} (d_{1}^{2} + d_{2}^{2} )^{2} + 2a_{3} c_{1} c_{2} d_{1} d_{2} - a_{3} c_{1}^{2} d_{2}^{2} + a_{3} c_{2}^{2} d_{2}^{2} }}{{a_{3} d_{2}^{2} }}.$$
(44)

Substituting (42) (44) into (4), the one-rogue wave is conducted:

$$u = 4\left( { - \frac{{2(d_{1} A + d_{2} B)^{2} }}{{\Theta^{2} }} + \frac{{d_{1}^{2} + d_{2}^{2} }}{\Theta }} \right).$$
(45)
$$\Theta = c_{0} + A^{2} + B^{2} ,$$
$$\begin{gathered} A = c_{1} - a_{3} d_{1} T + d_{1} \xi , \hfill \\ B = c_{2} + d_{2} \xi . \hfill \\ \end{gathered}$$

In Fig. 6, by choosing proper parameters for (45), the dynamic diagrams of one-rogue wave can be described: \(d_{1} = 1,d_{2} = 1/2,c_{1} = - 1,c_{2} = - 1,c_{0} = 0,a_{2} = 1/6,\)(g1) \(a_{3} = 2\);(g2)\(a_{3} = 4\);(g3) \(a_{3} = 7\). From (g1)—(g3), the same values of \(d_{1} ,d_{2} ,c_{1} ,c_{2} ,c_{0}\) and \(a_{2}\), along with \(a_{3}\) changing, the wave propagation direction changes clockwise. From (g4) and (g5), different values of \(a_{3}\) lead to a big change of density. From (g6), (g7), when \(\xi = 0\) and \(T = 0\), along with \(a_{3}\) increasing, amplitudes decrease and shapes change.

Fig. 6
figure 6

One-rogue wave of Eq. (3). 3D graphs when \(d_{1} = 1,d_{2} = 1/2,c_{1} = - 1,c_{2} = - 1,\) \(c_{0} = 0,\)\(a_{2} = 1/6,\) (g1) \(a_{3} = 2\);(g2) \(a_{3} = 4\);(g3) \(a_{3} = 7\). Contour figures with \(d_{1} = 1,d_{2} = 1/2,\) \(c_{1} = - 1,c_{2} = - 1,c_{0} = 0,a_{2} = 1/6,\) (g4) \(a_{3} = 2\); (g5) \(a_{3} = 4\). g(6) g(7) are 2D graphs of the one-rogue wave.

Full size image

7 The interactions of two-soliton and one-rogue

Supporting by the symbolic computation approach, the interaction of two-soliton and one-rogue of Eq. (3) is obtained, suppose:

$$f = \theta_{1}^{2} + \theta_{2}^{2} + {\text{e}}^{{p\theta_{3} }} + {\text{e}}^{{ - p\theta_{3} }} ,$$
(46)

where \(\theta_{i} = \lambda_{i} \xi + w_{i} T + c_{i} ,(i = 1,2,3)\), \(\lambda_{i} ,w_{i}\) are real constant.

Putting (46) in (7) and setting the coefficients of \({\text{e}}^{{ - p\theta_{3} }} ,{\text{e}}^{{p\theta_{3} }} ,T,T^{2} ,T\xi ,\xi ,\xi^{2}\) and the coefficients of the cross terms be equal to zero, this results in a group of eighteen equations, we select one of the solutions to continue analysis:

$$w_{1} = \frac{{ - a_{3} \lambda_{1}^{2} - w_{2} \lambda_{2} - a_{3} \lambda_{2}^{2} }}{{\lambda_{1} }},$$
$$w_{2} = - a_{3} \lambda_{3}^{{}} - a_{2} p^{2} \lambda_{3}^{2} .$$
(47)

Substituting (46) (47) into (4), the interaction of two-soliton and onebreather is gained:

$$\begin{gathered} u = 2\left( {\frac{{2\lambda _{1}^{2}+2\lambda _{2}^{2}+p^{2}\lambda _{3}^{2}{\text{e}}^{{ -p(\lambda _{3} \xi + w_{3} T+c_{3})}} +p^{2}\lambda _{3}^{2}{\text{e}}^{p(\lambda _{3} \xi + w_{3} T+c _{3})}}}{{{\text{e}}^{{-p(\lambda _{3} \xi + w_{3} T+c _{3} )}} +{\text{e}}^{p(\lambda _{3} \xi + w_{3} T+c _{3})}+( \lambda _{1}\xi + w_{1} T +c _{1})^{2} +( \lambda _{2}\xi + w_{2} T +c _{2})^{2} }}} \right. \hfill \\ \quad \quad \left. { - \frac{{( -p\lambda _{3}{\text{e}}^{{-p( \lambda _{3} \xi + w_{3} T +c_{3})}} +p\lambda _{3}{\text{e}}^{{p( \lambda _{3} \xi + w_{3} T +c_{3})}} +2\lambda _{1}( \lambda _{1}\xi + w_{1} T +c_{1}) +2\lambda _{2}( \lambda _{2}\xi + w_{2} T +c_{2}) ) ^{2} }}{{{(\text{e}}^{{-p(\lambda _{3} \xi + w_{3} T +c_{3})}} +\text{e}^{{p(\lambda _{3} \xi + w_{3} T +c_{3})}}+ (\lambda _{1}\xi + w_{1} T+c_{1} ) ^{2} +(\lambda _{2}\xi + w_{2} T +c_{2})^{2} )^{2} }}} \right). \hfill \\ \end{gathered}$$
(48)

where \(w_{1} ,w_{2}\) satisfy (47).

In Fig. 7, by choosing proper parameters for (48), the dynamic diagrams of the interaction of two-soliton and one-rogue can be described: \(\lambda_{1} = 1/2,\lambda_{2} = \lambda_{3} = 2,\)\(w_{1} = 1,c_{i} = 1,(i = 1,2,3),p = 1,a_{2} = 1,\)(h1) \(a_{3} = - 4\); (h2) \(a_{3} = - 3\); (h3)\(a_{3} = - 2\). From (h1), (h2) and (h3), the same values of \(\lambda_{1} ,\lambda_{2} ,\lambda_{3} ,w_{1} ,c_{i}\) and \(a_{2}\), along with \(a_{3}\) increasing, the wave propagation direction changes clockwise and the shape of both waves’ changes. At same time, the angle between the two solitons decreases. We can see that the two solutions are bright solitons, and the collisions are elastic. Their speeds and shapes keep no change after collision; two solitons have phase shifts after the interactions, and as \(a_{3}\) changes, the position of the interaction between solitons does not change, and one-rogue wave is always at the center of the collision. From density Figures (h4) (h5) and (h6), we can clearly see the interaction of the two waves and notice that the moment of interaction of the two waves does not change with the changing of \(a_{3}\). From 2D Figures (h7) and (h8), as \(a_{3}\) increases, the waves move parallel to the right, along \(T\) increasing, the shape and amplitude of wave change the one-rogue wave in the center position of the two solitons.

Fig. 7
figure 7

Interaction solutions of two-soliton and one-rogue of Eq. (3). 3D graphs with \(\lambda_{1} = 1/2,\lambda_{2} = \lambda_{3} = 2,w_{1} = 1,c_{i} = 1,(i = 1,2,3),p = 1,a_{2} = 1\)(h1)\(a_{3} = - 4\); (h2)\(a_{3} = - 3\); (h3) \(a_{3} = - 2\). (h4) (h5) (h6) are the corresponding density plots. (h7) (h8) are the 2D plots

Full size image

8 Conclusions

This manuscript investigates the wave–wave interaction of the extended KdV equation with complete Coriolis parameters. Mainly apply Hirota bilinear method, and with the assistance of small parameter perturbation, N-soliton solution is represented. Application of the symbolic computation approach, one-breather, one-rogue wave and interaction between one-soliton and one-breather, interaction between two-soliton and one-rogue solutions are obtained. These solutions are new solutions, which are helpful to understand diverse physical phenomena in the atmosphere and ocean.

The effect of the horizontal Coriolis parameters \(a_{3}\) on propagation direction, period, and shape of wave is revealed. From all figures, it can be found that the change of Coriolis parameter \(a_{3}\) affects the propagation direction of the wave, and the wave rotates clockwise with the Coriolis parameter \(a_{3}\) increasing. If it is a periodic wave, an increase in \(a_{3}\) will also decrease the period. Figure 5 shows the inelastic collision of one-soliton and one-breather, which eventually form a Y-type wave. Figure 7 shows the elastic collision of two solitons, and one-rogue wave is always at the center of the collision. From Fig. 2, 3, 5, 7, the moment of interaction of the waves does not change with the change of \(a_{3}\).