Influence of Off-Axis Neutral Beam Injection on Resistive Wall Mode Stability

Abstract

Investigated are the effects of energetic particles (EPs), arising from off-axis neutral beam injection, on the resistive wall mode (RWM) instability in tokamaks. The analytic results for a cylindrical plasma show that EPs contribute the strongest kinetic damping to the RWM, as the deposition radius approaches the peak location of the mode eigenfunction. Toroidal computations are also carried out utilizing the MARS-K code, which includes EPs with anisotropic equilibrium distribution in the particle pitch angle space. These self-consistent numerical results confirm the analytic finding, that the RWM growth rate decreases as the peak of the EPs’ radial density profile approaches the maximum of the mode displacement. This study thus demonstrates the possibility of the RWM stabilization by the off-axis neutral beam injection in tokamak experiments.

Introduction

Suppression of the resistive wall mode (RWM) instability has been a significant concern for the magnetic confinement of toroidal plasmas, such as that in the future international thermonuclear experimental reactor (ITER) device. For exameple, in order to achieve high fusion power (proportional to the square of the normalized plasma pressure), the ITER 9 MA steady-state scenario was designed with the target plasma pressure exceeding the Troyon no-wall beta limit [1], resulting in potentially unstable RWM. The RWM is a global kink-like, non-axisymmetric instability, with the growth time of the order of the eddy current decay time in the surrounding resistive wall. The mode is driven by the plasma equilibrium pressure and/or the current density gradients.

Two approaches for suppressing RWM have been extensively pursued during recent years: the so-called active control and passive stabilization, with the drift kinetic damping physics playing a key role in the latter [2,3,4,5,6,7]. It has been shown that the kinetic effects associated with the resonance between the RWM and the toroidal precession drift motions of thermal particles can provide a partial or full stabilization of the mode, at very slow toroidal flow speed of the plasma [2]. The self-consistent magneto-hydrodynamic (MHD)-kinetic hybrid modeling [3, 8] has shown that either thermal particles or trapped energetic particles (EPs) can contribute to stabilization of the mode, where the free energy dissipation arises primarily from the mode-particle resonances.

Understanding the kinetic effect of EPs on the RWM is of significant importance for predicting the RWM stability in present day tokamaks as well as in the future devices such as ITER. The influence of EPs on the RWM stability, has however so far not been thoroughly investigated, in particular with regard to the dependence of mode stabilization on the configuration of the neutral beam injection (NBI) [9, 10]. In DIII-D, e.g., the off-axis neutral beam injection was used to broaden the current and pressure profiles, in order to achieve high beta plasma operations in conjunction with the RWM feedback control [11]. It is therefore certainly worthy theoretical efforts in assessing kinetic damping of the RWM associated with off-axis NBI.

In this work, we apply our previous theory model [7] to investigate the radial deposition effect of trapped EPs from off-axis NBI on the RWM instability. The results show that the spatial deposition of EPs indeed significantly affects the RWM stability, compared with the on-axis case. The off-axis deposition of trapped EPs can contribute substantial stabilization to the RWM instability. The optimal deposition radius is mainly determined by the eigen-structure of the RWM. Furthermore, we apply the linear MHD-kinetic hybrid code MARS-K to self-consistently model the effect of off-axis EPs, with an anisotropic distribution in particle pitch angle space, on the RWM instability. The self-consistent hybrid model implies that both the eigenvalue and the eigenfunction of the mode are modified by drift kinetic effects [4]. The toroidal modeling results qualitatively confirm that obtained with the analytic theory.

The remaining part of this paper is organized as follows. “Analytic Model” section presents an analytic model. “Numerical Results from MARS-K Code” section describes the computational results obtained by the MARS-K code. Conclusion is given in “Conclusions” section.

Analytic Model

The RWM dispersion relation, including the contribution from trapped EPs, can be written as [2, 4, 7, 12]:

$$\begin{aligned} D(\omega ) \equiv -i \omega \tau _{\rm w}^{*}+\frac{\delta W_{\rm f}^{\infty }+\delta W_{K 0}}{\delta W_{\rm f}^{b}+\delta W_{K 0}}=0, \end{aligned}$$

(1)

where $\omega =\omega _{r}+i \gamma$ is the mode eigenvalue. $\tau _{\rm w}^{*}$ is the typical wall eddy current decay time of a resistive wall. $\delta W_{\rm f}^{\infty }$ and $\delta W_{\rm f}^{b}$ represent the perturbed fluid potential energies without wall and with an ideal wall placed at the radial position b, respectively. The fluid potential energy includes the contributions from both the plasma and the vacuum region. $\delta W_{K 0}$ denotes the perturbed drift kinetic energy associated with trapped EPs, which is a net contribution after integrating along the plasma minor radius

$$\begin{aligned} \delta W_{K 0}=\int _{r_{\min }}^{1} W(r) {\rm d}r \end{aligned}$$

(2)

where [13]

$$\begin{aligned}W(r)&=\beta _{h} \frac{8 \pi R}{\mathrm {A} a}\left( 1-\alpha _{0} B_{0}/2\right) ^{2} a^{2 m-2} \Omega _{p f} n(r)|f(r)|^{2} r^{-1/2}\nonumber \\&\quad\times \left[ \frac{{\hat{A}}-{\hat{B}}}{\Omega _{d, e}} \ln \left( 1-\Omega _{d, e} / \Omega _{p f}\right) -\frac{{\hat{B}}}{\Omega _{p f}-\Omega _{d, e}}\right] . \end{aligned}$$

(3)

In $\delta W_{K 0}$, only the resonance between the precessional drift motion of trapped EPs and the mode is included. In Eq. (3), $A\equiv \int _{r_{\min }}^{1} r^{1 / 2} n(r) \mathrm {K} {\rm d} r$ with n(r) being the density distribution function of EPs. $\beta _{h}$ denotes the EPs’ pressure. $\alpha _0B_0(=0.99)$ specifies the EPs’ pitch angle. We assume that all EPs have the same pitch angle, with a slowing down distribution in the particle energy space as discussed in [7, 13]. r is the radial variable, normalized by the minor radius a of the plasma. f(r) is the perpendicular plasma displacement associated with the mode. $\Omega _{p f} \equiv \omega _{p f} / \omega _{d s}=i \gamma \tau _{\rm w}^{*} /\left( \tau _{\rm w}^{*} \omega _{d s}\right) +\Omega _{r}-\Omega _{0}$ and $\Omega _{d, e} \equiv \omega _{d, e} / \omega _{d s}=E_{m} K_{2} q /\left( \omega _{d s} K_{b} r \omega _{c} R\right)$, with $\omega _{p f}\left( \equiv \omega _{r}+i \gamma -\omega _{0}\right)$ being the mode complex frequency in the plasma frame and q being the safety factor. We have introduced $\gamma \tau _{\rm w}^{*}$, $\Omega _{r}=\omega _{r} / \omega _{d s}$ and $\Omega _{0}=\omega _{0} / \omega _{d s}$ to denote the normalized mode growth rate, the mode real frequency and the plasma rotation frequency, respectively. We also use $\omega _{d s}=K_{2}(a) E_{m} q /\left[ K_{b}(a) a \omega _{c} R\right]$ to label the bounce-averaged precession drift frequency of trapped EPs at the plasma boundary, with $m_{h} E_{m}\left( \equiv E_{b}\right)$ being the birth energy of the beam-driven EPs. The remaining quantities are defined in Ref. [13].

The normalized forms of the fluid potential energies, without and with an ideal wall, are given [4], respectively, as

$$\begin{aligned} \delta W_{\rm f}^{\infty }=\frac{-4 \pi }{m} \frac{(m-n q)^{2}}{q^{2}}\left( \frac{1}{m-n q}-1\right) , \end{aligned}$$

(4)

and

$$\begin{aligned} \delta W_{\rm f}^{b}=\frac{-4 \pi }{m} \frac{(m-n q)^{2}}{q^{2}}\left( \frac{1}{m-n q}-\frac{1}{1-b^{-2 m}}\right) , \end{aligned}$$

(5)

where the (ideal) wall minor radius b is normalized to the plasma minor radius a. m and n are poloidal and toroidal mode numbers, respectively. The above energy perturbation terms are valid for a cylindrical plasma with circular cross section.

We numerically solve the dispersion relation (1) while choosing the following parameters: the poloidal mode number $m=2$, the toroidal mode number $n=1$, the minor radius $a=1$ m, the major radius $R=3$ m, the magnetic field $B_0=2.3$ T, the EPs’ birth energy $E_b=85$ keV, the safety factor $q=1.42$ with flat profile, the plasma thermal beta $\beta _{th}=0.055$, the normalized wall radial position $b=1.2$, the wall conductivity $\sigma =10^{6}$ $\Omega ^{-1} \mathrm {m}^{-1}$, the wall thickness $d=0.01a$ and a flat plasma density $n_{0}=10^{20}$ $\mathrm {m}^{-3}$. These operating conditions are chosen mainly to access the fluid-wise unstable RWM regime in the absence of drift kinetic effects. In particular, the choices of the mode numbers and the q-value yield $\delta W_{\rm f}^{\infty }=-0.76<0$ and $\delta W_{\rm f}^{b}=0.22>0$, resulting in an unstable mode according to Eq. (1) at vanishing $\delta W_{K 0}$.

In this work, we focus on the influence of the change of density profile of trapped EPs arising from off-axis NBI heating, on the RWM stability. For this purpose, a normalized, spatially non-uniform density profile of EPs, $n(r)={\rm e}^{-u^{2}\left( r-r_{0}\right) ^{2}}$, is considered, where $r_0$ denotes the radial position of the peak of n(r). The circular equilibrium given above has analytic solution for the normalized perpendicular displacement as $f=f_{1}(r)=r^{(m-1)}$ [4], reaching its peak value at the plasma boundary. We shall also consider an artificial profile $f=f_{2}(r)=\left[ \left( r-r_{2}\right) ^{2}+1\right] ^{-10}$ which peaks at $r_2$, in order to demonstrate the influence of the off-axis NBI on the RWM. Figure 1 plots $f_1$ and $f_2$ as functions of r with $r_2=0.6$. Figure 2 plots the EPs’ density profiles with various choices of the u-value at fixed $r_{0}=0.6$.

Fig. 1

Two trial functions for the mode displacement, versus the plasma minor radius

Fig. 2

Various radial profiles of the energetic particle density n(r), corresponding to various choices of parameter u

Figure 3 shows the normalized RWM growth rate $\gamma \tau _{\rm w}^{*}$ as functions of the peak position $r_0$ of the EPs’ density profile, with various choices of the EPs’ beta $\beta ^{*}$ ($\beta ^{*} \equiv \beta _{h}/\beta _{th}$ is the ratio of the EPs’ pressure to the total thermal plasma pressure). Here, the trial function $f_1$ is used, which peaks at the plasma edge. For the case of $\beta ^{*}=0.3$, the RWM growth rate decreases and crosses the marginal stability point with increasing $r_{0}$. This shows that the off-axis deposition of EPs enhances the stabilization effect of EPs on the RWM. The stabilization becomes stronger as $r_0$ approaches the plasma edge. In fact, the calculation results indicate that the value of ${\text {Im}}\left( \delta W_{K 0}\right)$ is proportional to $r_0$. The imaginary part of the perturbed drift kinetic energy always contributes stabilization to the RWM and thus reduces the mode growth rate with increasing $r_0$.

Comparison between different curves in Fig. 3 shows that the growth rate decreases with increasing $\beta ^*$ at fixed $r_0$. Furthermore, compared to the case of $\beta ^*=0.1$, the effect of the EPs’ density peaking alignment with the mode structure, for the mode stabilization, becomes more prominent at higher $\beta ^*$ values. This is again related to the fact that the term $\ln \left( 1-\Omega _{d, e} / \Omega _{p f}\right)$ from Eq. (3) can always contribute an imaginary part to $\delta W_{K 0}$, arising mainly from the mode-particle resonance [13]. Moreover, Eq. (3) shows that ${\text {Im}}\left( \delta W_{K 0}\right)$ is proportional to the product of $n(r)|f(r)|^{2}$, which reaches the maximum if the peak position of n(r) aligns with that of $|f(r)|^{2}$.

Fig. 3

The normalized growth rate of the RWM $\gamma \tau _{\rm w}^{*}$ versus the peaking position $r_0$ of the EPs’ density profile for the choice of the mode eigenfunction $f_1(r)$. Various values of the normalized beta ($\beta ^{*} \equiv \beta _{h} / \beta$) are chosen for the EPs

Next, we carry out calculations assuming the artificial trial function $f_2$ as shown in Fig. 1. Although $f_2$ is not the true eigenfunction for the given equilibrium, it helps to further illustrate the importance of alignment between the MHD perturbation and the EPs’ equilibrium density distribution. Moreover, the RWM eigenfunction in a toroidal plasma often peaks near low-order rational surfaces. This also motivates our choice of the trial function $f_2$ here. Figure 4 compares the computed RWM growth rate $\gamma \tau ^*_{\rm w}$ as functions of $r_0$, assuming the peaking location of $r_2=0.6$ for $f_2$. It is evident that the mode growth rate is sensitive to $r_0$, and the strongest stabilization occurs when $r_0=r_2$, i.e. when the radial peaking of the EPs’ density aligns with that of the perturbation. For the case of $\beta ^{*}=0.3$, the mode is fully stabilized in a wide window near $r_0=0.6$. Figure 4 thus further confirms that the maximal drift kinetic damping on the RWM is provided by trapped EPs, when the latter has a radial deposition that peaks near the maximum of the plasma displacement associated with the mode.

Fig. 4

The growth rate of the RWM versus $r_{0}$ for various values of $\beta ^{*}$, where the trial eigenfunction $f_{2}$, with $r_{2}=0.6$ is used for the RWM

Trapped EPs affect the RWM stability via two physics mechanisms. One is the wave-particle Landau resonance, where the free energy associated with the instability is tapped by the EPs. The other is associated with the conservation of the so-called third adiabatic invariant, where the perturbed magnetic flux, enclosed by the center of the banana orbit (of EPs), is constrained (thus stabilization of the instability) as soon as the precessional motion of the banana orbit is sufficiently fast compared to the perturbation frequency. The latter mechanism is similar to that of the internal kink stabilization by EPs [14].

The Landau resonance stabilization can be understood by examining the real part of Eq. (1).

$$\begin{aligned} \gamma \tau ^*_{\rm w}=\frac{(\delta W^b_{\rm f}-\delta W^\infty _{\rm f})[\delta W^b_{\rm f}+\text {Re}(\delta W_{K0})]}{[\delta W^b_{\rm f}+\text {Re}(\delta W_{K0})]^2+\text {Im}(\delta W_{K0})^2}-1 . \end{aligned}$$

(6)

Since $|\text {Re}(\delta W_{K0})|\sim 0.1$ (shown in Fig. 5) is smaller than the fluid term $\delta W^b_{\rm f}=0.22$, we approximately obtain $\gamma \tau ^*_{\rm w}\propto \frac{(\delta W^b_{\rm f}-\delta W^\infty _{\rm f})\delta W^b_{\rm f}}{(\delta W^b_{\rm f})^2+\text {Im}(\delta W_{K0})^2}-1.$ This formula implies that the growth rate $\gamma \tau ^*_{\rm w}$ decreases with increasing the imaginary part of perturbed kinetic energy $\text {Im}(\delta W_{K0})$ . Hence, the dependence of ${\text {Im}}\left( \delta W_{K 0}\right)$ on $r_0$ shown in Fig. 5 results in the dependence of $\gamma \tau _{\rm w}^{*}$ on $r_{0}$ as reported in Fig. 4. Here, $\text {Im}(\delta W_{K0})$ is mainly induced by the resonance between the mode and the precession drift motion of trapped EPs (i.e. $\omega _r - \omega _d=0$), which occurs at certain EP energy similar to that shown in Fig. 9 from Ref. [13]. We point out that the precession drift frequency $\omega _d$ depends on both the radial location and energy of EPs.

We have so far fixed the Guassian width factor at $u=5$ in specifying the EPs’ radial density profile for the RWM stability calculations. Figure 6 shows the effect of varying u on the mode stability, while fixing the EP’s pressure fraction $\beta ^{*}$ at 0.14. It is evident that the narrower density profile of EPs, the more sensitive dependence of the mode growth rate on $r_{0}$. A broader radial distribution of EPs thus ensures a more robust mode stabilization, but at the expense of less degree of stabilization even with the optimal radial deposition of EPs.

We emphasize that the aforementioned alignment between the EPs’ density peaking and the mode peaking, for achieving the best RWM stabilization, is systematically obeyed. Indeed, by varying the mode peaking location $r_2$, the optimal density peaking location $r_0$ follows, as shown in Fig. 7. The exception here is for the case of $r_{2}=0.8$, where a very broad minimum in the mode growth rate is obtained. If we instead choose $u=8$ for this case (corresponding to a narrower EP distribution in real space) , we again finds (not shown here) that the minimal value of $\gamma \tau _{\rm w}^{*}$ is achieved at $r_{0}=r_{2}=0.8$. As an obvious implication to experiments, the NBI should be mostly deposited at the peaking position of the RWM eigenmode (in terms of the associated plasma radial displacement), in order to maximize the kinetic stabilization on the mode due to trapped EPs. As mentioned before, this usually implies NBI deposition near low-order rational surfaces. An obvious caution from the practical point of view is to avoid NBI being deposited too close to the plasma edge, which can cause shine-through issue and damage the plasma facing components.

Fig. 5

The perturbed drift kinetic energy due to trapped EPs as functions of $r_{0}$, for various choices of $\beta ^{*}$ value, corresponding to that shown in Fig. 4

Fig. 6

The growth rate of the RWM versus $r_{0}$ for different values of u, where $\beta ^{*}=0.14$ and $r_{2}=0.6$ are used

Fig. 7

The RWM growth rates versus $r_{0}$ for different choices of $r_{2}$, with $\beta ^{*}=0.12$ and $u=5$ being fixed

In the above analytic model, large aspect ratio expansion is implicitly assumed in evaluating the drift kinetic energy ($\delta W_{K 0}$) in order to allow particle trapping (for EPs). On the other hand, the perturbed fluid potential energies ($\delta W_{\rm f}^{\infty }$ and $\delta W_{\rm f}^{b}$) are calculated based on a straight cylinder. Therefore, strictly speaking, the kinetic dispersion relation (1), combined with Eqs. (2, 4, 5), is consistent only at the limit of infinite aspect ratio. Nevertheless, the model is capable of providing qualitative assessment of the influence of off-axis NBI on the RWM stability. Moreover, the analytic model assumes a mono-pitch angle EPs beam, i.e. equilibrium distribution function of EPs is a delta-function in the particle pitch angle space (and the particle pitch angle is chosen such that all particles remain trapped). In realistic situations, EPs of course have a spread-distribution in the pitch angle space. Moreover, the fraction of trapped EPs (out of the total number of EPs) varies with the plasma minor radius. All the aforementioned model simplifications are avoided in the full toroidal MHD-kinetic hybrid formulation adopted by the MARS-K code, which will be utilized to study the RWM stability in “Numerical Results from MARS-K Code” section.

Numerical Results from MARS-K Code

The MARS-K code allows us to study the effect of EPs with anisotropic distribution along the particle pitch angle [15]. A toroidal tokamak equilibrium is considered in the following study. This Solovev-type of equilibrium is specified in Ref. [3], cf. Eq. (23) therein, with the inverse aspect ratio of $\epsilon _a=0.33$ and the plasma boundary surface elongation of $\kappa =1.6$ are assumed. Furthermore, the equilibrium safety factor is chosen such that the on-axis value is $q_{0}=1.4$ and the edge value is $q_{\text{ edge } }=2.5$, allowing only one rational surface ($q=2$) inside the plasma for the $n=1$ perturbation. This equilibrium is unstable to the $n=1$ fluid RWM without kinetic effects.

In MARS-K, the perturbed pressure, below, is a tensor term that enters into the perturbed MHD force balance equation

$$\begin{aligned} {\mathbf {p}}=p_{th} {\mathbf {I}}+p_{\parallel } {\mathbf {b}} {\mathbf {b}}+p_{\perp }({\mathbf {I}}-{\mathbf {b}} {\mathbf {b}}). \end{aligned}$$

(7)

where $p_{\parallel }$ and $p_{\perp }$ are perturbed pressures due to EPs, being parallel along, and perpendicular to, the un-perturbed (equilibrium) magnetic field lines, respectively. Both adiabatic and non-adiabatic contributions are computed for these two terms, by solving the perturbed drift kinetic equation (i.e. Vlasov equation) for EPs in the continuous form [16]. The first term $p_{th}$ denotes the perturbed isotropic pressure associated with thermal particles, which are treated within the single fluid framework in this study. In other words, no drift kinetic contributions from thermal particles are included in this study. Such contribution, for the same type of Solovev equilibrium, was investigated in Ref. [3]. Excluding the kinetic contribution from thermal particles in this work allows better comparison with the analytic results presented in Sec. II. Symbols ${\mathbf {I}}$ and ${\mathbf {b}}$ denote the unit tensor and unit vector of the equilibrium magnetic field, respectively.

The normalized equilibrium pressure and density profiles of EPs are specified as $P_{h}=0.3 {\rm e}^{-u^{2}\left( \psi -r_{0}\right) ^{2}}$ and $N_{h}=0.05 {\rm e}^{-u^{2}\left( \psi -r_{0}\right) ^{2}}$, respectively, where $\psi$ (the normalized equilibrium poloidal flux) labels the magnetic flux surface, $r_{0}$ defines the peak position of $P_{h}$ and $N_{h}$ along the plasma minor radius. We assume that the EPs, driven by perpendicular NBI, have an equilibrium distribution function which is slowing-down in the particle energy space and anisotropic in the particle pitch angle space.

$$\begin{aligned} f^{0}=\frac{C(\psi )}{\varepsilon _{k}^{3 / 2}+\varepsilon _{c}^{3 / 2}} {\hat{f}}^0. \end{aligned}$$

(8)

where ${\hat{f}}^0=\frac{1}{\delta \zeta \sqrt{\pi }}\left[ {\rm e}^{-\zeta ^{2} / \delta \zeta ^{2}}+{\rm e}^{-(\zeta -2)^{2} / \delta \zeta ^{2}}\right]$ and $\delta \zeta ^{2}\left( \psi , \xi _{k}\right) =\delta \zeta _{0}^{2}-\frac{1}{3} \ln \left[ \frac{{\mathcal {E}}_{k}^{3 / 2}\left( \varepsilon _{\alpha }^{3 / 2}+\varepsilon _{c}^{3 / 2}\right) }{\varepsilon _{k}^{3 / 2}+\varepsilon _{c}^{3 / 2}}\right]$ [15, 17]. $\varepsilon _{k}$, $\varepsilon _{\alpha }$ and $\zeta$ denote the kinetic energy, birth energy and the pitch angle of EPs, respectively. $\varepsilon _{c}$ is a quantity (“cross-over” energy) proportional to the temperature of thermal electrons [18]. The coefficient $C(\psi )$ is determined by the surface averaged equilibrium density $N_{h}$ of EPs. As $\delta \zeta \rightarrow 0$, the above distribution function (8) approaches a delta-function along the particle pitch angle, recovering the analytic model assumed in Sec. II.

Figure 8 shows the MARS-K computed growth rate and real frequency of the $n=1$ RWM while scanning the peak position ($r_0$) of the EPs’ density profile $N_{h}$. The mode growth rate first decreases with increasing $r_{0}$, reaching a minimum at $r_{0}\sim 0.8$. The mode frequency meanwhile increases with $r_{0}$ before reaching $r_0=0.8$. This happens because the kinetic damping from trapped EPs increases as the peak position of $N_{h}$ approaches the maximum of the plasma displacement (Fig. 9), confirming the analytic finding from “Analytic Model” section.

Note that, as in the analytic theory, we include the kinetic contribution from trapped EPs alone. MARS-K computations confirm that the passing EPs play a negligible role on the RWM here. The mode’s eigenvalue almost does not change when the kinetic effect from passing EPs is included. For example, the additional contribution from passing EPs changes the mode growth rate $\gamma \tau _A$ and frequency $\omega _r \tau _A$ from $3.48387\times 10^{-4}$ and $2.90762\times 10^{-4}$ to $3.48160\times 10^{-4}$ and $2.90645\times 10^{-4}$, respectively, for the case with EPs density peaking at $r_0=0.8$. There are two main reasons for this: (1) the fraction of passing EPs is small for the studied case in fact less than 3% in the region $\psi ^{1/2} >0.3$ ; (2) the transit frequency of passing EPs is very high in the bulk region of plasma where the $(m-nq)$ factor is not small. Since the RWM is a global mode, the resonance effect (from passing EPs) in the small region near rational surfaces $m=nq$ plays a limited role.

Fig. 8

The computed mode eigenvalue as functions of the peaking position of the EPs density $N_{h}$. The value of $\delta \zeta _{0}=0.3$ is used. $\omega _{A}$ is the Alfven frequency at the plasma centre. No plasma rotation is assumed

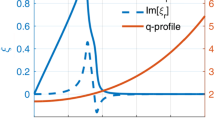
Figure 9 shows one example of the MARS-K computed eigenmode structure for the RWM for this Solovev equilibrium. Plotted are the poloidal Fourier harmonics of the plasma radial displacement, for the case of $r_{0}=0.7$. For comparison, we show eigenfunctions for both kinetic (Fig. 9a) and fluid (Fig. 9b) RWM. Figure 9a shows certain modification of the RWM eigenmode structure by drift kinetic effects from EPs. The change is particularly pronounced near and beyond the $q=2$ rational surface. Note that the sharp features near the rational surface are numerically well resolved, as shown by the inset in Fig. 9a, thanks to a strong radial mesh packing near the rational surface. This self-consistent modification of the mode eigenfunction shows the importance of the non-perturbative MHD-kinetic approach in capturing all relevant effects for the kinetic RWM.

Fig. 9

a The radial profiles of the poloidal harmonics of the computed normal displacement of the kinetic RWM, corresponding to the case of $r_0=0.7$ as shown in Fig. 8. b The fluid RWM case. The equal-arc flux coordinate system is used

Figure 10 compares two-dimensional plots of the perturbed drift kinetic pressure $\delta p_{/ /}$ and $\delta p_{\perp }$ associated with EPs. Note that, as mentioned before, the perturbed (scalar) pressure associated with thermal particles is modeled via single fluid adiabatic closure and is not shown here. The EPs due to normal NBI mainly drive the perpendicular component of the drift kinetic pressure perturbation, as is evident from Fig. 10. Note also that these kinetic pressure perturbations due to EPs are large mainly at the low field side of the poloidal cross section, reflecting the kink-ballooning nature of the RWM instability. This is also where the trapped EPs are primarily populated.

Fig. 10

Two-dimensional plots of the perturbed a parallel and b perpendicular kinetic pressures, computed from the self-consistent approach. No plasma rotation is assumed

Conclusions

In this work, we have investigated the influence of the off-axis NBI induced EPs on the RWM instability, employing both an analytic model and the full toroidal MHD-kinetic hybrid code MARS-K. The results from both approaches show that the kinetic damping effect, arising from the mode-particle resonances, is enhanced as the radial deposition of energetic particles approaches the peak position of the plasma radial displacement associated with the RWM. The strongest mode stabilization occurs, when the EPs’ peak radial deposition aligns with the peak location of the RWM perturbation. Furthermore, the MARS-K numerical results indicate that the EPs’ kinetic effect significantly modifies the RWM eigenfunction. With the normal neutral beam injection, the MARS-K toroidal modeling results show that the trapped EPs mostly drive the perpendicular component of the kinetic pressure perturbation, and mainly at the low field side of the torus. Overall, the off-axis NBI injection is found to enhance the RWM stability. It is possible to optimize the off-axis NBI deposition position to maximize this stabilization effect in experiments. Finally, we remark that a large fraction of NBI induced EPs may also trigger the fishbone instability. A systematic investigation of this aspect, employing the MARS-K code, remains a future work.