1 Introduction

As per observational evidences we are living in an expanding and accelerating universe (Permutter et al. [1], Riess et al. [2], Spergel et al. [3], Anderson et al. [4], Hinshaw et al. [5], Suzuki et al. [6], Ade et al. [7]). The cosmic accelerating expansion is assumed to be guided by a fluid called mysterious energy in cosmology i.e. dark energy. It is also known that the accelerating expansion of the universe is driven by negative pressure of dark energy which tends to increase the rate of expansion of the universe. During the investigation of literature it has been observed that many sources of dark energy such as cosmological constant, quintessence, tachyon, phantom, k-essence, chaplygin gas etc have been studied by many researchers [8–14]. In this paper we have studied the expanding and accelerating behavior of the universe with cosmological constant and EoS parameter. As we know cosmological constant Λ was proposed by Einstein in 1917 as the universal repulsion force to allow static homogeneous solution to Einstein field equations in the presence of matter in accordance with generally accepted theory at that time. After few year some researchers realized that the cosmological constant may be measure as the energy density of the vacuum which is the state of lowest energy more over the vacuum energy momentum tensor. \(T^{vac}_{ij}=-\rho ^{vac}g_{ij}\) and vacuum may be also treated as perfect fluid with EoS as P v a c = −ρ v a c , by taking \(\rho _{vac}=\rho _{\Lambda }=\frac {\Lambda }{8\pi G}\) and moving the Λg i j one can say that the effect of energy momentum tensor for vacuum is equivalent to Λ.

In recent research findings it has been established that hypothetical fluid (DE) is tied with cosmological constant. It means Λ is assumed to be source of dark energy i.e. ΛCDM, as we know that the density of dark energy evolve with the expansion of the universe, which is described by the EoS parameter \(\omega (t)=\frac {p}{\rho }\), where ρ and p are energy density and pressure respectively.

Here in this study we have presented the cosmological models of the universe in the frame work of modified gravity theory. Modified gravity theory provides a platform to understand the problem of dark energy more smoothly, this also indicate the possibilities to reconstruct the gravitational field theory which may be capable to reproduce the late time acceleration. The f(R) gravity theory suggests us a very natural unification of early time inflation and late time expansion of the universe. Allemandi et al. [15] have proposed a modified gravity theory by including an coupling of arbitrary function of R with the matter Lagrangian density. Harko et al. [16] have suggested a generalization of f(R) gravity theory which is known as f(R, T) gravity theory involving the dependence of the trace T of energy momentum tensor T μ ν . We have also emphasized that due to coupling of matter and geometry this gravity theory depends on the source term representing the variation of stress-energy tensor with respect to the metric.

Recently many researchers tried to explain the nature of dark energy by assuming ω, is not a constant, but a function of cosmic time (Akarsu and Kilinc [17, 18], Carroll and Hoffman [19], Ray and Rehman et al. [20] Yadav et al. [21], Yadav and Yadav [22], Pradhan et al. [23–25], Amirhashchi et al. [26] and Pradhan et al. [27]). Also some authors investigated Bianchi type dark energy models in the frame work of modified f(R, T) gravity theory by assuming deceleration parameter as a constant quantity [28, 29].

Motivated from above research findings, we have explored the dynamic nature of the universe with the help of variable deceleration (DP) parameter (as suggested by Mishra and Chawla et al. [30, 31]) along with EoS parameter and cosmological constant in the frame work of anisitropic cosmological models in string theory. For the purpose of the study we have presented the solution of field equation with and without presence of magnetic field along with known form of evolution of the universe. As we know that in power law model the scale factor and potential are assumed to be evolve exponentially with a scalar field. The present paper is organized in six different sections, Section 1 contains introduction, in Section 2 we have presented brief derivation of f(R, T) gravity theory whereas the metric and equations governing the cosmological models have been placed in Section 3, in Section 4 the exact solution of field equations have been given under both the cases. The physical and kinematical behavior of parameters have been presented under Section 5 whereas the result and discussion are given in brief in the last section i.e. in Section 6.

2 Brief of f(R, T) Gravity Theory

In continuation of above introduction presented in Section 1, we may say that the f(R, T) theory of gravity is the generalization or modification of general theory of gravity. The action for this theory may be expressed as:

$$ S=\frac{1}{16\pi}\int f(R,T)\sqrt{-g}d^{4}x + \int \pounds_{m} \sqrt{-g} d^{4}, $$
(1)

where f(R, T) is an arbitrary function of the Ricci scalar R and T (trace of energy momentum tensor), £ m is the matter Lagrangian density. The stress-energy tensor of the matter is defined as

$$ T_{ij} = \frac{-2}{\sqrt{-g}}\frac{\delta(\sqrt{-g}\pounds_{m})} {\delta g^{ij}} $$
(2)

and the trace T is define as T = g ij T i j , Assuming that the Lagrangian density £ m of matter depends on the metric tensor components g i j only. After simplification of (2) we may express T i j as

$$ T_{ij} = g_{ij}\pounds_{m}- 2\frac{\partial \pounds_{m}}{\partial g^{ij}}, $$
(3)

Varying the action S with respect to the metric tensor components g ij, the gravitational field equations of f(R, T) gravity is obtained as

$$\begin{array}{@{}rcl@{}} &&f_{R}(R,T)R_{ij}-\frac{1}{2}f(R,T)g_{ij} + (g_{ij}\Box-\nabla_{i} \nabla_{j})f_{R}(R,T)\\ &=& 8\pi T_{ij} - f_{T}(R,T)T_{ij} - f_{T}(R,T){\Theta}_{ij}, \end{array} $$
(4)

here \({\Theta }_{ij} = g^{\mu \nu } \{\frac {\delta T^{\mu \nu }}{\delta g^{ij}} \}\) which follows from the relation \( \partial \left \{\frac { g^{\mu \nu }T_{\mu \nu }}{\delta g^{ij}}\right \}=T_{ij} + {\Theta } \) and \(\Box = \nabla ^{i}\nabla _{i} f_{R}(R,T) = \frac {\partial f(R,T)}{\partial T}\) here ∇ i denote the co variant derivative. If we go for contraction of (4) then we have

$$ f_{R}(R,T)R+3\Box f_{R}(R,T)-2f(R,T) = (8\pi-f_{T}(R,T)T-f_{T}(R,T){\Theta}, $$
(5)

with Θ=g ijΘ i j . Combining (4) and (5) and eliminating the □f R (R, T) term from these equations, we obtain

$$\begin{array}{@{}rcl@{}} &&f_{R}(R,T)\left\{R_{ij} - \frac{1}{3}R g_{ij}\right\} +\frac{1}{6} f(R,T) g_{ij}\\ &=& \! (8\pi\! -\! f_{T}(R,T)) \left\{ T_{ij}-\frac{1}{3} Tg_{ij}\right\} -f_{R}(R,T)\left\{ {\Theta}_{ij}-\frac{1}{3} {\Theta} g_{ij}\right\} + \nabla_{i} \nabla_{j} f_{R}(R,T), \end{array} $$
(6)

using the covariant divergence of (1) as well energy-momentum conservation law

$$ \nabla^{i} \left\{ f_{R}(R,T)-\frac{1}{2}f(R,T)g_{ij} + (g_{ij}\Box -\nabla^{i}\nabla_{j}) f_{R}(R,T)\right\}\equiv 0, $$
(7)

which corresponds to the divergence of the left hand side of (1), we acquire the divergence of T i j as

$$ \nabla^{i} T_{ij} = \frac{f_{r}(R,T)}{8\pi - f_{r}(R,T)}\left\{ (T_{ij}+ {\Theta}_{ij}) \nabla^{i} ln f_{r}(R,T)+ \nabla^{i} {\Theta}_{ij}\right\}, $$
(8)

From (3) we have

$$ \frac{\delta T_{ij}}{\delta g^{\mu\nu}}= \left[\frac{\delta g_{ij}}{\delta g^{\mu\nu}} + \frac{1}{2}g_{ij} T_{\mu\nu} - 2\frac{\partial^{2}\pounds_{m}}{\partial g^{\mu\nu}g^{ij}}\right] $$
(9)

Using the relation \(\frac {\delta g_{ij}}{\delta g_{\mu \nu }} =-g_{i\gamma }g_{j\sigma }\delta ^{\gamma \sigma }_{\mu \nu }\) with \(\delta ^{\gamma \sigma }_{\mu \nu }= \frac {\delta g_{\gamma \sigma }}{\delta g_{\mu \nu }} \), which follow \(g_{i\gamma }g^{\gamma j}= {\delta ^{j}_{i}}\), with the help of above assumption we may re-express Θ i j as

$$ {\Theta}_{ij} = -2 T_{ij} + g_{ij}\pounds_{m}-2g{\Theta}^{\mu\nu}\frac{\partial^{2}\pounds_{m}} {\partial g^{\mu\nu}\partial g^{ij}}, $$
(10)

For perfect fluid the energy-momentum tensor T i j is given by

$$ T_{ij} =(\rho + p)u_{i} u_{j} - p g_{ij}, $$
(11)

where ρ and p are the energy density and pressure of the fluid respectively. u i = (0,0,0,1) is the four velocity vector in co-moving coordinates which satisfies the conditions u i u i = 1 and u i∇ j u i = 0. From (10) and (11), we have

$$ {\Theta}_{ij} = -2T_{ij} - p g_{ij}, $$
(12)

Now we wish to consider f(R, T) as suggested by Harko et al. [16].

$$ f(R,T) =R + 2f(T), $$
(13)

where f(T) is an arbitrary function of trace T. Now using (12) and (13) into the field (4) taken the form

$$ R_{ij} - R g_{ij} = 8\pi T_{ij} + 2 f^{\prime}(T) T_{ij} + [2p f^{\prime}(T) + f(T)]g_{ij}, $$
(14)

We may also agree with the following assumption

$$ f(T) = \eta T, $$
(15)

where η is a constant.

3 Metric and Equations Governing the Cosmological Model

In present communication we consider Bianchi type-II space time as

$$ ds^{2}=-dt^{2}+A^{2}(dx-zdy)^{2}+B^{2}dy^{2}+C^{2}dz^{2} $$
(16)

Here potential A, B and C are the functions of time t only. This ensure that the model of universe is spatially homogeneous and totally anisotropic.

Energy momentum tensor T i j for anisotropic dark energy is given by

$$\begin{array}{@{}rcl@{}} T_{ij} &=& diag[\rho, -p_{x},-p_{y},-p_{z}]\\ T_{ij}&=&diag[1,-\omega_{x},-\omega_{y},-\omega_{z}]\rho. \end{array} $$
(17)

where ρ is the energy density of the fluid while p x , p y and p z are the pressure components along the x, y and z axes respectively. Here ω is the EoS parameter of the fluid with no deviation and ω x , ω y and ω z are the EoS parameter in the directions of x, y and z respectively. The energy momentum tensor can be parameterized as

$$ T_{ij}=diag[1,-(\omega + \delta),-\omega, -\omega]\rho . $$
(18)

For sake of simplicity we choose ω y = ω z = ω and the skewness parameter δ is a deviation from ω on x axis. In co-moving coordinate system the velocity components are u i = (0,0,0,1). which satisfies the conditions u i u i = 0.

The electromagnetic field tensor F i j has only one non-zero component F 31 because the magnetic field is assumed to be only along the y axes. Subsequently Maxwell’s equations may be expressed as

$$ F_{ij;k}+F_{jk;i}+F_{ki;j}=0, $$
(19)
$$F_{;j}^{ij}=0 $$

which on simplification, we obtain

$$ F_{31}=K $$
(20)

where K is the constant.

Let us introduce some physical parameters such as the spatial volume V, the expansion scalar θ, the Hubble parameter H, the mean anisotropy parameter A m , the shear scalar σ and the deceleration parameter q for the metric (16)

$$ V = a^{3} = ABC $$
(21)
$$ \theta=3H=\frac{3\dot{a}}{a} = \frac{\dot{V}}{V}=(H_{x} + H_{y} + H_{z}), $$
(22)

where \(H_{x} = \frac {\dot {A}}{A}, H_{y} = \frac {\dot {B}}{B}, H_{z} = \frac {\dot {C}}{C}\) are the directional Hubble’s parameters in directions of x, y and z axis respectively.

$$ A_{m} = \frac{1}{3}\sum\limits_{i=1}^{3}\left[\frac{\Delta H_{i}}{H}\right]^{2} $$
(23)

where

$$\begin{array}{@{}rcl@{}} {\Delta} H_{i}&=&H_{i}-H, \hspace{1cm} i=1,2,3\\ \sigma^{2} &=& \frac{1}{2}\left[\sum\limits_{i=1}^{3} {H_{i}^{2}} - 3 H^{2}\right] \end{array} $$
(24)

The deceleration parameter q in cosmology is the measure of the cosmic acceleration of the universe expansion and is defined as

$$ q=-\frac{a\ddot{a}}{a^{2}}=-\left[\frac{\dot{H}+ H^{2}}{H^{2}}\right] $$
(25)

3.1 Field Equations with Presence of Magnetic Field

Now assuming co-moving coordinates system the field equations (14) for the metric (16) with the help of (15), (18) and (20) we will get following set of equations:

$$\begin{array}{@{}rcl@{}} \frac{\dot{A}\dot{B}}{A B} + \frac{\dot{B}\dot{C}}{B C} + \frac{\dot{A}\dot{C}}{A C}- \frac{1}{4}\hat{A^{2}}&=& \rho \{8\pi-\eta(3\omega+\delta-3)\}+2p\eta- \eta B^{2} \hat{B^{2}}\\ &&+ (4\pi + 2\eta)(A^{2} z^{2} + B^{2})\hat{B^{2}} \end{array} $$
(26)
$$\begin{array}{@{}rcl@{}} \frac{\ddot{B}}{B}+ \frac{\ddot{C}}{C}+\frac{\dot{B}\dot{C}}{B C}-\frac{3}{4}\hat{A^{2}} &=& -\rho \{8\pi(\omega+\delta) +\eta(5\omega+3\delta-1)\} + 2p\eta - (8\pi+3\eta)B^{2}\hat{B^{2}}\\ &&+ (4\pi + 2\eta)(A^{2} z^{2} + B^{2})\hat{B^{2}} \end{array} $$
(27)
$$ \frac{\ddot{A}}{A}+ \frac{\ddot{C}}{C}+\frac{\dot{A}\dot{C}}{A C}+\frac{1}{4}\hat{A^{2}} = -\rho \{8\pi\omega+\eta(5\omega+\delta-1)\}+2p\eta + 4\pi B^{2} \hat{B^{2}} + \eta(A^{2} z^{2} + B^{2})\hat{B^{2}} $$
(28)
$$ \frac{\ddot{A}}{A}+ \frac{\ddot{B}}{B}+\frac{\dot{A}\dot{B}}{A B}+\frac{1}{4}\hat{A^{2}} = -\rho \{8\pi\omega+\eta(5\omega+\delta-1)\}+2p\eta - \eta B^{2} \hat{B^{2}}-4\pi (A^{2} z^{2} + B^{2})\hat{B^{2}} $$
(29)

Now it is mandatory for us to test these equations in the absence of magnetic field which being presented in the next Section 3.2.

3.2 Field Equations Without Presence of Magnetic Field

Re-write the set of field equations from (26)–(29) by putting K = 0 as

$$ \frac{\dot{A}\dot{B}}{A B} + \frac{\dot{B}\dot{C}}{B C} + \frac{\dot{A}\dot{C}}{A C}-\frac{1}{4}\hat{A^{2}} = \rho \{8\pi-\eta(3\omega+\delta-3)\}+2p\eta $$
(30)
$$ \frac{\ddot{B}}{B}+ \frac{\ddot{C}}{C}+\frac{\dot{B}\dot{C}}{B C}-\frac{3}{4}\hat{A^{2}} = -\rho \{8\pi(\omega+\delta) +\eta(5\omega+3\delta-1)\}+2p\eta $$
(31)
$$ \frac{\ddot{A}}{A}+ \frac{\ddot{C}}{C}+\frac{\dot{A}\dot{C}}{A C}+\frac{1}{4}\hat{A^{2}} = - \rho \{8\pi\omega+\eta(5\omega+\delta-1)\}+2p\eta $$
(32)
$$ \frac{\ddot{A}}{A}+ \frac{\ddot{B}}{B}+\frac{\dot{A}\dot{B}}{A B}+\frac{1}{4} \hat{A^{2}} = -\rho \{8\pi\omega+\eta(5\omega+\delta-1)\}+2p\eta $$
(33)

where an overhead dot denotes derivatives with respect to cosmic time t. Also we have assume \(\hat {A^{2}}=\frac {A^{2}}{B^{2}C^{2}}\) and \(\hat {B^{2}}=\frac {A^{2}C^{2}K^{2}}{4\pi B^{2}}\) in all of above equations.

4 Solution of Field Equations

As we know that the (26)–(29) are the set of four independent equations along with six unknown A, B, C, η, ρ and p and therefore some additional constraint equations require for the solution of field equations,relating these parameters. For exact solution of EFE we have used two well accepted assumptions such as, we introduce deceleration parameter q as a function to time ‘t’, as suggested by Mishra et al. [30] and Chawla et al. [32]. i.e. q = b(t)

$$ q=-\frac{a\ddot{a}}{a^{2}}=-\left( \frac{\dot{H}+ H^{2}}{H^{2}}\right)= b(t) (say) $$
(34)

In this section main purpose of the study is to see the nature of model by assuming variable DP which is being presented below

$$ \frac{\ddot{a}}{a}+ b\frac{\dot{a}^{2}}{a^{2}} = 0 $$
(35)

In order to solve the (35), it is important to note here that one can assume b = b(t) = b(a(t)), as a is also a time dependent function.

$$ \int e^{\int \frac{b}{a}da}da=t+k $$
(36)

where k is an integrating constant. One cannot solve (36) in general as b is variable. So, in order to solve the problem completely, we have to choose \(\int \frac {b}{a} da\) in such a manner that (36) be integrable without any loss of generality. Hence we consider

$$ \int \frac{b}{a}da= \ln f(a), $$
(37)

From (36) and (37), we obtain

$$ \int f(a)da = t + k $$
(38)

Of course the choice of f(a) is in quite arbitrary, but for the sake of physically viable models of the universe with observations, we choose

$$ f(a)=\frac{na^{n-1}}{\alpha\sqrt{1+a^{2n}}}, $$
(39)

where α and n > 0 are arbitrary constants. In this case, on integrating (39) and neglecting the integration constant k, we obtain the exact solution as

$$ a(t)=[\sinh(\alpha t)]^{1/n} $$
(40)

Since the set of non-linear differential equations are always difficult to solve so remove this complication in secondly we may assume power law as suggested by Thorne [33],

$$ A = C^{r} $$
(41)
$$ B = C^{s} $$
(42)

where r and s are the proportionality constant.

From (40), (41), (42) and (21), we get

$$ C^{(r + s + 1)} = [\sinh(\alpha t)]^{\frac{3}{n}} \Rightarrow C = [\sinh(\alpha t)]^{\frac{3}{n(r + s + 1)}} $$
(43)

putting the value of C into the (41)and (42)

$$ A = [\sinh(\alpha t)]^{\frac{3r}{n(r + s + 1)}} $$
(44)
$$ B = [\sinh(\alpha t)]^{\frac{3s}{n(r + s + 1)}} $$
(45)

The directional Hubble parameters may be expressed as

$$ H_{x} = \frac{3\alpha r}{n(r+s+1)}\coth(\alpha t) $$
(46)
$$ H_{y} = \frac{3\alpha s}{n(r+s+1)}\coth(\alpha t) $$
(47)
$$ H_{z} = \frac{3\alpha}{n(r+s+1)}\coth(\alpha t) $$
(48)

The form of metric (16) after substituting the value of A, B and C is

$$\begin{array}{@{}rcl@{}} ds^{2}&=&-dt^{2}+[\sinh(\alpha t)]^{\frac{6r}{n(r + s + 1)}}(dx-zdy)^{2}+[\sinh(\alpha t)]^{\frac{6s}{n(r + s + 1)}}dy^{2}\\ &&+[\sinh(\alpha t)]^{\frac{6}{n(r + s + 1)}}dz^{2} \end{array} $$
(49)

The some parameters such as spatial volume, Hubble parameter, deceleration parameter (q), expansion scalar (θ), shear scalar σ 2 and anisotropy parameter A m are obtain by following mathematical expression:

$$ V = ABC = [\sinh(\alpha t)]^{\frac{3}{n}} $$
(50)
$$ H = \frac{\alpha }{n}\coth(\alpha t) $$
(51)
$$ \theta = 3H = \frac{3 \alpha}{n}\coth(\alpha t) $$
(52)
$$ q=n(1-tanh^{2}(\alpha t))-1 $$
(53)

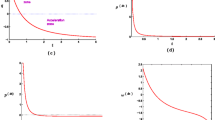
Here it is worthwhile to mention that the sign of q indicate the rate of expansion of the universe is accelerating or decelerating (Fig. 1).

$$ \sigma^{2} = \frac{3 \alpha^{2}(r^{2}+s^{2}-rs-r-s+1)}{n^{2}k^{2}}\coth^{2}(\alpha t) $$
(54)
$$ A_{m} = \frac{2(r^{2} + s^{2} - rs -r-s+1)}{k^{2}} $$
(55)

Here k is constant and it is equivalent to k = r+s+1.

Fig. 1
figure 1

The plot of deceleration parameter q versus time t for n = 0.8,1.0,1.5,2.0

Full size image

Now we have to discuss the physical & kinematical behavior of the model given by (49).

5 Physical and Kinematical Behavior

After calculating all the above mention cosmological parameter we feel necessary to discuss physical and kinematical behavior of the models under both the cases with presence and without presence of magnetic field in Sections 5.1 and 5.2

5.1 With Presence of Magnetic Field

Multiplying (28) by 2 then subtracting from the sum of (27) and (29), then substitute the values of A, B and C from (43)–(45), we get skewness scalar δ as

$$\begin{array}{@{}rcl@{}} \delta&=&\frac{1}{\rho(8\pi+2\eta)}\left\{\frac{3\alpha^{2}\left\{3(r^{2}-2s^{2}-rs-s+2r+1)-nk(r-2s+1)\right\}}{n^{2}k^{2}}. \right.\\ &&\left..\coth^{2}(\alpha t)+ \frac{3\alpha^{2}(r-2s+1)}{nk}+\left.\sinh(\alpha t)\right]^{\frac{6(r-s-1)}{nk}} -\frac{K^{2}}{\pi}[\sinh(\alpha t)]^{\frac{6(r+1)}{nk}}\right\} \end{array} $$
(56)

Subtracting (27) from (26), then put A, B and C from (43)–(45) also use the relation p = ω ρ, we have

$$\begin{array}{@{}rcl@{}} p+\rho&=&\frac{1}{(8\pi+2\eta)}\left\{ \frac{3\alpha^{2} \left\{3(s^{2}-r^{2}+2rs+s-r)+nk(r-s+2)\right.}{n^{2}k^{2}}\coth^{2}(\alpha t)\right.\\ &&\left.+\frac{3\alpha^{2}(r-s+2)}{nk}-\frac{1}{2}[\sinh(\alpha t)]^{\frac{6(r-s-1)}{nk}}\right\} + \frac{K^{2}}{4\pi}[\sinh(\alpha t)]^{\frac{6(r+1)}{nk}} \end{array} $$
(57)

Multiply (29) by \(\frac {\eta }{4\pi }\) and (57) by η, then adding these new equations into (28), we get the following expression

$$\begin{array}{@{}rcl@{}} p &=& \frac{-1}{(8\pi+2\eta)(8\pi +4\eta)}\left\{\left( \frac{3\alpha^{2}\{(8\pi+4\eta)(3r^{2}-nkr)-3\eta rs-3 \eta s^{2}-6\eta s\}}{n^{2}k^{2}}\right.\right.\\ &&\left.+\frac{3\alpha^{2}\{(3\eta+8)(3r+3-nk)+nk s\eta \}}{n^{2}k^{2}}\right).\coth^{2}(\alpha t)+2(\pi+\eta)[\sinh(\alpha t)]^{\frac{6(r-s-1)}{nk}}\\ &&\left.-\frac{3\alpha^{2}\{(8\pi+4\eta)r-\eta s+3\eta+8\}}{nk}-\frac{K^{2}(3\eta^{2}+20\eta+32\pi^{2})}{4\pi}[\sinh(\alpha t)]^{\frac{6(r+1)}{nk}}\right\}\qquad\! \end{array} $$
(58)

From (57) and (58) the energy density for the model is expressed as (Fig. 2)

$$\begin{array}{@{}rcl@{}} \rho&=&\frac{1}{(8\pi+2\eta)}\left\{ \left( \frac{3\alpha^{2}\{(3s^{2}-kns+3)(8\pi+3\eta)+(3rs+kn)(16\pi+7\eta)\}}{n^{2}k^{2}}\right.\right.\\ &&\left.-\frac{3\alpha^{2}\{3r(8\pi+\eta-8)+6s(4\pi+\eta)+nk(-\eta s+4\eta+8)\}}{n^{2}k^{2}}\right).\coth^{2}(\alpha t)\\ &&-(2\pi+\eta)[\sinh(\alpha t)]^{\frac{6(s-1)}{nk}}+\frac{3\alpha^{2} \{-s(8\pi+4\eta)+16\pi+11\eta+8\}}{nk}\\ &&\left.+\frac{2K^{2}\left\{\left.8\pi^{2}+5\pi\eta+\eta^{2}\right)\right\}}{\pi}[\sinh(\alpha t)]^{\frac{6(r+1)}{nk}}\right\} \end{array} $$
(59)
Fig. 2
figure 2

The plot of energy density ρ versus time t with presence of M.F. Here η = 2, r = 2.432, s = 1.730, K = 0.1

Full size image

From (58) and (59) the EoS parameter may be expressed as (Fig. 3)

$$\begin{array}{@{}rcl@{}} \omega &=&\frac{1}{\rho(8\pi+2\eta)(8\pi +4\eta)}\left\{\left( \frac{3\alpha^{2}\{(8\pi+4\eta)(3r^{2}-nkr)-3\eta rs-3\eta s^{2}-6\eta s\}}{n^{2}k^{2}}\right.\right.\\ &&\left.+\frac{3\alpha^{2}\{(3\eta+8)(3r-nk+3)\}}{n^{2}k^{2}}\right).\coth^{2}(\alpha t)+\frac{3\alpha^{2}\{(8\pi+4\eta)r-\eta s+3\eta+8\}}{nk}\\ &&\left.+2(\pi+\eta)[\sinh(\alpha t)]^{\frac{6(r-s-1)}{nk}}-\frac{K^{2}(3\eta^{2}+20\eta+32\pi^{2})}{4\pi}[\sinh(\alpha t)]^{\frac{6(r+1)}{nk}}\right\} \end{array} $$
(60)

In literature the relation between matter energy density and dark energy is given by the equation

$$ {\Omega}_{m} + {\Omega}_{\Lambda}=1 $$
(61)

where \({\Omega }_{m} =\frac {\rho }{3H^{2}} \) and \( {\Omega }_{\Lambda }= \frac {\Lambda }{3H^{2}}\) so

$$ \frac{\rho}{3H^{2}} + \frac{\Lambda}{3H^{2}}=1 $$
(62)
Fig. 3
figure 3

The plot of EoS parameter ω versus time t with presence of magnetic field. Here η = 2, r = 2.432, s = 1.730, K = 0.1

Full size image

Using equations (47) and (59) into equation (62) we obtain the expression for Λ (Fig. 4)

$$\begin{array}{@{}rcl@{}} {\Lambda}&=&\frac{-1}{(8\pi+2\eta)}\left[ \left\{ \frac{3\alpha^{2}\{(3s^{2}-kns+3)(8\pi+3\eta) +(3rs+kn)(16\pi+7\eta)\}}{n^{2}k^{2}}\right.\right.\\ &&\left.-\frac{3\alpha^{2}\{3r(8\pi+\eta-8)-6s(4\pi+\eta)\} }{n^{2}k^{2}}+\frac{(4-s)\eta+8}{nk}\right\} \coth^{2}(\alpha t)\\ &&+\frac{3\alpha^{2} \{-s(8\pi+4\eta)+16\pi+11\eta+8\}}{nk} - (2\pi+\eta)[\sinh(\alpha t)]^{\frac{6(r-s-1)}{nk}}\\ &&\left.+\frac{2K^{2}\{8\pi^{2}+5\pi\eta+\eta^{2})\}}{\pi}[\sinh(\alpha t)]^{\frac{6(r+1)}{nk}}\right]+\frac{3\alpha^{2}}{n^{2}}coth^{2}(\alpha t) \end{array} $$
(63)
Fig. 4
figure 4

The plot of cosmological constant Λ versus time t with presence of M.F. Here η = 2, r = 2.432, s = 1.730, K = 0.1

Full size image

5.2 Without Presence of Magnetic Field

Here the set of (30)–(33) is the set of four equations in six unknown, for the explicit solution we use the same set of assumptions as used in model one.

Subtracting (32) from (31) then using the (43)–(45), we obtain the skewness parameter as

$$\begin{array}{@{}rcl@{}} \delta&=& \frac{1}{(8\pi+2\eta)\rho}\left\{ \frac{3\alpha^{2}\coth^{2}(\alpha t)\left\{3(r^{2}-s^{2}-s+r)-nk(r-s)\right\}}{n^{2}k^{2}} -\frac{3\alpha^{2} (r-s)}{nk}\right.\\ &&\left.\qquad\qquad\qquad+[\sinh(\alpha t)]^{\frac{6(r-s-1)}{nk}}\right\} \end{array} $$
(64)

Simplifying (33) with the help of (43)–(45) and p = −ρ, we obtain the EoS parameter ω as (Fig. 6),

$$\begin{array}{@{}rcl@{}} \omega&=&\frac{-1}{\rho(8\pi+5\eta)(8\pi+2\eta)}\left\{\frac{3\alpha^{2}\{(8\pi+3\eta)(3r^{2}+3r-nkr)-3\eta(s^{2}+s)+nk \eta s\}}{n^{2}k^{2}}\right.\\ &&+\frac{3\alpha^{2}\{(8\pi+2\eta)(3-nk)\}}{n^{2}k^{2}}. \coth^{2}(\alpha t)-\frac{3 \alpha^{2}\{ r(8\pi+3\eta)-\eta s+8\pi+2\eta \}}{nk}\\ &&\left.+\frac{4\pi+3\eta}{2} [\sinh(\alpha t)]^{\frac{6(r-s-1)}{k}}\right\}-\frac{\eta}{8\pi + 5 \eta} \end{array} $$
(65)

From (30), (64) and (65), we have (Fig. 5)

$$\begin{array}{@{}rcl@{}} p&=& -\rho\\ &=&\!\frac{-1}{16(2\pi+\eta)(4\pi+\eta)^{2}}\!\left[\left\{\frac{3\alpha^{2} \{(r-s)(8\pi+5\eta)+3\eta(8\pi r+ 3\eta r\,-\,\eta s\,+\,8\pi+2\eta)\}}{nk}\right.\right.\\ &&-\frac{9\alpha^{2}\{(2r^{2}+s^{2})(4\pi\eta+2\eta^{2})-rs(10\eta^{2}+56\pi\eta+64\pi^{2})- 2r(3\eta^{2}+32\pi^{2})\}}{n^{2}k^{2}}\\ &&\left.+\frac{9\alpha^{2}\{40\pi r \eta-8s(\eta^{2}-6\pi\eta+8\pi^{2})+24\pi\eta+3\eta^{2} \}}{n^{2}k^{2}}\right\}.\coth^{2}(\alpha t)\\ &&-\frac{3\alpha^{2} \{(r-s)(8\pi+5\eta)+3\eta(8\pi r+ 3\eta r-\eta s+8\pi+2\eta)\}}{nk}\\ &&\left.-(7\eta^{2}+20\pi\eta+16\eta^{2}-8\pi-5\eta)[\sinh(\alpha t)]^{\frac{6(r-s-1)}{nk}}\right] \end{array} $$
(66)
Fig. 5
figure 5

The plot of energy density ρ versus time t without presence of M.F. Here η = 2, r = 2.432, s = 1.730

Full size image

Using (47) and (66) into (62) we obtain the expression for Λ as (Fig. 7)

$$\begin{array}{@{}rcl@{}} {\Lambda}&=&\frac{3\alpha^{2}}{n^{2}}coth^{2}+\frac{-1}{16(2\pi+\eta)(4\pi+\eta)^{2}}.\\ &&.\left[\left\{\frac{3\alpha^{2} \{(r-s)(8\pi+5\eta)+3\eta(8\pi r+3\eta r-\eta s+8\pi+2\eta)\}}{nk}\right.\right.\\ &&-\frac{9\alpha^{2}\left\{(2r^{2}+s^{2})(4\pi\eta+2\eta^{2})-rs(10\eta^{2}+56\pi\eta+64\pi^{2})- 2r(3\eta^{2}+32\pi^{2})\right\}}{n^{2}k^{2}}\\ &&\left.+\frac{9\alpha^{2}\{40\pi r \eta-8s(\eta^{2}-6\pi\eta+8\pi^{2})+24\pi\eta+3\eta^{2} \}}{n^{2}k^{2}}\right\}.\coth^{2}(\alpha t)\\ &&-\frac{3\alpha^{2} \{(r-s)(8\pi+5\eta)+3\eta(8\pi r+ 3\eta r-\eta s+8\pi+2\eta)\}}{nk}\\ &&\left.-(7\eta^{2}+20\pi\eta+16\eta^{2}-8\pi-5\eta)[\sinh(\alpha t)]^{\frac{6(r-s-1)}{nk}}\right] \end{array} $$
(67)

6 Results and Discussion

Following (53) as presented in Section 4, which is a connection between time dependent deceleration parameter q, n and α may be re-written as

$$ \tanh(\alpha t)= \sqrt{1-\frac{q+1}{n}} $$
(68)

The above equation (68) is valid if \(0\leq |\frac {q+1}{n}|\leq 1\).

We may re-expressed the (68) in term of α i.e.

$$ \alpha= \frac{1}{t}\tanh^{-1}\left[1-\frac{q+1}{n}\right]^{\frac{1}{2}} $$
(69)

From observational data age of the universe is t 0 = 13.8G r and q 0 = −0.73 [34],

$$ \alpha= \frac{1}{13.8}\tanh^{-1}\left[1-\frac{0.27}{n}\right]^{\frac{1}{2}} $$
(70)

For real value of α we may have to impose the constraint i.e. n ≥ 0.27. Now for understand the nature of model we have decided to know the transition phase of the universe. For this purpose we have compiled the value of n, α and ω (with and without presence of magnetic field) given in Table 1.

Table 1 Nature of EoS parameter for different n and α
Full size table

7 Concluding Remarks

On the basis of above study following conclusions may summarized:

  • It is easy to analyze from (50) that the spatial volume V is zero at t = 0 and approaches to infinite as t→∞, this indicates that universe starts evolving with zero volume at t = 0 (i.e. singularity at t = 0) and expand with cosmic time t. Thus we can say that our constructed models compatible with standard Big-Bang model of the universe.

  • Also Fig. 1 indicates the accelerating nature of universe for n ≤ 1 and transition phase i.e. decelerating to accelerating nature for n > 1.

    It is easily seen that the nature of q agree with observational data from SNeIa, it also show that the value of q is −1≤q ≤ 1.

  • We observed that \(\frac {\sigma ^{2}}{\theta ^{2}}\) is constant, which show that the models does not approaches to isotropy throughout the evolution of the universe.

  • Figures 2 and 5 depict the positive behavior of energy density ρ with cosmic time t for both models with and without presence of magnetic field, it is clear that ρ is decreasing function of time, the value of ρ very large at the beginning (i.e. at t = 0) and converges to zero for large value of t.

  • As shown in Table 1 we have presented the values of EoS parameter ω for different value of n and α, at t 0 = 13.8 for both the cases with and without presence of magnetic field followed by Figs. 3 and 6, which clearly indicate the reason how the universe is behaving decelerating to accelerating. The value of EoS parameter is negative for all value of n at t 0.

  • As we already presented in the previous section regarding the importance of cosmological constant Λ in f(R, T) gravity theory so we have plotted the figure Λ versus time t, which have been presented in Figs. 4 and 7 for both the cases(with and without magnetic field ), it has been found that cosmological term Λ is decreasing function of time and it approaches to a small positive value at the present scenario which is the strong tuning with the recent observation [1, 2, 35, 36]. Thus we may say that cosmological constant Λ is potential candidate to discuss the nature of DE.

Fig. 6
figure 6

The plot of EoS parameter ω versus time t without presence of M.F. Here η = 2, r = 2.432, s = 1.730

Full size image
Fig. 7
figure 7

The plot of cosmological constant Λ versus time t without presence of M.F. Here η = 2, r = 2.432, s = 1.730

Full size image