1 Introduction

Nonlinear partial differential equations are vital in mathematical modeling. The equations are commonly used in modeling many phenomena encountered in nature [1,2,3,4]. Numerous PDE models are derived from a fundamental balancing or conservation law which is a mathematical identity to certain symmetry of a physical system. The propagation of nonlinear waves is a crucial phenomenon in nature, and there is an increasing interest in studying nonlinear waves in dynamical systems. In addition to the differential equations including integer orders, fractional partial differential equations (FPDEs) also occupy a large place in modeling. FPDEs have become very popular in recent years thanks to the analysis capability obtained depending on the change in fractional order and new fractional derivative operators. There are various forms of fractional derivative and integral operators in the literature. Which of these forms will be used depends on the properties of the equation to be used. For more detailed information, you can take a look at Riemann–Liouville [5], Grünwald–Letnikov [5], Caputo [6, 7], Caputo–Fabrizio [8, 9], Hadamard [10], Weyl [11], Atangana–Baleanu [12] derivatives, etc. Besides, there are also local fractional derivative operators on which there are discussions. The main reason for the discussions is that local derivative operators do not provide some of the properties that other fractional derivative forms provide. Some of the other derivatives operators, which satisfy the main properties of integer derivative operators, are conformable [13, 14], M-truncated [15, 16] and beta [17] fractional derivative operators. In the literature, some methods used in solving FPDEs are exp(\(-\phi (\epsilon )\))-expansion method [18], \(\Phi ^6\)-expansion method [19, 20], Sardar sub-equation method [21], Kudryashov-expansion method [22], homotopy analysis method [23] and homotopy decomposition method [24].

Many phenomenon equations are utilized to model the nonlinear propagation of long waves. One of the most important of the NLPDEs is the Korteveg de Vries (KdV) equation. There are many variations of the KdV equation in the literature [25]. Benjamin–Bona–Mahony (BBM) equation, one of the variations, is given by [26]:

$$\begin{aligned} \phi _{t} + \phi _{x} + {\phi }^{2}\phi _{x} - \phi _{xxt} = 0. \end{aligned}$$
(1)

Many researchers studied the BBM equation for obtaining an analytical solution with the first integral method [27], making a comparison between analytical and numerical study [28], investigating the existence and uniqueness of the equation [29] and analytical solution of the equation by Wazwaz [30]. Wazwaz also studied a generalization of the BBM equation to \((3+1)\)-dimensions. The equations named as Wazwaz–Benjamin–Bona–Mahony (WBBM) equations are given by [30]:

$$\begin{aligned}&\phi _{t} + \phi _{x} + {\phi }^{2}\phi _{y} - \phi _{xzt} = 0, \end{aligned}$$
(2)
$$\begin{aligned}&\phi _{t} + \phi _{z} + {\phi }^{2}\phi _{x} - \phi _{xyt} = 0, \end{aligned}$$
(3)
$$\begin{aligned}&\phi _{t} + \phi _{y} + {\phi }^{2}\phi _{z} - \phi _{xxt} = 0, \end{aligned}$$
(4)

in which \(\phi =\phi (x,y,z,t)\) denotes the wave propagation and the subscripts represent the partial derivatives of the unknown function \(\phi (x,y,z,t)\).

Obtaining the solutions of nonlinear partial differential equations such as WBBM equation that models wave propagation in ocean engineering is one of the remarkable topics to understand the behavior of wave phenomena. Especially, the WBBM equation with M- truncated derivative has been rarely studied in the literature yet. So, this article’s main aim is to derive various analytical solutions for the WBBM equation with conformable and M-truncated derivatives. To our best knowledge, the conformable and M-truncated WBBM equations have not been solved by the unified Riccati equation expansion method (UREEM) [31,32,33] and Kudryashov auxiliary equation method (KAEM) [34, 35]. Another important aspect of this study is examining wave behavior according to the effects of the parameters in the obtained solutions of the considered equation. On the other hand, these methods used in this article are easily applicable and are useful for producing various solitons for nonlinear models, especially in water waves and optics.

In the literature, some of the solution methods for the WBBM equation are modified extended \(\tanh \) method [36], hyperbolic solutions via simple ansatz method [37], Sardar sub-equation method [38], \(\left( \frac{G^\prime }{G} \, \text {and} \, \frac{1}{G} \right) \)-expansion method [39], Kudryashov method and new extended direct algebraic method [40], new \(\Phi ^6\)-model method [41], bifurcation method and investigation of existence of solution [42]. Also, some of the used methods for solving the 3D fractional WBBM equation are improved auxiliary equation technique [43], tanh-coth method [44], sine-Gordon method [45] and modified auxiliary equation mapping method [46].

The structure of the paper can be given as follows: In Sect. 2, the preliminaries are given. The governing model with various derivative operators are dealt with and the methods are applied to the considered models in Sect. 3. The methods to be used are analyzed in Sect. 4 and are applied to the considered equation in Sect. 5. In Sect. 6, some graphs of the obtained solutions and the discussion about the results are included.

2 Preliminaries

2.1 Conformable derivative

Definition 1

Suppose that \(v:[0, \infty ) \rightarrow {\mathbb {R}}\) is a function. Conformable derivative of v(y) of order \(\gamma \) w.r.t. y is given as follows [13]:

$$\begin{aligned} {\mathcal {D}}_{y}^{\gamma }(v(y))=\lim _{h \rightarrow 0} \frac{v(y+h y^{1-\gamma })-v(y)}{h},\quad \end{aligned}$$
(5)

where \( \gamma \in (0,1],\; y>0\).

Theorem 1

[13] Let v(y) and w(y) be \(\gamma \)-differentiable functions for \(\gamma \in (0,1], \; y>0\). Then,

  1. 1.

    \({\mathcal {D}}_{y}^{\gamma }\big (c v(y)+d w(y)\big )=c {\mathcal {D}}_{y}^{\gamma } v(y)+d {\mathcal {D}}_{y}^{\gamma } w(y),\;\) for \( c, d \in {\mathbb {R}},\)

  2. 2.

    \({\mathcal {D}}_{y}^{\gamma }\left( y^{n}\right) =n y^{n-\gamma },\; n \in {\mathbb {R}}\),

  3. 3.

    If \(v(y)=c\) where c is a constant, then \({\mathcal {D}}_{y}^{\gamma }(c)=0,\)

  4. 4.

    \({\mathcal {D}}_{y}^{\gamma }\big (w(y) v(y)\big )=w(y) {\mathcal {D}}_{y}^{\gamma }v(y)+v(y) {\mathcal {D}}_{y}^{\gamma }w(y),\)

  5. 5.

    \({\mathcal {D}}_{y}^{\gamma }\left( \frac{v(y)}{w(y)}\right) =\frac{w(y) {\mathcal {D}}_{y}^{\gamma }v(y)-v(y) {\mathcal {D}}_{y}^{\gamma }w(y)}{w^{2}(y)}, \quad w(y) \ne 0,\)

  6. 6.

    When the first derivative of w(y) exists, we have \({\mathcal {D}}_{y}^{\gamma }(w(y))=y^{1-\gamma } \frac{d w(y)}{d y}.\)

2.2 M-truncated derivative

Definition 2

The truncated Mittag–Leffler function is given by [15]:

$$\begin{aligned} {}_i \mathbb {E}_{\beta }(w)=\sum _{k=0}^{i} \frac{w^{k}}{\Gamma (\beta k+1)}, \end{aligned}$$
(6)

where \(\beta >0\) and \(w \in C\).

Definition 3

M-truncated derivative of \(h:[0, \infty ) \rightarrow {\mathbb {R}} \) of order \(\gamma \in (0,1)\) with respect to y is defined [15]:

$$\begin{aligned} {\mathscr {D}}_{M,y}^{\gamma , \beta } h(t)=\lim _{\varepsilon \rightarrow 0} \frac{h\left( t+ {}_i \mathbb {E}_{\beta }\left( \varepsilon y^{-\gamma }\right) \right) -h(y)}{\varepsilon }, \end{aligned}$$
(7)

where \(\beta , y>0\) and \( {}_i \mathbb {E}_{\beta }()\) is truncated Mittag–Leffler function.

Theorem 2

Let h(y) be \(\gamma \)-order differentiable function at \(y_{0}>0\) with \(\gamma \in (0,1]\) and \(\beta >0\). Then, h(y) is continuous at \(y_{0}\) [15].

Theorem 3

[15] Let \(0<\gamma \le 1, \beta >0, p, q \in {\mathbb {R}}\) and suppose that g, h are \(\gamma \)-differentiable at a point \(y>0.\) Then,

  1. 1.

    \({\mathscr {D}}_{M,y}^{\gamma , \beta } (p g+f h)(y)=p\, {\mathscr {D}}_{M,y}^{\gamma , \beta }g(y)+f\,{\mathscr {D}}_{M,y}^{\gamma , \beta }h(y),\) where p, q are real constants,

  2. 2.

    \({\mathscr {D}}_{M,y}^{\gamma , \beta } (gh)(y)=g(y)\;{\mathscr {D}}_{M,y}^{\gamma , \beta }h(y)+h(y)\;{\mathscr {D}}_{M,y}^{\gamma , \beta }g(y),\)

  3. 3.

    \({\mathscr {D}}_{M,y}^{\gamma , \beta } \left( \frac{g}{h}\right) (y)=\frac{g(y)\;{\mathscr {D}}_{M,y}^{\gamma , \beta }h(y)-h(y)\;{\mathscr {D}}_{M,y}^{\gamma , \beta }g(y)}{h(y)^{2}},\)

  4. 4.

    \({\mathscr {D}}_{M,y}^{\gamma , \beta } \left( \frac{g}{h}\right) (y)=\frac{g(y)\;{\mathscr {D}}_{M,y}^{\gamma , \beta }h(y)-h(y)\;{\mathscr {D}}_{M,y}^{\gamma , \beta }g(y)}{h(y)^{2}},\)

  5. 5.

    If g is differentiable, then \({\mathscr {D}}_{M,y}^{\gamma , \beta }(g)(y)=\frac{t^{1-\gamma }}{\Gamma (\beta +1)} \frac{d g(y)}{d y}\).

3 Governing equation

In this section, the nonlinear WBBM equation with different definitions of derivatives is considered.

3.1 WBBM equation with conformable derivative

The WBBM equation with conformable derivative considered equation with conformable derivative can be given as follows [37]:

$$\begin{aligned} {\mathcal {D}}_{t}^{\alpha }\phi + {\mathcal {D}}_{y}^{\alpha }\phi + {\mathcal {D}}_{z}^{\alpha }\phi ^3 - {\mathcal {D}}_{xxt}^{3\alpha }\phi =0. \end{aligned}$$
(8)

For conformable derivative, we consider the following wave transformation [37]:

$$\begin{aligned} \phi (x,y,z,t)={\mathcal {U}}(\eta ) ,\; \eta = a\frac{x^\alpha }{\alpha } + b\frac{y^\alpha }{\alpha } + c\frac{t^\alpha }{\alpha } -d\frac{z^\alpha }{\alpha }. \end{aligned}$$
(9)

Applying the wave transformations in Eqs. (9)–(8), we obtain the following ODE:

$$\begin{aligned} (-d+a){\mathcal {U}} + b{{\mathcal {U}}}^{3} + acd{\mathcal {U}}^{\prime \prime }=0, \end{aligned}$$
(10)

where \({\mathcal {U}}={\mathcal {U}}(\eta )\) and the superscript \(^{\prime \prime }\) denotes second derivative of \({\mathcal {U}}\) w.r.t. \(\eta \). Applying the balancing principle to the equation in Eq. (10), we get \(N + 2 = 3N\Rightarrow N = 1.\)

3.2 WBBM equation with M-truncated fractional derivative

The WBBM equation with M-truncated fractional derivative can be given as follows [37]:

$$\begin{aligned} {\mathscr {D}}_{M,t}^{\alpha , \beta }\phi +{\mathscr {D}}_{M,y}^{\alpha , \beta }\phi +{\mathscr {D}}_{M,z}^{\alpha , \beta }\phi ^3 -{\mathscr {D}}_{M,xxt}^{3\alpha , \beta }\phi =0. \end{aligned}$$
(11)

For M-truncated fractional derivative, we consider the following wave transformation:

$$\begin{aligned} \phi (x,y,z,t)={\mathcal {U}}(\eta ) ,\; \eta =\frac{\Gamma (1+\beta )}{\alpha }\left( a x^\alpha + b y^\alpha + c t^\alpha -d z^\alpha \right) . \end{aligned}$$
(12)

Inserting the wave transformations in Eqs. (12)–(11), we obtain the same nonlinear ODE in Eq. (10) and same balancing constant \(N=1\).

4 Methods

In this section, we focus on finding \({\mathcal {U}}(\eta )\), the solutions of Eq. (10), using the UREEM and KAEM.

Let us assume that Eq. (10) have some solutions as follows:

$$\begin{aligned} {\mathcal {U}}(\eta )=\sum _{i=0}^{N} \sigma _{i}(R(\eta ))^{i}, \; \sigma _{N} \ne 0, \end{aligned}$$
(13)

where \(\sigma _{0}, \sigma _{1}, \sigma _{2}, \ldots , \sigma _{N}\) are constants to be determined, N is the balancing number and \(R(\eta )\) is a trial solution function that varies on the considered methods.

4.1 Unified Riccati equation expansion method (UREEM)

According to the UREEM, \(R(\eta )\) in Eq. (13) can be considered as follows:

$$\begin{aligned} R(\eta )= {\left\{ \begin{array}{ll} R^{+}(\eta ), & \Delta =c_{1}^{2}-4 c_{0} c_{2}>0, \\ R^{-}(\eta ), & \Delta =c_{1}^{2}-4 c_{0} c_{2}<0,\\ R^{0}(\eta ), & \Delta =c_{1}^{2}-4 c_{0} c_{2}=0, \end{array}\right. } \end{aligned}$$
(14)

where \(R(\eta )\) is the solution of the differential equation below:

$$\begin{aligned} R^{\prime }(\eta ) =c_0+c_1 R(\eta ) +c_2 R(\eta )^2. \end{aligned}$$
(15)

In Eq. (14), \(R^{+}(\eta ), R^{-}(\eta )\) and \(R^{0}(\eta )\) are defined by:

$$\begin{aligned} R^{+}(\eta )=-\frac{c_{1}}{2 c_{2}}-\frac{\sqrt{\Delta }\left( r_{1} \tanh \left( \frac{\sqrt{\Delta }}{2} \eta \right) +r_{2}\right) }{2 c_{2}\left( r_{1}+r_{2} \tanh \left( \frac{\sqrt{\Delta }}{2} \eta \right) \right) }, \end{aligned}$$
(16)

where it is non-trivial and nondegenerate if and only if \(r_{2} \ne \pm r_{1}, r_{1}^{2}+r_{2}^{2} \ne 0. \)

$$\begin{aligned} R^{-}(\eta )=-\frac{c_{1}}{2 c_{2}}+\frac{\sqrt{-\Delta }\left( r_{3} \tan \left( \frac{\sqrt{-\Delta }}{2} \eta \right) -r_{4}\right) }{2 c_{2}\left( r_{3}+r_{4} \tan \left( \frac{\sqrt{-\Delta }}{2} \eta \right) \right) }, \end{aligned}$$
(17)

where it is non-trivial and nondegenerate if and only if \( r_{3}^{2}+r_{4}^{2} \ne 0.\)

$$\begin{aligned} R^{0}(\eta )=-\frac{c_{1}}{2 c_{2}}-\frac{1}{c_{2} \eta +c}, \quad \Delta =c_{1}^{2}-4 c_{0} c_{2}=0. \end{aligned}$$
(18)

4.2 Kudryashov auxiliary equation method (KAEM)

The novel approach named KAEM has been recently introduced by Kudryashov [34]. According to the KAEM, \(R(\eta )\) in Eq. (13) can be considered as follows:

$$\begin{aligned} R(\eta )=\frac{4 \gamma }{\left( \varphi ^2 +4 \gamma \chi \right) {\mathrm e}^{\sqrt{\gamma }\delta \eta }+2 \varphi +{\mathrm e}^{-\sqrt{\gamma }\delta \eta }}, \end{aligned}$$
(19)

where \(R(\eta )\) is the solution of the differential equation below:

$$\begin{aligned} \left[ R^{\prime }(\eta )\right] ^{2}=\left[ \frac{d R(\eta )}{d \eta }\right] ^{2}=\sqrt{ \mathrm {\delta }^{2} R\left( \mathrm {\eta }\right) ^{2} \left( \gamma -\varphi R\left( \mathrm {\eta }\right) -\chi R\left( \mathrm {\eta }\right) ^{2}\right) }. \end{aligned}$$
(20)

5 Application

In this section, we apply UREEM and KAEM to the WBBM equation with conformable and M-truncated derivatives.

5.1 UREEM

Substituting \(N=1\) into Eq. (13), we derive:

$$\begin{aligned} {\mathcal {U}}(\eta )=\sigma _{0}+\sigma _{1} R(\eta ). \end{aligned}$$
(21)

Inserting Eq. (21) and its required derivatives into Eq. (10) by considering Eq. (20), we can find a polynomial in powers of \(R(\eta )\). Gathering the terms with the same power of \(R(\eta )\) and then setting each coefficient to zero, we obtain the algebraic equations given below:

$$\begin{aligned}&R^0\left( \eta \right) : \, ac\delta \sigma _{1}c_{1}c_{0}+b\sigma _{0}^{3}+a\sigma _{0}-\delta \sigma _{0}=0, \\&R^1\left( \eta \right) : \, 2a c c_{0}c_{2}\delta \sigma _{1}+acc_{1}^{2}\delta \sigma _{1}+3b\sigma _{0}^{2}\sigma _{1}+a\sigma _{1}-\delta \sigma _{1}=0, \\&R^2\left( \eta \right) : \, 3a c c_{1}c_{2}\delta \sigma _{1}+3b\sigma _{0}\sigma _{1}^{2}=0, \\&R^3\left( \eta \right) : \, 2acc_{2}^{2}\delta \sigma _{1}+b\sigma _{1}^{3}=0. \end{aligned}$$
(22)

The following set is extracted when the system in Eq. (22) is solved by a computer algebraic system:

$$\begin{aligned} \begin{aligned} \Bigg \{\delta&= -\frac{2 a}{4 a c c_{0} c_{2} -a c \,c_{1}^{2}-2}, \sigma _{0} = \pm \frac{c_{1} \sqrt{b \left( 4 a c c_{0} c_{2} -a c \,c_{1}^{2}-2\right) c}\, a}{b \left( 4 a c c_{0} c_{2} -a c \,c_{1}^{2}-2\right) },\\ \sigma _{1}&= \pm \frac{2 \sqrt{b \left( 4 a c c_{0} c_{2} -a c \,c_{1}^{2}-2\right) c}\, c_{2} a}{b \left( 4 a c c_{0} c_{2} -a c \,c_{1}^{2}-2\right) } \Bigg \}, \end{aligned} \end{aligned}$$
(23)

So, we get the solutions of the main FPDE as follows:

For \(\Delta >0\),

$$\begin{aligned} {}^{\pm } \phi ^{C}_{1}(x,y,z,t)&= {\mp } \frac{T_1 \left( r_{1}\tanh \! \left( \frac{\sqrt{\Delta }\,\left( \frac{a\,t^{\alpha }}{2}+\left( a\,x^{\alpha }+b\,y^{\alpha }+c\,z^{\alpha }\right) \left( -\frac{1}{2}+c\left( c_{0}c_{2}-\frac{c_{1}^{2}}{4}\right) a\right) \right) }{2\left( -\frac{1}{2}+c\left( c_{0}c_{2}-\frac{c_{1}^{2}}{4}\right) a\right) \alpha }\right) +r_{2}\right) }{b\left( r_{1}+r_{2}\tanh \! \left( \frac{\sqrt{\Delta }\,\left( \frac{a\,t^{\alpha }}{2}+\left( a\,x^{\alpha }+b\,y^{\alpha }+c\,z^{\alpha }\right) \left( -\frac{1}{2}+c\left( c_{0}c_{2}-\frac{c_{1}^{2}}{4}\right) a\right) \right) }{2\left( -\frac{1}{2}+c\left( c_{0}c_{2}-\frac{c_{1}^{2}}{4}\right) a\right) \alpha }\right) \right) }, \end{aligned}$$
(24)
$$\begin{aligned} {}^{\pm } \phi ^{M}_{1}(x,y,z,t)&= {\mp } \frac{T_1 \left( r_{1}\tanh \! \left( \frac{\sqrt{\Delta }\,\Gamma \left( \beta +1\right) \left( -2a\,t^{\alpha }+\left( a\,x^{\alpha }+b\,y^{\alpha }+c\,z^{\alpha }\right) \left( 2+c \Delta a\right) \right) }{2\left( 2+c \Delta a\right) \alpha }\right) +r_{2}\right) }{bT_2\left( r_{1}+r_{2}\tanh \! \left( \frac{\sqrt{\Delta }\,\Gamma \left( \beta +1\right) \left( -2a\,t^{\alpha }+\left( a\,x^{\alpha }+b\,y^{\alpha }+c\,z^{\alpha }\right) \left( 2+c \Delta a\right) \right) }{2\left( 2+c \Delta a\right) \alpha }\right) \right) }, \end{aligned}$$
(25)

where

$$\begin{aligned} T_1 =\sqrt{b\left( 4acc_{0}c_{2}-acc_{1}^{2}-2\right) c}\,a\sqrt{-4c_{0}c_{2}+c_{1}^{2}}\,,T_2=4acc_{0}c_{2}-acc_{1}^{2}-2, \end{aligned}$$
(26)

and the constrain condition for the existence of the solutions in Eqs. (24) and (25) is \( b \left( 4 a c c_{0} c_{2} -a c \,c_{1}^{2}-2\right) c>0.\)

For \(\Delta <0\),

$$\begin{aligned} {}^{\pm } \phi ^{C}_{2}(x,y,z,t)&= {\mp } \frac{\sqrt{bT_2c}\,a\sqrt{ -\Delta }\,\left( r_{3}\tan \! \left( \frac{\sqrt{ -\Delta }\,\left( \frac{a\,t^{\alpha }}{2}+\left( a\,x^{\alpha }+b\,y^{\alpha }+c\,z^{\alpha }\right) \left( -\frac{1}{2}+c\left( c_{0}c_{2}-\frac{c_{1}^{2}}{4}\right) a\right) \right) }{2\left( -\frac{1}{2}+c\left( c_{0}c_{2}-\frac{c_{1}^{2}}{4}\right) a\right) \alpha }\right) -r_{4}\right) }{\left( r_{3}+r_{4}\tan \! \left( \frac{\sqrt{ -\Delta }\,\left( \frac{a\,t^{\alpha }}{2}+\left( a\,x^{\alpha }+b\,y^{\alpha }+c\,z^{\alpha }\right) \left( -\frac{1}{2}+c\left( c_{0}c_{2}-\frac{c_{1}^{2}}{4}\right) a\right) \right) }{2\left( -\frac{1}{2}+c\left( c_{0}c_{2}-\frac{c_{1}^{2}}{4}\right) a\right) \alpha }\right) \right) bT_2}, \end{aligned}$$
(27)
$$\begin{aligned} {}^{\pm } \phi ^{M}_{2}(x,y,z,t)&= {\mp } \frac{\sqrt{bT_2c}\,a\sqrt{ -\Delta }\,\left( r_{3}\tan \! \left( \frac{\sqrt{ -\Delta }\,\Gamma \left( \beta +1\right) \left( -2a\,t^{\alpha }+\left( a\,x^{\alpha }+b\,y^{\alpha }+c\,z^{\alpha }\right) \left( 2+c \Delta a\right) \right) }{2\left( 2+c \Delta a\right) \alpha }\right) -r_{4}\right) }{\left( 2+c \Delta a\right) \left( r_{3}+r_{4}\tan \! \left( \frac{\sqrt{ -\Delta }\,\Gamma \left( \beta +1\right) \left( -2a\,t^{\alpha }+\left( a\,x^{\alpha }+b\,y^{\alpha }+c\,z^{\alpha }\right) \left( 2+c \Delta a\right) \right) }{2\left( 2+c \Delta a\right) \alpha }\right) \right) b}, \end{aligned}$$
(28)

where the constrain condition for Eqs. (27) and (28) is \( b \left( 4 a c c_{0} c_{2} -a c \,c_{1}^{2}-2\right) c>0.\)

For \(\Delta =0\),

$$\begin{aligned} {}^{\pm } \phi ^{C}_{3}(x,y,z,t)=\mp \frac{\alpha \sqrt{bT_2c}\,a}{2\left( \frac{a\,t^{\alpha }}{2}+\left( a\,x^{\alpha }+b\,y^{\alpha }+c\,z^{\alpha }\right) \left( -\frac{1}{2}+c\left( c_{0}c_{2}-\frac{c_{1}^{2}}{4}\right) a\right) \right) b}, \end{aligned}$$
(29)
$$\begin{aligned} {}^{\pm } \phi ^{M}_{3}(x,y,z,t) = \mp \frac{2 \alpha a \sqrt{ b T_2 c}}{b \left( -2 a \,t^{\alpha }+\left( 2+c \left( -4 c_{2} c_{0}+c_{1}^{2}\right) a\right) \left( a \,x^{\alpha }+b \,y^{\alpha }+c \,z^{\alpha }\right) \right) \Gamma \! \left( \beta +1\right) }, \end{aligned}$$
(30)

where the constrain condition for Eqs. (29) and (30) is \( b \left( 4 a c c_{0} c_{2} -a c \,c_{1}^{2}-2\right) c>0.\)

Fig. 1
figure 1

Comparison between Eqs. (24) and (25) for \(a=0.3,b=-0.2,c=0.3,\) and \(d=0.4\)

Full size image

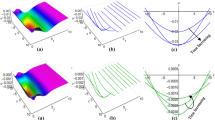
Figure 1 shows the plots of the solutions in Eqs. (24) and (25) for the appropriate parameters. In Fig. 1a, 3D view of the conformable solution \({}^{+}\phi _1^C(x,1,1,t)\) in Eq. (24) is depicted with \(\alpha =0.7, c=1, y=1, z=1, c_0=-1, c_1=4, c_2=6, a=-1, b=1, r_1=1\) and \(r_2=-0.6\) values. Figure 1b shows the plots of the M- truncated solution \({}^{+}\phi ^{M}_1(x,1,1,t)\) in Eq. (25) with \(\beta =0.7\) value. In Fig. 1c, we depict 2D plots of both conformable and M-truncated solutions. According to Fig. 1c, the wave travels along the negative \(x-\)direction. In addition, the solutions are almost overlapped due to both blue and yellow lines or red and purple lines. When the fractional orders \(\alpha \) and \(\beta \) are equal, the solutions overlap. In Fig. 1d, we depict the M-truncated solution in Eq. (25) with \(\alpha ,\beta \) parameters. There is a negative correlation between fractional order parameters and the wavelength. In Fig. 1d, when the parameter of the fractional order increases, the wave has a smaller wavelength (purple-styled plot). On the other hand, all sub-figures in Fig. 1 show that the solutions in Eqs. (24) and (25) are kink soliton solution.

Fig. 2
figure 2

Comparison between Eqs. (27) and (28) for \(a=0.3,b=-0.2,c=0.3,\) and \(d=0.4\)

Full size image

Figure 2 demonstrates the solutions in Eqs. (27) and (28). Figure 2a, b shows the 3D plots of the solutions in Eqs. (27) and (28) as conformable and M-truncated respectively, where \(y=1,z=1,c=1,c_{0}=1,c_{1}=1,c_{2}=2,a=-1,b=-1,r_{3}=- 0.1,r_{4}=- 0.3,\alpha = 0.7\) and \(\beta =0.7\) values. Figure 2a, b clearly shows that the solutions are periodic-singular soliton solutions. In Fig. 2c, we depict 2D plots of both conformable solution in Eq. (27) and M-truncated solution in Eq. (28). According to Fig. 2c, the wave travels along the negative \(x-\)direction. Lastly, Fig. 2d represents M-truncated solution \({}^{+}\phi ^M_2(x,1,1,t)\) with different \(\alpha \) and \(\beta \) values. While the parameters of the fractional order increase, the wave moves through the positive \(x-\)direction.

Fig. 3
figure 3

Comparison between Eqs. (29) and (30) for \(a=0.3,b=-0.2,c=0.3,\) and \(d=0.4\)

Full size image

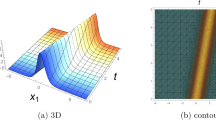
Figure 3 shows the results obtained in Eqs. (29) and (30). In Fig. 3a, b, we depict the 3D view of conformable solution \({}^{+}\phi ^C_3(x,y,z,t)\) in Eq. (29) and M-truncated solution \({}^{+}\phi _3^M(x,y,z,t)\) in Eq. (30), respectively, where \(z=1,y=1,c=1,c_{0}=1,c_{1}=1,c_{2}= 0.2,a=- 0.1,b=-1,\alpha = 0.7\) and \(\beta =0.7\) values. According to these Fig. 3a, b, the solution is singular-soliton solution. Figure 3c shows the 2D plots of both conformable solution in Eq. (29) and M-truncated solution in Eq. (30). It is clearly seen that the wave travels in positive \(x-\)direction and the solutions almost overlap at the same \(\alpha \) and \(\beta \) values. Lastly, Fig. 3d shows the 2D plots of M-truncated solution in Eq. (30) with different \(\alpha \) and \(\beta \) values. The wave goes to the left while the parameter of the fractional order increases.

Fig. 4
figure 4

Comparison between Eqs. (34) and (35) when \(a=0.3,b=-0.2,c=0.3,\) and \(d=0.4\)

Full size image

In Fig. 4, we represent some effects of the parameter on wave behavior. In Fig. 4a, we depict 2D plots of conformable solution \({}^{+}\phi _{1}^{C}(x,y,z,t)\) in Eq. (24) according to the parameter a and time. The decrease in the parameter a causes an increase in the wavelength and a decrease in the speed of the wave. This change is seen in the blue and yellow styled wave at \(t=0\) and the red and purple styled wave at \(t=14\). When \(a=-1\) which are blue and red-styled waves, the wavelength is less, but the displacement is more. In Fig. 4b, we depict conformable solution \({}^{+}\phi ^{C}_{2}(x,y,z,t)\) in Eq. (27). We aim to investigate wave behavior according to change in the parameter b. There are four different styled waves in Fig. 4b. Red and blue-styled waves are plotted for \(b=-1\); on the other hand, yellow and purple-styled waves are plotted for \(b=4\). According to the decrease in the parameter b, affects the displacement of waves increasingly. As can be seen from Fig. 4b, the distance between the yellow and purple-styled wave, where b decreases, is greater than the other red and blue-styled waves. In Fig. 4c, we plot 2D graphs of conformable solution \({}^{+}\phi ^{C}_{3}(x,y,z,t)\) in Eq. (29). We represent the change of the parameter b effects on wave behavior. There are four different styled waves. When the parameter b decreases in red and purple-styled waves, the wave displacement increases according to blue and yellow-styled waves.

5.2 KAEM

Substituting \(N=1\) into Eq. (13), we derive:

$$\begin{aligned} {\mathcal {U}}(\eta )=A_0+A_1 R(\eta ). \end{aligned}$$
(31)

Inserting Eq. (31) and its required derivatives into Eq. (10) by considering Eq. (15), we can find a polynomial in powers of \(R(\eta )\). Gathering the terms with the same power of \(R(\eta )\) and then setting each coefficient to zero, we obtain the algebraic equations given below:

$$\begin{aligned}&R^0\left( \eta \right) : \, b\sigma _{0}^{3}+a\sigma _{0}-\delta \sigma _{0}=0, \\&R^1\left( \eta \right) : \, ac\delta ^{3}\sigma _{1}+3b\sigma _{0}^{2}\sigma _{1}+a\sigma _{1}-\delta \sigma _{1}=0, \\&R^2\left( \eta \right) : \, 3 b \sigma _{0} \sigma _{1}^{2}-\frac{3}{2} a c \delta ^{3} \sigma _{1} \varphi =0, \\&R^3\left( \eta \right) : \, -2ac\delta ^{3}\sigma _{1}\chi +b\sigma _{1}^{3}=0. \end{aligned}$$
(32)

When we solve the system in Eq. (32) using a computer algebraic system, we get the set below:

$$\begin{aligned} \left\{ c = \frac{2 \left( -\delta +a\right) }{a \delta ^{3} \gamma },\chi = -\frac{\varphi ^{2}}{4 \gamma },\sigma _{0} = \pm \frac{\sqrt{-b \left( -\delta +a\right) }}{b}, \sigma _{1}=\pm \frac{\left( -\delta +a\right) \varphi }{\sqrt{-b \left( -\delta +a\right) }\, \gamma }\right\} . \end{aligned}$$
(33)

So, we get the solutions of the main FPDE as follows:

$$\begin{aligned} {}^{\pm } \phi ^{C}_{1}(x,y,z,t)&= \pm \frac{\sqrt{-b T_3}}{b}\pm \frac{4 T_3 \varphi }{\sqrt{-b T_3}\, \left( 2 \varphi +{\mathrm e}^{-\frac{\sqrt{\gamma }\, \delta \left( a \,x^{\alpha }+b \,y^{\alpha }+\frac{2 T_3 \,z^{\alpha }}{a \delta ^{3} \gamma }-\delta t^{\alpha }\right) }{\alpha }}\right) }, \end{aligned}$$
(34)
$$\begin{aligned} {}^{\pm } \phi ^{M}_{1}(x,y,z,t)&= \pm \frac{\sqrt{-b T_3}}{b}\pm \frac{4 T_3 \varphi }{\sqrt{-b T_3}\, \left( 2 \varphi +{\mathrm e}^{-\frac{\sqrt{\gamma }\, \delta \Gamma \left( \beta +1\right) \left( a \,x^{\alpha }+b \,y^{\alpha }+\frac{2 T_3 \,z^{\alpha }}{a \delta ^{3} \gamma }-\delta t^{\alpha }\right) }{\alpha }}\right) }, \end{aligned}$$
(35)

where \(T_3=a -\delta \) and the constrain condition for Eqs. (34) and (35) is:

$$\begin{aligned} -b \left( -\delta +a\right) >0. \end{aligned}$$
(36)
Fig. 5
figure 5

Comparison between Eqs. (34) and (35) for \(a=0.3,b=-0.2,c=0.3, \gamma =\varphi =1\) and \(d=0.4.\)

Full size image

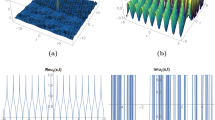
In Fig. 5, we depict the obtained solutions via KAEM in Eqs. (34) and (35). Firstly, in Fig. 5a, b, we plot the 3D view of conformable solution \({}^{+}\phi ^C_1(x,y,z,t)\) in Eq. (34) and M-truncated solution \({}^{+}\phi _1^M(x,y,z,t)\) in Eq. (35), respectively, where \(\gamma =\varphi =1,b=-1,a=2,\delta =-1,y=1,z=1,\alpha = 0.7\) and \(\beta =0.7\) values. Figure 5c shows 2D plots of the solutions in Eqs. (34) and (35) for various t values. According to Fig. 5c, the both of solutions travel along the negative \(x-\)direction according to time also conformable and M-truncated solutions overlap almost for some values. Lastly, Fig. 5d shows the wave behavior due to the changing of fractional order \(\alpha \) and \(\beta \). In Fig. 5d, the wave shifts along to the negative \(x-\)direction while \(\alpha \) and \(\beta \) increase.

6 Conclusion

In this paper, we have investigated the analytical solutions of the WBBM equation with conformable and M-truncated derivatives. The solutions have been obtained via two techniques named UREEM and KAEM. As a result of the methods, we have obtained kink, singular, and periodic-singular soliton solutions. We have included 3D and 2D graphics of the derived solutions and also compared conformable and M-truncated derivative operators with 2D graphics by selecting different values of the fractional orders. In addition, we have shown the effects of some parameters and fractional operators on wave behavior in 2D graphics. Thus, the paper has novel results because of investigating wave behavior when the parameters change. Also, we have checked that the derived solutions satisfy the WBBM equation with the different derivative operators via Maple. Consequently, we believe that both the derived solutions might contribute to the literature, and the figures and interpretations of the solutions might be useful for understanding the physical aspects of the solutions of the equation used to model long waves. Since the approaches are efficient, reliable, and simple, the methods may help finding some analytical solutions to many physical events in nature.