Entanglement sudden death with quasi-static approximation

Abstract

In this paper, we investigate the entanglement sudden death with a two-level system and plasmonic surface. We determine the collective damping and qubit–qubit interaction by employing the quasi-static approximation. To illustrate this approach, we first derive the Markovian master equation in the Lindblad form using frequency-domain Green function approach. The Wootter’s concurrence with Dicke states is used to measure the entanglement between two dipoles (two two-level systems). This approach enabled the present scheme to be applied in the field of quantum information theory.

1 Introduction

The primary premise of quantum information is the entanglement, which has been extensively studied theoretically [1, 2]. However, the decay of entanglement due to the inevitable system–environment interaction generates the obstacle “entanglement sudden death (ESD)” in quantum information processing [3,4,5,6]. Since the pioneering research of Eu and Eberly [4], the researchers have investigated ESD for various physical situations [7,8,9]. Recent study on Dark soliton qubits with Bose–Einstein condensates also confirms the occurrence of ESD [8], and the interaction of Bose–Einstein condensate atoms with a single-mode laser field reveals the collapse–revival phenomenon [10, 11]. Contrary to ESD, the investigations have shown the irreversible process of entanglement sudden birth, i.e. implying a kind of quantum coherence induced in the emission [12,13,14,15,16].

The investigation of quantum information protocols in the context of plasmonic waveguides [17], nanotubes or quantum dots [18, 19] and phonons [8, 20] has attracted an enormous interest during recent years. ESD has been confirmed with experiments performed with both photonic [3] and atomic systems [21]. Recently, Silveirinha et al. [22] have studied an interesting problem using the Markov approximation and modelling the point dipole as a two-level atom. To determine the spontaneous emission rate and to understand the quantum mechanical properties, they employ the Green’s function approach with quasi-static approximation to two-level atom and the metallic surface, for reciprocal and nonreciprocal systems [22, 23]. Enlightened by these recent investigations [22, 23], we employ this approach to determine the entanglement dynamics taking into account the loss effects of the metallic surface. We compute the collective damping resulting from the mutual exchange of the mediating particle and the dipole–dipole interaction. We believe this approach enabled the present scheme to be applied in the field of quantum information theory.

The paper is organized as follows: In Sect. 2, we describe the theoretical model and Markovian master equation to determine the collective damping resulting from mutual exchange of the mediating particle and qubit–qubit interaction by considering quasi-static approximation. The implication of this approximation to find the entanglement dynamics for different initial states is described in Sect. 3. In what follows, we conclude the results of present investigation in Sect. 4. Some of the technical aspects are described in the Appendix.

2 Theoretical model

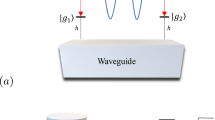
Considering two dipoles (two two-level systems) separated by distance d, placed at distance h from a plasmonic surface (Fig. 1), the Hamiltonian can be written as

$$\begin{aligned} H= & {} H_\mathrm{at.}+ H_\mathrm{field}+H_\mathrm{int.} \nonumber \\= & {} \frac{\hbar \omega _0}{2} (\sigma _1^z+\sigma _2^z)+\sum _{\omega _{n\mathbf{k}>0}}\frac{\hbar \omega _{n\mathbf{k}}}{2} \left( a_{n\mathbf{k}}^{\dagger } a_{n\mathbf{k}}+a_{n\mathbf{k}}a_{n\mathbf{k}}^{\dagger }\right) \nonumber \\&+ \sum _{j,\omega _{n\mathbf{k}>0}} \sqrt{\frac{\hbar \omega _{n\mathbf{k}}}{2}} \mathrm {\mathbf{p}_d} \cdot a_{n\mathbf{k}} \mathrm{\mathbf{F}}_{n\mathbf{k}}(r_j)+\mathrm{H.c.} \end{aligned}$$

(1)

where $\omega _0$ is the transition frequency of the states separated by energy $(E_e-E_g)/\hbar$ and $\sigma _z$=$\vert e \rangle \langle e \vert - \vert$g$\rangle \langle$g$\vert$ is the inversion operator. The operators $a_{n\mathbf{k}}^{\dagger }$ ($a_{n\mathbf{k}}$) denote the creation (annihilation) operator of the bosonic field, satisfying the commutation relation $[a_{n\mathbf{k}}, a_{n\mathbf{k}'}^{\dagger }]=\delta _{\mathbf{k},\mathbf{k}'}$ and $\omega _{n\mathbf{k}}$ is the oscillation frequency. The term $\mathrm{\mathbf{p}_d}=(\varvec{\tilde{\gamma }}^*_j \sigma _+^j + \varvec{\tilde{\gamma }}_j \sigma _-^j )$ denotes the dipole moment with dipole moment element $\gamma$ and the raising $\sigma _+ =\vert e \rangle \langle g\vert$ and lowering $\sigma _- =\vert g \rangle \langle e\vert$ operators. The function $\mathbf{F}_{n\mathbf{k}}(\mathbf{r})=\mathbf{f}_{n\mathbf{k}}(z)e^{i\mathbf{k}.\mathbf{r}}$ denotes the electromagnetic modes with the field $\mathbf{f}_{n\mathbf{k}}$ [22].

Fig. 1

Theoretical model describes the two dipoles separated by distance d and placed at distance h from the plasmonic surface

In order to characterize the entanglement dynamics, we derive the Markovian master equation (see Appendix A) to obtain the elegant description of physics involved in the dynamics of interacting system by following the procedure outlined in Ref. [24,25,26],

$$\begin{aligned} \partial _t{\hat{\rho }_{s}(t)}= & {} -\frac{i}{2}\sum _i \left( \omega _0+g^-_{ii}-g^+_{ii} \right) \left[ \sigma _z^i, \hat{\rho }_s(t)\right] \nonumber \\&- \sum _{i,j} \frac{\Gamma _{ij}}{2} \left( \sigma _{+}^{i}\sigma _{-}^{j}\hat{\rho }_s(t)+\hat{\rho }_{s}(t) \sigma _{+}^{j}\sigma _{-}^{i} - \sigma _{-}^{j}\hat{\rho }_{s}(t)\sigma _{+}^{i}\right. \nonumber \\&\left. -\sigma _{-}^{i}\hat{\rho }_{s}(t)\sigma _{+}^{j}\right) + \sum _{i\ne j}ig_{ij}\left( \sigma _{+}^{i}\sigma _{-}^{j} \hat{\rho }_{s}(t) \right. \nonumber \\&\left. -\sigma _{-}^{j}\hat{\rho }_{s}(t)\sigma _{+}^{i} \right) +H.c., \end{aligned}$$

(2)

with the collective damping term $\Gamma _{ij}=2 \mathrm{Im}\left\{ \varvec{\tilde{\gamma }}_i ^*.\mathcal {G}(\mathbf{r}_i, \mathbf{r}_j; \omega _0).\varvec{\tilde{\gamma }}_j \right\} /\hbar$ arises due to the mutual exchange of photons and qubit–qubit interaction term $g_{ij}= \mathrm{Re}\left\{ \varvec{\tilde{\gamma }}_i ^*.\mathcal {G}(\mathbf{r}_i, \mathbf{r}_j; \omega _0).\varvec{\tilde{\gamma }}_j \right\} /\hbar$. We employ the quasi-static approximation (see Appendix B) to compute the collective damping and qubit–qubit interaction term,

$$\begin{aligned} \Gamma _{12}= & {} \frac{ \tilde{\gamma }^2 \omega _{sp}^2 \Gamma }{ 4\pi \hbar \epsilon _0 \omega _{sp}'} \left\{ \frac{2 h^2-d^2}{ \left( d^2+4 h^2\right) ^{5/2} } \right\} \left[ \frac{\Delta _2-\Delta _1}{\Delta _1\Delta _2} \right] , \end{aligned}$$

(3)

$$\begin{aligned} g_{12}= & {} \frac{ \tilde{\gamma }^2 \omega _{sp}^2 }{4 \pi \hbar \epsilon _0 \omega _{sp}'} \left\{ \frac{2 h^2-d^2}{ \left( d^2+4 h^2\right) ^{5/2} } \right\} \nonumber \\&\left[ \frac{(\Delta _1+\Delta _2)\omega _{sp}'+(\Delta _1-\Delta _2)\omega _0}{\Delta _1\Delta _2} \right] , \end{aligned}$$

(4)

where

$$\begin{aligned} \Delta _1= & {} \frac{1}{\left( \omega _{sp}'-\omega _0 \right) ^2+\left( \frac{\Gamma }{2}\right) ^2}, \nonumber \\ \Delta _2= & {} \frac{1}{\left( \omega _{sp}'+\omega _0 \right) ^2+\left( \frac{\Gamma }{2}\right) ^2}, \end{aligned}$$

(5)

with $\omega _{sp}'=\sqrt{\omega _{sp}^2 - (\Gamma /2)^2}$, the losses in the metal half space $\Gamma$, the distance between two dipoles d, and the separation of the dipole and plasmonic slab h. For simplicity, the electric dipole is assumed to be oriented along x-direction $\gamma _{eg}=\tilde{\gamma } \hat{x}$. The spontaneous decay rate $\Gamma _{11}$ can be obtained by putting $d=0$ in Eq. (3). The variation of both collective damping and qubit–qubit interaction with distance d between qubits is depicted in Fig. 2. Both functions become vanish after long distance $d\sim 5h$. Dicke bases ($\left| e\right\rangle = \left| e_{1},e_{2}\right\rangle$, $\left| g\right\rangle = \left| g_{1},g_{2}\right\rangle$, $\left| \pm \right\rangle = \left( {\left| e_{1},g_{2}\right\rangle \pm \left| g_{1},e_{2}\right\rangle }\right) /{\sqrt{2}}$) [27] are used to solve master Eq. (2) as follows,

$$\begin{aligned} \rho _{++}(t)= & {} e^{-\Gamma _{+} t}\rho _{++}(0) + \frac{\Gamma _{+}}{\Gamma _{-}}\left( e^{-\Gamma _{+} t}-e^{-2\Gamma _{11} t}\right) \rho _{ee}(0),\nonumber \\ \rho _{--}(t)= & {} e^{-\Gamma _{-} t}\rho _{--}(0)+ \frac{\Gamma _{-} }{\Gamma _{+}}\left( e^{-\Gamma _{-} t}-e^{-2\Gamma _{11} t}\right) \rho _{ee}(0),\nonumber \\ \rho _{ee}(t)= & {} e^{-2\Gamma _{11} t}\rho _{ee}(0), \end{aligned}$$

(6)

with $\rho _{gg}(t)=1-\rho _{ee}(t)-\rho _{++}(t)-\rho _{--}(t)$. Here $\Gamma _{\pm }=\Gamma _{11} \pm \Gamma _{12}$. Equation (6) determines that the transition to and from the state $\rho _{++}(t)$ is superradiant ($\Gamma _+$) and from the state $\rho _{--}(t)$ is subradiant ($\Gamma _-$).

Fig. 2

Collective damping $\Gamma _{12}$ and qubit–qubit interaction $g_{12}$ (inset) as a function of the dipole–dipole separation d, where $\omega _{0}=0.5\omega _{sp}$ and $\Gamma =0.1\omega _{sp}$

3 Entanglement dynamics

How to quantify the entanglement is a central topic within QI theory. There are many measures for the quantification of entanglement, but a most widely spread measure is the concurrence defined by Wootter’s [28],

$$\begin{aligned} C\left( \rho \right) = \max \left\{ {0,\sqrt{\xi _1} - \sum _{j=2}^4 \sqrt{\xi _j}} \right\} , \end{aligned}$$

(7)

where ${\xi _i}$’s are the eigenvalues (in decreasing order) of the Hermitian matrix $R=\rho \tilde{\rho }$, where the spin flip density matrix $\tilde{\rho }= \left( {{\sigma _y} \otimes {\sigma _y}} \right) {\rho ^*}\left( {{\sigma _y} \otimes {\sigma _y}} \right)$, with ${\rho ^*}$ and ${\sigma _y}$ being the complex conjugate of $\rho$ and the Pauli matrix, respectively. In the Dicke Basis, the eigenvalues of the matrix R are given by [8]

$$\begin{aligned} \sqrt{\xi _{1,2}}= & {} \sqrt{\rho _{ee}\rho _{gg}} \pm \vert \rho _{eg} \vert , \nonumber \\ \sqrt{\xi _{3,4}}= & {} \frac{1}{2} \left( \sqrt{\left( \rho _{++}+\rho _{--}\right) ^2-\left( \rho _{+-}+\rho _{-+}\right) ^2} \right. \nonumber \\&\pm \left. \sqrt{\left( \rho _{++}-\rho _{--}\right) ^2-\left( \rho _{+-}-\rho _{-+}\right) ^2}\right) . \end{aligned}$$

(8)

It is easy to verify that, depending on the largest eigenvalue (either $\sqrt{\xi _{1}}$ or $\sqrt{\xi _{3}}$), the concurrence $C(t)=max\{0, C_1(t), C_2(t)\}$ can be defined in two alternative ways, i.e.

$$\begin{aligned} C_1(t)= & {} 2\vert \rho _{eg} \vert - \sqrt{\left( \rho _{++}+\rho _{--}\right) ^2-\left( \rho _{+-}+\rho _{-+}\right) ^2}, \nonumber \\ C_2(t)= & {} \sqrt{\left( \rho _{++}-\rho _{--}\right) ^2-\left( \rho _{+-}-\rho _{-+}\right) ^2} -2\sqrt{\rho _{ee}\rho _{gg}}. \end{aligned}$$

(9)

It is easy to verify from Eq. (9) that the concurrence $C_{1}(t)$ measures the entanglement produced by the non zero coherence term $\rho _{eg}(t)$, while $C_{2}(t)$ measures the entanglement produced by the density matrix of states $\left| \pm \right\rangle$ with positivity condition $\rho _{++}(t)\ne \rho _{--}(t)$. The density matrix elements can be obtained by solving Eq. (2). Hereafter, we are going to determine the dependence of entanglement sudden death on different initial states.

3.1 Sudden death and revival of entanglement

3.1.1 Entangled state

Two alternative ways to define the concurrence Eq. (9) lead to an interesting phenomenon of entanglement revival [8, 29,30,31], for which we initially assume a nonmaximally entangled state of excited ($\vert e \rangle$) and ground ($\vert g \rangle$) states.

$$\begin{aligned} \left| \Psi \right\rangle =\sqrt{1-q}\left| g \right\rangle + \sqrt{q}\left| e\right\rangle , \end{aligned}$$

(10)

Fig. 3

Time variation of the concurrence C(t) for initial entangled state $\left| \Psi \right\rangle$ at interatomic distance $d\simeq h$

By inspecting Eq. (9) at $t=0$, the initial degree of entanglement is $C_{1}(0)=2\sqrt{q(1-q)}$. It is not possible to observe the entanglement in the independently radiating two level system ($\Gamma _{12}=0$), because of equally populated $\left| \pm \right\rangle$ states. Therefore, the death time of entanglement can be found via the condition $C_{1}(t)=0$, that yields

$$\begin{aligned} t_\mathrm{d}=\frac{1}{\Gamma _{11}}\mathrm{ln}\left( \frac{q}{q - \sqrt{q(1-q)}}\right) , \end{aligned}$$

(11)

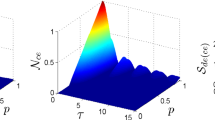
from which it is worthy to note that the two qubits are disentangled at $q >1/2$. However, the appearance of collective effects may lead to entanglement sudden birth (ESB) at later time ($t_\mathrm{r}$), which can be controlled by changing the interatomic distance. The transient evolution of concurrence for an initial state $\vert \Psi \rangle$ is shown in Fig. 3. It is depicted that the death of entanglement occurs due to the spontaneous emission but rebirth occurs due to the collective damping term after a collapse of time $t_\mathrm{r}\simeq 5/\gamma$, for $\alpha \simeq 1/2$ and separation $d \simeq h$ of qubits. After a careful inspection of Eq. (6), it can be concluded that the concurrence $C_{1}(t)$ is short lived, i.e. $C_{1}(t)<0$ at longer times, where the entanglement survives due to concurrence $C_{2}(t)$ that provides

$$\begin{aligned} t_\mathrm{r} \simeq \frac{3}{4\Gamma _{12}}\mathrm ln\left( \frac{4\Gamma _{11}}{\sqrt{q}(\Gamma _{11}-\Gamma _{12})}\right) . \end{aligned}$$

(12)

Moreover, Fig. 4 depicts the decay of entanglement at $d \simeq 5h/2$ that does not undergo any revival, due to impartiality between the term $\rho _{eg}(t)$ and $\rho _{++}(t)$. In other words, the latter terms go almost to zero at long times. Both two-level systems can be treated as being independent, equivalent to the situation when each system interacts with its own environment at $d \simeq 7h$, because of very small collective damping term ($\Gamma _{12} \approx 0$).

Fig. 4

Evolution of state population $\rho _{ge}$ (dotted curve), $\rho _{++}$ (dashed curve) and $\rho _{--}$ (dotted–dashed curve) with concurrence $C_1(t)$ (solid curve) at $d \simeq 5h/2$ and $q=0.6$

A limiting case ($q=1$) generates an unentangled state $\left| \Psi \right\rangle = \vert e \rangle$. Therefore, the density matrix $\rho (t)$ remains diagonal with nonzero elements,

$$\begin{aligned} \rho _{ee}(t)= & {} e^{-2\Gamma _{11} t},\nonumber \\ \rho _{++}(t)= & {} \frac{\Gamma _{+}}{\Gamma _{-}}e^{-2\Gamma _{11} t}\left( e^{-\Gamma _{-} t}-1\right) ,\nonumber \\ \rho _{--}(t)= & {} \frac{\Gamma _{-}}{\Gamma _{+}}e^{-2\Gamma _{11} t}\left( e^{-\Gamma _{+} t}-1\right) . \end{aligned}$$

(13)

One would expect that no entanglement could build up with Eq. (13). However, after some algebra we arrive at concurrence $C_2(t)$ of Eq. (9). It can be analysed from Fig. 5 that the transient entanglement for the limiting case $q=1$ of state $\vert \Psi \rangle$ generates at a later time, due to the large value of symmetric and anti-symmetric states population. In other words, the evolution of the concurrence follows the evolution of the population of the antisymmetric state because when the symmetric state becomes depopulated due to faster superradiant decay rate $\Gamma _+=\Gamma _{12}+\Gamma _{11}$, the state of the system reduces to the maximally entangled antisymmetric state.

Fig. 5

Panel a shows the time evolution of transient concurrence $C_2 (t)$ for the limiting case ($q=1$) of initial state $\vert \Psi \rangle$ and Panel b depicts the first (dashed) and second (dotted) term of concurrence $C_2 (t)$. The interatomic distance is considered to be $d\simeq h$

3.1.2 Mixed state

Here, we consider a two-qubit system to be initially prepared in a diagonal basis of the collective states, having initial density matrix of the form [4]

$$\begin{aligned} \rho (0) =\frac{1}{3}\left( \begin{array}{cccc} q &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 2 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad r \end{array} \right) , \end{aligned}$$

(14)

where $r=1-q$. At time $t=0$, the initial concurrence is $C_{2}(0)=2\left( 1-\sqrt{q(1-q)}\right) /3$, and the time for disappearance of concurrence is given by

$$\begin{aligned} t_\mathrm{d}=\frac{1}{\Gamma _{11}}\mathrm{ln}\left( \frac{q}{\sqrt{q(3q+5)}-(1+q)}\right) . \end{aligned}$$

(15)

It is easy to verify from Eq. (15) that the sudden death of concurrence for independent qubits is possible only for $q \gtrsim 1/3$. The time evolution of the concurrence for interacting qubits is depicted in Fig. 6. The entanglement decays for the whole range of parameter q, but it revives at $q \gtrsim 0.2$. In the physical terms, the location of the dipoles at a distance $d\simeq h$ from the plasmon interface leads to a strong collective behaviour of dipoles, resulting in the revival of entanglement. At $q=1/2$, ESD happens at $t_\mathrm{d} \sim 0.7/\gamma$, then it revives at $t_\mathrm{r}\sim 5.1/\gamma$. It is pertinent to mention here that going beyond $d\simeq h$ (i.e. the greater distance between two dipoles than to the plasmon field) destroys the collective behaviour of the dipoles and no revival occurs.

Fig. 6

Time variation of the concurrence C(t) for initial mixed state prepared in diagonal basis of the collective states at interatomic distance $d\simeq h$

3.1.3 Werner state

We assume the initial Werner state [32], which is a mixture of isotropic state and maximally entangled symmetric state $\vert s \rangle$,

$$\begin{aligned} \left| \psi _1\right\rangle =(1-p)\frac{\mathrm{I}}{4}+p \vert s \rangle \langle s \vert , \end{aligned}$$

(16)

where $\mathrm I$ is the $4 \times 4$ identity matrix and p determines the population of the symmetric state $\vert s \rangle$. Equation (16) interpolates between separable and entangled state, depending on the parameter p. Figure 7 depicts the time evolution of concurrence for various values of parameter p at long distance $d \simeq 7h$, when both the atoms act like an independent systems. It is shown that the state is separable for $p < 1/3$ and the initial concurrence appears as $C(0)=(3p-1)/2$ with sudden death in the range $1/3 \le p \le 3/5$ and follows the asymptotic decay for $p \ge 3/5$. It is pertinent to mention here that the greater distance between two dipoles than to the plasmon field destroys the collective behaviour of the dipoles and no revival occurs. In Fig. 8, entanglement sudden death appears for almost the whole range of parameter p (except $p = 1$) at interatomic distance $d\simeq h$. The more interesting feature is the appearance of entanglement for $p<1/3$ at later times, which is called entanglement sudden birth. This behaviour appears due to the collective dynamics of the two two-level systems and is more effective for the isotropic case ($p=0$), when all the levels are equally populated, i.e. $\rho (0)=\mathrm{I}/4$. For $p>0.7$, the entanglement dies out in a finite time and did not appear again. The practical realization of quantum computation and information requires a prolong entanglement. Thus, the local unitary operators can be applied to qubits to avert or delayed the dark period of entanglement [33, 34].

Fig. 7

Time evolution of concurrence C(t) for initial Werner state $\vert \psi _1 \rangle$ at interatomic distance $d \simeq 6h$

Fig. 8

Time evolution of concurrence C(t) for initial Werner state $\vert \psi _1 \rangle$ at interatomic distance $d \simeq h$

4 Conclusion

In summary, we use the green function approach with quasi-static approximation to explore the decay of entanglement for different initial states. In what follows, we first derive the Markovian master equation to extract the collective damping resulting from the mutual exchange of mediating particle and dipole–dipole interaction. Our results reveal the sudden death and birth of the entanglement depending on distance d between dipoles. This approach opens up new possibilities for systematically studying a wide class of open quantum systems and applications of quantum information theory.

Appendices

Appendix 1: Derivation of Born–Markov master equation

The Liouville–von Neumann equation by writing the global density matrix $\rho _{QP}$ is found to be

$$\begin{aligned} \frac{d\rho _{QP}}{dt}=-\frac{\imath }{\hbar }[H_0+H_\mathrm{int},\rho _{QP}], \end{aligned}$$

(A1)

where $H_0=H_{d}+H_{p}$. It is convenient to write Eq. (A1) in the interaction picture of $H_0$, for which we define

$$\begin{aligned} H_\mathrm{int}(t)=e^{\frac{i}{\hbar }H_0 t}H_{int}e^{-\frac{i}{\hbar }H_0 t}, \end{aligned}$$

(A2)

and

$$\begin{aligned} \rho (t)=e^{-\frac{i}{\hbar }H_0 t}\rho _{QP}e^{\frac{i}{\hbar }H_0 t}. \end{aligned}$$

(A3)

With the new definition of Hamiltonian and density operator, we can decompose Eq. (A1) as

$$\begin{aligned} \rho (t)=\rho (t_0)-\frac{i}{\hbar }\int _{t_0}^{t}[H(\tau ),\rho (\tau )]d\tau \end{aligned}$$

(A4)

Using Eq. (A4) in Eq. (A1), we get

$$\begin{aligned} \partial _t \rho= & {} -\frac{i}{\hbar }[H_\mathrm{int}(t),\rho (t_0)] \nonumber \\&+\frac{1}{\hbar ^{2}}\left[ H_\mathrm{int}(t),\int _{t_0}^{t}\left[ H_\mathrm{int}(\tau ),\rho (\tau )\right] d\tau \right] \end{aligned}$$

(A5)

With the Markov approximation and letting $t_0 \rightarrow - \infty$, it is possible to write

$$\begin{aligned} \partial _t \rho= & {} \frac{i}{\hbar }\left[ \rho (t_0),H_\mathrm{int}(t)\right] \nonumber \\&-\frac{1}{\hbar ^{2}}\int _{0}^{\infty }\left[ \left[ \rho (t), H_\mathrm{int}(t-\tau )\right] , H_\mathrm{int}(t)\right] d\tau \end{aligned}$$

(A6)

Let assume that the density matrix is of the form $\rho =\sum _n p_n \vert n(t), E_0 \rangle \langle n(t), E_0 \vert$ at all times, so that the degrees of freedom of the environment are to a first approximation unaffected by the dynamics of the atom (Born approximation). Hence, defining $\rho _s=\sum _E 1_s \otimes \langle E \vert \rho _I 1_s \otimes \vert E \rangle = \mathrm{tr_E} \rho _I (t)$, it follows that $\mathrm{tr}_E\left( \left[ \rho (t_0),H_{int}(t)\right] \right) =0$,

$$\begin{aligned} \partial _t \rho _s = -\frac{1}{\hbar ^{2}}\int _{0}^{\infty } \mathrm{tr}_E\left[ \left[ \rho (t), H_\mathrm{int}(t-\tau )\right] , H_\mathrm{int}(t)\right] d\tau , \end{aligned}$$

(A7)

where

$$\begin{aligned} H_\mathrm{int}= & {} -\sum _j \left( \tilde{\gamma }^*_j \sigma _+^j e^{i \omega _{0,j} t} + \tilde{\gamma }_j \sigma _-^j e^{-i \omega _{0,j} t} \right) . \hat{F}(r_j, t) \nonumber \\ \hat{F}(r, t)= & {} \sum _{\omega _{nk}>0} \sqrt{\frac{\hbar \omega _{nk}}{2}}\left( \hat{ a}_{nk}e^{-i\omega _{nk}t} F_{nk}(r)\right) +H.c. \end{aligned}$$

(A8)

Equation (A7) is the Born–Markov master equation. To proceed, we assume that the environment is in ground state for which we define the parameter

$$\begin{aligned} \mathcal {A}_{\omega }^{ij} =\frac{1}{\hbar ^{2}} \sum _{\omega _{nk}>0} \varepsilon _{0,\omega _{nk}} \frac{1}{i\left( \omega _{nk}-\omega -i0^+\right) } F_{nk}^*(r_i) F_{nk}^*(r_j), \end{aligned}$$

(A9)

where $\varepsilon _{0,\omega _{nk}}=\hbar \vert \omega _{nk} \vert /2$. Hereafter, we introduce a frequency-domain Green function $\mathcal {G}=\mathcal {G}^++\mathcal {G}^-+M_{\infty }^{-1}\delta (r-r_0)/i\omega$, where $\mathcal {G^{\pm }}=-i\omega \bar{\mathcal {G}}^{\pm }$ denotes the positive and negative frequency parts of the Green function,

$$\begin{aligned} \mathcal {G^+}= & {} \sum _{\omega _{nk}>0} \frac{\omega _{nk}}{2}\frac{1}{\omega _{nk}-\omega }F_{nk} (r_i) \otimes F^*_{nk} (r_j), \nonumber \\ \mathcal {G^-}= & {} \sum _{\omega _{nk}>0} \frac{\omega _{nk}}{2}\frac{1}{\omega _{nk}+\omega }F^*_{nk} (r_i) \otimes F_{nk} (r_j), \end{aligned}$$

(A10)

corresponding to the poles on the positive and negative real frequency axes, respectively. Therefore, Eq. (A9) can be written as

$$\begin{aligned} \mathcal {A}_{\omega }^{ij} =\frac{1}{i\hbar } \left( -i\omega \bar{\mathcal {G}}^{+}\right) (r_i, r_j; \omega -i0^+). \end{aligned}$$

(A11)

Using $\left( -i\omega \bar{\mathcal {G}}^{+}(r_i, r_j, \omega )\right) \vert _{-\omega }=\left( -i\omega \bar{\mathcal {G}}^{-}(r_i, r_j, \omega )\right) ^*\vert _{\omega ^*}$, we introduce

$$\begin{aligned} g_{ij}^{\pm }= & {} \frac{1 }{\hbar } \mathrm{Re} \left\{ \tilde{\gamma }_i ^*.\mathcal {G}^{\pm }(r_i, r_j; \omega _0).\tilde{\gamma }_j \right\} , \nonumber \\ \Gamma _{ij}^{\pm }= & {} \frac{2 }{\hbar } \mathrm{Im}\left\{ \tilde{\gamma }_i ^*.\mathcal {G}^{\pm }(r_i, r_j; \omega _0).\tilde{\gamma }_j \right\} . \end{aligned}$$

(A12)

Therefore, Eq. (A7) can be written as

$$\begin{aligned} \partial _t{\rho _{s}(t)}= & {} \sum _{i,j}\left( \frac{\Gamma ^+_{ij}}{2}+ig^+_{ij}\right) \left[ \sigma _{-}^{i}\rho _{s}(t)\sigma _{+}^{j}- \rho _{s}(t) \sigma _{+}^{j}\sigma _{-}^{i} \right] \nonumber \\&+ \sum _{i,j}\left( \frac{\Gamma ^+_{ij}}{2}-ig^+_{ij}\right) \left[ \sigma _{-}^{j}\rho _{s}(t)\sigma _{+}^{i}- \sigma _{+}^{i}\sigma _{-}^{j} \rho _{s}(t) \right] \nonumber \\&+ \sum _{i,j}\left( \frac{\Gamma ^-_{ij}}{2}+ig^-_{ij}\right) \left[ \sigma _{-}^{i}\sigma _{+}^{j}\rho _{s}(t)- \sigma _{+}^{j}\rho _{s}(t)\sigma _{-}^{i} \right] \nonumber \\&+ \sum _{i,j}\left( \frac{\Gamma ^-_{ij}}{2}-ig^-_{ij}\right) \left[ \rho _{s}(t)\sigma _{-}^{j}\sigma _{+}^{i}- \sigma _{+}^{i}\rho _{s}(t)\sigma _{-}^{j} \right] . \end{aligned}$$

(A13)

By employing the series expansion, it is easy to verify for the nonresonant part (−) of the Green function that $\Gamma _{ii}^-=0$, $\Gamma _{ij}^-=-\Gamma _{ji}^-$ and $g_{ij}^-=g_{ji}^-$. Using the relations $\hat{\sigma }_z = 2\hat{\sigma }_+ \hat{\sigma }_- -1$, $\hat{\sigma }_-\hat{\sigma }_+ = 1- \hat{\sigma }_+ \hat{\sigma }_-$ and again transforming Eq. (A13) to the Schrodinger picture, we obtain

$$\begin{aligned} \partial _t{\rho _{s}(t)}= & {} -\frac{i}{2}\sum _i \left( \omega _0+g^-_{ii}-g^+_{ii} \right) \left[ \sigma _z^i, \rho _s(t)\right] \nonumber \\&- \sum _{i,j} \frac{\Gamma _{ij}}{2} \left( \sigma _{+}^{i}\sigma _{-}^{j}\rho _s(t)+\rho _{s}(t) \sigma _{+}^{j}\sigma _{-}^{i} - \sigma _{-}^{j}\rho _{s}(t)\sigma _{+}^{i}\right. \nonumber \\&\left. -\sigma _{-}^{i}\rho _{s}(t)\sigma _{+}^{j}\right) + \sum _{i\ne j}ig_{ij}\left( \sigma _{+}^{i}\sigma _{-}^{j} \rho _{s}(t) \right. \nonumber \\&- \left. \sigma _{-}^{j}\rho _{s}(t)\sigma _{+}^{i} \right) +H.c., \end{aligned}$$

(A14)

where

$$\begin{aligned} \Gamma _{ij}= \frac{2 }{\hbar } \mathrm{Im}\left\{ \tilde{\gamma }_i ^*.\mathcal {G}(r_i,r_j, \omega _0).\tilde{\gamma }_j \right\} , \nonumber \\ g_{ij}= \frac{1 }{\hbar } \mathrm{Re}\left\{ \tilde{\gamma }_i ^*.\mathcal {G}(r_i,r_j, \omega _0).\tilde{\gamma }_j \right\} . \end{aligned}$$

(A15)

Equation (A14) determines the Markovian master equation and used to obtain elegant description of physics involved in the dynamics of interacting atoms. Equation (A14) is consistent with the results of Ref. [20, 24,25,26].

Appendix 2: Quasi-static approximation

To illustrate the concept developed throughout this paper, we employ the quasi static approximation [22, 35, 36] by assuming the fields are purely electric $\mathbf{F}_{n\mathbf{k}} \simeq \left( \mathbf{E}_{\mathbf{k}} 0\right) ^T \simeq \left( -\nabla \phi _\mathbf{k} 0\right) ^T$ ($\phi _\mathbf{k}$ represents the electric potential), satisfying $\nabla \cdot \left( \epsilon (\omega ,z) \nabla \phi _\mathbf{k} \right) =0$, with the general solution of the form

$$\begin{aligned} \phi _\mathbf{k} =\frac{A_{\mathbf{k}_{||}}}{\sqrt{S}}e^{i \mathbf{k_{||}}.\mathbf{r}} \left\{ \begin{array}{l} e^{-k_{||}z}, z > 0, \\ e^{+k_{||}z}, z < 0 , \\ \end{array} \right. \end{aligned}$$

(B1)

where $A_{\mathbf{k}_{||}}$ denotes the normalization constant and the wave vector $k_{||}=k_x \hat{x} + k_y \hat{y}$ is parallel to the interface of dipole and plasmonic slab. In this case, the plasmonic slab is assumed to locate in the region $z<0$ (for which the metal–air boundary corresponds to $z=0$). Therefore, the relevant eigenfrequency $\omega _k=\omega _{sp}$ corresponds to the surface plasmon resonance $\epsilon (\omega _{sp})=-\epsilon _0$. To find the normalization constant $A_{k_{||}}$, we employ

$$\begin{aligned} \vert A_{k_{||}} \vert ^2 \int k_{||}^2 e^{-2k_{||}|z|}\frac{\partial (\omega \epsilon (\omega ,z))}{\partial \omega }d^3r=1, \end{aligned}$$

(B2)

that provides $A_{k_{||}}=\sqrt{1/2 k_{||}\epsilon _0 S}$, where S determines the surface area of plasmonic slab and by considering the lossless Drude model,

$$\begin{aligned} \frac{\partial (\omega \epsilon (\omega ,z))}{\partial \omega } \vert _{\omega =\omega _{sp}} \rightarrow \left\{ \begin{array}{l} \epsilon _0, z>0 \\ 3\epsilon _0, z<0. \\ \end{array} \right. \end{aligned}$$

(B3)

This procedure follows to write the green function $\mathcal {G}^{\pm }$ in a way such that

$$\begin{aligned} \mathcal {G}^{\pm }= & {} \frac{\varepsilon (\omega )-1}{\varepsilon (\omega )+1} \times \frac{1}{4\pi \epsilon _0} \overrightarrow{\nabla }_{r_2} \nonumber \\&\left\{ \frac{1}{\sqrt{\left( x_2-x_1 \right) ^2+\left( y_2-y_1 \right) ^2+\left( z_2+z_1 \right) ^2}} \right\} \overleftarrow{\nabla }_{r_1}, \end{aligned}$$

(B4)

with $\varepsilon (\omega )=\varepsilon _0\left( 1-\omega _{sp}^2/\omega (\omega +i\Gamma ) \right)$ for lossy metal surface, where $\Gamma$ denotes the losses in the metal half space. By employing the quasi-static approximation, the collective damping term $\Gamma _{12}$ and the dipole–dipole coupling parameter $g_{12}$ can be written as

$$\begin{aligned} \Gamma _{12}= & {} \frac{ \tilde{\gamma }^2 \omega _{sp}^2 \Gamma }{ 4\pi \hbar \epsilon _0 \omega _{sp}'} \left\{ \frac{2 h^2-d^2}{ \left( d^2+4 h^2\right) ^{5/2} } \right\} \left[ \frac{\Delta _2-\Delta _1}{\Delta _1\Delta _2} \right] , \end{aligned}$$

(B5)

$$\begin{aligned} g_{12}= & {} \frac{ \tilde{\gamma }^2 \omega _{sp}^2 }{4 \pi \hbar \epsilon _0 \omega _{sp}'} \left\{ \frac{2 h^2-d^2}{ \left( d^2+4 h^2\right) ^{5/2} } \right\} \nonumber \\&\left[ \frac{(\Delta _1+\Delta _2)\omega _{sp}'+(\Delta _1-\Delta _2)\omega _0}{\Delta _1\Delta _2} \right] , \end{aligned}$$

(B6)

with

$$\begin{aligned} \Delta _1= & {} \frac{1}{\left( \omega _{sp}'-\omega _0 \right) ^2+\left( \frac{\Gamma }{2}\right) ^2}, \nonumber \\ \Delta _2= & {} \frac{1}{\left( \omega _{sp}'+\omega _0 \right) ^2+\left( \frac{\Gamma }{2}\right) ^2}. \end{aligned}$$

(B7)

here $\omega _{sp}'=\sqrt{\omega _{sp}^2 - (\Gamma /2)^2}$, $d=x_2-x_1$ denotes the distance between two dipoles and $h=z$ determines the separation of the dipole and plasmonic slab. For simplicity, the electric dipole is assumed to be oriented along x-direction $\gamma _{eg}=\tilde{\gamma } \hat{x}$. The spontaneous decay rate $\Gamma _{11}$ can be obtained by putting $d=0$ in Eq. (B5).