Free and bound entanglement dynamics in qutrit systems under Markov and non-Markov classical noise

Abstract

We investigate in detail the dynamics of decoherence, free and bound entanglements, and the conversion from one to another (quantum state transitions), in a two non-interacting qutrits system initially entangled and subject to independents or a common classical noise. Both Markovian and non-Markovian environments are considered. Furthermore, isotropic and bound entangled states for qutrits systems are considered as initial states. We show the efficiency of the formers over the latters against decoherence, and in preserving quantum entanglement. The loss of coherence increases monotonically with time up to a saturation value depending upon the initial state parameter and is stronger in a collective Markov environment. For the non-Markov regime the presence or absence of entanglement revival and entanglement sudden death phenomena is deduced depending on both the peculiar characteristics of the noise, the physical setup and the initial state of the system. We demonstrate distillability sudden death for conveniently selected parameters in bound entangled states; meanwhile, it is completely absent for isotropic states, where entanglement sudden death is avoided for dynamic noise independently of the noise regime and the physical setup. Our results indicate that distillability sudden death under the Markov/non-Markov noise considered can be avoided depending upon the physical setup.

1 Introduction

Quantum information theory has recently drawn much attention, and in the quantum information theory, quantum entanglement plays an important role as it can be utilized to perform various intriguing global tasks in quantum computing and information processing in novel ways [1, 2]. It is a valuable resource for a number of quantum features such as quantum cryptography [3], teleportation [4], computation [5], sensitive measurements [6], quantum telecloning [7] and entanglement swapping [8], as well as quantum technologies and photonics [9,10,11] just to cite a few examples. In realistic world, due to the unavoidable interaction between the system and the environment, most states in nature are mixed and the set of all states is a convex set, which is a convex hull of pure states, thus destroying initial quantum entanglement in the system [12], the so-called decoherence phenomenon [13]. Decoherence is a complex and challenging problem, and many works have been dealt with various models [13,14,15,16,17,18,19,20,21]. Both theoretical and experimental studies have revealed that entanglement does not always decay in an asymptotic way and can exhibit sudden death phenomena [16, 17, 22]. On the other hand, environment can also revive quantum correlations or preserve them [23,24,25]. Both phenomena have been observed in quantum systems under environmental noise with different classical or quantum properties [26, 27]. Thus, it is very important to study, characterize and optimize dynamical properties of the various kind of environmental noise on entanglement dynamics in open quantum systems, which are of particular importance in practical quantum information processing. Environmental noises can be put into two categories according to their intrinsic features, namely Markovian (with short, or rather instantaneous self-correlations) [16] and non-Markovian (associated with environments with memory and may lead to the non-monotonic time dependence of entanglement) [28].

Previous works are mostly concentrated on quantum correlations dynamics for mixed states in two-dimensional systems [29,30,31,32,33,34]. But it has been shown that, compared to qubits, maximally entangled qudits violate local realism more strongly and are less affected by noise [35,36,37]. It is thus very important to study and characterize correlations dynamical behavior in systems of higher dimensions, so as to construct a useful parallel with the more extensively studied case of entanglement. In fact, systems with higher dimensions can be used to improve the efficiency of quantum information processing, [35, 38,39,40] and the dynamics of the high-dimensional bipartite entangled state have been investigated [41,42,43]. It has been revealed that higher-dimensional systems may have advantages over the qubit ones, as they provide higher channel capacities, more secure cryptography and superior quantum gates [44,45,46]. In view of this fact, there have been some investigations regarding qutrit systems in the recent years, namely quantum correlations dynamics under Dzyaloshinskii–Moriya interaction [47], quantum and classical noises [48,49,50,51,52,53,54,55], magnetic fields [56] and even teleportation under intrinsic decoherence [57].

On the other hand, bipartite entangled states can be divided into free entangled states (FES) and bound entangled states (BES) [58, 59]. FES can be distilled under local operations and classical communication (LOCC), whereas BES cannot be distilled to pure state entanglement. However, it is interesting that some bound entanglement can be distilled by certain procedures [60] or interaction with auxiliary systems [42, 61, 62]. These properties provide new quantum communication schemes, including remote information concentration [63], secure quantum key distribution [64], superactivation [62], convertibility of pure entangled states [65], activation of teleportation fidelity [42]. They further manifest the irreversibility in asymptotic manipulation of entanglement [66]. Bound entanglement constructed by purely mathematical arguments have existence in physical processes [67, 68]. It has been shown that certain free entangled states of qutrit–qutrit systems become non-distillable in a finite time under the influence of classical noise. Such behavior has been named distillability sudden death (DSD) [69].

The aim of this paper is to investigate the dynamics of decoherence, free and bound entanglements in a physical model consisting of two non-interacting spin-qutrit particles coupled to noise in different and common environments. In the spirit of Refs. [32, 70], we consider two different kinds of noise: first is the static noise recently used in describing electron transport and photon propagation in disordered structures [71, 72]. Next is the random telegraph noise (RTN), a dynamic noise model playing an important role in the building up of $1/f^{\alpha }$ noises affecting solid state systems [73, 74]. It represents one of the common environmental noises affecting charge carriers in nanodevices. The static noise here simulates a non-Markovian environment, while the dynamic disorder can model both a non-Markovian environment (in the limit of slow RTN) and a Markovian noise (expressed by a fast RTN). Furthermore, two different initial configurations are examined, namely the isotropic states and bound entangled states. We use analytical techniques to detect entangled states. Specifically, FES are detected by means of negativity measure [75] based on the Peres–Horodecki separability criterion [76, 77], while for BES we use the realignment criterion [78, 79]. Hence, we analyze the above-mentioned entanglement measures dynamics to investigate DSD phenomena. Furthermore, we characterize the environmental decoherence due to the system–environment interactions by means of the von Neumann entropy [13].

The paper is organized as follows: The physical model adopted is described in Sect. 2. In Sect. 3 are presented the results for the various cases considered: static and dynamic noise, different and common environments, Markov and non-Markov regime. Conclusions are given in Sect. 4.

2 Physical model

Spin-1 particles often called qutrits are defined as quantum three-level systems, with states in the three-dimensional Hilbert space $H_{3}$. Its orthonormal basis is denoted here as $\left| 0\right\rangle$,$\left| 1\right\rangle$ and $\left| 2\right\rangle$. The model consists of two identical and non-interacting three-level atoms (qutrits) a and b, assumed in the V type configuration where $\left| 0_k\right\rangle$,$\left| 2_k \right\rangle$ are the nearest degenerated states and $\left| 1_k \right\rangle$ are ground states $(k=a, b)$. They are initially entangled and subject to noisy environments. We assume that the interaction with the surroundings induces the process of spontaneous emission from the two excited levels to the ground state, but a direct transition between excited levels is not possible.

A static and a RTN are accounted for in different conditions. Specifically independent (local) and common (non-local) interactions between qutrits and environments are considered. In both configurations, the dynamics of the two qutrits system is ruled by the Hamiltonian:

$$\begin{aligned} \mathcal {H}(t)=\mathcal {H}_{a}(t)\otimes \mathbb {I}_{b}+\mathbb {I}_{a}\otimes \mathcal {H}_{b}(t), \end{aligned}$$

(1)

where $\mathbb {I}_{a(b)}$ is the identity matrix acting on the Hilbert space of qutrit a(b) and $\mathcal {H}_{a(b)}$ is the single-qutrit Hamiltonian describing its dynamics in the presence of noise, and written as:

$$\begin{aligned} \mathcal {H}_{k}(t)=\omega _{0}\mathbb {I}_{k}+g\chi _{k}(t)S_{x}^{k}. \end{aligned}$$

(2)

In the above expression, $\omega _{0}$ represents the energy of an isolated qutrit. (Degeneracy is assumed, and qutrits are identical in the sense that they are characterized by the same energy.) g stands for the system–environment coupling strength of one qutrit with the noisy environment. $\chi _{k}(t)$ ($k=a,b$) represents the stochastic parameter related to the specific characteristics of the noise. $S_{x}^{k}$ is the generalized Pauli matrix for spin-1 systems expressed in the subspace of qutrit k. It is given by:

$$\begin{aligned} S_{x}^{k}=\frac{1}{\sqrt{2}}\left( \left| 0_{k}\right\rangle \left\langle 1_{k}\right| +\left| 1_{k}\right\rangle \left\langle 0_{k}\right| +\left| 1_{k}\right\rangle \left\langle 2_{k}\right| +\left| 2_{k}\right\rangle \left\langle 1_{k}\right| \right) \end{aligned}$$

The Hamiltonian (1) is stochastic due to the random nature of the noise parameter $\chi _{k}(t)$, thus leading to a stochastic time evolution of the quantum states. Note that the specific Hamiltonian in Eq. (2) extended to qudits has also been used to investigate the entanglement dynamics in a continuous-time quantum walk of two indistinguishable and non-interacting particles on a one-dimensional noisy lattice [80].

Physically, this type of interaction may possibly be viewed as noise (lattice disorder electric and/or magnetic fields for example), interacting with the spatial modes (degrees of freedom) of entangled biphotonic quantum systems (used to experimentally generate systems of entangled qutrits [81, 82]. Specifically, in a real scenario, the stochastic variable (noise parameter) $\chi _{k}(t)$, in the case of a transmitting antenna, can be the noisy measurement of the angular position of a transmitting antenna with respect to a receiving antenna [83]. Similarly, it can also represent the effective detuning of a particular waveguide, in the case of a coupled array of waveguides [72].

Once a choice of the noise parameter is performed, the unitary time evolution operator corresponding to the various realizations of the selected stochastic process is given by $\mathcal {U}\left( \chi _{a},\chi _{b},t\right) =\mathcal {U}_{a}\left( \chi _{a},t\right) \otimes \mathcal {U}_{b}\left( \chi _{b},t\right)$, since the subsystems are isolated from each other and the noisy channels are uncorrelated. $\mathcal {U}_{k}\left( \chi _{k},t\right)$ is the single-qutrit evolution operator which expression reads:

$$\begin{aligned} \mathcal {U}_{k}\left( \chi _{k},t\right) =\exp \left[ -i\int _{0}^{t}\mathcal {H}_{k}(s)ds\right] \quad (\text {hereafter}~\hbar =1). \end{aligned}$$

(3)

Therefore, the specific system dynamics is obtained by applying $\mathcal {U}\left( \chi _{a},\chi _{b},t\right)$ to the initial state of the system. Its time-evolving state (density matrix) under the influence of the selected stochastic processes is evaluated by averaging the global state over different realizations of the sequences of $\chi (t)$ and reads

$$\begin{aligned} \rho (t)=\left\langle \rho (\chi _{a},\chi _{b},t)\right\rangle =\left\langle \mathcal {U}\left( \chi _{a},\chi _{b},t\right) \rho (0)\mathcal {U}^{\dagger }\left( \chi _{a},\chi _{b},t\right) \right\rangle . \end{aligned}$$

(4)

Here $\left\langle \ldots \right\rangle$ stands for the average over all possible realization of the stochastic process $\chi _{k}(t)$ and $\rho (0)$ is the initial state of the system at $t=0$. Specifically, we examine the time evolution of two classes of initially entangled states: the two-qutrit isotropic states (IS) and a second class which we later refer to as bound entangled states (BES). The former reads

$$\begin{aligned} \rho _{p}(0)=p\left| \psi _{+}\right\rangle \left\langle \psi _{+}\right| +\frac{1-p}{9}\mathbb {I}_{9}, \end{aligned}$$

(5)

where $\left| \psi _{+}\right\rangle =\frac{1}{\sqrt{3}}\left( \left| 00\right\rangle +\left| 11\right\rangle +\left| 22\right\rangle \right)$ is the two-qutrit maximally entangled state, $p\in \left[ 0;1\right]$ is the purity of the state. $\mathbb {I}_{9}$ is the $9\times 9$ identity matrix corresponding to full separable states. The other initial configuration reads

$$\begin{aligned} \rho _{\alpha }(0)=\frac{2}{7}\left| \psi _{+}\right\rangle \left\langle \psi _{+}\right| +\frac{\alpha }{7}\sigma _{+}+\frac{5-\alpha }{7}\sigma _{-} \end{aligned}$$

(6)

where $2\le \alpha \le 5$. The maximally entangled state $\left| \psi _{+}\right\rangle$ is mixed with separable states $\sigma _{+}=\frac{1}{3}\left( \left| 01\right\rangle \left\langle 01\right| +\left| 12\right\rangle \left\langle 12\right| +\left| 20\right\rangle \left\langle 20\right| \right)$ and $\sigma _{-}=\frac{1}{3}\left( \left| 10\right\rangle \left\langle 10\right| +\left| 21\right\rangle \left\langle 21\right| +\left| 02\right\rangle \right. \left. \left\langle 02\right| \right)$. It is worth mentioning that, as shown in Ref. [42], $\rho _{\alpha }(0)$ is separable for $2\le \alpha \le 3$, bound entangled for $3\le \alpha \le 4$ and free entangled for $4\le \alpha \le 5$.

Additionally, it was shown that BES have positive partial transpose (PPT) and therefore non-distillable under LOCC [59]. As such BES cannot be detected by measures based on the Peres–Horodecki separability criterion, which is essentially a negative partial transpose (NPT) criterion and a free entanglement measure. However, one can use the realignment criterion [78, 79] to detect certain bound entangled states. Hence, in the present study we use the negativity first introduced by Vidal and Werner [75] to detect FES, while BES are quantified using the realignment criterion. Considering a bipartite quantum state $\rho \equiv \rho _{ab}(t)$, both quantities are, respectively, defined as:

$$\begin{aligned} \mathcal {N}(\rho )= & {} \frac{\left\| \rho ^{\text {T}_{k}}\right\| -1}{2}, \end{aligned}$$

(7)

$$\begin{aligned} \mathcal {R}(\rho )= & {} \max \left[ 0,\frac{\left\| \rho ^{\text {R}}\right\| -1}{2}\right] . \end{aligned}$$

(8)

where $\left\| \text {A}\right\| =\text {Tr}\sqrt{\text {AA}^{\dagger }}$ is the trace norm, $\rho ^{\text {T}_{k}}$ is the partial transpose of state $\rho$ with respect to subsystem $k=a,b$ and $\left( \rho ^{\text {R}}\right) _{ij,mn}=\rho _{im,jn}$ is the realigned density matrix. Either $\mathcal {N}(\rho )>0$ or $\mathcal {R}(\rho )>0$ indicates that the state is entangled, $\mathcal {N}(\rho )=0$ and $\mathcal {R}(\rho )>0$ indicates that the state is bound entangled and $\mathcal {N}(\rho )>0$ means that the state is free entangled. Note that there are various BES and a single criterion is not capable to detect all of them [84]. Thus, the realignment criterion detects certain but not all BES.

Moreover, environmental decoherence in quantum information processing can be viewed as the loss of information in a system due to unavoidable interactions with its environment. To some extent, it may be used to evaluate the degree of entanglement between a system and its environment as well as to estimate the deviation from an ideal state [85]. In this paper, we quantify the environmental decoherence by means of the von Neumann entropy [86] of the time-evolved density matrix given by:

$$\begin{aligned} \mathcal {S}(t)=-\text {Tr}\left[ \rho (t)\ln \rho (t)\right] . \end{aligned}$$

(9)

It is worth noting that the von Neumann entropy is a valid measure of decoherence, only when the interaction of the system with its environment is described classically as in our case.

3 Results and discussion

In this section we present the results obtained for the two different ways of modeling classical noise, namely through static and dynamic (RTN) disorder for a two-qutrit system initially entangled in either states of Eqs. (5) and (6). In particular, the static noise is simulated by assuming random and time-independent values for each $\chi _{k}$, while the RTN is modeled by selecting the time-dependent $\chi _{k}(t)$ according to a random telegraph signal. In the following, a different (or independent) environments coupling is labeled “de”, while common environment coupling is labeled “ce”. Note that in the followings, analytical expressions for decoherence, negativity and the realignment are quite involved and cumbersome to be reported explicitly. Hence, we present only the corresponding results.

3.1 Static noise

In fact, the first noise we investigate is the static noise, bearing this name due to its time-independent stochastic variable $\chi _{k}$ characterized by the flat probability distribution $P(\chi _{k})=\frac{1}{\vartheta _{m}}$ for $\left| \chi _{k}-\vartheta _{0}\right| \le \vartheta _{m}/2$ and vanishes for all other choices [72]. Here, $\vartheta _{0}$ is the mean value of the distribution and $\vartheta _{m}$ quantifies the disorder of the environment. The autocorrelation function of $\chi _{k}$ reads $\left\langle \delta \chi (t)\delta \chi (0)\right\rangle =\frac{\vartheta _{m}^{2}}{12}$; hence, its power spectrum is given by a $\delta$-function centered on zero frequency. As a consequence, this kind of noise has a characteristic time which is always much longer than the characteristic time of the system–environment coupling. Therefore, the static disorder can be considered as representative of a non-Markovian noise. Note that physically, the static noise stems from medium disorder (in disordered structures) like the propagation of photons in a realistic waveguide array with controllable disorder.

As stated earlier, to describe the full dynamics of the system subjected to the disordered environment, one needs to perform the average in Eq. (4) over all the possible noise configurations. This corresponds to the integral of the time-evolved states, each corresponding to a specific choice of the noise parameters. Specifically, for the static disorder, in both cases of local coupling to different environments $\left( \chi _{a}\ne \chi _{b}\right)$ and non-local coupling to a common environment $\left( \chi _{a}=\chi _{b}\right)$, the two-qutrit evolved states at time t are, respectively, obtained from

$$\begin{aligned} \rho _{\text {de}}(t)=\int _{d^{-}}^{d^{+}}\int _{d^{-}}^{d^{+}}P(\chi _{a})P(\chi _{a})\rho (\chi _{a},\chi _{b},t)d\chi _{a}d\chi _{b} \end{aligned}$$

(10)

and

$$\begin{aligned} \rho _{\text {ce}}(t)=\int _{d^{-}}^{d^{+}}P(\chi _{a})\rho (\chi _{a},t)d\chi _{a}. \end{aligned}$$

(11)

In the above equations $d^{\pm }=\vartheta _{0}\pm \vartheta _{m}/2$. Their explicit forms each corresponding to the system initially prepared in either state of Eqs. (5) and (6) are presented in “Appendix”.

Fig. 1

Negativity (left and center panels) and decoherence (right panel) as a function of both the dimensionless time $\tau =gt$ and initial purity p of the isotropic state for two qutrits under a static noise ($\vartheta _m=1$) in different and common environments coupling

3.1.1 Isotropic states

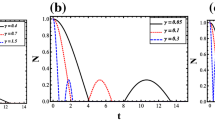
The composite system is initially prepared in the isotropic state given by Eq. (5) and then subject to static noise. The evolution of negativity and decoherence as a function of purity p and dimensionless time $\tau =gt$ are plotted in Fig. 1. The results show that for the pure state ($p=1$), entanglement is a non-monotonic and decreasing function of time exhibiting sudden death (ESD) and revival (ER) phenomena stemming from the non-Markovian nature of the static noise affecting the two-qutrit system. The oscillatory behavior is more prominent in non-local system–environment coupling (center panel) than in a local one (left panel). This demonstrates the relevance of the type of system–environment interaction over quantum entanglement preservation in bipartite systems. As the purity p decreases, revival phenomena vanish and disentanglement occurs abruptly. Precisely, optimization shows that the latter monotonic decay occurs for $p<0.95$ and $p<0.62$, respectively, in different and common system–environment(s) coupling. However, in both configurations and as expected, negativity vanishes for $p<0.25$, which corresponds for a ($d=3$)-dimensional system to $p<1/(d+1)$. On the other hand, Fig. 1 shows that decoherence (right panel) is a monotonic increasing function of time, reaching a corresponding saturation value with respect to the purity p of the initial state. Unlike negativity, the decoherence profile coincides for both physical system–environment configurations (either local or non-local) and hence is independent of the latter.

3.1.2 Bound entangled states

On the other hand, when the two-qutrit system is initially prepared in the bound entangled states of Eq. (6), the results for the evolution of free entanglement, bound entanglement and decoherence are, respectively, plotted in Figs. 2 and 3 as a function of time and entanglement parameter $\alpha$.

Fig. 2

Decoherence as a function of dimensionless time $\tau =gt$ and entanglement parameter $\alpha$ for two qutrits subject to a static noise ($\vartheta _m = 1$) for different (left panel) and common (right panel) environments coupling

Fig. 3

Negativity (left panel), realignment criterion (middle panel) and DSD occurence/avoided regions (right panel: contour plot) as a function of dimensionless time $\tau =gt$ and initial state parameter $\alpha$ for two qutrits subject to a static noise ($\vartheta _m = 1$) for different (upper panels) and common (lower panels) environments (Color figure online)

Under the degrading effects of a static noise, both realignment criterion and negativity are monotonic decaying functions of time and go through sudden death in a short time limit. Meanwhile, decoherence is also a monotonic but increasing function of time before reaching the saturation values. It is worth noting that unlike isotropic states, the long time saturation value of decoherence (Fig. 2) is independent of the state parameter $\alpha$, and decoherence, however, achieves its greatest level with time. Despite the non-Markovian nature of the considered noise that is generally a mean of entanglement revival, results highlight the absence of the latter when the system is initially prepared in the bound entangled states of Eq. (6) (unlike isotropic states shown in Fig. 1), thus demonstrating the relevance of the initial state of the system. Additionally, since negativity is essentially a NPT criterion, Fig. 3 clearly demonstrates that it is unable to detect bound entanglement (in the range $3\le \alpha \le 4$), shown to be present via the realignment criterion. While decoherence in stronger in different environments coupling than in common environment coupling with the static noise, the opposite is found for negativity; meanwhile, the realignment criterion is independent of the physical setup. On the other hand, analyzing the dynamics of both negativity and realignment criterion demonstrate entanglement distillability sudden death (i.e., a zero negativity but a nonzero realignment criterion in the free entangled state region $\alpha \in \left[ 4;5\right]$) in the qutrit–qutrit system under static noise. Moreover, in different environments, all the initially free entangled states can undergo DSD, while for a common environment, the latter phenomenon is avoided by some FES (red dashed dotted area on the lower right panel of Fig. 3), thus suggesting the sensitivity of the realignment criterion to both the physical setup and parameter $\alpha$. A similar result has previously been obtained in [43].

3.2 Dynamic noise: RTN

On the other hand, the second class of noise we investigate is the RTN [70, 87]. Physically, a RTN noise can result either from: (i) charges hopping between two locations in space (charge noise); (ii) electrons trapping in shallow subgap states formed at a superconductor–insulator boundary (noise of critical current); or (iii) spin diffusion on a superconductor surface generated by the exchange mediated by the conduction electrons (flux noise).

Here $\chi _{k}(t)$ mimicks a classical random fluctuating field such as a bistable fluctuator switching between two fixed values $\pm x$ at rate $\omega$. We consider the latter to be the same for both transitions. The autocorrelation function of the random variable $\chi _{k}(t)$ is $\left\langle \delta \chi (t)\delta \chi (t')\right\rangle =\exp \left[ -2\omega \left| t-t'\right| \right]$ with Lorentzian power spectrum $S_{rtn}(\omega _{r})=4\omega ^{2}/\left( \omega _{r}^{2}+4\omega ^{2}\right)$. Considering the ratio $q=g/\omega$, two regimes for the decay of quantum correlations are identified, namely the Markovian regime (for $q \ll 1$) and the non-Markovian regime (for $q \gg 1$). In the evolution of the composite system during the time interval $\left[ 0;t\right]$, each qutrit picks up a random noise phase factor $\varphi _{k}(t)=-\int _{0}^{t}\chi _{k}(t')dt'$. The averages in Eq. (4) for different environments coupling $\left( \varphi _{a}(t)\ne \varphi _{b}(t)\right)$ and for a common environment coupling $\left( \varphi _{a}(t)=\varphi _{b}(t)\right)$ read

$$\begin{aligned} \rho _{\text {de}}(t)=\left\langle \left\langle \rho \left( \varphi _{a},\varphi _{b},t\right) \right\rangle _{\varphi _{a}}\right\rangle _{\varphi _{b}}\quad \text {and}\quad \rho _{\text {ce}}(t)=\left\langle \rho \left( \varphi _{a},t\right) \right\rangle _{\varphi _{a}} \end{aligned}$$

(12)

The latter averages contain in their full expressions, terms of the form $\left\langle \exp \left( in\varphi _{k}(t)\right) \right\rangle$ ($n\in \mathbb {N}$), for which an analytical expression was found [88] and reads:

$$\begin{aligned} \left\langle \exp \left( in\varphi _{k}(t)\right) \right\rangle ={\left\{ \begin{array}{ll} e^{-\omega t}\left[ \cosh (\gamma _{ng}t)+\frac{\omega }{\gamma _{ng}}\sinh (\gamma _{ng}t)\right] &{} \;\text { for }\omega >ng\\ \\ e^{-\omega t}\left[ \cos (\gamma _{ng}t)+\frac{\omega }{\gamma _{ng}}\sin (\gamma _{ng}t)\right] &{} \;\text { for }\omega <ng \end{array}\right. } \end{aligned}$$

(13)

where $\gamma _{ng}=\sqrt{\left| \omega ^{2}-(ng)^{2}\right| }$. Also in this case, the explicit forms of $\rho _{\text {de}}(t)$ and $\rho _{\text {ce}}(t)$ each corresponding to the system initially prepared in either state of Eqs. (5) and (6) are given in “Appendix”.

3.2.1 Isotropic states

As we can see from Fig. 4, decoherence induced by the Markovian RTN noise increases monotonically with time until reaching the corresponding saturation values depending upon p. In the non-Markovian dynamics, decoherence exhibits some oscillations for lowest mixedness of quantum states (i.e., maximum purity) before achieving the corresponding saturation value. Oscillations are more pronounced in a common environment coupling than in independent ones, thus demonstrating the robustness of decoherence in the latter than in the former configuration. Meanwhile, the opposite behavior is found for Markovian environment(s) where for a given value of p, decoherence is stronger in common environment coupling than in independent ones. Unlike the case of the static noise, decoherence here is sensitive to the physical setup of the isotropic two-qutrit system, thus suggesting a potential connexion between the noise spectrum, the physical setup and the initial state of the system.

Fig. 4

Decoherence as a function of dimensionless time $\omega t$ and purity p of the initial state for two qutrits subject to different (left panels) and common (right panels) environments, modeled by a RTN in the Markovian (upper panels: $q=0.1$) and non-Markovian (lower panels: $q=10$) regime

Fig. 5

Negativity as a function of dimensionless time $\omega t$ and initial purity p of the isotropic state for two qutrits subject to RTN noise in the Markovian regime (left panel: $q=0.1$) and the non-Markovian regime (middle and right panels: $q=10$). Upper panels: different environments; lower panels: common environment

In accordance with the Markovian or non-Markovian nature of the noise, Fig. 5 shows that free entanglement (here quantified by negativity), decreases either monotonically (Markovian dynamics) or not (non-Markovian dynamics) with time before vanishing. The complete disentanglement time increases with increasing values of p. While negativity vanishes for values of $p \le 0.25$, initial entanglement of the system is a linear increasing function of p above 0.25. In fact, the two-dimensional dynamics for fixed values of purity p in Fig. 5 (right panels) clearly show that the oscillatory dynamics in the non-Markovian regime does not exhibit ESD phenomena. This represents one of the discrepancies among bipartite three-level (qutrits) and two-level (qubits) [32] systems under dynamical noise. However, like the two-qubit model [32], Markovian environments are less fatal to quantum entanglement than non-Markovian ones. In the latter, a common environment coupling is more effective in preserving free entanglement of the system than independent environments. The opposite is found in Markovian environments, where the relative weaker degradation of entanglement for greater values of initial purity can ensure persistent entanglement at long time in the system. The above-mentioned results in the case of disentanglement induced by the dynamic noise model are similar with some earlier findings concerning the disentanglement of Bell and Dicke states of two three-level atoms in a V type configuration, coupled to a common vacuum and separated by a distance comparable to the radiation wavelength [89]. ESD phenomena are totally removed from the dynamic, and we either observe an asymptotic or a non-monotonic decay of entanglement.

3.2.2 Bound entangled states

In this case, the dynamics of decoherence for bound entangled states shown in Fig. 6 is not too much different from that of Fig. 4, for isotropic states (free entangled states). Hence, the dynamics will not be discussed here in details due to dynamical similarities and we present just the major discrepancies. In fact unlike isotropic states, a free decoherence state (state with zero decoherence) cannot occur when the composite system is initially prepared in the bound entangled states of Eq. (6). Decoherence, however, achieves its greatest value in the long time limit independently of parameter $\alpha$.

Fig. 6

Decoherence as a function of dimensionless time $\omega t$ and entanglement parameter $\alpha$ of the initial state for two qutrits subject to different (left panels) and common (right panels) environments, modeled by a RTN in the Markovian (upper panels: $q=0.1$) and non-Markovian (lower panels: $q=10$) regime

Fig. 7

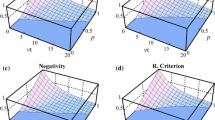
Negativity (left panel), realignment criterion (middle panel) and DSD occurence/avoided regions (right panel: contour plot) as a function of dimensionless time $\omega t$ and entanglement parameter $\alpha$, for two qutrits subject to a Markovian RTN noise ($q=0.1$) for different (upper panels) and common (lower panels) environments coupling (Color figure online)

Figure 7 shows the evolution of the negativity and realignment criterion for initially bound entangled states of Eq. (6), for the system interacting with a RTN noise in the Markovian regime. As a result of the nature of the environmental noise, both free entanglement (negativity) and bound entanglement (realignment criterion) decay abruptly in a monotonic manner going through sudden death. Disentanglement time increases with increasing values of the parameter $\alpha$ and free entanglement is more robust in non-local interaction than local one. Moreover, negativity is unable to detect bound entangled states (for $3 \le \alpha \le 4$) shown to be present via the realignment criterion. BES are degraded by environmental decohering effects, showing that under Markovian RTN noises, qutrit–qutrit bound entangled states cannot be converted into free entangled states. Meanwhile, for $4 \le \alpha \le 5$, we observe free entanglement distillability sudden death [43, 69], i.e., NPT states (free entangled) becoming PPT states after a certain time. In fact, Fig. 7 (right panels) clearly shows that under independents environments, all initially FES undergo DSD, whereas for a common environment, DSD can be avoided by some states presenting the sole phenomenon of ESD. Such a result simply highlights the sensitivity of DSD to both the entanglement parameter and the physical setup considered.

The same behavior is obtained in the case of a non-Markovian dynamic environment as shown in Fig. 8, but few revival phenomena can be observed for a common environment coupling and again, DSD phenomena are observed. Specifically, unlike FES subject to a common Markovian dynamic noise (Fig. 7), and alike FES under independent environments (no matter their nature), all initially FES considered in the present case are affected by DSD phenomena after a finite time. However, the realignment criterion fails to detect some entangled states in certain regions like the interval $0.048 \lesssim \omega t \lesssim 0.109$ (red dashed dotted regions). This highlights once again the sensitivity of the realignment criterion to the parameter $\alpha$ and the physical setup. Hence, although the initial free entangled states can become PPT after a finite time we cannot, however, conclude their separability/entanglement immediately. The PPT states might be entangled suffering distillability sudden death followed by entanglement sudden death. On the other hand, Fig. 8 shows that the memory effects of the non-Markovian RTN can be completely canceled by the system physical setup (the specific case of different environments coupling), leading to the absence of the oscillatory behavior that generally characterizes non-Markovian environments. However, an effect of delayed sudden birth of entanglement, has been invented by Ficek and Tanas [90] and observed by L. Derkacz, and L. Jakóbczyk [91]. In the same light, we demonstrate a similar phenomenon in the present study, where is observed a sort of delayed sudden rebirth of entanglement, occurring after an ESD phenomenon, for the system initially prepared in bound entangled states, and experiencing the effects of the collective/common non-Markovian dynamic noise. Hence, in view of the current finding and analyzing the earlier one, we suggest that the observed feature ((re)birth of entanglement) may be induced by either/both the type of system–environment interaction (the common environment) or/and the nature of the noise channel (dynamic and non-Markovian).

Fig. 8

Negativity (left panel), realignment criterion (middle panel) and DSD occurence/avoided regions (right panel: contour plot) as a function of dimensionless time $\omega t$ and entanglement parameter $\alpha$, for two qutrits subject to a non-Markovian RTN noise ($q=10$) for different (upper panels) and common (lower panels) environments coupling. Region (R1) corresponds to $\mathcal {N}(\rho )>0$ and $\mathcal {R}(\rho )>0$, while region (R2) is for $\mathcal {N}(\rho )=0$ and $\mathcal {R}(\rho )=0$ (Color figure online)

It is worth mentioning that for the static as for the dynamic noise models, we do not report the results of the realignment criterion when the composite system is initially prepared in the isotropic state Eq. (5). The reason is that after representation, both negativity and realignment criterion are equal:

$$\begin{aligned} \mathcal {N}\left( \rho _{\text {de(ce)}}(p,t)\right) =\mathcal {R}\left( \rho _{\text {de(ce)}}(p,t)\right) . \end{aligned}$$

(14)

Thus, free entanglement (quantified with negativity) and bound entanglement (quantified with the realignment criterion) coincide. This result suggests the complete absence of DSD phenomena, for qutrit–qutrit isotropic states under the classical environmental noise models here considered. However, they suffer ESD. A similar result has been demonstrated in [43, 51].

4 Conclusions

We have investigated the dynamics of decoherence, quantum free and bound entanglements in a model consisting of two initially entangled qutrits, not interacting among each other and coupled to independent sources or to a common source of classical noise, namely the static noise (non-Markovian) and the dynamic noise (RTN, modeling either a Markovian or a non-Markovian noise). Two initial states are considered: the isotropic states and the BES. Free and bound entanglement are, respectively, quantified with negativity and the realignment criterion, whereas environmental decoherence is evaluated using the von Neumann entropy. We further investigated the occurence of DSD.

We show that while decoherence is a monotonic increasing function of time with saturation value depending upon initial purity of the isotropic state, its maximum level is always achieved with time for bound entangled states, independently of the initial state parameter, hence being stronger in BES than isotropic ones. In the latter, the evolution profile under static noise is independent of the physical setup. For BES under non-Markovian noise, decoherence is stronger in “de” coupling than in “ce” coupling; meanwhile, the opposite is found under Markovian noise.

For isotropic states, both negativity and realignment criterion coincide, thus suggesting the complete absence of DSD. Non-Markovian environments lead to non-monotonic degradation of quantum entanglement with possible occurence of sudden death (SD) and revival (SR) phenomena depending on the noise spectrum. Specifically, SD and SR are observed only for the static noise model; meanwhile, for the non-Markovian dynamic environment, entanglement is a damped oscillating function of time, completely avoiding SD before vanishing with time. This is a specific feature of the two-qutrit system, since for the equivalent two-qubit model [32], SD are always present no matter the noise spectrum, thus suggesting the efficiency of the bipartite qutrit model over the qubit one.

Meanwhile, the Markovian RTN leads to a monotonic decaying profile of entanglement. Here, the relative weaker degradation of entanglement for greater values of initial purity ensures avoiding a long time complete disentanglement.

On the other hand, when the system is initially prepared in the BES, both free and bound entanglement decay abruptly going through ESD, no matter the noise regime, specifically in different environments coupling. It is worth mentioning that the physical setup and noise spectrum can serve as means of entanglement revival. Specifically few are observed for both negativity and realignment criterion for the system commonly coupled to a non-Markovian dynamic noise. However, negativity fails to detect bound entanglement; meanwhile, DSD phenomena are observed no matter the noise regime. But DSD can also be avoided depending on both the initial state parameter and the physical setup. Moreover, it is worth mentioning that the Hamiltonian here considered is of non-dissipative type, hence similar to the case of dissipative dynamical process [43, 51], we have found that certain free entangled qutrit–qutrit states also become bound entangled as a consequence of the interaction with the classical noises describes using a non-dissipative model. Finally, similar to the two-qubits model [32], a common environment coupling is more effective than different environments for free entanglement preservation under non-Markovian noise, while the opposite is found for Markovian ones. Meanwhile, bound entanglement may be insensitive to the physical setup.

Appendix: Explicit forms of the time-evolved states

We present the explicit forms of the various time-evolved states under the effects of the classical noise models considered, initially entangled in either state of Eqs. (5) and (6), and for both physical setups considered.

1.1 Static noise

1.1.1 Isotropic states

When the subsystems are initially entangled in isotropic states and subject to static noise, their density matrices from Eqs. (10) and (11) take the following form:

$$\begin{aligned}&\rho _{\text {de(ce)}}(p,t)\nonumber \\&\quad =\frac{1}{72}\left( \begin{array}{ccccccccc} \rho _{11}^{\text {de(ce)}} &{} \rho _{12}^{\text {de(ce)}} &{} \rho _{13}^{\text {de(ce)}} &{} \rho _{12}^{\text {de(ce)}} &{} \rho _{15}^{\text {de(ce)}} &{} \rho _{12}^{\text {de(ce)}} &{} \rho _{13}^{\text {de(ce)}} &{} \rho _{12}^{\text {de(ce)}} &{} \rho _{19}^{\text {de(ce)}}\\ -\rho _{12}^{\text {de(ce)}} &{} \rho _{22}^{\text {de(ce)}} &{} \rho _{23}^{\text {de(ce)}} &{} \rho _{24}^{\text {de(ce)}} &{} \rho _{25}^{\text {de(ce)}} &{} \rho _{24}^{\text {de(ce)}} &{} \rho _{23}^{\text {de(ce)}} &{} \rho _{24}^{\text {de(ce)}} &{} -\rho _{12}^{\text {de(ce)}}\\ \rho _{13}^{\text {de(ce)}} &{} -\rho _{23}^{\text {de(ce)}} &{} \rho _{33}^{\text {de(ce)}} &{} -\rho _{23}^{\text {de(ce)}} &{} \rho _{35}^{\text {de(ce)}} &{} -\rho _{23}^{\text {de(ce)}} &{} \rho _{37}^{\text {de(ce)}} &{} -\rho _{23}^{\text {de(ce)}} &{} \rho _{13}^{\text {de(ce)}}\\ -\rho _{12}^{\text {de(ce)}} &{} \rho _{24}^{\text {de(ce)}} &{} \rho _{23}^{\text {de(ce)}} &{} \rho _{22}^{\text {de(ce)}} &{} \rho _{25}^{\text {de(ce)}} &{} \rho _{24}^{\text {de(ce)}} &{} \rho _{23}^{\text {de(ce)}} &{} \rho _{24}^{\text {de(ce)}} &{} -\rho _{12}^{\text {de(ce)}}\\ \rho _{15}^{\text {de(ce)}} &{} -\rho _{25}^{\text {de(ce)}} &{} \rho _{35}^{\text {de(ce)}} &{} -\rho _{25}^{\text {de(ce)}} &{} \rho _{55}^{\text {de(ce)}} &{} -\rho _{25}^{\text {de(ce)}} &{} \rho _{35}^{\text {de(ce)}} &{} -\rho _{25}^{\text {de(ce)}} &{} \rho _{15}^{\text {de(ce)}}\\ -\rho _{12}^{\text {de(ce)}} &{} \rho _{24}^{\text {de(ce)}} &{} \rho _{23}^{\text {de(ce)}} &{} \rho _{24}^{\text {de(ce)}} &{} \rho _{25}^{\text {de(ce)}} &{} \rho _{22}^{\text {de(ce)}} &{} \rho _{23}^{\text {de(ce)}} &{} \rho _{24}^{\text {de(ce)}} &{} -\rho _{12}^{\text {de(ce)}}\\ \rho _{13}^{\text {de(ce)}} &{} -\rho _{23}^{\text {de(ce)}} &{} \rho _{37}^{\text {de(ce)}} &{} -\rho _{23}^{\text {de(ce)}} &{} \rho _{35}^{\text {de(ce)}} &{} -\rho _{23}^{\text {de(ce)}} &{} \rho _{33}^{\text {de(ce)}} &{} -\rho _{23}^{\text {de(ce)}} &{} \rho _{13}^{\text {de(ce)}}\\ -\rho _{12}^{\text {de(ce)}} &{} \rho _{24}^{\text {de(ce)}} &{} \rho _{23}^{\text {de(ce)}} &{} \rho _{24}^{\text {de(ce)}} &{} \rho _{25}^{\text {de(ce)}} &{} \rho _{24}^{\text {de(ce)}} &{} \rho _{23}^{\text {de(ce)}} &{} \rho _{22}^{\text {de(ce)}} &{} -\rho _{12}^{\text {de(ce)}}\\ \rho _{19}^{\text {de(ce)}} &{} \rho _{12}^{\text {de(ce)}} &{} \rho _{13}^{\text {de(ce)}} &{} \rho _{12}^{\text {de(ce)}} &{} \rho _{15}^{\text {de(ce)}} &{} \rho _{12}^{\text {de(ce)}} &{} \rho _{13}^{\text {de(ce)}} &{} \rho _{12}^{\text {de(ce)}} &{} \rho _{11}^{\text {de(ce)}} \end{array}\right) \nonumber \\ \end{aligned}$$

(15)

where

$$\begin{aligned} \rho _{11}^{\text {de(ce)}}= & {} \text {X}^{+};\quad \rho _{33}^{\text {de(ce)}}=\text {X}^{-}\quad \text {with}\quad \text {X}^{\pm }=8+p\left( 1\pm 12\alpha _{\text {de(ce)}}+3\xi _{\text {de(ce)}}\right) \\ \rho _{12}^{\text {de(ce)}}= & {} -\text {Y}^{+};\quad \rho _{23}^{\text {de(ce)}}=\text {Y}^{-}\quad \text {with}\quad \text {Y}^{\pm }=6ip\sqrt{2}\left( \Omega _{\text {de(ce)}}C_{2}(t)\pm \Pi _{\text {de(ce)}}\right) S_{2}(t)\\ \rho _{13}^{\text {de(ce)}}= & {} -\rho _{24}^{\text {de(ce)}}=3p\left( -1+\xi _{\text {de(ce)}}\right) ;\quad \rho _{22}^{\text {de(ce)}}=2\left( 4-p(1+3\xi _{\text {de(ce)}})\right) \\ \rho _{15}^{\text {de(ce)}}= & {} \text {B}^{+};\quad \rho _{35}^{\text {de(ce)}}=\text {B}^{-}\quad \text {with}\quad \text {B}^{\pm }=6p\left( 1\pm 2\alpha _{\text {de(ce)}}+\xi _{\text {de(ce)}}\right) \\ \rho _{19}^{\text {de(ce)}}= & {} \text {Z}^{+};\quad \rho _{37}^{\text {de(ce)}}=\text {Z}^{-}\quad \text {with}\quad \text {Z}^{\pm }=3p\left( 3\pm 4\alpha _{\text {de(ce)}}+\xi _{\text {de(ce)}}\right) \\ \rho _{25}^{\text {de(ce)}}= & {} 6ip\sqrt{2}\Omega _{\text {de(ce)}}S_{4}(t);\quad \rho _{55}^{\text {de(ce)}}=4\left( 2+p(1+3\xi _{\text {de(ce)}})\right) \end{aligned}$$

where

$$\begin{aligned} \alpha _{\text {de(ce)}}= & {} \Pi _{\text {de(ce)}}C_{2}(t);\quad \xi _{\text {de(ce)}}=\Omega _{\text {de(ce)}}C_{4}(t);\quad \Pi _{\text {de}}=K_{(1)}^{2};\quad \Pi _{\text {ce}}=K_{(2)};\\ \Omega _{\text {de}}= & {} K_{(2)}^{2};\quad \Omega _{\text {ce}}=K_{(4)}\\ \Pi _{\text {de}}= & {} K_{(1)}^{2};\quad \Pi _{\text {ce}}=K_{(2)};\quad \Omega _{\text {de}}=K_{(2)}^{2};\quad \Omega _{\text {ce}}=K_{(4)}\\ C_{n}(t)= & {} \cos (ngt\vartheta _{0});\quad S_{n}(t)=\sin (ngt\vartheta _{0});\\&K_{(n)}=\frac{2\sin (ngt\vartheta _{m}/2)}{ngt\vartheta _{m}},\quad n\in \left\{ 1,2,4\right\} \end{aligned}$$

1.1.2 Bound entangled states

When the subsystems are initially prepared in bound entangled states and then subject to a static noise, Eqs. (10) and (11) give:

$$\begin{aligned}&\rho _{\text {de(ce)}}(\alpha ,t)\nonumber \\&\quad =\frac{1}{2688}\left( \begin{array}{ccccccccc} s_{11}^{\text {de(ce)}} &{} s_{12}^{\text {de(ce)}} &{} s_{13}^{\text {de(ce)}} &{} s_{14}^{\text {de(ce)}} &{} s_{15}^{\text {de(ce)}} &{} s_{16}^{\text {de(ce)}} &{} s_{17}^{\text {de(ce)}} &{} s_{18}^{\text {de(ce)}} &{} s_{19}^{\text {de(ce)}}\\ -s_{12}^{\text {de(ce)}} &{} s_{22}^{\text {de(ce)}} &{} s_{23}^{\text {de(ce)}} &{} s_{24}^{\text {de(ce)}} &{} s_{25}^{\text {de(ce)}} &{} s_{26}^{\text {de(ce)}} &{} s_{27}^{\text {de(ce)}} &{} s_{28}^{\text {de(ce)}} &{} -s_{16}^{\text {de(ce)}}\\ s_{13}^{\text {de(ce)}} &{} -s_{23}^{\text {de(ce)}} &{} s_{33}^{\text {de(ce)}} &{} s_{34}^{\text {de(ce)}} &{} s_{35}^{\text {de(ce)}} &{} -s_{23}^{\text {de(ce)}} &{} s_{37}^{\text {de(ce)}} &{} s_{34}^{\text {de(ce)}} &{} s_{13}^{\text {de(ce)}}\\ -s_{14}^{\text {de(ce)}} &{} s_{24}^{\text {de(ce)}} &{} -s_{34}^{\text {de(ce)}} &{} s_{44}^{\text {de(ce)}} &{} s_{45}^{\text {de(ce)}} &{} s_{28}^{\text {de(ce)}} &{} s_{47}^{\text {de(ce)}} &{} s_{48}^{\text {de(ce)}} &{} -s_{18}^{\text {de(ce)}}\\ s_{15}^{\text {de(ce)}} &{} -s_{25}^{\text {de(ce)}} &{} s_{35}^{\text {de(ce)}} &{} -s_{45}^{\text {de(ce)}} &{} s_{55}^{\text {de(ce)}} &{} -s_{25}^{\text {de(ce)}} &{} s_{57}^{\text {de(ce)}} &{} -s_{45}^{\text {de(ce)}} &{} s_{15}^{\text {de(ce)}}\\ -s_{16}^{\text {de(ce)}} &{} s_{26}^{\text {de(ce)}} &{} s_{23}^{\text {de(ce)}} &{} s_{28}^{\text {de(ce)}} &{} s_{25}^{\text {de(ce)}} &{} s_{22}^{\text {de(ce)}} &{} s_{27}^{\text {de(ce)}} &{} s_{24}^{\text {de(ce)}} &{} -s_{12}^{\text {de(ce)}}\\ s_{17}^{\text {de(ce)}} &{} -s_{27}^{\text {de(ce)}} &{} s_{37}^{\text {de(ce)}} &{} -s_{47}^{\text {de(ce)}} &{} s_{57}^{\text {de(ce)}} &{} -s_{27}^{\text {de(ce)}} &{} s_{77}^{\text {de(ce)}} &{} -s_{47}^{\text {de(ce)}} &{} s_{17}^{\text {de(ce)}}\\ -s_{18}^{\text {de(ce)}} &{} s_{28}^{\text {de(ce)}} &{} -s_{34}^{\text {de(ce)}} &{} s_{48}^{\text {de(ce)}} &{} s_{45}^{\text {de(ce)}} &{} s_{24}^{\text {de(ce)}} &{} s_{47}^{\text {de(ce)}} &{} s_{44}^{\text {de(ce)}} &{} -s_{14}^{\text {de(ce)}}\\ s_{19}^{\text {de(ce)}} &{} s_{16}^{\text {de(ce)}} &{} s_{13}^{\text {de(ce)}} &{} s_{18}^{\text {de(ce)}} &{} s_{15}^{\text {de(ce)}} &{} s_{12}^{\text {de(ce)}} &{} s_{17}^{\text {de(ce)}} &{} s_{14}^{\text {de(ce)}} &{} s_{11}^{\text {de(ce)}} \end{array}\right) \nonumber \\ \end{aligned}$$

(16)

with

$$\begin{aligned} s_{11}^{\text {de}}= & {} 306-80\Pi _{\text {de}}+C_{2}(t)\left( -20\Pi _{\text {ce}}+48\Pi _{\text {de}}\right) +\left( -15+17C_{4}(t)\right) \Omega _{\text {de}}\\ s_{15}^{\text {de}}= & {} 64+8\Pi _{\text {de}}\left( 5+11C_{2}(t)\right) +2\Omega _{\text {de}}\left( 15+17C_{4}(t)\right) \\ s_{24}^{\text {de}}= & {} 64+40\Pi _{\text {de}}\left( -1+C_{2}(t)\right) -2\Omega _{\text {de}}\left( 15+17C_{4}(t)\right) \\ s_{25}^{\text {de}}= & {} -8i\sqrt{2}S_{1}\left( \Pi _{\text {ce}}C_{1}(t)\left( 5-17\Pi _{\text {ce}}C_{2}(t)\right) -(1+3C_{2}(t)\Pi _{\text {ce}})y_{1}(\alpha )\right) \\ s_{28}^{\text {de}}= & {} 44-40\Pi _{\text {ce}}C_{2}(t)+2\Omega _{\text {de}}\left( 15-17C_{4}(t)\right) \\ s_{45}^{\text {de}}= & {} 4i\sqrt{2}S_{1}(t)\left( -10\Pi _{\text {ce}}C_{1}(t)+17\Omega _{\text {de}}\left( C_{1}(t)+C_{3}(t)\right) -2(1+3\Pi _{\text {ce}}C_{2}(t))y_{1}(\alpha )\right) \\ s_{55}^{\text {de}}= & {} 328-80\Pi _{\text {ce}}C_{2}(t)+4\Omega _{\text {de}}\left( -15+17C_{4}(t)\right) \\ s_{12}^{\text {de}}= & {} \text {A}_{\text {de}}^{+};\quad s_{14}^{\text {de}}=\text {A}_{\text {de}}^{-};\quad s_{16}^{\text {de}}=\text {B}_{\text {de}}^{+};\quad s_{34}^{\text {de}}=\text {B}_{\text {de}}^{-};\quad s_{18}^{\text {de}}=\text {D}_{\text {de}}^{+};\quad s_{27}^{\text {de}}=-\text {D}_{\text {de}}^{-};\\ s_{35}^{\text {de}}= & {} \text {E}_{\text {de}}^{-}\\ s_{57}^{\text {de}}= & {} \text {E}_{\text {de}}^{+};\quad s_{19}^{\text {de}}=\text {F}_{\text {de}}^{+};\quad s_{37}^{\text {de}}=\text {F}_{\text {de}}^{-};\quad s_{33}^{\text {de}}=\text {G}_{\text {de}}^{+};\quad s_{77}^{\text {de}}=\text {G}_{\text {de}}^{-};\quad s_{26}^{\text {de}}=\text {H}_{\text {de}}^{+};\\ s_{48}^{\text {de}}= & {} \text {H}_{\text {de}}^{-}\\ s_{13}^{\text {de}}= & {} \text {I}_{\text {de}}^{+};\quad s_{17}^{\text {de}}=\text {I}_{\text {de}}^{-};\quad s_{22}^{\text {de}}=\text {J}_{\text {de}}^{-};\quad s_{44}^{\text {de}}=\text {J}_{\text {de}}^{+};\quad s_{23}^{\text {de}}=\text {L}_{\text {de}}^{+};\quad s_{47}^{\text {de}}=\text {L}_{\text {de}}^{-} \end{aligned}$$

with

$$\begin{aligned} \text {A}_{\text {de}}^{\pm }= & {} i\sqrt{2}\left( -17S_{4}(t)\Omega _{\text {de}}+2S_{2}(t)\left( 5\Pi _{\text {ce}}-12\Pi _{\text {de}}\right) \right. \\&\left. \pm \,2\left( -2S_{1}(t)+3\left( 3S_{1}(t)+S_{3}(t)\right) \Pi _{\text {ce}}\right) y_{1}(\alpha )\right) \\ \text {B}_{\text {de}}^{\pm }= & {} -i\sqrt{2}\left( 17S_{4}(t)\Omega _{\text {de}}+S_{2}(t)\left( 30\Pi _{\text {ce}}\pm 64\Pi _{\text {de}}\right) \right. \\&\left. -\,6\left( -S_{3}\Pi _{\text {ce}}+S_{1}(2+\Pi _{\text {ce}})\right) y_{1}(\alpha )\right) \\ \text {D}_{\text {de}}^{\pm }= & {} -2i\sqrt{2}S_{1}(t)\left( C_{1}(t)\left( \Pi _{\text {ce}}(30+17\Pi _{\text {ce}})\pm 64\Pi _{\text {de}}\right) +17C_{3}(t)\Omega _{\text {de}}\right. \\&\left. -\,6\left( -1+C_{2}\Pi _{\text {ce}}\right) y_{1}(\alpha )\right) \\ \text {E}_{\text {de}}^{\pm }= & {} 64-8\left( 5+11C_{2}\right) \Pi _{\text {de}}+\left( 30+34C_{4}\right) \Omega _{\text {de}}\pm 24\left( C_{1}-C_{3}\right) \Pi _{\text {ce}}y_{1}(\alpha )\\ \text {F}_{\text {de}}^{\pm }= & {} 66+4C_{2}(t)\left( 15\Pi _{\text {ce}}\pm 32\Pi _{\text {de}}\right) +\left( -15+17C_{4}(t)\right) \Omega _{\text {de}}\\ \text {G}_{\text {de}}^{\pm }= & {} 306+80\Pi _{\text {de}}-4C_{2}\left( 5\Pi _{\text {ce}}+12\Pi _{\text {de}}\right) +\left( -15+17C_{4}\right) \Omega _{\text {de}}\\&\pm \,8\left( 2C_{1}+3(C_{1}+C_{3})\Pi _{\text {ce}}\right) y_{1}(\alpha )\\ \text {H}_{\text {de}}^{\pm }= & {} 64-40\left( -1+C_{2}(t)\right) \Pi _{\text {de}}-2\left( 15+17C_{4}(t)\right) \Omega _{\text {de}}\\&\pm \,24\left( C_{1}(t)-C_{3}(t)\right) \Pi _{\text {ce}}y_{1}(\alpha )\\ \text {I}_{\text {de}}^{\pm }= & {} -22+20\Pi _{\text {ce}}C_{2}(t)-\Omega _{\text {de}}\left( 15-17C_{4}(t)\right) \\&\pm \,12\left( -2C_{1}(t)+\left( C_{1}(t)+C_{3}(t)\right) \Pi _{\text {ce}}\right) y_{1}(\alpha )\\ \text {J}_{\text {de}}^{\pm }= & {} 2\left( 142+20\Pi _{\text {ce}}C_{2}(t)-17\Omega _{\text {de}}C_{4}(t)+15\Omega _{\text {de}}\right. \\&\left. \pm \,4\left( 2C_{1}(t)+3\Pi _{\text {ce}}\left( C_{1}(t)+C_{3}(t)\right) \right) y_{1}(\alpha )\right) \\ \text {L}_{\text {de}}^{\pm }= & {} i\sqrt{2}\left( 17S_{4}(t)\Omega _{\text {de}}-2S_{2}(t)(5\Pi _{\text {ce}}+12\Pi _{\text {de}})\right. \\&\left. \pm \,2\left( 2S_{1}(t)+3\left( S_{1}(t)+3S_{3}(t)\right) \Pi _{\text {ce}}\right) y_{1}(\alpha )\right) \end{aligned}$$

where

$$\begin{aligned} y_{1}(\alpha )= & {} K_{(1)}(5-2\alpha )\\ y_{3}(\alpha )= & {} K_{(3)}(5-2\alpha ) \end{aligned}$$

and

$$\begin{aligned} s_{11}^{\text {ce}}= & {} 211+28\Pi _{\text {ce}}C_{2}(t)+17\Omega _{\text {ce}}C_{4}(t);\quad s_{15}^{\text {ce}}=2\left( 67+44\Pi _{\text {ce}}C_{2}(t)+17\Omega _{\text {ce}}C_{4}(t)\right) \\ s_{19}^{\text {ce}}= & {} 51+188\Pi _{\text {ce}}C_{2}(t)+17\Omega _{\text {ce}}C_{4}(t);\quad s_{24}^{\text {ce}}=-3+20\Pi _{\text {ce}}C_{2}(t)-17\Omega _{\text {ce}}C_{4}(t)\\ s_{28}^{\text {ce}}= & {} 2\left( 37-20\Pi _{\text {ce}}C_{2}(t)-17\Omega _{\text {ce}}C_{4}(t)\right) ;\quad s_{37}^{\text {ce}}=17\left( 3-4\Pi _{\text {ce}}C_{2}(t)+\Omega _{\text {ce}}C_{4}(t)\right) \\ s_{55}^{\text {ce}}= & {} 4\left( 67-20\Pi _{\text {ce}}C_{2}(t)+17\Omega _{\text {ce}}C_{4}(t)\right) ;\quad s_{12}^{\text {ce}}=\text {A}_{ce}^{+};\quad s_{14}^{\text {ce}}=\text {A}_{\text {ce}}^{-}\\ s_{16}^{\text {ce}}= & {} \text {B}_{\text {ce}}^{-};\quad s_{18}^{\text {ce}}=\text {B}_{\text {ce}}^{+};\quad s_{13}^{\text {ce}}=\text {D}_{\text {ce}}^{-};\quad s_{17}^{\text {ce}}=\text {D}_{\text {ce}}^{+};\quad s_{27}^{\text {ce}}=\text {E}_{\text {ce}}^{-};\quad s_{34}^{\text {ce}}=-\text {E}_{\text {ce}}^{+};\\ s_{22}^{\text {ce}}= & {} \text {F}_{\text {ce}}^{-};\quad s_{44}^{\text {ce}}=\text {F}_{\text {ce}}^{+};\quad s_{33}^{\text {ce}}=\text {G}_{\text {ce}}^{+};\quad s_{77}^{\text {ce}}=\text {G}_{\text {ce}}^{-};\quad s_{23}^{\text {ce}}=\text {H}_{\text {ce}}^{-};\quad s_{47}^{\text {ce}}=\text {H}_{\text {ce}}^{+};\\ s_{26}^{\text {ce}}= & {} \text {I}_{\text {ce}}^{+};\quad s_{48}^{\text {ce}}=\text {I}_{\text {ce}}^{-};\quad s_{35}^{\text {ce}}=\text {J}_{\text {ce}}^{-};\quad s_{57}^{\text {ce}}=\text {J}_{\text {ce}}^{+};\quad s_{35}^{\text {ce}}=\text {L}_{\text {ce}}^{-};\quad s_{57}^{\text {ce}}=\text {L}_{\text {ce}}^{+} \end{aligned}$$

with

$$\begin{aligned} \text {A}_{\text {ce}}^{\pm }= & {} -i\sqrt{2}\left( 14\Pi _{\text {ce}}S_{2}(t)+17\Omega _{\text {ce}}S_{4}(t)\pm 2\left( 7y_{1}(\alpha )S_{1}(t)+3S_{3}(t)y_{3}(\alpha )\right) \right) \\ \text {B}_{\text {ce}}^{\pm }= & {} -i\sqrt{2}\left( 94\Pi _{\text {ce}}S_{2}(t)+17\Omega _{\text {ce}}S_{4}(t)\pm \left( 18y_{1}(\alpha )S_{1}(t)-6S_{3}(t)y_{3}(\alpha )\right) \right) \\ \text {D}_{\text {ce}}^{\pm }= & {} -37+20\Pi _{\text {ce}}C_{2}(t)+17\Omega _{\text {ce}}S_{4}(t)\pm 12\left( C_{1}(t)y_{1}(\alpha )-C_{3}(t)y_{3}(\alpha )\right) \\ \text {E}_{\text {ce}}^{\pm }= & {} -i\sqrt{2}\left( 34\Pi _{\text {ce}}S_{2}(t)-17\Omega _{\text {ce}}S_{4}(t)\pm 6\left( 3y_{1}(\alpha )S_{1}(t)-S_{3}(t)y_{3}(\alpha )\right) \right) \\ \text {F}_{\text {ce}}^{\pm }= & {} 314+40\Pi _{\text {ce}}C_{2}(t)-34\Omega _{\text {ce}}C_{4}(t)\pm 8\left( 5C_{1}(t)y_{1}(\alpha )+3C_{3}(t)y_{3}(\alpha )\right) \\ \text {G}_{\text {ce}}^{\pm }= & {} 371-68\Pi _{\text {ce}}C_{2}(t)+17\Omega _{\text {ce}}C_{4}(t)\pm 8\left( 5C_{1}(t)y_{1}(\alpha )+3C_{3}(t)y_{3}(\alpha )\right) \\ \text {H}_{\text {ce}}^{\pm }= & {} -i\sqrt{2}\left( 34\Pi _{\text {ce}}S_{2}(t)-17\Omega _{\text {ce}}S_{4}(t)\pm 2\left( 5y_{1}(\alpha )S_{1}(t)+9S_{3}(t)y_{3}(\alpha )\right) \right) \\ \text {I}_{\text {ce}}^{\pm }= & {} 74-40\Pi _{\text {ce}}C_{2}(t)-34\Omega _{\text {ce}}C_{4}(t)\pm 24\left( C_{1}(t)y_{1}(\alpha )-C_{3}(t)y_{3}(\alpha )\right) \\ \text {J}_{\text {ce}}^{\pm }= & {} 54-88\Pi _{\text {ce}}C_{2}(t)+34\Omega _{\text {ce}}C_{4}(t)\pm 24\left( C_{1}(t)y_{1}(\alpha )-C_{3}(t)y_{3}(\alpha )\right) \\ \text {L}_{\text {ce}}^{\pm }= & {} 2i\sqrt{2}\left( -10\Pi _{\text {ce}}S_{2}(t)+17\Omega _{\text {ce}}S_{4}(t)\pm 2\left( y_{1}(\alpha )S_{1}(t)-3S_{3}(t)y_{3}(\alpha )\right) \right) \end{aligned}$$

1.2 Dynamic noise

1.2.1 Isotropic states

For the dynamic noise model, when the system is initially prepared in state of Eq. (5), density matrices from Eq. (12) take the following form:

$$\begin{aligned}&\rho _{\text {de(ce)}}(t)\nonumber \\&\quad =\frac{1}{72}\left( \begin{array}{ccccccccc} A_{\text {de(ce)}}^{+} &{} 0 &{} B_{\text {de(ce)}} &{} 0 &{} C_{\text {de(ce)}}^{+} &{} 0 &{} B_{\text {de(ce)}} &{} 0 &{} D_{\text {de(ce)}}^{+}\\ 0 &{} E_{\text {de(ce)}} &{} 0 &{} -2B_{\text {de(ce)}} &{} 0 &{} -2B_{\text {de(ce)}} &{} 0 &{} -2B_{\text {de(ce)}} &{} 0\\ B_{\text {de(ce)}} &{} 0 &{} A_{\text {de(ce)}}^{-} &{} 0 &{} C_{\text {de(ce)}}^{-} &{} 0 &{} D_{\text {de(ce)}}^{-} &{} 0 &{} B_{\text {de(ce)}}\\ 0 &{} -2B_{\text {de(ce)}} &{} 0 &{} E_{\text {de(ce)}} &{} 0 &{} -2B_{\text {de(ce)}} &{} 0 &{} -2B_{\text {de(ce)}} &{} 0\\ C_{\text {de(ce)}}^{+} &{} 0 &{} C_{\text {de(ce)}}^{-} &{} 0 &{} F_{\text {de(ce)}} &{} 0 &{} C_{\text {de(ce)}}^{-} &{} 0 &{} C_{\text {de(ce)}}^{+}\\ 0 &{} -2B_{\text {de(ce)}} &{} 0 &{} -2B_{\text {de(ce)}} &{} 0 &{} E_{\text {de(ce)}} &{} 0 &{} -2B_{\text {de(ce)}} &{} 0\\ B_{\text {de(ce)}} &{} 0 &{} D_{\text {de(ce)}}^{-} &{} 0 &{} C_{\text {de(ce)}}^{-} &{} 0 &{} A_{\text {de(ce)}}^{-} &{} 0 &{} B_{\text {de(ce)}}\\ 0 &{} -2B_{\text {de(ce)}} &{} 0 &{} -2B_{\text {de(ce)}} &{} 0 &{} -2B_{\text {de(ce)}} &{} 0 &{} E_{\text {de(ce)}} &{} 0\\ D_{\text {de(ce)}}^{+} &{} 0 &{} B_{\text {de(ce)}} &{} 0 &{} C_{\text {de(ce)}}^{+} &{} 0 &{} B_{\text {de(ce)}} &{} 0 &{} A_{\text {de(ce)}}^{+} \end{array}\right) \nonumber \\ \end{aligned}$$

(17)

where

$$\begin{aligned} A_{\text {de(ce)}}^{\pm }= & {} 8+p\left( 1\pm 12\Phi _{\text {de(ce)}}+3\Psi _{\text {de(ce)}}\right) \\ B_{\text {de(ce)}}= & {} 3p\left( \Psi _{\text {de(ce)}}-1\right) \\ C_{\text {de(ce)}}^{\pm }= & {} 6p\left( 1\pm 2\Phi _{\text {de(ce)}}+\Psi _{\text {de(ce)}}\right) \\ D_{\text {de(ce)}}^{\pm }= & {} 3p\left( 3\pm 4\Phi _{\text {de(ce)}}+\Psi _{\text {de(ce)}}\right) \\ E_{\text {de(ce)}}= & {} 2\left( 4-p(1+3\Psi _{\text {de(ce)}})\right) \\ F_{\text {de(ce)}}= & {} 4\left( 2+p\left( 1+3\Psi _{\text {de(ce)}}\right) \right) \\ \Phi _{\text {de}}= & {} \Gamma _{1}^{2}(t);\quad \Psi _{\text {de}}=\Gamma _{2}^{2}(t);\quad \Phi _{\text {ce}}=\Gamma _{2}(t);\quad \Psi _{\text {ce}}=\Gamma _{4}(t). \end{aligned}$$

1.2.2 Bound entangled states

Here Eq. (12) gives:

$$\begin{aligned} \tilde{\rho }_{\text {de}}(t)= & {} \frac{1}{1344}\left( \begin{array}{ccccccccc} A_{1} &{} 0 &{} B_{1}^{-} &{} 0 &{} C_{1} &{} 0 &{} B_{1}^{+} &{} 0 &{} D_{1}^{+}\\ 0 &{} E_{1}^{+} &{} 0 &{} F_{1} &{} 0 &{} F_{1} &{} 0 &{} G_{1} &{} 0\\ B_{1}^{-} &{} 0 &{} H_{1}^{-} &{} 0 &{} J_{1} &{} 0 &{} D_{1}^{-} &{} 0 &{} B_{1}^{-}\\ 0 &{} F_{1} &{} 0 &{} E_{1}^{-} &{} 0 &{} G_{1} &{} 0 &{} F_{1} &{} 0\\ C_{1} &{} 0 &{} J_{1} &{} 0 &{} K_{1} &{} 0 &{} J_{1} &{} 0 &{} C_{1}\\ 0 &{} F_{1} &{} 0 &{} G_{1} &{} 0 &{} E_{1}^{+} &{} 0 &{} F_{1} &{} 0\\ B_{1}^{+} &{} 0 &{} D_{1}^{-} &{} 0 &{} J_{1} &{} 0 &{} H_{1}^{+} &{} 0 &{} B_{1}^{+}\\ 0 &{} G_{1} &{} 0 &{} F_{1} &{} 0 &{} F_{1} &{} 0 &{} E_{1}^{-} &{} 0\\ D_{1}^{+} &{} 0 &{} B_{1}^{-} &{} 0 &{} C_{1} &{} 0 &{} B_{1}^{+} &{} 0 &{} A_{1} \end{array}\right) \end{aligned}$$

(18)

$$\begin{aligned} \tilde{\rho }_{\text {ce}}(t)= & {} \frac{1}{2688}\left( \begin{array}{ccccccccc} A_{2} &{} 0 &{} B_{2}^{+} &{} 0 &{} C_{2} &{} 0 &{} B_{2}^{-} &{} 0 &{} D_{2}\\ 0 &{} E_{2}^{+} &{} 0 &{} F_{2} &{} 0 &{} -B_{2}^{+} &{} 0 &{} H_{2} &{} 0\\ B_{2}^{+} &{} 0 &{} I_{2}^{-} &{} 0 &{} J_{2}^{+} &{} 0 &{} K_{2} &{} 0 &{} B_{2}^{+}\\ 0 &{} F_{2} &{} 0 &{} E_{2}^{-} &{} 0 &{} H_{2} &{} 0 &{} -B_{2}^{-} &{} 0\\ C_{2} &{} 0 &{} J_{2}^{+} &{} 0 &{} L_{2} &{} 0 &{} J_{2}^{-} &{} 0 &{} C_{2}\\ 0 &{} -B_{2}^{+} &{} 0 &{} H_{2} &{} 0 &{} E_{2}^{+} &{} 0 &{} F_{2} &{} 0\\ B_{2}^{-} &{} 0 &{} K_{2} &{} 0 &{} J_{2}^{-} &{} 0 &{} I_{2}^{+} &{} 0 &{} B_{2}^{-}\\ 0 &{} H_{2} &{} 0 &{} -B_{2}^{-} &{} 0 &{} F_{2} &{} 0 &{} E_{2}^{-} &{} 0\\ D_{2} &{} 0 &{} B_{2}^{+} &{} 0 &{} C_{2} &{} 0 &{} B_{2}^{-} &{} 0 &{} A_{2} \end{array}\right) \end{aligned}$$

(19)

where

$$\begin{aligned} A_{1}= & {} 153-16\Phi _{\text {de}}-(10-\Phi _{\text {ce}})\Phi _{\text {ce}}\\ B_{1}^{\pm }= & {} \left( -1+\Phi _{\text {ce}}\right) \left( 11+\Phi _{\text {ce}}\pm 12f(\alpha )\Gamma _{1}(t)\right) \\ C_{1}= & {} 32\left( 1+2\Phi _{\text {de}}+\Psi _{\text {de}}\right) \\ D_{1}^{\pm }= & {} 33\pm 64\Phi _{\text {de}}+\Phi _{\text {ce}}\left( 30+\Phi _{\text {ce}}\right) \\ E_{1}^{\pm }= & {} 2\left( 71+\left( 10-\Phi _{\text {ce}}\right) \Phi _{\text {ce}}\pm 4\Gamma _{1}(t)\left( 1+3\Phi _{\text {ce}}\right) f(\alpha )\right) \\ F_{1}= & {} 64\left( 1-\Psi _{\text {de}}\right) \\ G_{1}= & {} 2\left( 1-\Phi _{\text {ce}}\right) \left( 11+\Phi _{\text {ce}}\right) \\ H_{1}^{\pm }= & {} 153+16\Phi _{\text {de}}-\left( 10-\Phi _{\text {ce}}\right) \Phi _{\text {ce}}\pm 8\Gamma _{1}(t)\left( 1+3\Phi _{\text {ce}}\right) f(\alpha )\\ J_{1}= & {} 32\left( 1-2\Phi _{\text {de}}+\Psi _{\text {de}}\right) \\ K_{1}= & {} 4\left( 41-(10-\Phi _{\text {ce}})\Phi _{\text {ce}}\right) \end{aligned}$$

and

$$\begin{aligned} A_{2}= & {} 211+28\Phi _{\text {ce}}+17\Psi _{\text {ce}}\\ B_{2}^{\pm }= & {} -37+20\Phi _{\text {ce}}+17\Psi _{\text {ce}}\pm 12\left( \Gamma _{1}(t)-\Gamma _{3}(t)\right) f(\alpha )\\ C_{2}= & {} 2\left( 67+44\Phi _{\text {ce}}+17\Psi _{\text {ce}}\right) \\ D_{2}= & {} 188\Phi _{\text {ce}}+17\left( 3+\Psi _{\text {ce}}\right) \\ E_{2}^{\pm }= & {} 2\left( 157+20\Phi _{\text {ce}}-17\Psi _{\text {ce}}\pm 4\left( 3\Gamma _{3}(t)+5\Gamma _{1}(t)\right) f(\alpha )\right) \\ F_{2}= & {} 2\left( -3+20\Phi _{\text {ce}}-17\Psi _{\text {ce}}\right) \\ H_{2}= & {} 2\left( 37-20\Phi _{\text {ce}}-17\Psi _{\text {ce}}\right) \\ I_{2}^{\pm }= & {} 371-68\Phi _{\text {ce}}+17\Psi _{\text {ce}}\pm 8\left( 5\Gamma _{1}(t)+3\Gamma _{3}(t)\right) f(\alpha )\\ J_{2}^{\pm }= & {} 2\left( 27-44\Phi _{\text {ce}}+17\Psi _{\text {ce}}\pm 12\left( \Gamma _{1}(t)-\Gamma _{3}(t)\right) f(\alpha )\right) \\ K_{2}= & {} 17\left( 3-4\Phi _{\text {ce}}+\Psi _{\text {ce}}\right) \\ L_{2}= & {} 4\left( 67-20\Phi _{\text {ce}}+17\Psi _{\text {ce}}\right) \end{aligned}$$

with

$$\begin{aligned} f(\alpha )=-5+2\alpha . \end{aligned}$$