Soliton solutions and traveling wave solutions of the two-dimensional generalized nonlinear Schrödinger equations

Abstract

In this paper, the two-dimensional generalized nonlinear Schrödinger equations are introduced with the Lax pair. The existence of the Lax pair defines integrability for the partial differential equation, so the two-dimensional generalized nonlinear Schrödinger equations are integrable. Related to this development was the understanding that certain coherent structures called solitons play a basic role in nonlinear phenomena as fluid mechanics, nonlinear optics relativity, and lattice dynamics. Via the Hirota bilinear method, bilinear forms of the two-dimensional generalized nonlinear Schrödinger equations are obtained. Based on which one- and two-soliton solutions are derived. Furthermore, to find traveling wave solutions the extended tanh method is applied. Through 2D and 3D plots, the dynamical behavior of the obtained solutions is studied. The generalized form of the nonlinear Schrödinger equations has a mathematical and physical interest because a fundamental model in the field of nonlinear science. The used methods are quite useful in the solution of nonlinear partial differential equations.

1 Introduction

The investigation of nonlinear evolution equations is the main area of research in the field of nonlinear dynamics. One of the nonlinear equations is the nonlinear Schrödinger (NLS) equation which arises from a wide variety of fields, such as weakly nonlinear dispersive water waves, quantum field theory and nonlinear optics [1,2,3,4]. Different modifications and generalizations of the NLS equations were proposed and studied [5,6,7,8,9,10,11]. There are various methods to study nonlinear equations, such as the Darboux transformation [12,13,14,15,16], the Hirota method [17,18,19,20,21], the sine-cosine [22, 23], the extended tanh method [24,25,26], and so on. In two-dimension, the generalized form of the NLS equation has a mathematical and physical interest because it is nonlinear partial differential equation and describes many physical phenomena such as nonlinear optical fibers, Bose–Einstein condensates, and water waves. As a coupled system, a one-dimensional generalized nonlinear Schrödinger (GNLS) equation with Maxwell–Bloch system was studied in [27, 28].

In this work, by Lax pair we introduce a generalization of the two-dimensional NLS equation with additional parameters as $\alpha$ that denotes the amplification or absorption and $\beta$ that relates to dispersion. The obtained two-dimensional GNLS system of equations is

$$\begin{aligned} iq_{t}+q_{xy}-vq+\alpha q-i\beta q_x= & {} 0, \end{aligned}$$

(1)

$$\begin{aligned} v_{x}+2(|q|^2)_{y}= & {} 0, \end{aligned}$$

(2)

where q is complex function, v is real function, $\alpha$ and $\beta$ are the constants, the subscripts denote the partial derivatives with respect to the variables x, y, t. The equations (1)-(2) admit next reductions: if $\alpha =0,\beta =0$, we can obtain the two-dimensional nonlinear Schrödinger equations [29], if $x=y, \alpha =0,\beta =0$, we can get the one-dimensional nonlinear Schrödinger equation [2,3,4].

The aim of this paper is to find some new solutions of Eqs. (1)–(2). We apply Hirota’s bilinear method and obtain the bilinear form of the two-dimensional GNLS system of equations. One soliton and two soliton solutions are constructed based on the obtained bilinear form. We derive traveling wave solutions using the extended tanh-method that provides wider applicability for handling nonlinear wave equations. The figures have been plotted to analyze the dynamical features of obtained solutions.

The article is organized as follows. In Sect. 2, we present the Lax pair for the two-dimensional GNLS system of Eqs. (1)–(2). In Sect. 3, the Hirota bilinear method is applied to obtain soliton solutions for two-dimensional GNLS system of equations. In Sect. 4, we obtain traveling wave solution by the extended tanh method. In Sect. 5, we summarize the results of our study.

2 Lax pair

The Lax pair provides the complete integrability of the nonlinear equation [2, 3]. In this section, we present the Lax pair for Eqs. (1)–(2) that can be expressed as follows:

$$\begin{aligned} \varPsi _{x}= & {} U\varPsi , \end{aligned}$$

(3)

$$\begin{aligned} \varPsi _{t}= & {} 2\lambda \varPsi _y+V\varPsi , \end{aligned}$$

(4)

where $\varPsi =(\varPsi _1,\varPsi _2)^T$ (T denotes the transpose of a matrix), $\lambda$ is a spectral parameter and the matrices U and V have the form

$$\begin{aligned} U= & {} \left( \begin{array}{lll} -i\lambda &{}\quad q\\ -q^*&{}\quad i\lambda \end{array}\right) , \end{aligned}$$

(5)

$$\begin{aligned} V= & {} \left( \begin{array}{lll} -\lambda i \beta -\frac{iv}{2}+\frac{i\alpha }{2}&{}\quad iq_y+\beta q\\ iq^*_y-\beta q^*&{}\quad \lambda i \beta +\frac{iv}{2}-\frac{i\alpha }{2} \end{array}\right) . \end{aligned}$$

(6)

Through direct computations, it can be verified that the compatibility condition (also known as a zero-curvature condition):

$$\begin{aligned} U_t-V_x-2\lambda U_y+UV-VU=0, \end{aligned}$$

(7)

exactly gives rise to

$$\begin{aligned} iq_{t}+q_{xy}-vq+\alpha q-i\beta q_x= & {} 0, \\ iq^*_{t}-q^*_{xy}+vq^*-\alpha q^*-i\beta q^*_x= & {} 0,\\ v_{x}+2|q|^2_{y}= & {} 0. \end{aligned}$$

The above-coupled system can give two-dimensional GNLS Eqs. (1)–(2).

3 Soliton solutions

In order to obtain soliton solutions for the two-dimensional GNLS system of equations, we apply Hirota’s bilinear method. The method was suggested by Hirota [17, 19]. This approach provides a direct method for finding N-soliton solutions to nonlinear evolutionary equations. The stages of the method are described in the next section.

3.1 Description of Hirota’s bilinear method

The basic idea in Hirota’s bilinear method is as follows [3, 17, 19, 24]:

Bilinearization. At this stage, a dependent variable transformation is introduced. The transformation ought to reduce the nonlinear equation to the bilinear equation, which is quadratic in the dependent variables.

Transformation to the Hirota bilinear form. Hirota suggests the D-operator defined by

$$\begin{aligned} D^{l}_{x}D^{m}_{y}D^{n}_{t}(g\cdot f)= & {} \left( \frac{\partial }{\partial x}-\frac{\partial }{\partial x'}\right) ^l\left( \frac{\partial }{\partial y}-\frac{\partial }{\partial y'}\right) ^m \nonumber \\&\times \left( \frac{\partial }{\partial t}-\frac{\partial }{\partial t'}\right) ^n g(x,y,t)\cdot f(x',y',t')|_{x'=x,y'=y,t'=t} \end{aligned}$$

(8)

with $x',y'$ and $t'$ as three formal variables, g(x, y, t) and $f(x',y',t')$ being two functions, l, m and n being three nonnegative integers. The operator (8) rewrites the bilinear equation in terms of the D operator as a combination of variable coefficient bilinear equations.

Using the Hirota perturbation. Formal perturbation expansion into this bilinear equation is introduced. This expansion is truncated in the case of soliton solutions. To prove that the suggested soliton form is indeed correct, we use mathematical induction.

3.2 Application

Bilinear form

The two-dimensional GNLS system of Eqs. (1)–(2) can be rewritten as

$$\begin{aligned} {[}iD_t+D_xD_y+\alpha -i\beta D_x](g\cdot f)= & {} 0, \end{aligned}$$

(9)

$$\begin{aligned} D_xD_y (f\cdot f)+2D_{y}(h\cdot f)= & {} 0, \end{aligned}$$

(10)

$$\begin{aligned} D_x(h\cdot f)+|g|^2= & {} 0, \end{aligned}$$

(11)

with the dependent variable transformations

$$\begin{aligned} q= & {} \frac{g}{f}, \end{aligned}$$

(12)

$$\begin{aligned} v= & {} 2\left( \frac{h}{f}\right) _y, \end{aligned}$$

(13)

where g is the complex function of x, y and t, f, h-are real ones, $D_x$, $D_y$ and $D_t$ are the bilinear differential operators defined by (8).

To obtain the soliton solutions of Eqs. (9)–(11), we expand g, f, h with respect to a small parameter $\epsilon$ as follows:

$$\begin{aligned} g(x,y,t)= & {} \epsilon g_{1}(x,y,t)+\epsilon ^3 g_{3}(x,y,t)+\ldots , \end{aligned}$$

(14)

$$\begin{aligned} f(x,y,t)= & {} 1+\epsilon ^2 f_2(x,y,t)+\epsilon ^4 f_4(x,y,t)+..., \end{aligned}$$

(15)

$$\begin{aligned} h(x,y,t)= & {} 1+\epsilon ^2 h_{2}(x,y,t)+\epsilon ^4 h_4(x,y,t)+..., \end{aligned}$$

(16)

where $g_j$, $(j=1,3,5,...)$ are the complex functions of x, y and t, and $f_n,h_n$, $(n=2,4,6,...)$ are the real ones. Substituting expression (14)–(16) into (9)–(11) and collecting the coefficients of the same power of $\epsilon$, we have from Eq. (9)

$$\begin{aligned}&\epsilon ^1 : [iD_t+D_xD_y+\alpha -i\beta D_x](g_{1} \cdot 1)=0, \\&\epsilon ^3 :[iD_t+D_xD_y+\alpha -i\beta D_x](g_{3}\cdot 1+g_{1}\cdot f_{2})=0, \\&\epsilon ^5 :[iD_t+D_xD_y+\alpha -i\beta D_x](g_{5}\cdot 1+g_{1}\cdot f_{2}+g_{1}\cdot f_{4})=0,\\&\epsilon ^7 : [iD_t+D_xD_y+\alpha -i\beta D_x](g_{5}\cdot f_2+g_{3}\cdot f_4)=0,\\&\ldots \end{aligned}$$

from Eq. (10)

$$\begin{aligned}&\epsilon ^2 :D_xD_y (f_2\cdot 1+1\cdot f_2)+2D_{y}(h_{2}\cdot 1+1\cdot f_2)=0, \\&\epsilon ^4 : D_xD_y (f_4\cdot 1+f_2\cdot f_2+1\cdot f_4)+\\&\quad +2D_{y}(h_{4}\cdot 1+h_{1}\cdot f_2+1\cdot f_4)=0, \\&\epsilon ^6 : D_xD_y (f_4\cdot f_2+f_2\cdot f_4)+2D_{y}(h_{4}\cdot f_2+h_{2}\cdot f_4)=0,\\&\ldots \end{aligned}$$

and from Eq. (11)

$$\begin{aligned}&\epsilon ^2 : D_x (h_{2}\cdot 1+1\cdot f_2)+g_{1}^*g_{1}=0, \\&\epsilon ^4 : D_x (h_{4}\cdot 1+h_{2}\cdot f_2+1\cdot f_4)+(g_{3}g^*_{1}+g_{1}g^*_{3})=0, \\&\epsilon ^6 : D_x (h_{4}\cdot f_2+h_{2}\cdot f_4)+(g_{5}g^*_{1}+g_{3}g^*_{3}+g_{5}g^*_{1})=0,\\&\ldots \end{aligned}$$

With the benefit of the above expression and symbolic computation, we can obtain the one-, two-, and N-soliton solutions for Eqs. (1)–(2).

The one-soliton solutions

Truncating expressions (14)–(16) as

$$\begin{aligned} g=\epsilon g_{1}, \ \ \ \ f=1+\epsilon ^2f_2, \ \ h=1+\epsilon ^2h_{2}, \end{aligned}$$

(17)

setting $\epsilon =1$, and substituting them into bilinear forms (9)–(11), we can obtain the one-soliton solutions for the two-dimensional GNLS system of equations as follows:

$$\begin{aligned} q= & {} \frac{e^{\theta _1}}{1+ e^{\theta _1+\theta _1^*+R}}, \end{aligned}$$

(18)

$$\begin{aligned} v= & {} 2\left( \frac{1+ e^{\theta _1+\theta _1^*+S}}{1+ e^{\theta _1+\theta _1^*+R}}\right) _y, \end{aligned}$$

(19)

where

$$\begin{aligned} e^R= & {} \frac{1}{(k_1+k^*_1)^2}, \quad e^S=\frac{(1-k_1-k^*_1)}{(k_1+k^*_1)^2}, \\ \theta _1= & {} k_1x+p_1y+w_1t+\theta _{10}, \end{aligned}$$

with dispersion relation $w_1=-\beta k_1+ik_1p_1+i\alpha$ where $k_1=k_{1R}+ik_{1I},p_1=p_{1R}+ip_{1I},\theta _1=\theta _{1R}+i\theta _{1I}$.

The solutions (18)–(19) can also be written in the more conventional form

$$\begin{aligned} q= & {} \frac{k_{1R}e^{i\theta _{1I}}}{\cosh (\theta _{1R}+\phi _1)}, \\ v= & {} 2p_{1R}\sqrt{1-2k_{1R}}\frac{\cosh (\theta _{1R}+\phi _2)}{\cosh (\theta _{1R}+\phi _1)}, \end{aligned}$$

where $\phi _1=\frac{R}{2}, \quad \phi _2=\frac{S}{2}$ and we have introduced the subscripts R and I for the real and imaginary parts of the quantity in question. (A positive root has been used to define $e^{\frac{R}{2}}, e^{\frac{S}{2}}$ and hence $\phi _1,\phi _2$ are real.) From this form, it is easy to identify the amplitudes $k_{1R}, 2p_{1R}\sqrt{1-2k_{1R}}$ and the phases $\phi _1,\phi _2$. Propagation of the one-soliton solutions (18)–(19) is shown in Figs. 1 and 2.

Fig. 1

The time evolutions of the one-soliton solution (18). The parameters are: $k_1=1+i; p_1=1-i;\alpha =1;\beta =2$

Fig. 2

The time evolutions of the one-soliton solution (19). The parameters are: $k_1=1+i; p_1=1-i;\alpha =1;\beta =2$

The two-soliton solutions

To derive the two-soliton solutions for Eqs. (1)–(2), we truncate expressions (14)–(16) as

$$\begin{aligned} g= & {} \epsilon g_{1}+\epsilon ^3 g_{3}, \end{aligned}$$

(20)

$$\begin{aligned} f= & {} 1+\epsilon ^2f_2+\epsilon ^4f_4, \end{aligned}$$

(21)

$$\begin{aligned} h= & {} 1+\epsilon ^2h_{2}+\epsilon ^4h_{4}, \end{aligned}$$

(22)

set $\epsilon =1$ and substitute them into the bilinear Eqs. (9)–(11) than we get

$$\begin{aligned} q= & {} \frac{g_{1}+g_{3}}{1+ f_{2}+f_{4}}, \end{aligned}$$

(23)

$$\begin{aligned} v= & {} 2\left( \frac{1+h_2+h_4}{1+ f_{2}+f_{4}}\right) _{y}, \end{aligned}$$

(24)

where

$$\begin{aligned} g_{1}= & {} e^{\theta _1}+e^{\theta _2}, \\ g_{3}= & {} e^{\theta _1+\theta _2+\theta _2^*+\delta _1}+e^{\theta _1+\theta _2+\theta _1^*+\delta _2},\\ f_{2}= & {} e^{\theta _1+\theta _1^*+R_{11}}+e^{\theta _2+\theta _1^*+R_{21}}+e^{\theta _1+\theta _2^*+R^*_{21}}+e^{\theta _2+\theta _2^*+R_{22}},\\ f_{4}= & {} e^{\theta _1+\theta _1^*+\theta _2+\theta _2^*+R_3},\\ h_{2}= & {} e^{\theta _1+\theta _1^*+S_{11}}+e^{\theta _2+\theta _1^*+S_{21}}+e^{\theta _1+\theta _2^*+S^*_{21}}+e^{\theta _2+\theta _2^*+S_{22}},\\ h_{4}= & {} e^{\theta _1+\theta _1^*+\theta _2+\theta _2^*+S_3}, \end{aligned}$$

with

$$\begin{aligned} e^{R_{11}}= & {} \frac{1}{(k_1+k^*_1)^2},e^{R_{21}}=\frac{1}{(k_2+k^*_1)^2},\\ e^{R_{22}}= & {} \frac{1}{(k_2+k^*_2)^2},e^{S_{11}}=\frac{(1-k_1-k^*_1)}{(k_1+k^*_1)^2}, \\ e^{S_{21}}= & {} \frac{(1-k_2-k^*_1)}{(k_2+k^*_1)^2},e^{S_{22}}=\frac{(1-k_2-k^*_2)}{(k_2+k^*_2)^2},\\ e^{\delta _1}= & {} -\frac{e^{R_{21}}((k_2-k_1)(p_1^*+p_2)+(k_2+k^*_1)(p_2-p_1))}{((k_2+k^*_1)(p_1^*+p_1)+(k_1+k^*_1)(p_1^*+p_2))}\\&+\frac{e^{R_{11}}((k_1+k^*_1)(p_2-p_1)+(k_2-k_1)(p_1+p^*_1))}{((k_2+k^*_1)(p_1^*+p_1)+(k_1+k^*_1)(p_1^*+p_2))},\\ e^{\delta _2}= & {} -\frac{e^{R_{22}}((k_2-k_1)(p_2^*+p_2)+(k_2+k^*_2)(p_2-p_1))}{((k_2+k^*_2)(p_2^*+p_1)+(k_1+k^*_2)(p_2^*+p_2))}\\&+\frac{e^{R^*_{21}}((k_1+k^*_2)(p_2-p_1)+(k_2-k_1)(p_1+p^*_2))}{((k_2+k^*_2)(p_2^*+p_1)+(k_1+k^*_2)(p_2^*+p_2))},\\ e^{R_{3}}= & {} \frac{(e^{\delta _1}+e^{\delta _2}+e^{\delta _1^*}+e^{\delta _2^*})}{(k_1+k_2+k_1^*+k_2^*)^2},\\ e^{S_{3}}= & {} \frac{(1-k_1-k_2-k^*_1-k^*_2)(e^{\delta _1}+e^{\delta _2}+e^{\delta _1^*}+e^{\delta _2^*})}{(k_1+k_2+k_1^*+k_2^*)^2},\\ \theta _1= & {} k_1x+p_1y+w_1t+\theta _{10},\\ \theta _2= & {} k_2x+p_2y+w_2t+\theta _{20}, \end{aligned}$$

with dispersion relations $w_j=-\beta k_j+ik_jp_j+i\alpha$, where $k_j=k_{jR}+ik_{jI}, p_j=p_{jR}+ip_{jI}, \theta _j=\theta _{jR}+i\theta _{jI} \quad (j=1,2)$.

The multi-soliton solutions

To construct multi-soliton solutions for Eqs. (1)–(2), we have to expand g, f and h formally as power series expansions (14)–(16) in terms of a small arbitrary real parameter $\epsilon$. Then, by substituting Eqs. (14)–(16) into bilinear Eqs. (9)–(11) and solving the resultant set of equations recursively, we can obtain the explicit values for the functions g, f, h.

For multi-soliton solutions, the expansions (14)–(16) can be in the following form:

One-soliton solution

$$\begin{aligned} g=\epsilon g_{1}, \quad f=1+\epsilon ^2 f_2, \quad h=1+\epsilon ^2 h_{2}, \end{aligned}$$

where $g_{1}=e^{\theta _{1}}$, with $\theta _1=k_1x+p_1y+w_1t+\theta _{10}$, and $k_1, p_1, w_1, \theta _{10}$ are constants. The explicit values for the functions $f_2, h_2$ are determined from Eqs. (9)–(11). Note that $g_j = 0$ for $j=3,5,7,\ldots$ and $f_n=0,h_n=0$ for $n=4,6,8\ldots$.

Two-soliton solution

$$\begin{aligned} g=\epsilon g_{1}+\epsilon ^3 g_{3}, \quad f=1+\epsilon ^2 f_2+\epsilon ^4 f_4, \quad h=1+\epsilon ^2 h_{2}+\epsilon ^4 h_{4}, \end{aligned}$$

where $g_{1}=e^{\theta _{1}}+e^{\theta _{2}}$, with $\theta _i=k_ix+p_iy+w_it+\theta _{i0}$, and $k_i, p_i, w_i, \theta _{i0}, (i=1,2)$ are constants. The explicit values for the functions $g_3, f_2, f_4, h_2,h_4$ are determined from Eqs. (9)–(11). Note that $g_j = 0$ for $j=5,7,9 ...$ and $f_n=0,h_n=0$ for $n=6,8,10...$.

Three-soliton solution

$$\begin{aligned} g=\epsilon g_{1}+\epsilon ^3 g_{3}+\epsilon ^5 g_{5}, f=1+\epsilon ^2 f_2+\epsilon ^4 f_4+\epsilon ^6 f_6, h=1+\epsilon ^2 h_{2}+\epsilon ^4 h_{4}+\epsilon ^6 h_6, \end{aligned}$$

where $g_{1}=e^{\theta _{1}}+e^{\theta _{2}}+e^{\theta _{3}}$, with $\theta _i=k_ix+p_iy+w_it+\theta _{i0}$, and $k_i, p_i, w_i, \theta _{i0}, (i=1,2,3)$ are constants. The explicit values for the functions $g_3,g_5,f_2,f_4,f_6,h_2,h_4,h_6$ are determined from Eqs. (9)–(11). Note that $g_j = 0$ for $j=7,9,11\ldots$ and $f_n=0,h_n=0$ for $n=8,10,12\ldots$.

Four-soliton solution

$$\begin{aligned} g= & {} \epsilon g_{1}+\epsilon ^3 g_{3}+\epsilon ^5 g_{5}+\epsilon ^7 g_{7}, f=1+\epsilon ^2 f_2+\epsilon ^4 f_4+\epsilon ^6 f_6+\epsilon ^8 f_8,\\ h= & {} 1+\epsilon ^2 h_{2}+\epsilon ^4 h_{4}+\epsilon ^6 h_6+\epsilon ^8 h_8, \end{aligned}$$

where $g_{1}=e^{\theta _{1}}+e^{\theta _{2}}+e^{\theta _{3}}+e^{\theta _{4}}$, with $\theta _i=k_ix+p_iy+w_it+\theta _{i0}$, and $k_i, p_i, w_i, \theta _{i0}, (i=1,2,3,4)$ are constants. The explicit values for the functions $g_3, g_5, g_7, f_2,f_4,f_6,f_8, h_2,h_4,h_6,h_8$ are determined from Eqs. (9)–(11). Note that $g_j = 0$ for $j=9,11,13 ...$ and $f_n=0,h_n=0$ for $n=10,12,14...$.

and etc

The above procedure of obtaining soliton solutions can be extended to N soliton solutions with some effort, though the analysis is unwieldy. Unfortunately, if we try to continue to higher orders with the solution

$$\begin{aligned} g_{1}=\sum _{i=1}^Ne^{\theta _{i}}, \quad \theta _i=k_ix+p_iy+w_it+\theta _{i0}, \quad (i=1..N), \end{aligned}$$

the analysis becomes cumbersome. So, in this subsection, we only present a short explanation of deriving multi-soliton solutions.

Discussion on the soliton solutions

In this section, we graphically investigate solutions (18)–(19) and (23)–(24).

Figure 1 displays the evolution of the bright one-soliton for solution (18), and Fig. 2 displays the evolution of the dark one-soliton for solution (19). It can be seen that the bright one-soliton and dark one-soliton keep their directions, widths, and amplitudes invariant during the propagation on the $x-y$ plane.

In Figs. 3 and 4, we present 3D plot of the interaction between the two-solitons via solutions (23)–(24) on the $x-y$ plane. We notice that the bright two solitons (23) and dark two solitons (24) are traveling to the left by saving shape.

In order to study the direction of the two solitons, we consider next cases for the parameters:

• (I) $\alpha >\beta$; $k_{1R},p_{1R}>0; k_{2R},p_{2R}<0; k_{1R},p_{1R}>k_{2R},p_{2R}; k_{1I},k_{2I},p_{1I},p_{2I}>0; p_{1I},k_{1I}<k_{2I},p_{2I}$;

• (II) $\alpha <\beta$; $k_{1R},p_{1R}>0; k_{2R},p_{2R}<0; k_{1R},p_{1R}>k_{2R},p_{2R}; k_{1I},k_{2I},p_{1I},p_{2I}>0; p_{1I},k_{1I}<k_{2I},p_{2I}$;

• (III) $\alpha <\beta$; $k_{1R},p_{1R}<0; k_{2R},p_{2R}>0; k_{1R},p_{1R}<k_{2R},p_{2R}; k_{1I},k_{2I},p_{1I},p_{2I}>0; p_{1I},k_{1I}<k_{2I},p_{2I}$;

• (IV) $\alpha >\beta$; $k_{1R},p_{1R}<0; k_{2R},p_{2R}>0; k_{1R},p_{1R}<k_{2R},p_{2R}; k_{1I},k_{2I},p_{1I},p_{2I}>0; p_{1I},k_{1I}<k_{2I},p_{2I}$.

In Fig. 5, we present the result of case (I) as we notice that bright two-solutions q (blue solid line ) and dark solitons v (red dashed line) move to the right by keeping form and direction. In case (II), bright and dark two solitons change directions by traveling to the left (see Fig. 6). The result of case (III) we present in Fig. 7 where two solitons after interaction move to the right by saving shape and direction. In Fig. 8, interaction of case (IV) is shown. As we notice, bright two solitons q (blue solid line ) and dark two solitons v (red dashed line) travel to the left.

Fig. 3

The time evolutions of the two-soliton solution (23). The parameters adopted here are: $k_1=0.8+0.8i; p_1=1-4i;k_2=-1+0.8i; p_2=-1+i; \alpha =1; \beta =2$

Fig. 4

The time evolutions of the two-soliton solution (24). The parameters adopted here are: $k_1=0.8+0.8i; p_1=1-4i;k_2=-1+0.8i; p_2=-1+i; \alpha =1; \beta =2$

Fig. 5

Evolution of the two soliton solutions q (blue solid line) and v (red dashed line) given by expression (23) and (24) at $y = 0$ with parameters $k_1=1+i; p_1=1+i; k_2=-1.5+1.5i; p_2=-1.5+1.5i; \alpha =3; \beta =1$

Fig. 6

Evolution of the two soliton solutions q (blue solid line) and v (red dashed line) given by expression (23) and (24) at $y = 0$ with parameters $k_1=1+i; p_1=1+i;k_2=-1.5+1.5i; p_2=-1.5+1.5i; \alpha =1; \beta =3$

Fig. 7

Evolution of the two soliton solutions q (blue solid line) and v (red dashed line) given by expression (23) and (24) at $y = 0$ with parameters $k_1=-1+i; p_1=-1+i; k_2=1.5+1.5i; p_2=1.5+1.5i; \alpha =3; \beta =1$

Fig. 8

Evolution of the two soliton solutions q (blue solid line) and v (red dashed line) given by expression (23) and (24) at $y = 0$ with parameters $k_1=-1+i; p_1=-1+i; k_2=1.5+1.5i; p_2=1.5+1.5i; \alpha =1; \beta =3$

4 Traveling wave solutions

We use the extended tanh method [24] to obtain traveling wave solutions for the two-dimensional GNLS system of equations. The tanh method was suggested by Malfliet [30] and then was extended by Wazwaz [24]. In the next section, the description of the method is presented.

4.1 Description of the extended tanh method

The partial differential equation (PDE)

$$\begin{aligned} E_1(q,q_t,q_x,q_y,q_{tt},q_{xx},q_{yy},\ldots )=0, \end{aligned}$$

(25)

where $E_1$ is a polynomial of q(x, y, t) and its partial derivatives in which the highest order derivatives and nonlinear terms are involved, can be converted to the ordinary differential equation (ODE)

$$\begin{aligned} E_2(Q, Q', Q'', Q''',\ldots )=0, \end{aligned}$$

(26)

by using a wave variable

$$\begin{aligned} q(x,y,t)=Q(\xi ),\quad \xi =x+y-ct, \end{aligned}$$

(27)

where c is the constant. We integrate Eq. (26) as long as all terms contain derivatives. Constants of integration are considered zeros. By using a new independent variable

$$\begin{aligned} Y=\tanh (\mu \xi ), \quad \xi =x+y-ct, \end{aligned}$$

(28)

where $\mu$ is the wave number, we have the following change of derivatives:

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}\xi }= & {} \mu (1-Y^2)\frac{\mathrm{d}}{\mathrm{d}Y}, \\ \frac{\mathrm{d}^2}{\mathrm{d}\xi ^2}= & {} -2\mu ^2Y(1-Y^2)\frac{\mathrm{d}}{\mathrm{d}Y}+\mu ^2(1-Y^2)\frac{\mathrm{d}^2}{\mathrm{d}Y^2}. \end{aligned}$$

The extended tanh method admits the use of the finite expansion in the following form:

$$\begin{aligned} Q(\xi )=\sum ^M_{n=0} a_n Y^n+\sum ^M_{n=1} b_n Y^{-n}, \end{aligned}$$

(29)

where $a_0,a_1,a_2,a_3,\ldots ,a_N$ and $b_1,b_2,b_3,\ldots ,b_N$ are unknown constants. M is obtained balancing the highest order derivative term and the nonlinear terms in Eq. (26). Then, put the value of $Q(\xi )$ from (29) in Eq. (26), and comparing the coefficient of $Y^n$ we can obtain the values of the coefficients $a_0,a_1,a_2,a_3,\ldots ,a_N$ and $b_1,b_2,b_3,\ldots ,b_N$.

4.2 Application

In this section, we obtain exact traveling wave solutions of the two-dimensional GNLS system of equations using the extended $\tanh$ method [24, 26]. For applying this method, we ought to reduce the system (1)–(2) to the system of ordinary differential equations. If we consider the transformation

$$\begin{aligned} q(x,y,t)=e^{i(ax+by+dt)}Q(x,y,t), \end{aligned}$$

(30)

where a, b, d are the constants, Q(x, y, t) is the real-valued function, then the system (1)–(2) reduced to the following system of differential equations

$$\begin{aligned} Q(-d-ba+\alpha +\beta a)+Q_{xy}-vQ= & {} 0, \end{aligned}$$

(31)

$$\begin{aligned} Q_t+aQ_y+(b-\beta )Q_x= & {} 0, \end{aligned}$$

(32)

$$\begin{aligned} v_x+2 (Q^2)_y= & {} 0. \end{aligned}$$

(33)

Substituting the wave transformation

$$\begin{aligned}&Q(x,y,t)=Q(\xi )=Q(x+y-ct), \end{aligned}$$

(34)

$$\begin{aligned}&v(x,y,t)=V(\xi )=V(x+y-ct), \end{aligned}$$

(35)

into system (31)–(33), we obtain that

$$\begin{aligned} Q(-d-ba+\alpha +\beta a)+Q^{''}-VQ= & {} 0, \end{aligned}$$

(36)

$$\begin{aligned} Q^{'}(-c+a+b-\beta )= & {} 0, \end{aligned}$$

(37)

$$\begin{aligned} V^{'}+2(Q^2)^{'}= & {} 0. \end{aligned}$$

(38)

From Eq. (37), we have that

$$\begin{aligned} c=a+b-\beta . \end{aligned}$$

(39)

Integrating Eq. (38) with respect to $\xi$ and taking integration constant zero for simplicity, we find

$$\begin{aligned} V=-2Q^2. \end{aligned}$$

(40)

Substituting Eq. (40) into Eq. (36), we obtain the following ordinary differential equation

$$\begin{aligned} Q(-d+(\beta -b)a+\alpha )+ Q^{''}+2Q^3= & {} 0, \end{aligned}$$

(41)

where prime denotes the derivation with respect to $\xi$. Balancing the nonlinear term $Q^3$, which has the exponent 3M, with the highest order derivative $Q^{''}$, which has the exponent $M+2$, in (41) yields $3M=M+2$ that gives $M=1$. Then, the extended tanh method allows us to use the substitution

$$\begin{aligned} Q(\xi )=a_0+a_1Y+\frac{b_1}{Y}. \end{aligned}$$

(42)

Substituting (42) into (41) and collecting the coefficients of Y, we obtain a system of algebraic equations for $a_0,a_1,b_1,\mu$. Solving this system with the aid of Maple, we obtain the following results:

Result 1:

$$\begin{aligned} a_0=0, \quad c=a+b-\beta , \end{aligned}$$

(43)

$$\begin{aligned} a_1=\pm \frac{1}{2}\sqrt{\frac{1}{2}(a(b-\beta )-\alpha +d)}, \end{aligned}$$

(44)

$$\begin{aligned} b_1=\pm \frac{1}{2}\sqrt{\frac{1}{2}(a(b-\beta )-\alpha +d)}, \end{aligned}$$

(45)

$$\begin{aligned} \mu =\pm \frac{1}{2}\sqrt{-\frac{1}{2}(a(b-\beta )-\alpha +d)}. \end{aligned}$$

(46)

Result 2:

$$\begin{aligned} a_0= & {} 0,\quad a_1=0, \quad c=a+b-\beta , \end{aligned}$$

(47)

$$\begin{aligned} b_1= & {} \pm \sqrt{\frac{1}{2}(a(b-\beta )-\alpha +d)}, \end{aligned}$$

(48)

$$\begin{aligned} \mu= & {} \pm \sqrt{-\frac{1}{2}(a(b-\beta )-\alpha +d)}. \end{aligned}$$

(49)

Result 3:

$$\begin{aligned} a_0= & {} 0,\quad b_1=0, \quad c=a+b-\beta , \end{aligned}$$

(50)

$$\begin{aligned} a_1= & {} \pm \sqrt{\frac{1}{2}(a(b-\beta )-\alpha +d)}, \end{aligned}$$

(51)

$$\begin{aligned} \mu= & {} \pm \sqrt{-\frac{1}{2}(a(b-\beta )-\alpha +d)}. \end{aligned}$$

(52)

Result 4:

$$\begin{aligned} a_0= & {} 0, \quad c=a+b-\beta , \end{aligned}$$

(53)

$$\begin{aligned} a_1= & {} {\mp } \frac{1}{2}\sqrt{-(a(b-\beta )-\alpha +d)}, \end{aligned}$$

(54)

$$\begin{aligned} b_1= & {} \pm \frac{1}{2}\sqrt{(-a(b-\beta )-\alpha +d)}, \end{aligned}$$

(55)

$$\begin{aligned} \mu= & {} \pm \frac{1}{2}\sqrt{(a(b-\beta )-\alpha +d)}. \end{aligned}$$

(56)

By substituting Eq. (42) into (34), (40) and then the obtained expressions into (30) and (35), we can obtain solutions for the two-dimensional GNLS system of Eqs. (1)–(2) in the following form

$$\begin{aligned} q(x,y,t)= & {} e^{i(ax+by+dt)}[a_0+a_1\tanh (\mu \xi ) \nonumber \\&+b_1\coth (\mu \xi )], \end{aligned}$$

(57)

$$\begin{aligned} v(x,y,t)= & {} -2(a_0+a_1\tanh (\mu \xi ) \nonumber \\&+b_1\coth (\mu \xi ))^2, \end{aligned}$$

(58)

where $\xi =x+y-ct$.

Finally, substituting the results (43)–(56) into (57)–(58), we can obtain traveling wave solutions in the next forms

$$\begin{aligned} q_1(x,y,t)= & {} e^{i(ax+by+dt)}\left[ \pm \frac{1}{2}\sqrt{\frac{1}{2}(a(b-\beta )-\alpha +d)} \nonumber \right. \\&\times \left( \tanh \left( \pm \frac{1}{2}\sqrt{-\frac{1}{2}(a(b-\beta )-\alpha +d)}\xi \right) \nonumber \right. \\&\left. \left. +\coth (\pm \frac{1}{2}\sqrt{-\frac{1}{2}(a(b-\beta )-\alpha +d)}\xi )\right) \right] , \end{aligned}$$

(59)

$$\begin{aligned} v_1(x,y,t)= & {} -2\left( \pm \frac{1}{2}\sqrt{\frac{1}{2}(a(b-\beta )-\alpha +d)} \nonumber \right. \\&\times \left( \tanh \left( \pm \frac{1}{2}\sqrt{-\frac{1}{2}(a(b-\beta )-\alpha +d)}\xi \right) \nonumber \right. \\&\left. \left. +\coth \left( \pm \frac{1}{2}\sqrt{-\frac{1}{2}(a(b-\beta )-\alpha +d)}\xi \right) \right) \right) ^2, \end{aligned}$$

(60)

$$\begin{aligned} q_2(x,y,t)= & {} e^{i(ax+by+dt)}\left( \pm \sqrt{\frac{1}{2}(a(b-\beta )-\alpha +d)} \nonumber \right. \\&\left. \times \coth \left( \pm \sqrt{-\frac{1}{2}(a(b-\beta )-\alpha +d)}\xi \right) \right) , \end{aligned}$$

(61)

$$\begin{aligned} v_2(x,y,t)= & {} -2\left( \pm \sqrt{\frac{1}{2}(a(b-\beta )-\alpha +d)}\times \nonumber \right. \\&\left. \times \coth \left( \pm \sqrt{-\frac{1}{2}(a(b-\beta )-\alpha +d)}\xi \right) \right) ^2, \end{aligned}$$

(62)

$$\begin{aligned} q_3(x,y,t)= & {} e^{i(ax+by+dt)}\left( \pm \sqrt{\frac{1}{2}(a(b-\beta )-\alpha +d)} \nonumber \right. \\&\left. \times \tanh \left( \pm \sqrt{-\frac{1}{2}(a(b-\beta )-\alpha +d)}\xi \right) \right) , \end{aligned}$$

(63)

$$\begin{aligned} v_3(x,y,t)= & {} -2\left( \pm \sqrt{\frac{1}{2}(a(b-\beta )-\alpha +d)} \nonumber \right. \\&\left. \times \tanh \left( \pm \sqrt{-\frac{1}{2}(a(b-\beta )-\alpha +d)}\xi \right) \right) ^2, \end{aligned}$$

(64)

$$\begin{aligned} q_4(x,y,t)= & {} e^{i(ax+by+dt)}\left[ {\mp } \frac{1}{2}\sqrt{-(a(b-\beta )-\alpha +d)} \nonumber \right. \\&\times \tanh \left( \pm \frac{1}{2}\sqrt{(a(b-\beta )-\alpha +d)} \xi \right) \pm \nonumber \\&\pm \frac{1}{2}\sqrt{-(a(b-\beta )-\alpha +d)}\times \nonumber \\&\left. \times \coth \left( \pm \frac{1}{2}\sqrt{(a(b-\beta )-\alpha +d)} \xi \right) \right] , \end{aligned}$$

(65)

$$\begin{aligned} v_4(x,y,t)= & {} -2\left( {\mp } \frac{1}{2}\sqrt{-(a(b-\beta )-\alpha +d)} \nonumber \right. \\&\times \tanh \left( \pm \frac{1}{2}\sqrt{(a(b-\beta )-\alpha +d)} \xi \right) \pm \nonumber \\&\pm \frac{1}{2}\sqrt{-(a(b-\beta )-\alpha +d)}\times \nonumber \\&\left. \times \coth \left( \pm \frac{1}{2}\sqrt{(a(b-\beta )-\alpha +d)} \xi \right) \right) ^2, \end{aligned}$$

(66)

where $\xi =x+y-(a+b-\beta )t$.

Discussion on the traveling wave solutions

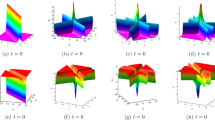
In this section, we analyze obtained traveling wave solutions (59)–(66). In Figs. 9, 10, 11 and 12, we present propagation of solutions (59)–(62) on the $x-y$ plane at $t=0$ and $t=3$. As we notice from 3D plots and density plots, the solutions $q_1, v_1 , q_2, v_2$ give the bright solitons. The evolution of the dark soliton solutions $q_3,v_3$ in 3D and density plot at $t=0$ is displayed in Figs. 13 and 14. It can be seen that the dark solitons and bright solitons keep their directions invariant during the propagation on the $x-y$ plane. Moreover, periodic type solutions $q_4,v_4$ at $t=0$ and $t=3$ are presented in Figs. 15 and 16. Analyzing the graphs of obtained solutions, we notice that in case $q_1, v_1, q_2, v_2$ we can obtain bright solitons which are almost similar to the one-soliton solutions obtained by Hirota’s bilinear method in Sect. 3. But in case $q_3, v_3, q_4, v_4$, dark solitons and periodic solutions can be derived. Thus, the extended tanh method can yield various types of solutions compared to Hirota’s bilinear method.

The algorithms described in Sects. 3 and 4 can be applied to a wide class of nonlinear partial differential equations. The main advantage of the extended tanh method is the possibility of reducing the size of computational work in contrast to Hirota’s bilinear method. Moreover, the extended tanh method can give a different type of solutions such as soliton, kink, periodic solutions, peakon. However, for deriving multi-soliton solutions, Hirota’s bilinear method is a very helpful tool compared to the extended tanh method. The disadvantages of Hirota’s bilinear method are cumbersome calculation, and also sometimes, it is difficult to find a bilinear form for nonlinear partial differential equations.

Fig. 9

Propagation of the solution $q_1$ via (59) with the $\alpha =1;\beta =3$

Fig. 10

Propagation of the solution $v_1$ via (60) with the $\alpha =1;\beta =3$

Fig. 11

Propagation of the solution $q_2$ via (61) with the $\alpha =1;\beta =3$

Fig. 12

Propagation of the solution $v_2$ via (62) with the $\alpha =1;\beta =3$

Fig. 13

Propagation of the solution $q_3$ via (63) with the $\alpha =1;\beta =3$

Fig. 14

Propagation of the solution $v_3$ via (64) with the $\alpha =1;\beta =3$

Fig. 15

Propagation of the solution $q_4$ via (65) with the $\alpha =1;\beta =3$

Fig. 16

Propagation of the solution $v_4$ via (66) with the $\alpha =1;\beta =3$

5 Conclusion

In this work, we presented the two-dimensional generalized nonlinear Schrödinger system of equations with the Lax pair. The Lax pair plays an important role in the study of the integrability of the differential system. By employing two methods, we have obtained the nonlinear wave solutions for the two-dimensional generalized nonlinear Schrödinger equations. Soliton solutions are derived by Hirota’s bilinear method. This method gives a mechanism for finding arbitrary N-soliton solutions for PDEs which can be written in bilinear form in the D-operator via a transformation of the dependent variable. We obtained the traveling wave solutions using the extended tanh method that provides wider applicability for handling nonlinear wave equations. The figures are plotted to display the dynamical features of those solutions. Moreover, the presented methods can be applied to obtain new solutions for other nonlinear equations.