1 Introduction

Despite the fact that nano-materials are nowadays considered as essential constituents of pioneering engineering, peculiar mechanical responses are reported through experimental results and numerical simulations [1,2,3,4]. The classical elasticity theory is imprecise in describing the physics of nano-materials, and accordingly, studying the behavior of media with nano-structural features via augmented elasticity theories has been the focus of numerous investigations, where recent reviews are tackled in [5, 6].

The smaller-is-stiffer phenomenon, detected by laboratory experiments [7,8,9], can be properly taken into account in the framework of the strain gradient theory. The kinematics of the strain gradient continuum is assumed to have additional degrees of freedom, and consequently, the response of the medium is described by incorporating the gradients of the displacement field [10]. Among various forms of the strain gradient elasticity, the modified strain gradient theory, introduced by Lam et al. [9], has drawn more attentions in the literature. The elastic strain energy associated with the modified strain gradient theory comprises both the first- and second-order gradients of the displacement field and can be described in terms of the strain tensor, dilatation gradient vector, deviatoric stretch gradient tensor, and symmetric rotation gradient tensor. The modified strain gradient theory is, therefore, supplied with three gradient length-scale parameters reflecting the dilatation gradients, deviatoric stretch gradients, and rotation gradients. The stiffening response of nano-structures, realized via utilizing the modified strain gradient theory, is widely addressed in the literature; to mention some representative works, let us recall [11,12,13,14,15,16,17].

The smaller-is-softer phenomenon, observed in experimental studies [18,19,20], can be alternatively captured consistent with the nonlocal elasticity theory. The nonlocal stress field at any material point is assumed to be affected by the strain field at not only that material point but also those of its vicinity. The nonlocality is described through an integral convolution between an attenuation kernel and the kinematic field. The nonlocal kernel, enriched with a nonlocal characteristic length, drastically decreases with distance based on the axiom of attenuating neighborhood [21]. Restoring the nonlocal integral convolution with the differential constitutive law, however, leads to anomalous structural results [22,23,24]. Advanced remedies are proposed in the literature to overcome the intrinsic anomalies associated with the nonlocal differential formulation [25,26,27,28,29]. Nonlocal elasticity approach has been broadly implemented to simulate the softening behavior of nano-structures, where recent contributions are addressed in [30,31,32,33,34,35,36,37,38].

The lack of consensus on the mechanical behavior of nano-sized structures, in solely exhibiting the stiffening or softening effects, is revealed in view of experimental observations. Nano-materials can, de facto, demonstrate both the structural responses depending on particular state conditions of the material [18, 22]. The nonlocal gradient theory of elasticity is conceived as a response to the need to entail a more comprehensive elasticity theory which is capable of capturing and describing both the structural responses at small scale. The nonlocal gradient elasticity is established via unification of the nonlocal differential and the simplified stain gradient models [39]. The resulted constitutive law is of higher order than the one of the classical elasticity theories and accordingly should be equipped with additional nonstandard boundary conditions. The proper choice of the nonstandard boundary conditions is still an open controversial issue in the literature [40, 41]. The nonlocal gradient elasticity theory, nevertheless, has recently received much attention and has been widely applied to investigate various nano-structural problems; as representative recent advances are reported in [42,43,44,45,46].

The present study aimed to consistently introduce the contribution of the nonlocal integral elasticity to the modified strain gradient theory. In comparison with the classical nonlocal gradient model, the proposed nonlocal modified gradient elasticity theory, enriched with four intrinsic length scales, can appropriately characterize the effects of nonlocality, dilatation gradient, deviatoric stretch gradient, and symmetric rotation gradient. The nonlocal modified gradient theory is applied to nano-sized beams in flexure with the intention of more accurately describing the inherent size effects. The paper is structured as follows. The flexure of nano-beams consistent with the modified strain gradient theory is briefly recalled in Sect. 2. The constitutive law of the nonlocal modified gradient theory is established utilizing a consistent variational approach and the nonstandard boundary conditions, required to close the constitutive problem, is also introduced. In Sect. 3, the wave dispersion response of nano-materials within the framework of the nonlocal modified gradient elasticity is analytically investigated and validated with the molecular dynamics simulation results. Section 4 is devoted to rigorously examine the elastostatic flexure of nano-beams via a practical solution approach and, furthermore, is enriched by illustrative numerical results and discussions. Section 5 summarizes the main outcomes and draws the concluding remarks.

2 Nonlocal modified gradient mechanics of beams in flexure

A homogenous elastic beam of length \(L = b - a\) and cross section \(\Xi\) is considered and referred to the orthogonal Cartesian coordinates where the x abscissa coincides with the longitudinal centroidal axis and the z ordinate is oriented downwards. The beam ends, at \(x = a\) and \(x = b\), are restrained to prevent any rigid motion, as illustrated in Fig. 1. The beam is subjected to a transverse loading q applied downwards at the top surface of the beam. The material possesses the density \(\rho\) and elastic and shear moduli E and \(\mu\), respectively. The elasticity solution of the flexure of cylinders [47, 48] can be applied to set forth the displacement field of the beam consistent with the Euler–Bernoulli model as

$$ u_{1} = - z\partial_{x} w\left( {x,t} \right),\,u_{2} = 0,\,u_{3} = w\left( {x,t} \right) $$
(1)
Fig. 1
figure 1

Coordinate system and configuration of a beam in flexure

Full size image

with w being the transverse deflection. The total elastic strain energy \({\mathbb{U}}\) and the kinetic energy \({\mathbb{T}}\) of the Euler–Bernoulli beam consistent with the modified strain gradient theory [49, 50] are written as

$$ \begin{aligned} {\mathbb{U}} & = \frac{1}{2}\int_{a}^{b} {\left[ {D_{E} \left( {\chi \left( {x,t} \right)} \right)^{2} + D_{\mu } \left( {\partial_{x} \chi \left( {x,t} \right)} \right)^{2} } \right]} {\text{d}}x - \int_{a}^{b} {q\left( x \right)w\left( {x,t} \right)} {\text{d}}x \\ {\mathbb{T}} & = \frac{1}{2}\int_{a}^{b} {\left[ {A_{\rho } \left( {\partial_{t} w\left( {x,t} \right)} \right)^{2} + I_{\rho } \left( {\partial_{xt} w\left( {x,t} \right)} \right)^{2} } \right]} {\text{d}}x \\ \end{aligned} $$
(2)

where \(\chi = \partial_{xx} w\) denotes the curvature of the beam centroidal axis along with the so-called higher-order stiffness parameters \(D_{E} ,D_{\mu }\) defined as

$$ D_{E} = I_{E} + A_{\mu } \left( {2\ell_{0}^{2} + \frac{8}{15}\ell_{1}^{2} + \ell_{2}^{2} } \right),\;D_{\mu } = I_{\mu } \left( {2\ell_{0}^{2} + \frac{4}{5}\ell_{1}^{2} } \right) $$
(3)

where \(\ell_{0} ,\ell_{1} ,\ell_{2}\) are the gradient length-scale parameters related to the dilatation gradients, deviatoric stretch gradients, and rotation gradients, correspondingly. The classical cross-sectional mass \(A_{\rho }\), rotatory inertia \(I_{\rho }\), flexural stiffness \(I_{E}\), shear stiffness \(I_{\mu }\), and shear area \(A_{\mu }\) are furthermore defined by

$$ \begin{aligned} A_{\rho } & = \iint\limits_{\Xi } {\rho {\text{d}}A},\;I_{\rho } = \iint\limits_{\Xi } {\rho z^{2} {\text{d}}A}, \\ A_{\mu } & = \iint\limits_{\Xi } {\mu {\text{d}}A},\;I_{E} = \iint\limits_{\Xi } {Ez^{2} {\text{d}}A},\;I_{\mu } = \iint\limits_{\Xi } {\mu z^{2} {\text{d}}A}. \\ \end{aligned} $$
(4)

In view of the kinematic compatibility condition \(\chi = \partial_{xx} w\), performing the first-order variation of the Lagrangian functional \({\mathbb{L}} = {\mathbb{T}} - {\mathbb{U}}\), followed by integration by parts, yields

$$ \begin{aligned} \delta {\mathbb{L}} &= \int_{a}^{b} \left[ - A_{\rho } \partial_{tt} w\left( {x,t} \right) + I_{\rho } \partial_{xxtt} w\left( {x,t} \right) + q\left( x \right) - D_{E} \partial_{xxxx} w\left( {x,t} \right)\right.\\ &\quad \left.+ D_{\mu } \partial_{xxxxxx} w\left( {x,t} \right) \right]\delta w {\text{d}}x \left.+ {\left( { - D_{E} \partial_{xx} w + D_{\mu } \partial_{xxxx} w} \right)\partial_{x} \delta w} \right|_{x = a,b}\\ &\quad + \left. {\left( {D_{E} \partial_{xxx} w - D_{\mu } \partial_{xxxxx} w} \right)\delta w} \right|_{x = a,b} - \left. {D_{\mu } \partial_{xxx} w\partial_{xx} \delta w} \right|_{x = a,b}. \hfill \\ \end{aligned} $$
(5)

To simplify the first-order variation of the Lagrangian functional \(\delta {\mathbb{L}}\), the resultant flexural moment M is introduced as

$$ M = D_{E} \chi \left( {x,t} \right) - D_{\mu } \partial_{xx} \chi \left( {x,t} \right) = D_{E} \partial_{xx} w\left( {x,t} \right) - D_{\mu } \partial_{xxxx} w\left( {x,t} \right). $$
(6)

Applying the Hamilton’s variational principle, the differential and boundary conditions of dynamic equilibrium of the modified strain gradient beam, while assuming arbitrary variations of the curvature field, are determined

$$ \begin{aligned} \partial_{xx} M\left( {x,t} \right) & = q\left( x \right) - A_{\rho } \partial_{tt} w\left( {x,t} \right) + I_{\rho } \partial_{xxtt} w\left( {x,t} \right) \\ \left. {M\partial_{x} \delta w} \right|_{x = a,b} & = \left. {\partial_{x} M\delta w} \right|_{x = a,b} = 0 \\ \left. {D_{\mu } \partial_{x} \chi } \right|_{x = a,b} & = 0. \\ \end{aligned} $$
(7)

To appropriately introduce the contribution of nonlocality to the modified strain gradient beam model, the constitutive law is assumed to be governed by the elastic potential functional \({\mathbb{F}}\) as

$$ {\mathbb{F}} = \frac{1}{2}D_{E} \int_{a}^{b} {\int_{a}^{b} {\chi \left( {x,t} \right)\varphi \left( {x - \xi ,\ell_{c} } \right)\chi \left( {\xi ,t} \right){\text{d}}\xi {\text{d}}x} } + \frac{1}{2}D_{\mu } \int_{a}^{b} {\int_{a}^{b} {\partial_{x} \chi \left( {x,t} \right)\varphi \left( {x - \xi ,\ell_{c} } \right)\partial_{\xi } } \chi \left( {\xi ,t} \right){\text{d}}\xi {\text{d}}x} $$
(8)

where \(x,\xi\) are the points of the beam domain. The attenuation nonlocal kernel \(\varphi\) is assumed to depend on a nonlocal characteristic length \(\ell_{c}\) and moreover meet the positivity, symmetry, normalization, and impulsivity properties [51].

The resultant moment in the nonlocal modified gradient beam is detected via setting equal the directional derivative of the elastic potential functional \({\mathbb{F}}\) along a virtual curvature field \(\delta \chi\) (with compact support in the domain) to the virtual work of the flexural moment field. Utilizing a standard variational procedure, the constitutive law of the flexural moment in the framework of the nonlocal modified gradient elasticity theory is provided by

$$ M\left( {x,t} \right) = D_{E} \int_{a}^{b} {\varphi \left( {x - \xi ,\ell_{c} } \right)\chi \left( {\xi ,t} \right){\text{d}}\xi } - D_{\mu } \partial_{x} \int_{a}^{b} {\varphi \left( {x - \xi ,\ell_{c} } \right)\partial_{\xi } } \chi \left( {\xi ,t} \right){\text{d}}\xi. $$
(9)

To derive the equivalent differential constitutive law, the attenuation nonlocal kernel is considered to be the Helmholtz kernel function, defined as

$$ \varphi \left( {x - \xi ,\ell_{c} } \right) = \frac{1}{{2\ell_{c} }}\exp \left( { - \frac{{\left| {x - \xi } \right|}}{{\ell_{c} }}} \right). $$
(10)

In view of the mathematical approach addressed in [52, 53], the integro-differential constitutive model Eq. (9), enriched with the Helmholtz kernel function Eq. (10), can be demonstrated to be equivalent to the differential formulation

$$ \frac{1}{{\ell_{c}^{2} }}M\left( {x,t} \right) - \partial_{xx} M\left( {x,t} \right) = \frac{{D_{E} }}{{\ell_{c}^{2} }}\chi \left( {x,t} \right) - \frac{{D_{\mu } }}{{\ell_{c}^{2} }}\partial_{xx} \chi \left( {x,t} \right) $$
(11)

subject to the nonstandard boundary conditions at the beam ends

$$ \begin{aligned} & \partial_{x} M\left( {a,t} \right) - \frac{1}{{\ell_{c} }}M\left( {a,t} \right) = \frac{{D_{\mu } }}{{\ell_{c}^{2} }}\partial_{x} \chi \left( {a,t} \right) \\ & \partial_{x} M\left( {b,t} \right) + \frac{1}{{\ell_{c} }}M\left( {b,t} \right) = \frac{{D_{\mu } }}{{\ell_{c}^{2} }}\partial_{x} \chi \left( {b,t} \right). \\ \end{aligned} $$
(12)

Prescribing the nonstandard boundary conditions closes the constitutive problem on bounded domains, and thus, the equivalence of the differential formulation to the integro-differential constitutive model is assured. The flexural moment, as the output of the integral convolutions of the constitutive law, can properly meet the equilibrium conditions. The conceived nonlocal modified gradient elasticity theory, therefore, results in well-posed problem, as put into evidence in the elastostatic and elastodynamic analyses of inflected beams.

Taking into consideration the impulsivity property of the nonlocal kernel, the modified strain gradient model of nano-beams in flexure can be recovered as a special limiting case of the conceived nonlocal modified gradient theory. The modified strain gradient law of the flexural moment field and the corresponding higher-order boundary conditions can be restored via vanishing of the nonlocal characteristic length as

$$ \begin{aligned} M\left( {x,t} \right) & = D_{E} \chi \left( {x,t} \right) - D_{\mu } \partial_{xx} \chi \left( {x,t} \right) \\ D_{\mu } \partial_{x} \chi \left( {a,t} \right) & = D_{\mu } \partial_{x} \chi \left( {b,t} \right) = 0. \\ \end{aligned} $$
(13)

The constitutive model of the nonlocal gradient beam in flexure and the associated nonstandard boundary conditions can be furthermore obtained via setting the stiffness parameters as \(D_{E} = I_{E}\) and \(D_{\mu } = \ell_{s}^{2} I_{E}\), where \(\ell_{s}\) is the gradient characteristic length consistent with the simplified strain gradient theory,

$$ \begin{aligned} & \frac{1}{{\ell_{c}^{2} }}M\left( {x,t} \right) - \partial_{xx} M\left( {x,t} \right) = \frac{{I_{E} }}{{\ell_{c}^{2} }}\chi \left( {x,t} \right) - \frac{{\ell_{s}^{2} I_{E} }}{{\ell_{c}^{2} }}\partial_{xx} \chi \left( {x,t} \right) \\ & \partial_{x} M\left( {a,t} \right) - \frac{1}{{\ell_{c} }}M\left( {a,t} \right) = \frac{{\ell_{s}^{2} I_{E} }}{{\ell_{c}^{2} }}\partial_{x} \chi \left( {a,t} \right) \\ & \partial_{x} M\left( {b,t} \right) + \frac{1}{{\ell_{c} }}M\left( {b,t} \right) = \frac{{\ell_{s}^{2} I_{E} }}{{\ell_{c}^{2} }}\partial_{x} \chi \left( {b,t} \right). \\ \end{aligned} $$
(14)

To study the diverse gradient effects, detectable in the framework of the nonlocal modified gradient elasticity, the nonlocal gradient model can be considered as a suitable counterpart for the comparison sake.

The so-called nonlocal couple stress model is introduced in the literature by integrating the nonlocal differential model and the modified couple stress theory, while nanoscopic effects of the dilatation gradient and the deviatoric stretch gradient are overlooked [54]. Close examination of the conceived size-dependent formulation reveals that the higher-order stiffness parameter \(D_{\mu }\) vanishes by setting zero the gradient length-scale parameters \(\ell_{0} ,\ell_{1}\). A comparison of the homogenous nonstandard boundary conditions Eq. (12), in the absence of the dilatation gradient and the deviatoric stretch gradient effects, with the equilibrium conditions Eq. (7)1–2 will evince that the requirements dictated by the equilibrium cannot be fulfilled. Indeed, the elastostatic flexure problem of a nano-sized beam consistent with the nonlocal couple stress model incorporates a governing differential equation of the fourth-order subjected to six boundary conditions including four classical boundary conditions and two homogenous nonstandard boundary conditions. The resulted over-constrained boundary value problem admits no solution, and the nonlocal couple stress model, therefore, results in ill-posed problems defined on bounded domains. A similar anomalous issue with reference to the nonlocal differential model of elastic beams in flexure is addressed in [51]. Nevertheless, the nanoscale effects of the gradient length-scale parameters along with the nonlocality can be consistently characterized in the conceived framework of the nonlocal modified gradient elasticity theory.

3 Wave dispersion

A suitable augmented elasticity theory should be capable of effectively capturing the dispersive behavior of waves in materials with nanoscopic features. The wave dispersion relation can be, furthermore, utilized in identification of the characteristic length-scale parameters of the augmented elasticity theories; see e.g., recent researches on the wave propagation phenomenon in nano-materials [55,56,57,58].

To determine the phase velocity of the wave dispersion, the differential condition of equilibrium should be described in terms of the displacement field. The flexural moment is first obtained employing the nonlocal modified gradient constitutive law Eq. (11) and the dynamic equilibrium condition Eq. (7)1 as

$$ M\left( {x,t} \right) = \ell_{c}^{2} \left( { - A_{\rho } \partial_{tt} w\left( {x,t} \right) + I_{\rho } \partial_{xxtt} w\left( {x,t} \right)} \right) + D_{E} \partial_{xx} w\left( {x,t} \right) - D_{\mu } \partial_{xxxx} w\left( {x,t} \right) $$
(15)

where the transverse loading is allowed to vanish to study the elastodynamic response. The dynamic equilibrium condition is then determined in terms of the transverse deflection as

$$ \partial_{xx} \left( {D_{E} \partial_{xx} w\left( {x,t} \right) - D_{\mu } \partial_{xxxx} w\left( {x,t} \right)} \right) = - A_{\rho } \partial_{tt} w\left( {x,t} \right) + \left( {I_{\rho } + \ell_{c}^{2} A_{\rho } } \right)\partial_{xxtt} w\left( {x,t} \right) - \ell_{c}^{2} I_{\rho } \partial_{xxxxtt} w\left( {x,t} \right). $$
(16)

In dealing with the wave dispersion response, the condition of decay at infinity can be suitably assumed, i.e., vanishing of the nonstandard boundary conditions at infinity is tacitly met. The general solution of the wave response is accordingly expressed as

$$ w\left( {x,t} \right) = W\exp \left( {ik\left( {x - vt} \right)} \right) $$
(17)

where \(i = \sqrt { - 1}\), k and v correspondingly stand for the wave number and the phase velocity along with W denoting the wave amplitude. Imposing the wave dispersion solution to the differential condition of dynamic equilibrium results in the sought phase velocity of flexural waves associated with the nonlocal modified gradient elasticity theory

$$ v = \frac{{k\sqrt {D_{E} + k^{2} D_{\mu } } }}{{\sqrt {A_{\rho } + k^{2} I_{\rho } } \sqrt {1 + k^{2} \ell_{c}^{2} } }} = \frac{{k\sqrt {I_{E} + A_{\mu } \left( {2\ell_{0}^{2} + \frac{8}{15}\ell_{1}^{2} + \ell_{2}^{2} } \right) + k^{2} I_{\mu } \left( {2\ell_{0}^{2} + \frac{4}{5}\ell_{1}^{2} } \right)} }}{{\sqrt {A_{\rho } + k^{2} I_{\rho } } \sqrt {1 + k^{2} \ell_{c}^{2} } }} $$
(18)

where the stiffness parameters \(D_{E} ,D_{\mu }\) are restored from Eq. (3). Notably, the phase velocity of flexural waves consistent with the nonlocal gradient theory can be also obtained via substituting the corresponding stiffness parameters [28].

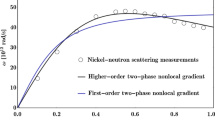
To examine the effectiveness of the proposed nonlocal modified gradient elasticity in describing the dispersive behavior of flexural waves, the phase velocity detected by molecular dynamics (MD) simulations for \(\left( {10,10} \right)\) armchair CNTs is employed [59]. Implementing the inverse theory approach, unknown parameters of a mathematical field can be determined via minimizing the discrepancy between the reconstructed results and the limited data measurements [60,61,62]. The physical properties of CNTs \(\left( {10,10} \right)\) as referenced in [58, 63] are applied in the present inverse analysis. The wave dispersion response of CNTs \(\left( {10,10} \right)\) is reconstructed via a nonlinear least square optimization procedure. The identified characteristic length-scale parameters associated with the nonlocal modified gradient elasticity and the nonlocal gradient theory are given in Table 1.

Table 1 Characteristic parameter identification for MD simulations of CNT \(\left( {10,10} \right)\)
Full size table

The results of MD simulations in comparison with the predicted wave response associated with the nonlocal modified gradient theory and the nonlocal gradient elasticity are graphically illustrated in Fig. 2. The goodness of fit is assessed in the framework of the Chi-squared statistics [64]. The reduced Chi-squared value is calculated as 5.37246 and 13.2994, respectively, consistent with the nonlocal modified gradient elasticity and the nonlocal gradient theory. Detected reduced Chi-squared values noticeably demonstrate that a better model fit, i.e., less discrepancy between the reconstructed wave dispersion response and the MD simulations, is attained utilizing the nonlocal modified gradient elasticity theory. Accordingly, the nonlocal modified gradient elasticity can better capture the wave dispersion characteristics in a wider range of wave numbers, compared to the counterpart results of the nonlocal gradient theory. The qualitative aspects of the dispersive behavior, achieved by the MD simulation, can be also captured with better accuracy in the framework of the nonlocal modified gradient elasticity theory. This issue evidently exposes the importance of applying the appropriate augmented elasticity theory, consistently enriched with intrinsic length-scale parameters, for nanoscopic analysis of the field quantities.

Fig. 2
figure 2

Comparison of the wave dispersion in CNT \(\left( {10,10} \right)\) by MD simulations and augmented elasticity theories

Full size image

Nanoscopic effects of the nonlocal and gradient characteristic parameters on the dispersive behavior of flexural waves are also graphically depicted. The non-dimensional form of the gyration radius \(\overline{r}\), nonlocal characteristic parameter \(\zeta\), gradient characteristic parameters \(\eta_{j} ,\eta_{s}\), wave number \(\overline{k}\), and phase velocity \(\overline{v}\) are introduced for the sake of consistency

$$ \overline{r} = \frac{1}{L}\sqrt {\frac{{I_{\mu } }}{{A_{\mu } }}} ,\;\zeta = \frac{{\ell_{c} }}{L},\;\eta_{j} = \frac{{\ell_{j} }}{L},\;\eta_{s} = \frac{{\ell_{s} }}{L},\;\overline{k} = kL,\;\overline{v} = vL\sqrt {\frac{{A_{\rho } }}{{I_{E} }}}. $$
(19)

3D variation of the phase velocity in terms of the logarithmic scaling of the non-dimensional wave number \(\overline{k}\)[65] is shown in Figs. 3 through 5 where the size effects of each characteristic parameter are separately investigated. In all the numerical illustrations, the varying gradient and nonlocal parameters are assumed to range in the interval \([0,0.5]\), as the (logarithm of) non-dimensional wave number \(\overline{k}\) is ranging in the interval \(\left[ {10^{ - 1} ,10^{1} } \right]\). The non-dimensional gyration radius is also prescribed as \(\overline{r} = 1/20\).

Fig. 3
figure 3

Wave dispersion by nonlocal modified gradient theory: effects of gradient parameters on the phase velocity

Full size image

The effects of the gradient length-scale parameters associated with the nonlocal modified gradient elasticity are studied in Fig. 3 in the absence of the nonlocal parameter \(\zeta \to 0^{ + }\). It is deduced from the illustrative results that a larger value of each gradient parameter \(\eta_{j}\) involves a larger value of the phase velocity. The phase velocity of flexural waves, accordingly, reveals a stiffening response in terms of the gradient characteristic parameter \(\eta_{j}\). Remarkably, the dilatation gradient parameter \(\eta_{0}\) and the deviatoric stretch gradient parameter \(\eta_{1}\), respectively, have the highest and the lowest stiffening effects. While the phase velocity of the wave dispersion associated with the non-vanishing rotation gradient \(\eta_{2}\) overestimates the counterpart result corresponding to the deviatoric stretch gradient \(\eta_{1}\), it is strictly lower than the phase velocity associated with the non-vanishing dilatation gradient \(\eta_{0}\). The stiffening effect of the deviatoric stretch gradient parameter \(\eta_{1}\) in the framework of the nonlocal modified gradient elasticity is consequently compared with the counterpart results of the nonlocal gradient theory in Fig. 4, as the nonlocal characteristic parameter tends to zero \(\zeta \to 0^{ + }\). The phase velocity of the wave dispersion corresponding to the nonlocal gradient theory underestimates the counterpart results consistent with the nonlocal modified gradient elasticity with non-vanishing deviatoric stretch gradient \(\eta_{1}\). In comparison with the nonlocal gradient theory, the dominant stiffening effect of the gradient characteristic parameters associated with the nonlocal modified gradient elasticity is thus confirmed. Effects of the nonlocal length-scale parameter on the dispersive behavior of flexural waves are studied in Fig. 5, for equal values of the gradient parameters assumed as \(\eta_{1} = \eta_{s} = 1/4\). The phase velocity associated with both the augmented elasticity theories decreases by increasing the nonlocal parameter \(\zeta\), and consequently, a softening response in terms of the nonlocal characteristic parameter is realized. The wave dispersion response of the nonlocal modified gradient elasticity is observed to overestimate the counterpart results of the nonlocal gradient theory. In all the numerical illustrations, the phase velocity of the augmented elasticity theories remains unchanged for low wave numbers, as the phase velocity is well known not to be sensitive to the nano-material properties for large wavelengths. The discrepancy between the dispersive behaviors of flexural waves is significantly enhanced at higher wave numbers.

Fig. 4
figure 4

Wave dispersion by augmented elasticity theories: effects of gradient parameters on the phase velocity

Full size image
Fig. 5
figure 5

Wave dispersion by augmented elasticity theories: effects of the nonlocal parameter on the phase velocity

Full size image

4 Elastostatic flexure

To capture the nanoscopic effects in the elastostatic flexure, the flexural response of structural schemes of applicative interest as fixed-end and cantilever beams is investigated. The beam is considered to be subjected to a uniform transverse loading \(q_{0}\). A practical solution approach is employed to derive the analytical solution of the flexure problem by integrating differential equations of lower orders. Integrating the differential condition of equilibrium Eq. (7)1, while ignoring the inertial terms, leads to the expression of the equilibrated flexural moment M in terms of integration constants \(\Gamma_{1} ,\Gamma_{2}\)

$$ M\left( x \right) = \int_{a}^{x} {\int_{a}^{\xi } {q\left( \varsigma \right){\text{d}}\varsigma {\text{d}}\xi } } + \Gamma_{1} x + \Gamma_{2}. $$
(20)

The flexural curvature \(\chi\) is determined up to integration constants \(\Gamma_{3} ,\Gamma_{4}\) via solving the constitutive differential law Eq. (11)

$$ \begin{aligned} \chi \left( x \right) & = \Gamma_{3} \exp \left( {\sqrt {\frac{{D_{E} }}{{D_{\mu } }}} x} \right) + \Gamma_{3} \exp \left( { - \sqrt {\frac{{D_{E} }}{{D_{\mu } }}} x} \right) \\ & \quad - \exp \left( {\sqrt {\frac{{D_{E} }}{{D_{\mu } }}} x} \right)\int_{a}^{x} {\frac{1}{{2\sqrt {D_{E} D_{\mu } } }}\exp \left( { - \sqrt {\frac{{D_{E} }}{{D_{\mu } }}} \xi } \right)} \left( {M\left( \xi \right) - \ell_{c}^{2} \partial_{\xi \xi } M\left( \xi \right)} \right){\text{d}}\xi \\ & \quad + \exp \left( { - \sqrt {\frac{{D_{E} }}{{D_{\mu } }}} x} \right)\int_{a}^{x} {\frac{1}{{2\sqrt {D_{E} D_{\mu } } }}\exp \left( {\sqrt {\frac{{D_{E} }}{{D_{\mu } }}} \varsigma } \right)} \left( {M\left( \varsigma \right) - \ell_{c}^{2} \partial_{\varsigma \varsigma } M\left( \varsigma \right)} \right){\text{d}}\varsigma. \\ \end{aligned} $$
(21)

The transverse deflection w is lastly detected via integrating the kinematic compatibility condition \(\chi = \partial_{xx} w\) up to integrations constant \(\Gamma_{5} ,\Gamma_{6}\) as

$$ w\left( x \right) = \int_{a}^{x} {\int_{a}^{\xi } {\chi \left( \varsigma \right){\text{d}}\varsigma {\text{d}}\xi } } + \Gamma_{5} x + \Gamma_{6}. $$
(22)

Unknown integration constants \(\Gamma_{j} \left( {j = 1..6} \right)\) are evaluated by prescribing four classical boundary conditions Eq. (7)2 in addition to two nonstandard boundary conditions Eq. (12). The exact analytical solution of the flexure problem of nano-sized beams is accordingly derived.

Numerical behavior of the elastostatic flexure of a nonlocal modified gradient beam with kinematic constraints of applicative interest as subjected to a uniform transverse loading \(q_{0}\) is graphically demonstrated and compared with the counterpart result corresponding to the nonlocal gradient theory. For the consistency of illustrations, the non-dimensional transverse deflection of the beam \(\overline{w}\) is introduced in the numerical illustrations as

$$ \overline{w} = \frac{{I_{E} }}{{q_{0} L^{4} }}w. $$
(23)

The normalized maximum transverse deflections of fixed-end and cantilever nonlocal modified gradient beams under uniform transverse load are studied here. Analytically detected deflections are, moreover, normalized utilizing the corresponding transverse deformations of the local beam model \(\overline{w}_{{{\text{LOC}}}}\). Effects of the nonlocal characteristic parameter \(\zeta\) and the dilatation gradient parameter \(\eta_{0}\), deviatoric stretch gradient parameter \(\eta_{1}\), and rotation gradient parameter \(\eta_{2}\) on the flexural response of nano-beams are studied in Figs. 6 and 7, correspondingly, for fixed-end and cantilever beams. The comparison of the flexural behavior of nano-beams in the frameworks of the nonlocal modified gradient elasticity and the nonlocal gradient theory is shown in Figs. 8 and 9, respectively, for fixed-end and cantilever beams. The varying gradient and nonlocal parameters are assumed to range in the same interval as the wave dispersion analysis. The non-dimensional gyration radius is again set to \(1/20\).

Fig. 6
figure 6

Fixed-end nano-beams subject to a uniform load: effects of characteristic parameters on the normalized deflection

Full size image
Fig. 7
figure 7

Cantilever nano-beams subject to a uniform load: effects of characteristic parameters on the normalized deflection

Full size image
Fig. 8
figure 8

Comparison of augmented elasticity theories for uniformly loaded fixed-end nano-beams

Full size image
Fig. 9
figure 9

Comparison of augmented elasticity theories for uniformly loaded cantilever nano-beams

Full size image

It is deduced from the illustrated flexural behavior of nano-beams associated with either of the augmented elasticity theories that the nonlocal characteristic parameter \(\zeta\) has the effect of increasing the transverse deflection, and accordingly, a softening response in terms of the nonlocal characteristic parameter is confirmed. The transverse deflection of nano-beams associated with the nonlocal modified gradient elasticity and the nonlocal gradient theory decreases by increasing either of the gradient characteristic parameters \(\eta_{j} ,\eta_{s}\), and thus, a stiffening response in terms of the gradient characteristic parameters is realized. In the framework of the nonlocal modified gradient theory, the dilatation gradients parameter \(\eta_{0}\) and the deviatoric stretch gradient parameter \(\eta_{1}\) exhibit the highest and the lowest stiffening response, as deducible from Figs. 6 and 7. While the transverse deflection of nonlocal modified gradient beams with non-vanishing values of the rotation gradient parameter \(\eta_{2}\) is strictly lower than the flexural response of nano-beams with non-vanishing deviatoric stretch gradient parameter \(\eta_{1}\), it overestimates the transverse deflection of nonlocal modified gradient beams with non-vanishing dilatation gradient parameter \(\eta_{0}\). Nanoscopic effects of the nonlocal modified gradient elasticity with non-vanishing deviatoric stretch gradient parameter \(\eta_{1}\) are thus compared with the counterpart flexural results of the nonlocal gradient theory in Figs. 8 and 9. The transverse deflections of nano-beam consistent with the nonlocal gradient elasticity overestimate the counterpart flexural response of nonlocal modified grained beams with non-vanishing deviatoric stretch gradient parameter \(\eta_{1}\). This issue is notably occurred in consequence of the dominant stiffening effect of the gradient characteristic parameters \(\eta_{j}\) corresponding to the nonlocal modified gradient elasticity in comparison with the gradient parameter \(\eta_{s}\) associated with the nonlocal gradient theory. For vanishing of the gradient characteristic parameters, the flexural response of nano-beams in either of frameworks of the augmented elasticity theories coincides in terms of the nonlocal characteristic parameter. The local flexural behavior is inevitably recovered, as the characteristic parameters tend to zero. The size-dependent flexure of a fixed-end nano-beam is observed to be more affected by the characteristic parameters compared with the cantilever beam. Tables 2, 3, 4 and 5, respectively, summarize the normalized maximum transverse deflections of fixed-end and cantilever nano-beams, detected in the frameworks of the nonlocal modified gradient elasticity and the nonlocal gradient theory, for different values of the characteristic parameters.

Table 2 Normalized maximum deflection of a fixed-end nano-beam: (a) Nonloc. grad. elast. and (b) Nonloc. mod. grad. \(\left( {\eta_{1} \ne 0} \right)\)
Full size table
Table 3 Normalized maximum deflection of a fixed-end nonlocal modified gradient beam: (a) Nonloc. mod. grad. elast. \(\left( {\eta_{0} \ne 0} \right)\) and (b) Nonloc. mod. grad. elast. \(\left( {\eta_{2} \ne 0} \right)\)
Full size table
Table 4 Normalized maximum deflection of a cantilever nano-beam: (a) Nonloc. grad. elast. and (b) Nonloc. mod. grad. elast. \(\left( {\eta_{1} \ne 0} \right)\)
Full size table
Table 5 Normalized maximum deflection of a cantilever nonlocal modified gradient beam: (a) Nonloc. mod. grad. elast. \(\left( {\eta_{0} \ne 0} \right)\) and (b) Nonloc. mod. grad. elast. \(\left( {\eta_{2} \ne 0} \right)\)
Full size table

5 Concluding remarks

Two main frameworks of the gradient elasticity theory and the nonlocal elasticity model are widely applied in the literature to address the structural response of materials at nanoscale. The gradient and nonlocal theories of elasticity yield to dissimilar stiffening and softening responses of nano-structures. Integrating the nonlocal and gradient approaches is accordingly of major interest in nano-mechanics. In the present study, the contribution of the nonlocal integral elasticity is appropriately introduced to the modified strain gradient theory via a consistent variational scheme. The conceived nonlocal modified gradient elasticity theory can suitably characterize the nonlocality effects as well as the effects of the dilatation gradient, deviatoric stretch gradient, and symmetric rotation gradient, overlooked in the framework of the classical nonlocal gradient model. The established augmented elasticity theory is applied to nano-sized beams in flexure with kinematic constrains of applicative interest in nano-engineering. The integro-differential constitutive law is consistently restored with the equivalent differential formulation equipped with the proper form of the nonstandard boundary conditions. The size-dependent constitutive law and associated higher-order boundary conditions of the nonlocal elasticity model, modified strain gradient theory, and nonlocal gradient elasticity are demonstrated to be restored under particular ad hoc assumptions. A further discussion is made on the so-called nonlocal couple stress framework, deduced via overlooking the nanoscopic effects of the dilatation gradient and the deviatoric stretch gradient. The over-constrained boundary value problem governing the flexure of a nano-sized beam consistent with the nonlocal couple stress model is evinced to be ill-posed. On the contrary, the well posedness of the introduced nonlocal modified gradient problem is illustrated by rigorous examination of the elastostatic flexure and the wave dispersion phenomenon. The MD simulations results are utilized to successfully identify the characteristic parameters associated with the nonlocal modified gradient theory. The qualitative aspects of the wave dispersive behavior are realized to be captured with a better accuracy in the framework of the nonlocal modified gradient elasticity theory. The importance of applying the proposed augmented elasticity theory to more accurately reflect the size-dependency of nano-structured materials is therefore demonstrated. A practical solution approach is applied to derive the analytical solution of the flexure problem. Numerical behavior of the transverse deflection of the nonlocal modified gradient beam is graphically illustrated in comparison with the nonlocal gradient elasticity counterpart results. Nanoscopic effects of different gradient length-scale parameters are thoroughly studied, and the dominant stiffening effect of the gradient characteristic parameters associated with the nonlocal modified gradient elasticity theory is confirmed. The established augmented elasticity theory can advantageously capture and simulate both the stiffening and softening structural responses of nano-materials and, accordingly, provides a beneficial approach for nanoscopic analysis of the field quantities.