Survey of third- and fourth-order dispersions including ellipticity angle in birefringent fibers on W-shaped soliton solutions and modulation instability analysis

Abstract

In this work, the modified Sardar sub-equation method is used to construct optical soliton solutions to the coupled nonlinear Schrödinger equation (CNLSE) having third-order and fourth-order dispersions describing short-pulse propagation in two-core fibers. Several solutions are determined including W-shaped bright, dark soliton solutions, singular soliton solutions, periodic function solutions and the combined complex soliton solutions. It should be noted that this integration scheme is very powerful mathematical tools for obtaining exact optical soliton solutions of nonlinear evolution equations. Under suitable values for the physical parameters, some representative wave structures are graphically displayed. In addition, the linear stability technic is used to analyze the modulation gain spectra in the birefringence associated with an ellipticity angle. In our knowledge, these obtained results are new in the context of nonlinear birefringent optical fibers.

1 Introduction

The greatest concern nowadays is localized waves known for their wide application in various fields of science and engineering. The best known are bright and dark solitons used in optical fibers communication systems. To this aim, numerous works have known exhilarating successes followed by their direct application [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38]. It should be emphasized that the results obtained are subject to the parameters which constitute the nonlinear equations, as well as the constraint conditions necessary for their validity. To achieve this, many works were highlighted concerning temporal, spatiotemporal and gray solitons associated with high-order dispersions terms and several nonlinearities terms like Kerr, power law, parabolic law type and so on [1,2,3,4,5,6,7,8,9,10,11,12].

Obtaining these solitons has been facilitated by the advent of mathematical methods in the last decade. Diverse works have been done successfully using these methods, see Refs. [21,22,23,24,25,26,27,28,29,30,31,32,33,34]. However, getting these solutions does not guarantee the stability of the latter, because the presence of the dispersion and nonlinearity terms can generate the phenomenon of modulation instability (MI). To show out the effects of the dispersions and nonlinearities on the MI gain spectra, many authors have used the manner of birefringent associate to an ellipticity angle. The most studied and used MI gain spectra have been pointed out in linear and circular birefringence and zero-birefringence in nonlinear optical fibers [6, 8, 10, 11].

MI is one of the phenomena which is essential in study of nonlinear systems. Concerning the MI analysis, several works have been carried out in such models to describe this aspect inside optical fiber and MI phenomenon in Refs. [1,2,3,4,5,6,7,8,9,10,11,12,13]. MI having effects in birefringent two-core fiber (TCF) in normal and anomalous dispersive regime has motivated extensive inducement in nonlinear propagation of wave in optical fibers [9,10,11]. Solitons in birefringent optical fibers possess are polarized into two pulses owing to fibers non-consistencies and other mechanism elements that take place from fibers devices. These have resulted in many issues including rise to many matter between other, the differential group delay, the polarization mode dispersion and so on [39,40,41,42]. To carry out analytical investigation of specific shapes of the solitons “called” W-shaped bright and dark solitons in nonlinear TCFs associated with third- and fourth-order dispersion terms in birefringent fibers, we considered the dimensionless CNLSE describing short-pulse propagation in birefringent fibers given by [43]

$$\begin{aligned}&iu_t+\beta _2u_{xx}+i\beta _3u_{xxx}+\beta _4u_{xxxx}+\lambda \left( |u|^2+\delta |v|^2 \right) u=0,\nonumber \\&iv_t+\beta _2v_{xx}+i\beta _3v_{xxx}+\beta _4v_{xxxx}+\lambda \left( |v|^2+\delta |u|^2 \right) v=0. \end{aligned}$$

(1)

where draws $\beta _2, \beta _3, \beta _4$, are, respectively, the group velocity dispersion (GVD), the third-order 3OD and fourth-order dispersion 4OD. However, $\delta$ and $\lambda$ denote the nonlinearity coefficient and cross-phase modulation term (XPM) in birefringent fibers, respectively. Furthermore, ellipticity angle is expressed in the form of $\delta =\frac{2+2\sin ^2(\theta )}{2+\cos ^2(\theta )}$. We notice that three forms of birefringence are known in the literature. The first named zero-birefringence corresponds to ($\delta =0$) (i.e., total absence of XMP). The second and third are called linear and circular birefringence (i.e., $\theta =0^{\circ }$ and $\theta =90^{\circ }$), respectively [43]. It is important to notice that XPM, higher-order dispersions terms and birefringent could help to provoke the MI.

We organized the work as follows: Sect. 2 gives the survey of the mathematical algorithm named the modified Sardar sub-equation method. In Sect. 3, we apply the method to take out W-shaped bright, W-shaped dark optical solitons and other solutions of the CNLSE. However, in Sect. 4 the linear stability technic is applied to study numerically the MI gain spectra under the effects of 3OD and 4OD including the effects of ellipticity angle in birefringent fibers. In the last section, we conclude and give some perspectives.

2 Survey of the modified Sardar sub-equation method

The first step is constituted by the following nonlinear equations (NLEs)

$$\begin{aligned}&F(u, u_x, u_t, u_{xx}, u_{tt}, \ldots )=0, \end{aligned}$$

(2)

and H is the polynomial function in terms of an unknown u(x, t).

The solutions of Eq. (2) consist to adopt the transformation assumption as

$$\begin{aligned}&u(x,t)=U(\xi ), \quad \xi =x-\mu t. \end{aligned}$$

(3)

Here, $\mu$ is different to zero. To obtain the nonlinear ordinary differential equation (NODE) of Eq. (2), we use Eq. (3) into Eq. (2), which gives the following NODE

$$\begin{aligned}&G(U,U^\prime ,\mu U^\prime , U^{\prime \prime }, \mu ^2 U^{\prime \prime }, \ldots )=0, \end{aligned}$$

(4)

where ($\prime$) denotes $\frac{\hbox {d}U}{\hbox {d}\xi }$ and so on. Estimate the solution of Eq. (4) in the form of [8]

$$\begin{aligned}&U(\xi )=H_0+\sum ^n_{i=1}H_i\left[ \phi (\xi )\right] ^i, \end{aligned}$$

(5)

where $\phi (\xi )$ satisfies the following nonlinear ordinary equation [8]

$$\begin{aligned}&(\phi ^\prime (\xi ))^2=\rho +a\phi (\xi )^2+b\phi (\xi )^4. \end{aligned}$$

(6)

The parameters $\rho$, $H_{i}\ne 0$($i=1, 2,\ldots , N$) are constants to be determined later. Otherwise, Eq. (6) is an ordinary differential equation which is not totally dependent of integrability of nonlinear equation and can be used to large numbers of nonlinear partial differential equations without complication compared to [22, 27, 28, 31, 44,45,46,47,48,49,50].

The nonlinear ordinary equation Eq. (6) in terms of the parameters $\rho , \, a, \, b$ has the following solutions

• Case 1. For $\rho =0$.

When $a>0$ and $b\ne 0$, it is unearthed bright and singular soliton

$$\begin{aligned}&\phi ^{\pm }_{1}(\xi )=\pm \sqrt{-{\frac{{pqa}}{b}}}\hbox {sech}_{{{pq}}} \left( \sqrt{a}\xi \right) , \end{aligned}$$

(7)

and

$$\begin{aligned}&\phi ^{\pm }_{2}(\xi )=\pm \sqrt{{\frac{{pqa}}{b}}}\hbox {csch}_{{{pq}}} \left( \sqrt{a}\xi \right) . \end{aligned}$$

(8)

When $a<0$ and $b\ne 0$, we get periodic and singular function solutions

$$\begin{aligned}&\phi ^{\pm }_{3}(\xi )=\pm \sqrt{-{\frac{{pqa}}{b}}}\sec _{{{pq}}} \left( \sqrt{-a}\xi \right) , \end{aligned}$$

(9)

and

$$\begin{aligned}&\phi ^{\pm }_{4}(\xi )=\pm \sqrt{-{\frac{{pqa}}{b}}}\csc _{{{pq}}} \left( \sqrt{-a}\xi \right) . \end{aligned}$$

(10)

• Case 2. For $\rho =\frac{1}{4}\frac{a^2}{b}$.

When $a<0$ and $b>0$, the following dark, singular and the combined soliton solutions are obtained

$$\begin{aligned}&\phi ^{\pm }_{5}(\xi )=\pm \frac{1}{2}\sqrt{-{\frac{{2a}}{b}}}\tanh _{{{pq}}} \left( \frac{1}{2}\sqrt{-2a}\xi \right) , \end{aligned}$$

(11)

$$\begin{aligned}&\phi ^{\pm }_{6}(\xi )=\pm \frac{1}{2}\sqrt{-{\frac{{2a}}{b}}}\coth _{{{pq}}} \left( \frac{1}{2}\sqrt{-2a}\xi \right) , \end{aligned}$$

(12)

$$\begin{aligned}&\phi ^{\pm }_{7}(\xi )=\pm \frac{1}{2}\sqrt{-{\frac{2a}{b}}} \left( \tanh _{{{pq}}} \left( \sqrt{-2a}\xi \right) \pm i\sqrt{pq}\hbox {sech}_{{{pq}}} \left( \sqrt{-2a}\xi \right) \right) , \end{aligned}$$

(13)

$$\begin{aligned}&\phi ^{\pm }_{8}(\xi )=\pm \frac{1}{2}\sqrt{-{\frac{2a}{b}}} \left( \coth _{{{pq}}} \left( \sqrt{-2a}\xi \right) \pm \sqrt{pq}\hbox {csch}_{{{pq}}} \left( \sqrt{-2a}\xi \right) \right) , \end{aligned}$$

(14)

$$\begin{aligned}&\phi ^{\pm }_{9}(\xi )=\pm \frac{1}{4}\sqrt{-{\frac{2a}{b}}} \left( \tanh _{{{pq}}} \left( \sqrt{\frac{-a}{8}}\xi \right) \pm \sqrt{pq}\coth _{{{pq}}} \left( \sqrt{\frac{-a}{8}}\xi \right) \right) . \end{aligned}$$

(15)

• Case 3. For $\rho =\frac{1}{4}\frac{a^2}{b}$.

If $a>0$ and $b>0$, we obtain trigonometric function solutions as

$$\begin{aligned}&\phi ^{\pm }_{10}(\xi )=\pm \frac{1}{2}\sqrt{{\frac{{2a}}{b}}}\tan _{{{pq}}} \left( \frac{1}{2}\sqrt{2a}\xi \right) , \end{aligned}$$

(16)

$$\begin{aligned}&\phi ^{\pm }_{11}(\xi )=\pm \frac{1}{2}\sqrt{{\frac{{2a}}{b}}}\cot _{{{pq}}} \left( \frac{1}{2}\sqrt{2a}\xi \right) , \end{aligned}$$

(17)

$$\begin{aligned}&\phi ^{\pm }_{12}(\xi )=\pm \frac{1}{2}\sqrt{{\frac{2a}{b}}} \left( \tan _{{{pq}}} \left( \sqrt{2a}\xi \right) \pm \sqrt{pq}\sec _{{{pq}}} \left( \sqrt{2a}\xi \right) \right) , \end{aligned}$$

(18)

$$\begin{aligned}&\phi ^{\pm }_{13}(\xi )=\pm \frac{1}{2}\sqrt{{\frac{2a}{b}}} \left( \cot _{{{pq}}} \left( \sqrt{2a}\xi \right) \pm \sqrt{pq}\csc _{{{pq}}} \left( \sqrt{2a}\xi \right) \right) , \end{aligned}$$

(19)

$$\begin{aligned}&\phi ^{\pm }_{14}(\xi )=\pm \frac{1}{4}\sqrt{{\frac{2a}{b}}} \left( \tan _{{{pq}}} \left( \sqrt{\frac{a}{8}}\xi \right) \pm \sqrt{pq}\cot _{{{pq}}} \left( \sqrt{\frac{a}{8}}\xi \right) \right) . \end{aligned}$$

(20)

We noted that, $\hbox {sech}_{pq}(\xi )=\frac{2}{pe^\xi +qe^{-\xi }}$,   $\hbox {csch}_{pq}(\xi )=\frac{2}{pe^\xi -qe^{-\xi }}$,   $\sec _{pq}(\xi )=\frac{2}{pe^{i\xi }+qe^{-i\xi }}$, $\csc _{pq}(\xi )=\frac{2i}{pe^{i\xi }-qe^{-i\xi }}$,   $\tanh _{pq}(\xi )=\frac{pe^\xi -qe^{-\xi }}{pe^\xi +qe^{-\xi }}$,   $\coth _{pq}(\xi )=\frac{pe^\xi +qe^{-\xi }}{pe^\xi -qe^{-\xi }}$,  $\tan _{pq}(\xi )=-i\frac{pe^{i\xi }-qe^{-i\xi }}{pe^{i\xi }+qe^{-i\xi }}$ and $\cot _{pq}(\xi )=i\frac{pe^{i\xi }+qe^{-i\xi }}{pe^{i\xi }-qe^{-i\xi }}$.

Where p and q are constants greater than zero and called deformation parameters.

3 Application of the modified Sardar sub-equation method to the CNLSE in birefringence

In order to emphasize the attitude of exact solutions of the higher dispersive CNSE in birefringent fibers including the effects of the ellipticity angle, the initial condition is to adopt the transformation hypothesis in the form of

$$\begin{aligned}&u(x,t)=\phi _1(\xi )e^{i( x-\vartheta t)}, \end{aligned}$$

(21)

$$\begin{aligned}&v(x,t)=\phi _2(\xi )e^{i( x-\vartheta t)}, \end{aligned}$$

(22)

and $\xi =x-\vartheta t$.

Next, using Eqs. (21) and (22) in the set of CNLSE, the imaginary parts give

$$\begin{aligned}&\vartheta =2\left( \beta _2-\beta _3\right) , \, \beta _3=-4\beta _4. \end{aligned}$$

(23)

Therefore, from the real parts it is obtained

$$\begin{aligned}&m_1\phi _1+m_2\phi ^{\prime \prime }_1+\beta _4\phi ^{\prime \prime \prime \prime }_1+\lambda \phi ^3_1+\lambda \delta \phi ^2_2\phi _1=0, \end{aligned}$$

(24)

and

$$\begin{aligned}&m_1\phi _2+m_2\phi ^{\prime \prime }_2+\beta _4\phi ^{\prime \prime \prime \prime }_2+\lambda \phi ^3_2+\lambda \delta \phi ^2_1\phi _2=0, \end{aligned}$$

(25)

where

$$\begin{aligned}&m_1=\beta _2+5\beta _4, \quad m_2=6\beta _4+\beta _2. \end{aligned}$$

(26)

We assume the solution of Eqs. (24) and (25) as follows

$$\begin{aligned}&\phi _1(\xi )=H_0+\sum ^n_{i=1}H_i\left[ \phi (\xi )\right] ^i, \end{aligned}$$

(27)

$$\begin{aligned}&\phi _2(\xi )=E_0+\sum ^n_{i=1}E_i\left[ \phi (\xi )\right] ^i. \end{aligned}$$

(28)

Applying the homogeneous balance principle, it is revealed $n=2$. Therewith,

$$\begin{aligned}&\phi _1(\xi )=H_0+H_1\phi (\xi )+H_2\phi (\xi )^2, \end{aligned}$$

(29)

$$\begin{aligned}&\phi _2(\xi )=E_0+E_1\phi (\xi )+E_2\phi (\xi )^2. \end{aligned}$$

(30)

To construct the soliton solutions to the set of coupled of equations, we insert Eqs. (29, 30) and (6) into Eq. (24) or Eq. (25). With the aid of MAPLE 18, the system of algebraic equations is obtained. From there, solving the obtained system, gives

• Case 1. For $\rho =0$.

$$\begin{aligned} H_{{0}}= & {} 0, \, H_{{1}}=0, \, H_{{2}}=\sqrt{3}\sqrt{{\frac{560{a}^{2}{\beta ^2_{{4}}}-40\beta _{{4}}m_{{2}}a+3{m^2_{{2}}}-40\beta _{{4}}m_{{1}}}{\lambda \left( 16\,\beta _{{4}}{a}^{2}+m_{{1}}+4m_{{2}}a \right) }}}b, \,\nonumber \\ E_{{0}}= & {} \sqrt{-{\frac{16\,\beta _{{4}}{a}^{2}+m_{{1}}+4\,m_{{2}}a}{\lambda \delta }}},\nonumber \\ E_{{1}}= & {} 0, \, E_2=-\frac{3b (20 a\beta _4+m_2)}{\sqrt{-{\frac{16\,\beta _{{4}}{a}^{2}+m_{{1}}+4\,m_{{2}}a}{\lambda \, \delta }}}\delta \,\lambda }. \end{aligned}$$

(31)

and

$$\begin{aligned} H_{{0}}= & {} 0, \, H_{{1}}={\frac{\sqrt{-20\,\lambda \,a\beta _{{4}}b-2\lambda \,m _{{2}}b+4\sqrt{6{b}^{2}{\lambda }^{2}\beta _{{4}}\left( \beta _{{4}}{a}^{2}+m_{{2}}a+m_{{1}} \right) }}}{\lambda }}, \, H_2=0, \,\nonumber \\ E_0= & {} \frac{\sqrt{6{b}^{2}{\lambda }^{2}\beta _{{4}} \left( \beta _{{4}}{a}^{2}+m_{{2}}a+m_{{1}} \right) }}{{\lambda }^{2}\delta \sqrt{-{\frac{6\beta _{{4}}b}{\lambda \,\delta }}}},\nonumber \\ E_1= & {} 0, \, E_2=2\sqrt{-{\frac{6\beta _{{4}}b}{\lambda \delta }}}. \end{aligned}$$

(32)

The above results have been obtained based on the constraint relation below:

$$\begin{aligned}&-20\lambda a\beta _4b-2\lambda m_2b+4\sqrt{6b^2\lambda ^{2}\beta _4\left( \beta _4{a}^{2}+m_2a+m_1 \right) }>0,\\&\quad 6{b}^{2}\lambda ^{2}\beta _4\left( \beta _{{4}}{a}^{2}+m_{{2}}a+m_1\right)>0,\\&\qquad (-6\beta _4 b)\times (\lambda \delta )>0. \end{aligned}$$

We can thus formulate the general solutions as follows.

From Eq. (31), we write

$$\begin{aligned}&u^{\pm }_{m}(x,t)=e^{i(x-v t)}\left( H_2\left( \phi ^{\pm }_{m}\right) ^2\right) , \, m=1\ldots 4, \end{aligned}$$

(33)

and

$$\begin{aligned}&v^{\pm }_{m}(x,t)=e^{i(x-v t)}\left( E_0+E_2\left( \phi ^{\pm }_{m}\right) ^2\right) , \, m=1\ldots 4. \end{aligned}$$

(34)

At the same time, by referring to Eq. (32), we get to

$$\begin{aligned}&u^{\pm }_{m}(x,t)=e^{i(x-v t)}\left( H_1\phi ^{\pm }_{m}\right) , \, m=1\ldots 4, \end{aligned}$$

(35)

and

$$\begin{aligned}&v^{\pm }_{m}(x,t)=e^{i(x-v t)}\left( E_0+E_2\left( \phi ^{\pm }_{m}\right) ^2\right) , \, m=1\ldots 4. \end{aligned}$$

(36)

Therewith, using Eq. (31) fourth types of soliton solutions are obtained

• When $a>0$ and $b\ne 0$, bright optical soliton is unearthed

$$\begin{aligned}&u^{\pm }_{1}(x,t)=e^{i( x-\vartheta t)}\left( H_2\left( \sqrt{-{\frac{{pqa}}{b}}}\hbox {sech}_{{{pq}}} \left( \sqrt{a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right) ^2\right) , \end{aligned}$$

(37)

and

$$\begin{aligned}&v^{\pm }_{1}(x,t)=e^{i( x-\vartheta t)}\left( E_0\pm E_2\left[ \sqrt{-{\frac{{pqa}}{b}}}\hbox {sech}_{{{pq}}} \left( \sqrt{a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right] ^2\right) . \end{aligned}$$

(38)

Figures 1 and 2 illustrate the effects of the 4OD along with the parameter of the modified Sardar sub-equation method and $p=q=1$. The influence of these parameters pointed out W-chirped bright optical soliton solutions in TCFs. Furthermore, when the absolute value of the 4OD increases the maximum amplitude of the W-shaped bright is obtained (see Fig. 2 ($C_4)$).

Fig. 1

Spatiotemporal plot evolution of the W-chirped bright optical solitons in two-core fiber TCF $|v^+_1(x,t)|$ at $\mathbf{h}_\mathbf{1}$ [$\beta _4=-1.002 \, ps^4/\hbox {km}, E_0=0.015,\, E_1=0, \, E_2=1.015, \, \vartheta =0.015 \, \hbox {m/s}, \, a=0.4729, \, \theta =30^{\circ } \, b=20.027$], $\mathbf{h}_\mathbf{2}$ [$\beta _4=-1.002\, ps^4/\hbox {km}, E_0=0.015,\, E_1=0, \, E_2=1.015, \, \vartheta =0.015 \, \hbox {m/s}, \, a=0.4254, \, \theta =30^{\circ } \, b=20.027, \, \lambda =0.475$]

Singular soliton solutions are unearthed

$$\begin{aligned}&u^{\pm }_{2}(x,t)=e^{i( x-\vartheta t)}\left( H_2\left( \sqrt{{\frac{{pqa}}{b}}}\hbox {csch}_{{{pq}}} \left( \sqrt{a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right) ^2\right) , \end{aligned}$$

(39)

and

$$\begin{aligned}&v^{\pm }_{2}(x,t)=e^{i( x-\vartheta t)}\left( E_0\pm E_2\left( \sqrt{{\frac{{pqa}}{b}}}\hbox {csch}_{{{pq}}} \left( \sqrt{a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right) ^2\right) . \end{aligned}$$

(40)

For $a<0$ and $b\ne 0$, we get periodic and singular function solutions

$$\begin{aligned}&u^{\pm }_{3}(x,t)=e^{i( x-\vartheta t)}\left( H_2\left( \sqrt{-{\frac{{pqa}}{b}}}\sec _{{{pq}}}\left( \sqrt{-a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right) ^2\right) , \end{aligned}$$

(41)

$$\begin{aligned}&v^{\pm }_{3}(x,t)=e^{i( x-\vartheta t)}\left( E_0\pm E_2\left[ \sqrt{-{\frac{{pqa}}{b}}}\sec _{{{pq}}} \left( \sqrt{-a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right] ^2\right) .\qquad \end{aligned}$$

(42)

And

$$\begin{aligned}&u^{\pm }_{4}(x,t)=e^{i( x-\vartheta t)}\left( H_2\left( \sqrt{-{\frac{{pqa}}{b}}}\csc _{{{pq}}} \left( \sqrt{-a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right) ^2 \right) , \end{aligned}$$

(43)

$$\begin{aligned}&v^{\pm }_{4}(x,t)=e^{i( x-\vartheta t)}\left( E_0\pm E_2\left[ \sqrt{-{\frac{{pqa}}{b}}}\csc _{{{pq}}} \left( \sqrt{-a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right] ^2\right) .\qquad \end{aligned}$$

(44)

Employing result of Eq. (32), we have to write

• While $a>0$ and $b\ne 0$, bright optical soliton is unearthed

$$\begin{aligned}&u^{\pm }_{1}(x,t)=e^{i( x-\vartheta t)}\left( \pm H_1\sqrt{-{\frac{{pqa}}{b}}}\hbox {sech}_{{{pq}}} \left( \sqrt{a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right) , \end{aligned}$$

(45)

and

$$\begin{aligned}&v^{\pm }_{1}(x,t)=e^{i( x-\vartheta t)}\left( E_0\pm E_2\left( \sqrt{-{\frac{{pqa}}{b}}}\hbox {sech}_{{{pq}}} \left( \sqrt{a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right) ^2\right) . \end{aligned}$$

(46)

Figures 1 and 2 illustrate the effects of the 4OD along with the parameter of the modified Sardar sub-equation method. The influence of these parameters points out W-chirped bright optical soliton solutions in TCFs. Furthermore, when the absolute value of the 4OD increases the maximum amplitude of the W-shaped bright is obtained (see Fig. 2 ($C_4)$). Singular soliton solutions are unearthed

$$\begin{aligned}&u^{\pm }_{2}(x,t)=e^{i( x-\vartheta t)}\left( \pm H_1\sqrt{{\frac{{pqa}}{b}}}\hbox {csch}_{{{pq}}} \left( \sqrt{a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right) , \end{aligned}$$

(47)

and

$$\begin{aligned}&v^{\pm }_{2}(x,t)=e^{i( x-\vartheta t)}\left( E_0\pm E_2\left( \sqrt{{\frac{{pqa}}{b}}}\hbox {csch}_{{{pq}}} \left( \sqrt{a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right) ^2\right) . \end{aligned}$$

(48)

• For $a<0$ and $b\ne 0$, we get periodic and singular function solutions

$$\begin{aligned}&u^{\pm }_{3}(x,t)=e^{i( x-\vartheta t)}\left( \pm H_1\sqrt{-{\frac{{pqa}}{b}}}\sec _{{{pq}}} \left( \sqrt{-a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right) , \end{aligned}$$

(49)

$$\begin{aligned}&v^{\pm }_{3}(x,t)=e^{i( x-\vartheta t)}\left( E_0\pm E_2\left( \sqrt{-{\frac{{pqa}}{b}}}\sec _{{{pq}}} \left( \sqrt{-a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right) ^2\right) . \qquad \end{aligned}$$

(50)

$$\begin{aligned}&u^{\pm }_{4}(x,t)=e^{i( x-\vartheta t)}\left( \pm H_1\sqrt{-{\frac{{pqa}}{b}}}\csc _{{{pq}}} \left( \sqrt{-a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right) , \end{aligned}$$

(51)

and

$$\begin{aligned}&v^{\pm }_{4}(x,t)=e^{i( x-\vartheta t)}\left( E_0\pm E_2\left( \sqrt{-{\frac{{pqa}}{b}}}\csc _{{{pq}}} \left( \sqrt{-a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right) ^2\right) . \end{aligned}$$

(52)

• Case 2. For $\rho =\frac{1}{4}\frac{a^2}{b}$.

Fig. 2

Spatiotemporal plot evolution of the W-chirped bright optical solitons in two-core fiber TCF $|v^+_1(x,t)|$ with the effects of the 4OD at $\mathbf{C}_\mathbf{1}$ [$\beta _4=-0.5002 \, \, ps^4/\hbox {km}, \, a=0.9603$], $\mathbf{C}_\mathbf{2}$ [$\beta _4=-0.6002\, \, ps^4/\hbox {km},\, a=0.8077$], $\mathbf{C}_\mathbf{3}$ [$\beta _4=-0.7802\, ps^4/\hbox {km}, \, a=0.6929$] and $\mathbf{C}_\mathbf{4}$ [$\beta _4=-0.8002 \, ps^4/\hbox {km}, \, a=0.6036$] for [$E_0=0.015,\, E_1=0, \, E_2=1.015, \, \vartheta =0.015 \, \hbox {m/s},\, \theta =45^{\circ } \, b=20.027, \, \lambda =0.012$]

The following results are obtained

$$\begin{aligned} H_{{0}}= & {} H_{{0}}, \, H_{{1}}=2\sqrt{-{\frac{2bH^2_0}{a}}}, \, H_2=-\frac{2H_0b}{a}, \,\nonumber \\ E_0= & {} \frac{-5\,{\lambda }^{2}{H^4_{{0}}}+36{a}^{4}{\beta ^2_{{4}}}-384{H_{{0 }}}^{2}\beta _{{4}}\lambda \,{a}^{2}}{\lambda \,\delta \, \left( 24\,\beta _{{4}}{a}^{2}+5\,\lambda \,{H_{{0}}}^{2} \right) \sqrt{-{\frac{30\,\beta _{{4}}{a}^{2}+\lambda \,{H^2_{{0}}}}{\lambda \delta }}}}, \, E_1=\frac{2\left( -\lambda {H^2_{{0}}}+12\beta _{{4}}{a}^{2} \right) \sqrt{-{\frac{2b}{a}}}}{\lambda \delta \,\sqrt{-{\frac{30\beta _{{4}}{a}^{2}+\lambda {H^2_{{0}}}}{\lambda \delta }}}},\nonumber \\ E_2= & {} \frac{2\,\sqrt{-{\frac{30\beta _{{4}}{a}^{2}+\lambda {H^2_{{0}}}}{\lambda \delta }}}b}{a}, \,\nonumber \\ \beta _2= & {} {\frac{36{a}^{2} \left( 324{a}^{6}{\beta _{{4}}}^{3}-4764{H^2_{{0}}}{\beta ^2_{{4}}}\lambda {a}^{4}+3225{\lambda }^{2}{H^4_{{0}}}\beta _{{4}}{a}^{2}+100{\lambda }^{3}{H^6_{{0}}} \right) \beta _{{4}}}{ \left( 30\beta _{{4}}{a}^{2}+\lambda {H^2_{{0}}} \right) \left( 24\beta _{{4}}{a}^{2}+5\lambda {H^2_{{0}}}\right) ^{2}}}-5\beta _4,\nonumber \\ \beta _3= & {} \frac{4}{3}{\frac{a \left( 1224{a}^{4}{\beta _{{4}}}^{2}+3030\,{H^2_{{0}}}\beta _{{4}}\lambda \,{a}^{2}-65\,{\lambda }^{2}{H^4_{{0}}}\right) \beta _{{4}}}{ \left( 30\beta _{{4}}{a}^{2}+\lambda \,{H^2_{{0}}} \right) \left( 24\beta _{{4}}{a}^{2}+5\lambda {H^2_{{0}}}\right) }}+\frac{2}{3}\beta _2. \end{aligned}$$

(53)

Considering Eq. (53), we establish the following combined soliton solutions under the following conditions

• For $a<0$ and $b>0$, we can formulate dark optical solitons and other combined solitons solutions depending on the parameters a and b

With regard to dark optical solitons, we arrive at the following formulation

$$\begin{aligned} u^{\pm }_{5}(x,t)= & {} e^{i( x-\vartheta t)}\left\{ H_0\pm \frac{H_1}{2}\sqrt{-{\frac{{2a}}{b}}}\tanh _{{{pq}}} \left( \frac{1}{2}\sqrt{-2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right. \nonumber \\&\left. \pm H_2\left[ \frac{1}{2}\sqrt{-{\frac{{2a}}{b}}}\tanh _{{{pq}}} \left( \frac{1}{2}\sqrt{-2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right] ^2\right\} , \end{aligned}$$

(54)

$$\begin{aligned} v^{\pm }_{5}(x,t)= & {} e^{i( x-\vartheta t)}\left\{ E_0\pm \frac{1}{2}E_1\sqrt{-{\frac{{2a}}{b}}}\tanh _{{{pq}}} \left( \frac{1}{2}\sqrt{-2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right. \nonumber \\&\left. \pm E_2\left[ \frac{1}{2}\sqrt{-{\frac{{2a}}{b}}}\tanh _{{{pq}}} \left( \frac{1}{2}\sqrt{-2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right] ^2\right\} . \end{aligned}$$

(55)

Fig. 3

Spatiotemporal plot evolution ($S_1$)3D and ($S_2$) 2D of the bright optical solitons in two-core fiber TCF $|v^-_1(x,t)|$ with the parameters of Eq. (32) for [$E_0=-0.1789,\, E_1=0, \, E_2=1.2526, \, \vartheta =0.12 \, \hbox {m/s},\, \lambda =-1.01 \, b=-1.107, \, a=0.5, \, \beta _2=0.0202\, ps^2/\hbox {km}, \, \beta _4=-0.05102 \, ps^4/\hbox {km}, \, \theta =\frac{\pi }{6}, \, \vartheta =0.1420 \,\hbox {m/s}$]

Fig. 4

Spatiotemporal plot evolution ($S_3$)3D and ($S_4$) 2D the dark optical solitons in two-core fiber TCF $|v^+_1(x,t)|$ with the parameters of Eq. (32) for [$E_0=-0.1839,\, E_1=0, \, E_2=1.2526, \, \vartheta =0.1420 \, \hbox {m/s},\, \lambda =-1.01 \, b=-1.107, \, a=0.025, \, \beta _2=0.0202\, ps^2/\hbox {km}, \, \beta _4=-0.05102 \, ps^4/\hbox {km}, \, \theta =\frac{\pi }{6}, \, \vartheta =0.1420 \,\hbox {m/s}$]

Meantime, Fig. 3 shows the spatiotemporal evolution of bright optical soliton in TCFs with the effects of the 3OD, 4OD and the normal group velocity dispersion for $p=q=1$. Besides, Fig. 4 depicts dark optical soliton. Figure 5 shows the plot evolution of the analytical solution Eq. (54) at $p=q=1$ under the influence of the higher-order dispersions terms in normal group velocity dispersive regime. The obtained dark soliton is well known in optical fibers communication because of its robustness and the stability. It can travel over long distance without any distortion and can help to secure information in case of digital signals. Considering the effects of the ellipticity angle, the behavior of the W-shaped dark optical soliton in different gaps of the ellipticity angle is highlighted (see Figs. 6, 7). It is important to notice that, in this case, higher-order dispersion is also present. In optical fibers, the 4OD is very important when the pulse becomes shorter than 10 fento-second [6].

Fig. 5

Spatiotemporal plot evolution of optical solitons in two-core fiber TCF $|u^+_5(x,t)|$ including higher-order dispersions and zero-birefringence. We employ the parameters of Eq. (53). The following parameters are used (i)[$H_0=0.24, \, H_1=1.2978, \, H_2=12.1348, \, \beta _2=0.6 \,ps^2/\hbox {km}, \, \beta _3=0.58\, ps^3/\hbox {km}, \, v=0.04, p=q=1$ ],   (ii)[$H_0=0.5, \, H_1=1.8732, \, H_2=0.8772, \, \beta _2=0.6 \,ps^2/\hbox {km}, \, \beta _3=0.58\, ps^3/\hbox {km}, \, v=0.04, p=q=1$ ],  (iii)[$H_0=1.5, \, H_1=3.2444, \, H_2=2.6316, \, \beta _2=0.6 \,ps^2/\hbox {km}, \, \beta _3=0.58 ps^3/\hbox {km}, \, v=0.04, p=q=1$ ],   (4i)[$H_0=2.5, \, H_1=4.1885\, H_2=4.3860, \, \beta _2=0.6 \,ps^2/\hbox {km}, \, \beta _3=0.58\, ps^3/\hbox {km}, \, a=-10.0712, \, b=0.8, \, v=0.04, p=q=1$],  (5i)[$H_0=0.8, \, H_1=2.3694,\, H_2=1.4035, \, \beta _2=0.6 \,ps^2/\hbox {km}, \, \beta _3=0.58\, ps^3/\hbox {km}, \, a=-0.312, \, b=0.8, \, v=0.04, p=q=1$ ],   (6i)[$H_0=4.5, \, H_1=5.6195,\, H_2=7.8947, \, \beta _2=0.6 \,ps^2/\hbox {km}, \, \beta _3=0.58\, ps^3/\hbox {km}, \, a=-0.912, \, b=0.8, \,v=0.04, \, p=q=1$ ]

Fig. 6

Spatiotemporal plot evolution the W-shaped dark optical solitons in two-core fiber TCF $|v^-_5(x,t)|$ with the effect of the ellipticity angle in birefringent fiber. We use the parameters of Eq. (45) when the FOD is present at ($Z_1$) [$\theta =\frac{\pi }{30},\, E_0=0.0866\, E_1=0.278, \, E_2=0.2166,\, \beta _2=210.006 ps^2/\hbox {km}, \, \beta _3=-100.014\, ps^3/\hbox {km}$], ($Z_2$) [$\theta =\frac{\pi }{3}, \, E_0=0.0418, \, E_1=0.8701, \, E_2=0.1045, \, \beta _2=154.016\, \beta _3=-98.075$], ($Z_3$) [$\theta =\frac{\pi }{4}, \, E_0=0.0528, \, E_1=0.1789, \, E_2=0.1320, \, \beta _2=108.035, \, \beta _3=-74.58$], ($Z_4$) [$\theta =\frac{\pi }{6}, \, E_0= 0.0670, \, E_1=0106.124\, \beta _3=-67.245, \, \beta _2=102.65 \, E_2=0.1677$], respectively. The parameters used are [$H_0=0.1005, \, E_1=0, \, \vartheta =0.12 \, m/s, \, b=0.0107, \, a=-0.2140, \, \beta _4=0.1002 \,ps^4/km, p=q=1$]

Fig. 7

Spatiotemporal plot evolution the W-shaped dark optical solitons in two-core fiber TCF $|v^-_5(x,t)|$ in zero-birefringence. We use the parameters of Eq. (45) when the FOD is present. The suitable parameters are [$\theta =0^{\circ }\, a=-0.2140, \, E_1=0.245, \, H_0=0.1005,\, E_2=0.2194,\, E_0=0.0877\, \vartheta =0.12\, m/s, \, b=0.0107, \, a=-0.2140, \, \beta _4=0.1002 \,ps^4/km, \, \beta _2=230.45 \,ps^2/km, \, \beta _3=-90.45 \,ps^3/km, \, \delta =2, \, \lambda =0.001$]

For trigonometric solutions type, the results are as follows

$$\begin{aligned} u^{\pm }_{6}(x,t)= & {} e^{i( x-\vartheta t)}\Bigg \{H_0\pm H_1\frac{1}{2}\sqrt{-{\frac{{2a}}{b}}}\coth _{{{pq}}} \left( \frac{1}{2}\sqrt{-2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \nonumber \\&\pm H_2\left[ \frac{1}{2}\sqrt{-{\frac{{2a}}{b}}}\coth _{{{pq}}} \left( \frac{1}{2}\sqrt{-2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right] ^2\Bigg \}, \end{aligned}$$

(56)

$$\begin{aligned} v^{\pm }_{6}(x,t)= & {} e^{i( x-\vartheta t)}\left\{ E_0\pm \frac{1}{2}E_1\sqrt{-{\frac{{2a}}{b}}}\coth _{{{pq}}} \left( \frac{1}{2}\sqrt{-2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right. \nonumber \\&\left. \pm E_2\left[ \frac{1}{2}\sqrt{-{\frac{{2a}}{b}}}\coth _{{{pq}}} \left( \frac{1}{2}\sqrt{-2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right] ^2\right\} . \end{aligned}$$

(57)

Those which are combined are expressed as indicated by the following solutions

$$\begin{aligned} u^{\pm }_{7}(x,t)= & {} e^{i( x-\vartheta t)}\Bigg \{H_0 \pm H_1\left[ \frac{1}{2}\sqrt{-{\frac{2a}{b}}} \left( \tanh _{{{pq}}} \left( \sqrt{-2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right. \right. \nonumber \\&\left. \left. \pm i\sqrt{pq}\hbox {sech}_{{{pq}}} \left( \sqrt{-2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right) \right] \nonumber \\&\pm H_2\left[ \frac{1}{2}\sqrt{-{\frac{2a}{b}}} \left( \tanh _{{{pq}}} \left( \sqrt{-2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right. \right. \nonumber \\&\left. \left. \pm i\sqrt{pq}\hbox {sech}_{{{pq}}} \left( \sqrt{-2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right) \right] ^2\Bigg \}, \end{aligned}$$

(58)

$$\begin{aligned} v^{\pm }_{7}(x,t)= & {} e^{i( x-\vartheta t)}\Bigg \{E_0\pm E_1\left[ \frac{1}{2}\sqrt{-{\frac{2a}{b}}} \left( \tanh _{{{pq}}} \left( \sqrt{-2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right. \right. \nonumber \\&\left. \left. \pm i\sqrt{pq}\hbox {sech}_{{{pq}}} \left( \sqrt{-2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right) \right] \nonumber \\&\pm E_2\left[ \frac{1}{2}\sqrt{-{\frac{2a}{b}}} \left( \tanh _{{{pq}}} \left( \sqrt{-2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right. \right. \nonumber \\&\left. \left. \pm i\sqrt{pq}\hbox {sech}_{{{pq}}} \left( \sqrt{-2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right) \right] ^2\Bigg \}. \end{aligned}$$

(59)

The combined trigonometric and singular functions solutions are obtained

$$\begin{aligned} u^{\pm }_{8}(x,t)= & {} e^{i( x-\vartheta t)}\Bigg \{H_0\pm H_1\left[ \frac{1}{2}\sqrt{-{\frac{2a}{b}}} \left( \coth _{{{pq}}} \left( \sqrt{-2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right. \right. \nonumber \\&\left. \left. \pm \sqrt{pq}\hbox {csch}_{{{pq}}} \left( \sqrt{-2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right) \right] \nonumber \\&\pm H_2\left[ \frac{1}{2}\sqrt{-{\frac{2a}{b}}} \left( \coth _{{{pq}}} \left( \sqrt{-2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right. \right. \nonumber \\&\left. \left. \pm \sqrt{pq}\hbox {csch}_{{{pq}}} \left( \sqrt{-2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right) \right] ^2\Bigg \}, \end{aligned}$$

(60)

$$\begin{aligned} v^{\pm }_{8}(x,t)= & {} e^{i( x-\vartheta t)}\Bigg \{E_0\pm E_1\left[ \frac{1}{2}\sqrt{-{\frac{2a}{b}}} \left( \coth _{{{pq}}} \left( \sqrt{-2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right. \right. \nonumber \\&\left. \left. \pm \sqrt{pq}\hbox {csch}_{{{pq}}} \left( \sqrt{-2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right) \right] \nonumber \\&\pm E_2\left[ \frac{1}{2}\sqrt{-{\frac{2a}{b}}} \left( \coth _{{{pq}}} \left( \sqrt{-2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right. \right. \nonumber \\&\left. \left. \pm \sqrt{pq}\hbox {csch}_{{{pq}}} \left( \sqrt{-2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right) \right] ^2\Bigg \}. \end{aligned}$$

(61)

The combined dark and trigonometric function solutions give

$$\begin{aligned} u^{\pm }_{9}(x,t)= & {} e^{i( x-\vartheta t)}\Bigg \{H_0\pm H_1\left[ \frac{1}{4}\sqrt{-{\frac{2a}{b}}} \left( \tanh _{{{pq}}} \left( \sqrt{\frac{-a}{8}}\left( x-2(\beta _2-\beta _3) t\right) \right) \right. \right. \nonumber \\&\left. \left. \pm \sqrt{pq}\coth _{{{pq}}} \left( \sqrt{\frac{-a}{8}}\left( x-2(\beta _2-\beta _3) t\right) \right) \right) \right] \nonumber \\&\pm H_2\left[ \frac{1}{4}\sqrt{-{\frac{2a}{b}}} \left( \tanh _{{{pq}}} \left( \sqrt{\frac{-a}{8}}\left( x-2(\beta _2-\beta _3) t\right) \right) \right. \right. \nonumber \\&\left. \left. \pm \sqrt{pq}\coth _{{{pq}}} \left( \sqrt{\frac{-a}{8}}\left( x-2(\beta _2-\beta _3) t\right) \right) \right) \right] ^2\Bigg \}, \end{aligned}$$

(62)

$$\begin{aligned} v^{\pm }_{9}(x,t)= & {} e^{i( x-\vartheta t)}\Bigg \{E_0\pm \left[ \frac{1}{4}E_1\sqrt{-{\frac{2a}{b}}} \left( \tanh _{{{pq}}} \left( \sqrt{\frac{-a}{8}}\left( x-2(\beta _2-\beta _3) t\right) \right) \right. \right. \nonumber \\&\left. \left. \pm \sqrt{pq}\coth _{{{pq}}} \left( \sqrt{\frac{-a}{8}}\left( x-2(\beta _2-\beta _3) t\right) \right) \right) \right] \nonumber \\&\pm E_2\left[ \frac{1}{4}\sqrt{-{\frac{2a}{b}}} \left( \tanh _{{{pq}}} \left( \sqrt{\frac{-a}{8}}\left( x-2(\beta _2-\beta _3) t\right) \right) \right. \right. \nonumber \\&\left. \left. \pm \sqrt{pq}\coth _{{{pq}}} \left( \sqrt{\frac{-a}{8}}\left( x-2(\beta _2-\beta _3) t\right) \right) \right) \right] ^{2}\Bigg \}. \end{aligned}$$

(63)

• Adopting $a>0$ and $b>0$, we formulate the following trigonometric relations as

$$\begin{aligned} u^{\pm }_{10}(x,t)= & {} e^{i( x-\vartheta t)}\left\{ H_0\pm \frac{1}{2}H_1\sqrt{{\frac{{2a}}{b}}}H_1\tan _{{{pq}}} \left( \frac{1}{2}\sqrt{2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right. \nonumber \\&\left. \pm H_2\left[ \frac{1}{2}\sqrt{{\frac{{2a}}{b}}}H_1\tan _{{{pq}}} \left( \frac{1}{2}\sqrt{2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right] ^2\right\} , \end{aligned}$$

(64)

and

$$\begin{aligned} v^{\pm }_{10}(x,t)= & {} e^{i( x-\vartheta t)}\left\{ E_0\pm \frac{1}{2}\sqrt{{\frac{{2a}}{b}}}E_1\tan _{{{pq}}} \left( \frac{1}{2}\sqrt{2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right. \nonumber \\&\left. \pm E_2\left[ \frac{1}{2}\sqrt{{\frac{{2a}}{b}}}\tan _{{{pq}}} \left( \frac{1}{2}\sqrt{2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right] ^2\right\} . \end{aligned}$$

(65)

$$\begin{aligned} u^{\pm }_{11}(x,t)= & {} e^{i( x-\vartheta t)}\left\{ H_0\pm \frac{1}{2}H_1\sqrt{{\frac{{2a}}{b}}}H_1\cot _{{{pq}}} \left( \frac{1}{2}\sqrt{2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right. \nonumber \\&\left. \pm H_2\left[ \frac{1}{2}\sqrt{{\frac{{2a}}{b}}}H_1\cot _{{{pq}}} \left( \frac{1}{2}\sqrt{2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right] ^2\right\} , \end{aligned}$$

(66)

and

$$\begin{aligned} v^{\pm }_{11}(x,t)= & {} e^{i( x-\vartheta t)}\left\{ E_0\pm \frac{1}{2}\sqrt{{\frac{{2a}}{b}}}E_1\cot _{{{pq}}} \left( \frac{1}{2}\sqrt{2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right. \nonumber \\&\left. \pm E_2\left[ \frac{1}{2}\sqrt{{\frac{{2a}}{b}}}\cot _{{{pq}}} \left( \frac{1}{2}\sqrt{2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right] ^2\right\} . \end{aligned}$$

(67)

$$\begin{aligned} u^{\pm }_{12}(x,t)= & {} e^{i( x-\vartheta t)}\Bigg \{H_0\pm H_1\left[ \frac{1}{2}\sqrt{{\frac{2a}{b}}} \left( \tan _{{{pq}}} \left( \sqrt{2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right. \right. \nonumber \\&\left. \left. \pm \sqrt{pq}\sec _{{{pq}}} \left( \sqrt{2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right) \right] \nonumber \\&\pm H_2\left[ \frac{1}{2}\sqrt{{\frac{2a}{b}}} \left( \tan _{{{pq}}} \left( \sqrt{2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right. \right. \nonumber \\&\left. \left. \pm \sqrt{pq}\sec _{{{pq}}} \left( \sqrt{2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right) \right] ^2\Bigg \}, \end{aligned}$$

(68)

and

$$\begin{aligned} v^{\pm }_{12}(x,t)= & {} e^{i( x-\vartheta t)}\Bigg \{E_0\pm E_1\left[ \frac{1}{2}\sqrt{{\frac{2a}{b}}} \left( \tan _{{{pq}}} \left( \sqrt{2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right. \right. \nonumber \\&\left. \left. \pm \sqrt{pq}\sec _{{{pq}}} \left( \sqrt{2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right) \right] \nonumber \\&\pm E_2\left[ \frac{1}{2}\sqrt{{\frac{2a}{b}}} \left( \tan _{{{pq}}} \left( \sqrt{2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right. \right. \nonumber \\&\left. \left. \pm \sqrt{pq}\sec _{{{pq}}} \left( \sqrt{2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right) \right] ^2\Bigg \}. \end{aligned}$$

(69)

$$\begin{aligned} u^{\pm }_{13}(x,t)= & {} e^{i( x-\vartheta t)}\Bigg \{H_0\pm H_1\left[ \frac{1}{2}\sqrt{{\frac{2a}{b}}} \left( \cot _{{{pq}}} \left( \sqrt{2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right. \right. \nonumber \\&\left. \left. \pm \sqrt{pq}\csc _{{{pq}}} \left( \sqrt{2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right) \right] \nonumber \\&\pm H_2\left[ \frac{1}{2}\sqrt{{\frac{2a}{b}}} \left( \cot _{{{pq}}} \left( \sqrt{2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right. \right. \nonumber \\&\left. \left. \pm \sqrt{pq}\csc _{{{pq}}} \left( \sqrt{2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right) \right] ^2\Bigg \}, \end{aligned}$$

(70)

and

$$\begin{aligned} v^{\pm }_{13}(x,t)= & {} e^{i( x-\vartheta t)}\Bigg \{E_0\pm E_1\left[ \frac{1}{2}\sqrt{{\frac{2a}{b}}} \left( \cot _{{{pq}}} \left( \sqrt{2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right. \right. \nonumber \\&\left. \left. \pm \sqrt{pq}\csc _{{{pq}}} \left( \sqrt{2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right) \right] \nonumber \\&\pm E_2\left[ \frac{1}{2}\sqrt{{\frac{2a}{b}}} \left( \cot _{{{pq}}} \left( \sqrt{2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right. \right. \nonumber \\&\left. \left. \pm \sqrt{pq}\csc _{{{pq}}} \left( \sqrt{2a}\left( x-2(\beta _2-\beta _3) t\right) \right) \right) \right] ^2\Bigg \}. \end{aligned}$$

(71)

$$\begin{aligned} u^{\pm }_{14}(x,t)= & {} e^{i( x-\vartheta t)}\Bigg \{H_0\pm H_1\left[ \frac{1}{4}\sqrt{{\frac{2a}{b}}} \left( \tan _{{{pq}}} \left( \sqrt{\frac{a}{8}}\left( x-2(\beta _2-\beta _3) t\right) \right) \right. \right. \nonumber \\&\left. \left. \pm \sqrt{pq}\cot _{{{pq}}} \left( \sqrt{\frac{a}{8}}\left( x-2(\beta _2-\beta _3) t\right) \right) \right) \right] \nonumber \\&\pm H_2\left[ \frac{1}{4}\sqrt{{\frac{2a}{b}}} \left( \tan _{{{pq}}} \left( \sqrt{\frac{a}{8}}\left( x-2(\beta _2-\beta _3) t\right) \right) \right. \right. \nonumber \\&\left. \left. \pm \sqrt{pq}\cot _{{{pq}}} \left( \sqrt{\frac{a}{8}}\left( x-2(\beta _2-\beta _3) t\right) \right) \right) \right] ^{2}\Bigg \}, \end{aligned}$$

(72)

and

$$\begin{aligned} v^{\pm }_{14}(x,t)= & {} e^{i( x-\vartheta t)}\Bigg \{E_0\pm E_1\left[ \frac{1}{4}\sqrt{{\frac{2a}{b}}} \left( \tan _{{{pq}}} \left( \sqrt{\frac{a}{8}}\left( x-2(\beta _2-\beta _3) t\right) \right) \right. \right. \nonumber \\&\left. \left. \pm \sqrt{pq}\cot _{{{pq}}} \left( \sqrt{\frac{a}{8}}\left( x-2(\beta _2-\beta _3) t\right) \right) \right) \right] \nonumber \\&\pm E_2\left[ \frac{1}{4}\sqrt{{\frac{2a}{b}}} \left( \tan _{{{pq}}} \left( \sqrt{\frac{a}{8}}\left( x-2(\beta _2-\beta _3) t\right) \right) \right. \right. \nonumber \\&\left. \left. \pm \sqrt{pq}\cot _{{{pq}}} \left( \sqrt{\frac{a}{8}}\left( x-2(\beta _2-\beta _3) t\right) \right) \right) \right] ^2\Bigg \}. \end{aligned}$$

(73)

The above analytical investigation helped to get optical solitons solutions in two-core fibers associated with the ellipticity angle and the effects of higher dispersions, we have got some new results such as Eqs. (59), (60), (61), (62) and (63) compared to Refs. [24,25,26,27,28,29,30]. These results are the combined soliton solutions which are usually obtained by employing some mathematical tools namely tanh method, hyperbolic function structure, extended hyperbolic functions method, bifurcation method and sine–cosine method [14,15,16,17,18,19]. While taking $\rho =0$, $a>0$ and $b\ne 0$, we realized numerical simulations of the W-shaped bright solitons solutions for suitable parameters of the model. In addition, for $\rho =\frac{1}{4}\frac{a^2}{b}$, $a<0$ and $b>0$, chose parameters to produce W-shaped dark optical solitons. These results will certainly have an application in telecommunication system and could improve the previous works in the context of two-core fibers.

In addition, we have found W-shaped optical solutions including ordinary bright and dark optical solitons in the presence of high-order dispersions and ellipticity angle in birefringent. More precisely, the new forms of bright and dark optical solitons were obtained under an impeccable influence of the dispersions terms of the model studied. As a reminder, the physical effects of higher-order dispersions are capital for short waves, and the obtained results in this work may help to build more on the propagation of waves in picosecond conditions. They will probably be used for fento-second laser application and raise the bit rate during communication through the two-core fibers.

4 Modulation instability

4.1 Linear stability analysis

Recently, some authors have exhibited in Refs. [6, 8, 11, 12] the effect of the ellipticity angle on MI gain spectra in normal and anomalous dispersion regime. It is important equally to highlight the fact that the model was used recently in previous works [43], however the system of coupled equations does not include 3OD and 4OD dispersions. In this work, the main goal is to emphasize the effect of the third-order and fourth-order dispersion associated with the ellipticity angle to the MI gain spectra in birefringent fibers. In this section, we emphasize the effect of the 3OD, 4OD and the ellipticity angle on the MI gain spectra in normal dispersive regime ($\beta _{2}>0$) /anomalous dispersive regime ($\beta _{2}<0$).

We suppose the continuous-wave CW solutions for the coupled of NLSE Eq. (1) as

$$\begin{aligned}&u(x,t)=P_{1}e^{iqt}, \end{aligned}$$

(74)

$$\begin{aligned}&v(x,t)=P_{2}e^{iqt}, \end{aligned}$$

(75)

$P_{1}$ and $P_{2}$ are, respectively, power incident and q the propagation constant of the polarization component in t-direction.

The linear stability analysis consists of perturbing a continuous-wave solutions and then analyzing whether the perturbation grows or decays. So, the linear stability of the steady state can be investigated by adding small disturbance to the above CW solutions, which reads

$$\begin{aligned}&u(x,t)=(P_{1}+A(x,t))e^{iqt},\end{aligned}$$

(76)

$$\begin{aligned}&v(x,t)=(P_{2}+B(x,t))e^{iqt}. \end{aligned}$$

(77)

Here, A(z, t) and B(z, t) are the perturbed terms and the ratio of the power incident $f=\frac{P_{1}}{P_{2}}$, and $\beta =1+f^{2}$, while the total power incident $P=P_{1}^{2}+P_{2}^{2}$. Using Eqs. (76) and (77) into the set of coupled Eq. (1), the linearizing technic gives

$$\begin{aligned}&iA_t+\beta _2 A_{xx}+i\beta _3 A_{xxx}+\beta _4 A_{xxxx}+\lambda P^2_1(2A+A^*)+\lambda \delta P_1P_2(2B+B^*)=0, \end{aligned}$$

(78)

$$\begin{aligned}&iB_t+\beta _2 B_{xx}+i\beta _3 B_{xxx}+\beta _4 B_{xxxx}+\lambda P^2_2(2B+B^*)+\lambda \delta P_1P_2(2A+A^*)=0. \end{aligned}$$

(79)

$A^{*}$ and $B^{*}$ are the complex conjugated of A and B, respectively.

Adopting the following plane-wave equations

$$\begin{aligned}&A(x,t)=r_{1}e^{i(Kx- \Omega t)}+h_{1}e^{-i(Kx- \Omega t)},\end{aligned}$$

(80)

$$\begin{aligned}&B(x,t)=r_{2}e^{i(Kx- \Omega t)}+h_{2}e^{-i(Kx- \Omega t)}, \end{aligned}$$

(81)

as solutions of the set of linear equations Eqs. (78) and (79), while $r_{1}$, $h_{1}$, $r_{2}$ and $h_{2}$ are reals. Whereas K and $\Omega$ are the wave number and the frequency of MI, respectively. Inserting Eqs. (80) and (84) into Eqs. (78) and (79), it is revealed the below $4 \times 4$ matrix which has non-trivial solution when the determinant vanishes.

$$\begin{aligned} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} a_{11} &{} a_{12} &{} a_{13} &{} a_{14} \\ a_{21} &{} a_{22} &{} a_{23} &{} a_{24} \\ a_{31} &{} a_{32} &{} a_{33} &{} a_{34} \\ a_{41} &{} a_{42} &{} a_{43} &{} a_{44} \\ \end{array} \right) \left( \begin{array}{c} r_{1} \\ r_{2} \\ h_{1} \\ h_{2} \\ \end{array} \right) =\left( \begin{array}{c} 0 \\ 0 \\ 0 \\ 0 \\ \end{array} \right) , \end{aligned}$$

while the parameters ($a_{ij}$) ($i=1,2,3,4. \, j=1,2,3,4$) are given in “Appendix.” The associated dispersion relation of the obtained matrix reads

$$\begin{aligned}&\alpha _{16} K^{16}+\alpha _{14} K^{14}+\alpha _{12} K^{12}+\alpha _{11} K^{11}+\alpha _{10} K^{10}+\alpha _9 K^9+\alpha _8 K^8+\alpha _7 K^7\nonumber \\&\quad +\alpha _6 K^6+\alpha _5 K^5+\alpha _4 K^4+\alpha _3 K^3 +\alpha _2 K^2+\alpha _0=0, \end{aligned}$$

(82)

where

$$\begin{aligned} \alpha _{16}= & {} {\frac{ \left( {f}^{8}+4\,{f}^{6}+6\,{f}^{4}+4\,{f}^{2}+1\right) {\beta _{{4}}}^{4}}{ \left( {f}^{2}+1 \right) ^{4}}}, \nonumber \\ \alpha _{14}= & {} {\frac{ \left( -4\,{f}^{8}-16\,{f}^{6}-24\,{f}^{4}-16\,{f}^{ 2}-4 \right) \beta _{{2}}{\beta _{{4}}}^{3}}{ \left( {f}^{2}+1 \right) ^ {4}}}\nonumber \\&+{\frac{ \left( -2\,{f}^{8}-8\,{f}^{6}-12\,{f}^{4}-8\,{f}^{2}-2 \right) {\beta _{{3}}}^{2}{\beta _{{4}}}^{2}}{ \left( {f}^{2}+1 \right) ^{4}}} ,\nonumber \\ \alpha _{12}= & {} {\frac{ \left( 4\,{f}^{8}+16\,{f}^{6}+24\,{f}^{4}+16\,{f}^{2}+4\right) P\lambda \,{\beta _{{4}}}^{3}}{ \left( {f}^{2}+1 \right) ^{4}}}\nonumber \\&+{\frac{ \left( 6\,{f}^{8}+24\,{f}^{6}+36\,{f}^{4}+24\,{f}^{2}+6\right) {\beta _{{2}}}^{2}{\beta _{{4}}}^{2}}{ \left( {f}^{2}+1\right) ^{4}}}\nonumber \\&+{\frac{ \left( 4\,{f}^{8}+16\,{f}^{6}+24\,{f}^{4}+16\,{f}^{2}+4 \right) \beta _{{2}}{\beta _{{3}}}^{2}\beta _{{4}}}{ \left( {f}^{2}+1 \right) ^{4}}}\nonumber \\&+{\frac{ \left( {f}^{8}+4\,{f}^{6}+6\,{f}^{4}+4\,{f}^{2}+1 \right) {\beta _{{3}}}^{4}}{ \left( {f}^{2}+1 \right) ^{4}}},\nonumber \\ \alpha _{11}= & {} {\frac{ \left( -4\,{f}^{8}-16\,{f}^{6}-24\,{f}^{4}-16\,{f}^{2}-4\right) \Omega \,\beta _{{3}}{\beta _{{4}}}^{2}}{ \left( {f}^{2}+1\right) ^{4}}},\nonumber \\ \alpha _{10}= & {} {\frac{ \left( -12\,{f}^{8}-48\,{f}^{6}-72\,{f}^{4}-48\,{f}^{2}-12 \right) P\lambda \,\beta _{{2}}{\beta _{{4}}}^{2}}{ \left( {f}^{2}+1 \right) ^{4}}}\nonumber \\&+{\frac{ \left( -4\,{f}^{8}-16\,{f}^{6}-24\,{f}^{4}-16\,{f}^{2}-4 \right) P\lambda \,{\beta _{{3}}}^{2}\beta _{{4}}}{ \left( {f}^{2}+1 \right) ^{4}}}\nonumber \\&+{\frac{ \left( -4\,{f}^{8}-16\,{f}^{6}-24\,{f}^{4}-16\,{f}^{2}-4 \right) {\beta _{{2}}}^{3}\beta _{{4}}}{ \left( {f}^{2}+1 \right) ^{4}}}\nonumber \\&+{\frac{ \left( -2\,{f}^{8}-8\,{f}^{6}-12\,{f}^{4}-8\,{f}^{2}-2 \right) {\beta _{{2}}}^{2}{\beta _{{3}}}^{2}}{ \left( {f}^{2}+1 \right) ^{4}}},\nonumber \\ \alpha _{9}= & {} {\frac{ \left( 8\,{f}^{8}+32\,{f}^{6}+48\,{f}^{4}+32\,{f}^{2} +8 \right) \Omega \,\beta _{{2}}\beta _{{3}}\beta _{{4}}}{ \left( {f}^{2}+ 1 \right) ^{4}}}\nonumber \\&+{\frac{ \left( 4\,{f}^{8}+16\,{f}^{6}+24\,{f}^{4}+16 \,{f}^{2}+4 \right) \Omega \,{\beta _{{3}}}^{3}}{ \left( {f}^{2}+1 \right) ^{4}}},\nonumber \\ \alpha _{8}= & {} {\frac{ \left( -2\,{f}^{8}-8\,{f}^{6}-12\,{f}^{4}-8\,{f}^{2}- 2 \right) {\Omega }^{2}{\beta _{{4}}}^{2}}{ \left( {f}^{2}+1 \right) ^{4 }}}\nonumber \\&+{\frac{ \left( -4\,{f}^{6}-8\,{f}^{4}-4\,{f}^{2} \right) {P}^{2}{ \delta }^{2}{\lambda }^{2}{\beta _{{4}}}^{2}}{ \left( {f}^{2}+1 \right) ^ {4}}}\nonumber \\&+{\frac{ \left( 3\,{f}^{8}+22\,{f}^{6}+38\,{f}^{4}+22\,{f}^{2}+3 \right) {P}^{2}{\lambda }^{2}{\beta _{{4}}}^{2}}{ \left( {f}^{2}+1 \right) ^{4}}}\nonumber \\&+{\frac{ \left( 12\,{f}^{8}+48\,{f}^{6}+72\,{f}^{4}+48 \,{f}^{2}+12 \right) P\lambda \,{\beta _{{2}}}^{2}\beta _{{4}}}{ \left( { f}^{2}+1 \right) ^{4}}}\nonumber \\&+{\frac{ \left( 4\,{f}^{8}+16\,{f}^{6}+24\,{f} ^{4}+16\,{f}^{2}+4 \right) P\lambda \,\beta _{{2}}{\beta _{{3}}}^{2}}{ \left( {f}^{2}+1 \right) ^{4}}}\nonumber \\&+{\frac{ \left( {f}^{8}+4\,{f}^{6}+6 \,{f}^{4}+4\,{f}^{2}+1 \right) {\beta _{{2}}}^{4}}{ \left( {f}^{2}+1 \right) ^{4}}},\nonumber \\ \alpha _{7}= & {} {\frac{ \left( -8\,{f}^{8}-32\,{f}^{6}-48\,{f}^{4}-32\,{f}^{2 }-8 \right) \Omega \,P\lambda \,\beta _{{3}}\beta _{{4}}}{ \left( {f}^{2}+ 1 \right) ^{4}}}\nonumber \\&+{\frac{ \left( -4\,{f}^{8}-16\,{f}^{6}-24\,{f}^{4}- 16\,{f}^{2}-4 \right) \Omega \,{\beta _{{2}}}^{2}\beta _{{3}}}{ \left( {f }^{2}+1 \right) ^{4}}},\nonumber \\ \alpha _{6}= & {} {\frac{ \left( 4\,{f}^{8}+16\,{f}^{6}+24\,{f}^{4}+16\,{f}^{2} +4 \right) {\Omega }^{2}\beta _{{2}}\beta _{{4}}}{ \left( {f}^{2}+1 \right) ^{4}}}\nonumber \\&+{\frac{ \left( 6\,{f}^{8}+24\,{f}^{6}+36\,{f}^{4}+24 \,{f}^{2}+6 \right) {\Omega }^{2}{\beta _{{3}}}^{2}}{ \left( {f}^{2}+1 \right) ^{4}}}\nonumber \\&+{\frac{ \left( 8\,{f}^{6}+16\,{f}^{4}+8\,{f}^{2} \right) {P}^{2}{\delta }^{2}{\lambda }^{2}\beta _{{2}}\beta _{{4}}}{ \left( {f}^{2}+1 \right) ^{4}}}\nonumber \\&+{\frac{ \left( -6\,{f}^{8}-44\,{f}^{ 6}-76\,{f}^{4}-44\,{f}^{2}-6 \right) {P}^{2}{\lambda }^{2}\beta _{{2}} \beta _{{4}}}{ \left( {f}^{2}+1 \right) ^{4}}}\nonumber \\&+{\frac{ \left( -3\,{f}^ {8}-6\,{f}^{6}-6\,{f}^{4}-6\,{f}^{2}-3 \right) {P}^{2}{\lambda }^{2}{ \beta _{{3}}}^{2}}{ \left( {f}^{2}+1 \right) ^{4}}}\nonumber \\&+{\frac{ \left( -4 \,{f}^{8}-16\,{f}^{6}-24\,{f}^{4}-16\,{f}^{2}-4 \right) P\lambda \,{ \beta _{{2}}}^{3}}{ \left( {f}^{2}+1 \right) ^{4}}},\nonumber \\ \alpha _{5}= & {} {\frac{ \left( 8\,{f}^{8}+32\,{f}^{6}+48\,{f}^{4}+32\,{f}^{2} +8 \right) \Omega \,P\lambda \,\beta _{{2}}\beta _{{3}}}{ \left( {f}^{2}+1 \right) ^{4}}},\nonumber \\ \alpha _{4}= & {} {\frac{ \left( -4\,{f}^{8}-16\,{f}^{6}-24\,{f}^{4}-16\,{f}^{2 }-4 \right) {\Omega }^{2}P\lambda \,\beta _{{4}}}{ \left( {f}^{2}+1 \right) ^{4}}}\nonumber \\&+{\frac{ \left( -2\,{f}^{8}-8\,{f}^{6}-12\,{f}^{4}-8\, {f}^{2}-2 \right) {\Omega }^{2}{\beta _{{2}}}^{2}}{ \left( {f}^{2}+1 \right) ^{4}}}\nonumber \\&+{\frac{ \left( -4\,{f}^{6}-8\,{f}^{4}-4\,{f}^{2} \right) {P}^{3}{\delta }^{2}{\lambda }^{3}\beta _{{4}}}{ \left( {f}^{2}+ 1 \right) ^{4}}}+{\frac{ \left( 12\,{f}^{6}+24\,{f}^{4}+12\,{f}^{2} \right) {P}^{3}{\lambda }^{3}\beta _{{4}}}{ \left( {f}^{2}+1 \right) ^{ 4}}}\nonumber \\&+{\frac{ \left( -4\,{f}^{6}-8\,{f}^{4}-4\,{f}^{2} \right) {P}^{2} {\delta }^{2}{\lambda }^{2}{\beta _{{2}}}^{2}}{ \left( {f}^{2}+1 \right) ^{4}}}\nonumber \\&+{\frac{ \left( 3\,{f}^{8}+22\,{f}^{6}+38\,{f}^{4}+22\,{f}^{2}+ 3 \right) {P}^{2}{\lambda }^{2}{\beta _{{2}}}^{2}}{ \left( {f}^{2}+1 \right) ^{4}}},\nonumber \\ \alpha _{3}= & {} {\frac{ \left( 4\,{f}^{8}+16\,{f}^{6}+24\,{f}^{4}+16\,{f}^{2} +4 \right) {\Omega }^{3}\beta _{{3}}}{ \left( {f}^{2}+1 \right) ^{4}}}\nonumber \\&+{ \frac{ \left( -6\,{f}^{8}-12\,{f}^{6}-12\,{f}^{4}-12\,{f}^{2}-6 \right) \Omega \,{P}^{2}{\lambda }^{2}\beta _{{3}}}{ \left( {f}^{2}+1 \right) ^{4}}},\nonumber \\ \alpha _{2}= & {} {\frac{ \left( 4\,{f}^{8}+16\,{f}^{6}+24\,{f}^{4}+16\,{f}^{2} +4 \right) {\Omega }^{2}P\lambda \,\beta _{{2}}}{ \left( {f}^{2}+1 \right) ^{4}}}\nonumber \\&+{\frac{ \left( 4\,{f}^{6}+8\,{f}^{4}+4\,{f}^{2} \right) {P}^{3}{\delta }^{2}{\lambda }^{3}\beta _{{2}}}{ \left( {f}^{2}+ 1 \right) ^{4}}}\nonumber \\&+{\frac{ \left( -12\,{f}^{6}-24\,{f}^{4}-12\,{f}^{2} \right) {P}^{3}{\lambda }^{3}\beta _{{2}}}{ \left( {f}^{2}+1 \right) ^{ 4}}},\nonumber \\ \alpha _{0}= & {} {\frac{ \left( {f}^{8}+4\,{f}^{6}+6\,{f}^{4}+4\,{f}^{2}+1 \right) {\Omega }^{4}}{ \left( {f}^{2}+1 \right) ^{4}}}\nonumber \\&+{\frac{ \left( -3\,{f}^{8}-6\,{f}^{6}-6\,{f}^{4}-6\,{f}^{2}-3 \right) {\Omega }^{2}{P}^{2}{\lambda }^{2}}{ \left( {f}^{2}+1 \right) ^{4}}}-4\,{\frac{{f}^{4}{\lambda }^{4}{P}^{4}{\delta }^{2}}{ \left( {f}^{2}+1 \right) ^{ 4}}}\nonumber \\&+9\,{\frac{{f}^{4}{\lambda }^{4}{P}^{4}}{ \left( {f}^{2}+1 \right) ^{4}}}. \end{aligned}$$

(83)

The MI is deliberated by a gain given by

$$\begin{aligned}&Gain=\mathbf{max} (Im (K_{max})), \end{aligned}$$

(84)

while $K_{\max }=\mathbf{eig} (A)$ where A is a matrix having elements ($a_{ij}$) ($i=1,2,3,4. \, j=1,2,3,4$) given in “Appendix,” max and eig are two functions of the MATLAB software. The function eig(A) returns a column vector containing the eigenvalues of square matrix A and $\mathbf{max} (Im (K_{\max }))$ returns the largest element of $Im (K_{\max })$.

4.2 MI gain spectra

Without doubt, high-order dispersions play an important role in MI dynamics. In this work, the presence of 4OD particularly will certainly set out the new behavior of high-order dispersion in birefringent mode, despite the assumption that 4OD over the 3OD is usually immaterially because of their tiny magnitude. So, it is for this reason that it will be supposed either $\beta _3=0$ or $\beta _4=0$ to emphasize the effect of each of them separately in which will follow. This study will be done in the context of normal and anomalous dispersion regime on the one hand and the zero-birefringence, circular and linear-birefringence, respectively, on the other hand.

4.2.1 Anomalous dispersion regime ($f<0$)

• The effects of third order and fourth order in anomalous dispersion regime associated with an ellipticity angle in birefringent fiber

In this section, we study the behavior of the MI gain spectra in anomalous dispersion regime. Figure 8 shows the variation of the MI gain spectrum versus anomalous group velocity dispersion regime with the effect of the third-order 3OD dispersion for [$\beta _3=1.1\, ps^3/\hbox {km}, \, \beta _3=0.51\, ps^3/\hbox {km}, \, \beta _3=0.25\, ps^3/\hbox {km}$], respectively. In addition, the MI gain spectra decrease when the value of the 3OD dispersion decreases, while the stability zones increase. However, when the anomalous group velocity dispersion values tend to zero, there are overlaps between the MI gain bands (see Fig. 8$D_1$). Figure 9 shows the variation of the MI gain spectra versus the ellipticity angle $\theta \epsilon [0^{\circ }, 15^{\circ }]$ in anomalous dispersion regime along with the effect of third-order dispersion in birefringent fiber. Scrutinizing Fig. 9 ($G_1$), for [$\beta _3=-100\, ps^3/\hbox {km}, \, \beta _3=-50\, ps^3/\hbox {km}$], the MI grows exponentially and the width of the instability gap increases. Besides, for [$\beta _3=-200\, ps^3/\hbox {km}$], the instability band proportionally decreases showing out the stability band. Moreover, the scenario changes when the third-order dispersion values become more important. In the event that, the instability band increases the stability zones vanish (see Fig. 10). The effect of the third-order dispersion 3OD in anomalous dispersion regime on the MI gain spectra is shown in Fig. 11 for $\theta \epsilon [30^{\circ }, 45^{\circ }]$. The width of the MI band increases with the 3OD values and for large values of 3OD additional sides lobes are obtained (see Fig. 11 ($H_4$)). Therewith, the situation becomes different with the effects of 4OD in anomalous dispersive regime for $\theta \epsilon [45^{\circ }, 60^{\circ }]$. The MI bands shrink and the amplitude grows for large values of the 4OD (see Fig. 12b). In Fig. 13, the variation of the MI gain spectra versus the ellipticity angle in birefringent two-core optical fibers under the effect of third-order and fourth-order dispersion in anomalous dispersion regime for $\theta \epsilon [60^{\circ }, 75^{\circ }]$, $P=1500 \,\hbox {kW}, \, f=-0.5, \, \lambda =100\,(/\hbox {kW}\,\hbox {m})$ is depicted. The maximum magnitude of the MI bands is obtained for slight values of the 3OD and 4OD (see Fig. 13 (green color)). It is observed from Fig. 14, that the MI gain spectrum in anomalous dispersive regime with the effects of 3OD and 4OD leads to important sides lobes. Alongside of this variation, extra small sides lobes are obtained for small values of the 3OD and 4OD (see Fig. 14c).

Fig. 8

Variation of the MI gain spectrum versus the anomalous group velocity with the effect of third-order dispersion in birefringent fiber at $(D_1)$ [$\beta _3=1.1\, ps^3/\hbox {km}, \, \beta _3=0.51\, ps^3/\hbox {km}, \, \beta _3=0.25\, ps^3/\hbox {km}$], respectively, and $\theta =30^{\circ }$, $P=1500 \, \hbox {kW}, \, f=-0.001, \, \beta _4=0\, ps^4/\hbox {km}$

Fig. 9

Variation of the MI gain spectrum versus the ellipticity angle with the effect of third-order dispersion in birefringent fiber at $(G_1)$ [$\beta _3=0.4\, ps^3/\hbox {km}, \, \beta _3=10.4\, ps^3/\hbox {km}, \, \beta _3=20.4\, ps^3/\hbox {km}$] and $(G_2)$ [$\beta _3=-200\, ps^3/\hbox {km}, \, \beta _3=-100\, ps^3/\hbox {km}, \, \beta _3=-50\, ps^3/\hbox {km}$], respectively, and $\theta \epsilon [0^{\circ }, 15^{\circ }]$, $P=1000 \, \hbox {kW}, \, f=-0.5, \, \beta _4=0\, ps^4/\hbox {km}$

Fig. 10

Variation of the MI gain spectrum versus the ellipticity angle with the effect of third-order dispersion in birefringent fiber at $(R_1)$ [$\beta _3=1$] and $(R_2)$ [$\beta _3=50\, ps^3/\hbox {km}$], $(R_3)$ [$\beta _3=100 ps^3/\hbox {km}$], $(R_4)$ [$\beta _3=150\, ps^3/\hbox {km}$], respectively, and $\theta \epsilon [15^{\circ }, 35^{\circ }]$, $P=1500 \, \hbox {kW}, \, f=-0.5, \, \beta _4=0\, ps^4/\hbox {km}, \, \beta _2=-0.001\,ps^2/\hbox {km}, \, \lambda =100\, (/\hbox {kW}\,\hbox {m})$

Fig. 11

Variation of the MI gain spectrum versus the ellipticity angle with the effect of third-order dispersion in birefringent fiber at $(H_1)$ [$\beta _3=0.75$], $(H_2)$ [$\beta _3=140.4\, ps^3/\hbox {km}$], $(H_3)$ [$\beta _3=-140.4\,ps^3/\hbox {km}$], $(H_4)$ [$\beta _3=-200.4\, ps^3/\hbox {km}$], respectively, and $\theta \epsilon [30^{\circ }, 45^{\circ }]$, $P=1500 \, \hbox {kW}, \, f=-0.5, \, \beta _4=0\,ps^4/\hbox {km}, \, \beta _2=-0.001\,ps^2/\hbox {km}, \, \lambda =100\, (/\hbox {kW}\,\hbox {m})$

Fig. 12

Variation of the MI gain spectrum versus the ellipticity angle with the effect of fourth-order dispersion in anomalous dispersion regime. The parameters of the obtained results are given by a [$\beta _4=-10.5\, ps^4/\hbox {km},\, \beta _4=-.5\, ps^4/\hbox {km},\, \beta _4=5.01\, ps^4/\hbox {km},\, \beta _2=-0.0001\,ps^2/\hbox {km}$], b [$\beta _4=50.1\, ps^3/\hbox {km},\, \beta _4=100.1 ps^4/\hbox {km},\, \beta _4=125.1\, ps^4/\hbox {km}, \, \beta _2=-1\, ps^2/\hbox {km}$] for $\theta \epsilon [45^{\circ }, 60^{\circ }]$, $\beta _3=-1.75\, ps^2/\hbox {km}, \, P=1500 \,\hbox {kW}, \, f=-0.5, \, \lambda =100\,(/\hbox {kW}\,\hbox {m})$

Fig. 13

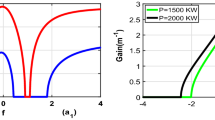
Variation of the MI gain spectra versus the ellipticity angle with the effect of the third-order and fourth-order dispersion in anomalous dispersion regime for $\theta \epsilon [60^{\circ }, 75^{\circ }]$, $\beta _2=-1\, ps^2/\hbox {km}, \, P=1500 \,\hbox {kW}, \, f=-0.5, \, \lambda =100\,(/\hbox {kW}\,\hbox {m})$

Fig. 14

Variation of the MI gain spectra versus the ellipticity angle with the effect of the third-order and fourth-order dispersion in anomalous dispersion regime for $\theta \epsilon [75^{\circ }, 90^{\circ }]$, c [$(\beta _4=1.5\, ps^4/\hbox {km},\, \beta _3=2.75\, ps^3/\hbox {km}), (\beta _4=-1.5\, ps^4/\hbox {km},\, \beta _3=-2.75\,ps^3/\hbox {km})$], d [$\beta _4=-50.1\, ps^4/\hbox {km},\, \beta _3=-100.001\, ps^3/\hbox {km}$] and $\beta _2=-1\, ps^2/\hbox {km}, \, P=1500 \,\hbox {kW}, \, f=-0.5, \, \lambda =100\,(/\hbox {kW}\,\hbox {m})$

Fig. 15

Variation of the MI gain spectra versus the ellipticity angle with the effect of the third-order and fourth-order dispersion in normal dispersion regime for $\theta \epsilon [0^{\circ }, 15^{\circ }]$, i [$(\beta _4=20.5\, ps^4/\hbox {km},\, \beta _3=200.25\, ps^3/\hbox {km}), (\beta _4=50.5\, ps^4/\hbox {km},\, \beta _3=250.25\,ps^3/\hbox {km}), \, (\beta _4=100.5\, ps^4/\hbox {km},\, \beta _3=300.25\, ps^3/\hbox {km})$], j [$(\beta _4=200.5\, ps^4/\hbox {km},\, \beta _3=50.25\, ps^3/\hbox {km}), \, (\beta _4=250.5\, ps^4/\hbox {km},\, \beta _3=25.25\, ps^3/\hbox {km}), (\beta _4=300.5\, ps^4/\hbox {km},\, \beta _3=15.25\, ps^3/\hbox {km})$] and $P=1500\,\hbox {kW}, \, f=10.5, \, \lambda =100\,(/\hbox {kW}\,\hbox {m})$

Fig. 16

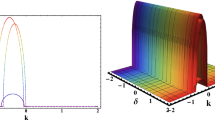
Variation of the MI gain spectra versus the ellipticity angle with the effect of the fourth-order dispersion in normal dispersion regime for $\theta \epsilon [15^{\circ }, 30^{\circ }]$, k [$\beta _4=150\, ps^4/\hbox {km},\, \beta _4=100\, ps^4/\hbox {km}, \beta _4=50\, ps^4/\hbox {km}$], n [$\beta _4=25\, ps^4/\hbox {km},\, \beta _4=10\, ps^3/\hbox {km}, \, \beta _4=5\,ps^4/\hbox {km}$] for $\beta _2=0.1\, ps^2/\hbox {km}, \, \beta _3=50\, ps^3/\hbox {km},\, P=2500\,\hbox {kW}, \, f=0.1, \, \lambda =250\,(/\hbox {kW}\,\hbox {m})$

Fig. 17

Variation of the MI gain spectra versus the ellipticity angle with the effect of the third-order dispersion in normal dispersion regime for $\theta \epsilon [30^{\circ }, 45^{\circ }]$, f [$\beta _4=-450\, ps^3/\hbox {km},\, \beta _3=-250\, ps^3/\hbox {km}, \beta _3=-50\, ps^3/\hbox {km}$], g [$\beta _3=50\, ps^3/\hbox {km},\, \beta _3=25\, ps^3/\hbox {km}, \, \beta _3=0.5\, ps^3/\hbox {km}$] for $\beta _2=0.1\, ps^2/\hbox {km}, \, \beta _4=5\,ps^4/\hbox {km},\, P=2500\,\hbox {kW}, \, f=0.1, \, \lambda =250\,(/\hbox {kW}\,\hbox {m})$

4.2.2 Normal dispersion regime ($f>0$)

• The effects of third order and fourth order in normal dispersion regime associated with ellipticity angle in birefringent fiber

In this part of the work, we emphasized the behavior of the MI gain spectra in normal dispersion regime under the effects of the third-order and fourth-order dispersion. We set $\beta _2=150\, ps^2/\hbox {m}$,  $P=2500\,\hbox {kW}$, $\lambda =100.5\,(/\hbox {kW}\,\hbox {m}), \, f=10.5$. Figure 15 shows the behavior of the MI gain spectra in normal dispersion regime with the effects of 3OD and 4OD. The ellipticity angle in birefringent is taking on $\theta \epsilon [0^{\circ }, 15^{\circ }]$. The magnitude of the MI gain spectra increases when the value of the 3OD increases, and the MI bands also increase. However, when the value of the 3OD tends to be small, while the 4OD increases in value, it is formed sides lobes with small amplitudes and the MI spectra bands shrink. Figure 16 gives the MI gain spectra with the effects of 4OD in normal dispersion regime for $\theta \epsilon [15^{\circ }, 30^{\circ }]$. An examination of Fig. 16k yields to the generation of the stability zones for $15^{\circ } <\theta \le 20^{\circ }$, $\theta =25^{\circ }$, respectively. Besides, a new MI band is produced when the 4OD takes small values and the stability zones vanish, see Fig. 16n. The situation is now different under the effects of the 3OD in normal dispersion regime in birefringent fiber for $\theta \epsilon [30^{\circ }, 45^{\circ }]$ at (f) [$\beta _4=-450\, ps^3/\hbox {km},\, \beta _3=-250\, ps^3/\hbox {km}, \beta _3=-50\, ps^3/\hbox {km}$], (g) [$\beta _3=50 ps^3/\hbox {km},\, \beta _3=25\, ps^3/\hbox {km}, \, \beta _3=0.5\, ps^3/\hbox {km}$] (see Fig. 17). The MI gain spectra band is seriously different from the situation for $\theta \epsilon [15^{\circ }, 30^{\circ }]$. Meanwhile, for positive values of the 3OD, new sides lobes are generated (see Fig. 17g). Observing the results obtained, the maximum initial expansion rate of the disturbances is estimated to be in the closeness of the prevalent MI frequency, which corresponds to the higher gain (see Fig. 18g).

• The effects of the ratio power incident in normal dispersion regime associated with an ellipticity angle in birefringent fiber

Fig. 18

Variation of the MI gain spectra versus the ellipticity angle with the effect of the ratio power in normal dispersion regime for $\beta _2=0.1\, ps^2/\hbox {km}, \, \beta _4=5\, ps^4/\hbox {km},\, P=2500\,\hbox {kW},\, \lambda =250\,(/\hbox {kW}\,\hbox {m})$

Fig. 19

Variation of the MI gain spectra versus the ellipticity angle with the effect of the ratio power in normal dispersion regime w [$f=0.005$], v [$f=0.001$] for $\beta _2=0.01\, ps^2/\hbox {km}, \, \beta _4=0\, ps^4/\hbox {km},\, \beta _3=0\, ps^3/\hbox {km}, \, P=2500\,\hbox {kW}, \, \lambda =-0.51\,(/\hbox {kW}\,\hbox {m})$

Fig. 20

Variation of the MI gain spectra versus the ellipticity angle with the effect of the ratio power in normal dispersion regime $\mathbf{a}_\mathbf{1}$ [$f=2.5$], $\mathbf{a}_\mathbf{2}$ [$f=1.5$], $\mathbf{a}_\mathbf{3}$ [$f=1.25$] and $\mathbf{a}_\mathbf{4}$ [$f=0.5$] for $\beta _2=0.5\, ps^2/\hbox {km}, \, \beta _4=0\, ps^4/\hbox {km},\, \beta _3=0\, ps^3/\hbox {km}, \, P=2500\,\hbox {kW}, \, \lambda =-0.01\,(/\hbox {kW}\,\hbox {m})$

Figure 18 shows the impacts of the ratio power to the MI gain spectra in normal dispersion regime for $\theta \epsilon [45^{\circ }, 60^{\circ }]$ and $\beta _2=0.1\, ps^2/\hbox {km}, \, \beta _4=4.5\, ps^4/\hbox {km},\, \beta _3=2.5\, ps^3/\hbox {km}, P=2500\,\hbox {kW}, \, \lambda =250\,(/\hbox {kW}\,\hbox {m})$. We observed two and three slides lobes. In case of total absence of the 3OD and 4OD dispersion in normal group velocity dispersion, two slides lobes with the effects of the ratio power (see Figs. 19, 20) for $\theta \epsilon [60^{\circ }, 75^{\circ }]$ and $\theta \epsilon [75^{\circ }, 90^{\circ }]$ are generated, respectively. It is also pointed out two and three stabilities zones, respectively.

From the various results obtained, the behavior of the MI Gain spectra in different ranges of ellipticity angle in birefringent fiber is emphasized. The effects of third-order dispersion and those of fourth-order dispersion have been highlighted in the normal and anomalous dispersion regime in birefringence. Likewise, in the absence of dispersions 3OD and 4OD, the effects of the ratio power (f) are exhibited on the MI Gain spectra. In presence of the third-order dispersion 3OD, in normal and anomalous dispersion regime, the effects of the fourth-order dispersion 4OD are less important on the MI gain spectra (see Fig. 14). To overcome this restriction, it is necessary to mix the third-order dispersion 3OD and the fourth-order dispersion to which the group velocity dispersion GVD is added to obtain an improved MI gain spectra (see Fig. 13). More precisely, in anomalous or normal dispersion regime, the effects of the third-order dispersion 3OD in the absence of the fourth-order dispersion 4OD are evident and we achieve a maximum amplitude of the MI gain spectra. In addition, we observe the appearance of new MI gain spectra as well as stability zone (see Figs. 9, 10, 11). However, excluding the third-order dispersion 3OD coefficient, new sides lobes of MI gain spectra are generated, reflecting the formation of new regions of instability. When the values of the 4OD become more important in the absence of the 3OD, the peak and some new stability regions are set out (see Fig. 12b).

5 Conclusion

In this paper, the analytical solutions survey of the CNLSE having 3OD and 4OD in birefringent TCFs have been studied by using the modified Sardar sub-equation method. From there, a new shape of solitons solutions known as W-shaped bright and dark solitons solutions, singular solitons solutions, periodic solutions are unearthed. These results have been secured under certain constraint conditions. Whatever, the medium is favorable to the formation of solitons due to the competition between dispersion and nonlinearity terms. These parameters are also good arguments to study MI. Furthermore, the study of MI gain spectra with the effects of the high-order dispersion and power ratio (f) in anomalous and normal dispersion regime is done.

We expanded the work on different ranges of ellipticity angle in birefringent, which consisted to use six ranges of ellipticity angle $\theta \epsilon [0^{\circ }, 15^{\circ }]$, $\theta \epsilon [15^{\circ }, 30^{\circ }]$, $\theta \epsilon [30^{\circ }, 45^{\circ }]$, $\theta \epsilon [45^{\circ }, 60^{\circ }]$, $\theta \epsilon [60^{\circ }, 75^{\circ }]$ and $\theta \epsilon [75^{\circ }, 90^{\circ }]$. For each case, the behavior of the MI gain spectra under the effects of 3OD and 4OD together with the influence of the ratio of power incident has been emphasized. These results generated additional MI gain spectra and new instability bands to the well-known classic ones which are related to linear and circular birefringent in two-core fibers. Comparing these results with Refs. [2,3,4,5,6, 8, 11, 43], Figs. 9, 10, 11, 12, 13, 14 and 15 show out a new behavior of the MI gain spectra with the effect of the 3OD and 4OD associated with an ellipticity angle in birefringent two-core fiber. Certainly, these results could improve the MI analysis in birefringent fibers with the effects of high-order dispersions including ellipticity angle effects in normal and anomalous dispersion regime. In the future, we aim at adding the numerical simulations of the obtained W-shaped bright and dark soliton solutions to more appreciate the behavior of the latter in TCFs.

Appendix

$$\begin{aligned} a_{11}= & {} K^{3}\beta _{{3}}+\Omega -K^{2}\beta _{{2}}+K^{4}\beta _{{4}}+{\frac{2P{f}^{2}\lambda }{{f}^{2}+1}} , \, a_{12}={\frac{\delta \,\lambda \,Pf}{1+{f}^{2}} }, \, a_{13}={\frac{\lambda \,P{f}^{2}}{1+{f}^{2}}}, \, \\ a_{14}= & {} {\frac{\delta \,\lambda \,Pf}{ 1+{f}^{2}}}; \, a_{21}={\frac{\lambda \,P{f}^{2}}{1+{f}^{2}}}, \, a_{22}={\frac{\delta \,\lambda \,Pf}{1+{f}^{2}}}, \,\\ a_{23}= & {} -K^{3}\beta _{{3}}-\Omega -K^{2}\beta _{{2}}+K^{4}\beta _{{4}}+{\frac{2P{f}^{2}\lambda }{{f}^{2}+1}}, \,\\ a_{24}= & {} {\frac{\delta \,\lambda \,Pf}{1+{f}^{2}}}, \, a_{31}={\frac{\delta \,\lambda \,Pf}{1+{f}^{2}}}, \, a_{32}=K^{3}\beta _{{3}}+\Omega -K^{2}\beta _{{2}}+K^{4}\beta _{{4}}+{\frac{2\lambda \,P}{{f}^{2}+1}}, \, \\ a_{33}= & {} {\frac{\delta \,\lambda \,Pf}{1+{f}^{2}}}, \, a_{34}={\frac{\lambda \,P}{1+{f}^{2}}}, \, a_{41}={\frac{\delta \,\lambda \,Pf}{1+{f}^{2}}}, \, a_{42}={\frac{\lambda \,P}{1+{f}^{2}}}, \, \\ a_{43}= & {} {\frac{\delta \,\lambda \,Pf}{1+{f}^{2}}}, \,a_{44}=-K^{3}\beta _{{3}}-\Omega -K^{2}\beta _{{2}}+K^{4}\beta _{{4}}+{\frac{2\lambda \,P}{{f}^{2}+1}} . \end{aligned}$$