1 Introduction

With the development of numerical analysis technique [1,2,3,4,5] and the gradual maturation of nonlinear dynamics theory [6,7,8,9], scientists have undeniably opened a new chapter in the pendulum studies; especially, an explosion of pendulum studies has produced a flood of information on nonlinear phenomenon in terms of the oscillations [10], rotations [11,12,13], bifurcations [14,15,16], chaos [17,18,19], synchronization [20, 21], experiment [22,23,24], energy absorption [25], vibration reduction [26], etc. However, many scholars are regularly faced with a big challenge which is how to precisely deal with the practical engineering systems with trigonometric, fractional, irrational and non-smooth terms by means of an approximately analytic method instead of a truncated Taylor series. In particular, a class of geometrical nonlinear systems of which the nonlinear term must be considered in the analysis of dynamic mechanism is mainly characterized by multiple coupling and strong nonlinearity. The emergence of such systems with trigonometric, fractional and irrational terms brings a great impact toward the traditional approximate method, especially the polynomial approximation.

Traditionally, large numbers of researchers often use the polynomial system derived by Taylor expansion to describe the local dynamic characteristics of the complex nonlinear system; especially, an approximate approach allows reducing the problem to the Duffing equation [27,28,29,30] with adequate initial conditions. For example, Tian et al. investigated the codimension-two bifurcation of a smooth and discontinuous oscillator with irrational nonlinearity which can be simplified as the Duffing equation [31] with Vander Pol damping; Zhang et al. studied the chaotic behaviors of a nanoplate postulating nonlinear Winkler foundation based upon the Duffing equation with a pair of heteroclinic orbits [32]; Hou et al. reported the mechanism of a complex bifurcation behavior caused by flight maneuvers in an aircraft rub-impact rotor system with Duffing-type nonlinearity by means of the harmonic balance method combined with an alternating frequency/time domain procedure (HB-AFT method [33]; Han et al. demonstrated the chaotic thresholds [34] and codimension-three bifurcation [35] of a coupled smooth and discontinuous oscillator which can be described by the quintic polynomial system. Based upon the quartic and quintic polynomial systems [36], Lai et al. investigated analytically the nonlinear free and forced vibration responses of a nonlinear micro-electro-mechanical system by using the Newton harmonic balance (NHB) method. Tang et al. studied the nonlinear free vibration of a dielectric elastomer balloon subjected to both pressure and voltage qualitatively and quantitatively, and the deformation of the spherical balloon is modeled as a general non-odd nonlinear differential system containing a polynomial term [37]. Many quasi-zero stiffness (QZS) isolators are simplified into the polynomial system to study their transmission performance analytically. Zhou et al. presented a torsion QZS vibration isolator [38] whose the approximate torque–torsion angle relationship can be written as seventh-degree polynomial system and then the transmission of torsional vibration can be derived by using the harmonic balance method. Yan et al. designed a large stroke QZS vibration isolator [39] using three-link mechanisms whose the dimensionless expression of the dynamic equation can be written as a fourth-degree polynomial system. Unlike the above studies, we introduce a simplified approximate system rather than the Duffing equation to study the local accurate dynamics of a pendulum system with an irrational and fractional nonlinear restoring force.

It is well known that the small oscillation of the simple pendulum is best modeled using the small-angle approximation. As a basic example [40], the small oscillation of the simple pendulum features prominently in mechanics where the small-angle approximation is absolutely essential to making any useful analytic progress. Obviously, the small-angle approximation is a useful simplification of the basic trigonometric functions which is approximately true in the limit where the angle approaches zero [41]. Due to the limitation of non-smooth feature, the traditional approximation is invalid to describe the local dynamics of the non-smooth dynamical system in the qualitative and quantitative analysis. This study focuses on the oscillatory motions of a classical pendulum system [42, 43] subjected to the viscous damping and periodic excitation and provides an effective approximation to analytically study the oscillating periodic solution around the stable equilibrium \(x=0\) in the complex pendulum system with the irrational and fractional nonlinear restoring force.

In fact, the headline finding of this study is to introduce an effectively simplified approximate system rather than the traditionally polynomial approximation to investigate the oscillating periodic solutions of a typical pendulum system with smooth and discontinuous dynamics. To this end, this paper is organized as follows. In Sect. 2, the equation of motion for the pendulum system subjected to both the viscous damping and external harmonic forcing is derived. It is found that this pendulum system exhibits both smooth and discontinuous dynamics depending on a geometrical parameter \(\lambda \). In Sect. 3, the unperturbed dynamics of this pendulum system with an irrational and fractional nonlinear restoring force is directly analyzed without using Taylor expansion. Compared with the Duffing system derived by Taylor unfolds at \(x=0\), a simplified approximate system not only successfully retains the non-smooth characteristics but also completely reflects the local feature of the complex restoring force. In Sect. 4, the averaging method is carried out to derive the response curve of the simplified approximate system with small oscillations within the margin of error. Furthermore, the corresponding oscillating periodic solutions around the position \(x=0\) for this pendulum system and the simplified approximate system can be investigated by means of the response curve. Then, the numerical simulations are carried out to verify the efficiency of the theoretical analysis. Finally, we summarize the conclusions and provide the further challenges in Sect. 5.

2 Equation of motion

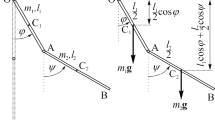
Figure 1a shows a classical mechanical model which is composed of a simple pendulum, a linear spring, an electrifying circuit that generates an electric current I and a magnetic field that provides the periodic magnetic intensity \(B \cos \Omega {\overline{t}}\). More specifically, a simple pendulum (with the mass m and the rod length L) linked by an oblique spring with a fixed end (with the free length l and the stiffness k) moves in a vertical plane and cuts vertically the horizontal magnetic field line. In other words, we also consider this mechanical model subjected a viscous damping (with coefficient C) and an external harmonic excitation (with amplitude \(F_{0}\) and frequency \(\Omega \)) in the direction of motion; the details can be seen in Fig. 1b. With the help of Lagrange equation, the differential equation can be derived as

$$\begin{aligned} \begin{array}{l} mL{x}^{\prime \prime }+ CL{x^{\prime }}+mg\sin {x}+ kh\sin {x}\left( 1-\frac{l}{\sqrt{L^{2}+h^{2}-2hL\cos {x}}}\right) =F_{0}\cos \Omega {\overline{t}}, \end{array} \end{aligned}$$
(1)

where the prime denotes derivative with respect to \({\overline{t}}\), x represents the angular displacement and the variable parameter h is the distance between the point A and point B, always assumed \(h \ge L\), respectively. Assuming \(L=l\), this pendulum system (1) can be rewritten in the following form

$$\begin{aligned} \begin{array}{l} \ddot{x}+\xi {\dot{x}}+\sin {x}+ q\lambda \sin {x}\left( 1-\frac{1}{\sqrt{1+\lambda ^{2}-2\lambda \cos {x}}}\right) =f_{0}\cos \omega t, \end{array} \end{aligned}$$
(2)

where

$$\begin{aligned} t=\sqrt{\frac{{g}}{{L}}}~{\overline{t}}, \xi =\frac{C}{m}\sqrt{\frac{L}{g}}, \omega =\sqrt{\frac{{L}}{{g}}}\Omega , \omega _{p}=\sqrt{\frac{g}{{L}}},\omega _{s}=\sqrt{\frac{k}{{m}}}, q=\frac{\omega _{s}^{2}}{\omega _{p}^{2}},\lambda =\frac{h}{L},~f_{0}=\frac{F_{0}}{mg}. \end{aligned}$$

Note that one dimensionless parameter q in system (2) mainly reflects the natural frequency ratio of the spring–mass system \(\omega _{s}\) and simple pendulum \(\omega _{p}\), the other dimensionless parameter \(\lambda \) represents the geometric structure of the pendulum model.

Fig. 1
figure 1

(a) The mechanical model: a pendulum which is tied a live wire moves in a periodic magnetic field, (b) the corresponding simplified plane model with \(F_{0}=BIL/2\)

Full size image

3 A simplified approximate system

Due to the discontinuous feature of this pendulum system, it is found that the traditional approximate method cannot completely and accurately describe the local dynamics in the qualitative and quantitative analysis. A simplified approximate system with an irrational and fractional nonlinear restoring force is introduced by means of the unperturbed dynamics of the original system (2), which bears significant similarities to an archetypal oscillator with smooth and discontinuous dynamics [44] rather than the softening Duffing oscillator.

3.1 Unperturbed dynamics of this pendulum system

When \(f_{0}=0\) and \(\xi =0\), the corresponding unperturbed dynamical system of the pendulum (2) is described by

$$\begin{aligned} \begin{array}{l} \ddot{x}+\sin {x}+q\lambda \sin {x}\left( 1-\frac{1}{\sqrt{1+\lambda ^{2} -2\lambda \cos {x}}}\right) =0. \end{array} \end{aligned}$$
(3)

It is worth reiterating here that the discontinuous dynamics is obtained by changing the parameter \(\lambda \) to 1 smoothly, which is the limit case from the mathematical point of view. Thus, the unperturbed discontinuous system can be written as

$$\begin{aligned} \begin{array}{l} \ddot{x}+\left( 1+q\right) \sin {x}-q\cos {\frac{x}{2}}~\text {sgn} \left( {\sin {{\frac{x}{2}}}}\right) =0, \end{array} \end{aligned}$$
(4)

where the piecewise defined function is

$$\begin{aligned} \text {sgn}\left( \sin {\frac{x}{2}}\right) =\left\{ \begin{array}{l} 1,~~~~{x}\in \left( 0,\pi \right] ,\\ 0,~~~~x=0,\\ [0.1 cm] -1,~~{x}\in \left[ -\pi ,0\right) . \end{array}\right. \end{aligned}$$
(5)

Due to its periodicity, we will consider dynamical behaviors of the pendulum system over a period \(x\in [-\pi ,\pi ]\) in the following analysis. Letting \(\ddot{x}=F(x)\), the restoring forces for smooth and discontinuous cases can be easily obtained as

$$\begin{aligned} F(x)=\left\{ \begin{array}{l} -\sin {x}-q\lambda \sin {x}\left( 1-\frac{1}{\sqrt{1+\lambda ^{2}-2\lambda \cos {x}}}\right) , ~~\lambda >1,\\ -\left( 1+q\right) \sin {x}+q\cos {\frac{x}{2}}~\mathrm {sgn}\left( {\sin {{\frac{x}{2}}}}\right) , ~~~~~~~~~~~~\lambda =1. \end{array}\right. \end{aligned}$$
(6)

Even the stiffness of the spring is linear and the resistance force supplied to the pendulum system is strongly irrational nonlinearity due to geometry configuration. Furthermore, a pitchfork bifurcation set B can be computed through \(F^{\prime }(0)=0\) where the prime denotes derivative of restoring force F(x) with respect to x. Thus, the corresponding expression of the pitchfork bifurcation set is

$$\begin{aligned} \begin{array}{lll}B=\left\{ (\lambda ,q)~\bigg |~q=\frac{\lambda -1}{\lambda \left( 2-\lambda \right) }, ~\lambda \in (1,2), ~q\in (0,+\infty ) \right\} . \end{array} \end{aligned}$$
(7)

3.2 A simplified approximate system with smooth and discontinuous dynamics

It is well known that the small-angle approximation is considered to be a useful simplification of the basic trigonometric functions in simple pendulum. The small-angle approximation is approximately true in the limit where the angle approaches zero. In the following analysis, we assume that the pendulum system vibrates in the neighborhood of the static equilibrium position \(x=0\).

In order to detect the small-angle oscillations around a stable equilibrium \(x=0\), we introduce an approximation \(\sin x \approx x\) and \(\cos x \approx 1-x^{2}/2\) into the proposed pendulum system (3), for which the oscillatory approximation of this pendulum system (3) can be written as

$$\begin{aligned} \begin{array}{l} \ddot{x}+x+q\lambda x\left( 1-\frac{1}{\sqrt{\left( \lambda -1\right) ^{2} +\lambda x^{2}}}\right) =0. \end{array} \end{aligned}$$
(8)

Letting \(\ddot{x}=F_{{A}}(x)\), the nonlinear restoring forces of the simplified approximate system (8) can be written as

$$\begin{aligned} F_{{A}}(x)=\left\{ \begin{array}{l} -x-q\lambda x\left( 1-\frac{1}{\sqrt{\left( \lambda -1\right) ^{2}+\lambda x^{2}}}\right) , ~~\lambda >1,\\ -(1+q)x+q~\mathrm {sgn}{x},~~~~~~~~~~~~~~~~~~~~~~~~\lambda =1. \end{array}\right. \end{aligned}$$
(9)

Traditionally, this pendulum system (3) can be simplified as a polynomial system (Duffing system) with the help of a Taylor expansion for the nonlinear restoring force F(x) centered at \(x=0\), and can be expressed as

$$\begin{aligned} \begin{array}{l} \ddot{x} +a_{0}+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+a_{4}x^{4}+a_{5}x^{5}+o[x^{6}]=0,~~~~\lambda >1, \end{array} \end{aligned}$$
(10)

of which the nonlinear restoring force \(F_{{3}}(x)\) and \(F_{{5}}(x)\) can be expressed as

$$\begin{aligned} \begin{array}{ll} F_{{3}}(x)= a_{0}+a_{1}x+a_{2}x^{2}+a_{3}x^{3},\\ F_{{5}}(x)= a_{0}+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+a_{4}x^{4}+a_{5}x^{5}, \end{array} \end{aligned}$$
(11)

where

$$\begin{aligned} a_{0}= & {} 0, a_{1}=-\left( 1+q\lambda -\frac{q\lambda }{\lambda -1}\right) , a_{2}=0, a_{3}=-\frac{1}{6} \left( 1+q\lambda -\frac{q\lambda }{\lambda -1}-\frac{3q\lambda ^{2}}{\left( \lambda -1\right) ^{3}}\right) ,\\ a_{4}= & {} 0,~~~ a_{5}=\frac{1}{120} \left( 1+q\lambda -\frac{q\lambda }{\left( \lambda -1\right) }-\frac{15q\lambda ^{2}}{\left( \lambda -1\right) ^{3}}-\frac{45q\lambda ^{3}}{\left( \lambda -1\right) ^{5}}\right) . \end{aligned}$$

In fact, compared with the polynomial approximate system (10), the simplified approximate system (8) not only successfully retains the non-smooth characteristics but also accurately reflects the local dynamics of original system (3) in the neighborhood of \(x=0\). Interestingly, the simplified approximate system (8) with strongly irrational nonlinearity exhibits both smooth and discontinuous dynamics depending on same geometrical parameter \(\lambda \), which bears significant similarities to the pendulum system (3). In order to further understand the benefits of the simplified approximate system (8), we construct a detailed comparison among the simplified approximate system denoted by a blue dashed line, cubic polynomial system or Duffing system marked by a red dashed line, quintic polynomial system marked by a green dashed line and the pendulum system with a black solid line, as shown in Fig. 2. When \(q=0.1\), Fig. 2a shows a equilibrium bifurcation diagram of the geometrical parameter \(\lambda \) versus the angular displacement x, which indicates that the polynomial system (10) derived by Taylor expansion can not accurately reflect the local feature of the original system (3), especially in the case of discontinuity for \(\lambda =1\). Note that these four dynamical systems undergo a pitchfork bifurcation for same parameters q and \(\lambda \) satisfying Eq. (7). Clearly, the equilibrium bifurcation of the quintic polynomial system marked by a green dashed line in Fig. 2a cannot qualitatively describe the local characteristics of the original system, especially the number of equilibrium. The corresponding nonlinear restoring forces of the original system F(x), the simplified approximate system \(F_{A}(x)\) and the Duffing system \(F_{3}(x)\) are plotted in Fig. 2b, where the black solid lines correspond to the original system, the blue dashed lines represent the simplified approximate system and the red dashed lines are the Duffing system, respectively. Similarly, for \(q=1.0\), the other equilibrium bifurcation diagram of the geometrical parameter \(\lambda \) and the corresponding nonlinear restoring forces can be plotted in Fig. 2c and d, respectively. Furthermore, the absolute error is regularly employed to evaluate the degree of approximation in both smooth and discontinuous cases; the detailed description can be seen in Fig. 3. For the smooth case with \(q=0.1\), Fig. 3a shows the absolute error \(\delta (x)=|F(x)-F_{A}(x)|\) and \(\delta (x)=|F(x)-F_{3}(x)|\) for different values of parameter \(\lambda \). Note that the solid curves colored in blue, red and green correspond to the absolute error of the polynomial system (PS), and the dashed, dotted and dash-dotted curves correspond to the absolute error (\(\delta (x)<4\times 10^{-3}\) for \(x\in [-0.3,0.3]\)) of the simplified approximate system (AS). For the discontinuous case with \(\lambda =1\), Fig. 3b displays the absolute error (\(\delta (x)=|F(x)-F_{A}(x)|<9 \times 10^{-3}\) for \(x\in [-0.4,0.4]\)) of the simplified approximate system (AS) for different values of parameter q. From the comparisons depicted in Figs. 2 and  3, it is concluded that the simplified approximate system (8) is obviously more accurate than the polynomial system (10), especially for small values of two parameters q and \(\lambda \). Then, we will use the simplified approximate system to analyze the oscillatory motion around the position \(x=0\) in the following section.

4 Oscillating periodic solutions

In this section, the oscillating periodic solutions of the pendulum system with an irrational and fractional nonlinear restoring force are studied both theoretically and numerically under the sufficiently small perturbations of a viscous damping as well as a harmonic excitation by means of the primary response curve of the simplified approximate system.

Fig. 2
figure 2

Dynamical behaviors in the neighborhood of the position \(x=0\), (a) the comparison of the equilibrium bifurcations for \(q=0.1\) and (b) the comparison of the nonlinear restoring forces for \(\lambda =1.0,1.05,1.1\) and 1.2, (c) the comparison of the equilibrium bifurcations for \(q=1.0\) and (d) the comparison of the nonlinear restoring forces for \(\lambda =1.0,1.2,1.6\) and 2.0, respectively (the black solid line represents the pendulum system F(x), blue dashed line denotes the simplified approximate system \(F_{A}(x)\), and red dashed line is the polynomial system \(F_{3}(x)\))

Full size image
Fig. 3
figure 3

The diagram of the absolute error \(\delta (x)\) for the nonlinear restoring force: (a) the smooth case with \(q=0.1\) for different values of parameter \(\lambda \), (b) the discontinuous case with \(\lambda =1\) for different values of parameter q

Full size image

4.1 Theoretical analysis of the oscillatory motion around the position \(x=0\)

With the help of the averaging method [45, 46], the oscillatory motion around the position \(x=0\) of the perturbed pendulum system can be studied by means of the simplified approximate system. Under the sufficiently small perturbations of a viscous damping as well as a harmonic excitation, the corresponding perturbed approximate system is given by

$$\begin{aligned} \begin{array}{l} \ddot{x}+\xi {\dot{x}}+x+q\lambda x\left( 1-\frac{1}{\sqrt{\left( \lambda -1\right) ^{2} +\lambda x^{2}}}\right) =f_{0}\cos \omega t. \end{array} \end{aligned}$$
(12)

We introduce a periodic solution in the form of slowly varying amplitude a(t) and phase \(\theta (t)\), and the defined solution can be written as

$$\begin{aligned} \begin{array}{l} x(t)=a\cos {\varphi },~~ \dot{x}{(t)}=-a\omega \sin {\varphi },~~ \varphi =\omega t+\theta . \end{array} \end{aligned}$$
(13)

Based upon Eqs. (12) and (13), we have

$$\begin{aligned} \left\{ \begin{array}{l} ~~~\dot{a} \cos \varphi -a {\dot{\theta }} \sin \varphi =0,\\ -\dot{a}\omega \sin {\varphi }-a\omega {\dot{\theta }}\cos {\varphi }=f(t,a\cos {\varphi }, -a\omega \sin {\varphi }), \end{array}\right. \end{aligned}$$
(14)

where

$$\begin{aligned} \begin{array}{l} f(t,a\cos {\varphi },-a\omega \sin {\varphi })= f_{0}\cos \omega t \\ \quad +\,a\omega ^{2}\cos {\varphi } + \xi a\omega \sin {\varphi }-a\cos {\varphi } -q\lambda a\cos {\varphi }\left( 1-\frac{1}{\sqrt{\left( \lambda -1\right) ^{2}+\lambda \left( a\cos {\varphi }\right) ^{2}}}\right) . \end{array}\nonumber \\ \end{aligned}$$
(15)

By solving linear equation set (14) about \(\dot{a}\) and \({\dot{\theta }}\), we have

$$\begin{aligned} \left\{ \begin{array}{l} \dot{a}=-\frac{1}{\omega }f(t,a\cos {\varphi },-a\omega \sin {\varphi })\sin \varphi ,\\ {\dot{\theta }}=-\frac{1}{\omega a}f(t,a\cos {\varphi },-a\omega \sin {\varphi })\cos \varphi . \end{array}\right. \end{aligned}$$
(16)

Averaging Eq. (16) over a period \([0, 2\pi ]\), Eq. (16) becomes

$$\begin{aligned} \left\{ \begin{array}{l} \dot{a}=-\frac{1}{2\pi \omega }\displaystyle \int _{0}^{2\pi }f(t,a\cos {\varphi }, -a\omega \sin {\varphi })\sin \varphi ~\mathrm{d}\varphi ,\\ {\dot{\theta }}=-\frac{1}{2\pi \omega a}\displaystyle \int _{0}^{2\pi }f(t,a\cos {\varphi }, -a\omega \sin {\varphi })\cos \varphi ~\mathrm{d}\varphi .\\ \end{array}\right. \end{aligned}$$
(17)

Substituting Eq. (15) into Eq. (17) and introducing two functions \(\Phi (a,\omega )\) and \(\Psi (a,\omega )\), we have

$$\begin{aligned} \left\{ \begin{array}{l} \dot{a}=-\frac{1}{2\omega }\left( \xi a\omega + f_{0}\sin {\theta }\right) = -\frac{1}{2\omega }\left[ \Phi (a,\omega ) + f_{0}\sin {\theta }\right] ,\\ {\dot{\theta }}=-\frac{1}{2\omega a}\left( a\omega ^{2}-a-q\lambda a+aG(a) +f_{0}\cos {\theta }\right) =-\frac{1}{2\omega a}\left[ \Psi (a,\omega ) +f_{0}\cos {\theta }\right] ,\\ [0.1 cm] \end{array}\right. \nonumber \\ \end{aligned}$$
(18)

which leads to the amplitude equation by neglecting the phase variable

$$\begin{aligned} \begin{array}{l} \left( \xi \omega \right) ^{2}+\left[ \omega ^{2}-\left( 1+q\lambda \right) +G(a)\right] ^{2} =\left( \frac{f_{0}}{a}\right) ^{2}. \end{array} \end{aligned}$$
(19)

The function G(a) in Eq. (19) can be expressed as

$$\begin{aligned} \begin{array}{l} G(a)=\frac{4q}{a^{2}\pi }\left( \sqrt{{(\lambda -1)^{2}+\lambda a^{2}}} ~{EllipticE}\left[ k\right] -{\frac{(\lambda -1)^{2}}{\sqrt{(\lambda -1)^{2}+\lambda a^{2}}}}~ {EllipticK}\left[ k\right] \right) ,\\ \end{array} \end{aligned}$$
(20)

where

$$\begin{aligned} \begin{array}{l} k=\sqrt{\frac{a^{2}\lambda }{(\lambda -1)^{2}+a^{2}\lambda }}. \end{array} \end{aligned}$$
(21)

It is worth reiterating here that EllipticK [k] and EllipticE [k] are the complete Jacobian elliptic integrals of the first and second kind with \(0< k < 1\). Particularly, the amplitude equation of discontinuous case can be derived by letting \(\lambda = 1\) and defining

$$\begin{aligned} \lim _{\lambda \rightarrow 1^{+}}{EllipticE}~\left[ \sqrt{\frac{a^{2}\lambda }{(\lambda -1)^{2} +a^{2}\lambda }}\right]= & {} \lim _{k \rightarrow 1^{-}}{EllipticE}~\left[ k\right] \nonumber \\= & {} \lim _{k \rightarrow 1^{-}} \int _{0}^{\frac{\pi }{2}}\sqrt{1-k^{2}\sin ^{2}{\phi }}~\mathrm{d}\phi =1, \end{aligned}$$
(22)
$$\begin{aligned} \lim _{\lambda \rightarrow 1^{+}}{EllipticK}~\left[ \sqrt{\frac{a^{2}\lambda }{(\lambda -1)^{2} +a^{2}\lambda }}\right]= & {} \lim _{k \rightarrow 1^{-}}{EllipticK}~\left[ k\right] \nonumber \\= & {} \lim _{k \rightarrow 1^{-}} \int _{0}^{\frac{\pi }{2}}\frac{1}{\sqrt{1-k^{2}\sin ^{2}{\phi }}}~\mathrm{d}\phi =+\infty .\nonumber \\ \end{aligned}$$
(23)

When the parameter \(\lambda \) approaches 1 from the right, Eq. (20) becomes

$$\begin{aligned} \lim _{\lambda \rightarrow 1^{+}}G(a)=\frac{4q}{a\pi }. \end{aligned}$$
(24)

Thus, the corresponding amplitude equation of discontinuous case is given by

$$\begin{aligned} \begin{array}{l} \left( \xi \omega \right) ^{2}+\left[ \omega ^{2}-\left( 1+q\right) +\frac{4q}{a\pi }\right] ^{2}=\left( \frac{f_{0}}{a}\right) ^{2}. \end{array} \end{aligned}$$
(25)

Then, we define that the amplitude \(a_{s}\) and phase \(\theta _{s}\) of the steady states which are satisfying Eqs. (19) and (25). Notice that \(a_{s}\) and phase \(\theta _{s}\) are the equilibria of Eq. (18) and satisfy

$$\begin{aligned} \left\{ \begin{array}{l} \Phi (a_{s},\omega ) + f_{0}\sin {\theta _{s}}=0,\\ [0.3 cm] \Psi (a_{s},\omega )+f_{0}\cos {\theta _{s}}=0, \end{array}\right. \end{aligned}$$
(26)

which leads to

$$\begin{aligned} W(a_{s},\omega )= & {} \Phi ^{2} (a_{s},\omega ) + \Psi ^{2} (a_{s},\omega ) -\left( f_{0}\right) ^{2}=0,\nonumber \\ \theta _{s}= & {} \arctan {\left( \frac{ \Phi (a_{s},\omega )}{ \Psi (a_{s},\omega )}\right) }. \end{aligned}$$
(27)

For a better understanding of the stability of the solution of Eqs. (19) and (25), the perturbation variables \(\zeta =a+a_{s}\) and \(\eta =\theta +\theta _{s}\) are introduced. Such that the system (18) can be written as a linearized averaged equation related to \(\zeta \) and \(\eta \) as follows

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{\zeta }}=-\frac{1}{2\omega }\left[ \left( \frac{\partial ~\Phi (a,\omega )}{\partial ~ a}\right) _{s}~\zeta + f_{0}\cos {\theta _{s}}~\eta \right] ,\\ {\dot{\eta }}=-\frac{1}{2\omega }\left\{ \frac{1}{a_{s}} \left[ \left( \frac{\partial ~\Psi (a,\omega )}{\partial ~ a}\right) _{s} -\frac{1}{a^{2}_{s}}\left( \Psi (a_{s},\omega )+f_{0}\cos {\theta _{s}}\right) \right] ~\zeta - f_{0}\sin {\theta _{s}}~\eta \right\} .\\ \end{array}\right. \end{aligned}$$
(28)

If the zero solutions of \(\zeta \) and \(\eta \) in the above system (28) are asymptotic stable, the steady state \((a_{s}, \theta _{s})\) is stable, otherwise unstable. It is clear that the above linearized averaged equation can be reduced to

$$\begin{aligned} \left\{ \begin{array}{l} 2\omega {\dot{\zeta }}+ \left( \frac{\partial ~\Phi (a,\omega )}{\partial ~ a}\right) _{s}~\zeta - \Psi (a_{s},\omega )~\eta =0,\\ 2\omega {\dot{\eta }}+\frac{1}{a_{s}}\left( \frac{\partial ~\Psi (a,\omega )}{\partial ~ a}\right) _{s} ~\zeta + \frac{1}{a_{s}}\Phi (a_{s},\omega ) ~\eta =0. \end{array}\right. \end{aligned}$$
(29)

Hence, the stability can be derived by the characteristic equation of the system (29). The corresponding characteristic equation is given by

$$\begin{aligned} \begin{array}{l} \texttt {det}\left( \begin{array}{cc} 2\omega \Lambda + \left( \frac{\partial ~\Phi (a,\omega )}{\partial ~ a}\right) _{s} &{} - \Psi (a_{s},\omega )\\ \frac{1}{a_{s}}\left( \frac{\partial ~\Psi (a,\omega )}{\partial ~ a}\right) _{s} &{} 2\omega \Lambda + \frac{1}{a_{s}}\Phi (a_{s},\omega )\\ \end{array} \right) =4\omega ^{2}\left( \Lambda ^{2}+\alpha ~\Lambda +\beta \right) =0,\end{array} \end{aligned}$$
(30)

where \(\Lambda \) is the eigenvalues of the differential equations and

$$\begin{aligned} \left\{ \begin{array}{l} \alpha =\frac{1}{2\omega }\left[ \left( \frac{\partial ~\Phi (a,\omega )}{\partial ~ a}\right) _{s} +\frac{1}{a_{s}}\Phi (a_{s},\omega )\right] ,\\ \beta =\frac{1}{4\omega ^{2} a_{s}}\left[ \Phi (a_{s},\omega )\left( \frac{\partial ~\Phi (a,\omega )}{\partial ~ a}\right) _{s}+ \Psi (a_{s},\omega )\left( \frac{\partial ~\Psi (a,\omega )}{\partial ~ a}\right) _{s}\right] . \end{array}\right. \end{aligned}$$
(31)

Based upon the Routh–Hurwitz criterion [7, 45, 46], when all the real part of eigenvalues is negative, the zero solution is stable. Therefore, if it satisfies the conditions \(\alpha >0\) and \(\beta >0\), the steady state \((a_{s},\theta _{s})\) is stable.

4.2 Numerical simulations of the oscillatory motion around the position \(x=0\)

In order to verify the theoretical results derived by the averaging method, the numerical simulations including the phase portrait, attractive basin and time history are conducted to demonstrate the corresponding periodic solution around the position \(x=0\) in this subsection.

Fig. 4
figure 4

Response curves in the \(f_{0}-a\) plane, (a) the effect of the parameter \(\omega \) with \(q=0.1,\lambda =1.15,\xi =0.05\), (b) the effect of the parameter \(\xi \) with \(q=0.1,\lambda =1.15,\omega =0.8\), (c) the effect of the parameter q with \(\lambda =1.15,\xi =0.05,\omega =0.8\), (d) the effect of the parameter \(\lambda \) with \(q=0.1,\xi =0.05,\omega =0.8\), respectively

Full size image
Fig. 5
figure 5

Response curves in the \(\omega -a\) plane, (a) the effect of the parameter \(f_{0}\) with \(\xi =0.05, q=0.1, \lambda =1.15\), (b) the effect of the parameter \(\xi \) with \(f_{0}=0.015, q=0.1, \lambda =1.15\), (c) the effect of the parameter q with \(f_{0}=0.015,\xi =0.05,q=0.1\), (d) the effect of the parameter \(\lambda \) with \(f_{0}=0.015,\xi =0.05,\lambda =1.15\), respectively

Full size image

For example, the response curves in the \(f_{0}-a\) plane can be plotted with the help of Eq. (19) for different values of parameter \(\omega \), \(\xi \), q and \(\lambda \) in Fig. 4a, b, c and d, respectively. As an external parameter \(\omega \) increases from 0.5 to 0.8, the effects of the external frequency \(\omega \) on the related response curve are investigated in Fig. 4a, which indicates that a plurality of steady states can be observed beyond \(\omega \approx 0.645\). Similarly, increasing the external parameter \(\xi \), the influences of the external damping \(\xi \) on the related response curve is presented in Fig. 4b, which means that the plurality of steady states disappears at \(\xi \approx 0.15\), and then becomes only one steady state for \(\xi >0.15\). In order to detect the effects of internal parameter q on the relative response curves, the amplitude–amplitude curves for different values of parameter q can be plotted in Fig. 4c. To continue investigating the effects of the geometrical parameter \(\lambda \), we construct the relative response curves for different values of parameter \(\lambda \); the detailed description can be seen in Fig. 4d. Note that the response curves with the plurality of steady states can be denoted by red and blue curves in Fig. 4. Moreover, the stable and unstable branches are drawn with solid and dashed lines in Fig. 4, respectively, which can be proven by considering of the eigenvalues of the linearized averaged equation, see Ref. [45, 46].

Then, the response curves in the \(\omega -a\) plane are presented with the help of Eq. (19) for different values of parameter \(f_{0}\), \(\xi \), q and \(\lambda \) in Fig. 5a, b, c and d, respectively. Fixing parameters \(\xi \), q and \(\lambda \) and plotting the response amplitude a of Eq. (19) against \(\omega \), we obtain the frequency response curves for different values of parameter \(f_{0}\), seen in Fig. 5a. It is found from Fig. 5a that the peak value and multi-stable interval of the amplitude–frequency curves increase obviously with the increase of parameter \(f_{0}\). As the external parameter \(\xi \) increases from 0.06 to 0.10, the influences of the external damping \(\xi \) on the relative the response curve are studied in Fig. 5b, which indicates that a plurality of steady states and the peak value of the amplitude–frequency curve decrease obviously with the increase of parameter \(\xi \). Similarly, the effects of the internal parameters q and \(\lambda \) on the related response curves are plotted by means of Eq. (19) in Fig. 5c and d, respectively. Note that a plurality of steady states is disappeared beyond \(\lambda \approx 1.3\) and the peak value of the amplitude–frequency curve decreases with the increase of parameter \(\lambda \), seen in Fig. 5c. Moreover, a plurality of steady states can be observed beyond \(q\approx 0.05\) and the peak value of the amplitude–frequency curve increases with the increase of parameter q, seen in Fig. 5d. The details of the parameters taken in Fig. 5 can be found in the corresponding captions.

For clarity, a typical response curve in the \(f_{0}-a\) plane can be displayed with the help of Eq. (19) for \(q=0.1,\lambda =1.15,\xi =0.05\) and \(\omega =0.8\) in Fig. 6a, where nine particular points are listed in Table 1. Two forces that bound the interval on the existence of a plurality of steady states are termed as \(f_{1}\) and \(f_{2}\). In other words, for the forces extracted from \([f_{1},f_{2}]\), a plurality of steady states can be observed. When the parameter \(f_{0}\) increases from 0 to 0.03, the response curve undergoes a jump phenomenon at \(f_{0}=f_{2}\) traveling one branch \(\texttt {A}\rightarrow \texttt {B}\rightarrow \texttt {C}\rightarrow \texttt {D}\rightarrow \texttt {H} \rightarrow \texttt {I}\). On the contrary, decreasing the parameter \(f_{0}\) from 0.03 to 0, there exists a jump phenomenon at \(f_{0}=f_{1}\) with the other branch \(\texttt {I}\rightarrow \texttt {H}\rightarrow \texttt {G}\rightarrow \texttt {F}\rightarrow \texttt {B} \rightarrow \texttt {A}\), the detailed description can be shown in Fig. 6a. Then, we will consider phase portraits of the corresponding periodic solutions around the equilibrium (0, 0) in the simplified approximate system. The relative phase portraits are plotted in Fig. 6b–f by using Runge–Kutta method. Note that Fig. 6b shows a small stable periodic solution for \(f_{0}=0.005\). As parameter \(f_{0}\) increases approximately to 0.00832, there exists a small stable periodic solution and a large semi-stable periodic solution denoted by the red dotted line in Fig. 6c. By continuing increasing the parameter \(f_{0}\), the large semi-stable periodic solution bifurcates into two periodic solutions where the large one is stable and the other is unstable, coexisting of a small stable periodic solution as shown in Fig. 6d. When \(f_{0}\approx 0.01832\), the unstable periodic solution and the small stable periodic solution shrink to a small semi-stable periodic solution which coexists of a large stable periodic solution in Fig. 6e. When \(f_{0}>0.01832\), the small semi-stable periodic solution disappears and only one large periodic solution can be found in Fig. 6f. In order to detect the jump phenomenon in both the original system (OS) and the simplified approximate system (AS), the bifurcation diagrams for parameter \(f_{0}\) versus x are given in Fig. 7. It is clear that Fig. 7a and b describes the bifurcation diagram for the parameter \(f_{0}\) versus x starting from 0 to 0.03. Fig. 7a corresponds to the original system with a jump phenomenon at \(f_{0}\approx 0.018401\), and Fig. 7b represents the simplified approximate system with a jump phenomenon at \(f_{0}\approx 0.01832\). Similarly, the bifurcation diagram for parameter \(f_{0}\) versus x from 0.03 to 0 can be plotted in Fig. 7c and d. It is found that the bifurcation diagram depicted in Fig. 7 shows a good agreement with the theoretical predictions depicted in Fig. 6a and an excellent efficiency of the analysis for this pendulum system; especially, the parameter values of the jump phenomenon occurring in two systems are well consistent with the theoretical analysis.

Table 1 The values of nine particular points in Fig. 6a
Full size table
Fig. 6
figure 6

When \(q=0.1,\lambda =1.15,\xi =0.05\) and \(\omega =0.8\): (a) a typical response curve in the \(f_{0}-a\) plane with \(f_{1} \approx 0.0083945\) and \(f_{2}\approx 0.018381\). The phase portraits of periodic solutions of the simplified approximate system (12) (the red solid, thin solid, dotted loops correspond to stable, unstable and semi-stable, respectively): (b) a small stable periodic solution for \(f_{0}=0.005\), (c) a stable periodic solution coexisting of a semi-stable periodic solution for \(f_{0} \approx 0.00839\), (d) two stable periodic solutions coexisting of an unstable periodic solution for \(f_{0}=0.014\), (e) a large stable periodic solution coexisting of a semi-stable periodic solution for \(f_{0}\approx 0.01832\), (f) a large stable periodic solution for \(f_{0}=0.025\), respectively

Full size image
Fig. 7
figure 7

Bifurcation diagrams for \(f_{0}\) versus x with \(q=0.1,\lambda =1.15,\omega =0.8,\xi =0.05\): one bifurcation diagram for \(f_{0}\) starting from 0 to 0.03: (a) the original system with a jump phenomenon at \(f_{2}\approx 0.018401\) and (b) the simplified approximate system with a jump phenomenon at \(f_{2}\approx 0.01832\); the other bifurcation diagram for \(f_{0}\) starting from 0.03 to 0: (c) the original system with a jump phenomenon and (b) the simplified approximate system with a jump phenomenon

Full size image
Fig. 8
figure 8

When \(q=0.1,\lambda =1.15,\omega =0.8,\xi =0.05\), the comparisons of phase portraits of the periodic solutions x(t) among the original system (blue lines), the simplified approximate system (red lines) and the corresponding theoretical results (black lines) starting from the initial condition \((x(0),y(0))=(0,0)\) for (a) \(f_{0}=0.005\) and (b) \(f_{0}=0.025\). (c) The comparisons of time histories for \(f_{0}=0.005\) and the amplified figure (d), (e) the comparisons of time histories for \(f_{0}=0.025\) and the amplified figure (f)

Full size image
Fig. 9
figure 9

Comparisons of phase portraits among the original system denoted by blue solid lines, the simplified approximate system marked by red solid lines and the theoretical results with black solid lines for \(q=0.1,\lambda =1.15,\omega =0.8,\xi =0.05\): (a) the coexistence of two stable periodic solutions for \(f_{0}=0.01\), (b) the coexistence of two stable periodic solutions for \(f_{0}=0.014\)

Full size image
Fig. 10
figure 10

When \(q=0.1,\lambda =1.15,\omega =0.8,\xi =0.05,f_{0}=0.01\), (a) the attractive basin of the pendulum system (2), (b) the attractive basin of the simplified approximate system (12). The corresponding comparisons of the stable periodic solution between the original system (blue solid lines) and the simplified approximate system (red dashed lines): (c) the comparison of time history x(t) for \(t\in [0,1000]\) starting from the initial condition \((x(0),y(0))=(0.2,0)\) and (d) the amplified description for \(t\in [980,1000]\), (e) the comparison of time history x(t) for \(t\in [0,1000]\) starting from the initial condition \((x(0),y(0))=(0,0)\) and (f) the amplified description for \(t\in [980,1000]\)

Full size image
Fig. 11
figure 11

When \(q=0.1,\lambda =1.15,\omega =0.8,\xi =0.05,f_{0}=0.014\), (a) the attractive basin of the pendulum system (2), (b) the attractive basin of the simplified approximate system (12). The corresponding comparisons of time histories of the stable periodic solution x(t) between the original system (blue solid lines) and the simplified approximate system (red dashed lines): (c) and (d) the time histories starting from the initial condition \((x(0),y(0))=(0.1,0)\) (the gray region of the attractive basin), (e) and (f) the time histories starting from the initial condition \((x(0),y(0))=(-0.1,0)\) (the blue region of the attractive basin)

Full size image
Fig. 12
figure 12

When \(q=0.1,\lambda =1.15,\omega =0.8,\xi =0.05\), (a) the attractive basin of the pendulum system (2) for \(f_{0}=0.018401\), (b) the attractive basin of the simplified approximate system (12) for \(f_{0}=0.01832\)

Full size image
Fig. 13
figure 13

When \(q=0.1,\lambda =1\) and \(\xi =0.05\), (a) the response curves of the discontinuous case for different values of parameter \(\omega \). The stable periodic solutions among the original system (blue), the simplified approximate system (red) and the corresponding theoretical results (black): the phase portraits of the original system (b) and approximate system (c) with similar parameters \(\omega =0.8,f_{0}=0.05\), the phase portraits of the original system (d) and approximate system (e) with similar parameters \(\omega =0.7,f_{0}=0.15\), the phase portraits of the original system (f) and approximate system (g) with similar parameters \(\omega =0.6,f_{0}=0.15\), (h) the corresponding time history x(t) for \(t\in [0,1000]\) starting from the initial condition \((x(0),y(0))=(1,0)\) and (i) the amplified description for \(t\in [800,1000]\), respectively

Full size image
Fig. 14
figure 14

Response curves of smooth and discontinuous systems with \(q=0.1,\xi =0.05,\omega =0.8\)

Full size image

In order to further understand the stable periodic solutions around the equilibrium (0, 0) depicted in Fig. 6, the comparisons of the phase portrait, time history and attractive basin between the pendulum system (2) and the simplified approximate system (12) can be introduced. When \(q=0.1,\lambda =1.15,\omega =0.8,\xi =0.05\) and \(f_{0}=0.005\), Fig. 8a shows a comparison of the phase portraits of a stable periodic solution, where the blue loop corresponds to the original system, the red loop represents the simplified approximate system, and the black loop denotes the theoretical result derived by the averaging method. It is worth pointing out that the phase trajectory of the theoretical results derived by the averaging method corresponds to the standard ellipses satisfying

$$\begin{aligned} \begin{array}{l} \frac{x^{2}}{a^{2}}+\frac{y^{2}}{\left( a\omega \right) ^{2}}=1. \end{array} \end{aligned}$$
(32)

The phase trajectories marked by the black loop are plotted with the help of Eq. (32), where the amplitude parameter a corresponds to a value of the response curve when \(f_{0}=0.005\). Then, the corresponding comparison of time histories can be displayed in Fig. 8b, where the blue line corresponds to the original system and the red dashed line represents the simplified approximate system. To show exactly the degree of approximation between the two systems, an amplified description of two time histories is presented in Fig. 8c. Similarly, for \(q=0.1,\lambda =1.15,\omega =0.8,\xi =0.05\) and \(f_{0}=0.025\), the comparisons of the phase portraits and time histories between the pendulum system (2) and the simplified approximate system (12) are plotted in Fig. 8d and e, respectively. In order to get a more accurate comparison, an amplified description of two time histories is introduced in Fig. 8f. Obviously, the oscillating periodic solutions of the approximate system colored in red coincide well with that of the original system by comparing with their phase trajectories and time histories. It is worth reiterating here that the black loops depicted in Fig. 8a (with \(a=0.0173\) and \(\omega =0.8\)) and Fig. 8d (with \(a=0.2810\) and \(\omega =0.8\)) can be potted by means of Eq. (32). The smaller the amplitude a of the response curve is, the higher the precision of the approximate analytical solution will be.

Fig. 15
figure 15

When \(q=0.1,\lambda =1.15,\xi =0.05\), (a) the function \(\Psi (a,\omega )\) of the smooth case for different values of parameter \(\omega \). When \(q=0.1,\lambda =1,\xi =0.05\), (b) the function \(\Psi (a,\omega )\) of the discontinuous case for different values of parameter \(\omega \)

Full size image
Fig. 16
figure 16

When \(q=0.1,\lambda =1.15,\omega =0.8,\xi =0.05\), the comparisons of the stable periodic solution x(t) between the original system (OS: blue solid lines) and the theoretical results (TR: red dotted lines) in the smooth case for (a) \(f_{0}=0.005\), (b) \(f_{0}=0.01\), (c) and (d) \(f_{0}=0.014\), (e) \(f_{0}=0.025\). (f) The time history of the discontinuous case for \(q=0.1, \lambda =1,\omega =0.8,\xi =0.05\) and \(f_{0}=0.025\). (Note that the initial conditions (x(0), y(0)) for the stable solutions of the original system correspond to (a) (0,0), (b) (0,0), (c), (0.1,0), (d) (\(-0.1\),0), (e) (0,0), (f) (1,0))

Full size image

Interestingly, it is found that both the original system (2) and the simplified approximate system (12) exhibit the coexistence of stable periodic solutions for \(f_{0}\in [f_{1},f_{2}]\), which shows a good agreement with the theoretical analysis in Fig. 6a. Taking \(f_{0}=0.01\) and \(f_{0}=0.014\) for example, the corresponding phase portraits of the coexistence of stable periodic solutions are presented in Fig. 9a and b, respectively, where two blue closed orbits correspond to the original system, two red closed orbits correspond to the approximate system and two black closed orbits are the theoretical results derived by the averaging method. Note that the black loops depicted in Fig. 9a (with \(a=0.2265\) and \(\omega =0.8\)) and Fig. 9b (with \(a=0.2449\) and \(\omega =0.8\)) can be potted by means of Eq. (32). For a better understanding of the coexistence of stable periodic solutions, the attractive basins can be introduced in Fig. 10a (the original system denoted by OS) and Fig. 10b (the approximate system marked by AS). It is worth pointing out that the blue region corresponds to the attractive basin of a small stable periodic solution of which attractor can be denoted by red solid point. Similarly, the attractive basin of the gray region represents a large stable periodic solution whose attractor can be marked by green solid point. It is well known that the boundary of two attractive regions is the basin of a unstable periodic solution. Then, the comparisons of time histories of the small and large stable periodic solutions between the original system colored in blue and the simplified approximate system denoted by red dashed line can be displayed for \(f_{0}=0.01\) in Fig. 10c and e. It is clear that the time history of the simplified approximate system shows a good agreement with that of the original system; the detailed comparison is displayed in Fig. 10d and f. Similarly, for \(f_{0}=0.014\), the comparisons of the attractive basin and time history are carried out to describe the stable periodic solutions in both the original system and approximate system, seen in Fig. 11. More specifically, Fig. 11a and b presents the attractive basin of small and large periodic solutions in two systems, respectively. In order to detect the degree of proximity of two system, the corresponding comparisons of the time history can be displayed in Fig. 11c (the amplified description seen in Fig. 11d) and Fig. 11e (the amplified description shown in Fig. 11f). It is worth reiterating here that the smaller the response amplitude of the pendulum system is, the higher the accuracy of the theoretical periodic solution will be.

As can be seen from Fig. 6a, the response curve undergoes one jump phenomenon at \(f_{0}=f_{2}\) as the parameter \(f_{0}\) increases from 0 to 0.03. In order to detect the nonlinear dynamical behavior near the jump phenomenon, Fig. 12a and b depicts the attractive basins of the original system (OS) and approximate system (AS) by taking the value of parameters near the jump phenomenon. When the parameter \(f_{0}\) increases from 0 to 0.03, the attractive region colored in blue of small stable periodic solution gradually reduces until disappears, and the detailed changes for the original system can be seen from Fig. 10a to Fig. 11a to Fig. 12a. Moreover, it is found that the attractive basins for the oscillating periodic solutions of the simplified approximate system coincide well with that of the original system.

For the discontinuous case [44, 47], we choose the parameters \(q=0.1,\lambda =1\) and \(\xi =0.05\). The response curves in the \(f_{0}-a\) plane can be plotted with the help of Eq. (25) for different values of parameter \(\omega \) in Fig. 13a, where the solid curves represent the stable branch and the dashed curves are the unstable branch. When \(f_{0}=0.05\) and \(\omega =0.8\), Fig. 13b gives a phase portrait comparison of the stable periodic solutions between the original system colored in blue and the theoretical analysis denoted by black. Meanwhile, the corresponding phase portrait comparison of the stable periodic solutions between the simplified approximate system colored in red and the theoretical analysis denoted by black is demonstrated in Fig. 13c. Similarly, for \(f_{0}=0.15\) and \(\omega =0.7\), the phase portraits of the stable periodic solutions of the original system colored in blue and the simplified approximate system denoted by red are presented in Fig. 13d and e, respectively, where the black closed orbit corresponds to the theoretical result. Then, Fig. 13f and g describes the stable periodic solutions of the original system colored in blue and the simplified approximate system denoted by red for \(\omega =0.6\) and \(f_{0}=0.15\). Moreover, the corresponding time histories of two systems can be plotted in Fig. 13h and its amplified description is presented in Fig. 13i, which shows a good agreement with the theoretical predictions and an excellent efficiency of the analysis for this pendulum system. The detailed value of the parameters taken in Fig. 13 can be found in the corresponding captions. It is worth reiterating here that a smooth periodic solution denoted by black loop in Fig. 13b–g is used to approximately describe the periodic solution of the non-smooth system. For a better understanding of this approximation, Fig. 14 shows the transition characteristics of the resonance curves from smooth systems to discontinuous systems. From a mathematical perspective, we derive the response curve of the discontinuous system by using the idea of limit.

Based upon the above theoretical analysis and numerical simulations, it is found that the simplified approximate system completely reflects the local dynamic behaviors of the original system with small-angle oscillations in terms of the equilibrium bifurcation, nonlinear restoring force, parameter bifurcation, attractive basin, phase portrait and time history. So, the corresponding theoretical solution x(t) of the oscillating periodic motion of this pendulum system is given by

$$\begin{aligned} \left\{ \begin{array}{ll} x(t)=a\cos {\left( \omega t +\arctan {\left( \frac{\Phi (a,\omega )}{\Psi (a,\omega )}\right) } \right) },&{} \quad \Psi (a,\omega )<0,\\ x(t)=\mp a\cos {\left( \omega t +\arctan {\left( \pm \infty \right) } \right) },&{} \quad \Psi (a,\omega )=0,\\ x(t)=-a\cos {\left( \omega t +\arctan {\left( \frac{\Phi (a,\omega )}{\Psi (a,\omega )}\right) } \right) },&{} \quad \Psi (a,\omega )>0. \end{array}\right. \end{aligned}$$
(33)

In order to further understand the approximate analytic expression of the periodic solution (33), we construct a detailed diagram of the function \(\Psi (a,\omega )\) for different parameter \(\omega \) to detect parameter a satisfying \(\Psi (a,\omega )<0\) or \(\Psi (a,\omega )>0\) in both smooth and discontinuous cases, seen in Fig. 15a and b, respectively. With the help of the analysis of the averaging method and the approximate analytic expression of the periodic solution (33), the theoretical solution x(t) can be displayed with the red dotted lines for the smooth and discontinuous cases in Fig. 16. When \(q=0.1\), \(\lambda =1.15\), \(\omega =0.8\) and \(\xi =0.05\), Fig. 16a–e depicts five typical stable periodic solutions x(t) marked by the red dotted lines for different parameter \(f_{0}\), which shows a good agreement with the numerical solutions of the original system denoted by the blue solid lines. For the discontinuous case, the comparison of the stable periodic solution x(t) between the numerical and theoretical result is given in Fig. 16f with \(q=0.1, \lambda =1,\omega =0.8,\xi =0.05\) and \(f_{0}=0.025\). Obviously, the theoretical solutions coincide well with that of the original system. It is worth pointing out here that the analytic expression of the theoretical solution x(t) can be marked in Fig. 16, and the corresponding initial conditions for time history of the original system can be given in the captions.

By comparing the phase portraits, bifurcation diagrams, time histories and attractive basins between the original system and the simplified approximate system in this section, it is concluded that the periodic oscillatory motion of the simplified approximate system bears significant similarities to that of the original system regardless of the qualitative analysis and quantitative calculation in both smooth and discontinuous cases. Furthermore, we precisely calculate the approximate analytic expression of the periodic solution of this pendulum system based upon the primary resonance analysis of the simplified approximate system.

5 Conclusions

The oscillating periodic motions of a classical pendulum system with small-angle oscillations have been studied in terms of the qualitative analysis and quantitative calculation. Note that this pendulum system having an irrational and fractional nonlinear restoring force exhibits both smooth and discontinuous dynamics. Due to its intrinsic nonlinearity and discontinuous characteristics, the traditionally polynomial approximation derived by a Taylor expansion about the point \(x=0\) cannot precisely describe the local feature of this pendulum with the small-angle oscillations, especially the discontinuous case. By introducing a simplified approximate system, all the possible periodic solutions around the position \(x=0\) of this pendulum system have been investigated theoretically by using the averaging method in the smooth and discontinuous cases. Compared with the traditional polynomial system derived by the Taylor expansion, it is concluded that the simplified approximate system not only successfully retains the non-smooth characteristics but also completely reflects the local feature of the original system. Numerical calculations, including the phase portrait, time history, attractive basin, bifurcation diagram and response curve, have shown a good agreement with the theoretical predictions and an excellent efficiency of the analysis for this pendulum system with the small-angle oscillations. This study provides an effective approach to investigate analytically the oscillating periodic solution of the complex pendulum system with the small-angle oscillations with a given error. The future study on this classical pendulum system is being carried out by the current authors in two aspects: one is the oscillating periodic solution around the bi-stable position, and the other is the vibration isolation [48, 49] and the energy absorption [50,51,52].