1 Introduction

In modern technology, the elastic semiconductor materials are very important in various circuit applications. Most of semiconductor materials have economic importance because it is widely spread in the environment. In modern geophysics, the silicon (Si) and germanium have many applications specially for electrical renewable energy. To understand the physical properties of these materials, the surface wave propagations through the semiconductor media must be studied. The effect of laser beam on the semiconductor media is very useful with the applications in generating clean electrical energy. The internal structure of the semiconductor media may be depends on gravitational forces. Since recently, semiconductor materials have been studied in mechanical engineering with structure as elastic materials. In this case, the thermal effect of laser or light, gravity and the electrical connection was being neglected with neglected. But in modern studies, the thermal effect of laser, gravity and sunlight must be taken into account. In this case, the microelement structures of the semiconductors from electrons and holes must be inserted into the calculations. As a result of the thermal effect, vibrations (elastic wave) of the particles occur and the electrons on the surface move from one place to the other. However, a weak electrical current is generated due to the electronic deformation (ED) with carrier density which it occurs inside the material and the plasma wave is obtained. The heat source as a laser has a great significant to understand the microelement structure with thermoelastic deformation (TE) of the elastic semiconductor material. The thermal conductivity parameter is very important to discuss TE specially when it depends on the temperature. In this case, the thermoelastic mechanism based on the thermal conductivity. Based on all the above studies, the photo-thermoelasticity theory of elastic semiconductor with the effect of gravity and variable thermal conductive must be taken into consideration.

In the middle of the last century, it was introduced the coupled dynamic thermoelasticity theory with a paradox when it was studied the wave propagation in elastic medium by Biot [1]. Chadwick [2] predicted that during disturbance processes the wave propagation through the elastic medium has an infinite speed. To address this contradiction, Lord and Şhulman's (LS) [3] developed a new model for the thermoelasticity theory when insert in the heat (energy) equation one relaxation time which it called a single-phase-lag model. On the other hand, Green and Lindsay (GL) [4] investigated and modified the thermoelasticity theory when added a two thermal relaxation times which they called thermal memories to the main heat conduction equation. Several scientists have developed the generalized thermoelasticity theory [5,6,7]. Tzou [8, 9] introduced the new DPL model which is a modification of the classical thermoelastic theory. In this model, the interaction between electrons and phonons is described with the heat transfer behavior of microelement structural when an elastic medium is studied [10]. The DPL model introduced a two various type of translations (relaxation) time. However, in the micro-scale, the first time names the first phase-lag (PL) \(\tau_{q}\) which describe the heat flux, and the second describes the temperature gradient which it calls a second phase-lag (PL) \(\tau_{\theta }\). Ailawalia et al. [11, 12] studied the effect of gravitational field and the rotation with two temperature theory during the generalized thermoelastic medium in the context of the hydrostatic initial stress impact. Hosseinzadeh et al. [13, 14] modified many models during they studying the micropolar hybrid nanoparticles with mixture fluid flow in the context of the influence of radiation and magnetic field. On the other hand, Hosseinzadeh et al. [15,16,17,18] investigated a hydrothermal analysis during a cross-fluid flow for ethylene glycol nanoparticles and microorganisms in three-dimensional cylinder and used the numerical simulation to prove the obtained results.

The photothermal theory is used to study physical properties of a sample on the from intracavity spherical of semiconductor material [19]. The spectroscopy analyses are used during a photoacoustic processes with laser heat sources which it fall on a semiconductor medium [20]. In modern physics and electrical engineering, the photothermal phenomena are very important to study the semiconductors [21,22,23,24,25]. Many applications for photo-thermoelasticity theory are introduced with external many fields to study wave propagation during elastic semiconductors by Lotfy et al. [26,27,28,29,30]. The thermal conductivity parameter of elastic media may be constant and independents to temperature (when it is a constant). But in fact, the thermal conductivity in theoretical and experimental studies in modern physics changes with the gradient (change) in temperature. Many authors introduced a novel model when the thermal conductivity is changed (variable). For the elastic semiconductor material, the thermal conductivity may be depends on a liner presentation of temperature [31,32,33,34,35]. However, the thermal impact (temperature) of laser heat source on thermal conductivity parameter must be taken into consideration [36,37,38]. Ailawalia and Kumar [39] used the ramp-type heating with mechanical conditions to study a semiconductor medium during the photo-thermoelasticity theory. In all the above studies, the impact of gravity field is neglected and thermal laser as heat source is ignored in case of dependence of the thermal conductivity on temperature [26].

The main objective of this work is to investigate the interaction between the thermal-elastic-plasma waves during the photo-thermoelasticity theory. The photothermal excitation and transport processes are occurred when the thermal conductivity is changed in the context of the gradient temperature. The influence of gravitational field under the impact of thermal heat source of semiconductor medium is studied. The different thermal memories lead to various photo-thermoelasticity models (LS model and DPL model). The harmonic wave method in 2D deformation is applied of the governing equation to obtain the main expression of the dimensionless physical quantities. Various thermal and mechanical load conditions at the outer free surface of the medium are applied subjected to thermal shock. The effects of DPL models with thermal relaxation times are obtained graphically. The thermal conductivity parameters also are graphed and discussed theoretically in the context of the thermoelastic and thermoelectric coupling parameters.

2 Governing equations

Considering the elastic semiconductor medium has isotropic properties and it taken in a non-homogeneous case (the thermal conductivity is variable). The governing equations consider about the coupling between the carrier density (plasma distribution) C (\(r_{i}\), t), the thermal wave is the temperature distribution T (\(r_{i}\), t) and elastic mechanical wave is the displacement distribution u (\(r_{i}\), t) which (\(r_{i}\) is the space vector) in 2D deformation, the main quantities are taken in the space coordinates x and z (\(r_{i}\) (x, 0, z)) with independent to y-direction and the time coordinate t. The system of equations which describe the interaction between the plasma, thermal and elastic waves in gravitational field with laser heat source can be represented according to the following main equations [37, 38, 40, 41]:

$$ \frac{{\partial C(r_{i} ,t)}}{\partial t} = A_{E} N_{,ii} (r_{i} ,t) - \frac{{C(\mathop{r}\limits^{\rightharpoonup} ,t)}}{\tau } + \kappa \;T(r_{i} ,t), $$
(1)
$$ \begin{aligned} \rho \,C_{e} \left( {1 + \tau_{q} \frac{\partial }{\partial t}} \right)\frac{{\partial {\text{T}}(r_{i} ,t)}}{\partial t} & = \left( {1 + \tau_{\theta } \frac{\partial }{\partial t}} \right)(KT_{,i} (r_{i} ,t))_{,i} + \frac{{E_{g} }}{\tau }C(r_{i} ,t) \\ & \quad - \gamma T_{0} \left( {1 + \tau_{q} \frac{\partial }{\partial t}} \right)\frac{\partial }{\partial t}u_{,i} (r_{i} ,t) - \left( {1 + \tau_{q} \frac{\partial }{\partial t}} \right)\Theta . \\ \end{aligned} $$
(2)

The equation of motion when the gravitational field is ignored with strain–stress relation and carrier density without heat source can be represented in the following form [8, 42] (see schematic representation of the problem):

figure a
$$ \rho \,\frac{{\partial^{2} u_{i} }}{{\partial t^{2} }} = \sigma_{ij,j} . $$
(3)

The constitutive relations which describe strain–stress relation in 2D mechanical deformation can be expressed as [8, 42]:

$$ \sigma_{xx} = {(2}\mu + \lambda {)}\frac{\partial u}{{\partial x}} + \lambda \;\frac{\partial w}{{\partial z}} - (3\lambda + 2\mu )\left( {\alpha_{T} \left( {1 + \tau_{\theta } \frac{\partial }{\partial t}} \right)T\, + d_{n} C} \right), $$
(4)
$$ \sigma_{zz} = {(2}\mu + \lambda {)}\frac{\partial w}{{\partial z}}\, + \lambda \;\frac{\partial u}{{\partial x}} - (3\lambda + 2\mu )\left( {\alpha_{T} \left( {1 + \tau_{\theta } \frac{\partial }{\partial t}} \right)T + d_{n} C} \right), $$
(5)
$$ \sigma_{xz} = \mu \left( {\frac{\partial u}{{\partial z}} + \frac{\partial w}{{\partial x}}} \right). $$
(6)

The thermal activation coupling parameter \(\kappa = \frac{{\partial c_{0} }}{\partial T}\frac{T}{\tau }\) is taken in a nonzero form, where the carrier concentration at temperature \(T\) is \(c_{0}\) which is taken in equilibrium case [42]. The electrical physical constants are \(A_{E}\),\(E_{g}\), \(\delta_{n}\) and \(\tau\) which express the coefficient of carrier diffusion, energy of the gap, the deformation valence band and the carrier lifetime (which generated during photothermal transport), respectively. The elastic physical constants of the material sample are (\(\mu \;\), \(\lambda\)), \(\rho\), \(K\), \(T_{0}\), \(\gamma = (3\lambda + 2\mu )\alpha_{T}\) and \(C_{e}\) which they describe the elastic Lamé constant, the density, the thermal conductivity in steady case, the reference temperature, the volume thermal expansion and the specific heat respectively. On the other hand, the parameter \(\alpha_{T}\) is the linear thermal expansion coefficient. The DPL models with the thermal memories times \(\tau_{\theta } ,\;\tau_{q}\) must be satisfied the relation \(0 \)\(\le \tau_{\theta } < \tau_{q}\)\(\le \tau_{\theta } < \tau_{q}\)\(\le \tau_{\theta } < \tau_{q}\)\(\le \tau_{\theta } < \tau_{q}\le \tau_{\theta } < \tau_{q}\), \(\tau_{\theta } = 0\) reduced the model to LS case. The quantity term \(\Theta\) represents the effect of the volumetric absorption of uniform laser radiation heat source (input laser heat source). Our displacement analysis is taken in 2D plasma-elastic deformation as: \(u_{i} = (u_{1} ,\,0,\,u_{3} ) = (u,0,w),\quad u(x,z,t),\quad w(x,z,t)\).

Assume that the thermal conductivity \(K\) during the temperature gradient due to the laser thermal effect is taken as a linear function of temperature. In this case, thermal conductivity can be chosen variable, this case has many applications in devices industry which depends on thermal analysis of the thermal conductivity of elastic semiconductor medium. However, the thermal conductivity can be chosen under the impact of laser heat source as a temperature function [33, 36, 43]:

$$ K(T) = K_{0} (1 + K_{1} T). $$
(7)

In general case, a small non-positive parameter is \(K_{1}\) and \(K_{0}\) represents chosen constant which expresses the thermal conductivity when \(K_{1} = 0\) (independent of temperature). Using Kirchhoff transformation to describe the integral form of thermal conductivity [36, 38]:

$$ \hat{T} = \frac{1}{{K_{0} }}\int\limits_{0}^{T} {K(\Re ){\text{d}}\Re } . $$
(8)

The above transformation is used to exchange the nonlinear terms in the heat (energy) equation into linear terms.

3 Formulation of the problem

For more simplicity, the Helmholtzʼs theorem can be used to describe the displacement components in terms of the scalar function \(\Pi (x,\,z,\,t)\) (potential function) and the other in a vector function \(\psi (x,\,z,\,t)\), which can be expressed in vector form as:

$$ \vec{u} = {\text{grad}}\,\coprod + curl\vec{\psi },\quad \vec{\psi } = (0,\,\psi ,\,0). $$
(9)

In 2D elastic deformation, Eq. (9) takes the following form:

$$ u = \frac{\partial \coprod }{{\partial x}} + \frac{\partial \psi }{{\partial z}},\quad w = \frac{\partial \coprod }{{\partial z}} - \frac{\partial \psi }{{\partial x}}. $$
(10)

In 2D deformation, the general form of the equation of motion [Eq. (3)] under the effect of gravitational field \(g\) can be rewritten in two equations as [11]:

$$ \rho \left( {\frac{{\partial^{2} u}}{{\partial t^{2} }} - g\frac{\partial w}{{\partial x}}} \right) = \mu \nabla^{{2}} u + (\mu + \lambda )\frac{\partial e}{{\partial x}} - \gamma \left( {1 + \tau_{\theta } \frac{\partial }{\partial t}} \right)\frac{\partial T}{{\partial x}} + (3\lambda + 2\mu )d_{n} \frac{\partial C}{{\partial x}}, $$
(11)
$$ \rho \,\left( {\frac{{\partial^{2} w}}{{\partial t^{2} }} + g\frac{\partial u}{{\partial x}}} \right) = \mu \nabla^{{2}} w + (\mu + \lambda {)}\frac{\partial e}{{\partial z}} - \gamma \left( {1 + \tau_{\theta } \frac{\partial }{\partial t}} \right)\frac{\partial T}{{\partial z}} + (3\lambda + 2\mu )d_{n} \frac{\partial C}{{\partial z}}. $$
(12)

To insert the variable thermal conductivity in calculations, the transformation map Eq. (8) can be used with using the differentiation technique relative to the space coordinates \(x_{i}\) as:

$$ K_{0} \hat{T}_{,i} = K(T)T_{,i} . $$
(13)

Appling differentiation method again relative to the space coordinates \(x_{i}\) for Eq. (13), therefore:

$$ K_{0} \hat{T}_{,ii} = (K(T)T_{,i} )_{,i} . $$
(14)

The linear form of Eq. (14) (with neglected the nonlinear term) can be represented as:

$$ K_{0} \hat{T}_{,ii} = K_{,i} T_{,i} + KT_{,ii} = K_{0} (1 + K_{1} T)_{,i} T_{,i} + KT_{,ii} = K_{0} K_{1} (T_{,i} )^{2} + KT_{,ii} = KT_{,ii} . $$
(15)

Applying the time differentiation also, tend to:

$$ K_{0} \frac{{\partial \hat{T}}}{\partial t} = K(T)\frac{\partial T}{{\partial t}}. $$
(16)

Operating by \(\frac{\partial }{{\partial x_{i} }}\) on both sides of the coupling Eq. (1) and using Eq. (11), yields:

$$ \,\frac{\partial }{\partial t}C_{,i} = A_{E} (N_{,mm} )_{,i} - \,\frac{1}{\tau }C_{,i} + \frac{{\kappa K_{0} }}{K}\hat{T}_{,i} . $$
(17)

Using Taylor expand with linearity property for the last term in Eq. (17) (\(\frac{{\kappa K_{0} }}{K}\hat{T}_{,i}\)) with neglected the nonlinear terms, therefore

$$ \begin{aligned} \frac{{\kappa K_{0} }}{{K_{0} (1 + K_{1} T)}}\hat{T}_{,i} & = \kappa (1 + K_{1} T)^{ - 1} \hat{T}_{,i} = \kappa (1 - K_{1} T + (K_{1} T)^{2} - \cdots )\hat{T}_{,i} \\ & = \kappa \hat{T}_{,i} - \kappa K_{1} T\hat{T}_{,i} + (K_{1} T)^{2} \hat{T}_{,i} - \cdots = \kappa \hat{T}_{,i} . \\ \end{aligned} $$
(18)

In this case, Eq. (17) with a linearity form can be represented as:

$$ \,\frac{\partial }{\partial t}C_{,i} = A_{E} (N_{,mm} )_{,i} - \,\frac{1}{\tau }C_{,i} + \kappa \hat{T}_{,i} . $$
(19)

Using the integral property for Eq. (19) relative to the space coordinates \(x_{i}\), yields:

$$ \frac{\partial C}{{\partial t}} = A_{E} N_{,ii} - \frac{1}{\tau }C + \kappa \hat{T}. $$
(20)

The heat (energy) conduction Eq. (2) under the impact of map transform can be rewritten in the following form:

$$ \left( {1 + \tau_{\theta } \frac{\partial }{\partial t}} \right)\hat{T}_{,ii} = \left( {1 + \tau_{q} \frac{\partial }{\partial t}} \right)\left( {\frac{{\hat{T}}}{k} + \frac{{\gamma T_{0} }}{{K_{0} }}\frac{\partial }{\partial t}u_{,i} } \right) - \frac{{E_{g} }}{{\tau \,K_{0} }}C + \left( {1 + \tau_{q} \frac{\partial }{\partial t}} \right)\Theta . $$
(21)

The thermal diffusivity represents by \(\frac{{1}}{k} = \frac{{\rho C_{e} }}{{K_{0} }}\).

When a laser pulses fall on the outer surface of the elastic semiconductor, the volumetric absorption of uniform laser radiation is generated and consider it a heat source which can be expressed as:

$$ \Theta = \frac{{I_{0} \gamma^{\prime}t}}{{2\pi r^{2} t_{0}^{2} }}\exp \left( { - \frac{{z^{2} }}{{r^{2} }} - \frac{t}{{t_{0} }} - \gamma^{\prime}x} \right). $$

where \(I_{0}\) and \(t_{0}\) are the absorbed energy and the pulse rise time, respectively. The radius of the laser beam is \(r\) and \(\gamma^{\prime}\) is the heating energy which absorb at the depth (\(z\)).

For more simplicity, the dimensionless of the main quantities can be introduced as:

$$ \begin{aligned} & (x^{\prime},z^{\prime},\;u^{\prime},w^{\prime}) = \frac{(x,z,\;u,w)}{{C_{T} t^{*} }},\quad (t^{\prime},\tau^{\prime}_{q} ,\tau^{\prime}_{\theta } ) = \frac{{(t,\;\tau_{q} ,\tau_{\theta } )}}{{t^{*} }},\quad \hat{T^{\prime}} = \frac{{\gamma (\hat{T})}}{2\mu + \lambda } \\ & \sigma^{\prime}_{ij} = \frac{{\sigma_{ij} }}{\mu },\quad g^{\prime} = \frac{{t^{*} }}{{C_{T} }}g,\quad C^{\prime} = \frac{{\delta_{n} C}}{2\mu + \lambda },\quad (\coprod^{\prime},\psi^{\prime}) = \frac{(\coprod ,\psi )}{{(C_{T} t^{*} )^{2} }},\quad \Theta^{\prime} = \frac{{\gamma \,t^{*2} }}{{\rho K_{0} }}\Theta . \\ \end{aligned} $$
(23)

Substituting from Eq. (23) into the main equations after dropped the dashes, yields:

$$ \left( {\nabla^{2} - G_{1} - G_{2} \frac{\partial }{\partial t}} \right)C + q_{3} \,\hat{T} = 0, $$
(24)
$$ \left( {1 + \tau_{\theta } \frac{\partial }{\partial t}} \right)\nabla^{2} \hat{T} - \left( {1 + \tau_{q} \frac{\partial }{\partial t}} \right)q_{4} \frac{{\partial \hat{T}}}{\partial t} + q_{2} C + \left( {1 + \tau_{q} \frac{\partial }{\partial t}} \right)\left\{ {q_{1} \frac{\partial }{\partial t}\nabla^{2} \coprod } \right\} = - \Theta_{0} \Theta^{*} e^{{ - \gamma^{\prime}x}} , $$
(25)
$$ \left( {\nabla^{2} - \,\frac{{\partial^{2} }}{{\partial t^{2} }}} \right)\coprod + g\frac{\partial \psi }{{\partial x}} - \left( {1 + \tau_{\theta } \frac{\partial }{\partial t}} \right)\hat{T} - C = 0, $$
(26)
$$ \left( {\nabla^{2} - \,\beta^{2} \frac{{\partial^{2} }}{{\partial t^{2} }}} \right)\psi - g\frac{\partial \coprod }{{\partial x}} = 0. $$
(27)

where \(\,G_{1} = \frac{{K_{0} t^{*} }}{{A_{E} \rho \tau C_{e} }}\) , \(\,G_{2} = \frac{{K_{0} }}{{A_{E} \rho C_{e} }}\), \(\,q_{1} = \frac{{\gamma^{2} T_{0} t^{*2} }}{{K_{0} \rho }}\), \(\,q_{2} = - \frac{{\alpha_{T} E_{g} t^{*} }}{{d_{n} \rho \tau C_{e} }}\), \(q_{3} = \frac{{d_{n} K_{0} \kappa t^{*} }}{{\alpha_{T} \rho C_{e} A_{E} }}\), \(q_{4} = \frac{{K_{0} }}{{\rho C_{e} k}}\), \(C_{L}^{2} = \frac{\mu }{\rho }\), \(C_{T}^{2} = \frac{2\mu + \lambda }{\rho }\), \(\beta^{2} = \frac{{C_{T}^{2} }}{{C_{L}^{2} }}\), \(\delta_{n} = (2\mu + 3\lambda )d_{n}\), \(\,t^{*} = \frac{{K_{0} }}{{\rho C_{e} C_{T}^{2} }}\), \(\Theta_{0} = \frac{{I_{0} \gamma^{\prime}K_{0} }}{{2\pi a^{2} t_{0}^{2} }}\), \(\Theta^{*} = \left[ {1 + \tau_{q} (1 - \frac{t}{{t_{0} }})} \right]e^{{ - \left[ {\frac{{z^{2} }}{{r^{2} }} + \frac{t}{{t_{0} }}} \right]}}.\)

Where \(q_{1}\) and \(q_{2}\) are coupling parameters which reprsent the thermoelastic and thermo-energy (novel parameter) effects, respectively. On the other hand, the quantity \(\,q_{3}\) represents the effect of electricity conduction and named thermoelectric coupling parameter.

The stress–strain equation in non-dimension can be rewritten as follows:

$$ \sigma_{xx} = \frac{{{(2}\mu + \lambda {)}}}{\mu }\frac{{\partial^{2} \coprod }}{{\partial x^{2} }} + \frac{\lambda }{\mu }\;\frac{{\partial^{2} \coprod }}{{\partial z^{2} }} + 2\frac{{\partial^{2} \psi }}{\partial x\partial z} - \frac{{{(2}\mu + \lambda {)}}}{\mu }\left( {\left( {1 + \tau_{\theta } \frac{\partial }{\partial t}} \right)\hat{T} + C)} \right), $$
(28)
$$ \sigma_{zz} = \frac{{{(2}\mu + \lambda {)}}}{\mu }\frac{{\partial^{2} \coprod }}{{\partial z^{2} }} + \frac{\lambda }{\mu }\;\frac{{\partial^{2} \coprod }}{{\partial x^{2} }} - 2\frac{{\partial^{2} \psi }}{\partial x\partial z} - \frac{{{(2}\mu + \lambda {)}}}{\mu }\left( {\left( {1 + \tau_{\theta } \frac{\partial }{\partial t}} \right)\hat{T} + C} \right), $$
(29)
$$ \sigma_{xz} = \frac{{\partial^{2} \psi }}{{\partial z^{2} }} + 2\frac{{\partial^{2} \coprod }}{\partial x\partial z} - \frac{{\partial^{2} \psi }}{{\partial x^{2} }}. $$
(30)

4 Solution of the problem

In our analysis, the wave propagation is taken in 2D deformation, in this case all calculations must be obtained in the direction parallel to xz-plane. The harmonic wave plane propagation method can be used, the solutions of the physical quantities can be represented as [18]:

$$ \left[\coprod ,\psi ,\phi ,\hat{T},\sigma_{ij} ,C\right](x,z,t) = \left[\coprod^{*} (x),\psi^{*} (x),\phi^{*} (x),\,\hat{T}^{*} (x),\sigma_{ij}^{*} (x),C^{*} (x)\right]\,\exp (\omega t + ibz). $$
(31)

The parameter \(\omega\) is the complex circular time–frequency, \(i\) is the imaginary unit. The wave propagation is b which it taken in the direction of propagation (\(z\)-direction). The quantities \(\coprod^{*} (x),\psi^{*} (x)\),\(C^{*} (x),\phi^{*} (x),\hat{T}^{*} (x)\) and \(\sigma_{ij}^{*} (x)\) are the amplitude of the main physical quantities in this problem. Using the normal mode method which is defined in Eq. (31) of the main Eqs. (24)–(27) yields:

$$ \,(D^{2} - \alpha_{1} )C^{*} + \varepsilon_{3} \,\hat{T}^{*} = 0, $$
(32)
$$ (D^{2} - s_{2} )\hat{T}^{*} + s_{4} C^{*} + \alpha_{2} (D^{2} - b^{2} )\coprod^{*} = - \Theta_{0} \tilde{\Theta }e^{{ - \gamma^{\prime}x}} , $$
(33)
$$ (D^{2} - \,\alpha_{3} )\coprod^{*} + gD\psi^{*} - s_{5} \,\hat{T}^{*} - C{}^{*} = 0, $$
(34)
$$ (D^{2} - \,\alpha_{4} )\psi^{*} - gD\coprod^{*} = 0. $$
(35)

On the other hand, the harmonic wave method can be applied of stresses-strain relations (28)–(30), yield:

$$ \sigma_{xx}^{*} = \alpha_{5} D{}^{2}\coprod^{*} - \alpha_{6} \;b^{2} \coprod^{*} + 2ibD\psi^{*} - \alpha_{5} (\,\hat{T}^{*} + C^{*} ), $$
(36)
$$ \sigma_{zz}^{*} = - \alpha_{5} b^{2} \coprod^{*} + \alpha_{6} D{}^{2}\coprod^{*} - 2ibD\psi^{*} - \alpha_{5} (\hat{T}^{*} + C^{*} ), $$
(37)
$$ \sigma_{xz}^{*} = 2ibD\coprod^{*} - (D{}^{2} + b^{2} )\psi^{*} . $$
(38)

where \(D = \frac{d}{dx}\), \(\alpha_{1} = b^{2} + G_{1} + \omega \,G_{2}\),\(\alpha_{2} = q_{1} \omega (1 + \tau_{q} \omega )\),\(\alpha_{3} = b^{2} + \omega^{2}\), \(\alpha_{4} = b^{2} + \omega^{2} \beta^{2}\),\(s_{4} = \frac{{q_{2} }}{{s_{5} }}\),\(\alpha_{6} = \frac{\lambda }{\mu }\), \(s_{2} = b^{2} + s_{3}\), \(s_{3} = \frac{{\omega (1 + \tau_{q} \omega )}}{{s_{5} }}\), \(s_{5} = (1 + \tau_{\theta } \omega )\), \(\alpha_{5} = \frac{{{(2}\mu + \lambda {)}s_{5} }}{\mu }\), \(\tilde{\Theta } = \Theta^{*} \exp ( - \omega t - ibz)\).

Using the eliminate technique in terms of the amplitudes \(\hat{T}^{*} (x),\quad \coprod^{*} (x)\), \(C^{*} (x)\) and \(\psi^{*} (x)\) which are represented into the four Eqs. (32)–(35), therefore, the non-homogenous ordinary differential equation from eighth order in terms of \(\Pi^{*} (x)\) can be get as:

$$ [D^{8} - ED^{6} + FD^{4} - GD^{2} + H]\coprod^{*} (x) = - \Omega \exp ( - \gamma^{\prime}x). $$
(39)

where the coefficients of the above equation take the form:

$$ \begin{aligned} & \xi_{1} = s_{5} \alpha_{4} + q_{3} ,\quad \xi_{2} = \alpha_{4} + \alpha_{3} g^{2} ,\quad \xi_{3} = \alpha_{3} \alpha_{4} ,\quad E = \xi_{2} + \alpha_{1} + s_{2} - s_{5} \alpha_{2} , \\ & F = \xi_{3} + \alpha_{1} s_{2} + \xi_{2} (\alpha_{1} + s_{2} ) - s_{4} q_{3} - \alpha_{2} (\xi_{1} + s_{5} (b^{2} + \alpha_{1} )),\\ & \quad H = \xi_{3} (\alpha_{1} s_{2} - s_{4} q_{3} ) - \alpha_{2} \alpha_{1} b^{2} \xi_{1} , \\ & G = \xi_{3} (\alpha_{1} + s_{2} ) + \xi_{2} (\alpha_{1} s_{2} - s_{4} q_{3} ) - \alpha_{2} (\xi_{1} \alpha_{1} + b^{2} (\xi_{1} + s_{5} \alpha_{1} )),\\ &\quad \Omega = (\gamma^{{\prime}{2}} - \alpha_{1} )\left[ {(\gamma^{{\prime}{2}} - \alpha_{3} ) + g^{2} \gamma^{{\prime}{2}} } \right]\Theta_{0} \tilde{\Theta }. \\ \end{aligned} $$

The factorization form of the differential Eq. (39) can be rewritten as:

$$ \left( {D^{2} - \Im_{1}^{2} } \right)\left( {D^{2} - \Im_{2}^{2} } \right)\,\left( {D^{2} - \Im_{3}^{2} } \right)\,\left( {D^{2} - \Im_{4}^{2} } \right)\coprod^{*} (x) = - \Omega \exp ( - \gamma^{\prime}x). $$
(40)

The parameters \(\Im_{n}^{2} \,(n = 1\,,2,3,4)\) are the roots of the homogenous solution of Eq. (39). On the other hand, the homogenous characteristic equation of Eq. (40) can be represented as:

$$ k^{8} - Ek^{6} + Fk^{4} - Gk^{2} + H = 0. $$
(41)

However, the general solution form of Eq. (40) with the non-homogeneity property and bounded at \(x \to \infty\) which takes the following form:

$$ \coprod^{*} (x) = \sum\limits_{n = 1}^{4} {{\rm N}_{n} } (b,\omega )\,\exp ( - \Im_{n} x) + L_{1} \Omega \exp ( - \gamma^{\prime}x). $$
(42)

The value of the parameter \(L_{1}\) can obtained as: \(L_{1} = - \frac{1}{{\gamma^{{\prime}{8}} - E\gamma^{{\prime}{6}} + F\gamma^{{\prime}{4}} - G\gamma^{{\prime}{2}} + H}}\). By the same method, the other quantities can be represented as:

$$ \,\hat{T}^{*} (x) = \sum\limits_{n = 1}^{4} {N^{\prime}_{n} } (b,\omega )\,\exp ( - \Im_{n} x) + L_{2} \Omega \exp ( - \gamma^{\prime}x), $$
(43)
$$ C^{*} (x) = \sum\limits_{n = 1}^{4} {N^{\prime\prime}_{n} } (b,\omega )\,\exp ( - \Im_{n} x) + L_{3} \Omega \exp ( - \gamma^{\prime}x), $$
(44)
$$ \psi^{*} (x) = \sum\limits_{n = 1}^{4} {N_{n}^{m} (b,\omega )\exp ( - \Im_{n} x) + L_{4} \Omega \exp ( - \gamma^{\prime}x).} $$
(45)

where \(L_{2} = - \frac{{\xi_{3} }}{{\xi_{1} (\gamma^{{\prime}{8}} - E\gamma^{{\prime}{6}} + F\gamma^{{\prime}{4}} - G\gamma^{{\prime}{2}} + H)}}\), \(L_{3} = - \frac{{\varepsilon_{3} \xi_{3} }}{{\alpha_{1} \xi_{1} (\gamma^{{\prime}{8}} - E\gamma^{{\prime}{6}} + F\gamma^{{\prime}{4}} - G\gamma^{{\prime}{2}} + H)}}\), \(L_{4} = - \frac{g}{{\alpha_{4} H(\gamma^{{\prime}{8}} - E\gamma^{{\prime}{6}} + F\gamma^{{\prime}{4}} - G\gamma^{{\prime}{2}} + H)}}\).

The displacement components can be obtained from the amplitude of the two the potential functions \(\Pi^{*} (x)\) and \(\psi^{*} (x)\) as:

$$ \left. \begin{gathered} u^{*} (x) = D\coprod^{*} + i\,b{\kern 1pt} \psi^{*} \hfill \\ u^{*} (x) = - \sum\limits_{n = 1}^{4} {N_{n} } (b,\omega )\,\Im_{n} e^{{ - \Im_{n} x}} + ib\left(\sum\limits_{n = 1}^{4} {N^{\prime\prime\prime}_{n} } (b,\omega )\,e^{{ - \Im_{n} x}} + (L_{4} - \gamma^{\prime}L_{1} \right)\Omega \exp ( - \gamma^{\prime}x) \hfill \\ \end{gathered} \right\}, $$
(46)
$$ \left. \begin{gathered} w^{*} (x) = i\,b{\kern 1pt} {\kern 1pt} \coprod^{*} - D\,\psi^{*} \hfill \\ w^{*} (x) = ib(\sum\limits_{n = 1}^{4} {N_{n} } (b,\omega )\,e^{{ - \Im_{n} x}} + (L_{1} - L_{4} \gamma^{\prime})\Omega \exp ( - \gamma^{\prime}x) + \sum\limits_{n = 1}^{4} {k_{n} N^{\prime\prime\prime}_{n} } (b,\omega )\,e^{{ - \Im_{n} x}} \hfill \\ \end{gathered} \right\}. $$
(47)

The parameters \(N_{n} ,\,\,N^{\prime}_{n}\),\(N^{\prime\prime}_{n}\) and \(N^{\prime\prime\prime}_{n}\) are unknown on the other hand they depend on the values of the wave number \(b\) and \(\omega .\)

The relations between \(N_{n} ,\,\,N^{\prime}_{n}\),\(N^{\prime\prime}_{n}\) and \(N^{\prime\prime\prime}_{n}\) can be detriment from the Eqs. (32)–(35), which yield:

$$ N^{\prime}_{n} (b,\omega ) = H_{1n} N_{n} (b,\omega ),\quad n = 1,\,2,3,4, $$
(48)
$$ N^{\prime\prime}_{n} (b,\omega ) = H_{2n} N_{n} (b,\omega ),\quad n = 1,\,2,3,4, $$
(49)
$$ N^{\prime\prime\prime}_{n} \;(b,\omega ) = H_{3n} N_{n} (b,\omega ),\quad n = 1,\,2,3,4. $$
(50)

where \(H_{1n} = \frac{{(\Im_{n}^{4} - \xi_{2} \Im_{n}^{2} + \xi_{3} )}}{{(s_{5} \Im_{n}^{2} - \xi_{1} )}}\), \(H_{2n} = - \frac{{q_{3} (\Im_{n}^{4} - \xi_{2} \Im_{n}^{2} + \xi_{3} )}}{{(\Im_{n}^{2} - \alpha_{1} )(s_{5} \Im_{n}^{2} - \xi_{1} )}}\,\,\), \(H_{3n} = \frac{{g\Im_{n} }}{{\Im_{n}^{2} - \alpha_{4} }}\).

In this case, the complete solutions by the unknown parameters \(N_{n}\) for the amplitudes quantities of the main quantities can be represented as:

$$ \hat{T}^{*} (x) = \sum\limits_{n = 1}^{4} {H_{1n} \,N_{n} } (b,\omega )\,\exp ( - \Im_{n} x) + L_{2} \Omega \exp ( - \gamma^{\prime}x), $$
(51)
$$ C^{*} (x) = \sum\limits_{n = 1}^{4} {H_{2n} N_{n} } (b,\omega )\,\exp ( - \Im_{n} x) + L_{3} \Omega \exp ( - \gamma^{\prime}x), $$
(52)
$$ \psi^{*} (x) = \sum\limits_{n = 1}^{4} {H_{3n} N_{n} } (b,\omega )\,\exp ( - \Im_{n} x) + L_{4} \Omega \exp ( - \gamma^{\prime}x). $$
(53)
$$ \sigma_{xx}^{*} = \sum\limits_{n = 1}^{4} {h_{n} \,N_{n} } (b,\omega )\,\exp ( - \Im_{n} x) - \varsigma_{1} \Omega \exp ( - \gamma^{\prime}x), $$
(54)
$$ \sigma_{zz}^{*} = \sum\limits_{n = 1}^{4} {h^{\prime}_{n} \,N_{n} } (b,\omega )\,\exp ( - \Im_{n} x) - \varsigma_{2} , $$
(55)
$$ \sigma_{xz}^{*} = \sum\limits_{n = 1}^{4} {h^{\prime\prime}_{n} \,N_{n} } (b,\omega )\,\exp ( - \Im_{n} x) - \varsigma_{3} \Omega \exp ( - \gamma^{\prime}x), $$
(56)
$$ u^{*} (x) = - \sum\limits_{n = 1}^{4} {(\Im_{n} + ibH_{3n} )N_{n} } (b,\omega )\,e^{{ - \Im_{n} x}} + (L_{4} - \gamma^{\prime}L_{1} )\Omega \exp ( - \gamma^{\prime}x), $$
(57)
$$ w^{*} (x) = \sum\limits_{n = 1}^{4} {(ib + \Im_{n} H_{3n} )N_{n} } (b,\omega )\,e^{{ - \Im_{n} x}} + (L_{1} - L_{4} \gamma^{\prime})\Omega \exp ( - \gamma^{\prime}x). $$
(58)

where \(h_{n} = \alpha_{5} \Im_{n}^{2} - \alpha_{6} b^{2} - 2ib\Im_{n} H_{3n} - \alpha_{5} (H_{1n} + H_{2n} )\),\(\varsigma_{1} = - \alpha_{6} b^{2} + \alpha_{5} (\gamma^{{\prime}{2}} - 1) - 2ib - \gamma^{\prime}L_{4} + L_{2} + L_{3} )\), \(\varsigma_{2} = - \alpha_{6} b^{2} + \alpha_{5} (\gamma^{{\prime}{2}} - 1) - 2ib - \gamma^{\prime}L_{4} + L_{2} + L_{3} )\), \(\varsigma_{3} = \gamma^{{\prime}{2}} L_{4} - \gamma^{\prime}L_{1}\), \(h^{\prime\prime}_{n} = 2ib\Im_{n} - (b^{2} + \Im_{n}^{2} )H_{3n}\), \(h^{\prime}_{n} = - \alpha_{5} b^{2} + \alpha_{6} \Im_{n}^{2} - 2ib\Im_{n} H_{3n} - \alpha_{5} (H_{1n} + H_{2n} )\).

5 Boundary conditions

Using some mechanical and thermal loads at the boundary (\(\,x = 0\)) of the medium under investigation to determine the unknown parameters \(N_{n} (n = 1,2,3,4)\).

  1. 1.

    The thermal shock condition is taken at boundary surface (\(\,x = 0\)), which it can be represented as:

    $$ T(x,\,z,\,t) = f(z,t),\quad \frac{\partial T(0,\,z,\,t)}{{\partial x}} = 0. $$
    (59)
  2. 2.

    The mechanical force condition which can be expressed by the normal stress component is taken at the surface (\(\,x = 0\)) as a fallen load \(p_{1}^{*}\) on the semiconductor medium, which it can be expressed as:

    $$ \,\sigma_{xx} (0,\,z,\,t) = - p_{1}^{*} = p_{1} \exp (\omega t + ibz). $$
    (60)

    The parameter \(p_{1}\) is the mechanical force magnitude.

  3. 3.

    The tangential mechanical stress can be chosen as a second mechanical condition which can be expressed as a free traction at boundary of the semiconductor as:

    $$ \sigma_{xz} (0,\,z,\,t) = 0. $$
    (61)
  4. 4.

    The plasma condition can be expressed when a photothermal transport processes occur, in this case the mass diffusion process with carriers density can be obtained. This condition can be expressed by a finite probability of recombination process at the boundary which can be presented as:

    $$ \frac{\partial C(0,z,t)}{{\partial x}} = \frac{s}{{A_{E} }}. $$
    (62)

Using these conditions when the harmonic wave technique is applied of the considered quantities, yield:

$$ \sum\limits_{n = 1}^{4} {H_{1n} \,\Im_{n} N_{n} } \, + L_{2} \gamma^{\prime}\Omega = 0, $$
(63)
$$ \sum\limits_{n = 1}^{4} {h_{n} \,N_{n} } \, - \varsigma_{1} \Omega = - p_{1} , $$
(64)
$$ \sum\limits_{n = 1}^{4} {h^{\prime\prime}_{n} \,N_{n} } - \varsigma_{3} \Omega = 0, $$
(65)
$$ \sum\limits_{n = 1}^{4} {H_{2n} \Im_{n} N_{n} } + L_{3} \Omega \gamma^{\prime} = - \frac{s}{{A_{E} }}. $$
(66)

Expanding the summation notation of the system of Eqs. (63)–(66), in this case a four equation in terms of the unknown parameters \(N_{n}\). After that, the algebraic Cramer’s rule or the inverse of matrix method can be used to get the values of the parameters \(N_{n}\). In this case, the full solutions of the main quantities fields can be obtained.

Using the map transform to obtain the relation between \(T\) and \(\hat{T}\), in this case the following relation can be represented as:

$$ \hat{T} = \frac{1}{{K_{0} }}\int\limits_{0}^{T} {K_{0} (1 + K_{1} T){\text{d}}T = T + } \frac{{K_{1} }}{2}T^{2} = \frac{{K_{1} }}{2}\left( {T + \frac{1}{{K_{1} }}} \right)^{2} - \frac{1}{{2K_{1} }},\quad {\text{or}} $$
(67)
$$ T = \frac{1}{{K_{1} }}\left[ {\sqrt {1 + 2K_{1} \hat{T}} - 1} \right] = \frac{1}{{K_{1} }}\left[ {\sqrt {1 + 2K_{1} \hat{T}^{*} \exp (\omega t + ibz)} - 1} \right]. $$
(68)

6 Validation

6.1 The theory of thermoelasticity

The generalized thermoelasticity theory is obtained when the carrier density \(C{(}\mathop{r}\limits^{\rightharpoonup} { ,} t)\) effect is vanished. In this case, the photothermal transport with diffusion processes is neglected and the free electrons on the surface are not appear. On the other hand, the physical quantities are evaluated in the theory of thermoelasticity only [9].

6.2 Different theories of the photo-thermoelasticity

The photo-thermoelasticity theory with different models according to the thermal relaxation times can be obtained. The governing equation in a gravitational field with the effect of laser thermal source in equation of motion and heat conduction equation based on the thermal memories. The photo-thermoelasticity theory can be observed as follows:

  • When \(\tau_{\theta } = 0\), in this case the LS model is obtained and the heat conduction equation can be expressed in the following form [44]:

    $$ \rho \,C_{e} \left( {1 + \tau_{q} \frac{\partial }{\partial t}} \right)\frac{{\partial {\text{T}}}}{\partial t} = (KT_{,i} )_{,i} - \frac{{E_{g} }}{\tau }C + \gamma T_{0} \left( {1 + \tau_{q} \frac{\partial }{\partial t}} \right)\frac{{\partial u_{,i} }}{\partial t} + \left( {1 + \tau_{q} \frac{\partial }{\partial t}} \right)\Theta . $$
    (69)

  • The classical coupled photo-thermoelasticity theory (CT) can be obtained when neglected the thermal memories (\(\tau_{\theta } = \tau_{q} = 0\)). In this case, the heat equation under the effect of carrier density with laser heat source can be rewritten in the form [45]:

    $$ \rho \,C_{e} \frac{{\partial {\text{T}}}}{\partial t} = (KT_{,i} )_{,i} + \frac{{E_{g} }}{\tau }C - \gamma T_{0} \frac{{\partial u_{,i} }}{\partial t} + \Theta . $$
    (70)

  • The DPL model can be appeared when \(\tau_{q} = 1.85 \times 10^{ - 12} s > \tau_{\theta } = 1.5 \times 10^{ - 12} s \ge 0\).

6.3 Laser heat source effect

When the laser heat source is ignored (i.e.,\(\Theta = 0\)), the governing equations describe the photo-thermoelasticity theory in a gravitational field only. However, the heat conduction equation in DPL models can be expressed as [46]:

$$ \rho \,C_{e} \left( {1 + \tau_{q} \frac{\partial }{\partial t}} \right)\frac{{\partial {\text{T}}}}{\partial t} = \left( {1 + \tau_{\theta } \frac{\partial }{\partial t}} \right)(KT_{,i} )_{,i} + \frac{{E_{g} }}{\tau }C + \gamma T_{0} \left( {1 + \tau_{q} \frac{\partial }{\partial t}} \right)\frac{{\partial u_{,i} }}{\partial t}. $$
(71)

6.4 Gravity field impact

The photo-thermoelasticity theory with laser heat source can be obtained only when the gravitational field is neglected (i.e.,\(g = 0\)) [29].

6.5 The variable thermal conductivity

When the thermal conductivity parameter independent to temperature (i.e.,\(K_{1} = 0\), \(K = K_{0}\)), the elastic semiconductor problem with relaxation times is investigated with a constant thermal conductivity in the photo-thermoelasticity theory with laser heat source [26].

7 Numerical results and discussions

The semiconductor material in this investigation can be a chosen as silicon (Si) material to make the numerical simulation to understand the wave propagation in the medium. The following physical constants of Si material in SI unit can be introduced in Table 1 [45, 46]. The MATLAB 2018 program is used on the personal computer with accuracy 7 digits to make the numerical simulation. Graphically the real part of the main distributions of the physical quantities is used. For small value of the time, the complex circular frequency of the time can be given as \(\omega = \omega_{0} + i\xi\) where \(\omega = \omega_{0}\)(real) which can be expanded as \(e^{\omega t} = e^{{\omega_{0} t}} (\cos \xi t + i\sin \xi t)\).

Table 1 The physical constants of Si material
Full size table

7.1 Comparison between relaxation times

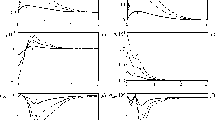
Figure 1 represents the first category which contain six subfigures express the variation of the main physical quantity distributions (temperature (\(T\)) (thermal distribution), two components of displacement (\(u\) and \(w\)) (elastic distributions), carrier density (\(N\)) (plasma wave distribution), normal stress force and tangent stress force (\(\sigma_{xx}\),\(\sigma_{xz}\)) (mechanical distributions) in the direction of the horizontal axis \(x\) (in the dimensionless form). The category displays the impact of different three values of thermal memories (presenting various choices of delay parameters) according to the thermal relaxation times, namely solid lines represent the CT theory at \(\tau_{\theta } = \tau_{q} = 0\), the dotted lines express the LS model when \(\tau_{\theta } = 0\) and third case which represented by the dash lines according to DPL model at \(\tau_{q} > \tau_{\theta } \ge 0\). This category is carried out numerically under the thermal impact of laser heat source in the gravitational field. On the other hand, all calculations are made under the effect of the variable thermal conductivity at \(K_{1} = - 0.04\) in weak electricity (the thermoelectric coupling parameter) at \(q_{3} = - 3 \times 10^{ - 12}\). From this six subfigures, all physical fields depend on the variations in the thermal memories which included in the general form of the heat (energy) equation. It is clear that the variation of the relaxation times have a very great effect on the all physical distribution. The main reason is due to the thermal effects (due to the impact of thermal memories) in the Fourier’s heat conduction equation, the thermal, plasma and stress-elastic waves propagate in infinite speed as opposed behavior to finite speed in the non-Fourier case.

Fig. 1
figure 1

The variations of the main physical fields in the direction of x-axis with different three theories under the effect of gravitational field and laser heat source when \(K_{1} = - 0.04\) and \(q_{3} = - 3 \times 10^{ - 12}\)

Full size image

7.2 The influence of the variable thermal conductivity

The second figure (Fig. 2) represents six subfigures which exhibit that the variations of the obtained physical fields in this phenomenon in the direction of the x-axis in different cases of the thermal conductivity parameters. All numerical results are carried out for DPL model (when delay parameters are \(\tau_{q} > \tau_{\theta } \ge 0\)) under the impact the thermal effect of laser heat source and gravity field \(g = 9.8\) in a weal electricity at the thermoelectric coupling parameter is \(q_{3} = - 6 \times 10^{ - 12}\). The three cases represented at \(K_{1} = 0.0\) which shows the non-dependence on temperature, classical case of thermal conductivity. On the other hand, the other two cases at negative parameters are \(K_{1} = - 0.02\) and \(K_{1} = - 0.04\). However, in these cases the thermal conductivity depends on the temperature effect. From this category, the conditions at the boundary are satisfied of all physical quantities. The behavior of physical field wave distribution has the different behaviors with respect to the various values of the thermal conductivity magnitude. The physical field distributions are very sensitive to the change of the thermal conductivity parameter. However, any little changes occur in the parameters of thermal conductivity lead to a great impact in the thermal, elastic, plasma and mechanical waves propagation.

Fig. 2
figure 2

The variations of the main physical fields in the direction of x-axis for DPL theory with different values of thermal conductivity parameters in a gravitational field with laser heat source when \(q_{3} = - 3 \times 10^{ - 12}\)

Full size image

7.3 The electrical conduction influence

Figure 3 which represents six subfigures shows the influence of the different values of the thermoelectric coupling parameter \(q_{3}\) on the physical quantity distributions when they studied in the direction of the \(x\)-axis. The obtained results are made numerically when delay parameters are \(\tau_{q} > \tau_{\theta } \ge 0\) (DPL theory) under the effect of input laser heat source with gravity field impact \(g = 9.8\) when the thermal conductivity depends on temperature at \(K_{1} = - 0.08\). From this category, the values of all physical field distributions investigated increase with an increase in the thermoelectric coupling parameter. However, the thermoelectric coupling parameter has a significant impact on the physical field distributions. All the amplitude of physical field distributions (\(T\), \(u\), \(w\), \(N\), \(\sigma_{xx}\) and \(\sigma_{xz}\)) match to the zero line with an increase in the distance \(x\).

Fig. 3
figure 3

The variations of the main physical fields in the direction of x-axis for DPL theory with various values of \(q_{3}\) in the gravitational field and laser heat source when \(K_{1} = - 0.04\)

Full size image

7.4 The impact of gravity field

Figure 4 which represents six subfigures exhibits the influence of the gravitational field on the wave distributions of thermal \(T\), elastic (\(u\) and \({\text{w}}\)), plasma \(N\) and mechanical (\(\sigma_{xx}\), \(\sigma_{xz}\)) in the direction of the \(x\)-axis. In this case, a two cases of gravity (\(g = 0.0\) and \(g = 9.8\)) are studied. All numerical calculations are made when delay parameters are \(\tau_{q} > \tau_{\theta } \ge 0\) (DPL theory) with input laser heat source when \(q_{3} = - 3 \times 10^{ - 12}\), when the thermal conductivity (\(K_{1} = - 0.04\)) depends on the temperature. From this category, the gravitational field has a great impact on all physical distributions and causes vary in movement of the waves. All physical field distributions have a great change in case of the presence of the gravity field.

Fig. 4
figure 4

The variations of the main physical fields in the direction of x-axis for DPL theory in two cases with gravity field and without it under the effect laser heat source when \(q_{3} = - 3 \times 10^{ - 12}\) and \(K_{1} = - 0.04\)

Full size image

7.5 Effect of internal steady heat source

Figure 5 which represents six subfigures shows the changes of the physical quantity distributions in the direction of the \(x\)-axis at two different cases of input laser heat source. The first case in the presence of input laser heat source (WLHS) and the other case in the absent of the input laser heat source (WOLHS). All obtained results are made numerically under the impact gravity field when the delay parameters are \(\tau_{q} > \tau_{\theta } \ge 0\) (DPL theory) at \(q_{3} = - 3 \times 10^{ - 12}\) when the thermal conductivity depends on temperature at \(K_{1} = - 0.04\). The presence of input laser heat source WLHS affects on all physical fields investigated and increase the wave propagation. However, the presence of input laser heat source (pulses) causes an increase in the inside particles movement and the internal collisions of the particles.

Fig. 5
figure 5

The variations of the main physical fields in the direction of x-axis for DPL theory in two cases, WOLHP and WLHP in gravitational field when \(q_{3} = - 3 \times 10^{ - 12}\) and \(K_{1} = - 0.04\)

Full size image

7.6 Three-dimensional representation

Figure 6 which represents a six subfigures shows the variation of the physical wave distributions with the \(x\)-axis and the vertical axis \(z\) (three-dimensional (3D) representation). All numerical results in this category are carried out when a delay parameters are \(\tau_{q} > \tau_{\theta } \ge 0\) (DPL theory) under the effect of gravity field in weak electricity conduction \(q_{3} = - 3 \times 10^{ - 12}\) in the context of the effect of the variable thermal conductivity \(K_{1} = - 0.04\) with input laser heat source. The magnitude values of the physical field distributions change with the change of the horizontal distance \(x\) and the vertical distance \(z\) axis and vanished with the increasing of the axial \(x\) and \(z\).

Fig. 6
figure 6

The variations of the main physical fields in 3D (x and z) for DPL theory with laser heat source under the effect of the gravitational field when \(q_{3} = - 3 \times 10^{ - 12}\) and \(K_{1} = - 0.04\)

Full size image

8 Conclusion

The main objective of this work is to focus on studying many parameters on the physical field distributions in the context of the photo-thermoelasticity theory of semiconducting medium. The problem is studied under the effect the various delay parameters with the CT, LS, and DPL models (different thermal relaxation times), various thermal conductivity parameters, gravity field and input laser heat source during electrical conduction. The harmonic wave technique is used to get the main physical distributions. Through the discussion, the delay parameters with DPL model (memories theory) have a significant effect and play an important role to understand the wave propagation of the main fields. The thermal conductivity when it changes (depends on the linear form of temperature) is clear to modify the wave propagations. On the other hand, the thermoelectric coupling parameters have an impact role on the wave propagations and used to improve of the physical field distributions. In the presence of gravitational field, input laser heat source is very sensible form in the physical quantities under investigation. The investigated results give the researches and engineers which they work in the geology, mechanical engineering and petroleum extracting ability to design and manufacture different semiconductor devices and reduce the cost of industries.