Analysis of Photo-Thermo-Elastic Response in a Semiconductor Media due to Moving Heat Source

Abstract

A mathematical model of Green–Naghdi photothermal theory is given to study the wave propagation in a two-dimensional semiconducting material due to moving heat source. By using the Fourier and Laplace transformations with the eigenvalues method, the physical quantities are obtained analytically. Initially, it is assumed that the medium is at rest and it is subject to a heat source in motion with a constant velocity, which is free of traction. A semiconductor media such as silicon has been studied. The derived method is evaluated with numerical results which are applied to the semiconductor medium in simplified geometry. The influences of the different values of moving heat source speed are discussed for all physical quantities.

1. Introduction

The most previous studies considering the thermal and elastic properties of the semiconducting elastic medium are isotropic and homogeneous. Whereas the equations of plasma, thermal and elastic waves are partially coupled and also the coupling between them was neglected. Solving the system with coupling the plasma, the thermal and elastic equation is very complex. But, the analysis with partially coupled is enough in most experimental studies. In those work, the coupling between the plasma, thermal, and elastic waves was neglected. As an especially cases the problem of thermoelastic and electronic distortion were taken into account. The effect of coupling was studied in terms of approximately quantitative analysis. Studying the excitation of short elastic pulses by photothermal means is important for engineers and physicists because it is applied in several areas, such as the monitoring of laser drilling, the determination of the parameters of the thermoelastic material, the photoacoustic microscope, the formation of images by thermal wave, laser annealing and fusion phenomena. The difference influences of thermoelastic and electronic deformations in semiconductor media with disregard the coupling between the plasma and thermoelastic equations have been analyzed. Todorovic et al. [1–3] performed the theoretical analysis to describe two phenomena that provide information about the transport properties and carrier recombination in the semiconductor material. The changes in the propagations of photothermal waves go back to the linear coupling between the heating and mass transports (i.e., thermodiffusions) has inclusive. In the materials science, the variable thermal conductivity that depends on temperature is very important and has many applications in nature. Recent studies of the thermal conductivity dependence of semiconductors on temperature showed that physical properties, especially deformation and thermomechanical behavior, are strongly affected by any change in material temperature. Rosencwaig et al. [4] studied the local thermoelastic deformations at the model flat cause to the excitation. Green and Naghdi [5, 6] proposed a new generalized thermoelasticity theorem by consists of the thermal-displacement gradient among the independent constitutive variables. Othman and Marin [7] studied the thermoelastic interactions on porous material under Green and Naghdi theory due to laser pulse. Abbas and Abbas et al. [8–17] applied the generalized thermoelastic theories to get the numerical and analytical solutions of physical quantities. Marin and Öchsner [18] have presented the effects of a dipolar structure under Green–Naghdi thermoelasticity. Moreover, Song et al. [19] presented the vibration by the generalized theory of thermoelasticity subject to optically excited semiconducting microconductors. Lotfy and Lotfy et al. [20–23] have solved some problems by applied various fields in semiconductors materials. The eigenvalue method gave an analytical solution without any supposed restrictions on the factual physical variables in the Laplace domain.

The aim of the present article is to introduce a unified mathematical Green–Naghdi model for photothermoelastic case. By using the eigenvalue approach and Fourier–Laplace transformations based on an analytical-numerical method, the governing equations are processed. For the considered variables, the numerical results are obtained and presented graphically.

2. Mathematical model

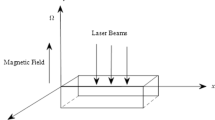
Consider an isotropic, homogeneous and elastic semiconducting media, the basic equation of plasma, thermal conduction and motion based on Green and Naghdi model can be expressed by [2, 24]

$$(\lambda + \mu)u_{j,ij} + \mu u_{i,jj} - \gamma_{n}N_{,i} - \gamma_{t}\Theta_{,i} - \rho\frac{\partial^{2}u_{i}}{\partial t^{2}} = 0,\ \ (1)$$

$$D_{e}N_{,jj} - \frac{N}{\tau} + \delta\frac{\Theta}{\tau} - \frac{\partial N}{\partial t} = 0,\ \ (2)$$

$$\left( K^{*} + K\frac{\partial}{\partial t} \right)\Theta_{,jj} + \frac{E_\mathrm{g}}{\tau}N - \frac{\partial}{\partial t}\left( \rho c_{e}\frac{\partial\Theta}{\partial t} + \gamma_{t}T_{0}\frac{\partial u_{j,j}}{\partial t} - Q \right) = 0.\ \ (3)$$

The stress-displacement relations can be expressed as

$$\sigma_{{ij}} = \mu(u_{i,j} + u_{j,i}) + (\lambda u_{k,k} - \gamma_{n}N - \gamma_{t}\Theta)\delta_{{ij}},\ \ (4)$$

where Q is the moving heat source, ρ is the material density, σ_ij are the components of stress,N = n – n₀,n₀ is the equilibrium carrier concentration, Θ = T – T₀,T₀ is the reference temperature, λ, μ are the Lame’s constants, u_i are the components of displacement, D_e is the coefficient of carrier diffusion, γ_t = (3λ + 2μ)α_t, α_t is the linear thermal expansion coefficient, γ_n = (3λ + 2μ)d_n,d_n is the electronic deformation coefficient, δ_E = E – E_g,E is the excitation energy,E_g is the semiconducting energy gap,K is the thermal conductivity,K^* is the material constant characteristic of the theory, c_e is the specific heat at constant strain, r is the position vector,t is the time, δ = ∂n₀/∂Θ is the thermal activation coupling parameter [25], τ is the photogenerated carrier lifetime, i,j, k = 1, 2, 3. Taking into account the stress state of the plane in a two-dimensional semiconducting problem, the components of the variables are defined by

$$\Theta = \Theta(x,\mspace{6mu} y,\mspace{6mu} t),\mspace{6mu} N = N(x,\mspace{6mu} y,\mspace{6mu} t),\mspace{6mu}\mathbf{u} = (u,\mspace{6mu} v,\mspace{6mu} 0),\mspace{6mu} u = u(x,\mspace{6mu} y,\mspace{6mu} t),\mspace{6mu} v = v(x,\mspace{6mu} y,\mspace{6mu} t).\ \ (5)$$

Subsequently, the Eqs. (1)–(4) can be given by

$$(\lambda + 2\mu)\frac{\partial^{2}u}{\partial x^{2}} + (\lambda + \mu)\frac{\partial^{2}v}{\partial x\partial y} + \mu\frac{\partial^{2}u}{\partial y^{2}} - \gamma_{n}\frac{\partial N}{\partial x} - \gamma_{t}\frac{\partial\Theta}{\partial x} - \rho\frac{\partial^{2}u}{\partial t^{2}} = 0,\ \ (6)$$

$$(\lambda + 2\mu)\frac{\partial^{2}v}{\partial y^{2}} + (\lambda + \mu)\frac{\partial^{2}u}{\partial x\partial y} + \mu\frac{\partial^{2}v}{\partial x^{2}} - \gamma_{n}\frac{\partial N}{\partial y} - \gamma_{t}\frac{\partial\Theta}{\partial y} - \rho\frac{\partial^{2}v}{\partial t^{2}} = 0,\ \ (7)$$

$$D_{e}\left( \frac{\partial^{2}N}{\partial x^{2}} + \frac{\partial^{2}N}{\partial y^{2}} \right) - \frac{N}{\tau} + \zeta\frac{\Theta}{\tau} - \frac{\partial N}{\partial t} = 0,\ \ (8)$$

$$\left( K^{*} + K\frac{\partial}{\partial t} \right)\left( \frac{\partial^{2}\Theta}{\partial x^{2}} + \frac{\partial^{2}\Theta}{\partial y^{2}} \right) + \frac{E_\mathrm{g}}{\tau}N - \frac{\partial}{\partial t}\left( \rho c_{e}\frac{\partial\Theta}{\partial t} + \gamma_{t}T_{0}\left( \frac{\partial^{2}u}{\partial t\partial x} + \frac{\partial^{2}v}{\partial t\partial y} \right) \right) - Q = 0,\ \ (9)$$

$$\sigma_{xx} = (\lambda + 2\mu)\frac{\partial u}{\partial x} + \lambda\frac{\partial v}{\partial y} - \gamma_{n}N - \gamma_{t}\Theta,\mspace{6mu}\sigma_{xy} = \mu\left( \frac{\partial u}{\partial y} + \frac{\partial v}{\partial x} \right).\ \ (10)$$

The problem initial and boundary conditions can be defined by

$$T(x,\mspace{6mu} y,\mspace{6mu} 0) = \frac{\partial T(x,\mspace{6mu} y,\mspace{6mu} 0)}{\partial t} = 0,\mspace{6mu} N(x,\mspace{6mu} y,\mspace{6mu} 0) = \frac{\partial N(x,\mspace{6mu} y,\mspace{6mu} 0)}{\partial t} = 0,\ \ (11)$$

$$u(x,\mspace{6mu} y,\mspace{6mu} 0) = \frac{\partial u(x,\mspace{6mu} y,\mspace{6mu} 0)}{\partial t} = 0,\mspace{6mu} v(x,\mspace{6mu} y,\mspace{6mu} 0) = \frac{\partial v(x,\mspace{6mu} y,\mspace{6mu} 0)}{\partial t} = 0,$$

$$\Theta(0,\mspace{6mu} y,\mspace{6mu} t) = 0,\mspace{6mu} D_{e}\frac{\partial N(0,\mspace{6mu} y,\mspace{6mu} t)}{\partial x} = s_{0}N(0,\mspace{6mu} y,\mspace{6mu} t),\mspace{6mu}\sigma_{xx}(0,\mspace{6mu} y,\mspace{6mu} t) = \sigma_{xy}(0,\mspace{6mu} y,\mspace{6mu} t) = 0, \ \ (12)$$

where s₀ is the surface recombination speed. For convenience, the dimensionless variables can be taken as

$$(t^{'},\mspace{6mu}\tau^{'}) = \zeta c^{2}(t,\mspace{6mu}\tau),\ (x^{'},\mspace{6mu} y^{'},\mspace{6mu} u^{'},\mspace{6mu} v^{'}) = \zeta c(x,\mspace{6mu} y,\mspace{6mu} u,\mspace{6mu} v),$$

$$N^{'} = \frac{N}{n_{0}},\mspace{6mu} Q^{'} = \frac{Q}{KT_{0}\zeta^{2}c^{2}},\mspace{6mu}\Theta^{*} = \frac{\Theta}{T_{0}},\ \ (13)$$

$$(\sigma_{xx}^{'},\mspace{6mu}\sigma_{xy}^{'}) = \frac{1}{\mu}(\sigma_{xx},\mspace{6mu}\sigma_{xy}),$$

where

$$c = \sqrt{\frac{\lambda + 2\mu}{\rho}},\mspace{6mu}\zeta = \frac{\rho c_{e}}{k}.$$

In these nondimensional terms of the physical quantities in Eq. (13), the above Eqs. (5)–(12) can be expressed as in the following forms (the dash has been dropped for convenience)

$$\frac{\partial^{2}u}{\partial x^{2}} + m_{1}\frac{\partial^{2}v}{\partial x\partial y} + m_{2}\frac{\partial^{2}u}{\partial y^{2}} - \beta_{n}\frac{\partial N}{\partial x} - \beta_{t}\frac{\partial\Theta}{\partial x} - \frac{\partial^{2}u}{\partial t^{2}} = 0,\ \ (14)$$

$$\frac{\partial^{2}v}{\partial y^{2}} + m_{1}\frac{\partial^{2}u}{\partial x\partial y} + m_{2}\frac{\partial^{2}v}{\partial x^{2}} - \beta_{n}\frac{\partial N}{\partial y} - \beta_{t}\frac{\partial\Theta}{\partial y} - \frac{\partial^{2}v}{\partial t^{2}} = 0,\ \ (15)$$

$$\frac{\partial^{2}N}{\partial x^{2}} + \frac{\partial^{2}N}{\partial y^{2}} - \alpha_{\mathrm{s}}\frac{N}{\tau} + \beta\frac{\Theta}{\tau} - \alpha_{\mathrm{s}}\frac{\partial N}{\partial t} = 0,\ \ (16)$$

$$\left( \gamma + \frac{\partial}{\partial t} \right)\left( \frac{\partial^{2}\Theta}{\partial x^{2}} + \frac{\partial^{2}\Theta}{\partial y^{2}} \right) + \eta_{2}\frac{N}{\tau} - \frac{\partial}{\partial t}\left\lbrack \frac{\partial\Theta}{\partial t} + \eta_{1}\left( \frac{\partial^{2}u}{\partial t\partial x} + \frac{\partial^{2}v}{\partial t\partial y} \right) - Q \right\rbrack = 0,\ \ (17)$$

$$\sigma_{xx} = \frac{\partial u}{\partial x} + m_{3}\frac{\partial v}{\partial y} - \beta_{n}N - \beta_{t}\Theta,\mspace{6mu}\sigma_{xy} = m_{2}\left( \frac{\partial u}{\partial y} + \frac{\partial v}{\partial x} \right),\ \ (18)$$

$$\Theta(0,\mspace{6mu} y,\mspace{6mu} t) = 0,\mspace{6mu}\frac{\partial N(0,\mspace{6mu} y,\mspace{6mu} t)}{\partial x} = \varphi N(0,\mspace{6mu} y,\mspace{6mu} t) = 0,\mspace{6mu}\sigma_{xx}(0,\mspace{6mu} y,\mspace{6mu} t) = \sigma_{xy}(0,\mspace{6mu} y,\mspace{6mu} t) = 0,\ \ (19)$$

where

$$m_{1} = \frac{\lambda + \mu}{\lambda + 2\mu},\mspace{6mu} m_{2} = \frac{\mu}{\lambda + 2\mu},\mspace{6mu} m_{3} = \frac{\lambda}{\lambda + 2\mu},\mspace{6mu}\eta_{1} = \frac{\gamma_{t}}{\rho c_{e}},$$

$$\gamma = \frac{K^{*}}{{kρ}c_{e}c^{2}},\mspace{6mu}\eta_{2} = \frac{E_\mathrm{g}n_{0}}{{ηK}T_{0}},\mspace{6mu}\varphi = \frac{s_{0}}{D_{e}{ηc}},\mspace{6mu}\beta_{n} = \frac{n_{0}\gamma_{n}}{\lambda + 2\mu},$$

$$\beta_{t} = \frac{T_{0}\gamma_{t}}{\lambda + 2\mu},\mspace{6mu}\alpha_{\mathrm{s}} = \frac{1}{\eta D_{e}},\mspace{6mu}\beta = \frac{\zeta T_{0}}{n_{0}\eta D_{e}}.$$

Now, we consider that the plane is induced by moving thermal source along x axis with a constant velocity ω which is assumed in the following nondimensional form

$$Q = Q_{0}\delta(x - \omega t)H(b - \left| y \right|),\ \ (20)$$

where δ is the delta function, Q₀ is constant and H is the step function of the Heaviside unit.

3. The Laplace–Fourier transforms

The Laplace transforms for any functionZ(x, y, t), can be expressed by

$$\bar{Z}(x,\mspace{6mu} y,\mspace{6mu} p) = \int_{0}^{\infty}{Z(x,\mspace{6mu} y,\mspace{6mu} t)e^{- {pt}}\mathrm{d}t,}\mspace{6mu} p > 0,\ \ (21)$$

while the Fourier transforms for any function can be defined by

$${\bar{Z}}^{*}(x,\mspace{6mu} q,\mspace{6mu} p) = \int_{- \infty}^{\infty}{\bar{Z}(x,\mspace{6mu} y,\mspace{6mu} p)e^{- {iqy}}\text{d}x.}\ \ (22)$$

Thus, the governing equations with initial and boundary conditions can be written to obtain the following ordinary differential equations system

$$\frac{d^{2}{\bar{u}}^{*}}{dx^{2}} = (p^{2} + m_{2}q^{2}){\bar{u}}^{*} - m_{1}{iq}\frac{\mathrm{d}\bar{v}}{{\text{d}x}} + \beta_{n}\frac{\mathrm{d}{\bar{N}}^{*}}{{\text{d}x}} + \beta_{t}\frac{\mathrm{d}{\bar{\Theta}}^{*}}{{\text{d}x}},\ \ (23)$$

$$\frac{d^{2}{\bar{v}}^{*}}{dx^{2}} = \frac{p^{2} + q^{2}}{m_{2}}{\bar{v}}^{*} + \frac{\beta_{n}{iq}}{m_{2}}{\bar{N}}^{*} + \frac{\beta_{t}{iq}}{m_{2}}{\bar{\Theta}}^{*} - \frac{m_{1}{iq}}{m_{2}}\frac{\mathrm{d}{\bar{u}}^{*}}{{\text{d}x}},\ \ (24)$$

$$\frac{\mathrm{d}^{2}{\bar{N}}^{*}}{\mathrm{d}x^{2}} = \left( p^{2}\alpha_{\mathrm{s}} + q^{2} + \frac{\alpha_{\mathrm{s}}}{\tau} \right){\bar{N}}^{*} - \frac{\beta}{\tau}_{n}{\bar{\Theta}}^{*},\ \ (25)$$

$$\frac{\mathrm{d}^{2}{\bar{\Theta}}^{*}}{\mathrm{d}x^{2}} = \eta_{1}{iq}\frac{p^{2}}{\gamma + p}{\bar{v}}^{*} - \frac{\eta_{2}}{\tau}{\bar{N}}^{*} + \left( q^{2} + \frac{p^{2}}{\gamma + p} \right){\bar{\Theta}}^{*} + \eta_{1}\frac{p^{2}}{\gamma + p}\frac{\mathrm{d}{\bar{u}}^{*}}{{\text{d}x}} - fe^{- {mx}},\ \ (26)$$

$${\bar{\sigma}}_{xx}^{*} = \frac{\mathrm{d}{\bar{u}}^{*}}{{\text{d}x}} + iqm_{3}{\bar{v}}^{*} - \beta_{n}{\bar{N}}^{*} - \beta_{t}{\bar{\Theta}}^{*},\mspace{6mu}{\bar{\sigma}}_{xy}^{*} = m_{2}\left( {iq}{\bar{u}}^{*} + \frac{\mathrm{d}{\bar{v}}^{*}}{{\text{d}x}} \right),\ \ (27)$$

$${\bar{\Theta}}^{*} = \frac{\mathrm{d}{\bar{N}}^{*}}{{\text{d}x}} - \varphi{\bar{N}}^{*} = {\bar{\sigma}}_{xx}^{*} = {\bar{\sigma}}_{xy}^{*} = 0,\ \ (28)$$

where

$$m = \frac{p}{\omega},\mspace{6mu} f = \frac{pQ_{0}}{\omega}\sqrt{\frac{2}{\pi}}\frac{\sin(qb)}{q}.$$

The vector-matrix differential equation of Eqs. (23)–(26) can be written by

$$\frac{\mathrm{d}\mathbf{V}}{{\text{d}x}} = A\mathbf{V} + Fe^{- {mx}},\ \ (29)$$

where

$$V = \begin{bmatrix} {\bar{u}}^{*} & {\bar{v}}^{*} & {\bar{N}}^{*} & {\bar{\Theta}}^{*} & \frac{\mathrm{d}{\bar{u}}^{*}}{{\text{d}x}} & \frac{\mathrm{d}{\bar{v}}^{*}}{{\text{d}x}} & \frac{\mathrm{d}{\bar{N}}^{*}}{{\text{d}x}} & \frac{\mathrm{d}{\bar{\Theta}}^{*}}{{\text{d}x}} \\ \end{bmatrix}^\mathrm{T},$$

$$F = \lbrack\begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 & - f \\ \end{matrix}\rbrack^\mathrm{T},$$

while the matrixA = [a_ij] = 0,i, j = 1, ..., 8, excepting

$$a_{15} = a_{26} = a_{37} = a_{48} = 1,\mspace{6mu} a_{51} = p^{2} + m_{2}q^{2},\mspace{6mu} a_{56} = - m_{1}iq,$$

$$a_{57} = \beta_{n},\mspace{6mu} a_{58} = \beta_{t},\mspace{6mu} a_{62} = \frac{p^{2} + q^{2}}{m^{2}},\mspace{6mu} a_{63} = \frac{\beta_{n}{iq}}{m_{2}},$$

$$a_{64} = \frac{\beta_{t}{iq}}{m_{2}},\mspace{6mu} a_{65} = - \frac{m_{1}{iq}}{m_{2}},\mspace{6mu} a_{73} = p\alpha_{\mathrm{s}} + q^{2} + \frac{\alpha_{\mathrm{s}}}{\tau},$$

$$a_{74} = - \frac{\beta}{\tau},\mspace{6mu} a_{82} = \frac{\eta_{1}{iq}p^{2}}{\gamma + p},\mspace{6mu} a_{83} = - \frac{\eta_{2}}{\tau(\gamma + p)},$$

$$a_{84} = q^{2} + \frac{p^{2}}{\gamma + p},\mspace{6mu} a_{85} = \frac{\eta_{1}p^{2}}{\gamma + p}.$$

The general solution V of the nonhomogeneous system (29) are the sum of the complementary solutionV_c of the homogeneous equation and a particular solution V_p of the nonhomogeneous system. By using the eigenvalues method which proposed in Ref. [25], the exact solutions of homogeneous system can be obtained. Then, the matrix A has the characteristic equation which can be given by

$$\xi^{8} - f_{1}\xi^{6} + f_{2}\xi^{4} + f_{3}\xi^{2} + f_{4} = 0,\mspace{6mu}(30)$$

where

$$f_{1} = a_{73} + a_{84} + a_{51} + a_{62} + a_{56}a_{65} + a_{58}a_{85},$$

$$f_{2} = a_{51}a_{84} + a_{62}a_{84} + a_{56}a_{65}a_{84} + a_{73}a_{84} + a_{51}a_{62} + a_{51}a_{73} + a_{62}a_{73} + a_{56}a_{65}a_{73}$$

$$- a_{64}a_{82} - a_{58}a_{65}a_{82} - a_{74}a_{83} + a_{58}a_{73}a_{85} - a_{57}a_{74}a_{85} + a_{58}a_{62}a_{85} - a_{56}a_{64}a_{85},$$

$$f_{3} = a_{64}a_{73}a_{82} + a_{58}a_{65}a_{73}a_{82} - a_{63}a_{74}a_{82} - a_{57}a_{65}a_{74}a_{82} - a_{51}a_{62}a_{73} + a_{51}a_{64}a_{82}$$

$$- a_{51}a_{62}a_{84} - a_{51}a_{73}a_{84} - a_{62}a_{73}a_{84} - a_{56}a_{65}a_{73}a_{84} - a_{58}a_{62}a_{73}a_{85} + a_{53}a_{64}a_{73}a_{85}$$

$$+ a_{57}a_{62}a_{74}a_{85} - a_{56}a_{63}a_{74}a_{85} + a_{51}a_{74}a_{83} + a_{62}a_{74}a_{83} + a_{56}a_{65}a_{74}a_{83},$$

$$f_{4} = a_{51}a_{62}a_{73}a_{84} - a_{51}a_{62}a_{74}a_{83} + a_{51}a_{63}a_{74}a_{82} - a_{51}a_{64}a_{73}a_{82}.$$

To obtain the solutions of Eq. (29), the eigenvalues and corresponding eigenvectors of matrix A must be calculated. If the eigenvalues take the form ±ξ₁, ±ξ₂, ±ξ₃, ±ξ₄, the corresponding eigenvectors of eigenvalues ξ can be considered as

$$Y = \begin{pmatrix} y_{1} \\ y_{2} \\ y_{3} \\ y_{4} \\ y_{5} \\ y_{6} \\ y_{7} \\ y_{8} \\ \end{pmatrix},\ \ (31)$$

where

$$y_{1} = a_{58}((a_{58}(a_{62} + \xi^{2}) - a_{64}a_{56})(\xi^{2} - a_{73}) - a_{74}((\xi^{2} - a_{62})a_{57} + a_{63}a_{56}))\xi^{2},$$

$$y_{2} = - \xi a_{58}((a_{64}(\xi^{2} - a_{51}) + \xi^{2}a_{65}a_{58})(\xi^{2} - a_{73}) + a_{74}(a_{63}(\xi^{2} - a_{51}) + \xi^{2}a_{63}a_{57})),$$

$$y_{3} = \xi a_{74}a_{58}(\xi^{2}a_{56}a_{65} - (\xi^{2} - a_{51})(\xi^{2} - a_{62})),$$

$$y_{4} = \xi a_{58}(\xi^{2} - a_{73})(\xi^{2}a_{56}a_{65} + (\xi^{2} - a_{51})(\xi^{2} - a_{62})),$$

$$y_{5} = (a_{58}\xi^{2}(a_{56}a_{64} + a_{58}(\xi^{2} - a_{62}))(a_{73} - \xi^{2}) + ((\xi^{2} - a_{62})a_{57} + a_{63}a_{56})a_{74}))\xi,$$

$$y_{6} = ( - \xi a_{58}(((\xi^{2} - a_{51})a_{64} + \xi^{2}a_{65}a_{58})(\xi^{2} - a_{73}) + (a_{63}(\xi^{2} - a_{51}) + \xi^{2}a_{65}a_{57})a_{74}))\xi,$$

$$y_{7} = (\xi a_{58}((\xi^{2} - a_{51})(a_{62} - \xi^{2}) + \xi^{2}a_{65}a_{56})a_{74})\xi,$$

$$y_{8} = (\xi a_{58}((\xi^{2} - a_{51})(a_{62} - \xi^{2}) + \xi^{2}a_{65}a_{56})(\xi^{2} - a_{73}))\xi.$$

Hence, the complementary solutions of Eq. (29) can be given by

$$V_\mathrm{c}(x,\mspace{6mu} q,\mspace{6mu} p) = \sum_{i = 1}^{4}{B_{i}Y_{i}}e^{- \xi_{i}x}.\mspace{6mu}(32)$$

From Eq. (29), in the inhomogeneous terms, there is the exponential function e^–mx, which in the homogeneous equation solution coincides with the exponential function. Thus, the particular solutions ${\bar{h}}_{p}^{*}$ should be sought in the form of a quasi-polynomial vector:

$$V_\mathrm{p} = Re^{- {mx}},\ \ (33)$$

where R depends on q andp. Thus, the general solutions of the field variables can be written for q, p andt as

$${\bar{N}}^{*}(x,\mspace{6mu} q,\mspace{6mu} p) = \sum_{i = 1}^{4}{B_{i}N_{i}e^{- \xi_{i}x} + \frac{s_{1}}{D}e^{- {mx}},}\ \ (34)$$

$${\bar{\Theta}}^{*}(x,\mspace{6mu} q,\mspace{6mu} p) = \sum_{i = 1}^{4}{B_{i}T_{i}e^{- \xi_{i}x} + \frac{s_{2}}{D}e^{- {mx}},}\ \ (35)$$

$${\bar{u}}^{*}(x,\mspace{6mu} q,\mspace{6mu} p) = \sum_{i = 1}^{4}{B_{i}u_{i}e^{- \xi_{i}x} + \frac{s_{3}}{D}e^{- {mx}},}\ \ (36)$$

$${\bar{v}}^{*}(x,\mspace{6mu} q,\mspace{6mu} p) = \sum_{i = 1}^{4}{B_{i}v_{i}e^{- \xi_{i}x} + \frac{s_{4}}{D}e^{- {mx}},}\ \ (37)$$

$${\bar{\sigma}}_\text{xx}^{*}(x,\mspace{6mu} q,\mspace{6mu} p) = \sum_{i = 1}^{4}{B_{i}( - \xi_{i}u_{i} + iqm_{3}v_{i}} - \beta_{n}N_{i} - \beta_{t}T_{i})e^{- \xi_{i}x} + \frac{s_{5}}{D}e^{- {mx}},\ \ (38)$$

$${\bar{\sigma}}_{xy}^{*}(x,\mspace{6mu} q,\mspace{6mu} p) = \sum_{i = 1}^{4}{B_{i}m_{2}( - \xi_{i}v_{i} + iqu_{i})}e^{- \xi_{i}x} + \frac{s_{6}}{D}e^{- {mx}},\ \ (39)$$

where the terms containing exponentials of growing nature in the space variable x have been discarded due to the regularity condition of the solution at infinity,B₁, B₂,B₃ and B₄ are constants which can be calculated by using the problem boundary conditions while u_i,v_i, N_i and Θ_i are the components of corresponding eigenvectors with

$$s_{1} = fa_{74}(a_{51}(m^{2} - a_{62}) + m^{2}( - m^{2} + a_{62} + a_{56}a_{65})),$$

$$s_{2} = - f(m^{2} - a_{73})(a_{51}( - m^{2} + a_{62}) + m^{2}(m^{2} - a_{56}a_{65} - a_{62})),$$

$$s_{3} = - fm(a_{58}(m^{2} - a_{62})(m^{2} - a_{73}) + a_{56}(a_{64}(m^{2} - a_{73}) + a_{63}a_{74}) + a_{57}(m^{2} - a_{62})a_{74}),$$

$$s_{4} = - f(a_{64}(m^{2} - a_{73})(m^{2} - a_{51}) + m^{2}a_{58}a_{65}(m^{2} - a_{73}) + ((m^{2} - a_{51})a_{63} + m^{2}a_{57}a_{65})a_{74}),$$

$$s_{5} = - ms_{3} + iqm_{3}s_{4} - \beta_{n}s_{1} - \beta_{t}s_{2},$$

$$s_{6} = m_{2}( - ms_{4} + iqs_{3}),$$

$$D = m^{8} - f_{1}m^{6} + f_{2}m^{4} + f_{3}m^{2} + f_{4}.$$

Now, for any function ${\bar{Z}}^{*}(x,\mspace{6mu} q,\mspace{6mu} p),$ its inversion of Fourier transform can be defined by

$$\bar{Z}(x,\mspace{6mu} y,\mspace{6mu} p) = \frac{1}{\sqrt{2\pi}}\int_{- \infty}^{\infty}{{\bar{Z}}^{*}(x,\mspace{6mu} q,\mspace{6mu} p)e^{{iqy}}\text{d}q.}\ \ (40)$$

Finally, to get the general solutions of temperature, the displacements, carrier density and stresses along distancesx, y at any time t, we choose the Stehfest numerical inversion approach [26]. In this approach, the inverse of Laplace transforms for $\bar{h}(x,\mspace{6mu} y,\mspace{6mu} p)$ can be approximated by

$$Z(x,\mspace{6mu} y,\mspace{6mu} t) = \frac{\text{ln2}}{t}\sum_{n = 1}^{N}{V_{n}\bar{Z}\left( x,\mspace{6mu} y,\mspace{6mu} n\frac{\text{ln2}}{t} \right)},\ \ (41)$$

where V_n is defined by the following relation:

$$V_{n} = ( - 1)^{(\frac{N}{2} + 1)}\sum_{p = \frac{(n + 1)}{2}}^{\min(n,\mspace{6mu}\frac{N}{2})}\frac{(2p)!p^{(\frac{N}{2} + 1)}}{p!(n - p)!(\frac{N}{2} - p)!(2n - 1)!},\ \ (42)$$

where N is the term numbers.

4. Numerical results and discussion

The polymeric silicone appears in the photovoltaic solar cell of the p-n junction and can be manufactured quickly and economically. The values of thermal properties for silicon (Si) like material have been written as [27] μ = 5.46 × 10¹⁰ N m^–2,p = 2330 kg m^–3, λ = 3.64 × 10¹⁰ N m^–2,E = 2.33 eV,D_e = 2.5 × 10^–3 m²s^–1,s₀ = 2 m s^–1,E_g = 1.11 eV, α_t = 3 × 10^–6 K^–1,n₀ = 10²⁰ m^–3,d_n = –9 × 10^–31 m³, τ = 5 × 10^–5 s, T₀ = 300 K,c_e = 695 J kg^–1 K^–1,b = 0.4.

The above data have been applied to study the effects of the moving heat source speed in the variations of temperature Θ, the variations of carrier density N, the components of displacementu, v and the stresses σ_xx, σ_xy. The media is considered to be an isotropic and homogeneous two-dimension semiconducting material. In addition, the thermal and elastic properties are considered without leaving the conjunction between the waves subjected to the plasma and the thermoelastic conditions.

Figure 1a predicts the increment of temperature along the distance x. It is noticed that it starts from zeros according to the application of boundary condition and increase with x to have utmost values atx = 0.3 and decreases gradually with increasingx to close to zero beyond a wave front for the generalized photothermal theory. Figure 1b shows the carrier density variation along x. It is observed that the carrier density increasing with increases x to have maximum values on x = 0.4 and decreases with the increasing x until attaining zero onx = 3. Figure 1c displays the variation of vertical displacement along x which have maximums values on x = 0 and decreases with increasing x. Figure 1d shows the variation of horizontal displacement u alongx. It is observed that it attains utmost negative value and progressively increases until it attains peak values at a particular location in close proximity to x = 0 and then continuously decreases to zero. Figure 1e display the stress component variation σ_xx along x. It is clear that the stress magnitude always starts from zero which satisfies the boundary conditions. Figure 1f predicts the variation of stress component σ_xy along x. The stress magnitude always starts from zero which satisfies the problem boundary conditions.

Fig. 1.

The variation of temperature Θ (a), carrier density N (b), horizontal u (c) and vertical displacement v (d), stress σ_xx (e) and σ_xy (f) along to distance x wheny = 0.5 for different values of heat source velocity ω = 0.01 (1), 0.03 (2), 0.05 (3).

Figures 2a and 2b show the variations of the increment of temperature Θ and the carrier densityN along y and they point that the carrier density and the increment of temperature have ultimate values at the length of thermal surface (|y| ≤ 0.4) and they start to reduce just near the edge (|y| ≤ 0.4) where they smoothly decrease and finally close to zero values. Figure 2c shows the variations of vertical displacement v along y. We find that it starts raising at the beginning and ending of the thermal surface (|y| ≤ 0.4), and has smallest values at the middle of the thermal surface, then it starts increasing and come to highest values just near the edge (y = ±0.4), after that it decreases to reach to zero. Figure 2d displays the variations of horizontal displacement u with respect to x and it indicates that it has ultimate values at the length of the thermal surface (|y| ≤ 0.4), and it begins to reduce just near the edge (y = ±0.4), and after that reduces to zero value. Respectively, stresses σ_xx and σ_xy with respect to y are shown in Figs. 2e and 2f. As expected, it can be found that the speed of moving heat source have the great effects on the values of all the studied fields.

Fig. 2.

The variation of temperature Θ (a), carrier density N (b), horizontal u (c) and vertical displacement v (d), stress σ_xx (e) and σ_xy (f) along to distance y whenx = 0.5 for different values of heat source velocity ω = 0.01 (1), 0.03 (2), 0.05 (3).