1 Introduction

In recent years, the vortical and skyrmionic states in superconductors with two or more coupled condensates have drawn a lot of attention [1]. Different from conventional superconducting states, the domain walls separate different chiral states [2,3,4,5,6,7,8] and the coreless skyrmionic structures [9,10,11,12] can be stabilized in spin-triplet \(p_{x}\pm {i}p_{y}\)-wave superconductors with broken time-reversal symmetry. Cantilever magnetometry measurements have revealed evidence for the existence of half-quantum vortices in \(\hbox {Sr}_{{2}}\) \(\hbox {RuO}_{{4}}\) which is most-likely a spin-triplet chiral p-wave material [13]. The half-quantum vortices may host Majorana states at exactly zero energy as bound states inside the vortex cores [14]. Moreover, several striking features, such as the vortex coalescence into clusters [15,16,17,18] and the type-1.5 behavior with attractive (repulsive) intervortex interaction at long (short) ranges [19], have been reported in \(\hbox {Sr}_{{2}}\)  \(\hbox {RuO}_{{4}}\) samples. Particularly, in the presence of mesoscopic boundaries, the spatial configurations of topological defects are strongly influenced by the geometric effect [20, 21]. At the boundary of superconducting domains of opposite chirality, the locally suppressed condensate can produce an intrinsic Josephson junction [6, 22]. Due to the interplay between the circular symmetry of the applied magnetic field and noncircular boundaries, unusual skyrmionic configurations containing half-quantum vortex–antivortex pairs can be found in finite-size p-wave superconducting systems [23, 24].

In addition, the competition between different pairing symmetries in \(s+is\) or \(s+id\) superconductors with time-reversal symmetry breaking can result in rich phenomena associated with the vortex matter [25,26,27]. Peculiar features of vortical configurations, such as the skyrmionic chains, can be realized by tunning the relative strength of competing pairing symmetries [27]. The nematic skyrmion consisting of two spatially separated half-quantum vortices has also been predicted in two-component superconductors [28]. When a mixed s-wave and d-wave superconducting order is coupled to the nematic order, the novel elliptical vortex and oblique vortex lattice have been revealed in FeSe superconducting systems [29]. Furthermore, mixed singlet-triplet pairing becomes possible in the superconducting system with lifted spin degeneracy [30, 31]. It has been predicted that an additional p-wave component can be generated by the surface induced spin-orbit coupling in the case of s-wave or d-wave superconductors [32,33,34,35,36]. For the material \(\beta \)-\(\hbox {Bi}_{{2}}\)Pd exhibiting classical s-wave bulk superconductivity [37], the experimental signature of Majorana zero modes [38] and half-integer magnetic flux quantization [39] has revealed the occurrence of a spin-triplet pairing symmetry. A novel vortex distribution, distinctly different from the well-studied disordered and glassy phases, was recently demonstrated in \(\beta \)-\(\hbox {Bi}_{{2}}\)Pd [40]. Notably, for a square lattice system with a nearest-neighbor attractive interaction, superconducting states with various symmetries can be found by changing the band structure (i.e., the shape of the Fermi surface) [41, 42]. Several peculiar vortical patterns have been obtained in a mesoscopic superconducting square loop when the p-wave, s-wave and d-wave pairing symmetries are coexisted [43]. However, the configurations of topological defect states remain little explored in bulk superconducting systems with mixed pairing orders up to now. One may expect to see whether the unusual vortical and skyrmionic modes can still be observed for such bulk samples when the quantum-confined effect is absent.

In the present work, we systematically investigate the spatial patterns of topological defects in bulk superconducting samples with mixed pairing orders by solving the Bogoliubov-de Gennes (BdG) equations [44] in a square unit cell with periodic boundary conditions along the x and y directions. Based on a tight-binding model Hamiltonian, the on-site repulsive interaction among the electrons is introduced to generate the mixed singlet-triplet pairing [43, 45]. For an appropriate chemical potential, the effect of next-nearest-neighbor (nnn) hopping will be applied to tune the stable spin-triplet p-wave superconducting order which can coexist with spin-singlet s-wave and d-wave superconducting ones. The influence of the Zeeman field on the order modulation are also discussed. Our numerical analysis tackles the issue of whether the novel topological defect structures similar to the features observed in recent experiments can be present in such a bulk system based on our microscopic model. The corresponding zero-energy local density of states (LDOS) and the relative phase differences useful to display the skyrmionic texture are demonstrated. We expect that our present results may provide useful information for future experiments.

2 The model and formulas

We start with an effective mean-field Hamiltonian:

$$\begin{aligned} {\hat{H}}_{\mathrm {eff}}= & {} -\sum _{\langle \mathbf {ij}\rangle ,\sigma }t_{\mathbf {ij}}\mathrm {exp}(i\varphi _{{\mathbf {i}}{\mathbf {j}}})c_{{\mathbf {i}}\sigma }^{\dagger }c_{{\mathbf {j}}\sigma }+\sum _{{\mathbf {i}},\sigma }(U{\langle }n_{{\mathbf {i}}{\bar{\sigma }}}{\rangle } \nonumber \\&-\mu )c_{{\mathbf {i}}\sigma }^{\dagger }c_{{\mathbf {i}}\sigma }-{\mathbf {h}}_{z}\sum _{{\mathbf {i}},\sigma ,{\bar{\sigma }}}(\mathbf {\sigma }_{z})_{\sigma {\bar{\sigma }}}c_{{\mathbf {i}}\sigma }^{\dagger }c_{{\mathbf {i}}{\bar{\sigma }}} \nonumber \\&+V\sum _{\langle \mathbf {ij}\rangle }(\varDelta _{\mathbf {ij}}c_{{\mathbf {i}}\uparrow }^{\dagger }c_{{\mathbf {j}}\downarrow }^{\dagger }+\varDelta _{\mathbf {ij}}^{*}c_{{\mathbf {j}}\downarrow }c_{{\mathbf {i}}\uparrow }), \end{aligned}$$
(1)

where \(t_{\mathbf {ij}}=t\) and \(t'\) are the nearest-neighbor (nn) and nnn hopping integrals, respectively. \(c_{{\mathbf {i}}\sigma }\) (\(c_{{\mathbf {i}}\sigma }^{\dagger }\)) are destruction (creation) operators for electron of spin \(\sigma \) (\(\sigma \)=\(\uparrow \) or \(\downarrow \)). U represents the on-site repulsion interaction, and the nearest-neighbor attraction V is responsible for the superconducting pairing. \(n_{{\mathbf {i}}\sigma }=c_{{\mathbf {i}}\sigma }^{\dagger }c_{{\mathbf {i}}\sigma }\) is the number operator, and \(\mu \) is the chemical potential determining the averaged electron density \({\bar{n}}\). \({\mathbf {h}}_{z}\) describes the Zeeman site energy in the z direction, and \(\mathbf {\sigma }_{z}\) the Pauli matrix. The Peierl’s phase factor is given by \(\varphi _{\mathbf {ij}}=\pi /\varPhi _{0}\int _{r_{{\mathbf {i}}}}^{r_{{\mathbf {j}}}}\mathbf {A(r)}\cdot {d{\mathbf {r}}}\), where the flux quantum \(\varPhi _{0}=hc/2e\) and the vector potential \(\mathbf {A(r)}=H(-y,x,0)/2\) with magnetic filed H in the symmetric gauge. Here, we have introduced the pairing amplitude on a bond \(\varDelta _{\mathbf {ij}}=\langle {c_{{\mathbf {i}}\uparrow }c_{{\mathbf {j}}\downarrow }}\rangle \). Using the Bogoliubov transformation: \(c_{{\mathbf {i}}\uparrow }=\sum _{n}[u_{{\mathbf {i}}\uparrow }^{n}\gamma _{n\uparrow }-v_{{\mathbf {i}}\uparrow }^{n*}\gamma _{n\downarrow }^{\dag }]\), \(c_{{\mathbf {i}}\downarrow }=\sum _{n}[u_{{\mathbf {i}}\downarrow }^{n}\gamma _{n\downarrow }+v_{{\mathbf {i}}\downarrow }^{n*}\gamma _{n\uparrow }^{\dag }]\), the Hamiltonian in Eq. (1) can be diagonalized by solving the resulting BdG equations self-consistently:

$$\begin{aligned} \sum _{{\mathbf {j}}}^{N}\left( \begin{array}{cc} {\mathcal {H}}_{\mathbf {ij}\sigma } &{} \varDelta _{\mathbf {ij}} \\ \varDelta _{\mathbf {ij}}^{\dagger } &{} -{\mathcal {H}}_{\mathbf {ij}{\bar{\sigma }}}^{*} \\ \end{array} \right) \left( \begin{array}{c} u_{{\mathbf {j}}\sigma }^{n} \\ v_{{\mathbf {j}}{\bar{\sigma }}}^{n} \\ \end{array} \right) =E_{n}\left( \begin{array}{c} u_{{\mathbf {i}}\sigma }^{n} \\ v_{{\mathbf {i}}{\bar{\sigma }}}^{n} \\ \end{array} \right) , \end{aligned}$$
(2)

where \(\mathcal {H}_{\mathbf {ij}\sigma }=-t_{\mathbf {ij}}\mathrm {exp}(i\varphi _{{\mathbf {i}}{\mathbf {j}}})+[U{\langle }n_{{\mathbf {i}}{\bar{\sigma }}}{\rangle }-{\mathbf {h}}_{z}\sigma -\mu ]\delta _{\mathbf {ij}}\). With the periodic boundary conditions, we can get the eigenvalues \(\{E_{n}\}\) with eigenvectors \(\{u_{{\mathbf {i}}}^{n}, v_{{\mathbf {i}}}^{n}\}\). The self-consistent conditions are

$$\begin{aligned}&\langle {n_{{\mathbf {i}}\uparrow }}\rangle =\sum _{n=1}^{2N}|u_{{\mathbf {i}}}^{n}|^{2}f(E_{n}), \end{aligned}$$
(3)
$$\begin{aligned}&\langle {n_{{\mathbf {i}}\downarrow }}\rangle =\sum _{n=1}^{2N}|v_{{\mathbf {i}}}^{n}|^{2}[1-f(E_{n})], \end{aligned}$$
(4)
$$\begin{aligned}&\varDelta _{\mathbf {ij}}=\sum _{n=1}^{2N}u_{{\mathbf {i}}}^{n}v_{{\mathbf {j}}}^{n*}[1-f(E_{n})], \end{aligned}$$
(5)

where \(f(E_{n})=(e^{{E_{n}}/k_{B}T}+1)^{-1}\) is the Fermi-Dirac distribution function. From the order parameter \(\varDelta _{\mathbf {ij}}\), it is possible to build the spin-singlet (S) and spin-triplet (T) pairing amplitudes in the \(S_{z}=0\) sector, given by [42, 46]

$$\begin{aligned}&\varDelta _{\mathbf {ij}}^{S}=(\varDelta _{\mathbf {ij}}+\varDelta _{\mathbf {ji}})/2, \end{aligned}$$
(6)
$$\begin{aligned}&\varDelta _{\mathbf {ij}}^{T}=(\varDelta _{\mathbf {ij}}-\varDelta _{\mathbf {ji}})/2. \end{aligned}$$
(7)

Then, the extended \(s-\), \(d_{x^{2}-y^{2}}-\), \(p_{x}-\) and \(p_{y}-\)wave symmetry can be defined, respectively, at site \({\mathbf {i}}\) as

$$\begin{aligned}&\varDelta _{s}({\mathbf {i}})=(\varDelta _{{\mathbf {i}}+{\mathbf {e}}_{{\mathbf {x}}},{\mathbf {i}}}^{S}+\varDelta _{{\mathbf {i}}-{\mathbf {e}}_{{\mathbf {x}}},{\mathbf {i}}}^{S}+\varDelta _{{\mathbf {i}},{\mathbf {i}}+\mathbf {e_{y}}}^{S}+\varDelta _{{\mathbf {i}},{\mathbf {i}}-\mathbf {e_{y}}}^{S})/4,\nonumber \\ \end{aligned}$$
(8)
$$\begin{aligned}&\varDelta _{d}({\mathbf {i}})=(\varDelta _{{\mathbf {i}}+{\mathbf {e}}_{{\mathbf {x}}},{\mathbf {i}}}^{S}+\varDelta _{{\mathbf {i}}-{\mathbf {e}}_{{\mathbf {x}}},{\mathbf {i}}}^{S}-\varDelta _{{\mathbf {i}},{\mathbf {i}}+\mathbf {e_{y}}}^{S}-\varDelta _{{\mathbf {i}},{\mathbf {i}}-\mathbf {e_{y}}}^{S})/4,\nonumber \\ \end{aligned}$$
(9)
$$\begin{aligned}&\varDelta _{p_{x}}({\mathbf {i}})=(\varDelta _{{\mathbf {i}}+{\mathbf {e}}_{{\mathbf {x}}},{\mathbf {i}}}^{T}-\varDelta _{{\mathbf {i}}-\mathbf {e_{x}},{\mathbf {i}}}^{T})/2, \end{aligned}$$
(10)
$$\begin{aligned}&\varDelta _{p_{y}}({\mathbf {i}})=(\varDelta _{{\mathbf {i}},{\mathbf {i}}+\mathbf {e_{y}}}^{T}-\varDelta _{{\mathbf {i}},{\mathbf {i}}-\mathbf {e_{y}}}^{T})/2, \end{aligned}$$
(11)

where \(\mathbf {e_{x(y)}}\) denotes the unit vector along the x(y) direction. For \(\sin {p_{x}}\pm {i}\sin {p_{y}}\)-wave superconductivity, we can define the pairing potential as \(\varDelta _{\pm }({\mathbf {i}})\equiv \varDelta _{p_{x}}({\mathbf {i}})\pm {i}\varDelta _{p_{y}}({\mathbf {i}})\).

The LDOS, proportional to the local differential tunneling conductance measured in a low-temperature scanning tunneling microscopic (STM) experiment, can be written as

$$\begin{aligned} \rho (E)=\sum _{n,\sigma }[|u_{{\mathbf {i}}\sigma }^{n}|^{2}\delta (E_{n}-E)+|v_{{\mathbf {i}}\sigma }^{n}|^{2}\delta (E_{n}+E)],\nonumber \\ \end{aligned}$$
(12)

where the Dirac delta-function \(\delta (x)\) is taken as \(\varGamma /\pi (x^{2}+\varGamma ^{2})\) with the quasiparticle damping \(\varGamma =0.01\).

Throughout this work, the distance is measured in units of the lattice constant a, the energy in units of t, and the magnetic flux in units of \(\varPhi _{0}=hc/e\). In the numerical calculations, we take \(k_{B}=a=t=1\) for simplicity. In what follows, we focus on the bulk superconducting system with a periodic \(N_{x}\times {N_{y}}\) unit cell. For an appropriate initial set of parameters \(n_{{\mathbf {i}}\sigma }\) and \(\varDelta _{\mathbf {ij}}\), the Hamiltonian is numerically diagonalized and the electron wave functions obtained are used to calculate the new parameters for the next iteration step. The calculations was repeated until the difference in the order parameters between two consecutive iterations is less than \(10^{-6}\).

3 Results and discussion

Fig. 1
figure 1

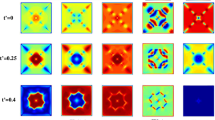
Contour plots of the total p-wave order-parameter amplitude \(|\varDelta _{p}|=\sqrt{|\varDelta _{+}|^2+|\varDelta _{-}|^2}\) [column (I)], the relative phase \(\phi _{xy}=cos(\phi _{x}-\phi _{y})\) between the \(p_{x}\)- and \(p_{y}\)-wave components [column (II)], the extended s-wave pairing \(\varDelta _{s}\) [column (III)], the d-wave pairing \(\varDelta _{d}\) [column (IV)], and the zero-energy LDOS \(\rho (0)\) [column (V)] in a \(40\times 40\) square unit cell accommodating the magnetic flux \(\varPhi =4\varPhi _{0}\) when \(t'=0\) (first row), \(t'=0.1\) (second row), and \(t'=0.2\) (third row). The calculation is performed with \(V=4\), \(U=1.5\), \(\mu =-2\), \({\mathbf {h}}_{z}=0\), and the temperature \(T=0\)

Full size image

For a finite out-of-plane magnetic field, we investigate the spatial profiles of topological defects in the bulk superconducting system at zero temperature. Here, the interaction strengths are chosen as \(V=4\), \(U=1.5\), leading to a favorable spin-triplet \(p_{x}\pm {i}p_{y}\)-wave pairing state. When the spin correlation is introduced, the spin-singlet s- and d-wave components of the order parameter can appear at the same time since the spin rotational symmetry is broken. It is known that the relative strength of three different orders can be tuned by the chemical potential [41, 42]. In contrast to our previous work [43], the chemical potential is chosen as \(\mu =-2\) in the present bulk case, that is, a subdominant s-wave state and a coexisted \(d_{x^{2}-y^{2}}\)-wave one can be stabilized. We assume that each unit cell with \(N_{x}\times {N_{y}}=40\times 40\) can accommodate the magnetic flux \(\varPhi =m\varPhi _{0}\), where m denotes an integer. First, we consider the case of the Zeeman field \({\mathbf {h}}_{z}=0\). For an applied flux \(\varPhi =4\varPhi _{0}\), Fig. 1 displays the contour plots of the quantized vortex state with point-like cores and the coreless skyrmionic state as well as their hybrid case in a \(40\times 40\) unit cell when the nnn hopping \(t'=0\) (first row), \(t'=0.1\) (second row), and \(t'=0.2\) (third row), respectively. As seen from column (I) when \(t'=0\), the total p-wave order-parameter amplitude \(|\varDelta _{p}|=\sqrt{|\varDelta _{+}|^2+|\varDelta _{-}|^2}\) shows a multivortex state carrying four separated flux quanta in the unit cell. For the dominant pairing symmetry, the bulk order-parameter amplitude \(|\varDelta _{p}(0)|\approx 0.18\), i.e., the BCS coherent length \(\xi (0)=\hbar {v_{F}}/\pi {|\varDelta _{p}(0)|}\approx 5.6a\), where \(v_{F}\) is the Fermi velocity. Correspondingly, the relative phase \(\phi _{xy}=cos(\phi _{x}-\phi _{y})\) of the p-wave components \(\varDelta _{p_{x}}\) and \(\varDelta _{p_{y}}\) exhibits cloverleaf patterns [see column (II)]. Likewise, the quantized vortex states with point-like cores appear in the profiles of s- and d-wave components [see columns (III) and (IV)]. We also calculate the distribution of the zero-energy LDOS \(\rho (0)\) in column (V). One can find that the zero-bias LDOS comes to peaks around the vortex cores, indicating the occurrence of vortex bound states.

Notice that the configuration of the vortex lattice in our simulation with the periodic boundary condition deviates from the conventional triangular mode. This is similar to the results revealed in FeSe superconducting systems [29], resulting from the anisotropic interactions among the mixed superconducting orders. In the second and third rows of Fig. 1, we introduce two finite nnn hopping \(t'\) in the effective model Hamiltonian and plot the spatial order-parameter distributions when \(\varPhi /\varPhi _{0}\)=4. Notably, the ratio between nn and nnn hopping is an important electronic parameter characterizing different superconducting materials [47, 48]. In contrast to the case of \(t'=0\) in row (I) at the same flux value, the mixed parity pairings can still be realized for an increased \(t'=0.1\), while the s- and d-wave orders are suppressed. Four vortices located near the outer boundary move toward the center in \(\varDelta _{p}\), \(\varDelta _{s}\) and \(\varDelta _{d}\) plots. Namely, the vortex lattice structure tends to evolve into a triangular shape in the order-parameter space. Furthermore, in the case of \(t'=0.2\), one can easily find that the mixed s- and d-wave orders almost disappear inside the sample. As a consequence, two bottom vortices transit to an enclosed skyrmionic structure and a hybrid mode with skyrmionic and vortex states can be obtained, similar to the feature obtained in the pure chiral p-wave state [49]. In this case, the chiral domain walls separating \(\varDelta _{+}\) and \(\varDelta _{-}\) regions occur, which can be clearly revealed by the \(|\varDelta _{p}|\) profile in column (I). Different from the conventional Abrikosov flux, four one-component vortex cores in the \(p_{x}\)- and \(p_{y}\)-wave pairings are spatially separated on the domain wall for a single-skyrmionic structure, leading to a coreless vortex state carrying two flux quanta with the topological charge \(Q=2\) [21, 23, 24]. Correspondingly, the relative phase \(\phi _{xy}\) in column (II) alternates four times between negative and positive values for the enclosed chain. Moreover, from the spatial variation of \(\rho (0)\) depicted in column (V), the zero-energy peaks mainly emerge at the circular-loop-like domain walls as a result of the existence of domain-wall bound states.

Fig. 2
figure 2

Contour plots of \(|\varDelta _{p}|\) [column (I)], \(\phi _{xy}\) [column (II)], \(\varDelta _{s}\) [column (III)], \(\varDelta _{d}\) [column (IV)], and \(\rho (0)\) [column (V)] in a \(40\times 40\) lattice accommodating \(\varPhi =4\varPhi _{0}\) when \(t'=0\) (first row), \(t'=0.1\) (second row), and \(t'=0.2\) (third row). The chosen parameters are the same as in Fig. 1 except \({\mathbf {h}}_{z}=0.2\)

Full size image

Next, we would like to examine the configurations of topological defects at \(\varPhi =4\varPhi _{0}\) for a nonzero \({\mathbf {h}}_{z}=0.2\). It is noted that the Zeeman field has a particularly important effect on the spin structure of the Cooper pairs [34,35,36, 50, 51]. Figure 2 displays the spatial profiles of quantities same as in Fig. 1 when \(t'=0\) (first row), \(t'=0.1\) (second row), and \(t'=0.2\) (third row). Clearly, in contrast to the case of \({\mathbf {h}}_{z}=0\) with \(t'=0\) [first row in Fig. 1], four flux quanta in the multivortex state tend to move inside the sample and try to assemble a triangular-like vortex lattice when a Zeeman filed is included into the system. When the combined effect of nnn hopping and Zeeman field is presented, the situation becomes quite different resulting from the modification of the relative strength of competing pairing symmetries. With increasing the finite \(t'\), the system will gradually achieve its minimum free energy by further arranging the vortices. Consequently, the vortex lattice favors the triangular one for the case of \(t'=0.2\) [see the third row of Fig. 2]. Interestingly, an enlarged \(t'\) also results in the change in the vortex structure from isotropic to the twofold anisotropic. As seen from the \(|\varDelta _{p}|\) profile shown in the column (I), two diagonal (antidiagonal) vortices are stretched along the vertical (horizontal) direction, i.e., the elliptical-like vortices show up. Simultaneously, the s-wave and d-wave orders with an elliptical-like shape are only generated in the regions of the vortex cores, as displayed in the columns (III) and (IV). Moreover, the corresponding spatial variations of \(\phi _{xy}\) [column (II)] and \(\rho (0)\) [column (V)] are depicted, and one can clearly observe these unique vortex states.

Fig. 3
figure 3

Contour plots of \(|\varDelta _{p}|\) [column (I)], \(\phi _{xy}\) [column (II)], \(\varDelta _{s}\) [column (III)], \(\varDelta _{d}\) [column (IV)], and \(\rho (0)\) [column (V)] in a \(40\times 40\) lattice accommodating \(\varPhi =5\varPhi _{0}\) when \({\mathbf {h}}_{z}=0\) and \(t'=0\) (first row), \({\mathbf {h}}_{z}=0\) and \(t'=0.2\) (second row), \({\mathbf {h}}_{z}=0.2\) and \(t'=0\) (third row), as well as \({\mathbf {h}}_{z}=0.2\) and \(t'=0.2\) (fourth row). The other chosen parameters are the same as in Fig. 2

Full size image

In the following, we turn to discuss the vortical patterns when the applied magnetic flux is enlarged. For a perpendicular flux, \(\varPhi =5\varPhi _{0}\) when \({\mathbf {h}}_{z}=0\) and \(t'=0\), a multivortex state carrying singly quantized vortices still shows up as compared to the above \(4\varPhi _{0}\) case, and the general picture of this state is depicted in the first row of Fig. 3. To keep five flux quanta in a \(40\times 40\) square unit cell, a singular vortex with the point-like core always appears at the square corner [see the cloverleaf profiles of the relative phase in column (II)]. Meanwhile, the other four vortices move inside the square due to the repulsion effect from the corner vortices. Once the nnn hopping effect is considered, the mixed s-wave and d-wave pairing symmetries are highly suppressed, and a multiskyrmionic state tends to stabilize inside the unit cell. As seen in the second row of Fig. 3 when \(t'=0.2\), one can clearly find two separated enclosed chains along the vertical direction, that is, two coreless \(Q=2\) skyrmions carrying four flux quanta are formed. Notice that the enclosed skyrmionic chains, especially the upper one, are stretched along the horizontal direction. Consequently, the elliptical-loop-like skyrmionic configurations are obtained. One can also clearly see this pattern in the zero-energy LDOS profile shown in column (V).

Fig. 4
figure 4

Spatial profiles of the amplitude [columns (I) and (III)] and phase [columns (II) and (IV)] for the p-wave components \(\varDelta _{p_{x}}\) and \(\varDelta _{p_{y}}\) corresponding to the enclosed skyrmionic state with \({\mathbf {h}}_{z}=0\) and \(t'=0.2\) (the upper row) as well as the state with unclosed vortex chains (the bottom row)

Full size image

Furthermore, for a finite \({\mathbf {h}}_{z}=0.2\), another type of stable topological-defect states can be found in such systems, and the two bottom rows of Fig. 3 depict the corresponding evolution of this state with increasing \(t'\). Similar to the mode obtained in the first row of Fig. 2 when \(t'=0\), the singly quantized vortices tend to rearrange in the presence of finite \({\mathbf {h}}_{z}\). Remarkably, for the case of \(t'=0.2\), one can find that two unclosed vortex chains take place with comparison to the enclosed skyrmionic configuration. In Fig. 4, we also display the amplitude and phase for the \(p_{x}\) and \(p_{y}\) order-parameter components since they are very useful in the analysis of unique topological defect states. As clearly displayed in the upper row of Fig. 4 corresponding to the case of the second row in Fig. 3, four individual one-component vortices can exist inside \(\varDelta _{p_{x}}\) and \(\varDelta _{p_{y}}\), respectively. Consequently, all eight one-component vortices generate two separated enclosed chains carrying two flux quanta each. In contrast, for the case of \({\mathbf {h}}_{z}=0.2\) (the bottom row of Fig. 4), one can see that four one-component vortices inside \(\varDelta _{p_{y}}\) try to stretch along the horizontal direction and the four ones in \(\varDelta _{p_{x}}\) do not nucleate aligning along the vertical direction, giving rise to two separated horizontal vortex chains in the order-parameter space as shown in the third row of Fig. 3.

Fig. 5
figure 5

Contour plots of \(|\varDelta _{p}|\) [column (I)], \(\phi _{xy}\) [column (II)], \(\varDelta _{s}\) [column (III)], \(\varDelta _{d}\) [column (IV)], and \(\rho (0)\) [column (V)] in a \(40\times 40\) lattice accommodating \(\varPhi =6\varPhi _{0}\) when \({\mathbf {h}}_{z}=0\) and \(t'=0\) (first row), \({\mathbf {h}}_{z}=0\) and \(t'=0.2\) (second row), \({\mathbf {h}}_{z}=0.2\) and \(t'=0\) (third row), as well as \({\mathbf {h}}_{z}=0.2\) and \(t'=0.2\) (fourth row). The other chosen parameters are the same as in Fig. 2

Full size image

Finally, for further increased external flux, more vortices nucleate inside the present mixed-parity system and peculiar skyrmion-vortex coexisting modes can occur. In Fig. 5, we present the spatial distributions for such stable states when \(\varPhi /\varPhi _{0}=6\). Besides the multivortex states consisting of six singly quantized vortices, two types of hybrid topological structures are depicted for the \(t'=0.2\) cases when \({\mathbf {h}}_{z}=0\) (the second row) and \({\mathbf {h}}_{z}=0.2\) (the fourth row). Similar to the \(Q=2\) case, the \(\varDelta _{p_{x}}\) and \(\varDelta _{p_{y}}\) components of the order parameter both contain three (or five) vortices which do not overlap in space, leading to the occurrence of a single-skyrmionic pattern with a larger \(Q=3\) (or 5). Also, these hybrid states can be easily distinguished according to their signatures in the phase difference and LDOS plots.

4 Conclusions

In summary, we have investigated the spatial configurations of topological defects in bulk superconducting systems with mixed pairing orders by numerically solving the BdG equations self-consistently. The on-site repulsive interaction among the electrons is introduced into the model Hamiltonian, giving rise to the mixed spin-triplet (dominant p-wave) and spin-singlet (subdominant s-wave and coexisted d-wave) pairing symmetries by suitable choice of the chemical potential. The influences of the Zeeman field and the next-nearest-neighbor hopping on the order-parameter modulations are mainly discussed. With increasing the applied magnetic flux in a periodic unit cell, the quantized multivortex states with point-like cores and the coreless \(Q=2\) skyrmionic structures as well as their hybrid modes can remain stable in such mixed-parity systems. Interestingly, the unclosed vortex chains and enclosed skyrmionic modes with \(Q>2\) can be obtained when the external magnetic flux becomes stronger. In particular, nonuniform patterns of the vortex lattice and the elliptical-like vortices take place at appropriate perpendicular flux. All these topological configurations can be resolved by the zero-energy peaks in the LDOS plots. It is noted that using the tight-binding model allows us to take certain aspects of the real band structure into account. Our theoretical calculations may be useful for some materials containing several competing order parameters, such as the proximity-induced two-dimensional topological superconducting systems near the surface of \(s+d\) or \(s+id\) superconductors as well as the noncentrosymmetric superconductors in which the singlet and the triplet components are intrinsically mixed [52]. We expect that our theoretical results will be verified experimentally in the future.