1 Introduction

There are two types of superconductors depending on the surface energy between the normal and superconducting phases, which is positive when \(\kappa \equiv \lambda / \xi <1 / {\sqrt 2 }\) (type I) and negative for \(\kappa >1 / {\sqrt 2 }\) (type II) where λ is the penetration depth and ξ the coherence length. For type-II superconductors, a mixed state formed by vortices with superconducting quantum magnetic fluxes \(({\Phi }_{0} \equiv {\pi \hbar c} / e)\) appears when an external magnetic field with strength between B c1 and B c2 is applied. A triangular vortex lattice is obtained if one starts from an isotropic electronic model. However, in real superconductors, the crystalline symmetry can make the square vortex lattice more favorable, since the energy difference between these two lattices is very small [1].

Virtually all superconducting compounds are type-II superconductors including the ceramic high-temperature ones, which have d-wave superconducting gaps [2]. It would be important to study the effects of the superconducting gap symmetry on the vortex structure as well as on the mixed state superconducting gap. On the theoretical side, the Bogoliubov-de Gennes formalism [3] provides a microscopic description of the vortex formation, vortex symmetry, and interaction between vortices [4]. Moreover, the generalized Hubbard model, which includes on-site (U), nearest-neighbor (V), and correlated hopping (Δt) interactions, has been used to investigate s- and d-wave superconductivity [5]. In this work, we report an extension of the Bogoliubov-de Gennes formalism for the generalized Hubbard model and a comparative study of the effects of both the pairing interaction and symmetry on the vortex structure and superconducting gap.

2 The Model

Let us consider a single-band Hubbard Hamiltonian on a square lattice given by [6]

$$\begin{array}{@{}rcl@{}} \hat{{H}}&=&t\sum\limits_{\left\langle {l,j} \right\rangle ,\sigma } {\hat{{c}}_{l,\sigma }^{\dag } \hat{{c}}_{j,\sigma } } +U\sum\limits_{l} {\hat{{n}}_{l,\uparrow } \hat{{n}}_{l,\downarrow } } +\frac{V}{2}\sum\limits_{\left\langle {l,j} \right\rangle } {\hat{{n}}_{l} {\kern 1pt}\hat{{n}}_{j} } \\&&+{\Delta} t\sum\limits_{\left\langle {l,j} \right\rangle ,\sigma } {\hat{{c}}_{l,\sigma }^{\dag } \hat{{c}}_{j,\sigma } \left( {\hat{{n}}_{l,-\sigma } {\kern 1pt}+\hat{{n}}_{j,-\sigma } } \right)} \end{array} $$
(1)

where \(\hat {{c}}_{j,\sigma }^{\dag } (\hat {{c}}_{j,\sigma } )\) is the creation (annihilation) operator with spin σ = ↑or↓ at site j, \(\hat {{n}}_{j,\sigma } =\hat {{c}}_{j,\sigma }^{\dag } {\kern 1pt}\hat {{c}}_{j,\sigma } \), \(\hat {{n}}_{j} =\hat {{n}}_{j,\uparrow } +\hat {{n}}_{j,\downarrow } \), and 〈l, j〉 denote nearest-neighbor sites. For a singlet superconductor with uniform electronic charge and spin densities in an external magnetic field (B = ∇ × A), Hamiltonian (1) in the mean-field approximation can be written as

$$\begin{array}{@{}rcl@{}} \hat{{H}}_{\text{MF}} {\kern 1pt}&=&\varepsilon_{0} {\kern 1pt}+\varepsilon \sum\limits_{l,\sigma } {\hat{{c}}_{l,\sigma }^{\dag } \hat{{c}}_{l,\sigma } } +\sum\limits_{<l,j>,\sigma } {t_{l,j} \hat{{c}}_{l,\sigma }^{\dag } \hat{{c}}_{j,\sigma } } \\&&+{\kern 1pt}\sum\limits_{j} {({\Delta}_{j,j}^{\ast } \hat{{c}}_{j,\downarrow } \hat{{c}}_{j,\uparrow } +{\Delta}_{j,j} \hat{{c}}_{j,\uparrow }^{\dag } \hat{{c}}_{j,\downarrow }^{\dag } )} \\&&+\sum\limits_{<l,j>} {({\Delta}_{l,j}^{\ast } \hat{{c}}_{j,\downarrow } \hat{{c}}_{l,\uparrow } +{\Delta}_{j,l} \hat{{c}}_{l,\uparrow }^{\dag } \hat{{c}}_{j,\downarrow }^{\dag } )} , \end{array} $$
(2)

where \(\varepsilon _{0} \,=\,-N_{\mathrm {S}} \left ({\frac {U}{4}+2V} \right )n^{2}{\kern 1pt}\,-\,2{\Delta } t\sum \limits _{<l,j>}{({\Lambda }_{l,{\kern 1pt}l}^{\ast } {\Lambda }_{l,j}+{\Lambda }_{l,l} }\) \({{\Lambda }_{l,j}^{\ast } )} \), \(\varepsilon =\frac {U}{2}n+4Vn\),

$$ t_{l,j} =(t+n{\Delta} t)\exp \left( {-\frac{i\pi }{{\Phi}_{0} }{\int}_{\mathbf{R}_{l} }^{\mathbf{R}_{j} } {\mathbf{A}(\mathbf{r})\cdot d\mathbf{r}} } \right), $$
(3)
$$ {\Delta}_{l,{\kern 1pt}l} =U{\Lambda}_{l,{\kern 1pt}l} +2{\Delta} t\sum\nolimits_{j} {{\Lambda}_{l,j} } ,\; \text{and}\; {\Delta}_{l,j} =V{\Lambda}_{j,{\kern 1pt}l} +{\Delta} t({\Lambda}_{l,l} +{\Lambda}_{j,j} ), $$
(4)

being \(n=\left \langle {\hat {{c}}_{j,\uparrow }^{\dag } \hat {{c}}_{j,\uparrow } } \right \rangle +\left \langle {\hat {{c}}_{j,\downarrow }^{\dag } \hat {{c}}_{j,\downarrow } } \right \rangle \), N S the total number of sites and

$$\begin{array}{@{}rcl@{}} {\Lambda}_{l,j} &=&\left\langle {\hat{{c}}_{l,\downarrow } \hat{{c}}_{j,\uparrow } } \right\rangle =-\left\langle {\hat{{c}}_{j,\uparrow } \hat{{c}}_{l,\downarrow } } \right\rangle \\&=&-\frac{1}{2}\sum\limits_{\alpha} {(u_{l}^{\alpha } \mathit{v}_{j}^{\alpha \ast } +u_{j}^{\alpha } \mathit{v}_{l}^{\alpha \ast } )} \tanh \left( {\frac{E^{\alpha }}{2k_{B} T}} \right). \end{array} $$
(5)

Applying the following unitary transformation

$$\begin{array}{@{}rcl@{}} \hat{{c}}_{j,\uparrow } &=&\sum\nolimits_{\alpha} {(u_{j}^{\alpha } \hat{{\gamma }}_{\alpha ,\uparrow } -\mathit{v}_{j}^{\alpha \ast } \hat{{\gamma }}_{\alpha ,\downarrow }^{\dag } )} ,\nonumber\\ \hat{{c}}_{j,\downarrow } &=&\sum\nolimits_{\alpha} {(u_{j}^{\alpha } \hat{{\gamma }}_{\alpha ,\downarrow } +\mathit{v}_{j}^{\alpha \ast } \hat{{\gamma }}_{\alpha ,\uparrow }^{\dag } )} , \end{array} $$
(6)

and the supercell technique by rewriting [7]

$$ \left( {{\begin{array}{*{20}c} {u_{j}^{\alpha } } \\ {\mathit{v}_{j}^{\alpha } } \end{array} }} \right)\Rightarrow e^{i\,\mathbf{k}\cdot \mathbf{r}_{j} }\left( {{\begin{array}{*{20}c} {u_{j}^{\alpha } (\mathbf{k})} \\ {\mathit{v}_{j}^{\alpha } (\mathbf{k})} \end{array} }} \right), $$
(7)

the Bogoliubov-de Gennes equations for \(u_{j}^{\alpha } (\mathbf {k})\) and \(v_{j}^{\alpha } (\mathbf {k})\) are

$$ \sum\limits_{j} {e^{i\,\mathbf{k}\cdot (\mathbf{r}_{j} -\mathbf{r}_{l} )}\left( {{\begin{array}{*{20}c} {H_{l,j} } & {{\Delta}_{l,j} } \\ {{\Delta}_{l,j}^{\ast } } & {-H_{l,j}^{\ast } } \end{array} }} \right)\left( {{\begin{array}{*{20}c} {u_{j}^{\alpha } (\mathbf{k})} \\ {\mathit{v}_{j}^{\alpha } (\mathbf{k})} \end{array} }} \right)} =E^{\alpha }(\mathbf{k})\left( {{\begin{array}{*{20}c} {u_{l}^{\alpha } (\mathbf{k})} \\ {\mathit{v}_{l}^{\alpha } (\mathbf{k})} \end{array} }} \right) $$
(8)

where subscripts l and j denote the sites of a N × N supercell, H l, j = ε δ l, j + t l, j , and Δ l, j is given by (4) with

$$\begin{array}{@{}rcl@{}} {\Lambda}_{l,j} &=&-\frac{1}{2}\sum\limits_{\alpha ,\mathbf{k}} {\left[ {u_{l}^{\alpha } (\mathbf{k})\,\mathit{v}_{j}^{\alpha \ast } (\mathbf{k})\,e^{-i{\kern 1pt}\mathbf{k}\cdot (\mathbf{r}_{j} -\mathbf{r}_{l} )}+u_{j}^{\alpha } (\mathbf{k})\,\mathit{v}_{l}^{\alpha \ast } (\mathbf{k})\,e^{i{\kern 1pt}\mathbf{k}\cdot (\mathbf{r}_{j} -\mathbf{r}_{l} )}} \right]}\\ &&\times\tanh \left( {\frac{E^{\alpha }(\mathbf{k})}{2k_{B} T}} \right). \end{array} $$
(9)

The local s-wave \(({{\Delta }_{l}^{s}} )\), anisotropic s-wave \(({\Delta }_{l}^{s\ast } )\), and d-wave \(({{\Delta }_{l}^{d}} )\) superconducting gaps can be written [4, 5] as \({{\Delta }_{l}^{s}} ={\Delta }_{l,l} \), \({\Delta }_{l}^{s\ast } =\frac {1}{4}\sum \nolimits _{j} {{\Delta }_{l,j} } \), and \({{\Delta }_{l}^{d}} =\frac {1}{4}\sum \nolimits _{j} {(-1)^{\gamma _{l,j} }{\Delta }_{l,j} } \), where the sum is over the nearest-neighbors of site l, \(\gamma _{l,j} {\kern 1pt}={\left | {\mathbf {r}_{l,j} \cdot \hat {\mathbf {e}}_{y} } \right |} / a\) and a is the lattice parameter. Equation (8) allows to determine the spatial variation of the superconducting gaps as a function of the electron concentration for a given applied magnetic field.

3 Results and Discussion

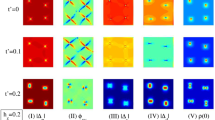
Equations (8) were self-consistently solved for s-, s*-, and d-wave superconducting gaps, respectively, induced by U, Δt, and V, starting from a homogeneous gap seed. We considered N × N-atom supercells containing two quantum fluxes at T = 0 K that corresponds to an external magnetic field (B) perpendicular to the square lattice given by B = 2Φ0/(N a)2 and a vector potential obtained by the symmetric gauge A = B × r/2. Figure 1a with B = 0 and Fig. 1b with B = 2Φ0/(13a)2, corresponding to a supercell of 13 × 13 atoms, show the supercell averaged superconducting gap amplitudes (< |Δ η | >) as functions of the electron density (n) for η = s induced by U = −1.09|t|, η = s by Δt = 0.225|t|, η = s* by Δt = 0.225|t|, and η = d by V = −|t|. The values of these interaction parameters were chosen to give the same maximum < |Δ η | >. For each case, the other electron-electron interactions in Hamiltonian (1) were taken equal to zero. Observe the significant reduction of the superconducting zones when a magnetic field is applied, being more pronounced for s-wave than d-wave.

Fig. 1
figure 1

Real-space averaged superconducting gap amplitudes (<|Δ η |>) as a function of the electron density (n) for s-, s*-, and d-wave symmetries a without and b with applied magnetic field (B)

Full size image

Figure 2 illustrates the variation of maximum < |Δ η | > at the optimal electronic density (n op) with the magnetic field strength (B) for (a) η = s induced by U = −1.09|t|, (b) η = s by Δt = 0.225|t|, (c) η = s* by Δt = 0.225|t|, and (d) η = d by V = −|t|. Notice that both isotropic and anisotropic s-wave superconducting gaps vanish around B a 2/Φ0 ≈ 0.04, whereas the d-wave superconducting gap remains about 60 % of its zero-field value. This fact is consistent with the experimental data of high- T c ceramic superconductors having B c2 higher than 100 T at optimal doping, as occurs in YBa2Cu3 O y [8].

Fig. 2
figure 2

Real-space averaged superconducting gap amplitude (<|Δ η |>) at the optimum electron concentration (n op) as a function of the magnetic field (B) for a η = s with \(n_{\text {op}} {\kern 1pt}=1\), b η = s with \(n_{\text {op}} {\kern 1pt}=1.82\), c η = s* with \(n_{\text {op}} {\kern 1pt}=1.82\), and d η = dwith \(n_{\text {op}} {\kern 1pt}=1\)

Full size image

The local superconducting gaps in a 19 × 19-atom supercell are shown in Fig. 3a–d for the same cases as in Fig. 2a–d with B = 2Φ0/(19a)2.

Fig. 3
figure 3

a–d Spatial distribution of the superconducting gap amplitude (<|Δ η |>) in a 19 × 19-atom supercell under an applied magnetic field \(B={2{\Phi }_{0} } / {(19a)}^{2}\) for the same cases as in Fig. 2

Full size image

It would be worth mentioning that these spatial distributions of superconducting gaps with applied magnetic field in Fig. 3 were spontaneously obtained from an initial homogenous gap distribution that corresponds to the zero magnetic field case, and (8) is then self-consistently solved.

4 Conclusions

In this article, we report a systematic study of the effects of applied magnetic field strength on isotropic and anisotropic superconducting gaps, through varying the size of square-lattice supercells. This study was carried out by using the Hubbard model within the Bogoliubov-de Gennes formalism. The attractive on-site (U) Hubbard model has been used to describe s-wave superconductors [9], whereas the repulsive U and attractive nearest-neighbor (V) electron-electron interactions have been successfully used to reproduce the antiferromagnetic-superconducting phase diagram for both electron-doped (Nd2−x Ce x CuO4−y ) and hole doped (La2−x Sr x CuO4−y ) d-wave superconductors [10].

The results of this work show that d-wave superconductors have upper critical magnetic fields (B c2) significantly larger than those of both isotropic and anisotropic s-wave ones with the same superconducting gap amplitude as d-wave systems in the absence of external magnetic field. This fact could be related to the phase change in the hopping integral induced by the magnetic field that is less harmful for anisotropic superconductors. Moreover, for small magnetic fields, the superconductivity induced by density-density interactions is more depleted than that induced by correlated hopping ones.