Kinetic Transport Coefficients through a Bilayer Ion Exchange Membrane during Electrodiffusion

Abstract

Analytical expressions for the specific coefficients of electrical conductivity and electrodiffusion of a bilayer ion exchange membrane have been obtained in terms of thermodynamics of irreversible processes and the homogeneous model of a fine-pore membrane. The influence of the physicochemical parameters of the modifying layer and the electrolyte concentration on the obtained values of the coefficients at fixed physicochemical characteristics of the substrate has been explored using mathematical modeling. It has been shown that the conductivity and electrodiffusion of the modified membrane increase with increasing the space charge density of the modifying layer when the signs of the space charges of the membrane layers are identical and decrease when they differ or the thickness of the modifying layer increases. With increasing electrolyte concentration, these characteristics of the modified membrane increase regardless of the sign of charges of the membrane layers. The obtained analytical expressions can be used in modeling electromembrane processes and predicting the characteristics of new surface-modified ion exchange membranes.

INTRODUCTION

The knowledge of analytical relationships between the kinetic coefficients of electrolyte transport through an ion exchange membrane (IEM) and its physicochemical characteristics (charge density, ion diffusion coefficients, etc.) makes it possible to evaluate and predict the performance of ion exchange membranes used in electromembrane processes and systems, such as electrodialysis [1–3], membrane electrolysis [4], and fuel cells [5–7], without resorting to complicated and time-consuming experiments. To find the kinetic transport coefficients in IEMs, nonequilibrium thermodynamics (NET) is commonly used, in which transport fluxes across an IEM under isothermal conditions are described by the linear Onsager equations [8–10]

$$\left\{ {\begin{array}{*{20}{c}} {{{J}_{{\text{w}}}} = {{{{L}_{{11}}}\Delta p} \mathord{\left/ {\vphantom {{{{L}_{{11}}}\Delta p} h}} \right. \kern-0em} h} + {{{{L}_{{12}}}\Delta \varphi } \mathord{\left/ {\vphantom {{{{L}_{{12}}}\Delta \varphi } h}} \right. \kern-0em} h} + {{{{L}_{{13}}}\Delta c} \mathord{\left/ {\vphantom {{{{L}_{{13}}}\Delta c} h}} \right. \kern-0em} h}} \\ {I = {{{{L}_{{21}}}\Delta p} \mathord{\left/ {\vphantom {{{{L}_{{21}}}\Delta p} h}} \right. \kern-0em} h} + {{{{L}_{{22}}}\Delta \varphi } \mathord{\left/ {\vphantom {{{{L}_{{22}}}\Delta \varphi } h}} \right. \kern-0em} h} + {{{{L}_{{23}}}\Delta c} \mathord{\left/ {\vphantom {{{{L}_{{23}}}\Delta c} h}} \right. \kern-0em} h}} \\ {{{J}_{{\text{d}}}} = {{{{L}_{{31}}}\Delta p} \mathord{\left/ {\vphantom {{{{L}_{{31}}}\Delta p} h}} \right. \kern-0em} h} + {{{{L}_{{32}}}\Delta \varphi } \mathord{\left/ {\vphantom {{{{L}_{{32}}}\Delta \varphi } h}} \right. \kern-0em} h} + {{{{L}_{{33}}}\Delta c} \mathord{\left/ {\vphantom {{{{L}_{{33}}}\Delta c} h}} \right. \kern-0em} h}} \end{array}} \right.,$$

(1)

where L_ij are the phenomenological kinetic Onsager transport coefficients; ∆p, ∆φ, and ∆c are the pressure, electrical potential, and concentration drops across the IEM, respectively; J_w and J_d are respectively the specific solvent and solute fluxes; I is the electric current density through the IEM, and h is the membrane thickness.

Note that it is impossible to directly obtain an explicit analytical form of phenomenological transport coefficients from system (1); for this purpose, some model of an ion exchange membrane has to be specified. Here we assume that the transport of ions of the electrolyte in question is described by the known homogeneous model of a fine-pore membrane (Nernst–Planck equations without taking account of convection with the corresponding boundary conditions and the electrical neutrality condition [9, 10]). To take into account the charge distribution in the IEM, one of two approaches is used. Within the framework of the phenomenological approach, the porous structure of the IEM is not specified and the charge of the membrane is formally characterized by space charge density ρ. Another approach uses IEM structural models, such as the charged pore model [11, 12], cell model [13, 14], microheterogeneous model [15, 16], and percolation theory-based models [17–19] that are detailed and analyzed in [3, 9, 10]. It should be noted that these models contain many structural IEM parameters, whose values are not always determinable without the use of additional experimental data. Thus, analytical expressions for the Onsager coefficients in terms of the microheterogeneous [15, 16, 20, 21] and cell [22–24] models contain six physicochemical parameters and the values of the Onsager coefficients in the case of the charged pore model [11, 12] can only be obtained numerically [25‒27]. Note also that almost all works on finding analytical transport coefficients were carried out only for a single-layer IEM.

Currently, in connection with intensive work on the surface modification of ion exchange membranes (SMIEM) [28–33], there is a demanding task that has barely been tackled until now to look for analytical expressions for kinetic transport coefficients across bilayer membranes.

The purpose of this work is to find analytical expressions for two kinetic transport coefficients of SMIEM (L₂₂ and L₃₂) depending on the electrolyte concentration, geometry, and physicochemical characteristics of the modifying layer (ML) of a bilayer SMIEM in terms of the nonequilibrium thermodynamics on the basis of the homogeneous model without taking into account the IEM structure.

GENERAL FORMULATION OF THE PROBLEM

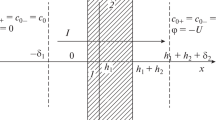
Let us consider the steady-state process of electrodiffusion of 1 : 1 electrolyte ions under an applied external electric field (voltage drop U is specified, and pressure and concentration drops are zero) through a surface-modified membrane (SMIEM) consisting of two layers, the initial ion exchange membrane itself (hereinafter called ion exchange layer 2 or substrate) (h₁ < x < h₁ + h₂) with a constant space charge density (−ρ₂) and modifying layer 1 (0 < x < h₁) applied onto one of the IEM surfaces and having a space density of fixed charges (−ρ₁) constant over the thickness. For definiteness, we will assume that the initial ion exchange membrane (layer 2) is a cation exchange membrane (Fig. 1). We neglect both the electroosmotic transport of the solvent through the ion exchange membrane and convective ion flows due to their smallness.

Fig. 1.

Scheme of electrodiffusion through a bilayer cation exchange membrane (MB) with adjacent diffuse layers (DL): (1) modifying layer with a thickness h₁, and (2) ion exchange layer (ion exchange membrane–substrate) with a thickness h₂; δ₁ and δ₂ are the thicknesses of the diffuse layers.

In both areas of intense mixing of the solution, the ion concentrations are constant and equal to each other: ${{c}_{0}} \equiv {{c}_{{0 + }}} = {{c}_{{0 - }}}$ at $x\left\langle { - {{{{\delta }}}_{1}};x} \right\rangle {{h}_{1}} + {{h}_{2}} + {{{{\delta }}}_{2}}$, where ± refer to cations and anions and c₀ is the electrolyte concentration in the regions of intense mixing of the solution.

We will assume that the characteristic pore size is much smaller than the membrane thickness, but much larger than the Debye parameter (thickness of the electrical double layer). In addition, for simplicity of calculations, the diffusion coefficients of anions and cations in each layer are assumed to be the same $D \equiv {{D}_{ + }} = {{D}_{ - }},$ ${{D}_{{m1}}} \equiv {{D}_{{m1 + }}} = {{D}_{{m1 - }}},$${{D}_{{m2}}} \equiv {{D}_{{m2 + }}} = {{D}_{{m2 - }}}$ (where D, D_m1, and D_m2 are the diffusion coefficients of the electrolyte molecule in the bulk solution and membrane layers, respectively).

In [35], it is shown that within the framework of the assumptions made, ion transport in the given membrane system is described in dimensionless variables by a closed system of equations (2)–(8), with the ion fluxes in diffusion layers and in the membrane layers being described by the Nernst–Planck equations:

$$\begin{gathered} {{j}_{ \pm }} = - \left( {\frac{{d{{\xi }_{ \pm }}}}{{dy}} \pm {{\xi }_{ \pm }}\frac{{d\varphi }}{{dy}}} \right);\,\,\,\, \\ - {{\Delta }_{1}} < y < 0,\,\,\,\,1 < y < 1 + {{\Delta }_{2}}, \\ \end{gathered} $$

(2)

$${{j}_{ \pm }}{{\nu }_{{m1}}} = - \left( {\frac{{d{{\xi }_{ \pm }}}}{{dy}} \pm {{\xi }_{ \pm }}\frac{{d\varphi }}{{dy}}} \right);\,\,\,\,0 < y < \frac{1}{{1 + H}},$$

(3)

$${{j}_{ \pm }}{{\nu }_{{m2}}} = - \left( {\frac{{d{{\xi }_{ \pm }}}}{{dy}} \pm {{\xi }_{ \pm }}\frac{{d\varphi }}{{dy}}} \right);\,\,\,\,\frac{1}{{1 + H}} < y < 1.$$

(4)

In this case, the conditions of electrical neutrality hold in the diffuse layers:

$${{\xi }_{ + }}\left( y \right) = {{\xi }_{ - }}\left( y \right);\,\,\,\, - {{\Delta }_{1}} < y < 0,\,\,\,\,1 < y < 1 + {{\Delta }_{2}},$$

(5)

and in the membrane layers:

$$\begin{gathered} {{\xi }_{ + }}\left( y \right) = {{\xi }_{ - }}\left( y \right) + {{\sigma }_{1}};\,\,\,\,0 \leqslant y \leqslant \frac{1}{{1 + H}}, \\ {{\xi }_{ + }}\left( y \right) = {{\xi }_{ - }}\left( y \right) + {{\sigma }_{2}};\,\,\,\,\frac{1}{{1 + H}} \leqslant y \leqslant 1. \\ \end{gathered} $$

(6)

The conditions for equality of electrochemical potentials of ions at the interfaces of the membrane layers and the solution/membrane interfaces (x = 0, x = h₁, x = h₁ + h₂) are written as follows:

$$\begin{gathered} {{\xi }_{ + }}\left( { - 0} \right) = {{\xi }_{ + }}\left( { + 0} \right){{\gamma }_{{1 + }}}\exp (\Delta {{\varphi }_{0}}), \\ {{\xi }_{ - }}\left( { - 0} \right) = {{\xi }_{ - }}\left( { + 0} \right){{\gamma }_{{1 - }}}\exp ( - \Delta {{\varphi }_{0}}), \\ {{\xi }_{ + }}\left( {\frac{1}{{1 + H}} - 0} \right){{\gamma }_{{1 + }}}\exp ( - \Delta {{\varphi }_{1}}) = {{\xi }_{ + }}\left( {\frac{1}{{1 + H}} + 0} \right){{\gamma }_{{2 + }}}, \\ {{\xi }_{ - }}\left( {\frac{1}{{1 + H}} - 0} \right){{\gamma }_{{1 - }}}\exp (\Delta {{\varphi }_{1}}) = {{\xi }_{ - }}\left( {\frac{1}{{1 + H}} + 0} \right){{\gamma }_{{2 - }}}, \\ {{\xi }_{ + }}\left( {1 - 0} \right){{\gamma }_{{1 + }}}\exp ( - \Delta {{\varphi }_{2}}) = {{\xi }_{ + }}\left( {1 + 0} \right), \\ {{\xi }_{ - }}\left( {1 - 0} \right){{\gamma }_{{1 - }}}\exp (\Delta {{\varphi }_{2}}) = {{\xi }_{ - }}\left( {1 + 0} \right). \\ \end{gathered} $$

(7)

The continuity conditions for concentrations and electric potential at the boundary of diffusion layers have the form:

$$\begin{gathered} {{\xi }_{ \pm }}\left( { - {{\Delta }_{1}}} \right) = {{\xi }_{ \pm }}\left( {1 + {{\Delta }_{2}}} \right) = 1,\,\,\,\,\varphi \left( { - {{\Delta }_{1}}} \right) = 0, \\ \varphi \left( {1 + {{\Delta }_{2}}} \right) = - u, \\ \end{gathered} $$

(8)

where ${{\xi }_{ \pm }} = \frac{{{{c}_{ \pm }}}}{{{{c}_{0}}}},$ $~\xi = {{\xi }_{ + }} + {{\xi }_{ - }},$ ${{j}_{ \pm }} = \frac{{{{J}_{ \pm }}\left( {{{h}_{1}} + {{h}_{2}}} \right)}}{{D{{C}_{0}}}},$ $i = \frac{{I\left( {{{h}_{1}} + {{h}_{2}}} \right)}}{{{{c}_{0}}FD}},$ $i = {{j}_{ + }} - {{j}_{ - }},$ $~H = \frac{{{{h}_{2}}}}{{{{h}_{1}}}} > 1,$ ${{\Delta }_{{1,2}}} = \frac{{{{\delta }_{{1,2}}}}}{{{{h}_{1}} + {{h}_{2}}}},$ ${{\sigma }_{{1,2}}} = \frac{{{{\rho }_{{1,2}}}}}{{F{{c}_{0}}}},$ ${{\nu }_{{m1,m2}}} = \frac{D}{{{{D}_{{m1,m2}}}}},$ $~{{\gamma }_{{1 \pm }}},$ ${{\gamma }_{{2 \pm ~}}}$ are the coefficients of the equilibrium distribution of ions in the membrane layers, ${{{{\gamma }}}_{1}} = \sqrt {{{{{\gamma }}}_{{1 + }}}{{{{\gamma }}}_{{1 - }}}} ,$ ${{{{\gamma }}}_{2}} = \sqrt {{{{{\gamma }}}_{{2 + }}}{{{{\gamma }}}_{{2 - }}}} ,$ φ is the dimensionless electric potential in RT/F units (F is the Faraday number, R is the universal gas constant, T is the absolute temperature), $y = \frac{x}{{{{h}_{1}} + {{h}_{2}}}},$ x is the coordinate normal to the membrane surface and directed along the outer electric field; ∆φ₀, ∆φ₁, and ∆φ₂ are the dimensionless electric potential drops across the membrane surface x = 0, x = h₁, and x = h₁ + h₂; $u = \frac{{FU}}{{RT}}$ is the dimensionless electric voltage in the system; and σ = σ₁ at $0 < y < \frac{1}{{1 + H}}$ and σ = σ₂ at $\frac{1}{{1 + H}} < y < 1$ are the dimensionless densities of fixed charges in the ML and IEM (substrate), respectively.

For the convenience of solving the boundary problem (2)–(8), instead of unknown constant ion flux densities j_±, we will use the dimensionless electric current density i = j₊ − j₋ and the salt flux density j = j₊ + j₋.

In [35], we obtained a general solution to the above boundary problem with allowance for the finiteness of the diffuse layers at ∆c = 0 and ∆p = 0. In this study we will consider the case when the resistances of the diffuse layers can be neglected ∆₁ = ∆₂ = 0. Then, as shown in [36], the solution to system (2)–(8) takes the form

$$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi } + j\frac{{{{{\bar {\nu }}}_{{m1}}}}}{{1 + H}} = \sqrt {\bar {\sigma }_{1}^{2} + 4} + \frac{i}{j}{{\bar {\sigma }}_{1}}\ln \frac{{\sqrt {\bar {\sigma }_{1}^{2} + 4} - \frac{i}{j}{{{\bar {\sigma }}}_{1}}}}{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi } - \frac{i}{j}{{{\bar {\sigma }}}_{1}}}},$$

(9)

$$\bar {\xi } - j\frac{{{{{\bar {\nu }}}_{{m2}}}H}}{{1 + H}} = \sqrt {\bar {\sigma }_{2}^{2} + 4} + \frac{i}{j}{{\bar {\sigma }}_{2}}\ln \frac{{\sqrt {\bar {\sigma }_{2}^{2} + 4} - \frac{i}{j}{{{\bar {\sigma }}}_{2}}}}{{\bar {\xi } - \frac{i}{j}{{{\bar {\sigma }}}_{2}}}},$$

(10)

$$\begin{gathered} u = \ln \frac{{\bar {\xi } + {{{\bar {\sigma }}}_{2}}}}{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi } + {{{\bar {\sigma }}}_{1}}}} + \ln \frac{{\sqrt {\bar {\sigma }_{2}^{2} + 4} - {{{\bar {\sigma }}}_{2}}}}{{\sqrt {\bar {\sigma }_{1}^{2} + 4} - {{{\bar {\sigma }}}_{1}}}} \\ - \,\,\frac{i}{j}{{{\bar {\sigma }}}_{2}}\ln \frac{{\sqrt {\bar {\sigma }_{2}^{2} + 4} - \frac{i}{j}{{{\bar {\sigma }}}_{2}}}}{{\bar {\xi } - \frac{i}{j}{{{\bar {\sigma }}}_{2}}}} + \frac{i}{j}{{{\bar {\sigma }}}_{1}}\ln \frac{{\sqrt {\bar {\sigma }_{1}^{2} + 4} - \frac{i}{j}{{{\bar {\sigma }}}_{1}}}}{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi } - \frac{i}{j}{{{\bar {\sigma }}}_{1}}}}, \\ \end{gathered} $$

(11)

$${{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi } }^{2}} - \bar {\sigma }_{1}^{2} = {{\bar {\xi }}^{2}} - \bar {\sigma }_{2}^{2},$$

(12)

$$\begin{gathered} {{\varphi }_{1}} = \frac{{\sqrt {\sigma _{1}^{2} + k_{1}^{2}} - \xi - {{\nu }_{{m1}}}jy}}{{{{\sigma }_{1}}}} + \frac{i}{j}\ln \frac{{{{\gamma }_{1}}{{k}_{1}}}}{2} \\ - \,\,\ln \left( {{{\gamma }_{{1 + }}}\frac{{{{\sigma }_{1}} + \sqrt {\sigma _{1}^{2} + k_{1}^{2}} }}{{{{\gamma }_{1}}{{k}_{1}}}}} \right), \\ \end{gathered} $$

(13)

$$\begin{gathered} {{\varphi }_{2}} = \frac{{\sqrt {\sigma _{2}^{2} + k_{2}^{2}} - \xi + {{\nu }_{{m2}}}j\left( {1 - y} \right)}}{{{{\sigma }_{2}}}} + \frac{i}{j}\ln \frac{{{{\gamma }_{2}}{{k}_{2}}}}{2} \\ - \,\,\ln \left( {{{\gamma }_{{2 + }}}\frac{{{{\sigma }_{2}} + \sqrt {\sigma _{2}^{2} + k_{2}^{2}} }}{{{{\gamma }_{2}}{{k}_{2}}}}} \right) - u, \\ \end{gathered} $$

(14)

where $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi } = {{\gamma }_{1}}\xi \left( {\frac{1}{{1 + H}} - 0} \right),$ $\bar {\xi } = {{\gamma }_{2}}\xi \left( {\frac{1}{{1 + H}} + 0} \right),$ ${{\bar {\sigma }}_{1}} = {{\gamma }_{1}}{{\sigma }_{1}},$ ${{\bar {\sigma }}_{2}} = {{\gamma }_{2}}{{\sigma }_{2}}.$ ${{\bar {\nu }}_{{m1}}} = {{\gamma }_{1}}{{\nu }_{{m1}}}$, ${{\bar {\nu }}_{{m2}}} = {{\gamma }_{2}}{{\nu }_{{m2}}}$, where $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\xi } = {{\gamma }_{1}}\xi \left( {\frac{1}{{1 + H}} - 0} \right),$ $\bar {\xi } = {{\gamma }_{2}}\xi \left( {\frac{1}{{1 + H}} + 0} \right),$ ${{\bar {\sigma }}_{1}} = {{\gamma }_{1}}{{\sigma }_{1}},$ ${{\bar {\sigma }}_{2}} = {{\gamma }_{2}}{{\sigma }_{2}}.$ ${{\bar {\nu }}_{{m1}}} = {{\gamma }_{1}}{{\nu }_{{m1}}}$, ${{\bar {\nu }}_{{m2}}} = {{\gamma }_{2}}{{\nu }_{{m2}}}$, and φ₁ and φ₂ are respectively the dimensionless electric potentials in the first and second layers.

To find analytical expressions for the transport coefficients, consider the case of low currents (i.e., i $\ll$ 1). Taking into account the given expressions (9)–(14) in this approximation, the following relations were obtained in [36]:

$$\Delta t = \frac{{\left( {{{R}_{2}}{{{\bar {\sigma }}}_{2}} + {{R}_{1}}{{{\bar {\sigma }}}_{1}}} \right)}}{{2\left[ {{{R}_{2}}\sqrt {\bar {\sigma }_{2}^{2} + 4} + {{R}_{1}}\sqrt {\bar {\sigma }_{1}^{2} + 4} } \right]}},$$

(15)

$$U = I\left( {{{\alpha }_{1}}{{R}_{1}} + {{\alpha }_{2}}{{R}_{2}}} \right),$$

(16)

where $\rho = \frac{{RT}}{{{{c}_{0}}{{F}^{2}}D}},$ ${{R}_{2}} = \rho {{\bar {\nu }}_{{m2}}}{{h}_{2}}$, ${{R}_{1}} = \rho {{\bar {\nu }}_{{m1}}}{{h}_{1}},$ α₁ = $\frac{{\left( {2\Delta t + 1} \right)\left( {\sqrt {\bar {\sigma }_{1}^{2} + 4} - {{{\bar {\sigma }}}_{1}}} \right)}}{4}$, ${{\alpha }_{2}} = \frac{{\left( {2\Delta t + 1} \right)\left( {\sqrt {\bar {\sigma }_{2}^{2} + 4} - {{{\bar {\sigma }}}_{2}}} \right)}}{4},$ U and I are respectively the dimensional voltage and current density, R_mc = (α₁R₁ + α₂R₂) is the resistance of the bilayer membrane, $\Delta t = \frac{I}{{2J}}$, and J is the dimensional salt flux.

We will assume that linear expressions for Onsager fluxes (1) also hold in the case of bilayer SMIEM. Since ∆c = 0 and ∆p = 0 within the framework of this consideration, then the current density through the SMIEM is given by

$$I = {{L}_{{22}}}\frac{U}{h}.$$

(17)

as follows from the second relation of system (1). Substituting Eq. (16) into (17), we get

$${{L}_{{22}}} = \frac{h}{{({{\alpha }_{1}}{{R}_{1}} + {{\alpha }_{2}}{{R}_{2}})}} = \frac{h}{{{{R}_{{mc}}}}}.$$

(18)

Similarly, from the third equation of system (1) follows the relation

$$J = {{L}_{{32}}}\frac{U}{h}.$$

(19)

Taking into account Eqs. (17) and (19), we obtain from Eq. (15) that

$$\Delta t = \frac{j}{{2i}} = \frac{{JF}}{{2I}} = \frac{{{{L}_{{32}}}F\frac{U}{h}}}{{2{{L}_{{22}}}\frac{U}{h}}} = \frac{{F{{L}_{{32}}}}}{{2{{L}_{{22}}}}}.$$

(20)

Substituting Eqs. (17) and (18) into (20), we obtain an expression for the electrodiffusive-transport coefficient of the SMIEM

$${{L}_{{32}}} = 2\Delta t{{L}_{{22}}}{\text{/}}F = \frac{{2\Delta t~h}}{{({{\alpha }_{1}}{{R}_{1}} + {{\alpha }_{2}}{{R}_{2}})F}}~.$$

(21)

RESULTS AND DISCUSSION

From Eq. (18) it follows that the coefficient 1/L₂₂ represents the resistivity of the SMIEM:

$$\frac{1}{{{{L}_{{22}}}}} = \frac{{{{R}_{{mc}}}}}{h} = \frac{{({{\alpha }_{1}}{{R}_{1}} + {{\alpha }_{2}}{{R}_{2}})}}{h}.$$

(22)

Let us analyze the influence of some physicochemical characteristics of the modifying layer on the coefficients of electrical conductivity and electrodiffusion of SMIEM, comparing them with the corresponding coefficients of the substrate of this membrane.

For this purpose, we introduce the coefficients ${{k}_{{22}}} = \frac{{{{L}_{{22}}}}}{{{{L}_{{220}}}}}~$ and ${{k}_{{32}}} = \frac{{{{L}_{{32}}}}}{{{{L}_{{320}}}}}$, where L₂₂₀ and L₃₂₀ are the conductivity and the electrodiffusion coefficient of the substrate, respectively, which will be found taking into account Eqs. (15), (18), and (21) and assuming that h₁ = 0,

$$\begin{gathered} \frac{1}{{{{L}_{{220}}}}} = \frac{{{{\alpha }_{{20}}}{{R}_{2}}}}{{{{h}_{2}}}} = \frac{{\left( {\frac{{{{{\bar {\sigma }}}_{2}}}}{{\sqrt {\bar {\sigma }_{2}^{2} + 4} }} + 1} \right)\left( {\sqrt {\bar {\sigma }_{2}^{2} + 4} - {{{\bar {\sigma }}}_{2}}} \right)}}{4}~\rho {{{\bar {\nu }}}_{{m2}}} \\ = \frac{{\rho {{{\bar {\nu }}}_{{m2}}}}}{{\sqrt {\bar {\sigma }_{2}^{2} + 4} }}, \\ \end{gathered} $$

(23)

$$\frac{1}{{{{L}_{{320}}}}} = \frac{F}{{2\Delta {{t}_{0}}{{L}_{{220}}}}}.$$

(24)

Then, taking into account Eqs. (15), (18), and (21) together with Eqs. (23) and (24), we obtain

$${{k}_{{22}}} = \frac{{{{L}_{{22}}}}}{{{{L}_{{220}}}}} = \frac{{4~~\left( {1 + \frac{{{{h}_{1}}}}{{{{h}_{2}}}}} \right)}}{{\left( {2\Delta t + 1} \right)\sqrt {\bar {\sigma }_{2}^{2} + 4} \left[ {\left( {\sqrt {\frac{{\bar {\sigma }_{1}^{2}}}{{\bar {\sigma }_{2}^{2}}} + \frac{4}{{\bar {\sigma }_{2}^{2}}}} - \frac{{{{{\bar {\sigma }}}_{1}}}}{{{{{\bar {\sigma }}}_{2}}}}} \right){{{\bar {\sigma }}}_{2}}\frac{{{{\gamma }_{1}}{{D}_{{m2}}}}}{{{{\gamma }_{2}}{{D}_{{m1}}}}}\frac{{{{h}_{1}}}}{{{{h}_{2}}}} + \left( {\sqrt {\bar {\sigma }_{2}^{2} + 4} - {{{\bar {\sigma }}}_{2}}} \right)} \right]}},$$

(25)

$${{k}_{{32}}} = \frac{{{{L}_{{32}}}}}{{{{L}_{{320}}}}} = \frac{{{{L}_{{22}}}}}{{{{L}_{{220}}}}}~\frac{{\Delta t}}{{\Delta {{t}_{0}}}} = {{k}_{{22}}}\frac{{\Delta t}}{{\Delta {{t}_{0}}}},$$

(26)

where $\Delta {{t}_{0}} = \Delta t\left( {{{h}_{1}} = 0{{\;}}} \right) = \frac{{{{{\bar {\sigma }}}_{2}}}}{{2\sqrt {\bar {\sigma }_{2}^{2} + 4} }}$.

Analysis of Eqs. (25) and (26) shows that the influence of the modifying layer on the transport coefficients is determined by the ratio of its thickness to the thickness of the substrate (i.e., $\frac{{{{h}_{1}}}}{{{{h}_{2}}}}$) and a number of the following ratios: σ₁/σ₂, $~\frac{{{{\gamma }_{1}}}}{{{{\gamma }_{2}}}}$, and $\frac{{{{D}_{{m1}}}}}{{{{D}_{{m~2}}}}}$. Moreover, the degree of this influence also depends on the value of the dimensionless parameter of the substrate ${{\bar {\sigma }}_{2}} = {{\gamma }_{2}}\frac{{{{\rho }_{2}}}}{{F{{c}_{0}}}}$, which is determined by the space charge density, the coefficient of equilibrium distribution of the electrolyte in the substrate, and the electrolyte concentration.

Using formulas (25)–(26) and the Mathcad 14 package with the given values of c₀₀ = 0.05 M; ρ₂ = 0.98 M, h₁ = 15 μm, h₂ = 220 μm; γ₁ = 1, γ₂ = 0.453; D = 3300 μm²/s; D_m1 = 91 μm²/s; and D_m2 = 31 μm²/s, we quantitatively assessed the influence of a number of parameters of the modifying layer on the conductivity and electrodiffusion coefficient of the modified membrane. The physicochemical parameters chosen qualitatively correspond to a modified MF-4SK/Pan membrane in a measuring cell filled with a 0.05 M aqueous solution of HCl [37].

Numerical calculation of the influence of the space charge density of the modifying layer (i.e., the 1st layer) showed (Fig. 2) that in the case of uncharged modifying layer (i.e., ρ₁ = 0), the conductivity and the electrodiffusion coefficient of the SMIEM are lower than those of the substrate (k₂₂ < 1 and k₃₂ < 1), which is due to the fact that the modifying layer increases the resistance of the modified membrane (Fig. 2). With identical signs of charges of both SMIEM layers $\left( {\frac{{{{\rho }_{1}}}}{{{{\rho }_{2}}}} > 0} \right)$, the conductivity of the SMIEM increases with increasing ρ₁; this is due to an increase in the concentration of counterions in the modifying layer, which leads to an increase in the conductivity and the electrodiffusion coefficient of the membrane (Fig. 2).

Fig. 2.

Effect of the space charge density of the modifying layer on dimensionless (1) electrical conductivity k₂₂ and (2) electrodiffusion coefficient k₃₂ of the modified membrane.

When the space charges of the SMIEM layers have different signs $\left( {\frac{{{{\rho }_{1}}}}{{{{\rho }_{2}}}} < 0} \right)$, the concentration of counterions in the modifying layer increases with an increase in the absolute value of space charge ρ₁, but they are co-ions for the substrate and, as a consequence, the conductivity of the modified membrane decreases and the values of the SMIEM electrodiffusion coefficient also decrease (Fig. 2).

Numerical simulation of the effect of the modifying-layer thickness is illustrated in Fig. 3. As can be seen from Fig. 3, in the case of uncharged modifying layer (i.e., ρ₁ = 0), the electrical conductivity and the electrodiffusion coefficient of SMIEM decrease noticeably with increasing thickness of this layer, which is due to an increase in the resistivity of the modifying layer. However, if the modifying layer has a space charge density ρ₁ of the same sign as the substrate $\left( {\frac{{{{\rho }_{1}}}}{{{{\rho }_{2}}}} > 0} \right)$, then the conductivity of SMIEM can increase with increasing membrane thickness (Fig. 3) because of an increase in the concentration of counterions in the modifying layer, which weakens the effect of the modifying-layer thickness. The electrodiffusion coefficient behaves similarly.

Fig. 3.

Effect of the thickness of the modifying layer on the dimensionless conductivity (k₂₂, red curves) and electrodiffusion coefficient (k₃₂, blue curves) of the modified membrane at different values of space charge density of the modifying layer: $\frac{{{{\rho }_{1}}}}{{{{\rho }_{2}}}} = 1.5$ (1); $\frac{{{{\rho }_{1}}}}{{{{\rho }_{2}}}} = 0.5~$ (2); $\frac{{{{\rho }_{1}}}}{{{{\rho }_{2}}}} = 0$ (3); $\frac{{{{\rho }_{1}}}}{{{{\rho }_{2}}}} = - 1$ (4).

When the space charges of the SMIEM membrane layers are of different signs $\left( {\frac{{{{\rho }_{1}}}}{{{{\rho }_{2}}}} < 0} \right)$, the concentration of counterions in the membrane layers decreases and the resistivity of the membrane increases with increasing thickness of the modifying layer; as a consequence, both of these factors lead to a decrease in the electrical conductivity and electrodiffusion of the modified membrane (Fig. 3).

The effect of electrolyte concentration c₀ on the electrical conductivity and electrodiffusion of the modified membrane was also simulated numerically using the Mathcad 14 package and the resulting expression (25). In this analysis, it was taken into account that the resistance of the substrate varies with the electrolyte concentration, since its parameter σ₂ depends on the concentration according to the expression ${{\sigma }_{{1,2}}} = \frac{{{{\rho }_{{1,2}}}}}{{F{{c}_{0}}}}$ = $\frac{{{{\rho }_{{1,2}}}}}{{F{{c}_{{00}}}}}\frac{{{{c}_{{00}}}}}{{{{c}_{0}}}} = {{\sigma }_{{10,20}}}\frac{{{{c}_{{00}}}}}{{{{c}_{0}}}}$, where ${{c}_{{00}}} = 0.05\,\,{\text{M}}$ and ${{\sigma }_{{10,20}}} = \frac{{{{\rho }_{{1,2}}}}}{{F{{c}_{{00}}}}}$. In addition, taking into account Eqs. (16) and (23), it is easy to find that the substrate resistivity can be written as $\frac{1}{{{{L}_{{220}}}}} = \frac{{\rho {{{\bar {\nu }}}_{{m2}}}}}{{\sqrt {\bar {\sigma }_{2}^{2} + 4} }}$ = $\frac{{RT{{{\bar {\nu }}}_{{m2}}}}}{{{{F}^{2}}D}}\frac{1}{{\sqrt {4c_{0}^{2} + \frac{{{{\rho }_{2}}}}{F}} }}$. It follows that the resistivity of the substrate decreases and its electrical conductivity increases with increasing electrolyte concentration, which is consistent with experimental data [38–40].

The effect of electrolyte concentration c₀ on the electrical conductivity and electrodiffusion of the modified membrane is shown in Fig. 4. As can be seen from Fig. 4 (curve 3), the electrical conductivity and electrodiffusion of SMIEM increases with increasing c₀ in the case of the uncharged modified layer, but due to the resistivity of the modifying layer, the former is slightly lower than the conductivity of the substrate. However, at high electrolyte concentrations, the resistance of the modifying layer weakens and their electrical conductivities become equal (Fig. 4). If the modified layer is charged and has the same sign as the substrate $\left( {\frac{{{{\rho }_{1}}}}{{{{\rho }_{2}}}} > 0} \right)$, then, as noted earlier, the charge of this layer weakens the effect of the resistance of the modifying layer on the conductivity and the conductivity of the SMIEM may be slightly greater than that of the substrate at small values of the c₀/c₀₀ ratio (curve 1 in Fig. 4). As the electrolyte concentration increases, the conductivities of the membrane and the substrate come closer and practically coincide. The electrodiffusion coefficient of SMIEM changes in a similar way: it also increases with increasing electrolyte concentration.

Fig. 4.

Effect of the electrolyte concentration on the dimensionless electrical conductivity (k₂₂) and electrodiffusion coefficient (k₃₂) of the modified membrane at different values of space charge density of the modifying layer: $\frac{{{{\rho }_{1}}}}{{{{\rho }_{2}}}} = 1.5~$ (1); $\frac{{{{\rho }_{1}}}}{{{{\rho }_{2}}}} = 0.5$ (2); $\frac{{{{\rho }_{1}}}}{{{{\rho }_{2}}}} = 0~$ (3); $\frac{{{{\rho }_{1}}}}{{{{\rho }_{2}}}} = - 1$ (4).

In the case of opposite space charges of MIEM membrane layers $\left( {\frac{{{{\rho }_{1}}}}{{{{\rho }_{2}}}} < 0} \right)$, as can be seen from Fig. 4 (curve 4), the values of the conductivity and electrodiffusion coefficient of the SMIEM are noticeably lower than those of the substrate (since k₂₂ < 1), which is due to the combined action of two factors: the difference in sign between charges of the membrane layers and the resistance of the modifying layer. However, as can be seen from Fig. 4, their influence decreases with increasing c₀ so that the dimensionless electrical conductivity and electrodiffusion coefficient of the modifying layer become almost the same as those of the substrate at high electrolyte concentrations.

CONCLUSIONS

In terms of the homogeneous model of a fine-pore membrane, analytical expressions for the Onsager transport coefficients—electrical conductivity and electrodiffusion—of a bilayer ion exchange membrane have been first obtained. The influence of a number of physicochemical characteristics of the modifying layer on the electrical conductivity and electrodiffusion coefficient of the membrane was studied using the method of mathematical modeling. It has been shown that an increase in the space charge density of the modifying layer increases the electrical conductivity and electrodiffusion coefficient of the membrane when the signs of the space charge densities of the modifying layer and the substrate are the same and decreases them when the signs are different. It has been established that increasing the thickness of the modifying layer reduces the electrical conductivity and electrodiffusion of the membrane if this layer is not charged. When the charge density of the modifying layer and the substrate are of the same sign, an increase in the charge density of the modifying layer weakens its resistance and can enhance the electrical conductivity and electrodiffusion of the membrane. But at different signs of space charge densities of the SMIEM membrane layers $\left( {\frac{{{{\rho }_{1}}}}{{{{\rho }_{2}}}} < 0} \right)$, electrical conductivity and electrodiffusion decrease with an increase in the absolute value of the space charge, with their values being noticeably lower than the respective coefficients of the substrate.

It has been shown that an increase in the electrolyte concentration enhances the electrical conductivity and electrodiffusion of the modified membrane for any charge sign of the modifying layer.

The obtained analytical expressions can be used in modeling electromembrane processes and predicting the parameters of new surface-modified ion exchange membranes.