1 INTRODUCTION

The efficient numerical simulation of flows around moving obstacles is quite a difficult task. From a mathematical point of view, the flow geometry is determined by the corresponding boundary conditions on the surface of moving solid bodies. At the moment, there are two main approaches to model flows with a complex geometry: the classical approach based on body-fitted meshes [1, 2], and the alternative flow approach, which uses immersed boundary methods [3, 4]. In the classical approach, when solving problems characterized by a complex geometric shape of the obstacles, the construction of a body-fitted computational mesh is often a resource-intensive task that cannot always be solved. The construction of body-fitted computational meshes becomes much more complicated for moving obstacles since it requires continuous adaptation or the construction of a new mesh. In this case, methods of modeling moving bodies for meshes can be used. The most common ones among them are the use of sliding meshes [5], the Chimera technology [6], and the transition to a non-inertial coordinate system [7]. The implementation of the first two approaches requires re-interpolation of the solution from mesh to mesh, which can lead to a significant loss in the accuracy of the numerical solution, especially in the case of a sharp contrast in the mesh resolution in areas of body fitted meshes or in the presence of shock waves. The main disadvantage of using a non-inertial coordinate system is its inapplicability for several obstacles moving according to different laws.

The immersed boundary method (IBM) makes it possible to avoid the cost and difficulties related to the construction of meshes and set boundary conditions on the surface of solid bodies without positioning mesh nodes on the boundary of the obstacles, which greatly simplifies the construction of the computational mesh, which is then solved in the entire domain of the problem definition, including the rigid body. In the IBM, the boundary conditions on the obstacle surface are specified by introducing additional terms in the system of equations, and depending on the way boundary conditions are imposed, the immersed boundary methods can be divided into two main classes: discrete [3, 8, 9] and differential (continuous) [10, 11] methods. Discrete approaches are based on changes in discretized equations by introducing additional feedbacks that ensure the satisfaction of boundary conditions, which makes them difficult to generalize due to their direct dependence on numerical methods. Perhaps, the biggest disadvantages of discrete immersed boundary methods are the lack of mathematical proofs of their convergence and the difficulty of controlling the error in approximating the boundary conditions [4].

The volume penalization methods (VPMs) constitute a separate subclass of differential immersed boundary methods, in which the effect of the presence of solid bodies is achieved by introducing additional terms in differential equations that describe the evolution of a liquid or gas flow, after which the modified equations are discretized and solved using an appropriate computational method. Starting with the work of Arquis and Caltagirone [10], which presented the formulation of the Brinkman VPM (BVPM), significant efforts were invested in the development of the BVPM for modeling viscous incompressible fluid flows around solid obstacles [11–13]. The main idea of this method is to model a solid as a porous medium with low permeability, approaching zero. The principal advantage of the BVPM in comparison to discrete immersed boundary methods lies in the possibility of analytical evaluation and active control of the error of the solution of the penalized equations by changing the values of the parameters of the penalty functions [11, 12].

The BVPM was generalized to compressible flows in [14], where, in addition to introducing penalty functions into the momentum and energy conservation equations, the continuity equation was also modified in such a way that the problem inside the body was reduced to a flow in a porous medium with a large acoustic impedance, leading to the slight penetration of acoustic waves. As in the case of an incompressible viscous flow, in the generalized BVPM, the error in solving the penalized equations can be strictly estimated and controlled by the values of the porosity and permeability parameters. The generalized BVPM has been successfully used to simulate viscous [14] and inviscid [15] subsonic compressible flows around stationary bodies. However, as was shown in [16], the original formulation of the generalized Brinkman penalty method [14] is not Galilean invariant. In [16], an extension of the generalized BMVP with a Galilean-invariant formulation of the continuity and momentum conservation equations was proposed. However, the formulation proposed by Komatsu et al. [16] is not Galilean-invariant for the energy conservation equation.

In this paper, we propose a fully Galilean-invariant generalization of the BVPM [14, 16] for the numerical simulation of compressible fluid flows around moving bodies. The effectiveness of the proposed formulation was demonstrated in solving test problems of the direct reflection of a one-dimensional acoustic pulse from a flat stationary and moving surface, scattering of an acoustic wave by a stationary cylinder, and subsonic flow of a viscous gas around an oscillating cylinder.

All problems considered in this paper were solved using the finite volume/finite difference method on unstructured computational meshes based on the edge-based reconstruction (EBR) scheme [17], whose accuracy is increased due to the quasi-one-dimensional edge-oriented reconstruction of variables.

The rest of the article is organized as follows. The second section describes the generalized BVPM. This section also provides a Galilean-invariant generalization of the BVPM for modeling a compressible viscous flow around moving bodies. The third section briefly describes the numerical method based on the finite volume EBR scheme. The results of numerical simulation of test problems are given in the fourth section. Finally, in the fifth section, conclusions are drawn and directions for further development of the topic are outlined.

2 BRINKMANN VOLUME PENALIZATION METHOD

2.1 Mathematical Model

As a basic mathematical model for describing the flows of a viscous compressible medium around solid obstacles, we use the system of Navier–Stokes equations, written with respect to physical variables: density ρ, component of the velocity vector ui, and specific internal energy ε in the following way:

$$\frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \rho {{u}_{j}}}}{{\partial {{x}_{j}}}} = 0,$$
$$\frac{{\partial {{u}_{i}}}}{{\partial t}} + {{u}_{j}}\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{j}}}} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial {{x}_{i}}}} + \frac{1}{{{{{\operatorname{Re} }}_{{\text{a}}}}}}\frac{1}{\rho }\frac{{\partial {{\tau }_{{ij}}}}}{{\partial {{x}_{j}}}},$$
(1)
$$\frac{{\partial \varepsilon }}{{\partial t}} + {{u}_{i}}\frac{{\partial \varepsilon }}{{\partial {{x}_{i}}}} = - \frac{p}{\rho }\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{i}}}} + \frac{1}{{{{{\operatorname{Re} }}_{{\text{a}}}}}}\frac{{{{\tau }_{{ij}}}}}{\rho }\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{j}}}} - \frac{1}{{{{{\operatorname{Re} }}_{{\text{a}}}}}}\frac{1}{\rho }\frac{{\partial {{q}_{i}}}}{{\partial {{x}_{i}}}}.$$

All variables of system (1) are assumed to be dimensionless. The characteristic size of body L and the characteristic parameters of the undisturbed medium—the speed of sound c0 and density ρ0, which determine the acoustic Reynolds number \({{\operatorname{Re} }_{{\text{a}}}} = {{\rho }_{0}}{{c}_{0}}L{\text{/}}{{\mu }_{0}}\)—are chosen as the nondimensionalization parameters. The pressure and specific internal energy are nondimensionalized by the values \({{\rho }_{0}}c_{0}^{2}\) and \(c_{0}^{2}\); and the temperature, by \({{c_{0}^{2}} \mathord{\left/ {\vphantom {{c_{0}^{2}} R}} \right. \kern-0em} R}\), where R is the gas constant. This implies that the relationship between dimensionless temperature and dimensionless specific internal energy \(T = (\gamma - 1)\varepsilon \).

The system of equations (1) is closed by the ideal gas equation of state \(p = (\gamma - 1)\rho \varepsilon \) and γ = 1.4 is the adiabatic index. The following notations are introduced in system (1):

\({{\tau }_{{ij}}} = \mu \left( {\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{j}}}} + \frac{{\partial {{u}_{j}}}}{{\partial {{x}_{i}}}}} \right) - \frac{2}{3}\mu \frac{{\partial {{u}_{i}}}}{{\partial {{x}_{i}}}}{{\delta }_{{ij}}}\) is the viscous stress tensor,

\({{q}_{i}} = - \frac{\gamma }{{\Pr }}\mu \frac{{\partial \varepsilon }}{{\partial {{x}_{i}}}}\) is the heat flux, \(\Pr = {{\mu {{c}_{p}}} \mathord{\left/ {\vphantom {{\mu {{c}_{p}}} \lambda }} \right. \kern-0em} \lambda }\) is the Prandtl number, and μ is the coefficient of molecular viscosity. Note that for convenience, we use implicit summation over repeating direction indices i, j = 1, …, d, where d is the dimensionality of the problem.

2.2 BVPM for Compressible Flows

We consider the problem of a viscous compressible flow around a rigid obstacle, described by the Navier–Stokes equations (1). We assume that the problem is solved in the domain Ω, containing a body occupying a region of space ΩB. The velocity and temperature of a fluid at the boundary of a solid body ∂ΩB satisfies the no-slip and isothermal conditions given as

$${{\left. {\mathbf{u}} \right|}_{{\partial {{\Omega }_{{\text{B}}}}}}} = {{{\mathbf{U}}}_{{\text{B}}}},\quad {{\left. T \right|}_{{\partial {{\Omega }_{{\text{B}}}}}}} = {{T}_{{\text{B}}}},$$

where \({{{\mathbf{U}}}_{{\text{B}}}}\) and \({{T}_{{\text{B}}}}\) are the speed and body temperature terms, respectively. In BVPM, generalized in [14] for a compressible gas, in addition to the no-slip condition and isothermality on the body surface, specified implicitly by adding Brinkman volume penalization to the momentum and energy conservation equations, the mass conservation equation was also modified so that inside a body the equation was reduced to the equations of conservation of mass in a porous medium. Thus, the dimensionless penalized Navier–Stokes equations for a compressible gas in the formulation of [14] for motionless obstacles, i.e., in the case \({{{\mathbf{U}}}_{{\text{B}}}} = 0\), can be written in the following form:

$$\begin{gathered} \frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \rho {{u}_{j}}}}{{\partial {{x}_{j}}}} = - \chi \left( {\frac{1}{\phi } - 1} \right)\frac{{\partial \rho {{u}_{j}}}}{{\partial {{x}_{j}}}}, \\ \frac{{\partial \rho {{u}_{i}}}}{{\partial t}} + \frac{{\partial \rho {{u}_{i}}{{u}_{j}}}}{{\partial {{x}_{j}}}} = - \frac{{\partial p}}{{\partial {{x}_{i}}}} + \frac{1}{{{{{\operatorname{Re} }}_{{\text{a}}}}}}\frac{{\partial {{\tau }_{{ij}}}}}{{\partial {{x}_{j}}}} - \frac{\chi }{{{{\eta }_{b}}}}\rho {{u}_{i}}, \\ \frac{{\partial E}}{{\partial t}} + \frac{{\partial ({{u}_{j}}(E + p))}}{{\partial {{x}_{j}}}} = \frac{1}{{{{{\operatorname{Re} }}_{{\text{a}}}}}}\frac{{\partial {{u}_{i}}{{\tau }_{{ij}}}}}{{\partial {{x}_{j}}}} - \frac{1}{{{{{\operatorname{Re} }}_{{\text{a}}}}}}\frac{{\partial {{q}_{i}}}}{{\partial {{x}_{i}}}} - \frac{\chi }{{{{\eta }_{T}}}}\rho (\gamma - 1)(\varepsilon - {{\varepsilon }_{{\text{B}}}}), \\ \end{gathered} $$
(2)

where \(E = {{\rho {{{\mathbf{u}}}^{2}}} \mathord{\left/ {\vphantom {{\rho {{{\mathbf{u}}}^{2}}} 2}} \right. \kern-0em} 2}{\text{ + }}{p \mathord{\left/ {\vphantom {p {(\gamma - 1)}}} \right. \kern-0em} {(\gamma - 1)}}\) is the total energy determined taking into account the ideal gas equation of state, φ is the porosity, \({{\eta }_{b}}\) is the normalized viscous permeability, \({{\eta }_{T}}\) is the normalized thermal permeability, and the spatial position of the solid body is determined by the marking function \(\chi ({\mathbf{x}},t)\):

$$\chi ({\mathbf{x}},t) = \left\{ \begin{gathered} 1,\quad {\mathbf{x}} \in {{{\bar {\Omega }}}_{{\text{B}}}}, \hfill \\ 0,\quad {\mathbf{x}} \notin {{{\bar {\Omega }}}_{{\text{B}}}}, \hfill \\ \end{gathered} \right.$$

where \({{\bar {\Omega }}_{{\text{B}}}} = {{\Omega }_{{\text{B}}}} \cup \partial {{\Omega }_{{\text{B}}}}\). It was shown in [14] that for small values of the parameters φ, \({{\eta }_{b}}\), and \({{\eta }_{T}}\), when \({{\eta }_{T}} = \operatorname{O} ({{\eta }_{b}})\), the error in solving the penalized system of equations (3) converges as \(\operatorname{O} ({{(\varphi {{\eta }_{b}})}^{{1/2}}})\).

2.3 Galilean-Invariant BVPM for Compressible Flows

When solving problems of the flow around moving objects, it is important that the equations and boundary conditions remain invariant in the moving reference frame; i.e., the penalized equations must satisfy the Galilean invariance conditions. In [16], an extension of the generalized BVPM [14] with the Galilean-invariant formulation of the continuity and momentum conservation equations was proposed. However, the formulation proposed by Komatsu et al. [16] is not Galilean-invariant for the energy conservation equation.

To derive a generalized BVPM that satisfies the conditions of Galileo invariance, we rewrite the penalized Navier–Stokes equations (2) for fixed bodies with respect to density variables ρ, a component of the velocity vector \({{u}_{i}}\), and specific internal energy ε:

$$\begin{gathered} \frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \rho {{u}_{j}}}}{{\partial {{x}_{j}}}} = - \chi \left( {\frac{1}{\phi } - 1} \right)\frac{{\partial \rho {{u}_{j}}}}{{\partial {{x}_{j}}}}, \\ \frac{{\partial {{u}_{i}}}}{{\partial t}} + {{u}_{j}}\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{j}}}} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial {{x}_{i}}}} + \frac{1}{{{\text{R}}{{{\text{e}}}_{{\text{a}}}}}}\frac{1}{\rho }\frac{{\partial {{\tau }_{{ij}}}}}{{\partial {{x}_{j}}}} - \frac{\chi }{{{{\eta }_{b}}}}{{u}_{i}}, \\ \frac{{\partial \varepsilon }}{{\partial t}} + {{u}_{i}}\frac{{\partial \varepsilon }}{{\partial {{x}_{i}}}} = - \frac{p}{\rho }\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{i}}}} + \frac{1}{{{\text{R}}{{{\text{e}}}_{{\text{a}}}}}}\frac{{{{\tau }_{{ij}}}}}{\rho }\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{j}}}} - \frac{1}{{{\text{R}}{{{\text{e}}}_{{\text{a}}}}}}\frac{1}{\rho }\frac{{\partial {{q}_{i}}}}{{\partial {{x}_{i}}}} - \frac{\chi }{{{{\eta }_{T}}}}\rho \left( {\gamma - 1} \right)\left( {\varepsilon - {{\varepsilon }_{{\text{B}}}}} \right). \\ \end{gathered} $$
(3)

System (3) can also be interpreted as a system of equations written in the coordinate system of a body moving at speed UB. Rewriting the system of equations (3) in a fixed coordinate system using the Galilean transformations

$$\frac{\partial }{{\partial t}} \to \frac{\partial }{{\partial t}} + {{U}_{{{\text{B}}i}}}\frac{\partial }{{\partial {{x}_{i}}}},\quad \frac{\partial }{{\partial {{x}_{i}}}} \to \frac{\partial }{{\partial {{x}_{i}}}},\quad {{u}_{i}} \to {{u}_{i}} - {{U}_{{{\text{B}}i}}},$$

we obtain the following Galilean-invariant form of the penalized Navier–Stokes equations, written for density variables ρ, the component of the velocity vector \({{u}_{i}}\), and specific internal energy:

$$\begin{gathered} \frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \rho {{u}_{j}}}}{{\partial {{x}_{j}}}} = - \chi \left( {\frac{1}{\phi } - 1} \right)\frac{{\partial \rho ({{u}_{j}} - {{U}_{{{\text{B}}j}}})}}{{\partial {{x}_{j}}}}, \\ \frac{{\partial {{u}_{i}}}}{{\partial t}} + {{u}_{j}}\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{j}}}} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial {{x}_{i}}}} + \frac{1}{{{{{\operatorname{Re} }}_{{\text{a}}}}}}\frac{1}{\rho }\frac{{\partial {{\tau }_{{ij}}}}}{{\partial {{x}_{j}}}} - \frac{\chi }{{{{\eta }_{b}}}}\left( {{{u}_{i}} - {{U}_{{{\text{B}}i}}}} \right), \\ \frac{{\partial \varepsilon }}{{\partial t}} + {{u}_{i}}\frac{{\partial \varepsilon }}{{\partial {{x}_{i}}}} = - \frac{p}{\rho }\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{i}}}} + \frac{1}{{{{{\operatorname{Re} }}_{{\text{a}}}}}}\frac{{{{\tau }_{{ij}}}}}{\rho }\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{j}}}} - \frac{1}{{{{{\operatorname{Re} }}_{{\text{a}}}}}}\frac{1}{\rho }\frac{{\partial {{q}_{i}}}}{{\partial {{x}_{i}}}} - \frac{\chi }{{{{\eta }_{T}}}}\rho \left( {\gamma - 1} \right)\left( {\varepsilon - {{\varepsilon }_{{\text{B}}}}} \right). \\ \end{gathered} $$
(4)

Rewriting the system of equations (4) with respect to conservative variables of the density ρ, the components of the momentum vector \(\rho {{u}_{i}}\), and full of energy E, we obtain the following Galilean-invariant system of penalized Navier–Stokes equations:

$$\frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \rho {{u}_{j}}}}{{\partial {{x}_{j}}}} = - \chi \left( {\frac{1}{\phi } - 1} \right)\frac{{\partial \rho ({{u}_{j}} - {{U}_{{{\text{B}}j}}})}}{{\partial {{x}_{j}}}},$$
$$\begin{gathered} \frac{{\partial \rho {{u}_{i}}}}{{\partial t}}{\text{ + }}\frac{{\partial \rho {{u}_{i}}{{u}_{j}}}}{{\partial {{x}_{j}}}}{\text{ = }} - \frac{{\partial p}}{{\partial {{x}_{i}}}}{\text{ + }}\frac{1}{{{{{\operatorname{Re} }}_{{\text{a}}}}}}\frac{{\partial {{\tau }_{{ij}}}}}{{\partial {{x}_{j}}}} - \frac{\chi }{{{{\eta }_{b}}}}\rho ({{u}_{i}} - {{U}_{{{\text{B}}i}}}) - \chi \left( {\frac{1}{\phi } - 1} \right){{u}_{i}}\frac{{\partial \rho ({{u}_{j}} - {{U}_{{{\text{B}}j}}})}}{{\partial {{x}_{j}}}}, \\ \frac{{\partial E}}{{\partial t}} + \frac{{\partial (E + p){{u}_{j}}}}{{\partial {{x}_{j}}}} = \frac{1}{{{{{\operatorname{Re} }}_{{\text{a}}}}}}\frac{{\partial {{u}_{i}}{{\tau }_{{ij}}}}}{{\partial {{x}_{j}}}} - \frac{1}{{{{{\operatorname{Re} }}_{{\text{a}}}}}}\frac{{\partial {{q}_{i}}}}{{\partial {{x}_{i}}}} \\ \end{gathered} $$
(5)
$$ - \;\frac{\chi }{{{{\eta }_{T}}}}\rho (\gamma - 1)(\varepsilon - {{\varepsilon }_{{\text{B}}}}) - \frac{\chi }{{\eta {{{\kern 1pt} }_{b}}}}\rho {{u}_{i}}({{u}_{i}} - {{U}_{{{\text{B}}i}}}) - \chi \left( {\frac{1}{\phi } - 1} \right)\frac{E}{\rho }\frac{{\partial \rho ({{u}_{j}} - {{U}_{{{\text{B}}j}}})}}{{\partial {{x}_{j}}}}.$$

One of the advantages of the BVPM is the ability to determine the total force F acting on the body and the heat flux, using the integration of the BVPM over the space occupied by this body. For this, the surface integral of the total stress tensor

$${{\sigma }_{{ij}}} = - p{{\delta }_{{ij}}} + \frac{1}{{{{{\operatorname{Re} }}_{{\text{a}}}}}}{{\tau }_{{ij}}}$$

is reduced to the volume integral

$${{F}_{i}} = \oint\limits_{\partial {{\Omega }_{{\text{B}}}}} {{{\sigma }_{{ij}}}{{n}_{j}}dS} = \int\limits_{{{\Omega }_{{\text{B}}}}} {\frac{{\partial {{\sigma }_{{ij}}}}}{{\partial {{x}_{j}}}}d{\mathbf{x}}} ,$$

where \({{n}_{j}}\) are the components of the outer normal n to the edge of the body \(\partial {\kern 1pt} {{\Omega }_{{\text{B}}}}\). Using the equation for the components of the velocity vector of system (4) under the assumption that there is no rotational motion of the streamlined body, we obtain the following chain of equalities:

$$\begin{gathered} \frac{{\partial {{\sigma }_{{ij}}}}}{{\partial {{x}_{j}}}} = \rho \frac{{\partial {{u}_{i}}}}{{\partial t}} + \rho {{u}_{j}}\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{j}}}} + \frac{\chi }{{{{\eta }_{b}}}}\rho ({{u}_{i}} - {{U}_{{{\text{B}}i}}}) \\ = \rho \frac{{d{{U}_{{{\text{B}}i}}}}}{{dt}} + \frac{\chi }{{\eta {{{\kern 1pt} }_{b}}}}\rho ({{u}_{i}} - {{U}_{{{\text{B}}i}}}) + \rho \frac{{\partial ({{u}_{i}} - {{U}_{{{\text{B}}i}}})}}{{\partial t}} + \rho {{u}_{j}}\frac{{\partial ({{u}_{i}} - {{U}_{{{\text{B}}i}}})}}{{\partial {{x}_{j}}}}. \\ \end{gathered} $$
(6)

Neglecting the contribution of the last two terms in the second equality of expression (6) due to their small magnitude, it is easy to obtain the following approximation for calculating the total force

$${\mathbf{F}} \approx \left( {\int\limits_{{{\Omega }_{{\text{B}}}}} {\rho d{\mathbf{x}}} } \right)\frac{{d{{{\mathbf{U}}}_{{\text{B}}}}}}{{dt}} + \frac{1}{{{{\eta }_{b}}}}\int\limits_{{{\Omega }_{{\text{B}}}}} \rho ({\mathbf{u}} - {{{\mathbf{U}}}_{{\text{B}}}})d{\mathbf{x}}.$$
(7)

Note that in formula (7), in addition to the second term, which represents the well-known formula for calculating forces when using the BVPM in the case of stationary obstacles [18], there is also a term associated with the acceleration of the added fluid mass inside the obstacle. We also note that formula (7) can also be used in the case of a non-inertial frame of reference. In this case, an additional term arises due to the presence of body forces caused by its acceleration.

3 NUMERICAL METHOD

The method proposed in this paper is implemented based on the NOISEtte software package described in [19, 20].

Spatial discretization of the convective part of the system of equations (5) is based on a finite-volume approach with the determination of the desired variables at the mesh nodes around which the computational cells (muzzle mesh) are built. To increase the order of accuracy, a scheme based on the quasi-one-dimensional reconstruction of variables along a mesh edge (EBR schemes) is used. This class of schemes is described in detail in [17]. For the spatial approximation of viscous terms, the Galerkin finite element method based on linear basis functions is used. The source nondifferential terms on the right-hand side of system (5) are specified at the mesh nodes. The differential terms on the right hand side are approximated similarly to the density transfer in the convective part of the system, except for the term \({{\partial \rho {{U}_{{{\text{B}}j}}}} \mathord{\left/ {\vphantom {{\partial \rho {{U}_{{{\text{B}}j}}}} {\partial {{x}_{j}}}}} \right. \kern-0em} {\partial {{x}_{j}}}}\), for which the flow on the edge of the computational cell separating nodes L and R and having an oriented area \({{{\mathbf{n}}}_{{LR}}}\), is defined as \(\sqrt {{{\rho }_{L}}{{\rho }_{R}}} ({{{\mathbf{U}}}_{{\text{B}}}} \cdot {{{\mathbf{n}}}_{{LR}}})\). Here it is assumed that the velocity vector \({{{\mathbf{U}}}_{{\text{B}}}}\) does not depend on the spatial variables.

Integration over time is carried out according to an implicit three-layer scheme of the 2nd order of approximation, followed by the Newton linearization of a spatially discretized system of equations. At each Newtonian iteration, the stabilized biconjugate gradient method (BiCGSTAB) is applied to solve the system of linear equations.

4 NUMERICAL RESULTS

4.1 Reflection of a One-Dimensional Acoustic Pulse

To estimate the accuracy of approximation of the boundary conditions when using the Galilean-invariant generalization of the BVPM for compressible flows, we consider the reflection and transmission of a one-dimensional acoustic pulse incident on a moving solid wall. This problem is a good test case for checking the amplitude and phase errors in the solution of penalized equations and was used as a test problem in [14] for the case of a fixed wall. The problem of reflection of an acoustic pulse has an exact solution for the Euler equations. In this paper, it is solved in the inviscid approximation, i.e., the system of Navier–Stokes equations was used for a large Reynolds number Re = 5 × 105. Periodic boundary conditions are set on the upper and lower boundaries of the computational domain; and the Dirichlet conditions determined by the undisturbed parameters of the medium, on the left and right boundaries.

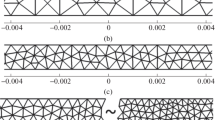
The problem is defined in a rectangular domain of \(\Omega = [ - 0.5,0.5]\) × \([0,0.003]\), consisting of the flow region \({{\Omega }_{F}} \equiv \Omega {{\backslash }}{{\bar {\Omega }}_{{\text{B}}}}\) = \([ - 0.5,0.0)\) × \([0,0.003]\) and porous media region of \({{\bar {\Omega }}_{{\text{B}}}}\) = \([0,0.5]\) × \([0,0.003]\), the interface between two media in the case of a fixed wall (\({{U}_{{\text{B}}}}\) = 0) corresponds to a straight line x = 0, and in the case of moving boundaries, a straight line \(x = {{U}_{{\text{B}}}}t\). The velocity of the walls was set to \({{U}_{{\text{B}}}}\) = ±0.2. To carry out numerical calculations in the region Ω, an unstructured triangular mesh with a characteristic element size of \(h = {{10}^{{ - 4}}}\) was built.

At the initial time, a one-dimensional acoustic pulse was set:

$$\rho = 1 + \rho {\kern 1pt} ',\quad u = {{U}_{{\text{B}}}} + u{\kern 1pt} ',\quad p = 1{\text{/}}\gamma + p{\kern 1pt} ',\quad - {\kern 1pt} 0.45 \leqslant x \leqslant - 0.05,$$

where \(p{\kern 1pt} ' = \rho {\kern 1pt} '\) = \(A\exp ( - \ln 2{{(x - 0.25)}^{2}}{\text{/}}0.004)\), \(u{\kern 1pt} ' = {v}{\kern 1pt} ' = 0\), \(A = {{10}^{{ - 3}}}\).

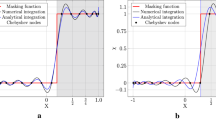
In Fig. 1a the solution of the reflected pulse for different values of porosity ranging from φ = 10−2 to φ = 1 and normalized permeabilities \({{\eta }_{b}}\) = \({{\eta }_{T}}\) = 10–3 is given. The comparison with the exact solution, also shown in the figure, shows the amplitude and phase errors decreasing from 15 to 2% with the decrease in the value of the porosity coefficient from the value φ = 1.0 to the value φ = 0.01.

Fig. 1.
figure 1

Reflection of an acoustic pulse from a solid wall: (a) the reflected wave profile, (b–e) the convergence of the solution with respect to penalty parameters.

Full size image

One of the important aspects of the Galilean-invariant generalized BVPM is the possibility of actively controlling the numerical solution error by changing the penalty function parameters φ, \({{\eta }_{b}}\), and \({{\eta }_{T}}\) to levels that provide the desired order of error. The efficiency of the generalized BVPM is shown in Figs. 1b and 1d, where the results of the convergence of the relative amplitude error of the reflected pulse are given as the penalty parameters tend to zero. The amplitude error was defined as \(|{\kern 1pt} A - p_{{\max }}^{'}{\kern 1pt} |{\kern 1pt} {\text{/}}A\), where \(p_{{\max }}^{'}\) is the magnitude of the pressure disturbance at the crest of the wave, and A = 10−3 is the exact value of the amplitude of the oncoming pulse.

Graphs illustrating the results of the convergence of the solution at fixed values \({{\eta }_{b}} = {{\eta }_{T}} = \eta \) and φ are shown in Figs. 1b and 1c, respectively. Note that the same mesh with the characteristic size \(h = {{10}^{{ - 4}}}\) was used in the calculations for all the porosity values φ and normalized permeability values η. As can be seen from Figs. 1b and 1c, the amplitude error converges as \(\operatorname{O} ({{\varphi }^{{1/2}}})\) for a fixed value of η and as \(\operatorname{O} ({{\eta }^{{1/2}}})\) for a fixed value of φ. The type of graphs in Fig. 1d confirms that the numerical convergence is on the order of \(\operatorname{O} ({{(\varphi \eta )}^{{1/2}}})\), which matches the results of the theoretical studies [14].

Satisfaction of the Galilean invariance condition follows from the convergence graphs shown in Fig. 1e for stationary and moving walls. We can see a satisfactory agreement between the graphs and the correspondence of the theory with respect to the order of convergence of \(\operatorname{O} ({{(\varphi \eta )}^{{1/2}}})\).

4.2 Scattering of a Two-Dimensional Acoustic Pulse

The second test problem considers the scattering by a cylinder of an acoustic wave generated by a localized acoustic source. This problem was considered as a test problem at the conference on computational acoustics [21]. Unlike most of the methods used to solve the test problems of the conference and based on solving the Euler equations, when solving the second test problem, the generalized BVPM was based on the Navier–Stokes equations for a compressible gas with an acoustic Reynolds number of Rea = 5 × 105. The numerical results are compared with the exact analytical solutions for the Euler equations.

Schematically, the problem statement is shown in Fig. 2a. A cylinder with diameter D = 1 is placed in a rectangular computational domain Ω = [−10, 15] × [−10, 10] at a point with coordinates (0, 0). At the initial moment of time at the point (4, 0), an acoustic disturbance is set in the form of a Gaussian pulse:

$$p{\kern 1pt} ' = \rho {\kern 1pt} ' = A\exp ( - \ln 2({{(x - 4)}^{2}} + {{y}^{2}}){\text{/}}{{0.2}^{2}}),\quad u{\kern 1pt} ' = {v}{\kern 1pt} ' = 0,\quad A = 0.001.$$
Fig. 2.
figure 2

Acoustic scattering on the cylinder: (a) formulation of the problem, (b–d) pressure pulsations at control points A, B, C, respectively.

Full size image

For the numerical simulation, an unstructured triangular computational mesh was constructed, which refines near the cylinder boundary with the characteristic size of the mesh element h = 0.001, while the mesh parameters outside the condensation region are chosen in such a way as to provide sufficient resolution of the acoustic source (h ~ 0.05).

The initial localized disturbance leads to the formation of a cylindrical acoustic wave propagating radially from the source. Upon reaching the surface of the cylinder, the wave is reflected from its surface and propagates towards the boundaries of the computational domain. The third wave is formed behind the cylinder as a result of the collision of two waves split by the cylinder. It should be noted that the error in solving the second and third reflected waves depends entirely on the accuracy of the generalized BVPM used to approximate the cylinder, and is a good test of the effectiveness of the method.

The calculation was carried out until the time t = 10. To assess the accuracy of the obtained numerical results, the evolution of the solution is considered at three control points located around the cylinder with coordinates: A(5, 0), B(0, 5), and C(–3.54, 3.54). Figures 2b–2d show the change in pressure fluctuations depending on time at these points, obtained by numerical calculation with the values of the porosity coefficient, φ = 1.0 and φ = 0.01; in this case, the permeability coefficient did not change: η = 10−4. Their comparison with the exact solution indicates sufficient accuracy of the numerical simulation of acoustic wave scattering on a cylinder by the generalized BVPM. It can be seen that the introduction of the mathematical model of a porous medium into the continuity equation (φ = 0.01) allows elimination of the phase and amplitude errors in the modeled reflected acoustic waves, which are observed for φ = 1.0.

4.3 Oscillation of a Two-Dimensional Cylinder in a Medium at Rest

In this subsection, we consider the problem of the oscillating motion of a two-dimensional cylinder in a viscous medium, where the position of the center of mass of the cylinder is determined by the harmonic law \(y(t) = - A\sin (2\pi ft)\), \(x(t) = 0\).

For an incompressible medium surrounding a cylinder, the problem depends on the following dimensionless parameters: Reynolds numbers \(\operatorname{Re} = {{{{U}_{{\max }}}D} \mathord{\left/ {\vphantom {{{{U}_{{\max }}}D} \nu }} \right. \kern-0em} \nu }\) = 100 and Keulegan–Carpenter number \({{K}_{c}} = {{{{U}_{{\max }}}} \mathord{\left/ {\vphantom {{{{U}_{{\max }}}} {Df}}} \right. \kern-0em} {Df}}\) = 5. Here, D is the diameter of the cylinder, \({{U}_{{\max }}}\) is the maximum speed of the cylinder, and f is the oscillation frequency. In the case of a compressible medium, an additional dimensionless parameter is added, the Mach number \({\text{M}} = {{U}_{{\max }}}{\text{/}}{{c}_{0}}\), where \({{c}_{0}}\) is the speed of sound in a gas at rest.

Since quantities D and \({{U}_{{\max }}}\) are the characteristic parameters of the problem, it is easy to obtain expressions for the dimensionless frequency and dimensionless displacement amplitude, which are defined as \(f = \;{1 \mathord{\left/ {\vphantom {1 {{{K}_{c}}}}} \right. \kern-0em} {{{K}_{c}}}}\) and \(A = {{{{K}_{c}}} \mathord{\left/ {\vphantom {{{{K}_{c}}} {2\pi \,f}}} \right. \kern-0em} {2\pi \,f}}\), respectively.

For the case of incompressible flows, the problem was solved by the authors using the BVPM in the incompressible flow formulation [22]. In this study, the oscillating cylinder interacts with a compressible flow at the Mach number M = 0.4.

The computational domain has the shape of a square with sides l = 20.0, whose center coincides with the origin.

Numerical calculations were carried out using an unstructured triangular mesh. In the region of motion of the cylinder, the mesh thickens with the characteristic size of the element h = 0.02. The problem was solved in three formulations:

1. In an inertial coordinate system, where the boundary condition is modeled by the Galilean-invariant BVPM (designated on the graphs by GI BVPM).

2. In a non-inertial coordinate system related to a cylinder, where the boundary condition is modeled by the Galilean-invariant BVPM (designated on the graphs by GI BVPM).

3. In a non-inertial coordinate system related to the cylinder and on a body-fitted mesh (designated on the graphs by BFM).

The results of numerical simulation demonstrated that a quasi-stationary periodic flow is achieved \((t > 10.0)\). In this case, a force induced by the external environment begins to act on the surface of the cylinder. For a comparative analysis of the calculation results, we considered the temporal distribution of the transverse component of the force Fy, expressed in terms of the lift coefficient: \({{C}_{{\text{l}}}} = 2{{F}_{y}}{\text{/}}{{\rho }_{0}}{{U}_{{\max }}}\) (\({{\rho }_{0}}\) is the density of the unperturbed gas).

To calculate the components of the force vector, formula (7) is proposed in this paper, which allows performing calculations without integrating directly over the body’s boundary. The latter circumstance becomes especially important for the methods of immersed boundaries, since when they are used, the interface between two media is not explicitly defined.

In Fig. 3a, the time distributions of the coefficient Cl are presented, determined in the numerical solution of the problem in three formulations. In this case, the coefficient was calculated according to the standard formula for determining forces without taking into account the acceleration of the added fluid mass (the second term in (7)). It can be seen that the results obtained using the BVPM for different coordinate systems coincide with each other, but differ markedly from the body-fitted mesh results. The difference is due to the need to take into account the non-inertial force. The application of formula (7) made it possible to obtain close agreement between the results of the numerical calculations of this problem in all three formulations (Fig. 3b).

Fig. 3.
figure 3

Flow around an oscillating cylinder. The distribution of the lift force coefficient, obtained by numerically solving the problem in various formulations, was used to calculate the coefficient: (a) formula (7) without taking into account the force related to the acceleration of the added mass, (b) formula (7).

Full size image

5 CONCLUSIONS

This paper proposes a Galilean-invariant generalization of the BVPM for compressible flows, which extends the applicability of the method to problems of the flow around moving bodies. The developed method provides the possibility of performing calculations on structured and unstructured non-body fitted computational meshes. The Galilean-invariant formulation is obtained using the Galilean transformations of the penalized Navier–Stokes equations for a compressible gas in a frame of reference related to a moving body.

The Galilean-invariant generalized BVPM allows numerical simulation of compressible flows around both stationary and moving bodies. The effectiveness of the developed method is demonstrated for test problems of the direct reflection of a one-dimensional acoustic pulse from a flat stationary and moving surface, scattering of an acoustic wave by a stationary cylinder, and the problem of subsonic flow of a viscous gas around an oscillating cylinder. The obtained numerical results are in close agreement with the reference solutions and theoretical estimates of the convergence of the method, and they confirm the invariance of the proposed formulation with respect to the Galilean transformations. This paper also proposes a method for calculating the total force acting on a body during its translational motion, using the integration of the BVP over the space occupied by this body, and taking into account the acceleration of the attached fluid mass inside it.

On the whole, the results obtained in this work indicate the effectiveness of the numerical simulation of problems of the aerodynamic flow using the Galilean-invariant generalization of the BVPM for compressible flows. Further development is connected with the use of the VPM together with mesh adaptation, which allows the local resolution of complex geometry with the given accuracy without excessive resolution far from the boundaries. Of particular interest is the joint application of the VPM and the node redistribution method, which allows, in addition to making a mesh more refined/coarse, to adapt the anisotropy of the mesh without changing the topology of the mesh. The potential benefit of such an ext-ension is a significant reduction in grid nodes with the optimal representation of the anisotropy of the solution.