INTRODUCTION

The most widespread and conventional approach to the numerical simulation of boundary conditions in aerodynamic flow problems is based on body-fitted meshes in which the interface between two media is determined by mesh nodes and boundary conditions are specified by algebraic relations at these nodes. If the body has complex geometry, body-fitted mesh generation becomes a resource-intensive problem. This approach also becomes highly complicated in the case of moving or deformable boundaries, since it requires continuous adaptation or the construction of a new mesh with solution interpolation from the old to new meshes [1]. In this case, more efficient can be an alternative approach based on the immersed boundary method. According to this method, the problem can be considered in a simply connected domain and the boundary condition on a solid surface can be satisfied without fitting mesh nodes with the boundary. This approach substantially simplifies the mesh generation procedure and makes it possible to use methods of dynamic adaptation of a moving grid to the immersed body surface with the preservation of the mesh topology, which is especially useful in the modeling of flows around moving objects.

Immersed boundary methods can be divided into two large classes: discrete and differential (volume) methods. Discrete approaches are based on direct transformations of discretized equations ensuring the fulfillment of the boundary conditions, so these approaches are difficult to generalize because of their direct dependence on discretization methods (see, e.g., [2–4]). The most serious shortcomings of discrete immersed boundary methods are that they lack mathematical proofs of their convergence and the approximation error of boundary conditions is difficult to control. Differential immersed boundary methods (see, e.g., [5–7]) are based on the solution of differential equations modified by introducing penalty functions in the form of additional forces or feedback terms ensuring the fulfillment of the boundary conditions.

The immersed boundary method as a class was formulated by Peskin for the numerical simulation of a heart valve [8]. A wide variety of immersed boundary methods for viscous incompressible flows has been developed to date (see, e.g., [1]). Examples are ghost cell methods [9], cut-cell methods [10, 11], the free-boundary method [12], penalization methods [13], and the fictitious domain method [14].

Penalization methods make up a subclass of differential immersed boundary methods in which solid bodies are modeled by adding source terms to the system of differential equations determining the mathematical model of the gasdynamic process. An example is the Brinkman penalization method (BPM), in which a solid obstacle is modeled as a porous medium with low permeability. For this purpose, penalty functions that are nonzero within the porous medium are added to the momentum and energy equations of the Navier–Stokes system. An advantage of the method is that the error can be controlled by monitoring the value of the penalty parameter. Moreover, mathematical justification of the method for incompressible flows is based on the proved result that the solution of the Navier–Stokes equations involving penalty functions converges to the exact solution as the penalty parameter tends to zero [15].

In the Russian-language literature, the differential subclass of immersed boundary methods was developed as an independent parallel research direction known as the fictitious domain method [14]. Its underlying idea is that an approximate problem is solved not in the original domain \({{\Omega }_{E}}\) of complex geometry, but rather in a simpler domain \(\Omega \) containing \({{\Omega }_{E}} \subset \Omega \). An auxiliary problem in the fictitious (complementary) domain \({{\Omega }_{B}} = \Omega {{\backslash }}{{\Omega }_{E}}\) is formulated so that it involves a small parameter η determining the size of the jump in the coefficients of the equations across the domain boundary \(\partial {{\Omega }_{B}}\) and the approximate solution of the parameterized problem converges to the exact solution in \({{\Omega }_{E}}\) as \(\eta \to 0\). A detailed literature review on the history and applications of this method can be found in [14]. Below, we briefly discuss works associated with the development and use of the fictitious domain method as applied to problems in hydromechanics. A fundamental work in this direction is due to Vishik [16], where the idea of the fictitious domain method on the transition to an expanded domain was formulated. For the first time, the fictitious domain method as a technique for numerical solution of elliptic problems with complex geometry was formulated in [17, 18]. Specifically, the method with extension with respect to leading coefficients was developed and the error of the approximate solution was estimated. A generalization of the fictitious domain method with extension with respect to smaller coefficients was suggested by Lebedev [19]. Extensions of the method to the incompressible Navier–Stokes equations were considered in numerous studies concerning the numerical simulation of steady (see, e.g., [20–25]) and unsteady (see, e.g., [6, 26, 27]) flows. Note that the fictitious domain method with extension with respect to smaller coefficients is mathematically identical to the Brinkman penalization method. In the English-language literature, both names are used interchangeably (see, e.g., [13, 28, 29]), but the latter is more popular, although the fictitious domain method was coined earlier. Since these two approaches are mathematically equivalent, to simplify the discussion, all differential subclasses of the immersed boundary method are referred to in this work as penalization methods.

The Brinkman penalization method was first proposed in [30] and was later successfully used for numerical simulation of incompressible flows [31–34]. Several attempts were made to adapt it to the simulation of compressible flows. Among them, we mention the approach suggested in [35] and successfully used, for example, in [36]. It was shown in [35, 36] that propagation of sound waves through a porous medium is correctly described by the proposed modification.

Practical application of the Brinkman penalization method was substantially limited by the fact that only Dirichlet boundary conditions can be specified at the interface between two media. This shortcoming was overcome in the characteristic-based volume penalization method proposed in [37]. The possibility of specifying Robin and Neumann boundary conditions in this method is of interest for the study of its practical applicability. Some results of this type can be found in [37], where the characteristic based volume penalization method is successfully used for numerical simulation of a number of benchmark problems, including diffusion in one-dimensional setting, reflection of an acoustic pulse, and laminar flow around a two-dimensional cylinder. In [38] a numerical solution technique on structured meshes was developed using the adaptive wavelet collocation method, which provides active error control and the necessary local grid resolution based on dynamic grid adaptation.

In this work, we refine the formulation of the characteristic based volume penalization method and use it to construct a finite-volume/finite-difference technique for numerical simulation of viscous compressible flows on unstructured meshes. Spatial discretization is based on high-accuracy quasi-one-dimensional edge-based reconstructions (EBR) of flux variables [39]. The accuracy and correctness of the new method are investigated through the numerical simulation of problems with an adiabatic boundary condition: reflection of an acoustic pulse, reflection of a shock wave from a wall, and the Couette flow.

1. CHARACTERISTIC BASED VOLUME PENALIZATION METHOD

As a baseline mathematical model for describing viscous compressible flows, we consider the Navier–Stokes equations written in terms of physical variables: the density \(\rho \), velocity components \({{u}_{i}}\), and specific internal energy \(\varepsilon \):

$$\begin{gathered} \frac{{\partial \rho }}{{\partial t}} = - \frac{{\partial \rho {{u}_{i}}}}{{\partial {{x}_{i}}}} = {\text{RH}}{{{\text{S}}}_{\rho }}, \\ \frac{{\partial {{u}_{i}}}}{{\partial t}} = - {{u}_{j}}\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{j}}}} - \frac{1}{\rho }\frac{{\partial p}}{{\partial {{x}_{i}}}} + \frac{1}{\rho }\frac{{\partial {{P}_{{ij}}}}}{{\partial {{x}_{j}}}} = {\text{RH}}{{{\text{S}}}_{{{{u}_{i}}}}}, \\ \frac{{\partial \varepsilon }}{{\partial t}} = - {{u}_{i}}\frac{{\partial \varepsilon }}{{\partial {{x}_{i}}}} - \frac{p}{\rho }\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{i}}}} + \frac{1}{\rho }D + \frac{1}{\rho }\frac{{\partial {{q}_{i}}}}{{\partial {{x}_{i}}}} = {\text{RH}}{{{\text{S}}}_{\varepsilon }}. \\ \end{gathered} $$
(1)

Here and below, the abbreviation \({\text{RHS}}\) with a subscript stands for corresponding physically justified right-hand sides of the system of equations. System (1) is closed by the ideal gas law \(p = \left( {\gamma - 1} \right)\rho \varepsilon \), where \({{\gamma }} = 1.4\) is the ratio of specific heats. The following notation was used in system (1):

• \({{P}_{{ij}}} = 2\mu {{S}_{{ij}}} - \frac{2}{3}\mu \frac{{\partial {{u}_{i}}}}{{\partial {{x}_{i}}}}{{\delta }_{{ij}}}\) is the viscous stress tensor, and \({{S}_{{ij}}} = \frac{1}{2}\left( {\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{j}}}} + \frac{{\partial {{u}_{j}}}}{{\partial {{x}_{i}}}}} \right)\) is the strain rate tensor;

• \(D = {{S}_{{ij}}}{{P}_{{ij}}}\) is a dissipative function;

• \({{q}_{i}} = \frac{\gamma }{{\Pr }}\mu \frac{{\partial \varepsilon }}{{\partial {{x}_{i}}}}\) is the heat flux, and \({\text{Pr}} = 0.72\) is the Prandtl number;

• \(\mu \) is the molecular viscosity.

Here, repeated direction indices \(i,j = 1, \ldots ,d\) imply summation over the directions and d is the dimension of the problem. In the case of external flow over a solid body, we use the following notation:

• \(\Omega \) is the domain of the problem;

• \({{\Omega }_{B}}\) is the internal domain of the solid body;

• \(\partial {\kern 1pt} {{\Omega }_{B}}\) is the boundary of the solid body;

• \({{\Omega }_{E}} = \Omega {{\backslash }}({{\Omega }_{B}} \cup \partial {{\Omega }_{B}})\) is the domain surrounding the solid body;

• \({\mathbf{n}}\) is the inward normal to the boundary \(\partial {{\Omega }_{B}}\).

In the test problems considered in this work, on the boundary of the solid body, we set the no-slip condition \({{\left. {\mathbf{u}} \right|}_{{\partial {{\Omega }_{B}}}}} = {\text{ }}{{{\mathbf{u}}}_{w}}\) and the adiabatic condition \({{\left. {(\nabla \varepsilon ,{\mathbf{n}})} \right|}_{{\partial {{\Omega }_{B}}}}} = 0\), where \({{{\mathbf{u}}}_{w}}\) is the velocity of the solid body.

According to the immersed boundary method, the location of the solid body is determined by the indicator function

$$\chi ({\mathbf{x}},t) = \left\{ \begin{gathered} 1,\quad {\mathbf{x}} \in {{{\bar {\Omega }}}_{B}}, \hfill \\ 0,\quad {\mathbf{x}} \notin {{{\bar {\Omega }}}_{B}}, \hfill \\ \end{gathered} \right.$$

where \({{\bar {\Omega }}_{B}} = {{\Omega }_{B}} \cup \partial {{\Omega }_{B}}\).

In the characteristic based volume penalization method, the no-slip boundary condition for velocity is satisfied by adding penalty functions to the equations for the velocity components:

$$\frac{{\partial {{u}_{i}}}}{{\partial t}} = (1 - \chi ){\text{RH}}{{{\text{S}}}_{{{{u}_{i}}}}} - \underbrace {\frac{\chi }{{{{\eta }_{b}}}}({{u}_{i}} - {{u}_{{w,}}}_{i})}_{{\text{penalty function}}} + \chi {{\nu }_{n}}\Delta {{u}_{i}}.$$
(2)

For the no-slip condition, the penalty functions have the same form as in the Brinkman penalization method with a penalty parameter \({{\eta }_{b}} \ll 1\). For the solution to be smooth in the domain \({{\bar {\Omega }}_{B}}\), we add a diffusion term with \(\Delta {\kern 1pt} {\kern 1pt} {{u}_{i}},\) where \({{\nu }_{n}}\) is an artificial viscosity coefficient proportional to the mesh size \(h\). This term introduces artificial viscosity in explicit form. For schemes of first-order accuracy in space, the role of artificial viscosity is played by numerical viscosity and diffusion does not need to be added in explicit form. In [16], to make the error of the numerical solution independent of the parameter \({{\eta }_{b}}\), the artificial viscosity was taken proportional to \({{{{h}^{2}}} \mathord{\left/ {\vphantom {{{{h}^{2}}} {{{\eta }_{b}}}}} \right. \kern-0em} {{{\eta }_{b}}}}\). The expression \((1 - \chi ){\text{RH}}{{{\text{S}}}_{{{{u}_{i}}}}}\) used in Eq. (2) means that the convective and diffuse transport terms are eliminated from Eqs. (1) at computational points inside the solid body. This is done to eliminate their possible influence on the relaxation of the solution toward the required boundary condition.

The boundary condition of surface adiabaticity means that the homogeneous Neumann boundary condition is set for internal energy (or temperature).

In the general case, the fulfillment of the Neumann condition \({{\left. {(\nabla f,{\mathbf{n}})} \right|}_{{\partial {{\Omega }_{B}}}}} = q({\mathbf{x}})\) in the direction of the inward normal \({\mathbf{n}} = ({{n}_{1}}, \ldots ,{{n}_{d}})\) to the obstacle surface in the characteristic based volume penalization method is ensured by solving the following hyperbolic equation with a penalty term:

$$\frac{{\partial f}}{{\partial t}} = (1 - \chi ){\text{RH}}{{{\text{S}}}_{f}} - \underbrace {\frac{\chi }{{{{\eta }_{c}}}}\left( {{{n}_{k}}\frac{{\partial f}}{{\partial {{x}_{k}}}} - {{q}_{w}}({\mathbf{x}})} \right)}_{{\text{characteristic penalty function}}},$$
(3)

where \({{\eta }_{c}} \ll 1\) is a small penalty parameter, which is generally different from the penalty parameter \({{\eta }_{b}}\) in Eq. (2).

The penalty source term in Eq. (3) is defined over the entire volume of the obstacle domain \({{\Omega }_{B}}\), rather than over its surface, so the definition of the normal to the surface \(\partial {{\Omega }_{B}}\) is generalized to the entire domain \({{\Omega }_{B}}\) by taking the gradient of the scalar distance function

$${\mathbf{n}}({\mathbf{x}}) = \nabla \delta ({\mathbf{x}}),\quad {\mathbf{x}} \in {{\Omega }_{B}},$$

where \(\delta \) is the distance to the nearest point of the boundary:

$$\delta ({\mathbf{x}}) = \left\{ \begin{gathered} \mathop {\min }\limits_{y \in \partial {{\Omega }_{B}}} \left\| {x - y} \right\|,\quad {\mathbf{x}} \in \Omega {{\backslash }}{{\Omega }_{B}}, \hfill \\ - {\kern 1pt} \mathop {\min }\limits_{y \in \partial {{\Omega }_{B}}} \left\| {x - y} \right\|,\quad {\mathbf{x}} \in {{\Omega }_{B}}. \hfill \\ \end{gathered} \right.$$

Mathematically, Eq. (3) describes transport of the solution into the interior of \({{\Omega }_{B}}\) along inward-directed characteristics, so that the derivative of the function  f in the direction of the normal n to the body boundary \(\partial {\kern 1pt} {{\Omega }_{B}}\) takes the required value. The matter is that the choice of \({{\eta }_{c}} \ll 1\) leads to Eq. (3) becoming quasi-stationary within \({{\Omega }_{B}}\) on the scale of the characteristic time \({{t}_{H}} = {L \mathord{\left/ {\vphantom {L {{{U}_{0}}}}} \right. \kern-0em} {{{U}_{0}}}}\) of the solution to the fluid dynamics equations (here, \(L\) is the characteristic size of the obstacle and \({{U}_{0}}\) is the characteristic flow velocity near the obstacle). In dimensionless variables (marked with a tilde) Eq. (3) in \({{\Omega }_{B}}\) can be written as

$$\frac{{{{t}_{R}}}}{{\mathop {{{t}_{H}}}\limits_{ \ll 1} }}\;\frac{{\partial \tilde {f}}}{{\mathop {\partial t}\limits_{ \sim O\left( 1 \right)} }} = \underbrace {{{n}_{k}}\frac{{\partial \tilde {f}}}{{\partial {{{\tilde {x}}}_{k}}}} - {{{\tilde {q}}}_{w}}({\mathbf{x}})}_{ \sim O\left( 1 \right)},$$
(4)

where \({{t}_{R}} = {{\eta }_{c}}L\) is the relaxation time. Since \({{{{t}_{R}}} \mathord{\left/ {\vphantom {{{{t}_{R}}} {{{t}_{H}} = {{U}_{0}}{{\eta }_{c}} \ll 1}}} \right. \kern-0em} {{{t}_{H}} = {{U}_{0}}{{\eta }_{c}} \ll 1}}\) at moderate characteristic flow velocities, Eq. (4) implies that the boundary condition holds on O(tR) time scales, i.e.,

$$\frac{{\partial f}}{{\partial n}} \to {{q}_{w}}({\mathbf{x}})\quad {\text{as}}\quad {{\eta }_{c}} \to 0$$

with an \(O({{U}_{0}}{{\eta }_{c}})\) asymptotic error. Thus, the adiabatic boundary condition on the surface is ensured by adding characteristic penalty functions to the specific internal energy equation

$$\frac{{\partial \varepsilon }}{{\partial t}} = (1 - \chi ){\text{RH}}{{{\text{S}}}_{{{\kern 1pt} \varepsilon }}} - \frac{\chi }{{{{\eta }_{c}}}}{{n}_{k}}\frac{{\partial \varepsilon }}{{\partial {{x}_{k}}}}.$$
(5)

In flows with attached boundary layers, such as flows in the linear acoustic approximation, the normal gradient of pressure on the boundary \({{\left. {(\nabla p,{\mathbf{n}})} \right|}_{{\partial {{\Omega }_{B}}}}}\) vanishes. For the equation of state to hold on the adiabatic boundary of the solid body, the normal gradient of density on the boundary has to vanish as well, i.e., \({{\left. {(\nabla \rho ,{\mathbf{n}})} \right|}_{{\partial {{\Omega }_{B}}}}} = 0\), which can be treated as an additional boundary condition on the solid surface for the discretized Navier–Stokes equations.

In the general case (e.g., for separated flows), when \({{\left. {(\nabla \rho ,{\mathbf{n}})} \right|}_{{\partial {{\Omega }_{B}}}}} \ne 0\), we set an inhomogeneous boundary condition on the derivative of density in the normal direction n:

$${{\left. {(\nabla \rho ,{\mathbf{n}})} \right|}_{{\partial {{\Omega }_{B}}}}} = \Phi ({\mathbf{x}}).$$
(6)

Then, according to the general definition (3) of Neumann conditions in the characteristic based volume penalization method, the fulfillment of boundary condition (6) is ensured by modifying the continuity equation:

$$\frac{{\partial \rho }}{{\partial t}} = (1 - \chi ){\text{RH}}{{{\text{S}}}_{{{\kern 1pt} \rho }}} - \underbrace {\frac{\chi }{{{{\eta }_{c}}}}\left( {{{n}_{k}}\frac{{\partial \rho }}{{\partial {{x}_{k}}}} - \Phi \left( {{\mathbf{x}},t} \right)} \right)}_{{\text{characteristic penalty function}}}.$$
(7)

Here, \(\Phi ({\mathbf{x}},t)\) is a function satisfying the following boundary value problem for the transport equation:

$$\frac{{\partial \Phi }}{{\partial t}} = - \frac{\chi }{{{{\eta }_{c}}}}\frac{{\partial \Phi }}{{\partial n}},\quad {{\left. \Phi \right|}_{{\partial {{\Omega }_{B}}}}} = {{\left. {\frac{{\partial \rho }}{{\partial n}}} \right|}_{{\partial {{\Omega }_{B}}}}}.$$
(8)

According to [40], the solution of problem (8) can be interpreted as extrapolation of the boundary value of \(\Phi \) to the interior of the domain.

For \(\chi = 1\), penalized equations (2), (5), (7), and (8) written in terms of the physical variables \({{(\rho ,{\mathbf{u}},\varepsilon )}^{\text{T}}}\) determine the solution of the problem inside \({{\Omega }_{B}}\); moreover, the no-slip boundary condition is satisfied and there is no heat flux across the boundary of the solid body.

Thus, the system of penalized equations (2), (5), (7), and (8) extends the Navier–Stokes equations (1) to the entire domain \(\Omega \) and determines a mathematical model of viscous compressible gas flow over a solid body with boundary conditions imposed automatically with the help of the characteristic based volume penalization method.

It was shown in [8] that the asymptotic error in the Dirichlet condition simulated by applying the Brinkman penalization method is \(O(\eta _{b}^{{1/2}})\). In the characteristic based volume penalization method, the error in Neumann conditions has \(O({{\eta }_{c}})\) asymptotics, which was shown in [37] and illustrated in Eq. (4).

2. NUMERICAL METHOD

System (2), (5), (7) written in terms of the vector of conservative variables \({{(\rho ,\rho {\mathbf{u}},E)}^{\text{T}}}\) is solved together with Eq. (8) by numerical integration over the entire domain \(\Omega \). Here, \(E = {{\rho {{{\mathbf{u}}}^{2}}} \mathord{\left/ {\vphantom {{\rho {{{\mathbf{u}}}^{2}}} 2}} \right. \kern-0em} 2} + {p \mathord{\left/ {\vphantom {p {(\gamma - 1)}}} \right. \kern-0em} {(\gamma - 1)}}\) is the total energy determined taking into account the ideal gas law. Time stepping is based on an implicit integration scheme with Newton linearization.

Spatial discretization of the equations in the domain \({{\Omega }_{E}} = \Omega {{\backslash }}{{\bar {\Omega }}_{B}}\) (with \(\chi = 1\)) is based on a finite-volume EBR scheme whose high accuracy is achieved due to quasi-one-dimensional edge-based reconstructions of flux variables on an unstructured mesh [39].

The numerical integration of system (2), (5), (7) in \({{\bar {\Omega }}_{B}}\) is described as follows.

Rewritten in terms of conservative variables, system (2), (5), (7), and (8) becomes

$$\begin{gathered} \frac{{\partial \rho }}{{\partial t}} = - \frac{1}{{{{\eta }_{c}}}}\frac{{\partial \rho }}{{\partial n}} + \frac{1}{{{{\eta }_{c}}}}\Phi , \\ \frac{{\partial \rho u}}{{\partial t}} = - \frac{1}{{{{\eta }_{c}}}}u\frac{{\partial \rho }}{{\partial n}} + \frac{1}{{{{\eta }_{c}}}}u\Phi - \frac{1}{{{{\eta }_{b}}}}\rho (u - {{u}_{w}}) + \rho {{\nu }_{n}}\Delta u, \\ \end{gathered} $$
$$\begin{gathered} \frac{{\partial \rho v}}{{\partial t}} = - \frac{1}{{{{\eta }_{c}}}}v\frac{{\partial \rho }}{{\partial n}} + \frac{1}{{{{\eta }_{c}}}}v\Phi - \frac{1}{{{{\eta }_{b}}}}\rho (v - {{v}_{w}}) + \rho {{\nu }_{n}}\Delta v, \\ \frac{{\partial E}}{{\partial t}} = \frac{1}{{{{\eta }_{c}}}}\left[ { - ({{u}^{2}} + {{v}^{2}})\frac{{\partial \rho }}{{\partial n}} + u\frac{{\partial \rho u}}{{\partial n}} + v\frac{{\partial \rho v}}{{\partial n}} - \frac{{\partial E}}{{\partial n}}} \right] \\ \end{gathered} $$
(9)
$$\begin{gathered} - \;\frac{1}{{{{\eta }_{b}}}}\left[ {\rho u(u - {{u}_{w}}) + \rho v(v - {{v}_{w}})} \right] + \frac{1}{{{{\eta }_{c}}}}\frac{E}{\rho }\Phi + \rho {{\nu }_{n}}(u\Delta u + v\Delta v), \\ \frac{{\partial \Phi }}{{\partial t}} = - \chi \frac{1}{{{{\eta }_{c}}}}\frac{{\partial \Phi }}{{\partial n}}. \\ \end{gathered} $$

The normal derivatives in system (9) are approximated by first-order upwind differences, which are characterized by numerical diffusion proportional to the mesh size. For this reason, the terms with artificial viscosity \({{\nu }_{n}}\Delta {\kern 1pt} {\kern 1pt} {\mathbf{u}}\) were dropped from the subsequent analysis.

System (9) can be written in matrix-vector form as

$$\frac{{\partial \operatorname{Q} }}{{\partial t}} = {\mathbf{A}}\frac{{\partial \mathbf{Q}}}{{\partial n}} + {\mathbf{S}},$$
(10)

where \(\mathbf{Q} = {{(\rho ,\;\rho u,\;\rho {v},\;E,\;\Phi )}^{\text{T}}}\) is the vector of conservative variables,

$${\mathbf{A}} = \frac{1}{{{{\eta }_{c}}}}\left( {\begin{array}{*{20}{l}} { - 1}&0&0&0&0 \\ { - u}&0&0&0&0 \\ { - {v}}&0&0&0&0 \\ { - ({{u}^{2}} + {{{v}}^{2}})}&u&{v}&{ - 1}&0 \\ 0&0&0&0&{ - 1} \end{array}} \right),\quad {\mathbf{S}} = \left( {\begin{array}{*{20}{l}} {\frac{1}{{{{\eta }_{c}}}}\Phi } \\ { - \frac{1}{{{{\eta }_{b}}}}\rho (u - {{u}_{w}}) + \frac{1}{{{{\eta }_{c}}}}u\Phi } \\ { - \frac{1}{{{{\eta }_{b}}}}\rho ({v} - {{{v}}_{w}}) + \frac{1}{{{{\eta }_{c}}}}{v}\Phi } \\ { - \frac{1}{{{{\eta }_{b}}}}\left[ {\rho u(u - {{u}_{w}}) + \rho {v}({v} - {{{v}}_{w}})} \right] + \frac{1}{{{{\eta }_{c}}}}\frac{E}{\rho }\Phi } \\ 0 \end{array}} \right).$$

Without loss of generality, we assume that the domain \({{\bar {\Omega }}_{B}}\) is covered by an unstructured mesh with triangular elements \({{T}_{j}}\) such that \({{\bar {\Omega }}_{B}} = \bigcup\nolimits_j^{} {{{T}_{j}}} \) and \({{T}_{j}} \cap {{T}_{i}} = \varnothing \) \({\text{(}}i \ne j{\text{)}}\). It follows that all nodes \({{{\mathbf{x}}}_{i}} \in {{\bar {\Omega }}_{B}}\), where \(i = 1, \ldots ,N.\) Note that the grid in \({{\bar {\Omega }}_{B}}\) may include quadrilateral cells, which can always be represented as the union of two triangles.

System (10) is solved numerically by applying the implicit difference scheme

$$\frac{{\mathbf{Q}_{i}^{{n + 1}} - \mathbf{Q}_{i}^{n}}}{\tau } = {{{\mathbf{A}}}^{n}}\frac{{\mathbf{Q}_{i}^{{n + 1}} - \mathbf{Q}_{{i'}}^{{n + 1}}}}{{\Delta {{r}_{{ii'}}}}} + \mathbf{S}_{i}^{{n + 1}}.$$
(11)

Here, the inward normal derivative is approximated by a one-sided difference and the point with index \(i{\kern 1pt} '\) is the nearest point of intersection of the inward normal starting at the point \(i\) and an edge of a triangular element. The value \({{\mathbf{Q}}_{{i'}}}\) is found by linear interpolation between \({{\mathbf{Q}}_{{{{i}_{1}}}}}\) and \({{\mathbf{Q}}_{{{{i}_{2}}}}}\), where \({{i}_{1}}\) and \({{i}_{2}}\) are the indices of the nodes forming the intersected face:

$${{\mathbf{Q}}_{{i'}}} = {{C}_{1}}{{\mathbf{Q}}_{{{{i}_{1}}}}} + {{C}_{2}}{{\mathbf{Q}}_{{{{i}_{2}}}}},$$

where \({{C}_{1}}\) and \({{C}_{2}}\) are coefficients of linear interpolation and \(\Delta {{r}_{{ii'}}}\) is the distance between the points with indices \(i\) and \(i{\kern 1pt} '\).

To solve the nonlinear difference equation (11) at a single time step, we construct the following iterative process (\(s\) is the iteration number) for finding the increment \({{\mathop {\Delta \mathbf{Q}}\limits^{(s)} }_{i}} = \mathop {{\mathbf{Q}}_{i}^{{n + 1}}}\limits^{(s + 1)} - \mathop {{\mathbf{Q}}_{i}^{{n + 1}}}\limits^{(s)} \):

$$\begin{gathered} \frac{{{{{\mathop {\Delta \mathbf{Q}}\limits^{(s)} }}_{i}}}}{\tau } = {\mathbf{A}}_{i}^{n}\frac{{{{{\mathop {\Delta \mathbf{Q}}\limits^{(s)} }}_{i}} - {{C}_{1}}{{{\mathop {\Delta \mathbf{Q}}\limits^{(s)} }}_{{{{i}_{1}}}}} - {{C}_{2}}{{{\mathop {\Delta \mathbf{Q}}\limits^{(s)} }}_{{{{i}_{2}}}}}}}{{\Delta {{r}_{{ii'}}}}} + \mathop {{\mathbf{S}}_{{{\mathbf{Q}},i}}^{{n + 1}}}\limits^{(s)} {{\mathop {\Delta \mathbf{Q}}\limits^{(s)} }_{i}} \\ + \;{\mathbf{A}}_{i}^{n}\frac{{\mathop {{\mathbf{Q}}_{i}^{{n + 1}}}\limits^{(s)} - {{C}_{1}}\mathop {{\mathbf{Q}}_{{{{i}_{1}}}}^{{n + 1}}}\limits^{(s)} - {{C}_{2}}\mathop {{\mathbf{Q}}_{{{{i}_{2}}}}^{{n + 1}}}\limits^{(s)} }}{{\Delta {{r}_{{ii'}}}}} - \frac{{\mathop {{\mathbf{Q}}_{i}^{{n + 1}}}\limits^{(s)} - {\mathbf{Q}}_{i}^{n}}}{\tau } + \mathop {{\mathbf{S}}_{i}^{{n + 1}}}\limits^{(s)} , \\ \end{gathered} $$

where \({{{\mathbf{S}}}_{{\mathbf{Q}}}}\) is the Jacobian matrix of the source term in scheme (11):

$${{{\mathbf{S}}}_{{\mathbf{Q}}}} = \frac{{\partial {\mathbf{S}}}}{{\partial {\mathbf{Q}}}} = ( - 1)\left( {\begin{array}{*{20}{c}} 0&0&0&0&{\frac{1}{{{{\eta }_{c}}}}} \\ { - \frac{{{{u}_{w}}}}{{{{\eta }_{b}}}} + \frac{u}{{{{\eta }_{c}}\rho }}\Phi }&{\frac{1}{{{{\eta }_{b}}}} + \frac{1}{{{{\eta }_{c}}\rho }}\Phi }&0&0&{ - \frac{1}{{{{\eta }_{c}}}}u} \\ { - \frac{{{{{v}}_{w}}}}{{{{\eta }_{b}}}} + \frac{{v}}{{{{\eta }_{c}}\rho }}\Phi }&0&{\frac{1}{{{{\eta }_{b}}}} + \frac{1}{{{{\eta }_{c}}\rho }}\Phi }&0&{ - \frac{1}{{{{\eta }_{c}}}}{v}} \\ { - \frac{1}{{{{\eta }_{b}}}}({{u}^{2}} + {{{v}}^{2}}) + \frac{E}{{{{\eta }_{c}}{{\rho }^{2}}}}\Phi }&{\frac{1}{{{{\eta }_{b}}}}(2u - {{u}_{w}})}&{\frac{1}{{{{\eta }_{b}}}}(2{v} - {{{v}}_{w}})}&{ - \frac{1}{{{{\eta }_{c}}\rho }}\Phi }&{ - \frac{1}{{{{\eta }_{c}}}}\frac{E}{\rho }} \\ 0&0&0&0&0 \end{array}} \right).$$

As a result, we obtain a system of linear algebraic equations (SLAE) for finding the block increment vector \(\mathop {\Delta \mathbf{Q}}\limits^{(s)} = {{\left( {{{{\mathop {\Delta \mathbf{Q}}\limits^{(s)} }}_{1}}, \ldots ,{{{\mathop {\Delta \mathbf{Q}}\limits^{(s)} }}_{i}}, \ldots {{{\mathop {\Delta \mathbf{Q}}\limits^{(s)} }}_{N}}} \right)}^{\text{T}}}\), namely,

$$\left( {\frac{1}{\tau }{\mathbf{I}} - {\mathbf{D}} - {\mathbf{M}}} \right)\mathop {\Delta \mathbf{Q}}\limits^{(s)} = {\mathbf{M}}\mathop {{{{\mathbf{Q}}}^{{n + 1}}}}\limits^{(s)} - \frac{{\mathop {{{{\mathbf{Q}}}^{{n + 1}}}}\limits^{(s)} - {{{\mathbf{Q}}}^{n}}}}{\tau } + \mathop {{{{\mathbf{H}}}^{{n + 1}}}}\limits^{(s)} ,$$
(12)

where \({\mathbf{I}}\) is the \(5N \times 5N\) identity matrix, \({\mathbf{D}}\) and \({\mathbf{M}}\) are \(N \times N\) block matrices (with \(5 \times 5\) blocks) having the following structure (\(i\) is the row number and \({{i}_{1}}\), \({{i}_{2}}\) are the column numbers):

• \({\mathbf{D}} = \operatorname{diag} \left\{ {\mathop {{\mathbf{H}}_{{{\mathbf{Q}},i}}^{{n + 1}}}\limits^{(s)} } \right\}\) is a diagonal matrix,

• \({\mathbf{M}} = \operatorname{diag} \{ {\mathbf{A}}_{i}^{n}\} + \operatorname{offdiag} \left\{ {{{{( - {{C}_{1}}{\mathbf{A}}_{i}^{n})}}_{{i{{i}_{1}}}}},{{{( - {{C}_{2}}{\mathbf{A}}_{i}^{n})}}_{{i{{i}_{2}}}}}} \right\}\) is a matrix having three nonzero blocks in a row.

Solving system (12) yields a vector of variables at the next iteration: \(\mathop {{\mathbf{Q}}_{i}^{{n + 1}}}\limits^{(s + 1)} = \mathop {{\mathbf{Q}}_{i}^{{n + 1}}}\limits^{(s)} + {{\mathop {\Delta \mathbf{Q}}\limits^{(s)} }_{i}}\). As an initial approximation of \(\mathop {{\mathbf{Q}}_{i}^{{n + 1}}}\limits^{(0)} \), we use \(\mathbf{Q}_{i}^{n}\).

Thus, the iterative time stepping process for Eqs. (2), (5), (7), and (8) can be organized in a unified manner for the entire domain \(\Omega \). The dependence of variables in the domains \(\Omega {{\backslash }}{{\bar {\Omega }}_{B}}\) and \({{\bar {\Omega }}_{B}}\) is determined, on the one hand, by the approximation stencil for the normal derivatives in Eqs. (9) and, on the other hand, by the reconstruction stencil for variables in the conservative form of the equations of system (1). At every iteration step, we obtain a unified SLAE, which is solved using the stabilized biconjugate gradient method (BiCGStab) [41] with ILU0 preconditioner.

3. NUMERICAL RESULTS

In this section, we consider numerical results obtained by solving benchmark problems having exact solutions.

The first two problems are the one-dimensional reflection of an acoustic pulse and a shock wave from a solid surface, which are considered in two-dimensional setting and in the inviscid approximation. The solutions of these initial-boundary value problems for the one-dimensional Euler equations are well-known, and they can be used for comparison with numerical results produced by two-dimensional computations of the Navier–Stokes equations at high Reynolds numbers (for example, \(\operatorname{Re} > {{10}^{6}}\)) with a zero heat flux on the solid wall (adiabatic surface). Indeed, on the solid surface, the impermeability condition (zero normal velocity on the boundary) for the Euler equations coincides with the no-slip condition for the Navier–Stokes equation in the one-dimensional case (\(u = 0\)). The natural condition for the Euler equations—no energy flux across the solid surface due to the zero normal velocity on the boundary—also holds for the Navier–Stokes equations in the case of the homogeneous Neumann boundary condition for temperature or internal energy (\({{\partial \varepsilon } \mathord{\left/ {\vphantom {{\partial \varepsilon } {\partial x}}} \right. \kern-0em} {\partial x}} = 0\)). Thus, the solutions of these two problems for the Euler equations can be regarded as solutions of the Navier–Stokes equations up to \(O\left( {{1 \mathord{\left/ {\vphantom {1 {\operatorname{Re} }}} \right. \kern-0em} {\operatorname{Re} }}} \right)\) and can be used to verify the treatment of the Neumann boundary condition in the characteristic based volume penalization method. Note that the estimate given above is valid only in the one-dimensional case. In the multidimensional case, in the presence of a solid surface, the solution of the Navier–Stokes equations has asymptotics of order \(O(1{\text{/}}{{\operatorname{Re} }^{{1/2}}})\).

As a third test problem, we consider the Couette flow between two plates, in which case the characteristic based volume penalization method can be verified in the presence of shear stress on the solid wall and in the case of a moving surface (inhomogeneous Dirichlet condition). In this problem, the pressure gradient is assumed to be zero and, to obtain a nontrivial solution (different from the “classical” linear one for the velocity profile), the viscosity is specified not by a constant, but rather as inversely proportional to the square root of temperature. For this formulation in the case of different boundary conditions (Neumann or Dirichlet) set on the opposite plates, the problem has an exact solution (see the documentation section at https://github.com/bahvalo/ColESo).

For a more complete analysis, the same problems were also solved numerically by applying the Brinkman penalization method. For this purpose, we used the same grid, time stepping, and spatial discretization [42]. Note that, in the Brinkman penalization method, there are no explicit tools (like penalty constraints on the temperature derivative in the normal direction) ensuring the fulfillment of the adiabatic condition on the body surface. Note also that, while applying this method, we did not modify the continuity equation in contrast to [35] and did not introduce porosity to control the acoustic impedance in the penalty domain and to ensure insignificant penetration and appropriate reflection of acoustic waves.

3.1. Reflection of a One-Dimensional Acoustic Pulse

The problem was considered in the two-dimensional formulation in the rectangular domain \(\Omega = \left[ { - 0.65,0.25} \right] \times \left[ {0,0.1} \right]\) with the immersed interface \(x = 0\) and the penalty domain \({{\bar {\Omega }}_{B}} = \left[ {0,0.25} \right] \times \left[ {0,0.1} \right]\). In \(\Omega \) we introduced a structured mesh and a sequence of refined unstructured quasi-uniform triangular meshes (with a halved element size). Additionally, a nonuniform triangular mesh was constructed in which the element size near the boundary was equal to its value in the fine grid and was further increased (with a coefficient of 1.02) to the element size in the coarse grid. The types and sizes of the grids are given in Table 1, and grid fragments are shown in Fig. 1.

Table 1.   Types of grids and their characteristic sizes
Full size table
Fig. 1.
figure 1

Fragments of unstructured triangular meshes: (a) UTM1, (b) UTM2, and (c) UTM4.

Full size image

The penalized system (2), (5), (7), and (8) rewritten in terms of conservative variables was solved at the Reynolds number \(\operatorname{Re} = {{10}^{8}}\) and the penalty parameters \({{\eta }_{b}}\) = 10–6 and \({{\eta }_{c}}\) = 10–2.

Periodic boundary conditions were used at the upper and lower boundaries of the computational domain, and Dirichlet conditions determined by parameters of the unperturbed medium were set at the left and right boundaries.

The problem was solved in dimensionless variables. As nondimensionalization parameters, we used the characteristic parameters of the unperturbed medium, namely, the speed of sound \({{c}_{0}}\) and the density \({{\rho }_{0}}\). The pressure was nondimensionalized by the quantity \({{\rho }_{0}}c_{0}^{2}\).

At the initial time, we specified the one-dimensional acoustic pulse

$$\rho = 1 + \rho {\kern 1pt} ',\quad u = u{\kern 1pt} ',\quad p = \frac{1}{\gamma } + p{\kern 1pt} ',\quad {-}0.45 \leqslant x \leqslant - 0.05,$$

where

$$\rho {\kern 1pt} ' = u{\kern 1pt} ' = p{\kern 1pt} ' = A{{\left( {\frac{{x + 0.25}}{{0.2}} - 1} \right)}^{4}}{{\left( {\frac{{x + 0.25}}{{0.2}} + 1} \right)}^{4}},\quad A = {{10}^{{ - 3}}}.$$

The presence of the small amplitude \(A\) in the initial perturbation determines the solution of the linear evolution problem with use of nonlinear equations.

Over time, the pulse moves from left to right, reflecting from the solid surface and changing the direction of motion.

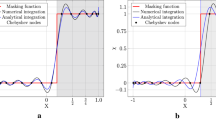
Figure 2a shows the pressure fluctuations near the wall at \(t = 0.25\) (the time of reflection from the wall) produced by the characteristic based volume penalization method (CBVPM) and the Brinkman penalization method (BPM) on various grids in comparison with the analytical solution. The CBVPM solution agrees well with the analytical one even on the coarse grids, in contrast to the BPM solution, which exhibits differences from the exact solution even on the fine grid. At \(t = 0.5,\) the acoustic wave reflected from the solid wall has the velocity profile shown in Fig. 2b. The profile of velocity fluctuations obtained with CBVPM on the coarse grid UTM1 agrees well with the exact solution, while a small discrepancy between the BPM and the analytical solution is observed at the minimum point.

Fig. 2.
figure 2

(a) Pressure fluctuations near the wall at the reflection time t = 0.25 and (b) velocity fluctuations at t = 0.5 (reflected wave).

Full size image

Figure 3 compares the profiles of pressure fluctuations produced by CBVPM and BPM on the UTM4 grid in a neighborhood of the extreme point and near the wall. It can be seen that the BPM solution exhibits a pressure peak near the boundary on the inner side of \({{\bar {\Omega }}_{B}}\); as a result, the profile of the reflected wave becomes slightly distorted, namely, its amplitude decreases. In contrast to BPM, the CBVPM-based energy flux across the boundary is correctly determined as zero, so the profile of the reflected wave is preserved. According to [35], the incorrect reflection of acoustic waves in BMP served as a motivating factor for the generalization of BPM and the inclusion of porosity in the continuity equation.

Fig. 3.
figure 3

Pressure fluctuations in the reflected wave near the maximum of fluctuations and near the wall.

Full size image

The grid convergence of CBVPM and BPM is demonstrated in Tables 2 and 3, which present the errors of the numerical solution for pressure fluctuations in the \({{L}_{2}}\) norm computed in the physical domain \(\Omega {{\backslash }}{{\Omega }_{B}}\) of the solution at the times \(t = 0.25\) and \(t = 0.5\).

Table 2.   Error of the numerical solution in the \({{L}_{2}}\) norm at the time \(t = 0.25\)
Full size table
Table 3.   Error of the numerical solution in the \({{L}_{2}}\) norm at the time \(t = 0.5\)
Full size table

Inspection of the tables (see the UTM1–UTM3 columns) suggests that the convergence is linear (when the mesh size is halved, the error is roughly halved as well).

The results obtained on the nonuniform UTM4 grid are similar to those on the fine UTM3 grid. This is explained by the fact that major errors arise in the course of reflection, while the element sizes of UTM3 and UTM4 near the boundary are identical.

The norms of the errors given in the tables also show that BPM is inferior to CBVPM in accuracy.

3.2. Shock Wave Reflection

Consider the problem of a plane shock wave reflecting from a solid wall. The shock front moves from left to right along the \(OX\) axis at the velocity corresponding to the Mach number \(\operatorname{M} = 2\). The problem was solved in two dimensions in the rectangular domain \(\Omega = \left[ {0,100} \right] \times \left[ {0,4} \right]\) with the immersed interface \(x = 80\) and the penalization domain \({{\bar {\Omega }}_{B}} = \left[ {80,100} \right] \times \left[ {0,4} \right]\). As in the preceding example, three sequentially refined quasi-uniform triangular meshes with a characteristic cell size of 1 (UTM1), 0.5 (UTM2), and 0.25 (UTM3) were constructed in \(\Omega \). The structures of these meshes were similar to the mesh structures presented in Fig. 1.

The problem was solved with initial piecewise constant conditions

$$\left( {\rho ,u,{v},p} \right) = \left\{ \begin{gathered} {{\left( {\rho ,u,{v},p} \right)}_{1}} = \left( {1,0,0,{1 \mathord{\left/ {\vphantom {1 \gamma }} \right. \kern-0em} \gamma }} \right),\quad x \geqslant 30, \hfill \\ {{\left( {\rho ,u,{v},p} \right)}_{2}},\quad x < 30, \hfill \\ \end{gathered} \right.$$

where the state \({{(\rho ,u,{v},p)}_{2}}\) ahead of the shock front is determined by the Rankine–Hugoniot relations. The problem was solved in dimensionless variables. As nondimensionalization parameters, we used the parameters ahead of the shock front, namely, the speed of sound \({{c}_{1}}\) and the density \({{\rho }_{1}}\). The pressure was nondimensionalized by \({{\rho }_{1}}c_{1}^{2}\).

The penalized system (2), (5), (7), and (8) rewritten in terms of conservative variables was solved at the Reynolds number \(\operatorname{Re} = {{10}^{7}}\) and the penalty parameters \({{\eta }_{b}} = {{10}^{{ - 6}}}\) and \({{\eta }_{c}} = {{10}^{{ - 6}}}\). The immersed solid surface (\(x = 80\)) was modeled by the immersed boundary method with no-slip and adiabatic conditions.

According to the formulation of the problem, the shock wave reflects from the surface and then moves from right to left. The profile of the reflected shock wave at the time \(t = 60\) is presented in Fig. 4, which also depicts the numerical results produced by BPM and the exact analytical solution of the problem. The figure shows that the CBVPM numerical solutions obtained on the fine (UTM3) and coarse (UTM1) grids agree well with the analytical solution, in contrast to the BPM solutions on the same grids. Specifically, the reflected shock wave in the BPM solutions has an underestimated amplitude and a phase lag, as in the previous problem of acoustic wave reflection. However, in the case of the nonlinear problem, this underestimation is more significant. The cause is the same as before: the energy flux across the boundary is incorrectly modeled by BPM. As was noted in [37], in contrast to acoustic waves, the porous extension of BPM [35] does not eliminate the error caused by the abrupt change in the gas pressure within the penalty domain and by the subsequent smooth decrease in the pressure due to infiltration. The CBVPM yields the correct pressure gradient on the modeled wall, since the density gradient (extrapolated from the surface \(\partial {\kern 1pt} {{\Omega }_{B}}\)) and the temperature gradient (relaxing to zero) are correctly determined in the immersed domain \({{\bar {\Omega }}_{B}}\). Altogether, these factors lead to a zero energy flux across the boundary and, as a consequence, to the correct reflection of the shock wave.

Fig. 4.
figure 4

Reflected shock wave at the time \(t = 60\).

Full size image

3.3. Couette Flow

Consider the two-dimensional compressible gas flow in a channel formed by two parallel impermeable plates. One plate has a given temperature (isothermal surface) and is stationary, while the other plate moves at a constant velocity and has an adiabatic surface. The considered medium is characterized by a variable dimensionless dynamic viscosity of the form \(\mu = {{{{{\left( {{T \mathord{\left/ {\vphantom {T {{{T}_{0}}}}} \right. \kern-0em} {{{T}_{0}}}}} \right)}}^{{ - 1/2}}}} \mathord{\left/ {\vphantom {{{{{\left( {{T \mathord{\left/ {\vphantom {T {{{T}_{0}}}}} \right. \kern-0em} {{{T}_{0}}}}} \right)}}^{{ - 1/2}}}} {\operatorname{Re} }}} \right. \kern-0em} {\operatorname{Re} }}\), where \({{T}_{0}}\) is the temperature of the plate. The problem is solved at the Reynolds number \(\operatorname{Re} = 1\).

For the numerical solution, the penalty parameters in CBVPM were specified as \({{\eta }_{b}} = {{10}^{{ - 3}}}\) and \({{\eta }_{c}} = {{10}^{{ - 2}}}\). The problem was considered in the rectangular domain \(\Omega = \left[ { - 0.5,0.5} \right] \times \left[ {0,0.02} \right]\), where three sequentially refined quasi-uniform triangular grids with a characteristic cell size of 0.02 (UTM1), 0.01 (UTM2), and 0.005 (UTM3) were constructed. The plates were perpendicular to the \(OX\) axis, and their boundaries crossed this axis at the points \({{x}_{L}} = - 0.5\) and \({{x}_{R}} = 0.2\). On the left boundary of the computational domain, which coincided with the surface of one of the plates \((x = {{x}_{L}})\), we specified the temperature \({{T}_{L}} = {3 \mathord{\left/ {\vphantom {3 \gamma }} \right. \kern-0em} \gamma }\) and the no-slip condition \({{{v}}_{L}} = 0\). The right plate \((x = {{x}_{R}})\) moved at the velocity \({{{v}}_{P}} = 10\) and was immersed in the rectangular penalty subdomain \({{\bar {\Omega }}_{B}} = \left[ {0.2,0.5} \right] \times \left[ {0,0.02} \right]\). The boundary conditions on its surface, namely, adiabaticity \({{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial x}}} \right. \kern-0em} {\partial x}} = 0\) and the no-slip condition \({{{v}}_{R}} = {{{v}}_{P}}\) were modeled using the CBVPM.

The exact solution of the problem for the temperature function is given by the expression

$$\begin{gathered} T(x) = {{\tau }^{2}}(x), \\ \tau (x) = \sqrt {{{T}_{L}}} \frac{{\cos \left( {c({{x}_{R}} - x)} \right)}}{{\cos \left( {c({{x}_{R}} - {{x}_{L}})} \right)}},\quad c = \frac{1}{{({{x}_{R}} - {{x}_{L}})}}{\text{arctan}}\left( {\frac{{{{{v}}_{R}}}}{{\sqrt {{{T}_{L}}} }}{{{\left( {\frac{{\Pr ({{\gamma }} - 1)}}{{2{{\gamma }}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right) \\ \end{gathered} $$

(see the documentation section at https://github.com/bahvalo/ColESo), and the solution for the velocity function is given by

$${v}(x) = {{{v}}_{R}} - {{\left( {\frac{{\Pr ({{\gamma }} - 1)}}{{2{{\gamma }}}}} \right)}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\sqrt {{{T}_{L}}} \frac{{\sin \left( {c({{x}_{R}} - x)} \right)}}{{\cos \left( {c({{x}_{R}} - {{x}_{L}})} \right)}}.$$

The computations produced a \(y\)-independent stationary numerical solution of the problem. Figures 5a and 5b present the velocity and temperature distributions along the \(OX\) axis as computed on the fine UTM3 grid. Additionally, the figures show the results produced by BPM and the exact solution. It can be seen that the numerical results agree well with the exact solution, except for the neighborhood of the right boundary. Figures 6a and 6b present the velocity and temperature profiles near the right boundary obtained on the coarse (UTM1) and fine (UTM3) grids. It can be seen that the CBVPM yields more accurate results than the BPM.

Fig. 5.
figure 5

Distributions of characteristics in the Couette flow along the OX axis: (a) transverse velocity and (b) temperature.

Full size image
Fig. 6.
figure 6

Distributions of characteristics in the Couette flow near the right boundary: (a) transverse velocity and (b) temperature.

Full size image

The grid convergence of CBVPM is demonstrated in Table 4, which presents the errors of the numerical solution for temperature in the \({{L}_{2}}\) norm as computed in the physical domain \({\Omega \mathord{\left/ {\vphantom {\Omega {{{\Omega }_{B}}}}} \right. \kern-0em} {{{\Omega }_{B}}}}\) of the solution. It can be seen that the convergence under mesh refinement is linear, because, as was shown in [37], the error of the numerical method prevails over the CBVPM error for given penalty parameters. Note that, in contrast to the preceding test problems, an inhomogeneous no-slip boundary condition is modeled with the help of CBVPM in this problem.

Table 4.   Error of the numerical solution for temperature in the \({{L}_{2}}\) norm
Full size table

CONCLUSIONS

A technique for the numerical simulation of aerodynamic flow problems based on the characteristic based volume penalization method, which belongs to the class of immersed boundary methods, has been presented. The method relies on a qualitatively new approach to the implementation of boundary conditions on grids that are not boundary-fitted. On the one hand, boundary conditions of different types (Dirichlet, Neumann) can be modeled with this method. On the other hand, as a penalization method, it allows a relatively simple numerical implementation.

The developed technique makes use of a mathematical model based on the viscous compressible Navier–Stokes equations. In the case of the characteristic based volume penalization method, the Navier–Stokes system is supplemented with an equation for computing the derivative of density with respect to the normal direction to the surface, which is involved in the source terms of the Navier–Stokes equations. According to the numerical method proposed for solving this system, the flow region and the domain inside the obstacle are computed simultaneously. Thus, the numerical solution is reduced to the integration a unified SLAE obtained by applying an implicit time differencing scheme with the use of the linearized Newton method.

For the characteristic based volume penalization method, the Dirichlet boundary condition in the mathematical model is implemented as in the Brinkman penalization method. However, in contrast to the latter, the characteristic based volume penalization method ensures the fulfillment of the Neumann boundary condition.

The technique based on the characteristic based volume penalization method was used for the numerical simulation of several benchmark problems having an analytical solution, namely, the reflection of an acoustic pulse, the reflection of a shock wave, and the Couette flow. The used mathematical models include Dirichlet and Neumann boundary conditions. The numerical results were compared with an analytical solution and the numerical solution produced by the Brinkman penalization method. The results based on the characteristic based volume penalization method were found to agree well with the analytical solutions. For the considered benchmark problems, this method was shown to yield more accurate results than the Brinkman penalization method.

Overall, the results obtained in this work suggest that the developed characteristic penalization technique is efficient as applied to the numerical simulation of aerodynamic flow problems. Its further development would be associated with an extension to three-dimensional flow formulations, including flows over moving bodies.