Gradient Computation

Abstract

As was shown in the previous chapter, the discretization of the gradients of $\phi$ at cell centroids and faces is fundamental to constructing the discretized sets of diffusion equations and, as will be revealed in later chapters, of equations involving the convection term. In addition, the evaluation of gradients is needed for the evaluation of various operators. For example, pressure derivatives are directly needed in the discretized momentum equations, while velocity gradients are required to compute the production term in turbulence models, and the strain rate in non-Newtonian viscosity models. This chapter describes several techniques for evaluating gradients on a general mesh topology. The chapter starts with a description of the techniques for computing the gradient on cartesian structured grids and proceeds with gradient evaluation on unstructured grids. The presented methods follow either the Green-Gauss or the least square approach. Methods to interpolate the gradient to element faces are also presented.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Computing Gradients in Cartesian Grids

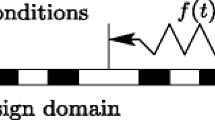
For the one-dimensional problem shown in Fig. 9.1 discretized using a uniform grid, a linear profile assumption for the variation of $\phi$ between cell centroids results in the following expression for the derivative at cell face e:

$$ \begin{aligned} \left( {\frac{d\phi }{dx}} \right)_{e} = & \frac{{\phi_{E} - \phi_{C} }}{{x_{E} - x_{C} }} \\ = & \frac{{\phi_{E} - \phi_{C} }}{{\delta x_{e} }} \\ \end{aligned} $$

(9.1)

Fig. 9.1

Computing the gradient on a uniform one dimensional grid

In the same way, the derivative at the cell centroid C (Fig. 9.1) can be written using the values at the two adjacent cells as

$$ \begin{aligned} \left( {\frac{d\phi }{dx}} \right)_{C} = & \frac{{\phi_{e} - \phi_{w} }}{{x_{e} - x_{w} }} = \frac{{\left( {\frac{{\phi_{E} + \phi_{C} }}{2}} \right) - \left( {\frac{{\phi_{C} + \phi_{W} }}{2}} \right)}}{{\Delta x_{C} }} \\ = & \frac{{\phi_{E} - \phi_{W} }}{{2\Delta x_{C} }} \\ \end{aligned} $$

(9.2)

This expression is usually referred to as the “central difference” approximation of the first derivative.

For Cartesian grids in multiple dimensions, the derivatives can be computed by applying the same principle along the respective coordinate directions. Consider, for example, the two dimensional grid shown in Fig. 9.2, using the central difference approximation introduced earlier, the partial derivatives in the x and y directions are obtained as

$$ \left( {\frac{\partial \phi }{\partial x}} \right)_{C} = \frac{{\phi_{E} - \phi_{W} }}{{x_{E} - x_{W} }}\quad \left( {\frac{\partial \phi }{\partial y}} \right)_{C} = \frac{{\phi_{N} - \phi_{S} }}{{x_{N} - x_{S} }} $$

(9.3)

Fig. 9.2

Computing the gradient on a two dimensional Cartesian grid

A similar equation holds in the z direction for three dimensional grids.

When dealing with unstructured grids the computation of the gradient using the above method becomes unpractical and leads to the use of more general methods, some of these are now presented.

2 Green-Gauss Gradient

This is one of the most widely used methods for computing the gradient. It was introduced in the previous chapter and will not be repeated here. Rather the final form of the equation will be given and some additional methods to compute the face values will be introduced.

As derived in the previous chapter, the gradient at the centroid of an element C with volume V _C ( Fig. 8.8) is computed as

$$ \nabla \phi_{C} = \frac{1}{{V_{C} }}\mathop \sum \limits_{f{\sim}nb\left( C \right)} \phi_{f} {\mathbf S}_{f} $$

(9.4)

where f refers to a face and S _f to its surface vector. The face values $\phi_{f}$ still need to be defined before the formula can be used. Two approaches are presented for computing $\phi_{f}$. One is face-based with a generally compact stencil involving face neighbors, and the second is vertex-based with a larger stencil involving vertex neighbors. The number of cells in this extended stencil is about twice the compact one.

The use of a compact stencil is attractive with implicit methods because it leads to more compact Jacobian matrices. However, the enlarged stencil brings more information into the reconstruction, and is therefore expected to be more accurate.

• Method 1: Compact Stencil [1]

For the two and three dimensional grid system shown in Fig. 9.3a, b, respectively, a simple approximation for calculating $\phi_{f}$ is to use the average values of the two cells sharing the face. In this case the value of $\phi_{f}$ is calculated as

$$ \phi_{f} = g_{C} \phi_{C} + \left( {1 - g_{C} } \right)\phi_{F} $$

(9.5)

where g _C is a geometric weighting factor equal to

$$ g_{C} = \frac{{\parallel {\mathbf{r}}_{F} - {\mathbf{r}}_{f} \parallel }}{{\parallel {\mathbf{r}}_{F} - {\mathbf{r}}_{C} \parallel }} = \frac{{d_{Ff} }}{{d_{FC} }} $$

(9.6)

where r designates the position vector and d the distance between two points. When the face is situated halfway between the two cell centers, $\phi_{f}$ is found to be

$$ \phi_{f} = \frac{{\phi_{C} + \phi_{F} }}{2} $$

(9.7)

Fig. 9.3

Conjunctional face in a a two dimensional and b a three dimensional configuration; non-conjunctional face in c a two dimensional and d a three dimensional configuration

This approach is simple to implement in two and three dimensional situations and all operations involved are face-based, not requiring any additional grid connectivity. Accuracy-wise, the above relation leads to a second order approximation of $\phi_{f}$ only when the segment [CF] and face S _f intersection point coincides with the centroid of the face S _f , i.e., with the Gaussian integration point f. Thus a second order accurate representation of the gradient is generally not achieved except for the above special case.

Such a condition is not usually satisfied with a general structured non-orthogonal or unstructured grid systems as shown for the two and three dimensional grid systems displayed in Fig. 9.3c, d, respectively. Rather, the skewness of the mesh (non-conjunctionality) results in the segment [CF] and the surface $S_{f}$ intersecting at a point $f'$, different from the face centroid f. In this case a correction is needed for the interpolated $\phi_{f'}$ value to get $\phi_{f}$. The correction equation is given by

$$ \begin{aligned} \phi_{f} = & \phi_{{f^{\prime}}} + correction \\ = & \phi_{{f^{\prime}}} + (\nabla \phi )_{{f^{\prime}}} \cdot ({\mathbf{r}}_{f} - {\mathbf{r}}_{{f^{\prime}}} ) \\ \end{aligned} $$

(9.8)

which may also be written in expanded form as

$$ \begin{aligned} \phi_{f} &= g_{C} \left\{ {\phi_{C} + \left( {\nabla \phi } \right)_{C} \,\cdot\, \left( {{\mathbf{r}}_{f} - {\mathbf{r}}_{C} } \right)} \right\} + \left( {1 - g_{C} } \right)\left\{ {\phi_{F} + \left( {\nabla \phi } \right)_{F} \,\cdot\,\left( {{\mathbf{r}}_{f} - {\mathbf{r}}_{F} } \right)} \right\} \\ &= \phi_{f'} + \underbrace {{g_{C} \left( {\nabla \phi } \right)_{C} \,\cdot\, \left( {{\mathbf{r}}_{f} - {\mathbf{r}}_{C} } \right) + \left( {1 - g_{C} } \right)\left( {\nabla \phi } \right)_{F} \,\cdot\, \left( {{\mathbf{r}}_{f} - {\mathbf{r}}_{F} } \right)}}_{correction} \\ \end{aligned} $$

(9.9)

Since g _C depends on $f^{\prime}$, Eq. (9.9) indicates that improved estimates of the gradient can be obtained iteratively. At each iteration, the average value at the face is computed using the gradients calculated in the pervious iteration. These face values are then used to compute new estimates of the gradients. Doing excessive number of iterations may cause oscillations and usually not more than two iterations are performed.

In this case, the calculation of g _C requires locating the intersection point $f^{\prime}$ between [CF] and the face S _f . For that purpose three options will be described.

Option 1:

In this option $f^{\prime}$ is taken to be the exact intersection between [CF] and the face S _f of surface vector S _f . With n denoting the surface unit vector (i.e., ${\mathbf{n}} = {\mathbf{S}}_{f} /\left\| {{\mathbf{S}}_{f} } \right\|$) and e the unit vector along CF (i.e., ${\mathbf{e}} = {\mathbf{CF}}/\left\| {{\mathbf{CF}}} \right\|$), the location of $f^{\prime}$ (Fig. 9.3c, d) can be found by exploiting the orthogonality condition that exists between n and the segment $ff^{\prime}$ (i.e., n is normal to the face S _f containing the segment $ff^{\prime}$) to write

$$ \left( {{\mathbf{r}}_{f} - {\mathbf{r}}_{f'} } \right) \cdot {\mathbf{n}} = 0 $$

(9.10)

Further, since $f^{\prime}$ is a point on CF the vector $\varvec{Cf^{\prime}}$ can be expressed in terms of e as

$$ \varvec{Cf}' = \left( {{\mathbf{r}}_{f'} - {\mathbf{r}}_{C} } \right) = k{\mathbf{e}} $$

(9.11)

where k is a scalar quantity. Combining Eqs. (9.10) and (9.11) yields

$$ {\mathbf{r}}_{f'} = \frac{{{\mathbf{r}}_{f} \cdot {\mathbf{n}}}}{{{\mathbf{e}} \cdot {\mathbf{n}}}}{\mathbf{e}} $$

(9.12)

with $f^{\prime}$ located, g _C is computed as

$$ g_{C} = \frac{{\left\| {{\mathbf{r}}_{F} - {\mathbf{r}}_{f'} } \right\|}}{{\left\| {{\mathbf{r}}_{F} - {\mathbf{r}}_{C} } \right\|}} = \frac{{d_{Ff'} }}{{d_{FC} }} $$

(9.13)

Then, the calculation procedure involves the following steps:

During the first iteration, calculate the gradient field over the entire domain as follows:

• 1. Calculate $\phi_{f^{\prime}}$ using $\phi_{f'} = g_{C} \phi_{C} + \left( {1 - g_{C} } \right)\phi_{F}$

• 2. Calculate $\nabla \phi_{C}$ using $\nabla \phi_{C} = \frac{1}{{V_{C} }}\sum\limits_{f{\sim}nb(C)} {\phi_{f'} {\mathbf{S}}_{f} }$

From the second iteration onward, correct the gradient field according to the following procedure:

• 3. Update $\phi_{f}$ using $\phi_{f} = \phi_{f'} + g_{C} \left( {\nabla \phi } \right)_{C} \cdot \left( {{\mathbf{r}}_{f} - {\mathbf{r}}_{C} } \right) + \left( {1 - g_{C} } \right)\left( {\nabla \phi } \right)_{F} \cdot \left( {{\mathbf{r}}_{f} - {\mathbf{r}}_{F} } \right)$

• 4. Update $\nabla \phi_{C}$ using $\nabla \phi_{C} = \frac{1}{{V_{C} }}\sum\limits_{f{\sim}nb(C)} {\phi_{f} {\mathbf{S}}_{f} }$

• 5. Go back to step 3 and repeat.

Option 2:

For $f^{\prime}$ chosen to be at the centre of segment [CF] [Fig. 9.4a in two dimensions and Fig. 9.4b in three dimensions] the equations become simpler and the calculation of the gradient field over the domain proceeds as follows:

Fig. 9.4

Correction to Non-Conjunctionality using the midpoint approach: a two dimensional configuration; b three dimensional configuration

During the first iteration, calculate the gradient field over the entire domain as follows:

• 1. Calculate $\phi_{{f^{\prime}}}$ _’ using $\phi_{f'} = \frac{{\phi_{C} + \phi_{F} }}{2}$

• 2. Calculate $\nabla_{{\phi_{C} }}$ using $\nabla \phi_{C} = \frac{1}{{V_{C} }}\sum\limits_{f{\sim}nb(C)} {\phi_{f'} {\mathbf{S}}_{f} }$

From the second iteration onward, correct the gradient field according to the following procedure:

• 3. Update $\phi_{f}$ using $\phi_{f} = \phi_{f'} + 0.5*\left[ {\left( {\nabla \phi } \right)_{C} + \left( {\nabla \phi } \right)_{F} } \right] \cdot \left[ {{\mathbf{r}}_{f} - 0.5*\left( {{\mathbf{r}}_{C} + {\mathbf{r}}_{F} } \right)} \right]$

• 4. Update $\nabla \phi_{{{C}}}$ using $\nabla \phi_{C} = \frac{1}{{V_{C} }}\sum\limits_{f{\sim}nb(C)} {\phi_{f} {\mathbf{S}}_{f} }$

• 5. Go back to step 3 and repeat

Option 3:

The position of $f^{\prime}$ can be chosen such that the distance $ff^{\prime}$ is the shortest possible [Fig. 9.5a in two dimensions and Fig. 9.5b in three dimensions], i.e., $\left[ {ff^{\prime}} \right]$ perpendicular to [CF]. This leads to a more accurate computation of the gradient during the first iteration. In this case $f^{\prime}$ is computed by minimizing the distance between f and $f^{\prime}$. In general ${\mathbf{r}}_{{f^{\prime}}}$ is described by

$$ {\mathbf{r}}_{f'} = {\mathbf{r}}_{C} + q\left( {{\mathbf{r}}_{C} - {\mathbf{r}}_{F} } \right) $$

(9.14)

where 0 < q < 1.

Fig. 9.5

Correction to Non-Conjunctionality using the minimum distance approach: a two dimensional configuration; b three dimensional configuration

Denoting the distance $f^{\prime}f$ by d, then its square is obtained as

$$ \begin{aligned} d^{2} = & \left( {{\mathbf{r}}_{f} - {\mathbf{r}}_{f'} } \right) \cdot \left( {{\mathbf{r}}_{f} - {\mathbf{r}}_{f'} } \right) \\ = & \left[ {{\mathbf{r}}_{f} - {\mathbf{r}}_{C} - q\left( {{\mathbf{r}}_{C} - {\mathbf{r}}_{F} } \right)} \right] \cdot \left[ {{\mathbf{r}}_{f} - {\mathbf{r}}_{C} - q\left( {{\mathbf{r}}_{C} - {\mathbf{r}}_{F} } \right)} \right] \\ = & \left( {{\mathbf{r}}_{f} - {\mathbf{r}}_{C} } \right) \cdot \left( {{\mathbf{r}}_{f} - {\mathbf{r}}_{C} } \right) - 2q\left( {{\mathbf{r}}_{f} - {\mathbf{r}}_{C} } \right) \cdot \left( {{\mathbf{r}}_{C} - {\mathbf{r}}_{F} } \right) + q^{2} \left( {{\mathbf{r}}_{C} - {\mathbf{r}}_{F} } \right) \cdot \left( {{\mathbf{r}}_{C} - {\mathbf{r}}_{F} } \right) \\ \end{aligned} $$

(9.15)

Minimizing the function d ² with respect to q, yields

$$ \frac{{\partial \left( {d^{2} } \right)}}{\partial q} = 0 \Rightarrow - 2\left( {{\mathbf{r}}_{f} - {\mathbf{r}}_{C} } \right) \cdot \left( {{\mathbf{r}}_{C} - {\mathbf{r}}_{F} } \right) + 2q\left( {{\mathbf{r}}_{C} - {\mathbf{r}}_{F} } \right) \cdot \left( {{\mathbf{r}}_{C} - {\mathbf{r}}_{F} } \right) = 0 $$

(9.16)

Solving, q is obtained as

$$ q = - \frac{{{\mathbf{r}}_{Cf} \cdot {\mathbf{r}}_{CF} }}{{{\mathbf{r}}_{CF} \cdot {\mathbf{r}}_{CF} }} $$

(9.17)

Knowing the q values, the gradient calculation over the domain proceeds as follows:

During the first iteration, calculate the gradient field over the entire domain as follows:

• 1. Calculate ${\mathbf{r}}_{{f^{\prime}}}$ using ${\mathbf{r}}_{f'} = {\mathbf{r}}_{C} - \frac{{{\mathbf{r}}_{Cf} \,\cdot\, {\mathbf{r}}_{CF} }}{{{\mathbf{r}}_{CF} \,\cdot\, {\mathbf{r}}_{CF} }}\left( {{\mathbf{r}}_{C} - {\mathbf{r}}_{F} } \right)$

• 2. Calculate g _C using $g_{C} = \left\| {{\mathbf{r}}_{F} - {\mathbf{r}}_{f'} } \right\|/\left\| {{\mathbf{r}}_{F} - {\mathbf{r}}_{C} } \right\|$

• 3. Calculate $\phi_{{f^{\prime}}}$ using $\phi_{f'} = g_{C} \phi_{C} + \left( {1 - g_{C} } \right)\phi_{F}$

• 4. Calculate $\nabla \phi_{C}$ using $\nabla \phi_{C} = \frac{1}{{V_{C} }}\sum\limits_{f{\sim}nb(C)} {\phi_{f'} {\mathbf{S}}_{f} }$

From the second iteration onward, correct the gradient field according to the following procedure:

• 5. Calculate $\nabla \phi_{{f^{\prime}}}$ using $\nabla \phi_{f'} = g_{C} \nabla \phi_{C} + \left( {1 - g_{C} } \right)\nabla \phi_{F}$

• 6. Update $\phi_{f}$ using $\phi_{f} = \phi_{f'} + \nabla \phi_{f'} \cdot \left( {{\mathbf{r}}_{f} - {\mathbf{r}}_{f'} } \right)$

• 7. Update $\nabla \phi_{C}$ using $\nabla \phi_{C} = \frac{1}{{V_{C} }}\sum\limits_{f{\sim}nb(C)} {\phi_{f} {\mathbf{S}}_{f} }$

• 8. Go back to step 5 and repeat

Example 1

For the mesh shown in Fig. 9.6 , the coordinates of the grid point C and its neighbors F ₁ through F ₆ are given by

$$ \begin{aligned} C\left( {13,11} \right)\quad & F_{1} \left( {4.5,9.5} \right)\quad F_{2} \left( {8,3} \right)\quad F_{3} \left( {17,3.5} \right) \\ & F_{4} \left( {22,10} \right)\quad F_{5} \left( {16,20} \right)\quad F_{6} \left( {7,18} \right) \\ \end{aligned} $$

Fig. 9.6

Grid layout for Examples 1 and 2

while the nodes n₁ through n₆ are located at

$$ \begin{aligned} & n_{1} \left( {9,14} \right)\quad n_{2} \left( {8,8} \right)\quad \quad n_{3} \left( {12,5} \right) \\ & n_{4} \left( {17,9} \right)\quad n_{5} \left( {17.5,14} \right)\;n_{6} \left( {12,17} \right) \\ \end{aligned} $$

If the values of the dependent variable $\phi$ at the centroids are known to be

$$ \begin{aligned} & \phi_{C} = 167 \\ & \begin{array}{*{20}c} {\phi_{{F_{1} }} = 56.75} & {\phi_{{F_{2} }} = 35} & {\phi_{{F_{3} }} = 80} \\ \end{array} \\ & \begin{array}{*{20}c} {\phi_{{F_{4} }} = 252} & {\phi_{{F_{5} }} = 356} & {\phi_{{F_{6} }} = 151} \\ \end{array} \\ \end{aligned} $$

and the values of the gradient of $\phi$, $\left( {\nabla \phi } \right)$ , at all neighboring elements to C are given by

$$ \begin{aligned} & \nabla \phi_{{F_{1} }} = 10.5{\mathbf{i}} + 5.5{\mathbf{j}}\quad \nabla \phi_{{F_{2} }} = 4{\mathbf{i}} + 9{\mathbf{j}}\quad \nabla \phi_{{F_{3} }} = 4.5{\mathbf{i}} + 18{\mathbf{j}} \\ & \nabla \phi_{{F_{4} }} = 11{\mathbf{i}} + 23{\mathbf{j}}\quad \quad \nabla \phi_{{F_{5} }} = 21{\mathbf{i}} + 17{\mathbf{j}}\quad \nabla \phi_{{F_{6} }} = 19{\mathbf{i}} + 8{\mathbf{j}} \\ \end{aligned} $$

If the volume of cell C is V _C  = 76, find the gradient $\nabla \phi_{C}$ using

• a. The Green-Gauss method with no correction

• b. The Green-Gauss method alongside correction to skewness with $f^{\prime}$ chosen to be at the centre of segment [CF].

Solution The Green-Gauss method with no correction

• a. The interpolation factors are needed to perform the calculations. This, in turn, necessitates computing the coordinates of the face centroids. The coordinates of the centroid f ₁ are found as

  $$ \left. {\begin{array}{*{20}c} {x_{{f_{1} }} = 0.5*\left( {x_{{n_{1} }} + x_{{n_{2} }} } \right) = 0.5*\left( {9 + 8} \right) = 8.5} \\ {y_{{f_{1} }} = 0.5*\left( {y_{{n_{1} }} + y_{{n_{2} }} } \right) = 0.5*\left( {14 + 8} \right) = 11} \\ \end{array} } \right\} \Rightarrow f_{1} \left( {8.5,11} \right) $$

In a similar way, the coordinates of other face centroids are found to be

$$ \begin{aligned} & f_{2} \left( {10,6.5} \right)\quad f_{3} \left( {14.5,7} \right) \\ & f_{4} \left( {17.25,11.5} \right)\quad f_{5} \left( {14.75,15.5} \right)\quad f_{6} \left( {10.5,15.5} \right) \\ \end{aligned} $$

The surface vectors are calculated as

$$ \begin{aligned} & {\mathbf{S}}_{{f_{1} }} = - 6{\mathbf{i}} + {\mathbf{j}}\quad \quad {\mathbf{S}}_{{f_{2} }} = - 3{\mathbf{i}} - 4{\mathbf{j}}\quad \quad {\mathbf{S}}_{{f_{3} }} = 4{\mathbf{i}} - 5{\mathbf{j}} \\ & {\mathbf{S}}_{{f_{4} }} = 5{\mathbf{i}} - 0.5{\mathbf{j}}\quad {\mathbf{S}}_{{f_{5} }} = 3{\mathbf{i}} + 5.5{\mathbf{j}}\quad \quad {\mathbf{S}}_{{f_{6} }} = - 3{\mathbf{i}} + 3{\mathbf{j}} \\ \end{aligned} $$

The interpolation factor (g _C )₁ is computed using

$$ \left. \begin{aligned} \left( {g_{C} } \right)_{1} = & \frac{{F_{1} f_{1} }}{{F_{1} f_{1} + Cf_{1} }} \\ F_{1} f_{1} = & \sqrt {\left( {4.5 - 8.5} \right)^{2} + \left( {9.5 - 11} \right)^{2} } = 4.272 \\ Cf_{1} = & \sqrt {\left( {13 - 8.5} \right)^{2} + \left( {11 - 11} \right)^{2} = 4.5} \\ \end{aligned} \right\} \Rightarrow \left( {g_{C} } \right)_{1} = 0.487 $$

In a similar way, the other interpolation factors are found to be

$$ \begin{array}{*{20}c} {\left( {g_{C} } \right)_{2} = 0.427}\,{\left( {g_{C} } \right)_{3} = 0.502}\,{\left( {g_{C} } \right)_{4} = 0.538}\,{\left( {g_{C} } \right)_{5} = 0.492}\,{\left( {g_{C} } \right)_{6} = 0.455} \\ \end{array} $$

Using Eq. (9.5) the $\phi_{f}$ values are computed as

$$ \begin{aligned} & \phi_{{f_{1} }} = 110.442\quad \phi_{{f_{2} }} = 91.364\quad \phi_{{f_{3} }} = 123.674 \\ & \phi_{{f_{4} }} = 206.27\quad \;\phi_{{f_{5} }} = 263.012\quad \phi_{{f_{6} }} = 158.28 \\ \end{aligned} $$

Using Eq. (9.4), $\nabla \phi_{C}$ is calculated as

$$ \begin{aligned} \nabla \phi_{C} & = \frac{1}{76}\left\{ {\begin{array}{*{20}c} {\left[ {\begin{array}{*{20}c} {110.442 \times \left( { - 6} \right) + 91.364 \times \left( { - 3} \right) + 123.674 \times 4 \,+ } \\ {206.27 \times 5 + 263.012 \times 3 + 158.28 \times \left( { - 3} \right)} \\ \end{array} } \right]{\mathbf{i}} + } \\ {\left[ {\begin{array}{*{20}c} {110.442 \times \left( 1 \right) + 91.364 \times \left( { - 4} \right) + 123.674 \times \left( { - 5} \right) \,+ } \\ {206.27 \times \left( { - 0.5} \right) + 263.012 \times 5.5 + 158.28 \times \left( 3 \right)} \\ \end{array} } \right]{\mathbf{j}}} \\ \end{array} } \right\} \\ & = 11.889{\mathbf{i}} + 12.433{\mathbf{j}} \\ \end{aligned} $$

• b. The Green-Gauss method alongside correction to skewness with $f^{\prime}$ chosen to be at the centre of segment [CF].

The values at the $f^{\prime}$ locations are computed as half the sum of the values at the nodes straddling the face and are given by

$$ \phi_{{f_{1} }} = 111.875\quad \phi_{{f_{2} }} = 101\quad \phi_{{f_{3} }} = 123.5\quad \phi_{{f_{4} }} = 209.5\quad \phi_{{f_{5} }} = 261.5\quad \phi_{{f_{6} }} = 158.5 $$

Using these values, the first estimate for the gradient is obtained using Eq. (9.4) as

$$ \nabla \phi_{C} = 11.53{\mathbf{i}} + 11.826{\mathbf{j}} $$

Defining d _f  = r _f  − 0.5 × (r _C  + r _F ), the various values are found to be

$$ \begin{aligned} & {\mathbf{d}}_{{f_{1} }} = - 0.25{\mathbf{i}} + 0.75{\mathbf{j}}\quad {\mathbf{d}}_{{f_{2} }} = - 0.5{\mathbf{i}} - 0.5{\mathbf{j}}\quad {\mathbf{d}}_{{f_{3} }} = - 0.5{\mathbf{i}} - 0.25{\mathbf{j}} \\ & {\mathbf{d}}_{{f_{4} }} = - 0.25{\mathbf{i}} + {\mathbf{j}}\quad \quad \;\;{\mathbf{d}}_{{f_{5} }} = 0.25{\mathbf{i}}\quad \quad \quad \;\;{\mathbf{d}}_{{f_{6} }} = 0.5{\mathbf{i}} + {\mathbf{j}} \\ \end{aligned} $$

Using $\phi_{f} = \phi_{{f^{\prime}}} + \, 0. 5 { }*[(\nabla \phi )_{C} + \, (\nabla \phi )_{F} ]\cdot\left[ {{\mathbf{r}}_{f} - 0. 5*\left( {{\mathbf{r}}_{C} + {\mathbf{r}}_{F} } \right)} \right]$ the updated values at the faces are obtained as

$$ \begin{aligned} & \phi_{{f_{1} }} = 115.619\quad \phi_{{f_{2} }} = 91.911\quad \;\phi_{{f_{3} }} = 115.764 \\ & \phi_{{f_{4} }} = 224.097\quad \phi_{{f_{5} }} = 265.566\;\;\phi_{{f_{6} }} = 176.046 \\ \end{aligned} $$

These values are used in Eq. (9.4) yielding the updated value of the gradient as

$$ \nabla \phi_{C} = 11.614{\mathbf{i}} + 13.761{\mathbf{j}} $$

• Method 2: Extended Stencil [2]

The value of $\phi_f$ at the surface centroid f can be computed as the mean of the values at the vertices defining the surface. This necessitates the estimation of the properties at the vertices. The properties at a vertex node are calculated using the weighted average of the properties within the cells surrounding that node. Figure 9.7 shows the cells that are considered for the weighted average of the properties at the vertex nodes n ₁ and n ₂. The weight is taken as the inverse of the distance of the vertex from the cell centre [3]. The resulting equation for the properties at the vertices are written as,

$$ \phi_{n} = \frac{{\sum\limits_{k = 1}^{NB(n)} {\mathop {\overline{{\left\| {{\mathbf{r}}_{n} - {\mathbf{r}}_{{F_{k} }} } \right\|}} }\limits^{{\phi_{{F_{k} }} }} } }}{{\sum\limits_{k = 1}^{NB(n)} {\mathop {\overline{{\left\| {{\mathbf{r}}_{n} - {\mathbf{r}}_{{F_{k} }} } \right\|}} }\limits^{1} } }} $$

(9.18)

where n refers to the vertex node, F _k to the neighboring cell node, NB(n) the total number of cell nodes surrounding the vertex node n, and $\left\| {{\mathbf{r}}_{n} - {\mathbf{r}}_{{F_{k} }} } \right\|$ the distance from the vertex node to the centroid of the neighboring cells.

Fig. 9.7

Cells Contributing to node n for the Weighted Average

Once the values $\phi_{n}$ at the vertices are found, the values $\phi_{f}$ at the surface centroids are calculated followed by the gradients at the control volume centroids. In two dimensional situations, $\phi_{f}$ is computed as

$$ \phi_{f} = \frac{{\phi_{n1} + \phi_{n2} }}{2} $$

(9.19)

Then the gradient at C is found using

$$ \nabla \phi_{C} = \frac{1}{{V_{C} }}\sum\limits_{f = nb(C)} {\phi_{f} {\mathbf{S}}_{f} = \frac{1}{{V_{C} }}\sum\limits_{f{\sim}nb(C)} {\left( {\frac{{\phi_{n1} + \phi_{n2} }}{2}} \right)_{f} {\mathbf{S}}_{f} } } $$

(9.20)

In three dimensional situations, the calculations are a little more involved as the number of a face vertices depends on the element type. The value of $\phi_{f}$ is found from the values at the vertices using

$$ \phi_{f} = \frac{{\sum\limits_{k = 1}^{nb(f)} {\frac{{\phi_{{n_{k} }} }}{{\left\| {{\mathbf{r}}_{{n_{k} }} - {\mathbf{r}}_{f} } \right\|}}} }}{{\sum\limits_{k = 1}^{nb(f)} {\frac{1}{{\left\| {{\mathbf{r}}_{{n_{k} }} - {\mathbf{r}}_{f} } \right\|}}} }} $$

(9.21)

where n represents the number of vertices of face f. Once the values $\phi_{f}$ are calculated, the gradient at C is computed using Eq. (9.4).

One of the disadvantages of this approach is that information from the wrong side of the cell face also contributes to the weighted average values of the conserved variables. This can be overcome by using upwind biased gradients as discussed by Cabello [4]. The higher order calculations based on the upwind biased gradients, however, have both higher memory overheads required to store the information about the cells used for the upwind biased gradient calculation and increased coding complexity.

Example 2

Using the data of example I, calculate $\phi_{{f_{1} }}$ using the extended stencil approach via Eq. (9.16).

Solution

First the distances have to be calculated and are given by

$$ \begin{aligned} \left\| {{\mathbf{r}}_{{n_{1} }} - {\mathbf{r}}_{{F_{6} }} } \right\| = & \sqrt {\left( {9 - 7} \right)^{2} + \left( {14 - 18} \right)^{2} } = 4.472 \\ \left\| {{\mathbf{r}}_{{n_{1} }} - {\mathbf{r}}_{{F_{1} }} } \right\| = & \sqrt {\left( {9 - 4.5} \right)^{2} + \left( {14 - 9.5} \right)^{2} } = 6.364 \\ \left\| {{\mathbf{r}}_{{n_{1} }} - {\mathbf{r}}_{C} } \right\| = & \sqrt {\left( {9 - 13} \right)^{2} + \left( {14 - 11} \right)^{2} } = 5 \\ \left\| {{\mathbf{r}}_{{n_{2} }} - {\mathbf{r}}_{{F_{1} }} } \right\| = & \sqrt {\left( {8 - 4.5} \right)^{2} + \left( {8 - 9.5} \right)^{2} } = 3.808 \\ \left\| {{\mathbf{r}}_{{n_{2} }} - {\mathbf{r}}_{{F_{2} }} } \right\| = & \sqrt {\left( {8 - 8} \right)^{2} + \left( {8 - 3} \right)^{2} } = 5 \\ \left\| {{\mathbf{r}}_{{n_{2} }} - {\mathbf{r}}_{C} } \right\| = & \sqrt {\left( {8 - 13} \right)^{2} + \left( {8 - 11} \right)^{2} } = 5.831 \\ \end{aligned} $$

The values at nodes n ₁ and n ₂ are computed using Eq. (9.15) as

$$ \phi_{{n_{1} }} = \frac{{\frac{151}{4.472} + \frac{56.75}{6.364} + \frac{167}{5}}}{{\frac{1}{4.472} + \frac{1}{6.364} + \frac{1}{5}}} = 131.009\quad \phi_{{n_{2} }} = \frac{{\frac{56.75}{3.808} + \frac{35}{5} + \frac{167}{5.831}}}{{\frac{1}{3.808} + \frac{1}{5} + \frac{1}{5.831}}} = 79.708 $$

The value of $\phi_{{f_{1} }}$ is found to be

$$ \phi_{{f_{1} }} = 0.5\left( {131.009 + 79.708} \right) = 105.3585 $$

3 Least-Square Gradient

Using least-square methods to compute the gradients [5] offers more flexibility with regard to the order of accuracy achieved [6] and the stencil used [7]. In the least-square method, the divergence-based gradient can be recovered as a special case. This flexibility comes at a cost, as proper weighting is needed for the stencil terms, and computation of the weights adds to the computational cost. The method is described next.

Considering a control volume and its immediate neighbors (Fig. 9.8), the change in centroid values between C and F is given by $(\phi_{F} - \phi_{C} )$, if the cell gradient ($\nabla \phi_{C}$) is exact, then the difference can also be computed as

$$ \phi_{F} = \phi_{C} + \left( {\nabla \phi } \right)_{C} \cdot \underbrace {{\left( {{\mathbf{r}}_{F} - {\mathbf{r}}_{C} } \right)}}_{{{\mathbf{r}}_{CF} }} $$

(9.22)

Fig. 9.8

A control volume with its immediate neighbors

However unless the solution field is linear the cell gradient cannot be exact because C has more neighbors than the gradient vector has components. In the least square methods, a gradient is computed by an optimization procedure that finds the minimum of the function G _C defined as

$$ \begin{aligned} G_{C} = & \sum\limits_{k = 1}^{NB(C)} {\left\{ {w_{k} \left[ {\phi_{{F_{k} }} - \left( {\phi_{C} + \nabla \phi_{C} \cdot {\mathbf{r}}_{{CF_{k} }} } \right)} \right]^{2} } \right\}} \\ = & \sum\limits_{k = 1}^{NB(C)} {\left\{ {w_{k} \left[ {\Delta \phi_{k} - \left( {\Delta x_{k} \left( {\frac{\partial \phi }{\partial x}} \right)_{C} } +\Delta y_{k} \left( {\frac{\partial \phi }{\partial y}} \right)_{C} +\Delta z_{k} \left( {\frac{\partial \phi }{\partial z}} \right)_{C} \right)} \right]^{2} } \right\}} \\ \end{aligned} $$

(9.23)

where w _k is some weighting factor. The various terms in the above equation represent

$$ \begin{aligned}\Delta \phi_{k} &= \phi_{{F_{k} }} - \phi_{C} \\\Delta x_{k} &= {\mathbf{r}}_{{CF_{k} }} \cdot {\mathbf{i}} \\\Delta y_{k} &= {\mathbf{r}}_{{CF_{k} }} \cdot {\mathbf{j}} \\\Delta z_{k} &= {\mathbf{r}}_{{CF_{k} }} \cdot {\mathbf{k}} \\ \end{aligned} $$

(9.24)

The function G _C is minimized by enforcing the conditions

$$ \frac{{\partial G_{C} }}{{\partial \left( {\frac{\partial \phi }{\partial x}} \right)}} = \frac{{\partial G_{C} }}{{\partial \left( {\frac{\partial \phi }{\partial y}} \right)}} = \frac{{\partial G_{C} }}{{\partial \left( {\frac{\partial \phi }{\partial z}} \right)}} = 0 $$

(9.25)

to yield the following set of three equations in three unknowns:

$$ \begin{aligned} & \sum\limits_{k = 1}^{NB(C)} {\left\{ {2w_{k}\Delta x_{k} \left[ { -\Delta \phi_{k} +\Delta x_{k} \left( {\frac{\partial \phi }{\partial x}} \right)_{C} +\Delta y_{k} \left( {\frac{\partial \phi }{\partial y}} \right)_{C} +\Delta z_{k} \left( {\frac{\partial \phi }{\partial z}} \right)_{C} } \right]} \right\} = 0} \\ & \sum\limits_{k = 1}^{NB(C)} {\left\{ {2w_{k}\Delta y_{k} \left[ { -\Delta \phi_{k} +\Delta x_{k} \left( {\frac{\partial \phi }{\partial x}} \right)_{C} +\Delta y_{k} \left( {\frac{\partial \phi }{\partial y}} \right)_{C} +\Delta z_{k} \left( {\frac{\partial \phi }{\partial z}} \right)_{C} } \right]} \right\} = 0} \\ & \sum\limits_{k = 1}^{NB(C)} {\left\{ {2w_{k}\Delta z_{k} \left[ { -\Delta \phi_{k} +\Delta x_{k} \left( {\frac{\partial \phi }{\partial x}} \right)_{C} +\Delta y_{k} \left( {\frac{\partial \phi }{\partial y}} \right)_{C} +\Delta z_{k} \left( {\frac{\partial \phi }{\partial z}} \right)_{C} } \right]} \right\} = 0} \\ \end{aligned} $$

(9.26)

which can be written in matrix form as

$$ \left[ {\begin{array}{*{20}c} {\sum\limits_{k = 1}^{NB(C)} {w_{k}\Delta x_{k}\Delta x_{k} } } & {\sum\limits_{k = 1}^{NB(C)} {w_{k}\Delta x_{k}\Delta y_{k} } } & {\sum\limits_{k = 1}^{NB(C)} {w_{k}\Delta x_{k}\Delta z_{k} } } \\ {\sum\limits_{k = 1}^{NB(C)} {w_{k}\Delta y_{k}\Delta x_{k} } } & {\sum\limits_{k = 1}^{NB(C)} {w_{k}\Delta y_{k}\Delta y_{k} } } & {\sum\limits_{k = 1}^{NB(C)} {w_{k}\Delta y_{k}\Delta z_{k} } } \\ {\sum\limits_{k = 1}^{NB(C)} {w_{k}\Delta z_{k}\Delta x_{k} } } & {\sum\limits_{k = 1}^{NB(C)} {w_{k}\Delta z_{k}\Delta y_{k} } } & {\sum\limits_{k = 1}^{NB(C)} {w_{k}\Delta z_{k}\Delta z_{k} } } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\left( {\frac{\partial \phi }{\partial x}} \right)_{C} } \\ {\left( {\frac{\partial \phi }{\partial y}} \right)_{C} } \\ {\left( {\frac{\partial \phi }{\partial z}} \right)_{C} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\sum\limits_{k = 1}^{NB(C)} {w_{k}\Delta x_{k}\Delta \phi_{k} } } \\ {\sum\limits_{k = 1}^{NB(C)} {w_{k}\Delta y_{k}\Delta \phi_{k} } } \\ {\sum\limits_{k = 1}^{NB(C)} {w_{k}\Delta z_{k}\Delta \phi_{k} } } \\ \end{array} } \right] $$

(9.27)

The solution to the above set of equations yields the gradient $\left( {\nabla \phi } \right)_{C}$. A solution exists provided that the matrix on the left hand side is not singular. Moreover, the choice of the w _k is important in determining the properties of the gradient. For example if w _k is chosen to be 1 for all neighbors of C, then all neighboring points will have the same weight in the computation of the gradient irrespective of whether they are near or far from point C. Actually points that are farther from C will have a more important influence as the error function will be more affected by their error.

Another choice for w _k , which was used earlier with the extended stencil method, is the inverse distance between C and F given by

$$ w_{k} = \frac{1}{{\left| {{\mathbf{r}}_{{F_{k} }} - {\mathbf{r}}_{C} } \right|}} = \frac{1}{{\sqrt {\Delta x_{{F_{k} }}^{2} + \,\Delta y_{{F_{k} }}^{2} +\Delta z_{{F_{k} }}^{2} } }} $$

(9.28)

Other options that can be pursued include the inverse distance raised to any power n such that

$$ w_{k} = \frac{1}{{\left| {{\mathbf{r}}_{{F_{k} }} - {\mathbf{r}}_{C} } \right|^{n} }} $$

(9.29)

where n can be set to 1, 2, 3, etc.

As mentioned above, the divergence based gradient is a special case of the least-square formulation. This can be shown for a Cartesian grid (see Fig. 9.9) where substituting the geometric quantities into Eq. (9.27) would yield the following set of three equations.

Fig. 9.9

A three dimensional Cartesian control volume

$$ \left[ {\begin{array}{*{20}c} {x_{E} - x_{W} } & 0 & 0 \\ 0 & {y_{N} - y_{S} } & 0 \\ 0 & 0 & {z_{T} - z_{B} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\left( {\partial \phi /\partial x} \right)_{C} } \\ {\left( {\partial \phi /\partial y} \right)_{C} } \\ {\left( {\partial \phi /\partial z} \right)_{C} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\phi_{E} - \phi_{W} } \\ {\phi_{N} - \phi_{S} } \\ {\phi_{T} - \phi_{B} } \\ \end{array} } \right] $$

(9.30)

Solving the above equation, the derivatives in the various directions are found to be

$$ \begin{array}{*{20}c} {\left( {\frac{\partial \phi }{\partial x}} \right)_{C} = \frac{{\phi_{E} - \phi_{W} }}{{x_{E} - x_{W} }}} & {\left( {\frac{\partial \phi }{\partial y}} \right)_{C} = \frac{{\phi_{N} - \phi_{S} }}{{y_{N} - y_{S} }}} & {\left( {\frac{\partial \phi }{\partial z}} \right)_{C} = \frac{{\phi_{T} - \phi_{B} }}{{z_{T} - z_{B} }}} \\ \end{array} $$

(9.31)

The obtained values are exactly the ones given in Eq. (9.3), demonstrating that the divergence-based gradient is a special case of the least-square method. Finally it can easily be demonstrated that the accuracy of the resulting gradient is at least first order. Indeed, the Taylor series expansion of the $\phi$ value around node C can be written as

$$ \phi \left( {\mathbf{r}} \right) - \phi \left( {{\mathbf{r}}_{C} } \right) = \left( {\nabla \phi } \right)_{C} \cdot \left( {{\mathbf{r}} - {\mathbf{r}}_{C} } \right) + O\left( {{\mathbf{r}}^{2} } \right) $$

(9.32)

which when solved for $\left( {\nabla \phi } \right)_{C}$ results in O(r).

4 Interpolating Gradients to Faces

It was shown in Chap. 8 that the discretization of the diffusion term in non-orthogonal grids requires the use of correction terms involving gradients at control volume faces. Thus in this situation the gradients need to be interpolated from the control volume centroids where they were computed to the control volume faces where they will be used. Figure 9.10a shows the stencil used in the Gauss gradient computation for two neighboring control volumes. The gradient at the face will have exactly the same stencil, while ideally it should be similar to that of Fig. 9.10b.

Fig. 9.10

a Interpolated and b corrected gradient at a control volume face

A better insight is gained by considering the configuration in Fig. 9.11a, which shows the gradients $\nabla \phi_{C}$ and $\nabla \phi_{F}$ of the variable $\phi$ at the two nodes C and F, respectively. The interpolated gradient at the face, $\overline{\nabla \phi }_{f}$, is obtained by averaging the values at nodes C and F, as shown in Fig. 9.11b. It is important for the stencil of the gradient at the face to be heavily based on the nodes straddling the face, which is not guaranteed by this simple averaging practice. As schematically displayed in Fig. 9.11c, this can be accomplished by forcing the face gradient along the CF direction to be equal to the local gradient defined by the values of $\phi$ at C and F. Mathematically this can be written as

$$ \nabla \phi_{f} = \overline{\nabla \phi }_{f} + \underbrace {{\left[ {\frac{{\phi_{F} - \phi_{C} }}{{d_{CF} }} - \left( {\overline{\nabla \phi }_{f} \cdot {\mathbf{e}}_{CF} } \right)} \right]{\mathbf{e}}_{CF} }}_{Correction \, interpolated \, face \, gradient} $$

(9.33)

where

$$ \overline{\nabla \phi }_{f} = g_{C} \nabla \phi_{C} + g_{F} \nabla \phi_{F} ,\quad {\mathbf{e}}_{CF} = \frac{{{\mathbf{d}}_{CF} }}{{d_{CF} }},\quad {\mathbf{d}}_{CF} = {\mathbf{r}}_{F} - {\mathbf{r}}_{C} $$

(9.34)

where r _F and r _C are position vectors, as displayed in Fig. 9.3. This approach is applicable to both structured and unstructured grids. For unstructured grids, while the stencil used for the face gradient might not be decreased, the gradient across a face will still be based on the nodes straddling that face.

Fig. 9.11

a Schematics of the gradients at the two nodes C and F straddling face f; b computing $\overline{\nabla \phi }_{f}$ as a simple average of $\nabla \phi_{C}$ and $\nabla \phi_{F}$ using Eq. (9.31); c the gradient at the face with its value heavily based on the nodes straddling the face

5 Computational Pointers

5.1 uFVM

In uFVM, the functions cfdComputeGradientGauss0 and cfdComputeGradientNodal are used to compute the element gradients. The Gauss gradient routine (Listing 9.1) takes as input the phi element array and returns the element gradient array. The values are interpolated to the faces using a weighted factor with no correction for non-conjunctionality, hence the 0 digit in the function name.

Listing 9.1

Function used in uFVM to compute the gradient field at the centroids of elements following the Green-Gauss approach with phi values at the face computed using simple a weighted average interpolation technique with no correction to non-conjunctionality

The nodal gradient routine, listed below (Listing 9.2), is very similar to the Gauss gradient routine except that it uses the functions cfdInterpolateFromElementsToNodes and cfdInterpolateFromNodesToFaces to interpolate phi values to the face that are subsequently used in the Gauss algorithm.

Listing 9.2

Function used in uFVM to compute the gradient field at the centroids of elements following the Green-Gauss approach with phi values at the face computed using nodal values, i.e., the extended stencil approach

For face interpolation of gradients, a variety of interpolation options are allowed in the function cfdInterpolateGradientsFromElementsToInteriorFaces. The input to the function is theInterpolationScheme, the element gradient grad, the element array phi and mdot for cases where an upwind or downwind scheme is used. The function is shown in Listing 9.3.

Listing 9.3

Function used to interpolation the element gradient field to the faces

It should be noted that theInterpolationScheme “Average:Corrected” implements the face gradient correction technique used to get a more accurate gradient representation along the CF direction, i.e., Eq. (9.33).

5.2 OpenFOAM^®

In OpenFOAM^® [8] several types of gradient evaluation techniques are defined: the standard Green-Gauss method, the second order least square method, and the fourth order least square method. Attention will be focussed here on the Green-Gauss method. Nonetheless the discretization in all cases is performed explicitly and is thus part of the fvc operator namespace. The Green-Gauss gradient is defined at the cell centre, as in Eq. (9.4), and its source code in OpenFOAM is located in the directory “src/finiteVolume/finiteVolume/gradSchemes/gaussGrad”.

Implementation-wise, the gradient evaluation is performed in the following two steps:

• Face interpolation of the variable

• Green-Gauss formula evaluation

The interpolation to the face is in the calcGrad routine listed below (Listing 9.4).

Listing 9.4

Script to interpolate variable values to cell faces

As a first step, values are interpolated to the faces and stored in the generic field “vsf” (the interpolation class will be described with more details in Chap. 11). Then the gradient is computed based on the Green-Gauss formula in the gradf routine shown in Listing 9.5

Listing 9.5

Routine used to compute the gradient using the Green-Gauss method

.

The sum over cell faces is performed using the LDU addressing. As such the “for” loop that evaluates the sum over the faces of the cell is based only on the global face numbering and uses the upper and lower addressing vectors to add or subtract (Listing 9.6) the flux to cell values. After all fluxes have been processed, the net value is divided by the volume to yield the gradient, as in Eq. 9.4.

Listing 9.6

Adding or subtracting fluxes to cell values

The type of gradient is defined in fvSchemes shown in Listing 9.7.

Listing 9.7

Defining the gradient calculation method

The face interpolation scheme is defined as displayed in Listing 9.8.

Listing 9.8

Defining the interpolation method used in calculating face values

The idea of evaluating the gradient based on a generic interpolation scheme that has to be defined by dictionary, allows computing the gradient with the Green-Gauss formula in several ways by just changing the interpolation scheme.

If skew correction, as defined in Eq. (9.8), is required then the above interpolation scheme definition should be replaced by (Listing 9.9)

Listing 9.9

Defining the interpolation scheme to calculate face values with skew correction

A more compact syntax can be used for defining the gradient in which the interpolation type is specified directly under gradSchemes shown in Listing 9.10.

Listing 9.10

Defining the gradient calculation method: compact syntax

In this case the interpolation method is defined directly in the gradient dictionary. The choice of the syntax type is up to the user keeping in mind that a separate definition of the interpolation scheme helps clarifying the various steps of the gradient calculation.

6 Closure

This chapter presented the discretization details of two methods for computing the gradient at the centroids of control volume meshes in general non-orthogonal grid systems. One method is based on the Green-Gauss theorem and the second on the Least-Square reconstruction approach. Chapter 10 will be devoted to methods used for solving systems of algebraic equations.

7 Exercises

Exercise 1

In the configuration depicted in Fig. 9.22, the values of the variable $\phi$ and its gradient $\nabla \phi$ at C are known. Using these known values estimate the value of $\phi$ at F.

Fig. 9.22

A two dimensional element of centroid C and neighbor F

Exercise 2

For the two cells shown in Fig. 9.23 the value of some scalar ϕ at their centroids C and F can be calculated from

$$ \phi \left( {x,y} \right) = 100\left( {x^{2} y + y^{2} x} \right) $$

Fig. 9.23

Two elements in a two dimensional plane with their centroids C and F

The gradient at C and F are also computed to be the exact gradient of the function at these points such that

$$ \nabla \phi \left( {x,y} \right) = 100\left( {2xy + y^{2} } \right){\mathbf{i}} + 100\left( {x^{2} + 2yx} \right){\mathbf{j}} $$

With C and F located at (0.32, −0.1) and (0.52, 0.31), respectively, find the value of the gradient at face f (0.43, 0.1) numerically (not from the expression for the gradient) using

• a. A simple averaging between C and F.

• b. A corrected averaging between C and F.

• c. Compare the two computed values with the exact gradient at point f.

Exercise 3

Consider the mesh composed of equilateral triangular elements shown in Fig. 9.24. The coordinates of the mesh vertices are as shown. The temperatures at the cell centroids are given by

$$ T\left( {x,y,z} \right) = 100\left( {x^{2} + y^{2} + 1} \right) $$

• a. Compute the gradient at 1 using the Green-Gauss method.

• b. Compute the gradient at 1 using the least squares approach with a limited stencil (i.e., nodes 2, 3 and 4) and with an extended stencil (i.e., nodes 2–13) used for the reconstruction.

• c. Compare the least squares gradient with the limited and extended stencil and the gauss gradient to the exact gradient.

Fig. 9.24

A domain discretized using triangular elements

Exercise 4

Consider the uniform mesh shown in Fig. 9.25. The coordinates of the mesh vertices are as shown. The temperatures at the cell nodes are given by

$$ T\left( {x,y} \right) = 100\left( {x^{3} + y^{3} + xy + 1} \right) $$

compute the gradient at the centroid of cell 1 using the gauss gradient with and without face corrections and compare to the exact gradient given by

$$ \nabla T\left( {x,y} \right) = 100\left( {3x^{2} + y} \right){\mathbf{i}} + 100\left( {3y^{2} + x} \right){\mathbf{j}} $$

Fig. 9.25

Mesh system for Exercise 4

Exercise 5 (uFVM, OpenFOAM^®)

Using uFVM and then OpenFOAM^® write a program that

• a. reads an OpenFOAM^® mesh and sets a scalar field with values equal to $\phi \left( {x,y,z} \right) = 10x^{2} y^{2} + 3y$

• b. computes the gradients using the second order least square method,

• c. computes the gradients using the gauss gradient method with linear interpolation,

• d. computes the gradients using the gauss gradient method with vertex interpolation,

• e. and computes the root mean square error between each of the computed gradients and the exact gradient.

Exercise 6 (uFVM, OpenFOAM^®)

Using uFVM and then OpenFOAM^® write a program that

• a. reads an OpenFOAM^® mesh and sets a scalar field with values equal to $\phi \left( {x,y,z} \right) \, = { 1}0x^{ 2} y^{ 2} + { 3}y$

Use the exact gradients at the element nodes to compute the gradients at the interior faces using

• b. simple linear interpolation,

• c. corrected linear interpolation,

• d. and exact gradient formulation at the face centroids.

• e. Compute the root mean square error between each of the computed gradients and the exact gradient.

Exercise 7

Starting with Eq. (9.8) derive Eq. (9.9).

Hint: ${\mathbf{r}}_{f} - {\mathbf{r}}_{{f^{\prime } }} = {\mathbf{r}}_{f} {-}{\mathbf{r}}_{C} - {\mathbf{r}}_{{cf^{\prime } }} = {\mathbf{r}}_{f} {-}{\mathbf{r}}_{f} - {\mathbf{r}}_{{Ff^{\prime } }}$.

Exercise 8 (OpenFOAM^®)

• a. List all possible gradient type definitions available in OpenFOAM^® by modifying the gradSchemes in the fvSchemes dictionary (Hint: just mistype a scheme, e.g., banana, and launch any solver or application, i.e., gradSchemes{default banana;}).

• b. Define in the dictionary file fvSchemes the option to evaluate the explicit gradient with the least square algorithm.

• c. Use the Doxygen documentation [9] to analyze the member function correctBoundaryConditions and explain its operations and aim.

• d. Define in the dictionary file fvSchemes the option to use a limited gradient (face and cell) (Gauss limited 0.8;).