The Number of 2-dominating Sets, and 2-domination Polynomial of a Graph

Abstract

Let $G=(V,E)$ be a simple graph. A set $D\subseteq V$ is a $2$-dominating set of $G$, if every vertex of $V\setminus D$ has at least two neighbors in $D$. The $2$-domination number of a graph $G$, is denoted by $\gamma_{2}(G)$ and is the minimum size of the $2$-dominating sets of $G$. In this paper, we count the number of $2$-dominating sets of $G$. To do this, we consider a polynomial which is the generating function for the number of $2$-dominating sets of $G$ and call it $2$-domination polynomial. We study some properties of this polynomial. Furthermore, we compute the $2$-domination polynomial for some of the graph families.

1 INTRODUCTION

A dominating set of a graph $G=(V,E)$ is any subset $D$ of $V$ such that every vertex not in $D$ is adjacent to at least one member of $D$. The minimum cardinality of all dominating sets of $G$ is called the domination number of $G$ and is denoted by $\gamma(G)$. This parameter has been extensively studied in the literature and there are hundreds of papers concerned with domination. For a detailed treatment of domination theory, the reader is referred to [1]. Also, the concept of domination and related invariants have been generalized in many ways. Among the best know generalizations are total, independent, and connected dominating, each of them with the corresponding domination number. Most of the papers published so far deal with structural aspects of domination, trying to determine exact expressions for $\gamma(G)$ or some upper and/or lower bounds for it. The domination polynomial of graph G is the generating function for the number of dominating sets of $G$, i.e., $D(G,x)=\sum_{i=1}^{|V(G)|}d(G,i)x^{i}$ (see [2, 3]). This polynomial and its roots have been actively studied in recent years [3–6]. It is natural to count the number of another kind of dominating sets [7]. In [8], we introduced the doubly connected domination polynomial of a graph. Some properties of these polynomials for some specific graphs are investigated. Motivated by these papers, we consider another type of dominating set of a graph in this paper.

A $2$-dominating set of $G$ is every vertex of $V(G)\setminus D$ has at least two neighbors in $D$. The $2$-domination number of $G$, denoted by $\gamma_{2}(G)$ is the minimum cardinality of $2$-dominating set of $G$ [1]. Let $d_{2}(G,i)$ be the number of the $2$-dominating sets of a graph $G$ with cardinality $i$ for $i\geq\gamma_{2}(G)$. The $2$-domination polynomial of $G$ is defined as $D_{2}(G,x)=\sum_{i=\gamma_{2}(G)}^{|V(G)|}d_{2}(G,i)x^{i}$.

The corona of two graphs $G_{1}$ and $G_{2}$ is the graph $G=G_{1}\circ G_{2}$ formed from one copy of $G_{1}$ and $|V(G_{1})|$ copies of $G_{2}$, where the $i$-th vertex of $G_{1}$ is adjacent to every vertex in the $i$-th copy of $G_{2}$. The corona $G\circ K_{1}$, in particular, is the graph constructed from a copy of $G$, where for each vertex $v\in V(G)$, a new vertex $v^{\prime}$ and a pendant edge $vv^{\prime}$ are added [9]. The join of two graphs $G_{1}$ and $G_{2}$, denoted by $G_{1}+G_{2}$, is a graph with vertex set $V(G_{1})\cup V(G_{2})$ and edge set $E(G_{1})\cup E(G_{2})\cup\{uv\ |\ u\in V(G_{1})\ and\ v\in V(G_{2})\}$.

We use $K_{n}$, $C_{n}$ and $P_{n}$ to denote a complete graph, cycle and a path of the order $n$, respectively. A wheel $W_{n}$, where $n\geq 3$, is a graph with $n+1$ vertices, formed by connecting a vertex to all vertices of a cycle $C_{n}$. By $K_{r,s}$ we denote a complete bipartite graph with partite sets of cardinalities $r$ and $s$. By a star we mean the graph $K_{1,n}$ of order $n+1$. A leaf of $G$ is the vertex of degree 1, while a support vertex of $G$ is a vertex adjacent to the leaf.

In this study, we obtain some properties of the $2$-domination polynomial on graphs. We determine this polynomial for some certain graphs. We consider three classes of graph family called the friendship graphs, helm graphs and gear graphs.

2 THE $2$-DOMINATION POLYNOMIAL OF CERTAIN GRAPHS

In this section, we shall obtain some results for the $2$-domination polynomial of some certain graphs. We obtain some of its properties.

Theorem 1. If a graph $G$ consists of $m$ components $G_{1},\ldots,G_{m}$ , then

$$D_{2}(G,x)=D_{2}(G_{1},x)\ldots D_{2}(G_{m},x).$$

Proof. It suffices to prove the theorem for $m=2$. A $2$-dominating set with cardinality $i$ in $G$, arises by choosing a $2$-dominating set of $j$ vertices in $G_{1}$ where $j\geq\gamma_{2}(G_{1})$ and a $2$-dominating set with $i-j$ vertices in $G_{2}$. Therefore, the coefficient of $x^{i}$ in $D_{2}(G_{1},x)D_{2}(G_{2},x)$ is equal to the coefficient of $x^{i}$ in $D_{2}(G,x)$. This complete the proof. $\Box$

The following theorem is a straightforward result of the definition of the $2$-domination polynomials.

Theorem 2. Let $G$ be a graph with $|V(G)|=n$.

• (i) If $G$ is connected, then $d_{2}(G,n)=1$.

• (ii) If $G$ is connected graph, then $d_{2}(G,n-1)=n-l$ in which $l$ is the number of the leaves of $G$.

• (iii) $d_{2}(G,i)=0$ if and only if $i<\gamma_{2}(G)$ or $i>n$.

• (iv) $D_{2}(G,x)$ has no constant term.

• (v) Let $G$ be a graph and $H$ be any induced subgraph of $G$. Then, $deg(D_{2}(G,x))\geq deg(D_{2}(H,x))$.

• (vi) Zero is a root of $D_{2}(G,x)$ with multiplicity $\gamma_{2}(G)$.

Now, we obtain some formulas for computing the $2$-domination polynomial of some certain graphs. We recall some results about the number of the $2$-dominating set.

Lemma 1. [10]

• (i) For every $n\geq 4$,

  $$\gamma_{2}(P_{n})=\begin{cases}\frac{n}{2}+1,\quad\text{if } n \text{ is even},\\ \frac{n-1}{2}+1,\quad\text{ if } n \text{ is odd}.\end{cases}$$

• (ii) For every $n\geq 4$,

  $$\gamma_{2}(C_{n})=\begin{cases}\frac{n}{2},\quad\text{if }n \text{ is even},\\ \frac{n+1}{2},\quad\text{if }n \text{ is odd}.\end{cases}$$

• (iii) For every $n\geq 3$,

  $$\gamma_{2}(W_{n})=\begin{cases}2,\quad\text{if }n=3,4,\\ \lfloor\frac{(n+1)}{3}\rfloor+1,\quad\text{if }n\geq\ 5.\end{cases}$$

• (iv) For every $n\geq 2$, $\gamma_{2}(K_{n})=2$.

• (v) $\gamma_{2}(K_{1,n})=n-1$.

Theorem 3. The number of $2$ -dominating sets of path $P_{n}$ with cardinality $i$ is given by

$$d_{2}(P_{n},i)=d_{2}(P_{n-1},i-1)+d_{2}(P_{n-2},i-1).$$

Proof. Let $P_{n}^{i}$ be the $2$-dominating set of $P_{n}$ with cardinality $i$. Let the vertices of $P_{n}$ are labeled by $v_{1},v_{2},\ldots,v_{n}$. According to the definition of a $2$-dominating set, it is easy to see that $v_{n}\in P_{n}^{i}$. Thus, we consider the following cases.

Case 1: If $v_{n-1}\in P_{n}^{i}$, then we get $P_{n}^{i}=P_{n-1}^{i-1}\cup\{v_{n}\}$. In this case, we have $d_{2}(P_{n},i)=d_{2}(P_{n-1},i-1)$.

Case 2: If $v_{n-1}\notin P_{n}^{i}$, then according to the definition of a $2$-dominating set must be $v_{n-2}\in P_{n}^{i}$. Thus, we have $P_{n}^{i}=P_{n-2}^{i-1}\cup\{v_{n}\}$. Therefore, $d_{2}(P_{n},i)=d_{2}(P_{n-2},i-1)$.

So, by the definition of the $2$-domination polynomial, we get

$$d_{2}(P_{n},i)=d_{2}(P_{n-1},i-1)+d_{2}(P_{n-2},i-1).$$

$\Box$

Theorem 4.

• (i) For every $n\geq 4$,

  $$D_{2}(P_{n},x)=\sum_{i=0}^{n}\binom{n-i-1}{i}x^{n-i}.$$

• (ii) For every $n\geq 3$,

  $$D_{2}(C_{n},x)=\sum_{i=0}^{n}\Bigg{[}\binom{n-i}{i}+\binom{n-i-1}{i-1}\Bigg{]}x^{n-i}.$$

• (iii) For every $n\geq 2$, $D_{2}(K_{n},x)=(1+x)^{n}-(1+nx)$.

• (iv) For any $r,s\geq 4$ , the $2$ -domination polynomial of the complete bipartite graph $K_{r,s}$ is equal to

  $$D_{2}(K_{r,s},x)=\sum_{i=4}^{r+s}\bigg{[}\sum_{j=2}^{i-2}\binom{r}{j}\binom{s}{i-j}\bigg{]}x^{i}.$$

• (v) For every $n\in\mathbb{N}$, $D_{2}(K_{1,n},x)=x^{n-1}(x+1)$.

Proof.

• (i) Using Theorem 3 we calculate a recursive formula for $2$-domination polynomial as following:

  $$D_{2}(P_{n},x)=\sum_{i=1}^{n}d_{2}(P_{n},i)x^{i}=\sum_{i=1}^{n}\Big{(}d_{2}(P_{n-1},i-1)+d_{2}(P_{n-2},i-1)\Big{)}x^{i}.$$

  Therefore, we get

  $$D_{2}(P_{n},x)=xD_{2}(P_{n-1},x)+xD_{2}(P_{n-2},x),$$

  (1)

  for $n\geq 3$ with the initial condition $D_{2}(P_{1},x)=x$. It is easy to see that $D_{2}(P_{2},x)=x^{2}$. For case $n=3$, $\gamma_{2}(P_{3})=2$ and the number of $2$-dominating set is 1. Therefore, using Theorem 2(i), $D_{2}(P_{3},x)=x^{2}+x^{3}$. Using the recursive formula (1) and simple calculations on $D_{2}(P_{n},x)$, it is easy to obtain $D_{2}(P_{n},x)=\sum_{i=0}^{n}\binom{n-i-1}{i}x^{n-i}$.

• (ii) Let the vertices of cycle $C_{n}$ are labeled by $v_{1},v_{2},\cdots,v_{n}$. By deleting the edge $v_{1}v_{n}$, we consider the path $P_{n}$ with the vertices $v_{1},v_{2},\cdots,v_{n}$. Let $D$ be the $2$- dominating set of $P_{n}$. We consider two cases for counting $2$-dominating sets.

  Case 1: If $v_{1},v_{n}\in D$, then we investigate all of the possibilities cases for selecting vertices of the set $\{v_{2},v_{3},\cdots,v_{n-1}\}$ in $D$. In this case, we get $d_{2}(C_{n},i)=\binom{n-i-1}{i-1}$ on path $P_{n}$ for $0\leq i\leq n$.

  Case 2: We add vertex $v_{n+1}$ by the edge $v_{n}v_{n+1}$ to path $P_{n}$. According to the definition $2$-dominating set, $v_{1}$ and $v_{n+1}$ are in $D$. Therefore, with similar argument of Case 1, on path $P_{n-1}$, we have $d_{2}(C_{n},i)=\binom{n-i}{i}$ for $0\leq i\leq n$. Therefore, by considering both cases and the definition $2$-domination polynomial of $C_{n}$, we get the result.

• (iii) Let $D$ be a $2$-dominating set of size $i$ in $K_{n}$. Using Lemma 1(iii), there are ${n\choose i}$ possibilities to choose $i$ vertices of $n$ vertices for $i\geq 2$. The proof is complete.

• (iv) Let $V_{1}$ and $V_{2}$ be partitions of graph $K_{r,s}$ such that $|V_{1}|=r$ and $|V_{2}|=s$. Since $r,s\geq 4$ by the definition of the $2$-dominating set, there are two vertices of $V_{1}$ and two vertices of $V_{2}$ in the $2$-dominating set and $\gamma_{2}(K_{r,s})=4$. Clearly, if $|V_{1}|<4$ or $|V_{2}|<4$, then the $2$-dominating set is the set with less size between $V_{1}$ and $V_{2}$. Assume, $D_{2}^{i}$, is the $2$-dominating set of cardinality $i$. If $j$ vertices select of the set $V_{1}$, then $i-j$ vertices of the set $V_{2}$ is in $D_{2}^{i}$. Since at least two vertices of any sets $V_{1}$ and $V_{2}$ exist in $D_{2}^{i}$ then, the number of the $2$-dominating set of cardinality $i$ in graph $K_{r,s}$ is equality to $d_{2}(K_{r,s},i)=\sum_{j=2}^{i-2}\binom{r}{j}\binom{s}{i-j}$.

  Therefore, the $2$-dominating set polynomial is as following

  $$D_{2}(K_{r,s},x)=\sum_{i=\gamma_{2}}^{|K_{r,s}|}d_{2}(K_{r,s},i)x^{i}=\sum_{i=4}^{r+s}\bigg{[}\sum_{j=2}^{i-2}\binom{r}{j}\binom{s}{i-j}\bigg{]}x^{i}.$$

• (v) Using Theorem 2(i) and Lemma 1(iv), the result follows.

$\Box$

Theorem 5. For $n\in\mathbb{N}$, $D_{2}(G\circ K_{1},x)=x^{n}D(G,x)$, where $D(G,x)$ is the domination polynomial of graph $G$.

Proof. Since every leaf of $G\circ K_{1}$, has just one neighbor in the graph, then the leaves are in $2$-dominating set of $G\circ K_{1}$. The set $L\cup D$ is a $2$-dominating set in $G\circ K_{1}$ where $L$ and $D$ are the set of leaves of graph $G\circ K_{1}$ and the dominating set in $G$, respectively. Therefore, $\gamma_{2}(G\circ K_{1})=n+\gamma(G)$. So, $d_{2}(G\circ K_{1},n+i)=d(G,i)$ for every $\gamma(G)\leq i\leq n$. Using the definition of the $2$-domination polynomial for $G\circ K_{1}$, we have

$$D_{2}(G\circ K_{1},x)=\sum_{i=n+\gamma(G)}^{2n}d_{2}(G\circ K_{1},i)x^{i}=\sum_{i=\gamma(G)}^{n}D(G,i)x^{n+i}=x^{n}D(G,x).$$

$\Box$

In the following theorem, we determine a formula for the $2$-domination polynomial of the join of two graphs.

Theorem 6. Let $G_{1}$ and $G_{2}$ be graphs of order $n_{1}$ and $n_{2}$ where $n_{1},n_{2}\geq 2$. Then

$$D_{2}(G_{1}+G_{2},x)=D_{2}(G_{1},x)+D_{2}(G_{2},x)+D(G_{1},x)D(G_{2},x),$$

where $D(G_{i},x)$ denotes the domination polynomial of graph $G_{i}$.

Proof. It is clear to achieve that $\gamma_{2}(G_{1}+G_{2})\geq 2$. Let $1\leq i\leq n_{1}+n_{2}$. We determine the number of $2$-dominating sets of size $i$. We can see that for every the dominating set $D_{1}\subseteq V(G_{1})$ and the dominating set $D_{2}\subseteq V(G_{2})$ such that $|D_{1}|=i_{1}$ and $|D_{2}|=i_{2}$, where $i_{1}+i_{2}=i$, $D_{1}\cup D_{2}$ is an $2$-dominating set of $G_{1}+G_{2}$. Moreover, if $D$ is an $2$-dominating $n$ set for $G_{1}$ or $G_{2}$ of size $i$ then $D$ is the $2$-dominating set for $G_{1}+G_{2}$. Thus, the proof is complete. $\Box$

In the next theorem, we obtain the $2$-domination polynomial for Wheel of order $n+1$. In first, we consider without proof the following result.

Lemma 2. [5] For every $n\geq 4$, the domination polynomial of cycle $C_{n}$ is as following

$$D(C_{n},x)=x\Big{(}D(C_{n-1},x)+D(C_{n-2},x)+D(C_{n-3},x)\Big{)}$$

with the initial values $D(C_{1},x)=x$, $D(C_{2},x)=x^{2}+2x$, $D(C_{3},x)=x^{3}+3x^{2}+3x$.

Theorem 7. Let $W_{n}$ be a wheel of order $n+1$ with cycle $C_{n}$ . Then

$$D_{2}(W_{n},x)=\sum_{i=0}^{n}\Bigg{[}\binom{n-i}{i}+\binom{n-i-1}{i-1}\Bigg{]}x^{n-i}+xD(C_{n},x),$$

where $D(C_{n},x)$ is the domination polynomial of cycle $C_{n}$.

Proof. Let $D_{n}^{i}$ be the $2$-dominating set of $W_{n}$ with cardinality $i$. Let the vertices of $W_{n}$ are labeled by $v_{1},v_{2},\ldots,v_{n+1}$ such that $v_{n+1}$ be the central vertex. According to the definition of the $2$-dominating set, we consider the following cases.

Case 1: Assume that $v_{n+1}\in D_{n}^{i}$. Since the central vertex $V_{n+1}$ is adjacent to all of the vertices on $C_{n}$ of wheel $W_{n}$, it is sufficient to consider the dominating set of cardinality $i-1$ on cycle $C_{n}$. Therefore,

$$d_{2}(W_{n},i)=d(C_{n},i-1).$$

Case 2: Assume that $v_{n+1}\notin D_{n}^{i}$. Then, we select the $2$-dominating set with cardinality $i$ of cycle $C_{n}$. Therefore, we get $d_{2}(W_{n},i)=d_{2}(C_{n},i).$ Thus, we calculate the $2$-dominating polynomial wheel graph $W_{n}$ as following

$$D_{2}(W_{n},x)=\sum_{i=1}^{n+1}(d_{2}(W_{n},i)x^{i}=\sum_{i=1}^{n+1}\Big{(}d(C_{n},i-1)+d_{2}(C_{n},i)\Big{)}x^{i}$$

$${}=\sum_{i=0}^{n}d(C_{n},i)x^{i+1}+\sum_{i=1}^{n}d_{2}(C_{n},i)x^{i}xD(C_{n},x)+D_{2}(C_{n},x).$$

Therefore, the result holds. $\Box$

3 $2$-DOMINATION POLYNOMIAL OF SPECIFIC GRAPHS

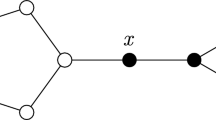
In this section, we study the $2$-domination polynomial of the friendship graphs. The friendship graph $F_{n}$ is a graph that can be constructed by coalescence $n$ copies of the cycle graph $C_{3}$ of length 3 with a common vertex. The friendship graph $F_{n}$ is a graph with the property that every two vertices have exactly one neighbor in common are exactly the friendship graphs [11]. Figure 1 shows a labeled friendship graph of length $n$ with cardinality $|F_{n}|=2n+1$.

Fig. 1

The labeled friendship graph $F_{n}$.

Theorem 8. Let $F_{n}$ be the friendship graph for every $n\geq 1$ . Then $\gamma_{2}(F_{n})=n+1.$

Proof. Let the vertices of $F_{n}$ are labeled by $v_{1},v_{2},\ldots,v_{2n+1}$ by Figure 1. It is easy to see that the set of vertices $\bigcup_{i=0}^{n}\{v_{1+2i}\}$ is an $2$-dominating set of $F_{n}$. Therefore, $\gamma_{2}(F_{n})\leq n+1$.

Let $D$ be a $2$-dominating set of $F_{n}$ and $|D|\leq n$. So, there exist $n+1$ vertices of $V(F_{n})$ that must dominate by $D$. We consider the following cases.

Case 1: If $v_{2n+1}\in D$, then according to Figure 1, since any vertex is dominated by two vertices of $D$ then, at least one vertex can not dominate by vertices of $D$.

Case 2: If $v_{2n+1}\notin D$, then according to Figure 1 and since every $v_{i}$ for $1\leq i\leq 2n$ is adjacent to $v_{i+1}$ and $v_{2n+1}$, it is a contradiction with the definition $2$-dominating set for the set $D$.

Thus, $|F_{n}|\geq n+1$. $\Box$

With regards to the friendship graphs, we obtain the $2$-domination polynomial for this family of graphs. At the first, we consider $F_{1}$ and obtain the following result.

Theorem 9. For the friendship graph $F_{1}$, $D_{2}(F_{1},x)=x^{2}(x+3).$

Proof. According to Figure 1, $F_{1}=C_{3}$ where is a cycle of order 3. Since $\gamma_{2}(F_{1})=2$ then, $d_{2}(F_{1},2)=3$ and $d_{2}(T_{1},3)=1$. Therefore, it is easy to get the $2$-domination polynomial of graph $F_{1}$ by the definition as following

$$D_{2}(F_{1},x)=\sum_{i=2}^{3}d_{2}(F_{1},i)x^{i}=3x^{2}+x^{3}=x^{2}(x+3).$$

$\Box$

Theorem 10. For every $n\geq 2$,

$$D_{2}(F_{n},x)=x^{2n+1}+(2n+1)x^{2n}+\sum_{i=0}^{n-2}\binom{n}{i}2^{n-i}x^{(n+1)+i}.$$

Proof. Let $D$ be the $2$-dominating set of $F_{n}$. Using Theorem 8, $\gamma_{2}(F_{n})=n+1$. Let $D_{n}^{i}$ be the $2$-dominating set of cardinality $i$ in graph $F_{n}$. According to the structure graph $F_{n}$, it is easy to see that $v_{2n+1}\in D$. We compute the number the sets $D_{n}^{i}$ based on the pigeonhole principle for $i\geq n+1$. Since $v_{2n+1}\in D$ and at least one of two vertices of $v_{j}$ and $v_{j+1}$ on any triangle that $1\leq j\leq 2n$ must be in the sets $D$, there are $\binom{2}{1}$ possibilities to choose one vertex of two vertices on any triangle. Therefore, the number of the $2$-dominating set of cardinality $n+1$ is $2^{n}$.

For $n+2\leq i\leq 2n-1$, by the pigeonhole principle there is at least one triangle that all of vertices is in the $2$-dominating set $D$. Thus, we get

$$d_{2}(F_{n},i)=\binom{n}{i}2^{n-i}\quad 0\leq i\leq n-2,$$

Also, by Theorem 2(i) and (ii), we have

$$d_{2}(F_{n},2n)=2n+1,\quad d_{2}(F_{n},2n+1)=1.$$

Therefore, the $2$-dominating polynomial is obtained as following

$$D_{2}(F_{n},x)=x^{2n+1}+(2n+1)x^{2n}+\sum_{i=0}^{n-2}\binom{n}{i}2^{n-i}x^{(n+1)+i}.$$

$\Box$

The following result is other formula for $2$-domination polynomial of the friendship graph $F_{n}$ for $n\geq 2$.

Corollary 1. For every $n\geq 2$,

$$D_{2}(F_{n},x)=x^{2n+1}+\sum_{i=1}^{n-1}\bigg{[}\binom{2n-i}{i}+\binom{2n-i-1}{i-1}+n^{i-1}\bigg{]}x^{2n+1-i}+2^{n}x^{n+1}.$$

Proof. Let $D_{n}^{i}$ be the $2$-dominating set of cardinality $i$ in graph $F_{n}$ and $d_{2}(F_{n},i)$ be the number of the sets $D_{n}^{i}$. According to the structure graph $F_{n}$, it is easy to see that the central vertex $v_{2n+1}\in D$. By Theorem 10 and Theorem 2 (i), we have $d_{2}(F_{n},n+1)=2^{n}$ and $d_{2}(F_{n},2n+1)=1$. Since $v_{2n+1}\in D_{n}^{i}$ for $n+2\leq i\leq 2n-1$, we can consider graph $F_{n}$ as cycle $C_{2n}$ with labeled vertices according to Figure 1 such that the edges $v_{2i}v_{2i+1}$ and $v_{2n}v_{1}$ are deleted of $C_{2n}$ for $1\leq i\leq n-1$. Thus, by induction on $n$ and the method of proving of Theorem 4(ii) on cycle $C_{2n}$ for $n+2\leq i\leq 2n-1$, the number of the $2$-dominating set of cardinality $i$ is computed. Therefore, the result completes. $\Box$

We consider another family of graphs as the helm graph. The helm graph $H_{n}$ is the graph obtained from an wheel graph with $n$ vertices by adjoining a pendant edge at each vertex of the cycle [12]. In the following theorem, the number of $2$-dominating sets and $2$-dominating polynomial of graph $H_{n}$ is obtained.

Theorem 11. For every $n\geq 5$,

$$D(H_{n},x)=x^{n}(1+x)^{n-1}+x^{n-1}D(C_{n-1},x).$$

Proof. Let $H_{n}$ be helm graph of order $2n-1$ with the set $L$ contains $n-1$ leaves, cycle $C_{n-1}$ and central vertex $v_{2n-1}$. Let $D$ be a $2$-dominating set of graph $H_{n}$. One can select the set $L\bigcup\{v_{2n-1}\}$ as the $2$-dominating set. Thus, $|D|\leq n$. Assume that $|D|\leq n-1$. Therefore, $n$ remaining vertices of $H_{n}$ dominate by at least two vertices of $D$. Since there are $n-1$ leaves in $H_{n}$, thus the set $D$ must contain these vertices. But, in this case, the central vertex cannot dominate by $D$. Thus, it is a contradiction. Therefore, $|D|=n$.

For computing $2$-domination polynomial of $H_{n}$, we get

$$D_{2}(H_{n},x)=\sum_{i=n}^{2n-1}d_{2}(H_{n},i)x^{i}.$$

It is easy to see that $d_{2}(H_{n},n)=1$ and using Theorem 2(i) $d_{2}(H_{n},2n-1)=1$. Thus, we investigate $d_{2}(H_{n},i)$ for $n+1\leq i\leq 2n-2$. Let $D_{n}^{i}$ be the $2$-dominating set of cardinality $i$ in graph $H_{n}$. We have two following cases.

Case 1: If $v_{2n-1}\in D_{n}^{i}$, then since $L\subseteq D_{n}^{i}$, there are $\binom{n-1}{i}$ possibilities to choose $i$ vertices of $n-1$ vertices for $1\leq i\leq n-2$ on cycle $C_{n-1}$ in graph $H_{n}$. Therefore, $d_{2}(H_{n},i+n)=\binom{n-1}{i}$, in which $1\leq i\leq n-2$.

Case 2: If $v_{2n-1}\notin D_{n}^{i}$, then since $L\subseteq D_{n}^{i}$, other vertices select on cycle $C_{n-1}$. Clearly, it is sufficient to consider the dominating set on cycle $C_{n-1}$. So, $d_{2}(H_{n},i+n-1)=d_{2}(C_{n-1},i)$ for $\gamma(C_{n-1})\leq i\leq n-1$. Therefore, we get

$$D_{2}(H_{n},x)=x^{n}+x^{2n-1}+\sum_{i=1}^{n-2}\binom{n-1}{i}x^{i+n}+\sum_{i=1}^{n-1}d(C_{n-1},i)x^{n-1+i}$$

$${}=x^{n}+x^{2n-1}+x^{n}\Big{(}(1+x)^{n-1}-x^{n-1}-1\Big{)}+x^{n-1}D(C_{n-1},x)$$

$${}=x^{n}(1+x)^{n-1}+x^{n-1}D(C_{n-1},x).$$

Therefore, by substituting for $D(C_{n-1},x)$ by Lemma 2 the result holds. $\Box$

In case $n=4$, it is easy to compute $D_{2}(H_{4},x)$. According to the structure graph $H_{4}$ clearly, $d_{2}(H_{4},4)=1$, $d_{2}(H_{4},5)=\binom{4}{2}$, $d_{2}(H_{4},6)=\binom{4}{3}$ and $d_{2}(H_{4},7)=1$. Thus, $d_{2}(H_{4},x)=x^{4}+6x^{5}+4x^{3}+x^{7}$.

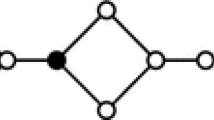
Finally, we consider gear graphs and calculate the $2$-domination polynomial for this family of graphs. The gear graph $G_{n}$, is the graph obtained from the wheel $W_{n}$ by inserting a vertex between any two adjacent vertices in its cycle $C_{n}$ [13].

Theorem 12. For every $n\geq 3$,

$$D_{2}(G_{n},x)=\sum_{i=0}^{n}\Bigg{[}\binom{2n-i}{i}+\binom{2n-i-1}{i-1}+\binom{2n-i+1}{i-1}+\binom{2n-i}{i-2}\Bigg{]}x^{2n+1-i}+x^{n}.$$

Proof. At the first, we show that $d_{2}(G_{n})=n$.According to Figure 2, label vertices of $G_{n}$ with $v_{i}$, $i=1,2,\cdots,n$ and the graph $G_{n}$ of order $2n+1$ contains a cycle $C_{2n}$. Let $D$ be the $2$-dominating set of graph $G_{n}$. According to Figure 2 one can consider the set $\{v_{1},v_{3},\cdots,v_{2n-1}\}$ as $2$-dominating set. So, $|D|\leq n$.

Fig. 2

A gear graph $G_{n}$.

If $|D|\leq n-1$, then $n+2$ remaining vertices in graph $G_{n}$ dominate by at least two vertices in $D$. We consider two following cases.

Case 1: If the central vertex $v_{2n+1}\in D$, then according to the structure graph $G_{n}$, $n$ vertices are adjacent to $v_{2n+1}$. Thus, $|D-\{v_{2n+1}\}|\leq n-2$ and these vertices are selected on cycle $C_{2n}$. Since at least two vertices of $G_{n}$ are not dominated by $D$, it is a contradiction.

Case 2: If $v_{2n+1}\notin D$, then all of the vertices of $D$ must select of cycle $C_{2n}$ such that at least two vertices are adjacent to $v_{2n+1}$. But, according to Figure 2, it is a contradiction. Therefore, $|D|=n$.

Now, we count the number of $2$-dominating sets of graph $G_{n}$. Let $D_{n}^{i}$ be $2$-dominating set of cardinality $i$ in graph $G_{n}$. There are two following cases.

Case i: If the central vertex $v_{2n+1}\in D$, then it is sufficient to compute $i$ vertices on cycle $C_{2n}$. Using Theorem 4 (ii) for $0\leq i\leq n$, we get

$$d_{2}(G_{n},2n+1-i)=\binom{2n-i}{i}+\binom{2n-i-1}{i-1}.$$

Case ii: If $v_{2n+1}\notin D$, then according to the definition $2$-dominating set, we consider $i$ vertices on cycle $C_{2n}$ such that the central vertex $v_{2n+1}$ is adjacent to at least two vertices of $D_{n}^{i}$. In this case, we get

$$d_{2}(G_{n},2n+1-i)=\binom{2n-i+1}{i-1}+\binom{2n-i}{i-2},$$

for $0\leq i\leq n$.

According to structure of graph $G_{n}$, vertex $v_{2n+1}$ is adjacent to vertices of $\{v_{1},v_{3},\cdots,v_{2n-1}\}$. Since $\gamma_{2}(G_{n})=n$, the set $D_{n}^{n}=\{v_{1},v_{3},\cdots,v_{2n-1}\}$ and $d_{2}(G_{n},\gamma_{2})=1$. Therefore, the proof completes. $\Box$