Graphs with Unique Minimum Specified Domination Sets

Abstract

In this paper, we consider the graphs that have a unique set that achieves a domination parameter and determine the maximum value of the associated parameter, both in graphs in general and in graphs without end-vertices. For example, for a graph G of order n without an end-vertex, we show an upper bound of n/3 if G has a unique minimum dominating set, an upper bound of $(n-1)/2$ if G has a unique minimum total dominating set or a unique minimum 2-dominating set, and an upper bound of n/2 if G has a unique paired dominating set.

1 Introduction

Many graph parameters are defined to be the minimum or maximum size of a set with some particular property. Examples include connectivity, independence number, and domination number. For such a parameter $\psi$, we say a graph is $\psi$ -unique if there is a unique set that achieves the extremum.

In this paper, we focus on domination parameters. In this regard, a $\gamma$-unique graph is one with a unique minimum dominating set, and these have been investigated by Gunther et al. [9], Fischermann and Volkmann [7] and others. A $\gamma _t$-unique graph is one with a unique minimum total dominating set, and these have been investigated by Fischermann [6], Haynes and Henning [12] and others. And other domination parameters have been discussed including paired [2], semipaired [13], independent [8, 14] and multiple [15]. Most of the research so far has focussed on trees, especially characterizations thereof, but there has been some work on general properties. Note that there are also several other notations for the concept including UTD [12] for total, UPD [1] for paired, and $\mathcal{U}\mathcal{I}$ [14] for independent.

In this paper, we investigate, for various domination parameters, the $\psi$-unique graphs G with the maximum value of the parameter as a function of the order n. For instance, we note that an isolate-free $\gamma$-unique graph G has $\gamma (G) \le n/3$ and this is sharp even for graphs without end-vertices. While Fischermann [6] showed that an isolate-free $\gamma _t$-unique graph has $\gamma _t(G) \le 3n/5$ in general, we show that if such a G has no end-vertex then $\gamma _t(G) \le (n-1)/2$, and this is sharp. We also show that for paired domination that an isolate-free $\gamma _{pr}$-unique graph has $\gamma _{pr}(G) \le n/2$, and this is sharp. At the same time, we provide results for connected, independent, semipaired and 2-domination, including a new bound on the latter parameter in isolate-free graphs with a constraint on the end-vertices.

2 Definitions and Some Constructions

A dominating set D of a graph G is a set of vertices such that every other vertex in the graph has at least one neighbor in D. It is total dominating if the subgraph G[D] induced by D has no isolates; independent dominating if G[D] has no edges; paired dominating if G[D] has a perfect matching; connected dominating if G[D] is connected; and k -dominating if every vertex outside D has at least k neighbors in the set D. The associated parameters are denoted $\gamma (G)$, $\gamma _t(G)$, i(G), $\gamma _{pr}(G)$, $\gamma _c(G)$ and $\gamma _k(G)$ respectively. (Note that the latter notation is also sometimes used for distance-k domination.) A semipaired dominating set D is such that there is a semi-matching for the vertices of D: this is a partition of D into pairs such that each vertex is within distance 2 of its partner (as measured in G). The associated parameter is denoted $\gamma _{pr2}(G)$. See for example [4, 10, 11] for more on these parameters.

Given a dominating set D and vertex $v\in D$, an external private neighbor of v (with respect to D) is a vertex outside D whose unique neighbor in D is v; an internal private neighbor of v is a vertex of D whose unique neighbor in D is v. A support vertex is a vertex adjacent to at least one end-vertex; a strong support is adjacent to at least two end-vertices.

A useful construction is the following graph, that is sometimes called a generalized corona. Given a graph F with distinguished root vertex v, take multiple disjoint copies of F and then add edges arbitrarily between the copies of the root v to make the graph connected. An example is given in Fig. 4.

For integers $m_1, m_2 \ge 3$ and $k\ge 0$, we define a dumbbell to be the graph of order $m_1+m_2+k$ obtained from the cycles $C_{m_1}$ and $C_{m_2}$ by joining a vertex of the first cycle to a vertex of the second cycle and subdividing the resulting edge k times. Note that the graph can also be defined by taking a path on $m_1+m_2+k$ vertices and then adding a suitable edge incident to each end-vertex. An example is given in Fig. 1.

3 Ordinary Domination

Graphs with unique minimum dominating sets, especially a construction for trees, were studied by Gunther et al. [9] and Fischermann and Volkmann [7] inter alia. The former proved the following:

Lemma 1

[9] If D is the unique dominating set of isolate-free graph G, then every vertex of D has at least two external private neighbors.

From this lemma the upper bound on the domination number is immediate:

Theorem 1

If isolate-free graph G on n vertices is $\gamma$-unique, then $\gamma (G) \le n/3$, and this is sharp even for graphs without end-vertices.

Proof

Let D be the unique minimum dominating set of G. By Lemma 1 there are at least 2|D| vertices outside D. The upper bound follows.

Equality in the bound is achieved for example by a generalized corona of $P_3$ with the center as root. But also consider the dumbbell $D(3r+1,3s+1,1)$ of order $3(r+s+1)$. Since this graph has a Hamiltonian path, the domination number is at most $r+s+1$. We need to argue that the parameter is uniquely attained. Say the subdivision vertex is x. Suppose one takes the neighbor of x in the $C_{3r+1}$ in a dominating set. One still needs r more vertices from that cycle, and $s+1$ vertices to dominate the other cycle, for a total of at least $r+s+2$ vertices. It follows that vertex x is in every $\gamma$-set. And then it can easily be observed that the minimum dominating set is unique within each cycle.$\square$

Note that one can generalize this construction by taking multiple cycles of length congruent to 1 mod 3 and identifying them at a single vertex, which is then used as the attacher. Thus there are example graphs with arbitrarily large maximum degree.

4 Total Domination

Graphs with unique minimum total dominating sets, in particular constructions for trees, were studied by Fischermann [6] and Haynes and Henning [12] inter alia. For general graphs, Fischermann showed:

Lemma 2

[6] If D is the unique minimum total dominating set of isolate-free graph G, then every vertex of D is either a support vertex or has at least two private neighbors (or both).

Using this, Fischermann [6] deduced the bound on the total domination number:

Theorem 2

[6] If isolate-free graph G on $n\ge 3$ vertices is $\gamma _t$-unique, then $\gamma _t(G) \le 3n/5$, and this is sharp.

Equality is achieved inter alia by a generalized corona of $P_5$ with the center as root. (See [6].) In contrast, we show that the upper bound for graphs without end-vertices is smaller:

Theorem 3

If graph G on n vertices with minimum degree $\delta (G) \ge 2$ is $\gamma _t$-unique, then $\gamma _t(G) \le (n-1)/2$, and this is sharp.

Proof

Let D be the unique minimum total dominating set of G. Consider a vertex v in D that does not have an external private neighbor. Then by Lemma 2, vertex v has at least two internal private neighbors, say w and $w'$. In particular, the vertex v is not a private neighbor of any vertex. Further, since each has no neighbor in D other than v, both w and $w'$ have at least two external private neighbors.

Form disjoint subsets of V(G) as follows. First, for each vertex v of D that has no external private neighbor, define subset $S_v$ to contain v, its internal private neighbors, and their (external) private neighbors. (So $|D\cap S_v|\ge 3$ and $|S_v|\ge 7$.) Second, for any vertex w of D not yet taken, define subset $T_w$ to contain w and its external private neighbors. (So $|D\cap T_w|=1$ and $|T_w|\ge 2$.) The subsets so defined are disjoint and collectively contain D. It follows that $|D| \le n/2$.

Suppose that $|D| = n/2$. By the above discussion, it is thus necessary that every vertex $w \in D$ has an external private neighbor and that neighbor is unique. Therefore by Lemma 2, the vertex w also has an internal private neighbor, say $w'$. By the same logic, vertex w is an internal private neighbor of $w'$. This implies that the subgraph induced by the set D forms a collection of disjoint $K_2$’s and that every vertex outside D has a unique neighbor in D.

But, then it follows that the complement of D is also a total dominating set of G. For, every vertex in D has an external neighbor, meaning a vertex in $V(G)-D$; and every vertex outside D has a neighbor outside D because of the minimum-degree condition. This is a contradiction. Hence $|D| < n/2$, as required.

A graph achieving equality in the bound of the result is the dumbbell $D(4r+1,4s+3,1)$ of order $4(r+s+1)+1$. (See Fig. 1 for the case $r=1$ and $s=0$.) We claim that the total domination number is $2(r+s)+2$. It is achieved by starting with x and its neighbor in the second cycle: then 2r vertices totally dominate the remaining vertices of the first cycle and 2s vertices totally dominate the remaining vertices of the second cycle. If the total dominating set does not include the vertex x, then one needs at least $2r+1$ vertices from the first cycle and at least $2s+2$ vertices from the second, which is too many. On the other hand, for a total dominating set we need a neighbor of x. If one takes the neighbor in first cycle, then it can be checked that one still needs 2r more vertices from that cycle, and more than 2s vertices from the second cycle, which is too many. The claim follows.$\square$

Fig. 1

A $\gamma _t$-unique graph where $n=9$ and $\gamma _t = 4$

5 Paired and Semipaired Domination

We consider paired domination next. Given a paired dominating set D with matching M, we refer to the partner of vertex $u\in D$ as that vertex $w\in D$ such that edge uw is in M. We begin with the following property. This property was observed for trees by Chen et al. [2]. Indeed, they proved for trees (and more generally graphs where every block is complete) that the converse is true as well, though it does not hold in general.

Lemma 3

If D is the unique minimum paired dominating set of connected graph G with order at least 3, then every vertex of D has an external private neighbor.

Proof

Suppose some vertex v in D does not have an external private neighbor. Consider its partner w in D. If w has a neighbor x outside D, then one can replace v by x and still have a paired dominating set. Thus every neighbor of w is in D. But then if v has a neighbor y outside D, one can similarly replace w by y. Thus every neighbor of v is in D. If neither v nor w is an end-vertex, one can delete both v and w and still have a paired dominating set. So say v is an end-vertex.

Let x be one of the other neighbors of w and let y be its partner. If vertex y has a neighbor z outside D, then one can replace v by z and still have a paired dominating set. On the other hand, if vertex y has no neighbor outside D, then one can delete both v and y and still have a paired dominating set. In all cases a contradiction is reached.$\square$

As a consequence we obtain immediately the following theorem. For $\gamma _{pr}$-trees the result is readily deduced from the characterization given by Chellali and Haynes [1] (and re-discovered in [2]).

Theorem 4

If isolate-free graph G on $n\ge 3$ vertices is $\gamma _{pr}$-unique, then $\gamma _{pr}(G) \le n/2$, and this is sharp even for graphs without end-vertices.

Proof

An example of graphs achieving the upper bound is the generalized corona of $P_4$ with an end-vertex as the root. But also consider the dumbbell $D(4r+1,4s+1,2)$ of order $4(r+s+1)$. Say the subdivision vertices are $x_1$ and $x_2$, with $x_1$ the one joined to $C_{4r+1}$. Since the graph has a Hamiltonian path, the paired domination number is at most $2(r+s+1)$. Suppose one builds a paired dominating set starting with one of the vertices of degree 3, say the one in $C_{4r+1}$. Then one still needs 2r vertices more from that cycle, and $2s+2$ vertices from what remains, for a total of at least $2(r+s)+3$ vertices. So neither degree-3 vertex is in a minimum paired dominating set. Without the degree-3 vertices, the remaining graph is a collection of paths of length 2 or a multiple of 4, and that has a unique minimum paired dominating set.$\square$

We consider semipaired domination next. Some of the results are similar to those for paired domination. In Lemma 1 of [13] the following result (or rather a stronger result) is proven for trees. We show that it holds for graphs in general. The proof is (very) similar to that of Lemma 3.

Lemma 4

If D is the unique semipaired dominating set of connected graph G of order at least 3, then every vertex of D has an external private neighbor.

Proof

Suppose some vertex v in D does not have an external private neighbor. Consider its partner w in the semi-matching of D.

If v has no neighbor in D, then let x be a common neighbor of v and w (exists since they are distance two apart). One can replace v by x and still have a semipaired dominating set. So assume vertex v has a neighbor in D. If w has a neighbor x outside D, then one can replace v by x and still have a semipaired dominating set. So every neighbor of w is in D. But then if v has a neighbor y outside D, one can replace replace w by y. So every neighbor of v is in D. If both v and w have a neighbor in D other than each other, then one can just delete them and still have a semipaired dominating set. So it follows that v and w are adjacent, and one is an end-vertex, say v.

Let x be one of the other neighbors of w, and let y be its partner in D. If vertex y has a neighbor z outside D, then one can replace v by z and still have a semipaired dominating set. On the other hand, if vertex y has no neighbor outside D, then one can delete both v and y and still have a semipaired dominating set. In all cases a contradiction is reached.$\square$

In Lemma 5 of [13] the following result is proved for trees. But by applying that result to a spanning tree of the graph, one immediately obtains the result for general graphs:

Lemma 5

If connected graph G has even order, then there exists a perfect semi-matching M of G with at least one pair of vertices that are adjacent.

Consequently we obtain the upper bound for general graphs, extending the result of [13] for trees:

Theorem 5

If connected graph G on $n\ge 3$ vertices is $\gamma _{pr2}$-unique, then $\gamma _{pr2}(G) \le (n-1)/2$, and this is sharp.

Proof

It is immediate from Lemma 4 that the semipaired domination number is thus at most n/2. Suppose that there is a semipaired dominating set D of half the order with semi-matching M. Then by that lemma, every vertex not in D is the private neighbor of some vertex of D; in particular every vertex in D has exactly one private neighbor. From this it follows that, for vertices at distance 2 in M, every common neighbor is in D. In particular, every component in the graph induced by D has even order. By Lemma 5, this means that the semi-matching M can be chosen so that some vertex $v \in D$ is adjacent to its partner in D. But then one can take D and replace v by its private neighbor and so get another semipaired dominating set of G. A contradiction of the uniqueness.$\square$

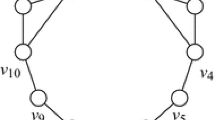
An example of equality is obtained from a star with an even number of edges by subdividing every edge once. (For the comprehensive list of trees, see [13].) However, it is unclear what the maximum value of the parameter is for graphs without end-vertices. The best examples we know have semipaired domination number asymptotically $\frac{2}{5}$ their order. Such an example is obtained for instance by taking a cycle with $5k+1$ vertices and adding one chord joining two vertices at distance 3. The value of the parameter is 2k. See Fig. 2 for the case that $k=3$.

Fig. 2

A $\gamma _{pr2}$-unique graph where $n=16$ and $\gamma _{pr2} = 6$

6 2-Domination

In this section we consider 2-domination. Consider first the restriction to graphs without end-vertices. For such a graph G, a general result of Cockayne et al. [3] shows that $\gamma _2(G) \le 2n/3$, and this is best possible because of the generalized corona of $K_3$. We show that the upper bound can be improved if the graph is also $\gamma _2$-unique. We will need the following observation:

Lemma 6

If G is a graph with $\delta (G) \ge 2$ and D is the unique minimum 2-dominating set of G, then $V(G)-D$ is a 2-dominating set of G.

Proof

Suppose $V(G)-D$ is not a 2-dominating set of G. Then there is some vertex v of D that has at most one neighbor in $V(G)-D$. By the minimum-degree condition, vertex v has at least one neighbor in D. If v has no neighbor in $V(G)-D$, then $D-\{v\}$ is a 2-dominating set of G, a contradiction. If v has a unique neighbor w in $V(G)-D$, then $(D-\{v\}) \cup \{ w \}$ is a 2-dominating set of G of the same size, again a contradiction.$\square$

As a consequence we obtain:

Theorem 6

If G is a graph of order n with $\delta (G) \ge 2$ that is $\gamma _2$-unique, then $\gamma _2(G) \le (n-1)/2$.

Proof

Suppose that $\gamma _2(G) \ge n/2$ and D is the unique minimum 2-dominating set. Then $V(G)-D$ is a 2-dominating set that contradicts either the minimality of D or the uniqueness of D.

We construct a graph that achieves the upper bound as follows. Let $n\ge 5$ be odd, and take an $(n-1)$-cycle and duplicate one vertex (so that the two vertices are not adjacent but have the same neighborhood). See Fig. 3 for $L_{11}$. It is easily checked that the resultant graph $L_n$ has a unique minimum 2-dominating set consisting of the neighbors of the twins and every alternate vertex on the cycle. Thus the graph $L_n$ is $\gamma _2$-unique with $\gamma _2(L_n) = (n-1)/2$.$\square$

Fig. 3

A $\gamma _2$-unique graph where $n=11$ and $\gamma _2 = 5$

6.1 Graphs with No Strong Support

If end-vertices are allowed, then the 2-domination number of a graph of order n can be as high as $n-1$ achieved by the star; and which is $\gamma _2$-unique. However, things are more interesting if one forbids a strong support; that is, no vertex is adjacent to more than one end-vertex. An immediate question is the upper bound for the parameter for such graphs. This we answer next.

Theorem 7

If G is a connected graph of order $n\ge 3$ and no vertex is adjacent to more than one end-vertex, then $\gamma _2(G) \le 3n/4$ and this is sharp.

Proof

The proof is by induction.

Claim

We may assume that:

• (i) there is no edge between vertices of degree 3 or more; and

• (ii) there is no edge between a vertex of degree 1 and a vertex of degree 2.

Proof

First, if there is an edge between two vertices of degree 3 or more, one can just delete it. (This cannot create a component of order 2.) Thus we may assume that the graph has the first property.

Now, suppose there exists some end-vertex u whose neighbor v has degree 2. Let w be the other neighbor of v. If w has degree at least 3, then proceed as follows. Add the edge between u and w. Any 2-dominating set D of the resultant graph must contain at least two vertices from the set $\{u,v,w\}$. Without loss of generality we may assume this pair is u and w; thus the set D is a 2-dominating set of the original graph. Further, the resultant graph still has the first property.

So assume that vertex w has degree 2. Say x is its other neighbor. If x has degree 2, then either we are in $P_5$, when the theorem is clear, or x does not have an end-vertex neighbor. In the latter case, the graph $G' = G - \{u,v\}$ satisfies the hypothesis of the theorem, and so we can induct to yield a 2-dominating set $D'$ of $G'$ of size at most $\frac{3}{4} \, (n-2)$. Since vertex w is in every 2-dominating set of $G'$, we can add just vertex u to $D'$ and obtain a 2-dominating set of G of the desired size.

Finally, if vertex x has degree 3 or more, then let $G'' = G - \{ u,v,w \}$. The graph $G''$ satisfies the hypothesis of the theorem, and so by the induction hypothesis has a 2-dominating set $D''$ of size at most $\frac{3}{4} \, (n-3)$. And $D'' \cup \{ u, w\}$ is a 2-dominating set of G of the desired size.$\square$

If the graph G is 2-regular, then the bound is trivial (and known). So assume G is not a cycle. Let X denote the vertices of degree at least 3 and define a “tract” as a maximal connected subgraph all of whose vertices have degree 2 in G. Note that a tract forms a path, and both ends of the path have a neighbor in X (by the claim).

Claim

We may assume that the number of tracts is at least |X|.

Proof

Suppose some vertex v of X is incident with (at most) one tract. Then it must be that v has an end-vertex neighbor and the graph contains only one tract, and both ends thereof are adjacent to v. That is, the graph G is a cycle with one end-vertex added adjacent to one vertex. The bound of the theorem is easily checked for such a graph. Thus we may assume that each vertex of X is incident with at least two tracts, and the bound follows.$\square$

Construct set D as follows. Start with X and all end-vertices. Then for each tract, take every alternate vertex, starting with the second. The set D is a 2-dominating set of G: one need only check that the degree-2 vertices are 2-dominated.

Now, for accountancy purposes, arbitrarily assign tracts to vertices of X such that each vertex $v\in X$ is assigned at least one tract. (This is possible by the above claim.) Then let $S_v$ be the set consisting of v, its end-vertex neighbor if it exists, and the one or more tracts assigned to v. The sets $S_v$ form a partition of V(G). Let s denote the number of vertices of D in the tract(s) assigned to v. Then $|D \cap S_v|/|S_v| \le (s+2)/(2s+2) \le 3/4$ if $s\ge 1$, and $|D \cap S_v|/|S_v| \le 2/3$ if $s=0$. The bound of the theorem follows.

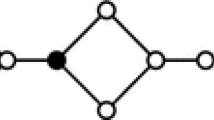
Equality in the bound is achieved by the corona of a corona, or equivalently the generalized corona using $P_4$ rooted at one of the inner vertices. See Fig. 4 for an illustration.$\square$

Fig. 4

A graph where $\gamma _2$ is $\frac{3}{4}$ the order

We consider next the restriction to graphs with unique minimum 2-dominating sets. We believe the upper bound is two-thirds the order. We can prove it for trees.

Theorem 8

If T is a $\gamma _2$-unique tree on $n\ge 3$ vertices with no vertex adjacent to more than one end-vertex, then $\gamma _2(T) \le 2n/3$ and this is sharp.

Proof

The proof is by induction on the order. Let D be the minimum 2-dominating set of T. Let X be the set of vertices of degree 3 or more.

Claim

We may assume that the vertices of X form an independent set.

Proof

Assume that vertices $x_1, x_2 \in X$ are adjacent. The removal of the edge $x_1x_2$ yields two trees, say $T_1$ and $T_2$, that have no strong support. So it suffices to show that both $T_1$ and $T_2$ are $\gamma _2$-unique.

If both $x_1$ and $x_2$ are in D, then clearly removing edge $x_1x_2$ does not affect the domination by D, and so D restricted to each subtree is a 2-dominating set of that subtree. If either subtree has a smaller 2-dominating set, it contradicts the minimality of D; and if either subtree has another 2-dominating set of the same size, it contradicts the uniqueness of D. The case that both $x_1$ and $x_2$ are out of D is identical.

So assume that every edge between vertices of X has one end in D and one out of D. Say $x_1 \in D$ and $x_2 \notin D$, and let y be a neighbor of $x_2$. Suppose y is not in D. Then y has at least two neighbors in D and hence y is in X; but that means that edge $x_2y$ contradicts our assumption. It follows that every neighbor of $x_2$ is in D. In particular, the set D restricted to $T_2$ is a 2-dominating set of $T_2$. The conclusion follows as before.$\square$

Now, consider a diametrical path P of T, say $abcd\ldots$ (Note that $P_3$ is precluded by the hypothesis.) By the maximality of P and the lack of strong supports, it follows that vertex b has degree 2. Furthermore, it holds that $b\notin D$, since otherwise $(D-b)\cup \{c\}$ is another 2-dominating set. Thus in particular $c\in D$.

Case 1: Vertex c has degree at least 3.

Then by the claim, every neighbor of c has degree at most 2. Let B denote the degree-2 neighbors of vertex c other than d. By the maximality of the path P, every vertex $b' \in B$ has an end-vertex neighbor. If every vertex of T is within distance 2 of c, then T is the graph obtained from a star centered at c by dividing all or all but one edges; and such a graph has $\gamma _2(T) \le \lfloor n/2+1\rfloor$. Since $P_4$ is not $\gamma _2$-unique, this quantity is at most 2n/3, as required.

So assume that there is some vertex at distance 3 or more from c. Let $T'$ be the tree obtained from T by deleting the end-vertex neighbor of c if it exists, all of B and all vertices thus isolated. We claim that $D\cap V(T')$ is the unique minimum 2-dominating set of $T'$. Note that c is an end-vertex in $T'$ and thus is in every 2-dominating set of $T'$. Every 2-dominating set of $T'$ can be extended to a 2-dominating set of T by adding the end-vertices of $V(T)-V(T')$. Conversely, every minimum 2-dominating set of T contains these end-vertices and a minimum 2-dominating set of $T'$. The claim follows.

Since we are assuming there is some vertex at distance 3 from c, and we know vertex d has degree 2, it follows that the tree $T'$ satisfies the hypothesis of the theorem. So by the induction hypothesis, it holds that $\gamma _2(T') \le 2n'/3$ where $n'$ denotes the order of $T'$. Let $\varepsilon =1$ if vertex c has an end-vertex neighbor in T and 0 otherwise. The number of vertices in $D-V(T')$ is $|B|+\varepsilon$ while the number in $T-V(T')$ is $2|B|+\varepsilon$. The ratio $(|B|+ \varepsilon )/ (2|B|+\varepsilon )$ is at most 2/3 (with equality only if $\varepsilon =|B|=1$). The bound follows.

Case 2: Vertex c has degree 2.

If vertex d does not have an end-vertex neighbor, then we can define $T'$ as above (which in this case means just removing vertices a and b), and induct as before. So assume vertex d has an end-vertex neighbor. If d has degree 2, then T is $P_5$, where the bound holds. Otherwise d has degree at least 3. Then either $d\in D$, or by the above claim all its neighbors have degree 2 or less and so are in D. In either case, we can define the tree $T'' = T - \{a,b,c\}$ and observe that D restricted to $V(T'')$ is a 2-dominating set thereof. And hence apply the induction hypothesis and add $\{a,c\}$. The bound follows.

Equality in the bound is obtained by the corona of the extremal $\gamma$-unique graphs. But there are more extremal graphs. For example, for $m\ge 2$ let $H_m$ be the caterpillar that is obtained from the spine $P_{2m+1}$ by adding an end-vertex at vertices $1,2,4,6,\ldots , 2m,2m+1$. The graph $H_5$ is shown in Fig. 5. The gaph $H_m$ is $\gamma _2$-unique.$\square$

Fig. 5

The $\gamma _2$-unique tree $H_5$ where $\gamma _2$ is $\frac{2}{3}$ the order

Fig. 6

An i-unique graph with maximum value of i

Fig. 7

A $\gamma$-unique graph where $\gamma$ is $\frac{2}{7}$ the order

7 Independent and Connected Domination

In contrast to the parameters discussed above, constraining the extremal set to be unique does not significantly affect the upper bound when it comes to independent and connected domination.

Favaron determined the maximum value of the independent domination number:

Theorem 9

[5] If G is an isolate-free graph on n vertices, then $i(G) \le n + 2 - 2\sqrt{n}$ and this is sharp.

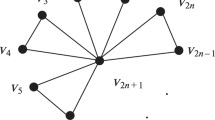
The maximum value is achieved by the generalized corona constructed by taking r copies of $K_{1,r-1}$ and adding all edges between the centers. If one now adds a single end-vertex and joins it to a vertex of the clique, then the resultant graph is i-unique, and has independence number $\lfloor n + 2 - 2\sqrt{n} \rfloor$. See Fig. 6. A similar idea is possible if there is a minimum-degree condition. The extremal graphs for the parameter are split graphs where, in particular, each vertex in the independent set I has the same degree $\delta$ and every vertex of the clique has the same degree. Again if we clone one vertex in I, we obtain an i-unique graph.

It is trivial and well-known that the path has maximum connected domination number (namely $n-2$) and it is $\gamma _c$-unique. If one forbid leaves, then consider the barbell $D(3,3,n-6)$. This graph is $\gamma _c$-unique, and the value $n-4$ is best possible.

8 Future Work

Apart from resolving the questions about semipaired and 2-domination discussed above, it would be interesting to determine what happens if the minimum degree is required to be at least 3. For example, for ordinary domination the best example we know is the generalized corona formed using the graph that is obtained from $K_{3,3}$ by subdividing one edge and setting that vertex to be the root. See Fig. 7.