An MHD Model of an Incompressible Polymeric Fluid: Linear Instability of a Steady State

Abstract

We study linear stability of a steady state for a generalization of the basic rheological Pokrovskii–Vinogradov model which describes the flows of melts and solutions of an incompressible viscoelastic polymeric medium in the nonisothermal case under the influence of a magnetic field. We prove that the corresponding linearized problem describing magnetohydrodynamic flows of polymers in an infinite plane channel has the following property: For some values of the conduction current which is given on the electrodes (i.e. at the channel boundaries), there exist solutions whose amplitude grows exponentially (in the class of functions periodic along the channel).

INTRODUCTION

In this article we study a generalization of the structurally phenomenological Pokrovskii–Vinogradov model describing the flows of melts and solutions of incompressible viscoelastic polymeric media to the nonisothermal case under the influence of a magnetic field. In the Pokrovskii–Vinogradov model, the polymeric system is considered as a suspension of polymer macromolecules moving in an anisotropic fluid formed, for example, by a solvent and other macromolecules. Impact of the environment to a real macromolecule is approximated by the action onto a linear chain of Brownian particles each of which is a rather large part of the macromolecule. The Brownian particles are often called the “beads,” they are connected to each other by the elastic forces called “springs.” In the case of slow motions, the macromolecule is modeled by a chain of two particles called a “dumbbell.”

The physical representation of linear polymeric flows described above results in the formulation of the Pokrovskii–Vinogradov rheological model [1–3]:

$$ \rho \bigg ( \frac {\partial }{\partial t} v_i + v_k \frac {\partial }{\partial x_k} v_i \bigg ) = \frac {\partial }{\partial x_k} \sigma _{ik}, \qquad \frac {\partial v_i}{\partial x_i} = 0, $$

(1)

$$ \sigma _{ik} = -p\delta _{ik} + 3 \frac {\eta _0}{\tau _0} a_{ik},$$

(2)

$$ \begin {gathered} \frac {d}{dt}a_{ik} - v_{ij}a_{jk} - v_{kj}a_{ji} + \frac {1 + (k - \beta )I}{\tau _0} a_{ik} = \frac {2}{3} \gamma _{ik} - \frac {3\beta }{\tau _0} a_{ij} a_{jk}, \\ I = a_{11} + a_{22} + a_{33}, \qquad \gamma _{ik} = \frac {v_{ik} + v_{ki}}{2}, \end {gathered} $$

(3)

where $\rho$ is the polymer density, $v_i$ is the $i$th component of the velocity, $\sigma _{ik}$ is the stress tensor, $p$ is the hydrostatic pressure, $\eta _0$ and $\tau _0$ are the initial values of the shear viscosity and the relaxation time for the viscoelastic component, $v_{ij}$ is the tensor of the velocity gradients, $a_{ik}$ is the symmetric tensor of anisotropic stresses of second rank, $I$ is the first invariant of the tensor of anisotropic stresses, $\gamma _{ik}$ is the symmetrized tensor of the velocity gradients, $k$ and $\beta$ are the phenomenological parameters accounting for the shape and the size of the coiled molecule in the dynamical equations of the polymer macromolecule. Here (1) is the equation of motion and the condition of incompressibility, (2) and (3) are the rheological relation that connects the kinematic characteristics of the flow and its thermodynamic parameters.

Some generalizations of model (1)–(3) (for example, when some term is added into (2) to take into account the so-called shear viscosity, and the parameter $\beta$ depends also on the first invariant of the anisotropy tensor) provide rather good results in numerical simulations of viscometric flows, i.e. when the components of the tensor of velocity gradients are some given functions of time [4]. Therefore, we can assume that some modifications of the basic Pokrovskii–Vinogradov model can be useful for modeling the polymer motion under complex conditions of deformation, for example, for the stationary and nonstationary flows in circular channels, flows in the channels with fast change of the sectional area, and the flows with free boundary. An important peculiarity of these flows is their two- and three-dimensional character.

In this article, we consider one of such generalizations that takes into account the influence of the heat and the magnetic field on the polymeric fluid motion. Our main interest is the linear stability of a steady state of the mathematical model in the case when the polymeric medium flows in an infinite plane channel.

Structurally, Section 1 is devoted to the statement of a nonlinear model that describes the MHD flow of an incompressible viscoelastic fluid provided that heat is supplied to the channel boundaries. In Section 2, we obtain some model linearized with respect to the steady state and formulate the main results of this article. The final Section 3 contains their proofs.

The results in this article are closely related to those of [5-11] in which, in particular, we obtained some asymptotic representations of the eigenvalues of the mixed problems arising in the description of the polymeric flows in an infinite plane channel. We use various generalizations of the Pokrovskii-Vinogradov model as the mathematical models, and the main solutions are analogous to a Poiseuille shear flow for the Navier–Stokes system. Finally, note that in [12] for the linear mixed problems the results are presented with some estimates of the real parts of the eigenvalues when the Reynolds number increases (as the main solutions, there are chosen some known shear flows). We use the Navier–Stokes model for a viscous fluid.

1. A NONLINEAR MODEL OF THE POLYMERIC FLUID FLOW IN A PLANE CHANNEL UNDER THE PRESENCE OF AN EXTERNAL MAGNETIC FIELD

Using the results of [3, 13–16] and following [17], we formulate the mathematical model that describes the magnetohydrodynamic flows of an nonisothermal incompressible polymeric fluid. Consider some variant of this model in which, by analogy with [18], we introduce some dissipative terms in the equation for the heat gain.

In dimensionless form this version of the mathematical model can be written as follows:

$$ {\mathop {\rm div}\nolimits \thinspace }\vec {u} = u_x + v_y = 0,$$

(4)

$$ {\mathop {\rm div}\nolimits \thinspace }\vec {H} = L_x + M_y = 0,$$

(5)

$$ \frac {d\vec {u}}{dt} + \nabla P = {\mathop {\rm div}\nolimits \thinspace }(Z\Pi ) + \sigma _m(\vec {H}, \nabla )\vec {H} + {\mathop {\rm Gr}\nolimits }(Z-1)\begin {pmatrix} \ 0 \ \\1\end {pmatrix}, $$

(6)

$$ \frac {da_{11}}{dt} - 2A_1 u_x - 2a_{12}u_y + L_{11} = 0, $$

(7)

$$ \frac {da_{22}}{dt} - 2A_2 v_y - 2a_{12}v_x + L_{22} = 0, $$

(8)

$$ \frac {da_{12}}{dt} - A_1 v_x - A_2 u_y + \frac {\widetilde {K}_I a_{12}}{\bar {\tau }_0(Z)} = 0,$$

(9)

$$ \frac {dZ}{dt} = \frac {1}{{\mathop {\rm Pr}\nolimits }}\ \Delta _{x,y}Z + \frac {A_r}{{\mathop {\rm Pr}\nolimits }}ZD + \frac {A_m}{{\mathop {\rm Pr}\nolimits }}\ \sigma _m D_m, $$

(10)

$$ \frac {d\vec {H}}{dt} - (\vec {H},\nabla )\vec {u} - b_m\Delta _{x,y}\vec {H} = 0.$$

(11)

Here $t$ is time, $\vec {u}=(u,v)$; $L$ and $1+M$ are the components of the magnetizing force $\vec {H}$ in the Cartesian coordinate system $x$ and $y$;

$$ P = p + \sigma _m \frac {L^2 + (1+ M)^2}2; $$

$p$ is the pressure; $a_{11}$, $a_{22}$, and $a_{12}$ are the components of the symmetrical anisotropy tensor of second rank;

$$ \Pi = \frac {1}{{\mathop {\rm Re}\nolimits }} (a_{ij}),\quad i,j = 1,2; \qquad L_{ii} = \frac {K_I a_{ii} + \beta (a_{ii}^2 + a_{12}^2)}{\bar {\tau }_0(Z)}, \quad i = 1,2;$$

$$ K_I = {\mathop {\rm W}\nolimits }^{-1} + \frac {\bar {k}}{3}I,\qquad \bar {k} = k - \beta ; $$

$I = a_{11} + a_{22}$ is the first invariant of the anisotropy tensor; $k$ and $\beta$ ($0 < \beta < 1$) are the phenomenological parameters of the rheological model (see [1]);

$$ A_i = W^{-1} + a_{ii},\quad i = 1,2;\qquad Z = T/T_0,$$

where $T$ is the temperature, $T_0$ is the average temperature (room temperature; we will further assume that $T_0 = 300$ K);

$$ \widetilde {K}_I = K_I + \beta I;\qquad \bar {\tau }_0(Z) = 1/(Z J(Z)),\qquad J(Z) = \exp \bigg \{\overline {E}_{A}\dfrac {Z-1}{Z}\bigg \},\qquad \overline {E}_A = E_A/T_0. $$

The constants are described in detail in [17, 19–21]: $E_A$ is the activation energy, $\mathop {\rm Re}\nolimits$ is the Reynolds number, $\mathop {\rm W}\nolimits$ is the Weissenberg number, ${\mathop {\rm Gr}\nolimits } ={\mathop {\rm Ra}\nolimits }/ {\mathop {\rm Pr}\nolimits }$ is the Grasshoff number, $\mathop {\rm Pr}\nolimits$ is the Prandtl number, $\mathop {\rm Ra}\nolimits$ is the Rayleigh number, $A_r$ and $A_m$ are the dissipative coefficients, $\sigma _m$ is the magnetic pressure coefficient, $b_m=1/{\mathop {\rm Re}\nolimits }_m$, and ${\mathop {\rm Re}\nolimits }_m$ is the magnetic Reynolds number. Further,

$$ D_{\Gamma } = a_{11}u_x + (v_x + u_y)a_{12} + a_{22}v_y,\qquad D_m = L^2 u_x + L(1 + M)(v_x + u_y) + (1 + M)^2 v_y,$$

$$ \frac {d}{dt} = \frac {\partial }{\partial t} + (\vec {u}, \nabla ) = \frac {\partial }{\partial t} + u\frac {\partial }{\partial x} + v\frac {\partial }{\partial y}, $$

and $\Delta _{x,y}$ is the Laplace operator

$$ \Delta _{x,y} = \frac {\partial ^2}{\partial x^2} + \frac {\partial ^2}{\partial y^2}.$$

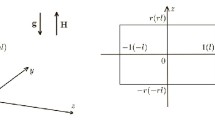
The variables $t$, $x$, $y$, $u$, $v$, $p$, $a_{11}$, $a_{22}$, $a_{12}$, $L$, and $M$ in (4)–(11) correspond to the following values: $l/u_H$, $l$, $u_H$, $\rho u_H^2$, ${\mathop {\rm W}\nolimits } /3$, and $H_0$, where $H_0$ is the characteristic magnetizing force (see Fig. 1)

Fig. 1.

A plane channel.

Remark 1$.$ The MHD equations (4)–(11) are derived with the use of the Maxwell equations (see [13, 15]). Moreover, the magnetic induction vector $\vec {B}$ is represented as

$$ \vec {B} = \mu \mu _0 \vec {H} = (1 + \chi ) \mu _0 \vec {H},$$

(12)

where $\chi$ is the magnetic susceptibility (see [22, 23]), $\chi =\chi _0/Z$, and $\chi _0$ is the magnetic susceptibility for $T = T_0$; $\mu$ is the magnetic penetration of the polymeric fluid, and $\mu _0$ is magnetic permeability in vacuum. In what follows, we assume that for a polymeric medium $\mu =1$ (i.e., $\chi _0 = 0$).

Remark 2$.$ Our main target is the problem of finding the solutions to (4)–(11) that describe magnetohydrodynamic flows of an incompressible polymeric fluid in a plane channel $S$ of depth $1(l)$. The cannel is bounded with the horizontal walls that are the electrodes $C^{+}$ and $C^{-}$ along which we have the conduction currents of current strengths of $J^{+}$ and $J^{-}$ respectively (see the figure). The domains $S_1^{+}$ and $S_1^{-}$ external to the channel are under the influence of the uniform magnetic fields with components $L_1^{\pm }$ and $M_1^{\pm }$ respectively:

$$ \begin {gathered} L_1^{+} = 0, \qquad M_1^{+}\big |_{y = 1/2+0} = -1 + \frac {1 + M(1/2)}{1 + \chi _0^{+}}, \\ L_1^{-} = 0, \qquad M_1^{-}\big |_{y=-1/2-0} = -1 + \frac {1 + M(-1/2)}{1 + \chi _0^{-}/(1 + \bar {\theta })}. \end {gathered}$$

Moreover, $\chi _1^{+}$ and $\chi _1^{-}$ are the magnetic susceptibilities of the magnets $S_1^{+}$ and $S_1^{-}$, while $\chi = \chi _0/Z$. The temperature values on the channel walls will be defined below on using (13). Finally, the correlations between the boundary values $M_1^{+} + 1$, $1 + M(1/2)$ and $M_1^{-} + 1$, $1 + M(-1/2)$ arise correspondingly due to continuity of the normal component of the magnetic induction vector on the channel walls and equality (12).

On the channel walls we have the boundary conditions:

$$ \begin {gathered} \vec {u}|_{y = \pm 1/2} = 0 \qquad \text {(no-slip condition)}, \\ Z|_{y = 1/2} = 1 \qquad (T = T_0), \\ Z|_{y = -1/2} = 1 + \bar {\theta } \qquad (\bar {\theta } = \theta /T_0, \ \ \theta = T - T_0). \end {gathered}$$

(13)

The temperature is given too:

$$ T = \begin {cases} T_0, & \text {in } \ S_1^{+}, \\ T_0 + \theta , & \text {in } \ S_1^{-}. \end {cases}$$

Moreover, for $\bar {\theta } > 0$ we have some heating from below; and for $\bar {\theta } < 0$ the heating occurs from above.

Remark 3$.$ We will consider the electrodes $C^{+}$ and $C^{-}$ as the boundaries between the two uniform isotropic magnetics. Therefore, the following well-known boundary conditions hold (see [22, 24]):

$$ \begin {gathered} L = -J^{+}, \quad M_y = 0 \qquad \text {for } \ y = 1/2 \ \ \qquad (\text {on }C^{+}), \\ L = -J^{-}, \quad M_y = 0\qquad \text {for } \ y = - 1/2 \qquad (\text {on }C^{-}). \end {gathered} $$

(14)

Assuming that (5) holds for $y = \pm 1/2$, $L = -J^{+}$ for $y = 1/2$, and $L = -J^{-}$ for $y = -1/2$ (see (14)), we arrive at the boundary condition $M_y = 0$ at $y = \pm 1/2$.

Remark 4$.$ Note that under the conditions

$$ \begin {aligned} d = L_x + M_y = 0 \qquad & \mbox {for} \quad y = \pm 1/2, \\ d = 0 \qquad & \mbox {for} \quad t=0,\quad |y| < 1/2,\quad x\in \mathbb {R}, \\ d \to 0 \quad \mbox {as} \quad |x|\to \infty ,\qquad &\mbox {for} \quad t > 0,\quad |y| < 1/2,\quad x\in \mathbb {R}, \end {aligned}$$

we have $d \equiv 0$ for $t > 0$, $|y| < 1/3$, and all $x \in \mathbb {R}$; i.e., (5) follows from (4) and (11).

To prove this we apply the operator $\mathop {\rm div}\nolimits \thinspace$ to (11). Taking (4) into account, we obtain

$$ d_t + (\vec {u},\nabla )d - b_m \Delta _{x,y}d = 0,$$

and then

$$ (d^2)_t + {\mathop {\rm div}\nolimits \thinspace }(d^2 \vec {u} - 2b_m d\cdot \nabla d) + 2 b_m |\nabla d|^2 = 0.$$

Integrating this relation with respect to $x$ from $-\infty$ to $+\infty$ and with respect to $y$ from $-1/2$ to $1/2$, we have

$$ \frac {d}{dt}\Bigg \{ \int \limits _{-1/2}^{1/2} \int \limits _{-\infty }^{+\infty } d^2(t,x,y)\thinspace dxdy \Bigg \} + 2b_m \int \limits _{-1/2}^{1/2} \int \limits _{-\infty }^{+\infty } |\nabla d(t,x,y)|^2\thinspace dxdy = 0,$$

which implies

$$ \int \limits _{-1/2}^{1/2} \int \limits _{-\infty }^{+\infty } d^2(t,x,y)\thinspace dxdy \leq 0;$$

i.e., $d \equiv 0$ for $t > 0$, $|y| < 1/2$, and $x\in \mathbb {R}$.

2. A STEADY STATE. THE LINEARIZED PROBLEM. FORMULATION OF THE MAIN RESULTS

As the main solution to problem (4)–(11),(13),(14) we take the steady state: $\hat {\vec {u}} \equiv 0$, $\hat {\alpha }_{11} = \hat {\alpha }_{12} = \hat {\alpha }_{22} \equiv 0$, $p(t,x,y) = \hat {p}_0 = {\mathrm {const}}$, $\widehat {Z} \equiv 1$ ($\bar {\theta } = 0$ and in what follows), $\hat {L} = J_0$ ($J^{\pm } = J_0$ and in what follows), and $\widehat {M} = \hat {\lambda } = \chi _0^{+} = \chi _0^{-}$.

Linearizing (4)–(11) with respect to the chosen steady state, we arrive at the linear system:

$$ \begin {gathered} u_t - (\alpha _{11})_x + (\alpha _{22})_x - (\alpha _{12})_y + \Omega _x + \sigma _m (1 + \hat {\lambda }) \omega _m = 0, \\ v_t - (\alpha _{12})_x + \Omega _y - {\mathop {\rm Gr}\nolimits } Z + \sigma _m J_0 \omega _m = 0, \\ (\alpha _{11})_t - 2\varkappa ^2 u_x + {\mathop {\rm W}\nolimits }^{-1} \alpha _{11} = 0, \\ (\alpha _{12})_t - \varkappa ^2 v_x - \varkappa ^2 u_y + {\mathop {\rm W}\nolimits }^{-1} \alpha _{12} = 0, \\ (\alpha _{22})_t - 2\varkappa ^2 v_y + {\mathop {\rm W}\nolimits }^{-1}\alpha _{222} = 0, \\ Z_t = \frac {1}{{\mathop {\rm Pr}\nolimits }}\ \Delta _{x,y}Z + \frac {A_m \sigma _m}{{\mathop {\rm Pr}\nolimits }} \ \big ( J_0^2 u_x - J_0(1 + \hat {\lambda }) v_x - J_0(1 + \hat {\lambda }) u_y + (1 + \hat {\lambda })^2 v_y \big ), \\ L_t + J_0 u_x - (1 + \hat {\lambda })u_y - b_m \Delta _{x,y} L = 0, \\ M_t + J_0 v_x - (1 + \hat {\lambda })v_y - b_m \Delta _{x,y} M = 0, \\ u_x + v_y = 0, \qquad t > 0, \quad |y| < 1/2,\quad x \in \mathbb {R}. \end {gathered} $$

(15)

Here

$$ \Omega = p - \alpha _{22},\qquad \omega _m = M_x - L_y,\qquad \varkappa ^2 = 1/({\mathop {\rm W}\nolimits } {\mathop {\rm Re}\nolimits }).$$

Note that (5) is omitted according to Remark 4. Moreover, if $(\alpha _{11} + \alpha _{22})|_{t =0} \equiv 0$ then from the third, fifth, and last equations of (15) it follows that

$$ \alpha _{11} = -\alpha _{22} \qquad \text {for} \ \|y| < 1/2,\ t > 0, \ x \in \mathbb {R}.$$

(16)

By (13) and (14), the boundary conditions for the linearized problem (15) are as follows:

$$ u = v = Z = L = M_{y} = 0 \qquad \text {for} \ \ y = \pm 1/2, \ t > 0,\ x \in \mathbb {R}.$$

(17)

Remark 5$.$ As was noted in Section 1, the boundary values of the components $M_1^{+}$ and $M_1^{-}$ in the domains $S_1^{+}$ and $S_1^{-}$ are determined as follows:

$$ \begin {gathered} M_1^{+}\big |_{y =1/2 + 0} = -1 + \frac {1 + M(1/2)}{1 + \chi _0^{+}}, \\[4pt] M_1^{-}\big |_{y = -1/2 - 0} = -1 + \frac {1 + M(-1/2)}{1 + \chi _0^{-}/{(1 + \bar {\theta }})} = -1 + \frac {1 + M(-1/2)}{1 + \chi _0^{+}}, \end {gathered}$$

(18)

where $M(1/2)$ and $M(-1/2)$ are the values of $M$ on the upper and lower electrodes respectively.

Suppose that $S_1^{\pm }$ are filled with nonconductive media. Then, owing to the Maxwell’s equations [23], we conclude that the small and time-independent perturbations of $M_1^{\pm }$ satisfy the Laplace equation and the additional conditions at infinity:

$$ \begin {aligned} \Delta _{x,y} M_1^{+} = 0 &\quad \text {in} \ \ S_1^{+},& & M_1^{+} \to 0 \quad \text {as} \ \ y \to \infty ,\qquad \qquad \\[3pt] \Delta _{x,y} M_1^{-} = 0 &\quad \text {in} \ \ S_1^{-},& & M_1^{-} \to 0 \quad \text {as} \ \ y \to -\infty .\qquad \qquad \end {aligned} $$

(19)

If the components of $M_1^{\pm }$ are periodic functions in $x$ so that

$$ M_1^{\pm }(x,y) = \widetilde {M}^{\pm }(y) e^{i\omega x}, \qquad \omega \in R;$$

then from (19) we obtain

$$ \begin {aligned} \tilde {M}_1^{+}(y) = M_1^{+}\big |_{y = 1/2 + 0}\thinspace e^{-|\omega |(y -1/2)}, &\qquad y > 1/2, \\ \tilde {M}_1^{-}(y) = M_1^{-}\big |_{y = 1/2 - 0}\thinspace e^{|\omega |(y + 1/2)}, &\qquad y < -1/2. \end {aligned}$$

Thus, by (18), the components $L_1^{\pm }$ and $1 + M_1^{\pm }$ are defined of the tension vector $\vec {H}$ in $S_1^{\pm }$.

Consider the particular case of the model (15), (17) for $b_m = 0$ (the absolute conductivity) and additionally assume that $A_m = 0$. Then (15), (17) will be much simpler and have only four unknowns: $u$, $v$, $\alpha _{12}$, and $\Omega$.

Let the class of admissible perturbations contain the periodic functions of $x$, namely,

$$ \begin {gathered} \vec {U} = (u,v,\alpha _{12})^\top = \vec {\widetilde {U}}(y)\exp \{\lambda t + i\omega x\}, \\ \Omega = \tilde {\Omega }(y) \exp \{\lambda t + i\omega x\}, \end {gathered} $$

(20)

where $\lambda = \eta + i\omega _0$, $\omega _0,\omega \in \mathbb {R}$ (in what follows we will omit the $\sim$ mark for the unknown functions).

Using (20), we transform the boundary value problem (15), (17), and obtain the spectral problem

$$ \begin {gathered} \vec {G}^{\prime } = A\vec {G}, \qquad |y| < 1/2, \\ L \vec {G}(\pm 1/2) = 0, \end {gathered} $$

(21)

where

$$ \begin {gathered} \vec {G} = (u,v,\alpha _{12},\Omega )^\top , \qquad L = \begin {pmatrix} 1 & \ 0 \ & \ 0 \ & \ 0 \ \\ \ 0 \ & 1 & 0 & 0 \end {pmatrix}, \qquad A = \begin {pmatrix} 0 & \ -i\omega \ & q_0 & 0 \\ \ -i\omega \ & 0 & 0 & 0 \\ \ \bar {\rho }_1/\rho _0 \ & a_1 & a_2 & \ i\omega /\rho _0 \ \\ b_1 & b_2 & b_3 & a_2 \end {pmatrix}, \\ \bar {\rho }_1 = \frac {\rho _1}{q_0} + 2\sigma _m (1 + \hat {\lambda })^2 \frac {\omega ^2}{\lambda }, \qquad q_0 = \frac {\lambda + {\mathop {\rm W}\nolimits }^{-1}}{\varkappa ^2}, \qquad \rho _1 = \lambda q_0 + 4\omega ^2, \qquad \rho _0 = 1 + \frac {\sigma _m (1 + \hat {\lambda })^2}{\lambda } q_0, \\ a_1 = \frac {2\sigma _m (1 + \hat {\lambda })\omega ^2}{\lambda \rho _0}\ J_0, \qquad a_2 = \frac {\sigma _m (1 + \hat {\lambda }) J_0 q_0}{\lambda \rho _0}\ i\omega , \\ b_1 = \frac {\bar {\rho }_1}{\rho _0} \frac {J_0 \sigma _m q_0 (1 + \hat {\lambda })}{\lambda } - \frac {2J_0 \sigma _m \omega ^2 (1 + \hat {\lambda })}{\lambda },\qquad b_2 = a_1 \frac {J_0 \sigma _m q_0 (1 + \hat {\lambda })}{\lambda } - \bigg ( \frac {2J_0 \sigma _m \omega ^2 (1 + \hat {\lambda })}{\lambda } + \lambda \bigg ), \\ b_3 = a_2 \frac {J_0 \sigma _m q_0 (1 + \hat {\lambda })}{\lambda } - \frac {J_0^2 \sigma _m \omega ^2 (1 + \hat {\lambda })}{\lambda } + i\omega . \end {gathered} $$

Remark 6$.$ The functions $L(y)$ and $M(y)$ are found as follows:

$$ M = -\frac {i\omega }{\lambda }(J_0 v + (1 + \hat {\lambda })u),\qquad L = -\frac {1}{\lambda }(i\omega J_0 u + i\omega (1 + \hat {\lambda })v - q_0 (1 + \hat {\lambda })\alpha _{12}); $$

and, moreover, $L_x + M_y = 0$.

Thus, we have

Proposition 1. $.$ If $J_0$ is small enough then some nontrivial solutions of $(21)$ exist with $\Re \lambda \thinspace (=\eta ) > 0$ .

And as a consequence, the following holds:

Proposition 2$.$ The steady state of $(4)$– $(11)$ with boundary conditions $(13)$ and $(14)$ $(\bar {\theta } = 0$, $J^{\pm } = J_0$, and $J_0$ is small enough $)$ in the case of absolute conductivity $(b_m = 0$, with additional $A_m = 0)$ is linearly unstable in the sense of Lyapunov.

3. PROOFS OF PROPOSITIONS 1 AND 2

The nontrivial solution of (21) can be written as follows:

$$ G(y) = \exp \{(y + 1/2)A\}G(-{1}/{2}), \qquad G(-1/2) \neq 0,$$

(22)

where $\exp \{(y + 1/2)A\}$ denotes the matrix exponent.

Therefore, the nontrivial solution to (21) exists if and only if the following is satisfied:

$$ \det \begin {pmatrix} R \\ \ R\exp \{A\} \ \end {pmatrix} = 0,$$

(23)

which is actually the equation for defining $\lambda$.

The columns of the matrix exponent $(Y_{ik})_{i,k = 1,2,3,4} = \exp \{A\}$ are the solution of the system (hereinafter, if this does not cause confusion, we omit the second index):

$$ \begin {gathered} Y_1^{\prime } = -i\omega Y_2 + q_0 Y_3, \\ Y_2^{\prime } = -i\omega Y_1, \\ Y_3^{\prime } = \frac {\bar {\rho }_1}{\rho _0} Y_1 + a_1 Y_2 + a_2 Y_3 + \frac {i\omega }{\rho _0} Y_4, \\ Y_4^{\prime } = b_1 Y_1 + b_2 Y_2 + b_3 Y_3 + a_2 Y_4, \qquad |y| < 1/2; \end {gathered} $$

(24)

and, moreover,

$$ Y_{k,k}(-1/2) = 1, \quad k = 1,2,3,4; \qquad Y_{i,k}(-1/2) = 0, \quad i\neq k,\quad i = 1,2,3,4. $$

Then it follows from the explicit form of the $R$-matrix that (23) is equivalent to the relation

$$ (Y_{1,3} Y_{2,4} - Y_{1,4} Y_{2,3})\big |_{y = 1/2} = 0. $$

(25)

For the third and fourth columns of $\exp \{A\}$ we obtain from (24)

$$ \begin {gathered} Y_1(y) = q_0 \int \limits _{-1/2}^y \cos \omega (y - \xi ) Y_3(\xi )\thinspace d\xi , \qquad Y_2(y) = -i q_0\int \limits _{-1/2}^y \sin \omega (y - \xi ) Y_3(\xi )\thinspace d\xi , \\ \eqalign { Y_3^{\prime }(y) &= \frac {\bar {\rho }_1 q_0}{\rho _0} \int \limits _{-1/2}^y \cos \omega (y - \xi )Y_3(\xi )\thinspace d\xi \\ &\qquad {}- i q_0 a_1 \int \limits _{-1/2}^y \sin \omega (y - \xi ) Y_3(\xi )\thinspace d\xi + a_2 Y_3(y) + \frac {i\omega }{\rho _0} Y_4(y),} \\ \eqalign { Y_4^{\prime }(y) &= b_1 q_0 \int \limits _{-1/2}^y \cos \omega (y - \xi ) Y_3(\xi )\thinspace d\xi \\ &\quad {}- i q_0 b_2 \int \limits _{-1/2}^y \sin \omega (y - \xi ) Y_3(\xi )\thinspace d\xi + b_3 Y_3(y) + a_2 Y_4(y),}\\ Y_{3,3}(-1/2) = Y_{4,4}(-1/2) = 1, \qquad Y_{4,3}(-1/2) = Y_{3,4}(-1/2) = 0. \end {gathered} $$

(26)

Rewrite the last two differential relations of (26) as

$$ \begin {gathered} \eqalign { \widetilde {Y}_3^{\prime }(y) &= \frac {\bar {\rho }_1 q_0}{\rho _0} \int \limits _{-1/2}^y e^{-a_2 (y-\xi )} \cos \omega (y - \xi )\widetilde {Y}_3(\xi )\thinspace d\xi \\ &\qquad {}- i q_0 a_1 \int \limits _{-1/2}^y e^{-a_2(y-\xi )} \sin \omega (y - \xi )\widetilde {Y}_3(\xi )\thinspace d\xi + \frac {i\omega }{\rho _0} \widetilde {Y}_4(y),} \\ \eqalign { \widetilde {Y}_4^{\prime }(y) &= b_1 q_0 \int \limits _{-1/2}^y e^{-a_2(y-\xi )} \cos \omega (y - \xi )\widetilde {Y}_3(\xi )\thinspace d\xi \\ &\qquad {}- iq_0 b_2 \int \limits _{-1/2}^y e^{-a_2(y-\xi )} \sin \omega (y - \xi )\widetilde {Y}_3(\xi )\thinspace d\xi + b_3 \widetilde {Y}_3(y).} \end {gathered} $$

(27)

Here $\widetilde {Y}_i (y) = e^{-a_2 (y + 1/2)} Y_i(y)$, $i = 3,4$. Taking (26) into account, from (27) we obtain

$$ \begin {gathered} \eqalign { \widetilde {Y}_4(y) &= b_1 q_0 \int \limits _{-1/2}^y\thinspace d\eta \int \limits _{-1/2}^{\eta } e^{-a_2 (\eta -\xi )} \cos \omega (\eta - \xi )\widetilde {Y}_3 (\xi )\thinspace d\xi \\ &\quad {}-iq_0 b_2 \int \limits _{-1/2}^y\thinspace d\eta \int \limits _{-1/2}^{\eta } e^{-a_2(\eta -\xi )} \sin \omega (\eta - \xi )\widetilde {Y}_3(\xi )\thinspace d\xi + b_3 \int \limits _{-1/2}^y \widetilde {Y}_3(\eta )\thinspace d\eta + \begin {cases} 0, \ \ & k = 3,\\ 1, & k = 4, \end {cases} \\ \widetilde {Y}_3(y)&= \frac {\bar {\rho }_1 q_0}{\rho _0} \int \limits _{-1/2}^y\thinspace d\eta \int \limits _{-1/2}^{\eta } e^{-a_2(\eta -\xi )}\cos \omega (\eta - \xi )\widetilde {Y}_3(\xi )\thinspace d\xi \\ &\quad {}- i q_0 a_1 \int \limits _{-1/2}^y\thinspace d\eta \int \limits _{-1/2}^{\eta }e^{-a_{2}(\eta -\xi )} \sin \omega (\eta - \xi )\widetilde {Y}_3(\xi )\thinspace d\xi \\ &\quad {}+ \frac {i\omega }{\rho _0} b_1 q_0 \int \limits _{-1/2}^y\thinspace d\eta \int \limits _{-1/2}^{\eta }\thinspace d\xi \int \limits _{-1/2}^{\xi } e^{-a_2(\xi -\theta )} \cos \omega (\xi - \theta )\widetilde {Y}_3(\theta )\thinspace d\theta \\ &\quad {}+ \frac {\omega }{\rho _0}\ b_2 q_0 \int \limits _{-1/2}^y\thinspace d\eta \int \limits _{-1/2}^{\eta }\thinspace d\xi \int _{-1/2}^{\xi } e^{-a_2(\xi -\theta )} \sin \omega (\xi -\theta ) \widetilde {Y}_3(\theta )\thinspace d\theta \\ &\quad {}+ \frac {i\omega }{\rho _0} \ b_3 \int \limits _{-1/2}^y\thinspace d\eta \int \limits _{-1/2}^{\eta } \widetilde {Y}_3(\xi )\thinspace d\xi + \begin {cases} 1, & k = 3, \\ \dfrac {i\omega }{\rho _0} \ (y + 1/2), \ & k = 4. \end {cases}} \end {gathered}$$

(28)

Using the Fubini Theorem to reduce the multidimensional integrals to the one-dimensional and returning to the vector function $Y_3(y)$, we infer

$$ \eqalign { (a^2+\omega ^2)Y_3(y)&=\int \limits _{-1/2}^y Y_3(y)\bigg \{[(Q_c a_2 + Q_s \omega )e^{a_2 (y-\xi )}-(Q_c a_2 + Q_s\omega )\cos \omega (y-\xi ) \cr &\qquad {}+ (Q_c \omega - Q_s a_2)\sin \omega (y - \xi )] + \frac {i\omega }{\rho _0} B_e (y - \xi ) e^{a_2(y - \xi )}\bigg \}d\xi \cr &\qquad {}+ \begin {cases} e^{a_2 (y + 1/2)}, & k = 3,\\ e^{a_2 (y + 1/2)} \dfrac {i\omega }{\rho _0}(y + 1/2), & k = 4, \end {cases} }$$

(29)

where

$$ \begin {gathered} Q_c = \frac {\bar {\rho }_1 q_0}{\rho _0} + \frac {i\omega }{\rho _0} \frac {q_0}{a^2 + \omega ^2} (i b_2\omega - b_1 a_2), \qquad Q_s = \frac {i\omega }{\rho _0} \frac {q_0}{a^2 + \omega ^2} (ib_2 a_2 + b_1\omega )- iq_0 a_1, \\[4pt] B_e = b_3 - \frac {q_0}{a^2 + \omega ^2}(ib_2\omega + b_1 a_2) \qquad \text {for}\quad a^2 + \omega ^2 \neq 0. \end {gathered}$$

(30)

Let us find a solution to (29). To this end, we first change the variables $\eta = \xi + 1/2$ and $x = y + 1/2$ and put $W(x) = Y_3(x - 1/2)$. Then (29) can be rewritten as

$$ \eqalign { W(x) &= \int \limits _0^x W(\eta ) \bigg \{ \bigg [ \frac {Q_c a_2 + Q_s \omega }{a^2 + \omega ^2} e^{a_2(x - \eta )} - \frac {Q_c a_2 + Q_s \omega }{a^2 + \omega ^2} \cos \omega (x - \eta ) \cr &\qquad {}+ \frac {Q_c \omega - Q_s a_2}{a^2 + \omega ^2} \sin \omega (x - \eta ) \bigg ] + \frac {i\omega }{\rho _0} B_e (x - \eta ) e^{a_2(x - \eta )} \bigg \}d\eta + \begin {pmatrix} 1\\ \dfrac {i\omega }{\rho _0} x \end {pmatrix} e^{a_2 x}.} $$

(31)

Applying the Laplace transform to (31), we obtain

$$ \eqalign { &\widehat {W}(p)\bigg ( 1 - \frac {Q_c a_2 + Q_s \omega }{a^2 + \omega ^2} (p - a_2)^{-1} + \frac {Q_c a_2 + Q_s\omega }{a^2 + \omega ^2}\frac {p}{p^2 + \omega ^2} \cr &\qquad {}- \frac {Q_c \omega - Q_s a_2}{a^2 + \omega ^2}\frac {\omega }{p^2 + \omega ^2} - \frac {i\omega }{\rho _0} B_e (p - a_2)^{-2} \bigg ) = \begin {cases}(p - a_2)^{-1}, & k = 3,\\ \dfrac {i\omega }{\rho _0}(p - a_2)^{-2}, \ & k=4. \end {cases}} $$

(32)

Here $\widehat {W}(p)$ is the image of $W(x)$. Then

$$ \widehat {W}(p) = \begin {cases} \dfrac {(p - a_2)(p^2 + \omega ^2)}{B(p)}, & k = 3,\\ \dfrac {i\omega }{\rho _0}\dfrac {p^2 + \omega ^2}{B(p)}, & k=4, \end {cases}$$

(33)

where $B(p)$ is the polynomial of degree $4$:

$$ \eqalign { B(p) &= (p^2 +\omega ^2)(p - a_2)^2 - \frac {(Q_c a_2 + Q_s\omega )(p - a_2)(p^2 + \omega ^2)}{a^2 + \omega ^2} \cr &\qquad {}+ \frac {Q_c a_2 + Q_s \omega }{a^2 + \omega ^2} p(p - a_2)^2 - \frac {Q_c \omega + Q_s a_2}{a^2 + \omega ^2} \omega (p - a_2)^2 - \frac {i\omega }{\rho _0} B_e (p^2 + \omega ^2) \cr &= p^4 - 2 a_2 p^3 + p^2 \bigg ( a_2^2 + \omega ^2 - \frac {\bar {\rho }_1 q_0}{\rho _0} - \frac {i\omega }{\rho _0} \ b_3\bigg ) + a_2^2 \omega ^2 - \frac {q_0}{\rho _0} \ b_2 \omega ^2 - \frac {i\omega }{\rho _0}\ b_3 \omega ^2 - i q_0 a_1 a_2\omega .}$$

(34)

Using the inverse transformation, in the case of simple zeros of $B(p)$, $p_l \neq p_k$, $l \neq k$, we find the solution to (29):

$$ Y_{3}(y) = \begin {cases} \sum \limits _{l = 1}^4 \dfrac {(p_l - a_2)(p_l^2 + \omega ^2)} {B^{\prime }(p_l)} e^{p_l(y + 1/2)}, \ \ & k = 3, \\ \dfrac {i\omega }{\rho _0} \sum \limits _{l = 1}^4 \dfrac {p_l^2 + \omega ^2}{B^{\prime }(p_l)} e^{p_l(y + 1/2)}, & k = 4, \end {cases} $$

(35)

and moreover,

$$ B^{\prime }(p) = 4p^3 - 6 a_2 p^2 + 2p\bigg (a^2 + \omega ^2 - \frac {\bar {\rho }_1 q_0}{\rho _0} - i\omega b_3 \bigg ).$$

By (35), we know the third and fourth components of the third column of $\exp \{A\}$ and transform (25) (we also take (26) into account) as follows:

$$ \eqalign { &\bigg [\sum _{l = 1}^4 (p_l - a_2)(p_l^2 + \omega ^2) \bigg ( \frac {e^{p_l + i\omega } - 1}{p_l + i\omega } + \frac {e^{p_l - i\omega } - 1}{p_l - i\omega }\bigg )\bigg ] \cr &\qquad \qquad {}\times \bigg [\sum _{l = 1}^4 (p_l^2 + \omega ^2) \bigg (\frac {e^{p_l + i\omega } - 1}{p_l + i\omega } - \frac {e^{p_l - i\omega } - 1}{p_l - i\omega }\bigg )\bigg ] \quad \ \cr &\qquad \qquad {}- \bigg [\sum _{l = 1}^4 (p_l^2 + \omega ^2) \bigg (\frac {e^{p_l + i\omega } - 1}{p_l + i\omega } + \frac {e^{p_l - i\omega } - 1}{p_l - i\omega }\bigg )\bigg ] \cr &\qquad \qquad {}\times \bigg [\sum _{l = 1}^4 (p_l - a_2)(p_l^2 + \omega ^2) \bigg (\frac {e^{p_l + i\omega } - 1}{p_l + i\omega } - \frac {e^{p_l - i\omega } - 1}{p_l - i\omega } \bigg )\bigg ] = 0. } $$

(36)

Note that the following is valid:

$$ \sum _{k=1}^4 L_k A_k \sum _{k=1}^4 B_k - \sum _{k = 1}^4 A_k \sum _{k=1}^4 L_k B_k = \sum _{i = 1}^3 \sum _{j = i + 1}^4 (L_i - L_j) (A_i B_j - A_j B_i).$$

(37)

Assuming in (37) that

$$ L_k = p_k - a_2,\qquad A_k = e^{p_k}(p_k\cos \omega + \omega \sin \omega ) - p_k,\qquad B_k = \omega + e^{p_k}(\sin \omega p_k - \omega \cos \omega ),$$

we obtain the equivalent form of (36):

$$ \eqalign { &\sum _{i = 1}^3 \sum _{j = i + 1}^4 (p_i - p_j) \bigg \{[(p_j - p_i) + (e^{p_i} p_i - e^{p_j} p_j) \cos \omega + (e^{p_i} - e^{p_j})\omega \sin \omega ] \cr &\qquad \qquad {}+ e^{p_i} e^{p_j} (p_j - p_i) + p_i p_j \frac {\sin \omega }{\omega }(e^{p_i} - e^{p_j}) + (e^{p_j} p_i - p_j e^{p_i}) \cos \omega \bigg \} = 0,}$$

(38)

which is the equation for $\lambda$ by analogy to (36).

Remark 7$.$ Owing to representation (33) of $B(p)$, we can remove the constraint $a^2 + \omega ^2 \neq 0$ imposed earlier.

In the particular case of $J_0 = 0$, the roots $p_k$ of $B(p)=0$ are found as follows:

$$ p_1 = K_{+}, \qquad p_2 = -K_{+}, \qquad p_3 = K_{-}, \qquad p_4 = -K_{-}.$$

(39)

Here

$$ K_{\pm } = |\omega |\sqrt {-\frac {A_2}{2} \pm \sqrt {\bigg (\frac {A_2}{2}\bigg )^2 - \frac {1 - q}{\rho _0}}}\thinspace , \qquad A_2 = \frac {1 + \rho _0}{\rho _0} - \frac {\bar {\rho }_1}{\rho _0\lambda }g, \qquad g = \frac {\lambda q_0}{\omega ^2},$$

(40)

or

$$ \begin {gathered} K_{\pm } = |\omega |\sqrt {Q\pm \sqrt {Q^2 - 4\rho _0(1 - q)}}\thinspace , \qquad Q = 2 + g + \sigma _m (1 + \hat {\lambda })^2 \frac {q}{\Lambda ^2}, \\ q = \frac {\Lambda (\Lambda + \chi ^2)}{\varkappa ^2}, \qquad \Lambda = \frac {\lambda }{|\omega |}, \qquad \chi ^2 = \frac {1}{W|\omega |}. \end {gathered}$$

(41)

Given $\sigma _m$, $\hat {\lambda }$, $|\omega |$, $\varkappa ^2$, and $\chi ^2$, we numerically found the positive reals $\Lambda ^{(0)} > 0$ (if any) satisfying condition (38) (see Table 1). For many collections of $\sigma _m$, $\hat {\lambda }$, $|\omega |$, $\varkappa ^2$, and $\chi ^2$, the reals $\Lambda ^{(0)} > 0$ were found (some of these calculations are presented in Table 1). In fact, to prove the Lyapunov instability (see below the proof of Proposition 2) we need to provide only one set of the parameters $\sigma _m$, $\hat {\lambda }$, $|\omega |$, $\varkappa ^2$, and $\chi ^2$ for which $\Lambda ^{(0)} > 0$ is found.

Table 1. Values of $\Lambda ^{(0)}$ for $\hat {\lambda } = 14 \cdot 10 ^{-6}$ (ebonite) and $\sigma _m = 1$

Remark 8$.$ The original problem does not contain the inherent velocity $u_H$. At the same time, the process of linearization of (4)–(11) proceeds provided that $|\vec {u}| = \sqrt {u^2 + v^2} < u^{*}$ is some characteristic quantity (rather small) that we take further as $u_H$. Therefore, the numerical results were obtained for some small values of the Reynolds and Weissenberg numbers: ${\mathop {\rm Re}\nolimits } = \rho u_H l/\eta _0$ and ${\mathop {\rm W}\nolimits } = \tau _0 u_H /l$, where $\rho \thinspace (={\mathrm {const}})$ is the density of the medium, while $\eta _0$ and $\tau _0$ are the initial values of shear viscosity and relaxation time at the room temperature $T_0$ (see [1]).

If $J_0 \neq 0$ is small; then, by the Rouche Theorem [25], we conclude that in some neighborhood of $\Lambda ^{(0)}$ on the complex plane there exist complex numbers $\Lambda$ satisfying (38) and such that $\Re \Lambda > 0$.

This completes the proof of Proposition 1.

The proof of Proposition 2 follows from Proposition 1 if to boundary value problem (4)–(11), (13), and (14) transformed in the case of absolute conductivity (recall that we consider $b_m=0$ and, moreover, $A_m=0$), we add the initial conditions of the form

$$ \begin {gathered} \vec {U}\big |_{t=0} = U(y)\exp \{i\omega x\} + U^{*}, \\[4pt] \Omega \big |_{t=0} = \Omega (y)\exp \{i\omega x\} + \Omega ^{*}, \qquad \omega \in \mathbb {R}, \end {gathered}$$

where $U^{*} = (0,0,0)^\top$, $\Omega ^{*} = \hat {p}_0$ is the steady state in this case. Then, by Proposition 1, this mixed problem has an exponentially runaway solution, which leads to the Lyapunov instability of the steady state. Proposition 2 is proved.

CONCLUSION

In this article we prove the linear instability in the sense of Lyapunov (at certain values of the conduction current) of the steady state of the MHD model flow of an incompressible viscoelastic polymeric medium in an infinite plane channel (conduction currents and heat are applied to the channel boundaries to the electrodes).