Simulation of the Stationary Nonisothermal MHD Flows of Polymeric Fluids in Channels with Interior Heating Elements

Abstract

Basing on the rheological mesoscopic Pokrovskii–Vinogradov model, the equations of nonrelativistic magneto-hydrodynamics, and the heat conduction equation with dissipative terms, we obtain a closed coupled system of nonlinear partial differential equations that describes the flow of solutions and melts of linear polymers. We take into account the rheology and induced anisotropy of a polymeric fluid flow as well as mechanical, thermal, and electromagnetic impacts. The parameters of the equations are determined by mechanical tests with up-to-date materials and devices used in additive technologies (as $3D$ printing). The statement is given of the problems concerning stationary polymeric fluid flows in channels with circular and elliptical cross-sections with thin inclusions (some heating elements). We show that, for certain values of parameters, the equations can have three stationary solutions of high order of smoothness. Just these smooth solutions provide the defect-free additive manufacturing. To search for them, some algorithm is used that bases on the approximations without saturation, the collocation method, and the relaxation method. Under study are the dependences of the distributions of the saturation fluid velocity and temperature on the pressure gradient in the channel.

INTRODUCTION

As is known [1], the solutions and melts of linear polymers are nonlinear viscoelastic media. In the article, we consider some model of the dynamics of these media that is a modification of the well-known rheological mesoscopic model due to Pokrovskii–Vinogradov [1-3] describing complex rheology and induced anisotropy of polymer solutions and melts with high degree of accuracy. In Section 1, the equations of the model with dimensionless variables are presented that also account for the influence of temperature and electromagnetic fields, which is impotrant for solving the problems of many applied fields; in particular, the problems related to the development and improvement of technology of additive manufacturing ($3D$ printing) of polymer-based products.

The first natural step in studying the described model is to identify the characteristic regimes of the stationary flow of polymers which are close in the qualitative features to the well-known Poiseuille flows for the system of Navier–Stokes equations (see [4] and Section 2). In particular, these flow regimes occur in the channels of printing devices at continuous supply of ink. Note that, for certain parameter values, the model admits the multiplicity of stationary smooth solutions (see Section 3). As a rule, the channels have circular or elliptical cross-section and include some internal heating elements. The statement of the boundary value problems in the domains of this type is described in Section 4.

Identification of the parameters of the developed model and formulated problems rests upon the data of the mechanical tests that involve up-to-date materials and devices used in additive technologies. These data are obtained from a wide set of sources [5–15]; their consolidated table as well as a brief summary are presented in the Appendix.

For numerical solution of the nonlinear boundary value problems with given parameters, the nonlocal method without saturation is used [16, 17] with application of the Chebyshev and Fourier approximations. This method allows us to carry out calculations with rather low consumption of memory and computer time and the error control in the problems with highly smooth solutions [18, 19]. The graphs of numerical solutions and comments to them are given in Section 5 together with some discussion of flow properties in dependence on the pressure gradient in the channel.

1. A MODIFIED POKROVSKII–VINOGRADOV MODEL

Following the monographs [1, 2, 4, 20–22] and articles [23, 24], we derive the equations of themodified rheological Pokrovskii–Vinogradov model which describes nonisothermal magneto-hydrodynamic (hereinafter MHD) flow of an incompressible viscoelastic polymeric fluid and takes into account the heat dissipation. In dimensionless form in a rectangular Cartesian coordinate system $(x,y,z)$ these equations are as follows:

$$ {\mathop {\rm div}\nolimits \thinspace } \mathbf {u}=0, $$

(1)

$$ {\mathop {\rm div}\nolimits \thinspace } \mathbf {H}=0, $$

(2)

$$ \frac {d\mathbf {u}}{dt} + \nabla \bigg (P+\frac {\sigma _m\|\mathbf {H}^2\|}{2}\bigg ) = \frac {1}{{\mathop {\rm Re}\nolimits }}{\mathop {\rm div}\nolimits \thinspace }(Y\Pi )+\sigma _m(\mathbf {H},\nabla )\mathbf {H} + \text {Ga}(Y-1) \begin {pmatrix} \ 1 \ \\ \ 0 \ \\ \ 0 \ \end {pmatrix},$$

(3)

$$ \frac {d\mathbf {H}}{dt}=(\mathbf {H},\nabla )\mathbf {u} + b_m\mathbf {\Delta _{x,y,z}}\mathbf {H},$$

(4)

$$ \frac {da_{11}}{dt}-2A_1u_x-2a_{12}u_y-2a_{13}u_z + \mathfrak {L}_{11}=0,$$

(5)

$$ \frac {da_{22}}{dt}-2a_{12}v_x-2A_2v_y-2a_{23}v_z + \mathfrak {L}_{22}=0,$$

(6)

$$ \\ \frac {da_{33}}{dt}-2a_{13}w_x-2a_{23}w_y-2A_3w_z + \mathfrak {L}_{33}=0,$$

(7)

$$ \frac {da_{12}}{dt}+w_za_{12}-A_1v_x-A_2u_y-v_za_{13} - u_z a_{23} + \mathfrak {L}_{12} = 0,$$

(8)

$$ \frac {da_{13}}{dt}-w_ya_{12}-A_1w_x-A_3u_z+v_ya_{13} - u_y a_{23} + \mathfrak {L}_{13} = 0,$$

(9)

$$ \frac {da_{23}}{dt}+u_xa_{23}-A_2w_y-A_3v_z - w_x a_{12} - v_x a_{13} + \mathfrak {L}_{23} = 0,$$

(10)

$$ \frac {dY}{dt}=\frac {1}{\text {Pr}} (\Delta _{x,y,z}Y+AY\Phi +A_m\Phi _m).$$

(11)

Here $t$ is time; $u$, $v$, and $w$ are the components of the velocity vector $\mathbf {u}$ in the Cartesian coordinate system $x$, $y$, and $z$; $\mathbf {H}=(L,M,N)$ is the vector of the magnetic field intensity; $P$ is the pressure; $a_{ij}$, $i,j=1,2,3$, are the components of the second rank symmetric anisotropy tensor $\Pi$; $\mathbf {a_1}$, $\mathbf {a_2}$, and $\mathbf {a_3}$ are the columns of the symmetric matrix $\Pi = (a_{ij}) = (\mathbf {a_1}, \mathbf {a_2}, \mathbf {a_3})$; $\|\mathbf {a_i}\|^2 = (\mathbf {a_i}, \mathbf {a_i})$, $i=1,2,3$;

$$ {\mathop {\rm div}\nolimits \thinspace }(Y\Pi ) = ({\mathop {\rm div}\nolimits \thinspace }(Y\mathbf {a_1}), {\mathop {\rm div}\nolimits \thinspace }(Y\mathbf {a_2}), {\mathop {\rm div}\nolimits \thinspace }(Y\mathbf {a_3}))^\top ; $$

and $Y = T/T_0$, $T$ is the temperature, $T_0=293.15~{\rm K}=20^{\circ }$ C is the environment temperature;

$$ \mathfrak {L}_{ij} = \big ( K_I a_{ij} + \beta (\mathbf {a_i},\mathbf {a_j}) \big ) /\bar {\tau }_0(Y), \qquad i,j=1,2,3;$$

$K_I = W^{-1}+ \bar {k}/3 \thinspace I$, $\bar {k} = k-\beta$, $I = (a_{11}+a_{22}+a_{33})$ is the first invariant of the anisotropy tensor $\Pi$, $A_i = a_{ii}+W^{-1}$, $i=1,2,3$; $k$ and $\beta$, $0 < \beta < 1$, are the phenomenological parameters of the model that characterize the contributions related to anisotropy ($\beta$ takes into account the orientation of the macromolecular coil, while $k$ stands for its size [1]);

$$ \bar {\tau }_0 = \dfrac {J(Y)}{Y},\qquad J(Y) = \exp \bigg (-\overline {E}_A\dfrac {Y-1}{Y}\bigg );$$

${\mathop {\rm Re}\nolimits } = \rho u_H l/\eta _0^*$ is the Reynolds number, $\rho = \mathrm{const}$ is the density of the medium; ${\mathop {\rm W}\nolimits } = \tau _0^* u_H/l$ is the Weissenberg number; $\eta _0^*$ and $\tau _0^*$ are the initial values of the shear viscosity and the relaxation time at $T = T_0$ [1, 5]; $\Phi$ and $\Phi _m$ are the dissipative functions (see Remark 2); the Laplace operator $\Delta _{x,y,z}$ has the form

$$ \begin {gathered} \Delta _{x,y,z} = \bigg ( \dfrac {\partial ^2}{\partial x^2} + \dfrac {\partial ^2}{\partial y^2} + \dfrac {\partial ^2}{\partial z^2} \bigg ) = \bigg (\dfrac {\partial ^2}{\partial x^2}+\Delta _{y,z}\bigg );\cr \Delta _{\mathbf {x,y,z}} \mathbf {H} =(\Delta _{x,y,z}L, \Delta _{x,y,z}M, \Delta _{x,y,z}N)^\top ;\qquad \dfrac {d}{dt} = \dfrac {\partial }{\partial t} + (\mathbf {u},\nabla ), \end {gathered}$$

where for arbitrary vector-functions $\mathbf {q}=(q_1,q_2,q_3)$ and $\mathbf {s}=(s_1,s_2,s_3)$ the vector $(\mathbf {q},\nabla )\mathbf {s}$ has the form

$$ (\mathbf {q},\nabla ) \mathbf {s} = \biggl ( q_1\dfrac {\partial s_1}{\partial x} + q_2\dfrac {\partial s_1}{\partial y} + q_3\dfrac {\partial s_1}{\partial z}, \ \ q_1\dfrac {\partial s_2}{\partial x} + q_2\dfrac {\partial s_2}{\partial y} + q_3\dfrac {\partial s_2}{\partial z}, \ \ q_1\dfrac {\partial s_3}{\partial x} + q_2\dfrac {\partial s_3}{\partial y} + q_3\dfrac {\partial s_3}{\partial z}\biggr )^\top ; $$

${\mathop {\rm Ga}\nolimits } = {\mathop {\rm Ra}\nolimits }/{\mathop {\rm Pr}\nolimits }$, $\overline {E}_A = E_A/T_0$; the Rayleigh number $\mathop {\rm Ra}\nolimits$, the Prandtl number $\mathop {\rm Pr}\nolimits$, and the activation energy $E_A$ are described in [4]; $A$ and $A_m$ are the dissipation coefficients of the heat equation (11); $\sigma _m = {\mu _0H_0^2}/\big (\rho u_H^2 \big )$ is the magnetic pressure coefficient; $b_m = 1/{\mathop {\rm Re}\nolimits }_m$, ${\mathop {\rm Re}\nolimits }_m = \sigma _e \mu _0 u_H l$ is the magnetic Reynolds number; $\mu _0$ is the magnetic permeability of vacuum; and $\sigma _e$ is the electrical conductivity of the medium.

System (1)–(11) is written in dimensionless form, where the time $t$, the coordinates $x$, $y$, and $z$, the velocity vector components $u$, $v$, and $w$, the pressure $P$, the components of the vector of the magnetic field intensity $L$, $M$, and $N$, and the components of the anisotropy tensor $a_{ij}$ are normalized by $l/u_H$, $l$, $u_H$, $\rho u_H^2$, $H_0$, and $W/3$, respectively, where $l$ is the characteristic length, $u_H$ is the characteristic velocity, and $H_0$ is the characteristic value of the magnetic field intensity.

It was possible to identify the most parameters of the above model using the results of mechanical tests with certain polymer materials and $3D$ printing devices. These values with the links to sources and comments are given in the Appendix.

Remark 1$.$ Magnetohydrodynamic equations (1)–(11) are derived involving the system of Maxwell’s equations [20, 21], whereas the magnetic induction vector $\mathbf B$ is taken in the form ${\mathbf B} = \mu _0 {\mathbf H}$. In fact, the more general formula holds [25, 26]:

$$ {\mathbf B} = \mu \mu _0 {\mathbf H} = (1+\chi )\mu _0 {\mathbf H},$$

(12)

where $\mu$ is the magnetic permeability $\chi$ is the magnetic susceptibility, and moreover

$$ \chi = \chi _0/Y,$$

(13)

$\chi _0$ is the magnetic susceptibility at $T=T_0$.

Remark 2$.$ Following [27], we use the binary tensor operation “:” to specify the dissipative functions $\Phi$ and $\Phi _m$ in (11):

$$ \begin {aligned} \Phi &= \Pi : \nabla \mathbf {u} := \sum \limits _{i,j=1}^3 a_{ij} \frac {\partial u_j}{\partial x_i} = a_{11} \frac {\partial u_1}{\partial x_1} + \bigg ( \frac {\partial u_1}{\partial x_2} + \frac {\partial u_2}{\partial x_1} \bigg ) a_{12}\cr &\qquad \qquad \qquad {}+ \bigg ( \frac {\partial u_1}{\partial x_3} + \frac {\partial u_3}{\partial x_1} \bigg ) a_{13} + a_{22} \frac {\partial u_2}{\partial x_2} + \bigg ( \frac {\partial u_2}{\partial x_3} + \frac {\partial u_3}{\partial x_2} \bigg ) a_{23} + a_{33} \frac {\partial u_3}{\partial x_3}, \end {aligned} $$

(14)

$$ \begin {aligned} \Phi _m &= \sigma _m\Pi _m : \nabla \mathbf {u} := \sigma _m\sum \limits _{i,j=1}^3 L_i L_j \frac {\partial u_j}{\partial x_i} = \sigma _m \bigg \{ L_1^2 \frac {\partial u_1}{\partial x_1} + \bigg (\frac {\partial u_1}{\partial x_2} + \frac {\partial u_2}{\partial x_1}\bigg ) L_1 L_2\cr &\qquad \qquad \qquad {}+ \bigg ( \frac {\partial u_1}{\partial x_3} + \frac {\partial u_3}{\partial x_1} \bigg ) L_1 L_3 + L_2^2 \frac {\partial u_2}{\partial x_2} + \bigg ( \frac {\partial u_2}{\partial x_3} + \frac {\partial u_3}{\partial x_2} \bigg ) L_2 L_3 + L_3^2 \frac {\partial u_3}{\partial x_3} \bigg \}.\qquad \end {aligned}$$

(15)

Here $u_1(=u)$, $u_2(=v)$, $u_3(=w)$ and $L_1(=L)$, $L_2(=M)$, $L_3(=N)$ are the components of the velocity vector $\mathbf u$ and the intensity vector $\mathbf H$ in the Cartesian coordinate system $x_1(=x)$, $x_2(=y)$, $x_3(=z)$; and $\Pi _m = (L_iL_j)$ for $i,j=1,2,3$.

Remark 3$.$ According to [28, 29], (1)–(11) should be supplemented by boundary conditions for the velocity vector components (no-slip condition on the channel wall) as well as for the temperature and magnetic field components on the channel walls. Below we obtain the resolving equations for the above variables in the channels with circular and elliptical cross-sections and internal heating elements. We give a specific type of boundary conditions for each problem.

As in [28, 29], we look for a particular solution to the original system (1)–(11) of the following form:

$$ \begin {gathered} v = w\equiv 0,\qquad u = \hat {u}(y,z), \\ P = \widehat {P}(x,y,z) = {\mathcal S}(y,z) - \hat {A}x, \\ a_{ij} = \hat {a}_{ij}(y,z),\quad i,j = 1,2,3,\qquad Y = \widehat {Y}(y,z). \end {gathered} $$

(16)

Moreover, assume that $M = N = 0$ and $L = \hat {L}(y, z)$. Such a situation is realized when a channel is wound with an electric wire or immersed into a coil.

Fig. 1.

A channel with rectangular section.

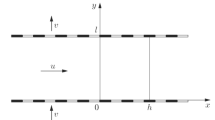
Solution (16) corresponds to a stationary flow of a polymeric fluid in a channel with rectangular cross section under the action of the constant pressure drop $\widehat {\Delta P}$ along the channel axis (see Fig. 1). Here

$$ \widehat {P}_x = -\hat {A}(=\mathrm{const}) = \dfrac {1}{{\mathop {\rm Re}\nolimits }} \{(\widehat {Y}\hat {a}_{12})_y+(\widehat {Y}\hat {a}_{13})_z\} + {\mathop {\rm Ga}\nolimits }(Y-1) + \hat {L}\hat {L}_x,\quad \ \hat {A}=\dfrac {\widehat {\Delta P}}{\rho u_H^2 h},\quad \ \hat {L}_x=0,$$

where $-\widehat {\Delta P}/\big (\rho u_H^2\big )$ is the dimensionless pressure drop on the segment $h$, while the dimensional quantity is positive, $\widehat {\Delta P} > 0$. To determine the functions $\hat {u}$, $\mathcal {S}$, $\hat {a}_{ij}$, and $\widehat {Y}$ (see (16)) from (3)–(11), we arrive at the following relations:

$$ (\widehat {Y}\hat {a}_{12})_y + (\widehat {Y} \hat {a}_{13})_z = - \widehat {D} = - {\mathop {\rm Re}\nolimits }[\hat {A} + {\mathop {\rm Ga}\nolimits }(\widehat {Y}-1)],$$

(17)

$$ \mathcal {S}_y = \frac {1}{{\mathop {\rm Re}\nolimits }} [(\widehat {Y}\hat {a}_{22})_y + (\widehat {Y}\hat {a}_{23})_z] - \sigma _m\hat {L}\hat {L}_y,\qquad \mathcal {S}_z = \frac {1}{{\mathop {\rm Re}\nolimits }} [(\widehat {Y}\hat {a}_{23})_y + (\widehat {Y}\hat {a}_{33})_z] - \sigma _m\hat {L}\hat {L}_z,$$

(18)

$$ \Delta _{y,z} \hat {L} = 0, $$

(19)

$$ K_{\hat {I}} \hat {a}_{11} + \beta \|\hat {\mathbf {a_1}}\|^2 = 2\bar {\tau }_0 (\widehat {Y}) (\hat {a}_{12}\hat {u}_y + \hat {a}_{13}\hat {u}_z),$$

(20)

$$ K_{\hat {I}}\hat {a}_{22} + \beta \|\hat {\mathbf {a_2}}\|^2 = 0,\qquad K_{\hat {I}}\hat {a}_{33} + \beta \|\hat {\mathbf {a_3}}\|^2 = 0,$$

(21)

$$ K_{\hat {I}} \hat {a}_{12} + \beta ( \hat {\mathbf {a_1}}, \hat {\mathbf {a_2}} ) = \bar {\tau }_0 (\widehat {Y}) ( \hat {A}_2 \hat {u}_y + \hat {a}_{23} \hat {u}_z ),$$

(22)

$$ K_{\hat {I}}\hat {a}_{13} + \beta ( \hat {\mathbf {a_1}},\hat {\mathbf {a_3}} ) = \bar {\tau }_0 (\widehat {Y}) ( \hat {A}_3 \hat {u}_z + \hat {a}_{23} \hat {u}_y),$$

(23)

$$ K_{\hat {I}} \hat {a}_{23} + \beta (\hat {\mathbf {a_2}},\hat {\mathbf {a_3}})=0,$$

(24)

$$ \Delta _{y,z} \widehat {Y} + A \widehat {Y}\widehat {\Phi } = 0.$$

(25)

Here $K_{\hat {I}} = W^{-1} + \bar {k}/3 \hat {I}$, $\hat {I} = \hat {a}_{11} + \hat {a}_{22} + \hat {a}_{33}$, $\hat {A}_i = W^{-1} + \hat {a}_{ii}$ for $i=2,3$; and $\widehat {\Phi } = \hat {u}_y \hat {a}_{12} + \hat {u}_z \hat {a}_{13}$.

Note that, by (15), in this formulation $\widehat {\Phi }_m = 0$.

Remark 4$.$ In Fig. 1 we show the vector ${\mathbf g} = - g_a(1,0,0)^\top$, where $g_a$ is the gravitational acceleration value that is used in the definition of the Rayleigh number $\mathop {\rm Ra}\nolimits$, whereas the corresponding vector is in the last term of (3).

In what follows, we omit caps over variables which denote that we consider the class of solutions of form (16).

2. DERIVATION OF THE RESOLVING SYSTEM OF EQUATIONS

In [28], the following relations are obtained for the components of the anisotropy tensor:

$$ a_{12}a_{23}-a_{13}a_{22}=0,\qquad a_{13}a_{23}-a_{12}a_{33}=0,\qquad a_{23}^2-a_{22}a_{33}=0. $$

(26)

Owing to (26), rewrite (22) and (23) as

$$ \widetilde {K}_{I}a_{12}=\bar {\tau }_0(A_2u_y+a_{23}u_z),\qquad \widetilde {K}_{I}a_{13}=\bar {\tau }_0(A_3u_z+a_{23}u_y);$$

i.e.,

$$ u_y = {\mathcal K} Y a_{12},\qquad u_z = {\mathcal K} Y a_{13}.$$

(27)

Here

$$ \widetilde {K}_I = K_I + \beta I,\qquad \mathcal {K}=\dfrac {W\widetilde {K}_I}{J(1+W\sigma )},\qquad \sigma = a_{22} + a_{33},\qquad I = a_{11} + \sigma .$$

From (24), taking (26) into account, we have

$$ a_{23} = -\frac {\beta a_{12}a_{13}}{K_I + \beta \sigma }.$$

(28)

Summing up the equations of (21) and taking (26) into account, we obtain

$$ K_I \sigma +\beta (\sigma ^2 + \mu ^2) = 0,\qquad \mu ^2 = a_{12}^2 + a_{13}^2.$$

(29)

It follows from (28) and (29) that $a_{23} = \sigma a_{12}a_{13} / \mu ^2$. Since $a_{22}a_{33} = a_{23}^2$ and $a_{22} + a_{33} = \sigma$, we find

$$ a_{22} = \sigma a_{12}^2 / \mu ^2,\qquad a_{33} = \sigma a_{13}^2 / \mu ^2.$$

(30)

Subtracting (29) from (20) and assuming that $\widetilde {K}_I \neq 0$, we have

$$ a_{11} = \sigma +\frac {2W\mu ^2}{1+W\sigma },\qquad I = 2\bigg (\sigma +\frac {W\mu ^2}{1+W\sigma }\bigg ). $$

(31)

Finally, using (27) and the expressions for $\bar {\tau }_0$, we arrive at the nonlinear equation to determine $\mu$:

$$ \widetilde {\mathcal K}(\mu ^2)\mu = \Lambda :=\bar {\tau }_0\lambda ,$$

(32)

where

$$ \lambda ^2=u_y^2+u_z^2,\qquad \widetilde {\mathcal K}(\mu ^2)= {\mathcal K}(\mu ^2)J = \frac {W\widetilde {K}_I(\mu ^2)}{1 + W\sigma (\mu ^2)}.$$

Thus, to determine $\mu (\Lambda )$ from (32) we must firstly to find the solutions $\sigma (\mu ^2)$ of nonlinear equation (29). Some study of these solutions is presented below, but first we formulate a boundary value problem with respect to the flow velocity $u$ in the channel with rectangular cross section (see Fig. 1).

In view of (27), it follows from (17) that

$$ (Ju_y / \widetilde {\mathcal K})_y + (Ju_z / \widetilde {\mathcal K})_z = - D.$$

(33)

Relation (32) determines $\mu = \mu (\Lambda )$. Hence, rewriting (33) by analogy with [28], we formulate the boundary value problem for $u$:

$$ \hat {a}u_{yy}-2\hat {b}u_{yz}+\hat {c}u_{zz}+\hat {d}u_y+\hat {e}u_z = - D\widetilde {\mathcal K},\qquad u=0\ \ \ \text {for} \ (y,z)\in \partial \Omega ,$$

(34)

where

$$ \begin {gathered} \hat {a} = 1-u_y^2{\mathcal L}, \qquad \hat {c} = 1-u_z^2{\mathcal L},\qquad \hat {b} = u_yu_z{\mathcal L}, \\ \hat {d}=(1-\Delta )\frac {Y_y}{Y}-\Delta \overline {E}_A \frac {Y_y}{Y^2},\qquad \hat {e}=(1-\Delta )\frac {Y_z}{Y}-\Delta \overline {E}_A \frac {Y_z}{Y^2}, \\ \mathcal {L} = \frac {1-\Delta }{\lambda ^2},\qquad \Delta = \frac {\Lambda }{\mu } \mu _{\Lambda }. \end {gathered} $$

Differentiating (32) with respect to $\Lambda$, using (31) and the expressions for $\widetilde {\mathcal K}$, we find

$$ \begin {gathered} \mu _{\Lambda }=\frac {1}{\widetilde {\mathcal {K}}_{\mu }\mu +\widetilde {\mathcal {K}}},\qquad \widetilde {\mathcal {K}} = \frac {1+W\sigma +2W(\bar {k}/3+\beta )(\sigma (1+W\sigma )+W\mu ^2)}{(1+W\sigma )^2}, \\[5pt] \widetilde {\mathcal {K}}_{\mu } = \frac {W\sigma _{\mu }}{(1+W\sigma )^2} \big [ 2(\bar {k}/3+\beta )-1 \big ] + \frac {4W^2\mu }{(1+W\sigma )^3} (\bar {k}/3+\beta ) \big [ W\sigma -W\mu \sigma _{\mu }+1 \big ]. \end {gathered}$$

Here the function $\sigma = \sigma (\mu ^2)$ can have three branches (the specific expressions are given below). Inserting the expressions of these branches into the expression for $\widetilde {\mathcal K}$, and the latter, in turn, into (32), we can compose a cumbersome nonlinear equation for writing the function $\mu$ in terms of $\Lambda$. In the analytical form, this equation cannot be solved. However, if the solution to the nonlinear equation (34) is sought numerically by some iterative method then it is natural to use (32) for the expression $\mu ^{[n]}$ at the $n$th iteration:

$$ \mu ^{[n]} = \frac {\bar {\tau }_0\lambda }{\widetilde {\mathcal K} \big ( (\mu ^{[n-1]})^2 \big )}.$$

(35)

Problem (34) should be supplemented by the boundary value problems for the temperature and magnetic field. Taking into account (25)–(27), we obtain

$$ \Delta _{y,z}Y+AY\lambda \mu =0. $$

(36)

The equation for $L$ remains the same (see (19)). The boundary conditions for these equations will be formulated in the next section.

After calculating the distributions $u(y,z)$, $Y(y,z)$, and $L(y,z)$, from equations (27), (30), and (31) together with $a_{23} = \sigma a_{12} a_{13}/\mu ^2$, we find the distributions of the components of the anisotropy tensor $\Pi$; and finally the pressure distribution is obtained using (18).

3. ANALYSIS OF THE MULTIPLICITY OF THE SOLUTIONS OF PROBLEM (34)

We now come back to search for solutions $\sigma (\mu ^2)$ of (29) appearing in the formulas for $\widetilde {\mathcal K}$ and $\widetilde {\mathcal K}_{\mu }$. Inserting the expressions for $K_I$ in (29) and taking $\sigma =a_{22}+a_{33}$ into account, after some transformations we arrive at the third degree equation

$$ \begin {gathered} a\sigma ^3+b\sigma ^2+c\sigma +d=0,\qquad \sigma \neq -1/W, \cr a = \tilde {\beta }W,\quad b = \tilde {\beta }+1,\qquad c = W^{-1}+W\mu ^2\tilde {\beta },\qquad d = \beta \mu ^2,\qquad \tilde {\beta } = 2\bar {k}/3 + \beta . \end {gathered}$$

(37)

Following the Cardano formulas for solution of a cubic equation, we introduce the notations

$$ p = \frac {3ac-b^2}{3a^2},\qquad q = \frac {2b^3-9abc+27a^2d}{27a^3},\qquad {\mathcal Q} = (p/3)^3+(q/2)^2.$$

After transformations we have $p = \mu ^2-\mathcal {A}$ and $q = \mathcal {B}\mu ^2+\mathcal {C}$, where

$$ \mathcal {A} = \frac {1-\tilde {\beta }+\tilde {\beta }^2}{3\tilde {\beta }^2W^2},\qquad \mathcal {B} = \frac {3\beta -\tilde {\beta }-1}{3W\tilde {\beta }},\qquad \mathcal {C} = \frac {(1+\tilde {\beta })(\tilde {\beta }-2) (2\tilde {\beta }-1)}{27W^3\tilde {\beta }^3}.$$

In what follows, we will be interested only in the real roots of (37).

For ${\mathcal Q}>0$ we have the single real root

$$ \sigma _1 = \sqrt [3]{-q/2 + \sqrt {\mathcal Q}} + \sqrt [3]{-q/2-\sqrt {\mathcal Q}} - b/3a;$$

for ${\mathcal Q} = 0$; the two roots

$$ \sigma _1 = -\sqrt [3]{4q} - b/3a,\qquad \sigma _2 = \sqrt [3]{q/2} - b/3a;$$

and for $\mathcal {Q} < 0$; the three real roots

$$ \begin {gathered} \sigma _1 = - 2 \cos \alpha |\sqrt [6]{q^2/4 - {\mathcal Q}}\thinspace | - b/(3a);\qquad \sigma _{2,3} = - |\sqrt [6]{q^2/4 -{\mathcal Q}}\thinspace | (-\cos \alpha \pm \sqrt {3} \sin \alpha ) - b/(3a), \\ \alpha = {\arctan (2\sqrt {-{\mathcal Q}}/q )}/3. \end {gathered}$$

Here and below, the absolute value signs are included to fulfill the condition of continuous dependence of the roots of (37) on $\mathcal Q$ in the neighborhood of the point ${\mathcal Q} = 0$.

In the first case, it is easy to calculate that

$$ \frac {\partial \sigma _1}{\partial \mu } = \sigma _1^{\prime } = \frac {(\mathcal {Q}^{\prime }/\sqrt {\mathcal Q}-q^{\prime })(\sqrt {\mathcal Q} + q/2)^{2/3} - ({\mathcal Q}^{\prime }/\sqrt {\mathcal Q} + q^{\prime }) (\sqrt {\mathcal Q} - q/2)^{2/3}}{6({\mathcal Q}-q^2/4)^{2/3}}.$$

In the third case,

$$ \frac {\partial \sigma _{1}}{\partial \mu }=\sigma _{1}^{\prime } = \frac {-2^{2/3}}{3\sqrt {-\mathcal {Q}}\thinspace |(q^2-4\mathcal {Q})^{5/6}|} \big ( (q\sin \alpha -2\sqrt {-\mathcal {Q}}\cos \alpha )\mathcal {Q}^{\prime } + (q\sqrt {-\mathcal {Q}}\cos \alpha -2\mathcal {Q}\sin \alpha )q^{\prime } \big ). $$

Next,

$$ \begin {aligned} \frac {\partial \sigma _{2,3}}{\partial \mu }=\sigma _{2,3}^{\prime } =\frac {-1}{3\sqrt [3]{2}\sqrt {-{\mathcal Q}}\thinspace |(q^2-4{\mathcal Q})^{5/6}|} &\big ( \pm (\sqrt {3}\cos \alpha \pm \sin \alpha )(2{\mathcal Q}q^{\prime }-q{\mathcal Q}^{\prime })\cr &\qquad {}+ (\cos \alpha \mp \sqrt {3}\sin \alpha )(2\mathcal {Q}^{\prime }-qq^{\prime }) \sqrt {-\mathcal {Q}}\thinspace \big ),\qquad \end {aligned} $$

where for $\sigma _2$ we choose the upper sign from $\pm$ and $\mp$; while for $\sigma _3$, the lower sign;

$$ q^{\prime } = \frac {\partial q}{\partial \mu } = - 2\mu \frac {1-3\beta +\tilde {\beta }}{3\tilde {\beta }W}, $$

$$ \begin {aligned} \mathcal {Q}^{\prime } = \frac {\partial \mathcal {Q}}{\partial \mu } = \frac {\mu }{27\tilde {\beta }^4W^4} \big \{ 27\beta ^2\tilde {\beta }^2 \mu ^2 W^2 &{}+ \tilde {\beta } \big (1 + \tilde {\beta }\mu ^2W^2 \big ) \big [ \tilde {\beta }(\tilde {\beta }(6\mu ^2W^2-1)+4)-1 \big ]\cr &\qquad {}- \beta (1 + \tilde {\beta }) \big [\tilde {\beta } \big ( 2 \tilde {\beta } (9\mu ^2W^2-1) +5 \big )-2 \big ] \big \}.\qquad \end {aligned} $$

In order to determine which of the indicated three options is realized, we denote ${\mathcal M} = \mu ^2 \geqslant 0$ and consider the function

$$ \mathcal {Q}(\mathcal {M}) = 1/27\thinspace {\mathcal M}^3 + ({\mathcal B}^2/4 - {\mathcal A}/9) {\mathcal M}^2 +({\mathcal A}^2/9 + {\mathcal B} {\mathcal C}/2) {\mathcal M} +({\mathcal C}^2/4 - {\mathcal A}^3/{27}).$$

The roots ${\mathcal M}_1$, ${\mathcal M}_2$, and ${\mathcal M}_3$ of equation ${\mathcal Q}({\mathcal M}) = 0$ can also be determined using the Cardano formulas. The number of real roots and their positions determine the domains of positive and negative $\mathcal Q$, i.e., the number of solutions to the original equation (37). Using the expression for the discriminant $\tilde {\Delta }$ of the equation ${\mathcal Q}({\mathcal M}) = 0$, we can calculate how many real roots this equation has. Here

$$ \tilde {\Delta } = \frac {a_1 a_2 a_3 a_4^3}{2^4 3^{12} \tilde {\beta }^{12} W^{12}},\quad a_1 = \beta ,\quad a_2 = 2\bar {k}/3,\quad a_3 = \beta -1,\quad a_4 = (1 + \tilde {\beta })^3 - 9 \beta (1 + (\tilde {\beta }-1)\tilde {\beta }). $$

Remark 5$.$ The inequality $\tilde {\Delta }<0$ means that

$$ {\mathcal M}_1\in {\mathbb R},\qquad {\mathcal M}_2=\overline {\mathcal M}_3 \in \mathbb {C}. $$

Hereinafter, it is used that $\mathcal {M}_2\mathcal {M}_3\in \mathbb {R}$ and $\mathcal {M}_2\mathcal {M}_3 \geqslant 0$. The equality $\tilde {\Delta }=0$ means that the roots $\mathcal {M}_1, \mathcal {M}_2, \mathcal {M}_3 \in {\mathbb R}$ and two of these coincide. The inequality $\tilde {\Delta } > 0$ means that $\mathcal {M}_1, \mathcal {M}_2, \mathcal {M}_3 \in {\mathbb R}$. Next, for such $\tilde {\Delta }$ we assume that $\mathcal {M}_1 < \mathcal {M}_2 <\mathcal {M}_3$.

We arrive at the following cases:

Case 1$.$ Equation (37) has a unique solution at all points of $\Omega$ if (1) $\tilde {\Delta }<0$ and ${\mathcal M}_1 < 0$ or (2) $\tilde {\Delta }\geqslant 0$ and ${\mathcal M}_1 \leqslant {\mathcal M}_2 \leqslant {\mathcal M}_3 < 0$.

Case 2$.$ Equation (37) has a unique solution at those points of $\Omega$, where $\mu$ is sufficiently small ($0 \leqslant \mu ^2 < {\mathcal M}_2$) or sufficiently large ($\mu ^2 > {\mathcal M}_3$), and nonunique solution at all other points if $\tilde {\Delta } \geqslant 0$ and ${\mathcal M}_1 \leqslant 0 < {\mathcal M}_2 \leqslant {\mathcal M}_3$.

Case 3$.$ Equation (37) has different solutions at those points $\Omega$ where $0 \leqslant \mu ^2 \leqslant {\mathcal M}_1$ ($\mu$ is sufficiently small) or ${\mathcal M}_2 \leqslant \mu ^2 \leqslant {\mathcal M}_3$, and a unique solution at other points if (1) $\tilde {\Delta } < 0$ and ${\mathcal M}_1>0$ or (2) $\tilde {\Delta } \geqslant 0$ and $0 < {\mathcal M}_1 \leqslant {\mathcal M}_2 \leqslant {\mathcal M}_3$.

Case 4$.$ Equation (37) has different solutions at those points of $\Omega$ where $\mu$ is sufficiently small ($0 \leqslant \mu ^2 \leqslant {\mathcal M}_3$) and a unique solution at the remaining points if $\tilde {\Delta } \geqslant 0$ and ${\mathcal M}_1 \leqslant {\mathcal M}_2 \leqslant 0 < {\mathcal M}_3$.

Let us note first that ${\mathcal Q}({\mathcal M}) \rightarrow \infty$ as ${\mathcal M} \rightarrow \infty$. Secondly, due to no-slip conditions on the channel walls, in the vicinity of the corners of the rectangular channel $\Omega$, the velocity $u$, its derivatives, and, thus, the values of $\lambda$ are close to zero. The only physically correct solution to equation (32) for $\lambda = 0$ is $\mu = 0$. Thus, under the assumption of continuity of the components of the stress tensor, there are points in the domain of the solution to the problem with the values $\mu = \sqrt {a_{12}^2 + a_{13}^2}$ that are arbitrarily close to zero.

Taking into account the inequalities of Cases 1–4 and the Vieta formulas for the solutions of the third degree equation, we arrive at the conditions for determining the right-hand side and the coefficients of boundary value problem (34).

In what follows, the above-described numbering of Cases 1–4 for (37) is preserved, but now these statements will be formulated for the right-hand side and coefficients of (34):

Case $\mathbf{1^{\prime }}$. The right-hand side and coefficients of (34) are uniquely determined if (1) $\tilde {\Delta } < 0$ and ${\mathcal M}_1 {\mathcal M}_2 {\mathcal M}_3 = {\mathcal A}^3 - 27{\mathcal C}^2/4 < 0$ or (2) $\tilde {\Delta }\geqslant 0$ and

$$ \begin {gathered} {\mathcal M}_1 + {\mathcal M}_2 + {\mathcal M}_3 = 3 {\mathcal A} - 27{\mathcal B}^2/4 < 0, \\ {\mathcal M}_1 {\mathcal M}_2 + {\mathcal M}_1 {\mathcal M}_3 + {\mathcal M}_2 {\mathcal M}_3 = 3 {\mathcal A}^2 + 27{\mathcal B} {\mathcal C}/2 > 0,\qquad {\mathcal M}_1 {\mathcal M}_2 {\mathcal M}_3 = {\mathcal A}^3 - 27 {\mathcal C}^2/4 < 0. \end {gathered} $$

Case $\mathbf{2^{\prime }}$. The right-hand side and coefficients of (34) are uniquely determined in the class of continuous functions but can have infinitely many values in the class of discontinuous functions if $\tilde {\Delta } \geqslant 0$ and ${\mathcal M}_1 {\mathcal M}_2 {\mathcal M}_3 = {\mathcal A}^3 - 27 {\mathcal C}^2/4 \leqslant 0$ and, in this case, either

$$ {\mathcal M}_1 + {\mathcal M}_2 + {\mathcal M}_3 = 3 {\mathcal A} - 27 {\mathcal B}^2/4 \geqslant 0, $$

or

$$ {\mathcal M}_1 {\mathcal M}_2 + {\mathcal M}_1 {\mathcal M}_3 + {\mathcal M}_2 {\mathcal M}_3 = 3 {\mathcal A}^2 + 27 {\mathcal B} {\mathcal C}/2 < 0.$$

Let us comment on this case. If the values of $\lambda$ at all points of $\Omega$ are so small that $\mu$ are in the neighborhood of the zero solution of (32), $\mu ^2 < {\mathcal M}_2$, then the right-hand side and coefficients of (34) are uniquely determined by expression of $\sigma _1(\mu ^2)$. Otherwise, there appear some points in the region $\Omega$, where each of $\sigma _i(\mu ^2)$, $i=1,2,3$, can be used to determine the right-hand side and coefficients; and then we have infinitely many variants to determine the coefficients and right-hand side of (34) in the class of discontinuous functions (problem with a multivalued operator) and the only variant in the class of continuous functions corresponding to the branch $\sigma _1(\mu ^2)$.

Case $\mathbf{3^{\prime }}$. The right-hand side and coefficients of (34) are not uniquely defined both in the class of continuous and discontinuous functions if

$$ {\mathcal M}_1 {\mathcal M}_2 {\mathcal M}_3 = {\mathcal A}^3 - 27 {\mathcal C}^2/4 > 0$$

and, in this case, either $\tilde {\Delta } < 0$, or

$$ {\mathcal M}_1 + {\mathcal M}_2 + {\mathcal M}_3 = 3 {\mathcal A} - 27 {\mathcal B}^2/4 > 0,\quad {\mathcal M}_1 {\mathcal M}_2 + {\mathcal M}_1 {\mathcal M}_3 + {\mathcal M}_2 {\mathcal M}_3 = 3 {\mathcal A}^2 + 27 {\mathcal B} {\mathcal C}/2 > 0. $$

In this case, for sufficiently small $\lambda$ there are the three different variants for setting the continuous right-hand side and coefficients of (34) using the values of $\sigma _i(\mu ^2)$, $i=1,2,3$. If at some point of $\Omega$ the values of $\lambda$ turn out to be greater than some threshold value $\lambda ^*$ (this fact is related to the inequality $\mu ^2 > {\mathcal M}_1$); then the right-hand side and coefficients of (34) in the neighborhood of this point are uniquely determined by $\sigma _1(\mu ^2)$.

Owing to the fact that, in the domain $\Omega$, there are always points with $\mathcal {M}$ arbitrarily close to $0$, the set of values of the differential operator of (34) has the cardinality of continuum.

Let us also note that, with the fixed temperature distribution $Y(y,z)$, the value $\lambda ^*$ corresponds to some threshold value of the pressure gradient $\hat {A}^*$ above which the velocity gradients become large enough; so that the solution $\mu$ of (32) is at sufficient distance from the zero solution of the same equation for $\lambda = 0$; more precisely, at some distance greater than $\sqrt {{\mathcal M}_1}$. From this it is easy to conclude that, for $\hat {A} < \hat {A}^*$, there are the three options in the class of continuous functions for obtaining the resolving equation (34), whereas for $\hat {A} > \hat {A}^*$, there is the only option.

Case $\mathbf{4^{\prime }}$. The right-hand side and the coefficients of equation (34) are determined nonuniquely in the classes of continuous and discontinuous functions if

$$ \tilde {\Delta }\geqslant 0,\qquad {\mathcal M}_1 {\mathcal M}_2 {\mathcal M}_3 = {\mathcal A}^3 - 27 {\mathcal C}^2/4 \geqslant 0 $$

and, in this case, either

$$ {\mathcal M}_1 + {\mathcal M}_2 + {\mathcal M}_3 = 3 {\mathcal A} - 27 {\mathcal B}^2/4 \leqslant 0, $$

or

$$ {\mathcal M}_1 {\mathcal M}_2 + {\mathcal M}_1 {\mathcal M}_3 + {\mathcal M}_2 {\mathcal M}_3 = 3 {\mathcal A}^2 + 27 {\mathcal B} {\mathcal C}/2 < 0.$$

This case is similar to the previous one with the exception that the fact of exceeding the threshold value $\lambda ^*$ is determined by the inequality $\mu ^2 > {\mathcal M}_3$.

In the conclusion of studying the set of values of the operator of problem (34) we note that

$$ \mathcal {M}_1\mathcal {M}_2\mathcal {M}_3=\mathcal {A}^3-\dfrac {27\mathcal {C}^2}{4} =\dfrac {(\widetilde {\beta }-1)^2}{4W^6\widetilde {\beta }^4}\geqslant 0. $$

This means that only the cases 3 or 4 are realized.

Remark 6$.$ Note that the question of uniqueness of solutions of quasilinear elliptic equations is difficult and can be solved only in some special cases. In this study, any rigorous analysis of the existence and uniqueness of solutions to problem (34), (36), (19) when using $\sigma _i(\mu )$, $i=1,2,3$, was not carried out. However, in numerical experiments while using $\sigma _1$ and $\sigma _3$, we succeeded in obtaining two different approximate solutions (see Section 5.1). To understand which of these solutions is realized in practice for the stationary flow of a polymeric fluid, the additional analysis of stability of each obtained solution is needed and, moreover, in the original spatial statement.

Remark 7$.$ For $\bar {k}=0$, instead of (37) it is not difficult to obtain some quadratic equation for $\sigma$. The roots of this equation can be easily found:

$$ \sigma = {\pm \sqrt {1-q^2}-1}/{(2\widetilde {W})},\qquad q^2=(2\widetilde {W}\mu )^2 < 1,\qquad \widetilde {W} = \beta W. $$

In this case, the expression for $\mathcal K$ has the form

$$ {\mathcal K} = \widetilde {\mathcal K}/J,\qquad \widetilde {\mathcal K} = \frac {2\beta (\rho \sqrt {1-q^2}+1)}{(\rho +\sqrt {1-q^2})^2},\qquad \rho = 2\beta -1,\qquad |\rho | < 1. $$

After cumbersome calculations in [28], it is obtained for the case of $\bar {k}=0$:

$$ \Delta = \frac {(1-\varkappa ^2\tilde {t}^2)(1+\tilde {t}^2)}{Q},\qquad Q = 1-\varkappa ^2\tilde {t}^4-\frac {6\rho }{1-\rho }\tilde {t}^2 + 4 \Lambda \frac {\tilde {t}(1-\tilde {t}^2)}{1-\rho }, $$

where $\tilde {t} = \tilde {g} \pm \sqrt {\tilde {g}^2-1}$ and $\tilde {g}>1$; moreover,

$$ \tilde {g} = \dfrac {1+\sqrt {1+4\Lambda ^2}}{2\Lambda }, \qquad \Lambda = \sqrt {1-\rho ^2}W\Lambda ,\qquad \varkappa = \sqrt {\dfrac {1+\rho }{1-\rho }}. $$

In this case,

$$ \sigma = - \dfrac {(\varkappa t)^2}{\beta W(1+(\varkappa t)^2)}.$$

4. STATEMENT OF BOUNDARY VALUE PROBLEMS IN CHANNELS WITH ELLIPTICAL AND CIRCULAR CROSS-SECTIONS AND HEATING ELEMENTS

4.1. A Channel with Elliptical Cross-Section

Under consideration is the flow in a cylindrical channel $\widetilde {\Omega }$ with an elliptical cross-section and some thin elliptical heating element with the same foci as for the outer boundary of the channel (Fig. 2a).

It is assumed that the inner wall of the channel (inner ellipse) is made of a substance that is a paramagnetic, for example, aluminum or tungsten, for which the magnetic susceptibility is $\chi _{0H}>0$. There is a winding on the surface of the inner ellipse so that there are $n$ turns per unit length ($1$ m in SI). In this case, a magnetic field appears inside the channel with a single nonzero component of the intensity vector $L$ (see (16)).

Fig. 2.

Cross-sections of an elliptical channel with a heating element (a) and a channel formed by two cylinders with distance $d$ between the axes (b).

Let us write problem (34) in the elliptic coordinates $\alpha$ and $\gamma$:

$$ y = \delta \cosh \alpha \sin \gamma ,\qquad z = \delta \sinh \alpha \cos \gamma ,$$

(38)

where $\delta = \sqrt {1-r_1^2}$ ($2\delta$ is the focal length), $0\leqslant \alpha <\infty$, and $0 \leqslant \gamma \leqslant 2\pi$. Owing to (38), we have

$$ y_{\alpha } = -z_{\gamma } = \delta \sinh \alpha \sin \gamma ,\qquad z_{\alpha } = y_{\gamma } = \delta \cosh \alpha \cos \gamma ,\qquad y_{\alpha \alpha } = -y_{\gamma \gamma } = y,\qquad y_{\alpha \gamma } = z. $$

(39)

$$ u_y = Ru_{\alpha }+Qu_{\gamma },\qquad u_z = Qu_{\alpha }-Ru_{\gamma }.$$

(40)

Here

$$ R = \dfrac {y_{\alpha }}{y_{\alpha }^2 + y_{\gamma }^2} = \dfrac {\delta \sinh \alpha \sin \gamma }{g^2},\qquad Q = \dfrac {y_{\gamma }}{y_{\alpha }^2 + y_{\gamma }^2} = \dfrac {\delta \cosh \alpha \cos \gamma }{g^2},\qquad g^2 = \delta ^2(\sinh ^2\alpha + \cos ^2\gamma ).$$

By (40), we obtain

$$ \lambda ^2 = u_y^2 + u_z^2 = \frac {1}{g^2} \big ( u_{\alpha }^2+u_{\gamma }^2 \big ).$$

(41)

Taking (40) into account, we successively infer

$$ \begin {gathered} u_{yy} = R^2 u_{\alpha \alpha } + 2 R Q u_{\alpha \gamma } + Q^2 u_{\gamma \gamma } + \big ( R R_{\alpha } + Q R_{\gamma } \big ) u_{\alpha } + \big ( R Q_{\alpha } + Q Q_{\gamma } \big ) u_{\gamma }, \\ u_{zz} = Q^2u_{\alpha \alpha } - 2 R Q u_{\alpha \gamma } + R^2 u_{\gamma \gamma } + \big ( Q Q_{\alpha } - R Q_{\gamma } \big ) u_{\alpha } + \big ( R R_{\gamma } - Q R_{\alpha } \big ) u_{\gamma }, \end {gathered}$$

(42)

whereas

$$ R_{\alpha } = Q_{\gamma } = \dfrac {\delta ^2 y(\cos ^2\gamma - \sinh ^2\alpha )}{g^4},\qquad R_{\gamma } = -Q_{\alpha } = \dfrac {\delta ^2 z(\cosh ^2\alpha + \sin ^2\gamma )}{g^4}.$$

By analogy, we find

$$ u_{yz} = R Q u_{\alpha \alpha } + (Q^2 - R^2) u_{\alpha \gamma } - R Q u_{\gamma \gamma } + (R Q_{\alpha } + Q Q_{\gamma }) u_{\alpha } - (R R_{\alpha } + Q R_{\gamma })u_{\gamma }.$$

(43)

In view of (42) and (43), quasilinear equation (34) assumes the following form:

$$ \tilde {a} u_{\alpha \alpha } - 2\widetilde {b} u_{\alpha \gamma } + \tilde {c} u_{\gamma \gamma } + \tilde {d} u_{\alpha } + \widetilde {e} u_{\gamma } = D\widetilde {\mathcal K},$$

(44)

where

$$ \begin {gathered} \tilde {a} = \hat {a}R^2 + \hat {c}Q^2 - 2\hat {b} R Q = \dfrac {1}{g^2}-\dfrac {u_{\alpha }^2}{g^4} {\mathcal L},\qquad \tilde {c} = \hat {a}Q^2 + \hat {c}R^2 + 2\hat {b} R Q = \dfrac {1}{g^2} - \dfrac {u_{\gamma }^2}{g^4} {\mathcal L},\cr \tilde {b} = \hat {b}(Q^2 - R^2) +R Q (\hat {c} - \hat {a}) = \dfrac {u_{\alpha }u_{\gamma }}{g^4} {\mathcal L},\cr \begin {aligned} \tilde {d} &= (\hat {a} - \hat {c}) (RR_{\alpha } + Q R_{\gamma }) - 2\hat {b} (QR_{\alpha }-RR_{\gamma }) + R \hat {d} + Q \hat {e}\cr &= \dfrac {\mathcal {L}}{g^2} [(R_{\gamma }Q - R_{\alpha }R)(u_{\alpha }^2-u_{\gamma }^2) - 2(R_{\gamma }R + R_{\alpha }Q)u_{\alpha }u_{\gamma }] + \dfrac {(1 - \Delta ) Y - \Delta }{(Y g)^2} Y_{\alpha }, \end {aligned}\cr \begin {aligned} \tilde {e} &= (\hat {a}-\hat {c})(QR_{\alpha }-RR_{\gamma }) + 2\hat {b}(RR_{\alpha }+QR_{\gamma })+Q\hat {d}-R\hat {e}\cr &= \dfrac {\mathcal {L}}{g^2}[(R_{\gamma }R + R_{\alpha }Q)(u_{\alpha }^2 - u_{\gamma }^2) + 2(R_{\gamma }Q - R_{\alpha }R) u_{\alpha } u_{\gamma }] + \dfrac {(1-\Delta )Y - \Delta }{(Y g)^2} Y_{\gamma },\qquad \end {aligned} \end {gathered} $$

whereas

$$ R_{\gamma }Q - R_{\alpha }R = \dfrac {\delta ^2}{g^4}\sinh \alpha \cosh \alpha ,\qquad R_{\gamma }R + R_{\alpha }Q = \dfrac {\delta ^2}{g^4}\sin \gamma \cos \gamma .$$

Equation (44) must be supplemented by the heat equation (it is derived from (36) on the basis of the change of coordinates (38) and formulas (39)–(41)):

$$ Y_{\alpha \alpha }+Y_{\gamma \gamma } + \left ( Ag\mu \sqrt {u_{\alpha }^2+u_{\gamma }^2} \right ) Y = 0. $$

(45)

The equation for $L$ takes the form

$$ L_{\alpha \alpha }+L_{\gamma \gamma }=0. $$

(46)

The domain of (44)–(46) is located between the confocal ellipses with small semiaxes $r_0 < r_1$ (see Fig. 2a); therefore, $\alpha _0 \leqslant \alpha \leqslant \alpha _1$ and, by (38),

$$ \alpha _{0,1} = \dfrac {1}{2} \ln \bigg (\dfrac {1+r_{0,1}}{1-r_{0,1}}\bigg ). $$

Thus, we will look for solutions of equation (44)–(46) in the class of sufficiently smooth functions which are $2\pi$-periodic with respect to the variable $\gamma$ and satisfy no-slip conditions for the velocity on the channel walls

$$ u=0\quad \text {for} \ \ \alpha = \alpha _0,\alpha _1 $$

(47)

and inhomogeneous Dirichlet conditions for temperature and magnetic field

$$ Y(\alpha _0,\gamma ) = \psi _0^Y(\gamma ),\qquad Y(\alpha _1,\gamma ) = \psi _1^Y(\gamma ),$$

(48)

$$ L(\alpha _0,\gamma ) = \psi _0^L(\gamma ),\qquad L(\alpha _1,\gamma ) = \psi _1^L(\gamma ).$$

(49)

Here $\psi _{0,1}^{Y,L}(\gamma )$ are the given temperature and magnetic field distributions on the inner and outer walls. When the current $I_H$ is passed along the winding of the inner channel, we have in accordance with [25, 26, 30] $\psi _0^L(\gamma )\equiv nI_H /H_0$ (here $H_0$ is the characteristic value of intensity for nondimensionalization). Under the assumption that the channel is in an external magnetic field that is codirectional with the axis of the channel and of intensity $\mathbf {H_0} = (L_0(\alpha ,\gamma ),0,0)$, while the outer wall of the channel has a small thickness; we obtain $\psi _1^L(\gamma ) = L_0(\alpha _1,\gamma )$. Using the Curie Law (see [25, 26, 30, 31]) it is possible to express the temperature on the inner wall through its magnetization $m$:

$$ \psi _0^Y(\gamma ) \equiv \chi _{H0} nI_H/m $$

(see Remark 1). The function $\psi _1^Y(\gamma )$ is determined by the external temperature field. In our calculations,

$$ \psi _1^Y(\gamma ) \equiv T_0 / T_0 = 1.$$

Note that for small values of $r_0$ at the points $\alpha = r_0$, $\gamma = \pi /2$ and $\alpha =r_0$, $\gamma = 3\pi /2$ (points $A$ and $B$ in Fig. 2a) the function $g$ in the denominators of the coefficients of (44) takes small values. If we multiply (44) by $g^6$ then we arrive at an equation with a small parameter $g^2$ at the higher derivatives. It means that, in the vicinity of these points, the solutions to this equation can have essential singularities.

Remark 8$.$ Note that, according to the reasoning in Section 3 and owing to the smoothness of the boundary of the channel under study, the minimum values of $\lambda$ and $\mu$ can be arbitrarily large, but they, as before, are proportional to the pressure gradient. For small gradients, $\lambda$ and $\mu$ are small; and so, in the class of continuous functions there are the three possible options for writing equation (44), which correspond to $\sigma _1$, $\sigma _2$, and $\sigma _3$. As pressure increases (when points with positive and negative values of $\mathcal Q$ appear in the region $\Omega$), the only one option remains of writing (44) with continuous coefficients and right-hand side but an infinite set of options in the class of discontinuous functions. With further increase in the pressure gradient, the values of $\mathcal Q$ become positive throughout $\Omega$; then there remains a unique option of writing (44) both in the classes of smooth and discontinuous functions.

4.2. A Channel with Circular Cross-Section

Let us pose a problem concerning the polymeric fluid flow in a channel $\widehat {\Omega }$ formed by two cylinders of radii $0 <r_0 <1$ and $r_1 = 1$ with parallel axes spaced at distance $d$, $0 \leqslant d <1 - r_0$. In Fig. 2b, the cross-section of the channel is shown. As in the above case, we assume that the inner wall of the channel (in this case, the cylinder) is wrapped with some thin wiring with $n$ turns per unit length that passes the current of strength $I_H$.

In (34) we make the change to the bipolar coordinate system. Within the scope of this subsection, we denote the bipolar coordinates by $(\alpha ,\gamma )$ so that

$$ \begin {gathered} y = \delta _0 \frac {\sinh \alpha }{\cosh \alpha - \cos \gamma },\qquad z = \delta _0 \frac {\sin \gamma }{\cosh \alpha - \cos \gamma }, \\ \delta _0 = 1-r_0^2/\nu ,\qquad \nu =\sqrt {d^2 \big ( 1 + r_0^2 \big ) + 2 d \omega },\qquad \omega = \sqrt {\big ( 1 - r_0^2 \big )^2 + (d r_0)^2}, \\ 0 \leqslant \alpha < \infty ,\qquad 0 \leqslant \gamma \leqslant 2\pi . \end {gathered}$$

(50)

After calculations, as in Section 4.1, for the temperature rate and the component $L$ of the magnetic field intensity, we obtain equations of the form (44)–(46) with the same expressions for the coefficients $\tilde {a}$–$\tilde {e}$ but with the following changes: $\delta$ should be replaced with $\delta _0$ and some items should be calculated as follows:

$$ \begin {gathered} y_{\alpha } = - z_{\gamma } = \delta _0 \frac {1-\cos \gamma \cosh \alpha }{(\cos \gamma -\cosh \alpha )^2},\qquad y_{\gamma } = z_{\alpha } = \delta _0 \frac {\sin \gamma \sinh \alpha }{(\cos \gamma -\cosh \alpha )^2}, \\ g = \frac {\delta _0}{(\cos \gamma -\cosh \alpha )},\qquad R = \frac {1-\cos \gamma \cosh \alpha }{\delta _0},\qquad Q = -\frac {\sin \gamma \sinh \alpha }{\delta _0}, \\ R_{\alpha } = Q_{\gamma } = -\frac {\cos \gamma \sinh \alpha }{\delta _0},\qquad R_{\gamma } = Q_{\alpha } = \frac {\sin \gamma \cosh \alpha }{\delta _0}, \\ R_{\gamma }Q - R_{\alpha }R = \frac {(\cos \gamma -\cosh \alpha )\sinh \alpha }{\delta _0^2}, \qquad R_{\gamma }R - R_{\alpha }Q = \frac {(\cosh \alpha -\cos \gamma )\sin \gamma }{\delta _0^2}. \end {gathered} $$

The equations of the circles of radii $r_0$ and $1$ (see Fig. 2b) in the bipolar coordinate system (50) have the form

$$ \alpha = \alpha _0 = {\mathop {\rm arctanh}\nolimits } \bigg (\dfrac { d r_0^2 + \omega }{1-r_0^2} \bigg ),\qquad \alpha = \alpha _1 = {\mathop {\rm arctanh}\nolimits } \bigg ( \dfrac { d +\omega }{1-r_0^2} \bigg ),$$

the coordinates of the centers of the circles in the bipolar system are $y_0 = \coth \alpha _0$ and $y_1 = \coth \alpha _1$.

As to the boundary conditions, it is also convenient to have expressions for the coordinates of points of the indicated circles in the bipolar system $(\alpha ,\gamma )$ through the polar coordinates $(r, \varphi )$ with the pole at $(y_0,0)$ for the inner circle:

$$ \begin {gathered} \alpha (\varphi ) = {\mathop {\rm arctanh}\nolimits } \bigg ( \dfrac {2 \big ( 1-r_0^2 \big ) (y_0 + r_0\cos \varphi )} { \big ( r_0^2 + 2 r_0 y_0 \cos \varphi + y_0^2 \big )\nu + \big ( 1-r_0^2 \big )^2/\nu } \bigg ), \\ \gamma (\varphi ) = \arctan \bigg ( \dfrac {2 r_0 (1 - r_0^2)\sin \varphi } { \big ( r_0^2 + 2r_0y_0\cos \varphi + y_0^2)\nu - (1 - r_0^2)^2/\nu } \bigg ) \end {gathered} $$

and the pole at $(y_1,0)$ for the outer circle:

$$ \begin {gathered} \alpha (\varphi ) = {\mathop {\rm arctanh}\nolimits } \bigg ( \dfrac {2 (1-r_0^2) (y_1+\cos \varphi )} {(1 + 2y_1 \cos \varphi + y_1^2)\nu + (1-r_0^2)^2/\nu }\bigg ), \\ \gamma (\varphi ) = \arctan \bigg ( \dfrac {2 (1-r_0^2) \sin \varphi } {(1+2y_1\cos \varphi +y_1^2) \nu - (1-r_0^2)^2/\nu } \bigg ). \end {gathered} $$

The solutions of (44) in the problem concerning the flow between two cylinders belong to the class of functions which are $2 \pi$-periodic in the variable $\gamma$ and satisfy the Dirichlet conditions:

$$ \begin {gathered} u(\alpha _0,\gamma ) = u(\alpha _1,\gamma ) = 0; \\ Y(\alpha _0,\gamma ) = \psi _0^Y(\gamma ) = \psi _0^Y(\gamma (\varphi )),\qquad Y(\alpha _1,\gamma ) = \psi _1^Y(\gamma ) = \psi _1^Y(\gamma (\varphi )), \\ L(\alpha _0,\gamma ) = \psi _0^L(\gamma ) = \psi _0^L(\gamma (\varphi )),\qquad L(\alpha _1,\gamma ) = \psi _1^L(\gamma ) = \psi _1^L(\gamma (\varphi )), \end {gathered}$$

where $\psi _{0,1}^{Y,L}(\gamma (\varphi ))$ are the given temperature and magnetic field distributions with respect to angular coordinates $\varphi$ on the outer and inner circles. They can be determined by analogy to those in Section 3.

It is easy that for small $r_0$ the parameter $\alpha _0$ takes large values; therefore, in a neighborhood of the circle $\alpha = \alpha _0$ the values of the function $g$ are small. Wherein there is a certain nonuniformity of this expression with respect to $\gamma$. However, for $d$ close to $0$ and $r_0$ close to $1$, the values of $g$ again turn out close to $0$ in the entire domain of the problem. As noted in Section 4.1, this circumstance can lead to essential singularities of the solution of (44).

5. NUMERICAL SIMULATION OF POLYMERIC FLUID FLOWS

To solve boundary value problem (44)–(49) in Section 4.1, the nonlocal method without saturation (hereinafter NMWS) is used which is implemented in Java as a computer software package [17]. In the works indicated in the list of references, the reader can find a detailed description of this method [16], estimates of the rate of convergence and the round-off error [18], results of tests of the method in the problems with singularities, as well as numerical justification of the absence of saturation of the method in solving nonlinear boundary value problems for equations of elliptic type [19]. As a result of approximation of unknown functions in (44)–(46) by direct (tensor) product of an interpolation polynomial with Chebyshev nodes with respect to the variable $\alpha$ and a trigonometric polynomial with Dirichlet kernel in the variable $\gamma$, using the collocation method and the relaxation method that are implemented within the framework of NMWS, we obtain the numerical solutions of the problem (regarding the use of polynomials with the Dirichlet kernel in the framework of this algorithm, see [16]).

Fig. 3.

Distribution of the flow velocity $u(y,z)$ (m/s) in an elliptical nozzle with a heating element at the different values of the pressure gradient in the nozzle: $\widehat {\Delta P}=0.7$ atm (a), $2.8$ (b), $4.8$ (c), and $6.9$ atm (d).

5.1. Flow in a Channel with Elliptical Cross-Section

Fig. 3 shows the distribution of the flow velocity of the polymeric fluid in a channel with elliptical cross-section for various values of the pressure gradient $\widehat {\Delta P}$ in the channel with the parameters corresponding to the experimental data in [5–15] (see the Appendix; hereinafter, for convenience, the pressure values are given in atmospheres (atm)).

According to the data from Table 1 (see the Appendix), the following values of physical parameters are used:

$$ \begin {gathered} \overline {E}_A=0.614,\qquad \beta =0.1,\qquad k=1.2\beta ,\qquad W=0.1,\qquad H_0=1~\text {A/m}, \\ n=22,\qquad I_H=22~\text {A},\qquad m=0.03~\text {A/m},\qquad \chi _{H0}=7.8\times 10^{-5} \end {gathered}$$

(we assume that the heating element is made of the paramagnet tungsten). The value of the following dissipation coefficient $A$ was not found in the literature; in the calculations, we put it equal to $3$. The next values of the geometric parameters were selected: $r_0=0.1$ and $r_1=0.5$. The degree of tensor product of interpolation polynomials (the number of the spatial grid nodes) was also fixed and equal to $21\times 21$. Note that for given parameter values $\tilde {\Delta } <0$; i.e. Case $3^{\prime }$ (see Section 3) is realized for the right-hand side and the coefficients of (34), wherein ${\mathcal M}_1\approx 1882.32$. In Fig. 4, the temperature distribution is given for the operation mode under consideration.

Fig. 4.

Distribution of the fluid temperature $T(y,z)$ ($^\circ$C) in an elliptical nozzle with a heating element at the different values of the pressure gradient in the nozzle: $\widehat {\Delta P}=0.7$ atm (a), $2.8$ (b), $4.8$ (c), and $6.9$ atm (d).

Note that the above values correspond to the solution $\sigma _1$ of (37). However, the given values of the pressure gradient are rather small, and there are two more options to write (44) with continuous coefficients and the right-hand side (see Remark 8). Let us note, however, the interesting fact: For the option of using $\sigma _2(\mu ^2)$, we cannot find solutions (the relaxation method does not converge with the variation of parameters of the numerical method in wide ranges), while with using $\sigma _3 (\mu ^2)$ it was possible to find solutions. Cross-sections of the distributions of flow velocity and temperature corresponding to the two branches $\sigma _1$ and $\sigma _3$ are given in Fig. 5 for the case of $\widehat {\Delta P} = 6.9$ atm. It can be seen that the maximum spread in the values of velocity and temperature for these two branches is large (solutions differ by $5$–$7$ times). In the original spatial statement, to determine a solution realized in practice, additional analysis of the stability of each obtained solution is needed.

Fig. 5.

Section by the plane $y = 0$ of the distribution of the velocity $u$ (m/s) (a) and the temperature $T$ (${}^\circ$C) (b) which correspond to the two different solutions $\sigma = \sigma _1$ and $\sigma = \sigma _3$ of equation (37) with $\widehat {\Delta P} = 6.9$ atm.

Concluding the analysis of the multiplicity of solutions, we note that, for the flow mode under consideration, the threshold pressure gradient value is $\widehat {\Delta P}^*\approx 90$ atm (see Remark 8). For $\widehat {\Delta P} < \widehat {\Delta P}^*$, it is possible to find two solutions with high smoothness; while for $\widehat {\Delta P}^* < \widehat {\Delta P} < \widehat {\Delta P}^{lim} \approx 248$ atm only one smooth solution can be found. With further increase of the pressure gradient, the relaxation method ceases to converge. The indicated threshold and limit values of the gradient $\widehat {\Delta P}^{lim}$ were obtained with accuracy of $1$ atm in numerical experiments.

5.2. Flow in a Channel with Circular Cross-Section

Applying NMWS, it was possible to find the approximate solutions to the equations describing nonisothermal magnetohydrodynamic flows of a polymeric fluid between two cylinders (see Section 4.2 and boundary value problem (44)–(49)). By analogy with the reasoning given in Section 5.1, we use the experimental data from Table 1 (see the Appendix) and set the following values of the physical parameters:

$$ \begin {gathered} E_A = 0.614,\qquad A=0.5,\qquad \beta =0.1,\qquad k=1.2\beta ,\qquad W=0.1, \\ H_0=1~\text {A/m},\qquad n=22,\qquad I_H = 22~\text {A},\qquad m=0.03~\text {A/m},\qquad \chi _{H0}=7.8\times 10^{-5}. \end {gathered} $$

The values of the geometric parameters were selected as follows: $r_0 = 0.4$ and $d = 0.2$. The degree of the tensor product of interpolation polynomials was fixed and equal to $31\times 31$. In Fig. 6 the values of the flow velocity are shown for the considered modes.

Fig. 6.

The flow velocity $u(y,z)$ (m/s) in a cylindrical nozzle with a heating element at the different values of the pressure gradient: $\widehat {\Delta P}=0.7$ atm (a), $2.8$ (b), $4.8$ (c), and $6.9$ atm (d).

APPENDIX. IDENTIFICATION OF PARAMETERS OF THE MODEL

We performed the analysis of the available literature sources containing data on the rheological and thermomechanical properties of polymer solutions with different conductivity as well as data on the main parameters of modern technologies of additive manufacturing the products from electrically conductive polymer materials. Based on the obtained data, the values of the main parameters of the above-developed model of the polymeric fluid flow are identified (see Table 1).

The rheological properties of polymer solutions and melts include, first of all, the values of shear viscosity and relaxation time, as well as their dependence on shear rates, temperature, and solution concentration. The thermomechanical properties include thermal diffusivity, heat capacity, the coefficient of thermal expansion, and the activation energy. Other properties of interest to researchers include magnetic susceptibility, current-voltage characteristics, maximal charge density, and the electron mobility.

For manufacturing electrically conductive devices, there are used polymer semiconductors such as polyethylene glycol, polyacrylamide, etc., high conductivity polymer materials (the most common is PEDOT:PSS) and polymer-based materials with the impurities of nanoparticles of electrically conductive metals (typically, silver or gold nanoparticles).

In the literature sources, there is also information about the mechanical characteristics of printing devices: the characteristic sizes of nozzles and drops of ink, the values of velocities and fluid flows in the nozzle, maximum resolution in printing, pressure in nozzles, etc. The most common printing technologies are piezoelectric and thermal inkjets.

All indicated data were used to identify the parameters of the above-developed model for calculating the flows of PEDOT:PSS (see Table 1). The values of the phenomenological parameters $\beta$ and $\bar {k}$ of the Pokrovskii–Vinogradov model were investigated in [1, 5]. It was found that for many linear polymers $\beta \in [0, 0.5]$, $\bar {k} = \beta$ or $\bar {k} = 1.2\beta$. |

Table 1. Values of the parameters of model (1)–(11) for calculating a stationary flow in the nozzle of a $3D$ printer

For calculating the Reynolds, Weissenberg, Rayleigh, and Prandtl numbers for the PEDOT: PSS solutions (see Table 2) the following formulas were used:

$$ {\mathop {\rm Re}\nolimits } = \dfrac {\rho u_H l}{\eta _0^*},\qquad {\mathop {\rm W}\nolimits } = \dfrac {\tau _0^*u_H}{l},\qquad {\mathop {\rm Ra}\nolimits } = \dfrac {g_ab\Delta T l^3c_P \rho ^2}{\eta _0^*c_T},\qquad {\mathop {\rm Pr}\nolimits } = \dfrac {\eta _0^*c_P}{c_T},$$

where $\Delta T = 200$ K is the characteristic temperature difference between the walls and the liquid, $g_a = 9.81$ m/s $^2$ is the gravity acceleration, and $\rho = 1000$ kg/m$^3$ is the fluid density. To calculate the relative dimensionless pressure gradient $\hat {A}$ (see (16)), it was assumed that the nozzle length is $100$ times greater than the characteristic section size $l$ and $h = 100$ (see also Fig. 1).

Table 2. Values of Reynolds, Weissenberg, Rayleigh, and Prandtl numbers for aqueous solutions PEDOT:PSS

CONCLUSION

We propose the model that describes stationary nonisothermal MHD flows of an incompressible viscoelastic polymeric fluid in the channels with rectangular, elliptical, and circular cross sections.

It is shown that the model allows multiple solutions and actually contains a multi-valued operator, whose range of values consists of finitely many points and is surely not convex. The model parameters are identified according to tests of the materials and devices used in the 3D printing.

We use the non-local algorithm without saturation to search for sufficiently smooth solutions to the problems posed and analyze their multiplicity.

Two different solutions were found for the flow regime under consideration. To determine which of these solutions is realized in practice, some additional analysis of their stability is needed.

FUNDING

The authors were supported by the Russian Science Foundation (project no. 20–11–20036).