3D Orbital Architecture of Exoplanetary Systems: KAM-Stability Analysis

Abstract

We study the KAM-stability of several single star two-planet nonresonant extrasolar systems. It is likely that the observed exoplanets are the most massive of the system considered. Therefore, their robust stability is a crucial and necessary condition for the long-term survival of the system when considering potential additional exoplanets yet to be seen. Our study is based on the construction of a combination of lower-dimensional elliptic and KAM tori, so as to better approximate the dynamics in the framework of accurate secular models. For each extrasolar system, we explore the parameter space of both inclinations: the one with respect to the line of sight and the mutual inclination between the planets. Our approach shows that remarkable inclinations, resulting in three-dimensional architectures that are far from being coplanar, can be compatible with the KAM stability of the system. We find that the highest values of the mutual inclinations are comparable to those of the few systems for which the said inclinations are determined by the observations.

1 INTRODUCTION

In his short and celebrated article [18] that marked the birth of the KAM theory, A. N. Kolmogorov explicitly mentioned celestial mechanics among the fields where it was natural to expect the most interesting applications of his statement¹ about the preservation of quasi-periodic motion in nearly integrable Hamiltonian systems. Nevertheless, the recent applications of KAM theory to extrasolar planetary systems were quite unexpected. Of course, the reason is not (only) due to the existence of planets outside our Solar System, as it was conjectured² centuries ago. The surprise is mainly due to the reverse way the KAM theorem is used in such a context: instead of being applied to celestial bodies with well-known motions, here from KAM theory one can deduce information about some unknown orbital properties of the exoplanets. Indeed, the main goal of the present work is the discussion of the results we can obtain by implementing this kind of approach.

To this day, the counting of discovered exoplanets has surpassed $5000$ units, and the number is set to rapidly increase in the future. Amongst other missions, after its first found candidate in early $2021$ (confirmed later on) GAIA has listed in its third data release (DR3) $72$ new candidates [1], with the prospect of thousands more discovered over the whole operating life. The PLATO mission is set to be launched in $2026$, with the objective of searching for new planets from the Sun-Earth $L_{2}$ Lagrangian point. As of early $2024$, the TESS mission had hit the milestone of more than $7000$ exoplanet candidates, waiting for confirmation.

Despite all these discovery missions, the limitations of the detection techniques remain and very few are the systems for which we have a set of complete orbital and planetary parameters. For example, the CHEOPS mission goal is to better characterize known Earth-to-Neptune size exoplanets, combining its observation with previous data to better understand the already discovered objects. Particularly interesting is the case of exoplanets discovered by means of the radial velocity method (hereafter, RV). Despite its efficiency in detecting new objects, the RV lacks the possibility of determining the inclinations of the systems, that is, both the orbital inclination with respect to the line of sight $i$ and the mutual inclination between the planets $i_{mut}$. The uncertainty on these parameters prevents a complete and clear understanding of the systems, as they are both quite relevant. Not knowing the value of $i$, in fact, implies that we only know minimal values for the masses of the planets. Considering that the correction factor to multiply the masses by is $1/\sin i$, even small values of the orbital inclinations can have a relevant impact on the nature of the system. Furthermore, complementing the data provided by RV with the ones given by other observational methods, it was possible for few extrasolar systems to determine the value of the mutual inclination between the planets, the most famous case being $\upsilon$ Andromedæ (see [9, 28]) with almost $30^{\circ}$. This proves that these systems can have planets that are not only noncoplanar, but also highly inclined between each other. To this, one should add the notion that the more massive the planet, the more probable is it to detect it. In the case of the RV, for example, this is due to the observation that a bigger planet contributes to a more noticeable shift in the spectrum of the observed star. Therefore, even in the multiplanetary systems already discovered³ there might be smaller planets that are still undetected. Taking the Solar System as an example, the survival of the smaller rocky planets is heavily due to the fact that the subsystem of the giant planets is in itself stable.

Considering all of the above, it is clear that a better understanding of the architecture of the already known exoplanetary systems is crucial. On the one hand, it has been proven that the systems can exhibit values of the inclinations that are very different from the low values seen in the Solar System, and therefore a complete study must take into account a wider range of values. On the other hand, the stability of the giant planets already detected is vital for the existence of smaller, undetected planets. Therefore, stability studies that consider wider sections of the parameter space of the inclinations are crucial in this sense.

There are different approaches that can be employed in this kind of study. In [35], for example, the authors tackled the problem by performing long-term n-body integrations of several systems, varying the values of the orbital and mutual inclination. More recently, in [21] the AMD stability criterion has been proposed, based on the angular momentum deficit of the system. A semianalytical approach is instead used in [38] and [36], where a secular approximation at order one in the masses is the base for the numerical exploration of the parameter space of the inclinations. From the last two works, we inherit the approach to the parameter space $(i_{mut},i)$, and the definition of the criteria to shortlist the systems to study.

The methodology and the criterion for the stability come instead from KAM theory. Indeed, we define a system to be KAM stable if it is possible to construct a Kolmogorov normal form ensuring the existence of an invariant torus which includes the initial conditions. Although it is well known that diffusion phenomena can originate from any open set of initial conditions in the phase space (for Hamiltonian systems having at least three degrees of freedom), a suitable normal form approach always allows one to prove the effective stability in small neighborhoods of KAM tori for intervals of times exceeding the expected lifetime of the physical system under consideration (see [13, 14, 30]). Thus, our definition of KAM stability surely requires a stronger condition to be satisfied with respect the simple assumption of existence of invariant tori (different thresholds of applicability for KAM theory, which come from rigorous results on normal forms or purely numerical methods, were compared in [34]). Nevertheless, in [37] some encouraging results were obtained by applying a reverse KAM approach. Starting from a secular approximation at order two in the masses, the main idea was to determine the stability of a system with respect to set values of the inclinations via the construction of normal forms corresponding to KAM tori. The stability was intended as a consequence of the algorithm, rather than a requirement for its implementation. For few systems it was possible to determine their stability up to nonnegligible values of the mutual inclination, albeit not considerably high. The main limitation encountered was the maximal eccentricity admissible, which was $\simeq 0.1$. It includes an extremely small portion of the exoplanetary systems known. A definite improvement was reached in [7], where an approach belonging to the same class was successfully applied to $\upsilon$ Andromedæ. This system is well known to have considerably relevant eccentricity and, of course, a high value of mutual inclination between the planets. The key to the success of the method lies in additional preliminary steps performed before the construction of the KAM tori. The system is found to be winding around a 1-dimensional elliptic torus, which is then used as a starting point for the procedure of constructing the Kolmogorov normal form. The initial values of the inclinations considered were within the ranges given by the observation, and it was possible to prove the stability of the secular dynamics. Indeed, the initial conditions were selected by applying a robustness criterion, which was derived (once again) from KAM theory according to the detailed explanations discussed in [25]. Furthermore, in [24] this constructive algorithm has been applied for a sparse study of the inclination parameter space in the case of the system HD $4732$. In the present work, we extend this last study not only to cover more widely the possible values of orbital and mutual inclination of the system HD $4732$, but also to discuss the robustness of the three-dimensional architecture for several other extrasolar systems with two nonresonant planets detected via RV.

The paper is organized as follows. The models of extrasolar planetary systems are defined in Section 2. Section 3 is devoted to explaining the computational procedure based on the construction of suitable normal forms. The results produced by such an approach are described in Section 4. The main conclusions are discussed in Section 5.

2 SELECTION OF THE EXTRASOLAR PLANETARY MODELS

In order to shortlist the single star exoplanetary systems that will be the object of this study, we follow a strategy similar to the one implemented in [38]. We select the RV-detected systems that host two exoplanets and satisfy the following criteria: $i)$ the system is far from mean-motion resonances involving the revolution periods; $ii)$ the observed eccentricities are smaller than $0.65$; $iii)$ the minimal masses of the planets are smaller than⁴$10$ $M_{J}$; $iv)$ the orbital period of both planets is greater than $45$ days; $v)$ the semimajor axis of the furthest planet is less than $10$ AU. We are then able to apply our purely gravitational secular, three-body, nonresonant model to the systems meeting these criteria. To reduce the parameter space, we set the initial values of some of the quantities as given by the observations. In Table 1 we list for each system the values of minimal masses, semimajor axes, eccentricities and arguments of the pericenters. It should be noted that the observations provide ranges, rather than a specific value. Further refinements to characterize the exact values that are more strongly linked to the stability of the system can be implemented (see, for example, [25], where a search of this kind was applied to the system $\upsilon$ Andromedæ), but it is beyond the scope of this work. Hence, we have reported in Table 1 the middle value of the parameters, and that is the value that we will consider. As per our secular approach, the mean anomalies are not taken into account. Therefore, the remaining parameters to completely define the initial conditions of the planetary system are the inclinations with respect to the line of sight $i_{1}$ and $i_{2}$, the mutual inclination $i_{mut}$ and the longitudes of the nodes $\Omega_{1}$ and $\Omega_{2}$. In the general reference plane these quantities depend on each other according to the following relation:

$$\cos i_{mut}=\cos i_{1}\cos i_{2}+\sin i_{1}\sin i_{2}\cos\Delta\Omega,$$

(2.1)

where $\Delta\Omega=\Omega_{1}-\Omega_{2}$. Generally speaking, the orbital inclinations with respect to the line of sight are unknown. This is particularly relevant as it implies that our knowledge of the mass of the $j$th planet is limited to its minimal mass $m_{j}\sin i_{j}$. In order to reduce the dimension of the parameter space to study, first of all, we set $i_{2}=180^{\circ}-i_{1}$, so as to have the two planes inclined symmetrically with respect to the line of sight. Therefore, for each value of $i$ we study the system corresponding to orbital inclinations of $(i,180^{\circ}-i)$. Hence, formula (2.1) becomes

$$\cos i_{mut}=-\cos^{2}i+\sin^{2}i\cos\Delta\Omega.$$

(2.2)

It should be noted that the equation above can be solved only if $i_{mut}\in[180^{\circ}-2i,180^{\circ}]$. As per the interval limits for the pair $(i,i_{mut})$, it has to be taken into account that both masses of the planets and the minimum value of $i_{mut}$ depend on $i$, so we decide to set it so as to have $i\in[0^{\circ},60^{\circ}]$, with a step size of $5^{\circ}$. Secondly, we set the mutual inclination to be at maximum $60^{\circ}$ with the constraint that $i_{mut}\in[\max(0,180^{\circ}-2i),60^{\circ}]$, with a step of $2^{\circ}$. On the one hand, the range set for $i$ ensures that the masses are not going to be multiplied by a factor $1/\sin i$ that would increase them close to the brown dwarf limit. On the other hand, preliminary studies showed that with the method here proposed it is not possible to obtain stability for extremely high values of mutual inclination. Considering the relation given by Eq. (2.1), we can then determine the value of $\Delta\Omega$ as a function of $i$ and $i_{mut}$. It should be stressed that, in the general reference frame, the longitudes of the nodes appear in the Hamiltonian only as their difference $\Delta\Omega$, therefore we have now set the values for all the parameters needed.

Table 1 Orbital parameters of the selected systems

3 CONSTRUCTION OF INVARIANT KAM TORI FOR THE SECULAR MODEL

The aim of this work is to present the practical results obtained by extensively applying the algorithm developed to construct KAM tori for the secular model of a gravitational three-dimensional three-body problem. This procedure has already been described in full detail in [24]. As our focus is on the applications of the algorithm and not on the algorithm itself, we do not describe the construction of the KAM tori in depth herein, but we will schematically recall the main points. In other words, this is mainly done for the sake of the proper definiteness of the computational methods that will be described in Section 4. For a deeper discussion about the details and the multiple steps of the procedure, we refer to [24], whose approach we adopt in the following.

There are three main blocks that constitute the core of our algorithm: $(i)$ the secular approximation at order two in the masses; $(ii)$ the normal form for the construction of elliptic tori; $(iii)$ the normal form for the construction of KAM tori. Each of these constructive steps is based on the application of a sequence of near-identity canonical transformations by Lie series⁵ (for an introduction to the Lie series formalism, see, for example, [12]), whose aim is to transform the Hamiltonian into a particular normal form.

Our starting point is the Hamiltonian of the purely gravitational three-body problem. The problem in itself would have nine degrees of freedom, which reduce to six once we take into account that three of them describe the uniform motion of the center of mass in an inertial frame, and therefore can be discarded. Considering the reduction of the total angular momentum of the system $\boldsymbol{C}$, which is constant in modulus and direction, we arrive at only four degrees of freedom (see, e.g., [19]). The resulting Hamiltonian describing the dynamics in the astrocentric frame can be expressed using the following Poincaré canonical variables:

$$\begin{aligned} \Lambda_j &=\frac{m_0 m_j}{m_0 + m_j}\sqrt{G(m_0+m_j)a_j}, &\xi_j=\sqrt{2 \Lambda_j}\sqrt{1-\sqrt{1-e_j^2}}\cos{(\omega_j)},\\ \lambda_j &= M_j + \omega_j, &\eta_j=-\sqrt{2 \Lambda_j}\sqrt{1-\sqrt{1-e_j^2}}\sin{(\omega_j)} \end{aligned}$$

(3.1)

$m_{0}$ being the mass of the central star and $m_{j}$, $a_{j}$, $e_{j}$, $\omega_{j}$ and $M_{j}$ the mass, the semimajor axis, the eccentricity, the argument of the pericenter and the mean anomaly of the $j$th planet, respectively. We introduce a translation $L_{j}=\Lambda_{j}-\Lambda^{*}_{j}$ such that $\Lambda^{*}_{j}$ corresponds to the quantity computed considering the value of $a_{j}$ given by the observations. Finally, we introduce an additional parameter $D_{2}$, the so-called angular momentum deficit⁶, defined as $D_{2}=\big{[}(\Lambda_{1}^{*}+\Lambda_{2}^{*})^{2}-C^{2}\big{]}\big{/}(\Lambda_{1}^{*}\Lambda_{2}^{*})$. We then expand the Hamiltonian $H_{\rm 3BP}$ describing the three-body problem around $\boldsymbol{L}=\boldsymbol{0}$ (and so, around the initial value of the semimajor axes) in Fourier series of angles $\boldsymbol{\lambda}$ and power series of parameter $D_{2}$ and canonical variables ${\boldsymbol{L}},\boldsymbol{\xi},\boldsymbol{\eta}$.

Given the nature of our study, we are interested in the long-term evolution of the systems. Therefore, our first aim is to obtain a secular approximation, disregarding the fast dynamics expressed by the variables $(\boldsymbol{L},\boldsymbol{\lambda})$. We opt for a secular approximation at order two in the masses, thus aiming to obtain a formulation of the Hamiltonian that is not dependent on the fast angles $\boldsymbol{\lambda}$ up to terms of order two in the ratio between the mass of the largest planet over the one of the star. This is done by computing a generating function $\chi_{1}^{(\mathcal{O}2)}(\boldsymbol{\lambda})$, such that its Lie series $\exp(\mathcal{L}_{\chi_{1}^{(\mathcal{O}2)}})$ transforms $H_{\rm 3BP}$ into

$$H^{(\mathcal{O}2)}=\exp(\mathcal{L}_{\chi_{1}^{(\mathcal{O}2)}})H_{\rm 3BP},$$

(3.2)

which satisfies the nondependence on the fast angles required. We then compute the value of the parameter $D_{2}$ as given by the particular choice of the initial conditions considered. Taking into account that we focus on the case ${\boldsymbol{L}}={\boldsymbol{0}}$ and that we truncate the otherwise infinite series up to a certain order $N_{S}$ (defined considering the characteristics of the systems), we finally obtain our secular approximation at order two in the masses:

$$H^{({\rm sec})}({\boldsymbol{\xi}},{\boldsymbol{\eta}})=\sum_{s=1}^{N_{S}/2}h^{({\rm sec})}_{2s}({\boldsymbol{\xi}},{\boldsymbol{\eta}}),$$

(3.3)

where $h_{2s}$ is a homogeneous polynomial of degree $2s$. Furthermore, we have again reduced the degrees of freedom of the problem, decreasing them to two. It should be noted that applying the Lie series $\exp(\mathcal{L}_{\chi_{1}^{(\mathcal{O}2)}})$ to $H_{\rm 3BP}$ is equivalent to perform a canonical transformation. As it is common practice when working in the framework of perturbation theory, by abuse of notation we have kept the symbols ${\boldsymbol{\xi}}$ and ${\boldsymbol{\eta}}$ for the variables. Nevertheless, being all the modifications due to near-identity transformations, the corrections are small. Let us recall that a step-by-step description of the method, complete with all details, can be found in [24].

Fig. 1

Poincaré sections of the system HD $4732$, considering $\eta_{2}=0$, with parameters $i=90^{\circ}$ and $i_{mut}=1^{\circ}$. The dark asterisks represent the true orbit as computed by integrating the secular model at order two in the masses. The black cross locates the elliptic torus.

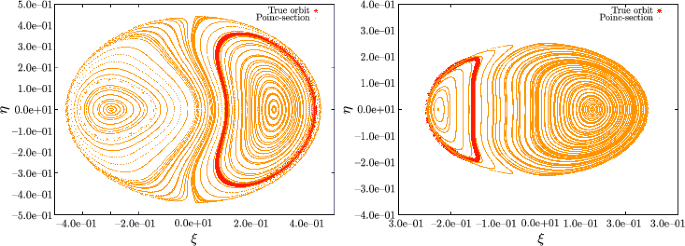
The next block concerns the construction of an invariant elliptic torus by a normal form algorithm. In order to fix the ideas, in Fig. 1 we show a plot referring to the specific case of the system HD $4732$, taken as an example. We plot the Poincaré sections obtained by setting $\eta_{2}=0$, with the additional condition of $\xi_{2}>0$. It should be noticed that setting $\eta_{2}=0$ is equivalent to considering the points of the orbits such that $\omega_{2}=0$. The dark asterisks represent the actual orbit of the system, whereas the light color points are the Poincaré sections obtained considering orbits with different initial conditions but the same level of the energy. It can be appreciated that there is a fixed point, highlighted as a black cross, which, being surrounded by closed curves, can be argued to be linearly stable with respect to the transverse dynamics. Elliptic tori are defined as compact invariant manifolds of smaller dimension than the maximal one (equal to the degrees of freedom of the problem). Therefore, the black cross represents a $1$-dimensional elliptic torus, namely, a linearly stable periodic orbit. The true orbit of the system is then enclosing such a point, and so we are going to construct the elliptic torus, aiming to use it as a base for the KAM torus construction. For this purpose, we have to preliminarly introduce suitable action-angle variables $(A,J,\alpha,\varphi)$ that are related to $({\boldsymbol{\xi}},{\boldsymbol{\eta}})$ by a canonical transformation. In the new canonical coordinates, the secular dynamics is described by the following Hamiltonian in the case of $r=0$:

$$\begin{aligned} \hfil\mathcal{H}^{(r)}(A,J,\alpha,\varphi)=&\mathcal{E}^{(r)}+\frac{2\pi}{T^{(r )}}A+\Omega^{(r)}J+\sum_{s\geqslant}\sum_{\ell\geqslant 3}f_{\ell}^{(r,s)}(A,J,\alpha, \varphi)\\ & +\sum_{s\geqslant r+1}\sum_{\ell=0}^{2}f_{\ell}^{(r,s)}(A,J,\alpha, \varphi), \end{aligned}$$

(3.4)

where $f_{\ell}^{(r,s)}\in{\mathfrak{P}}_{\ell,2s}$ $\forall\ \ell,\ s$. The set ${\mathfrak{P}}_{\ell,2s}$ includes all the real functions that are homogeneous polynomials of total degree $\ell$ in the square root of the actions and of trigonometric degree at most $2s$ with respect to the angle $\alpha$, where the pair of canonically conjugate variables $(J,\varphi)$ is of d’Alembert type. In more detail, this means that the expansion of a generic function belonging to the set ${\mathfrak{P}}_{\ell,2s}$ contains terms including factors $A^{l_{1}}\big{(}\sqrt{J}\big{)}^{l_{2}}$ and Fourier harmonics $k_{2}\varphi$ such that $2l_{1}+l_{2}=\ell$ and $|k_{2}|\leqslant l_{2}$, where the integers $k_{2}$ and $l_{2}$ have the same parity. The occurrence of d’Alembert type variables is common when a pair of polynomial canonical coordinates is replaced by the action and the angle that are usually introduced in the basic model of the harmonic oscillator. We also stress that the size of $f_{\ell}^{(r,s)}$ is expected to get smaller and smaller for increasing values of the index $s$, due to the decay of the Fourier coefficients. The algorithm of constructing the normal form for an invariant elliptic torus considers all the terms appearing in the second row of (3.4) as the perturbation to remove. In fact, every step of the computational procedure is defined by the composition of three canonical transformations and each of them is expressed in terms of a Lie series, with generating function ${\mathfrak{X}}_{\ell}^{(r+1)}$ that are determined so as to remove the angular dependence of the corresponding perturbing term $f_{\ell}^{(r,r+1)}=\mathcal{O}\big{(}\|(A,J)\|^{\ell/2}\big{)}$ $\forall\ \ell=0,1,2$. Such a computational algorithm is convergent if the perturbing part of the initial Hamiltonian is small enough (for a complete proof see [6]). Therefore, we can write

$$\lim_{r\to\infty}\mathcal{H}^{(r)}(A,J,\alpha,\varphi)=\mathcal{H}^{(\infty)}(A,J,\alpha,\varphi)=\mathcal{E}^{(\infty)}+\frac{2\pi}{T^{(\infty)}}A+\Omega^{(\infty)}J+\mathcal{O}\big{(}\|(A,J)\|^{3/2}\big{)}.$$

(3.5)

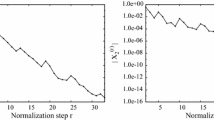
One can easily check that the Hamiltonian equations related to $\mathcal{H}^{(\infty)}$ admit the motion law $t\mapsto\big{(}A(t)=0,J(t)=0,\alpha(t)={2\pi t}/{T^{(\infty)}}+\alpha(0)\big{)}$ as a special solution⁷ that is an orbit on a 1-dimensional torus with period $T^{(\infty)}$; its corresponding energy level is equal to $\mathcal{E}^{(\infty)}$, while $\Omega^{(\infty)}$ is the angular velocity of the small oscillations which are transverse to such a periodic orbit. In the practical applications that will be described in Section 4, 20 normalization steps are sufficient to construct an excellent approximation of the final elliptic torus. Indeed, in Fig. 1 a “$+$” symbol is drawn every time that the solution of the equations of motion corresponding to the Hamiltonian⁸$\mathcal{H}^{(20)}$ intersects the hyperplane $\eta_{2}=0$ and all these plots exactly superpose each other as it is expected for a periodic orbit.

Finally, the third block concerns the construction of an invariant KAM torus. This requires one to preliminarily perform a canonical transformation aiming to translate the origin of the actions, i. e.,

$$A=A^{*}+p_{1}\>,\ \ J=J^{*}+p_{2}\>,\ \ \alpha=q_{1}\>,\ \ \varphi=q_{2}\>,$$

(3.6)

where $A^{*}$ and $J^{*}$ are constants that are given (as a first approximation) by the values $A(0)$ and $J(0)$ corresponding to the initial conditions, respectively; their determination will be refined later as it will be explained in the following. In these new canonical coordinates, the expansion of the Hamiltonian can be written as

$$\begin{aligned} \hfil{H}^{(r)}({\boldsymbol{p}},{\boldsymbol{q}})=&{E}^{(r)}+{{\boldsymbol{\nu}}}^{(r)}\cdot{\boldsymbol{p}}+\sum_{s\geqslant 0}\sum_{\ell\geqslant 2}{f}_{\ell}^{(r,s)}({\boldsymbol{p}},{\boldsymbol{q}})\\ &+\sum_{s\geqslant r+1}\sum_{\ell=0}^{1}{f}_{\ell}^{(r,s)}({\boldsymbol{p}},{\boldsymbol{q}}), \end{aligned}$$

(3.7)

with $r=0$ and ${f}_{\ell}^{(r,s)}\in\mathcal{P}_{\ell,2s}$ $\forall\ \ell,\ s$, where $\mathcal{P}_{\ell,2s}$ is the class of functions that are homogeneous polynomials of degree $\ell$ in the actions ${\boldsymbol{p}}$ and trigonometric polynomials of degree $\leqslant 2s$ with respect to the angles ${\boldsymbol{q}}$. Also, in the case of the construction of the Kolmogorov normal form, the terms appearing in the second row of formula (3.7) are considered as the perturbation to remove and this is done by performing a sequence of canonical transformations that are expressed by the composition of two Lie series. At the $(r+1)$th normalization step, the corresponding generation functions ${\chi}_{1}^{(r+1)}$ and ${\chi}_{2}^{(r+1)}$ are determined in such a way as to eliminate the angular dependence in the perturbing terms which appear in (3.7) and belong to the class of functions $\mathcal{P}_{j,2(r+1)}$ $\forall\ j=0,1$. Of course, these operations are started by considering the Hamiltonian ${H}^{(0)}$ as the initial one; also in this case, during the practical applications of the procedure we are describing, we perform 20 normalization steps so as to finally determine ${H}^{(20)}$. During this third block of the computational algorithm, we perform the Kolmogorov normalization in a way that is reminiscent of the version of the KAM theorem for isoenergetically nondegenerate systems (see [3]). This means that the generating function of the first Lie series to be applied at the $r$th normalization step is defined so that ${\chi}_{1}^{(r)}({\boldsymbol{q}})={X}^{(r)}({\boldsymbol{q}})+{\boldsymbol{\xi}}^{(r)}\cdot{\boldsymbol{q}}$ where ${X}^{(r)}({\boldsymbol{q}})\in{\mathcal{P}}_{0,2r}$ is a real function whose Fourier expansion includes harmonics with trigonometric degree not greater than $2r$, while the translation vector ${\boldsymbol{\xi}}^{(r)}\in\mathbb{R}^{2}$ is determined so as to satisfy⁹ the following two requirements: it must be parallel to the angular velocity vector and ${E}^{(r)}$ is approximately equal to the energy level $E^{*}$ of the Poincaré sections. We emphasize that this version of the Kolmogorov algorithm makes the angular velocity vector ${{\boldsymbol{\nu}}}^{(r)}$ slightly vary at every normalization step. As discussed in [24], under a few reasonable assumptions¹⁰ the normalization algorithm can be iterated so as to make the perturbing terms smaller and smaller. Therefore, if $r$ is large enough, then ${H}^{(r)}({\boldsymbol{p}},{\boldsymbol{q}})\simeq{E}^{(r)}+{{\boldsymbol{\nu}}}^{(r)}\cdot{\boldsymbol{p}}+\mathcal{O}(\|{\boldsymbol{p}}\|^{2})$. This means that the torus ${\boldsymbol{p}}={\boldsymbol{0}}$ is nearly invariant and the motions starting from the corresponding initial conditions (i.e., such that ${\boldsymbol{p}}(0)={\boldsymbol{0}}$) are well approximated by quasi-periodic motions with angular velocities equal to ${{\boldsymbol{\nu}}}^{(r)}$.

Once the secular model has been fixed by defining the expansion (3.3) in $H^{({\rm sec})}$, let us emphasize that the sequence of the angular velocities vectors ${{\boldsymbol{\nu}}}^{(r)}$ just depends on the energy level $E^{*}$ and the values of the translations on the actions, namely, $A^{*}$ and $J^{*}$, which appear in formula (3.6). On the other hand, starting from the initial conditions of a motion we want to study (in order to fix the ideas, one can refer to those which generate the Poincaré sections plotted with dark asterisks in Fig. 1), if such a motion is at least nearly quasi-periodic, then it is possible to compute the corresponding angular velocity vector, say ${\boldsymbol{\nu}}^{*}$, by using the frequency analysis method (for an introduction, see [20]). We have found that it is convenient to fix the values of $E^{*}$ and $A^{*}$ according to the initial conditions, hence, we consider the sequence of the angular velocity vectors as a function of the parameter $J^{*}$, i. e., ${{\boldsymbol{\nu}}}^{(r)}={{\boldsymbol{\nu}}}^{(r)}(J^{*})$. Therefore, we determine the value of $J^{*}$, by solving the implicit equation

$$\nu_{2}^{(20)}(J^{*})=\nu_{2}^{*},$$

(3.8)

where we recall that the twentieth normalization step is the final one we perform in our computational procedure and it produces ${H}^{(20)}$ whose expansion is written in (3.7) with $r=20$. The equation above can be numerically solved¹¹ by iterating the Newton method, starting from the approximation provided by the value of the action $J(0)$ which corresponds to the initial conditions. Of course, this requires that the construction of the Kolmogorov normal form be repeated several times starting from different corresponding values of $J^{*}$. If all the aforementioned assumptions are satisfied, then every normalization algorithm will converge as well as the Newton method. Therefore, the whole computational procedure can be stopped when the two equations

$$E^{(20)}=E^{*}\quad{\rm and}\quad\nu_{2}^{(20)}=\nu_{2}^{*}$$

(3.9)

are satisfied within a sufficiently good accuracy level. It is worth stressing the reasons why we have imposed so unusual¹² restrictions. Since we aim to compare the Poincaré sections with the solutions obtained by constructing a KAM torus, it looks natural to require that all of them correspond to the same energy level $E^{*}$, in order to make the numerical tests significant. Moreover, Fig. 1 highlights the strong dependence of the amplitude of the oscillations on the distance from the elliptic torus. The value of such a distance given in terms of the area enclosed by the orbit is expressed by the action $J$ (see [25]). On the other hand, for the kind of orbital motions we are interested in, the range of possible values which can be experienced by the other action (namely, $p_{1}$) is much more limited and so also its impact on the dynamics. Therefore, since the value of $J^{*}$ plays a much more crucial role with respect to $A^{*}$, it should be clear why we have chosen to impose also Eq. (3.8), which is reported as the second one in formula (3.9). This final part of the computational procedure which includes the Newton method to determine the parameter $J^{*}$ was missing in [24]. We stress that this additional improvement has allowed us to greatly extend our results, which will be discussed in Section 4.

The last iteration of the Kolmogorov normalization algorithm is the source of the data we are going to study in the light of the robustness criterion discussed in [7]. Indeed, a sharp decline of the norm $||\chi_{2}^{(r)}||$ is associated with the convergence of the algorithm, and therefore, the lowest the value of $||\chi_{2}^{(20)}||/||\chi_{2}^{(1)}||$, the better the convergence. This is not just a numerical feature, as in the context of this work a better convergence is linked to a most robust system.

4 RESULTS

The secular model at order two in the masses is a convenient way to reduce the number of degrees of freedom of the problem at hand while maintaning the most accuracy possible. It has been employed both in the framework of the Solar System (as in [26]) and in the one of extrasolar systems (see, for example, [7, 23, 37]). Overall, it has been found that, especially when the systems are far from mean-motion resonances, the qualitative description of the dynamics given by the secular approximation is in line with results provided by purely numerical integrations. The quasi-periodicity of the motions and the amplitude of the oscillations of the orbital parameters are among the quantities for which the agreement is quite solid. The differences between the two sets of results are usually found in the periods of the evolutions. Nevertheless, for the aim of this work it is sufficient to ensure that the main features of the systems are correctly represented. In particular, it is essential to check the coherence of the results up to high values of the mutual inclination between the planets, given the extent of our study. In Fig. 2 we show a comparison of the results obtained via the integration of the Hamiltonian equations given by the secular approximation, and the numerical integrations of the complete three-dimensional three-body problem¹³. Figure 2 refers to the particular system HD $4732$, but similar results are found for all the systems which are the object of this study. The plots are drawn as follows: on the x-axis we have the mutual inclination between the two planets, in the range $[0^{\circ},60^{\circ}]$, whereas on the y-axis we indicate the orbital inclination $i$ of the planes. This implies that following a horizontal line from left to right is equivalent to having fixed the multiplying parameter $1/\sin i$ for the masses, and to increasing the mutual inclination. The white areas of the plots are given by the restriction of the value of $i_{mut}$ with respect to that of $i$ given by the relation described by Eq. (2.2). In Fig. 2 (from left to right) we show the maximal libration amplitude of $\Delta\omega$ along the integration (i. e., $\max\Delta\omega-\min\Delta\omega$), the maximal value of the eccentricity of the inner planet $e_{1}$, and that of the outer planet $e_{2}$. The top row represents the results given by the secular approximation at order two in the masses, and the bottom row represents those of the purely numerical integrations. It can be appreciated that the agreement between the two models is very good, even for high values of the mutual inclination.

Fig. 2

Comparison of the results obtained by integrating the Hamiltonian equations given by the secular approximation at order two in the masses (top row) and numerically integrating the complete three-body problem (bottom row). From left to right: the maximal amplitude of the libration of the angle $\Delta\omega$, the maximal value of the eccentricity of the inner planet $e_{1}$, and of the outer planet $e_{2}$.

The aim of this work is to determine which values of the initial parameter $(i_{mut},i)$ are compatible with the stability in the KAM sense. Given the extent and the computationally demanding nature of this study, we need to determine an automatic criterion that allows us to establish the convergence of the procedure described in [24]. It is a common choice to consider the behavior of the norms of the second generating function of each step of the construction of the Kolmogorov normal form $\chi_{2}^{(r)}$ (briefly described in Section 3), with respect to its equivalent for the first step $\chi_{2}^{(1)}$.

Fig. 3

Poincaré section of the system HD $4732$, considering $\eta_{2}=0$. On the left, the case relative to the parameters $i=90^{\circ}$ and $i_{mut}=15^{\circ}$. On the right, the case for $i=74^{\circ}$ and $i_{mut}=37^{\circ}$.

In Fig. 3 we show the results of two initial configurations for which we reach the convergence of the algorithm. The graphs show the Poincaré sections obtained by considering $\eta_{2}=0$, with the additional condition that $\xi_{2}>0$. In the left panel, we report the case corresponding to $i=90^{\circ}$ and $i_{mut}=15^{\circ}$, therefore, considering minimal masses (since $\sin i=1$) and a medium mutual inclination value. In the right panel, we show the results for $i=74^{\circ}$ and $i_{mut}=37^{\circ}$, so with augmented masses and a quite relevant inclination between the planets. In both panels, the dark asterisks are the representation of the orbit integrated via the secular order two in the masses model. The orbit on the invariant KAM torus is represented by a set of black crosses forming what resembles an ellipse, whereas the elliptic torus is the single black cross centered in the said ellipse. It is possible to appreciate how the KAM torus given as the final result of the constructive algorithm presented in this work and in [24] perfectly overlaps with the true orbit. Therefore, the dynamics described by our final form are coherent with the ones given by the secular approximation.

It can be seen from Fig. 3 that the algorithm can converge in very different regimes. The left panel is an example of a pair $(i_{mut},i)$ for which the system shows the libration of the angle $\Delta\omega$, as it is highlighted by the fact that the orbit lies within one half of the graph ($\xi_{1}<0$, in particular). On the other hand, the right panel shows the case where $\Delta\omega$ is circulating, because the origin is surrounded by the closed orbit.

Fig. 4

Particular results for the system HD $4732$. On the left, the maximal amplitude of the angle $\Delta\omega$. On the right, the ratio of the norms of the generating function at the $r$th normalization step $\chi_{2}^{(r)}$ and at the beginning of the normalization process $\chi_{2}^{(1)}$.

To present a more general view of the HD $4732$ system, in Fig. 4 we compare the maximal amplitude of variation of $\Delta\omega$ with the numerical indicator to which we refer in order to evaluate the rate of convergence of the normalization algorithm, i.e., the ratio of the norms $||\chi_{2}^{(r)}||/||\chi_{2}^{(1)}||$. It can be seen that for this specific system the convergence of the algorithm up to $i_{mut}\simeq 30^{\circ}$ (that is, in the region of the right panel of Fig. 4 where darker colors can be observed) corresponds quite precisely to the change in the behavior of the angle $\Delta\omega$. We observe in fact that for lower values of $i_{mut}$, $\Delta\omega$ is librating, more precisely, around $180^{\circ}$ (not shown). As the value of the mutual inclination is increasing, we see that the angle changes to a circulation regime. Among the systems we study in the present work, this is the only one that presents a particular feature, namely, the existence of a small island of convergence (with $\Delta\omega$ circulating) that is clearly separated by the most consistent part at lower values of the mutual inclination (where $\Delta\omega$ librates). We find the said subset at $i_{mut}\simeq 39^{\circ}$ for values of $i\leqslant 80^{\circ}$. We investigate if the parameter space in between these two separate regions is characterized by more chaos. In order to study this possibility, we have performed a more detailed numerical study of the complete three-body problem, as shown in Fig. 5. We have considered a denser grid for the parameter space $(i_{mut},i)$, setting integrations each $0.1^{\circ}$ along the $i_{mut}$ axis. For each point, we consider the parameter space of the mean anomalies $(M_{1},M_{2})$, varying their values in $[0^{\circ},355^{\circ}]\times[0^{\circ},355^{\circ}]$ with a grid size of $5^{\circ}$. We have observed that usually the results obtained by integrating the complete three-body problem are qualitatively independent of the values of the mean anomalies (as the system is far from mean-motion resonances). That is to say, the bottom row of Fig. 2 does not change considerably when considering different values of $M_{1}$ and $M_{2}$. By means of these more refined computations we want to study if this is still the case in the region of the parameter space $(i_{mut},i)$ between the lower values of mutual inclination and the small island. In Fig. 5 we show the difference between a standard case ($i=80^{\circ},i_{mut}=35.4^{\circ}$, top row) and the only case it was possible to find where significant differences can be easily noticed when varying $(M_{1},M_{2})$ ($i=80^{\circ},i_{mut}=35.5^{\circ}$, bottom row). From left to right, the panels show the maximal amplitude of the libration of $\Delta\omega$, the maximal value of the eccentricity of the inner planet $e_{1}$, and of the outer one $e_{2}$. We see that for $i_{mut}=35.4^{\circ}$ the maximal values of the eccentricities do not change significantly, and more relevantly the behavior of $\Delta\omega$ remains unaltered. On the other hand, for $i_{mut}=35.5^{\circ}$, not only do we find that the maximal value of $e_{1}$ ranges between $0.22$ and $0.4$, but also $\Delta\omega$ can either circulate or librate depending on the values of $(M_{1},M_{2})$. As previously stated, though, this latter case constitutes a very specific exception, which was not found in other regions of the parameter space.

Fig. 5

Results obtained in the parameter space of the mean anomalies $(M_{1},M_{2})$ for a fixed value of $i=80^{\circ}$ and for $i_{mut}=35.4^{\circ}$ (top row) and $i_{mut}=35.5^{\circ}$ (bottom row). From left to right: the maximal amplitude of the libration of the angle $\Delta\omega$, the maximal value of the eccentricity of the inner planet $e_{1}$, and of the outer planet $e_{2}$.

Let us now discuss the results for all the different extrasolar planetary systems considered in the study. In Fig. 6 we show the results concerning the ratio of $||\chi_{2}^{(r)}||/||\chi_{2}^{(1)}||$, and consequently the convergence of the construction algorithm, as previously discussed. The darkest areas in the plots identify the subset of the parameter space $(i_{mut},i)$ for which we obtain the convergence of the algorithm, where in the light regions the procedure does not reach its completion. We see that for the nine systems displayed in Fig. 6 the main feature determining the convergence of the algorithm is the mutual inclination between the two planets. However, in some cases the border between the darker regions and the lighter ones (which are KAM stable/unstable, because our computational algorithm of invariant tori converges/diverges, respectively) is far from being a simple vertical segment. For instance, in the bottom-right panel referring to HD $74156$ we can appreciate that the rightmost dark pixels nicely describe a sort of arc; this suggests that in this case the transition from stability to instability should also depend on the orbital inclinations $i_{1}$ and $i_{2}$ in an untrivial way. Overall, we stress that we are able to construct KAM tori up to medium to high values of the mutual inclination, which are comparable with those actually observed in the few cases for which we have a clear estimate of $i_{mut}$, such as the almost $30^{\circ}$ of $\upsilon$ Andromedæ(see [7, 28]).

Fig. 6

Ratio of the norms of the second generating functions (as they are determined during the normalization algorithm) for all the initial conditions considered.

It seems hard to recognize general rules when Figs. 6 and 7 are compared. In the latter, the results about the maximal amplitude of the variation of $\Delta\omega$ are reported for the same exoplanetary systems already considered in the former. For most of them the stable region corresponding to low values of the mutual inclination has lighter color, because the angle $\Delta\omega$ experiences a full rotation. As far as HD $11506$, HD $207832$ and HD $12661$ are concerned, the difference of the arguments of the pericenters is in a libration regime. Except in the last case, the center of libration of $\Delta\omega$ (not shown) is $180^{\circ}$ for the HD $4732$ system, while the libration of $\Delta\omega$ is around $0^{\circ}$ for HD $12661$. We stress that, in our settings of coordinates, $0^{\circ}$ and $180^{\circ}$ correspond to the condition of the apsidal alignment and the anti-alignment configuration, respectively. The stabilizing role played by the latter configuration was discussed in [7, 32]. By comparing each panel of Fig. 6 with the corresponding one in Fig. 7, one can appreciate that the border of the region where the algorithm looks convergent has approximately the same shape of the transition zone from the librational regime to the rotational one. Moreover, the profile corresponding to the change of colors for the maximal amplitude of the variation of $\Delta\omega$ often overestimates the area where the normalization procedure is successful. This remark is not surprising at all, because the former quantity is evaluated thanks to purely numerical integrations of the secular model, while the latter is based on the semianalytical approach we widely described in the previous section.

Fig. 7

Maximal amplitude of the libration of the angle $\Delta\omega$ as a function of all the initial conditions considered. The exoplanetary systems considered here are exactly the same as in Fig. 6.

Of all the systems listed in Table 1, there are two which have not been discussed yet, i. e., HD $183263$ and HD $147873$. This is due to the fact that no points of the parameter space $(i_{mut},i)$ led to the successful conclusion of the constructive algorithm. In Fig. 8 we show the Poincaré sections for $i=90^{\circ}$ and $i_{mut}=1^{\circ}$, that is, the case in which we consider the masses to be minimal and the system to be almost coplanar. In the left panel, we present the results concerning HD $183263$, whereas in the right panel we show those relating to HD $147873$. It can be seen how the representation of the true orbit on the Poincaré section is quite distorted with respect to those pictured in Fig. 3. As the algorithm is optimized to cases as the ones presented in Fig. 3, which are found in the vast majority of the systems considered, it performs less well in this framework. More specifically, in the case of HD $183263$ the procedure for the construction of the KAM torus does not converge, whereas for HD $147873$ it is the procedure concerning the elliptic torus that could not be completed.

Fig. 8

Poincaré section for $\eta_{2}=0$. On the left, the case relating to the system HD $183263$ for $i=90^{\circ}$ and $i_{mut}=1^{\circ}$. On the right, the case relating to the system HD $147873$ for $i=90^{\circ}$ and $i_{mut}=1^{\circ}$.

5 CONCLUSIONS AND PERSPECTIVES

In this work, we studied the stability of $12$ extrasolar systems with respect to their orbital and mutual inclinations, which are currently unknown. Varying the values of these parameters drastically changes the structure of the systems. This concerns both their masses (which must be corrected by multiplying their values by the factor $1/\sin i$) and their mutual interaction. We studied their stability in the KAM sense, therefore, we evaluated the compatibility of the initial conditions with the construction of KAM tori. The complete procedure relies on three main blocks: the introduction of the secular model at order two in the masses, the construction of a $1$-dimensional elliptic torus, and the subsequent construction of a KAM torus well approximating the secular orbital motion. The adoption of the elliptic torus as seed for the KAM algorithm has proven to be crucial (see [7]) in order to be able to apply the method to systems that can be very different from the Solar System, for which the method was initially constructed (see, for example, [26]). A previous study missing this step gave encouraging but not completely satisfactory results, especially considering the limitations to the systems to which it was applicable (see [37]).

Here, we have applied the method to several systems. For most of them, it was possible to determine relevant subsets of the parameter space of the inclinations that are compatible with the stability in the KAM sense. From the results we achieved, it is clear that the main factor contributing to the stability or lack thereof is the mutual inclination between the planets. .Nevertheless, for most of the cases it was possible to reach values up to $\simeq 30^{\circ}$, or anyway values that are compatible with the few systems for which observations have provided clear evaluations of the mutual inclination. From an astronomical point of view, we think that the maps we produced about the KAM stability of the extrasolar planetary systems as functions of the (mutual) inclinations are the most interesting results of our work. In fact, they allow one to locate ranges of values of some unknown orbital elements, for which the mutual perturbations are so small that the three-body skeletons of those systems are robust enough to support the eventual presence of other exoplanets not yet detected. In other words, this provides a quantitative criterion to consider some orbital configurations more probable than others.

There are also two systems for which no results could be gathered, HD $183263$ and HD $147873$, because of a failure at some stage of our computational algorithm based on the previously described “three blocks scheme”. For both these extrasolar planetary systems, the Poincaré sections show that the actual orbits are quite different from the more regular ellipses drawn by the successful cases (for the sake of brevity, we limited the report of this kind of plots in the paradigmatic case we have studied more in depth, i.e., HD 4732). As a future challenge, we will try to further refine the whole algorithm constructing the final Kolmogorov normal form, so as to successfully extend it also to the configurations that have not yet been covered by our approach.