On the extension of the Laplace-Lagrange secular theory to order two in the masses for extrasolar systems

Abstract

We study the secular evolution of several exoplanetary systems by extending the Laplace-Lagrange theory to order two in the masses. Using an expansion of the Hamiltonian in the Poincaré canonical variables, we determine the fundamental frequencies of the motion and compute analytically the long-term evolution of the Keplerian elements. Our study clearly shows that, for systems close to a mean-motion resonance, the second order approximation describes their secular evolution more accurately than the usually adopted first order one. Moreover, this approach takes into account the influence of the mean anomalies on the secular dynamics. Finally, we set up a simple criterion that is useful to discriminate between three different categories of planetary systems: (i) secular systems (HD 11964, HD 74156, HD 134987, HD 163607, HD 12661 and HD 147018); (ii) systems near a mean-motion resonance (HD 11506, HD 177830, HD 9446, HD 169830 and $\upsilon$ Andromedae); (iii) systems really close to or in a mean-motion resonance (HD 108874, HD 128311 and HD 183263).

1 Introduction

The study of the dynamics of planetary systems is a long standing and challenging problem. The classical perturbation theory, mainly developed by Lagrange and Laplace, uses the circular approximation as a reference for the orbits. The discovery of extrasolar planetary systems has opened a new field in Celestial Mechanics and nowadays more than 100 multi-planetary systems have been discovered. In contrast to the Solar System, where the orbits of the planets are almost circular, the exoplanets usually describe true ellipses with high eccentricities. Thus, the applicability of the classical approach, using the circular approximation as a reference, can be doubtful for these systems. In this work we revisit the classical Laplace-Lagrange theory for the secular motions of the pericenters of the planetary orbits, based only on a linear approximation of the dynamical equations, by considering also higher order terms.

Previous works of Libert and Henrard (2005, 2006) for coplanar systems have generalized the classical expansion of the perturbative potential to a higher order in the eccentricities, showing that this analytical model gives an accurate description of the behavior of planetary systems which are not close to a mean-motion resonance, up to surprisingly high eccentricities. Moreover, they have shown that an expansion up to order 12 in the eccentricities is usually required for reproducing the secular behavior of extrasolar planetary systems. This expansion has also been used by Beaugé et al. (2006) to successfully reproduce the motions of irregular satellites with eccentricities up to 0.7. Veras and Armitage (2007) have highlighted the limitations of lower order expansions; using only a fourth-order expansion in the eccentricities, they did not reproduce, even qualitatively, the secular dynamics of extrasolar planetary systems. All the previous results have been obtained considering a secular Hamiltonian at order one in the masses. Let us also remark that an alternative octupole-level secular theory has been developed for systems that exhibit hierarchical behavior (see, e.g., Ford et al. 2000; Lee and Peale 2003; Naoz et al. 2011; Katz et al. 2011 and Libert and Delsate 2012). However, this approach is not suitable for our study, as we will also consider systems with large semi-major axes ratio.

Considering the secular dynamics of the Solar System, Lagrange and Laplace showed that the proximity to the 5:2 mean-motion resonance between Jupiter and Saturn leads to large perturbations in the secular motion, explaining the so-called “great inequality”. Let us stress that when referring to secular evolution we mean long-term evolution, possibly including the long-term effects of near resonances. Indeed the terms of the perturbation associated to mean-motion resonances have small frequencies and thus influence the secular behavior of the system. A good description of the secular dynamics of an exoplanetary system should include the effects of the mean-motion resonances on their secular long-term evolution. Therefore, we replace the classical circular approximation with a torus which is invariant up to order two in the masses, this is the so-called Hamiltonian at order two in the masses. The benefit of a second order approach has been clearly highlighted in (Laskar (1988), Table 2), where a comparison between the fundamental frequencies of the planetary motion of the Solar System, is given for different approximations. Concerning the problem of the stability of the Solar System, the celebrated theorems of Kolmogorov and Nekhoroshev allowed to make substantial progress. Nevertheless, in order to apply these theorems, a crucial point is to consider the secular Hamiltonian at order two in the masses in order to have a good approximation of the secular dynamics (e.g., this allows, in Locatelli and Giorgilli (2007), to deal with the true values of the planetary masses, while the first order approximation used in Locatelli and Giorgilli (2005) forces the authors to reduce the masses of the planets by a factor 10). In recent years, the estimates for the applicability of both Kolmogorov and Nekhoroshev theorems to realistic models of some part of the Solar System have been improved by some authors (e.g., Robutel 1995; Fejoz 2005; Celletti and Chierchia 2007; Gabern et al. 2005; Locatelli and Giorgilli 2007; Giorgilli et al. 2009 and Sansottera et al. 2011, 2013).

In the present contribution, we study the secular dynamics of extrasolar planetary systems consisting of two coplanar planets. The aim is to reconstruct the evolution of the eccentricities and pericenters of the planets by using analytical techniques, extending the Laplace-Lagrange theory to order two in the masses. To do so, we extend the results in Libert and Henrard (2005, 2006), replacing the first order averaged Hamiltonian, with the one at order two in the masses, and show the improvements of this approximation on the study of the secular evolution of extrasolar systems. In particular, we determine the fundamental frequencies of the motion and compute analytically the long-term evolution of the Keplerian elements. Furthermore, we show that the Hamiltonian at order two in the masses describes accurately the secular dynamics of systems close to a mean-motion resonance and, as a byproduct, we also give an estimate of the proximity to a mean-motion resonance of the two-planet extrasolar systems discovered so far.

The paper is organized as follows. In Sect. 2, we describe the expansion of the Hamiltonian of the planar three-body problem in Poincaré variables. Following the Lagrange approach, we focus, in Sect. 3, on the secular part of the Hamiltonian and derive the secular Hamiltonian at order two in the masses. In Sect. 4, we construct a high-order Birkhoff normal form, using the Lie series method, that leads to a very simple form of the equations of motion, being function of the actions only. We also show how to compute the secular frequencies and perform a long-term analytical integration of the motion of the planets. In Sect. 5, we apply our method to the $\upsilon$ Andromedae system and show that the second order approximation is well suited for systems close to a mean-motion resonance. Furthermore, the influence of the mean anomaly on the long-term evolution is pointed out in Sect. 6. In Sect. 7, we set up a criterion to evaluate the proximity of planetary systems to mean-motion resonances, and apply it to the two-planet extrasolar systems discovered so far. Finally, our results are summarized in Sect. 8. An Appendix containing the expansion of the secular Hamiltonian of the $\upsilon$ Andromedae extrasolar system, up to order 6, follows.

2 Expansion of the planetary Hamiltonian

We consider a system of three coplanar point bodies, mutually interacting according to Newton’s gravitational law, consisting of a central star $P_0$ of mass $m_0$ and two planets $P_1$ and $P_2$ of mass $m_1$ and $m_2$, respectively. The indices 1 and 2 refer to the inner and outer planet, respectively.

Let us now recall how the classical Poincaré variables can be introduced to perform the expansion of the Hamiltonian around circular orbits. We follow the formalism introduced by Poincaré (see Poincaré (1892, 1905); for a modern exposition, see, e.g., Laskar (1989) and Laskar and Robutel (1995)). To remove the motion of the center of mass, we adopt the heliocentric coordinates¹, $\mathbf{r }_j=\overrightarrow{P_0P_j}$, with $j=1,\,2$. Denoting by $\tilde{\mathbf{r }}_j$ the momenta conjugated to $\mathbf{r }_j$, the Hamiltonian of the system has four degrees of freedom, and reads

$$\begin{aligned} F(\mathbf{r },\tilde{\mathbf{r }})= T^{(0)}(\tilde{\mathbf{r }})+U^{(0)}(\mathbf{r })+ T^{(1)}(\tilde{\mathbf{r }})+U^{(1)}(\mathbf{r })\ , \end{aligned}$$

(1)

where

$$\begin{aligned} T^{(0)}(\tilde{\mathbf{r}})&= \frac{1}{2}\sum _{j=1}^2 \Vert \tilde{\mathbf{r}}_j\Vert ^2 \left( \frac{1}{m_0}+\frac{1}{m_j} \right) \ , \qquad T^{(1)}(\tilde{\mathbf{r}})= \frac{\tilde{\mathbf{r}}_1 \cdot \tilde{\mathbf{r}}_2}{m_0}\ ,\\ U^{(0)}(\mathbf{r})&= -\mathcal{G }\sum _{j=1}^2 \frac{m_0m_j}{\Vert \mathbf{r}_j\Vert }\ , \qquad \qquad \qquad \qquad U^{(1)}(\mathbf{r})= -\mathcal{G }\frac{m_1m_2}{\Vert \mathbf{r}_1-\mathbf{r}_2\Vert }\ . \end{aligned}$$

The plane set of Poincaré canonical variables is introduced as

$$\begin{aligned} \varLambda _j&= \frac{m_0\, m_j}{m_0+m_j}\sqrt{\mathcal{G }(m_0+m_j) a_j}, \quad \quad \quad \lambda _j = M_j+\omega _j,\nonumber \\ \xi _j&= \sqrt{ 2\varLambda _j}\, \sqrt{1-\sqrt{1-e_j^2}}\,\cos \omega _j , \quad \quad \eta _j=-\sqrt{2\Lambda _j}\, \sqrt{1-\sqrt{1-e_j^2}}\, \sin \omega _j, \end{aligned}$$

(2)

for $j=1,2$, where $a_j,\> e_j,\> M_j$ and $\omega _j$ are the semi-major axis, the eccentricity, the mean anomaly and the longitude of the pericenter of the $j$-th planet, respectively. One immediately sees that both $\xi _j$ and $\eta _j$ are of the same order as the eccentricity $e_j$. Using the Poincaré canonical variables, the Hamiltonian becomes

$$\begin{aligned} F({\varvec{\varLambda }},{\varvec{\lambda }}, {\varvec{\xi }}, {\varvec{\eta }})= F^{(0)}({\varvec{\varLambda }})+F^{(1)}({\varvec{\varLambda }}, {\varvec{\lambda }}, {\varvec{\xi }},{\varvec{\eta }}), \end{aligned}$$

(3)

where $F^{(0)}=T^{(0)}+U^{(0)}$ is the Keplerian part and $F^{(1)}=T^{(1)}+U^{(1)}$ the perturbation. Let us emphasize that the ratio $F^{(1)}/F^{(0)}=\mathcal{O }(\mu )$ with $\mu =\max \{m_1/m_0,m_2/m_0\}$. Therefore, the time derivative of each variable is of order $\mu$, except for ${\varvec{\lambda }}$. For this reason we will refer to $({\varvec{\varLambda }},{\varvec{\lambda }})$ as the fast variables and to $({\varvec{\xi }},{\varvec{\eta }})$ as the secular variables.

We proceed now by expanding the Hamiltonian (3) in Taylor-Fourier series. We pick a fixed value ${\varvec{\varLambda }}^*$ of the fast actions² and perform a translation, $\mathcal{T }_{F}$, defined as

$$\begin{aligned} \mathbf{L }={\varvec{\varLambda }}-{\varvec{\varLambda }}^*. \end{aligned}$$

This canonical transformation leaves the coordinates ${\varvec{\lambda }}$, ${\varvec{\xi }}$ and ${\varvec{\eta }}$ unchanged. The transformed Hamiltonian $\mathcal{H }^{(\mathcal{T })} = \mathcal{T }_{F}(F)$ can be expanded in power series of $\mathbf{L }$, ${\varvec{\xi }}$ and ${\varvec{\eta }}$ around the origin. Forgetting an unessential constant, we rearrange the Hamiltonian of the system as

$$\begin{aligned} \mathcal{H }^{(\mathcal{T })}=\mathbf{n }^*\cdot \mathbf{L }+\sum _{j_1=2}^{\infty } h_{j_1,0}^{\mathrm{(Kep)}}(\mathbf{L })+ \mu \sum _{j_1=0}^{\infty }\sum _{j_2=0}^{\infty } h^{(\mathcal{T })}_{j_1,j_2}(\mathbf{L },{\varvec{\lambda }},{\varvec{\xi }},{\varvec{\eta }}), \end{aligned}$$

(4)

where the functions $h^{(\mathcal{T })}_{j_1,j_2}$ are homogeneous polynomials of degree $j_1$ in the fast actions $\mathbf{L }$, degree $j_2$ in the secular variables $({\varvec{\xi }},{\varvec{\eta }})$, and depend analytically and periodically on the angles ${\varvec{\lambda }}$. The terms $h_{j_1,0}^{\mathrm{(Kep)}}$ of the Keplerian part are homogeneous polynomials of degree $j_1$ in the fast actions $\mathbf{L }$. We also expand $h^{(\mathcal{T })}_{j_1,j_2}$ in Fourier series of the angles ${\varvec{\lambda }}$. In the latter equation, the term which is both linear in the actions and independent of all the other canonical variables (i.e., $\mathbf{n }^*\cdot \mathbf{L }$) has been isolated in view of its relevance in perturbation theory, as it will be discussed in the next section.

All the expansions were carried out using a specially devised algebraic manipulator (see Giorgilli and Sansottera 2011). In our computations we truncate the expansion as follows. The Keplerian part is expanded up to the quadratic terms. The terms $h^{(\mathcal{T })}_{j_1,j_2}$ include the linear terms in the fast actions $\mathbf{L }$, all terms up to degree $12$ in the secular variables $({\varvec{\xi }},{\varvec{\eta }})$ and all terms up to the trigonometric degree $12$ with respect to the angles ${\varvec{\lambda }}$. The choice of the limits in the expansion is uniform for all the systems that will be considered. However, as we will explain in the next section, the actual limits for the computation of the secular approximation will be chosen as the lowest possible orders in ${\varvec{\lambda }}$ and $({\varvec{\xi }},{\varvec{\eta }})$, so as to include the main effects of the proximity to a mean-motion resonance.

3 Secular Hamiltonian

In this section we discuss the procedure for computing the secular Hamiltonian via elimination of the fast angles. The classical approach, usually found in the literature, consists in replacing the Hamiltonian $\mathcal{H }^{(\mathcal{T })}$, defined in (4), by

$$\begin{aligned} \overline{\mathcal{H }}= \frac{1}{4\pi ^2} \int \limits _{0}^{2\pi }\,\int \limits _{0}^{2\pi } \mathcal{H }^{(\mathcal{T })} \,\mathrm{d}\lambda _1\,\mathrm{d}\lambda _2. \end{aligned}$$

(5)

The idea is that the effects due to the fast angles are negligible on the long-term evolution and this averaged Hamiltonian represents a “good approximation” of the secular dynamics. This approach has been critically considered by Arnold, quoting his book (i.e., Arnold (1989), chapter 10) “this principle is neither a theorem, an axiom, nor a definition, but rather a physical proposition, i.e., a vaguely formulated and, strictly speaking, untrue assertion. Such assertion are often fruitful sources of mathematical theorems.”

The secular Hamiltonian obtained in this way is the so-called approximation at order one in the masses (or “averaging by scissors”) and is the basis of the Laplace-Lagrange theory for the secular motion of perihelia and nodes of the planetary orbits. This approximation corresponds to fixing the value of ${\varvec{\varLambda }}$, that remains constant under the flow, and thereby the semi-major axes. The averaged Hamiltonian, depending only on the secular variables, reduces the problem to a system with two degrees of freedom.

Let us remark that the Laplace-Lagrange secular theory was developed just considering the linear approximation of the dynamical equations. An extension of the Laplace-Lagrange theory for extrasolar systems, including also terms of higher order in the eccentricities, can be found in Libert and Henrard (2005, 2006), where the authors show that a secular Hamiltonian at order one in the masses gives an accurate description of the long-term behavior for systems which are not close to a mean-motion resonance.

One of the main achievements of the Laplace-Lagrange secular theory is the explanation of the “great inequality” between Jupiter and Saturn. Indeed, they have shown that the near commensurability of the two mean-motions (the 5:2 near resonance) has a great impact on the long-term behavior of the Solar System. For that reason, a good description of the secular dynamics of an exoplanetary system should include a careful treatment of the influence of mean-motion resonances on the long-term evolution.

Our purpose is to consider a secular Hamiltonian at order two in the masses. The idea is to remove perturbatively the dependency on the fast angles from the Hamiltonian (4), considering terms up to order two in the masses. This can be done using the classical generating functions of the Hamilton–Jacobi formalism. Here instead we use the Lie series formalism and implement the procedure in a way that takes into account the Kolmogorov algorithm for the construction of an invariant torus (see, Kolmogorov 1954). This is only a technical point and does not affect the results, our choice is a question of convenience since the Lie series approach is a direct method and is much more effective from the computational point of view (see, e.g., Giorgilli and Locatelli 2003).

3.1 Approximation at order two in the masses

Let us recall that in the expansion of the Hamiltonian $\mathcal{H }^{(\mathcal{T })}$, see (4), the perturbation is of order one in the masses and it is a polynomial in $\mathbf{L }$, ${\varvec{\xi }}$ and ${\varvec{\eta }}$, and a trigonometric polynomial in the fast angles ${\varvec{\lambda }}$. We remove part of the dependence on the fast angles performing a “Kolmogorov-like” normalization step, in the following sense. The suggestion of Kolmogorov is to give the Hamiltonian the normal form $H(\mathbf{L },{\varvec{\lambda }})= \mathbf{n }^*\cdot \mathbf{L }+ \mathcal{O }(\mathbf{L }^2)$, for which the existence of an invariant torus $\mathbf{L }=0$ is evident (where we consider the secular variables just as parameters). We give the Hamiltonian the latter form up to terms of order $\mathcal{O }(\mu ^2)$. More precisely, we perform a canonical transformation which removes the dependence on the fast angles from terms which are independent of and linear in the fast actions $\mathbf{L }$ (i.e., Eqs. (6) and (7), respectively). Therefore we replace the circular orbits of the Laplace-Lagrange theory with an approximate invariant torus, thus establishing a better approximation as the starting point of the classical theory. We also take into account the effects of near mean-motion resonances by including in the averaging process the corresponding resonant harmonics, as will be detailed hereafter. The procedure is a little cumbersome, and here we give only a sketch of the main path. For a detailed exposition one can refer to Locatelli and Giorgilli (2007) and Sansottera et al. (2013).

The expansion of the Hamiltonian $\mathcal{H }^{(\mathcal{T })}$, see (4), in view of the d’Alembert rules (see, e.g., Poincaré (1905); see also Kholshevnikov (1997, 2001) for a modern approach), contains only specific combinations of terms. Let us consider the harmonic $\mathbf{k }\cdot {\varvec{\lambda }}$, where $\mathbf{k }=(k_1,\,k_2)$, and introduce the so-called “characteristic of the inequality”

$$\begin{aligned} \mathcal C _\mathcal I (\mathbf{k }) = k_1 + k_2\ . \end{aligned}$$

The degree in the secular variables of the non-zero terms appearing in the expansion must have the same parity of $\mathcal C _\mathcal I (\mathbf{k })$ and is at least equal to $|\mathcal C _\mathcal I (\mathbf{k })|\,$.

It is well known that the terms of the expansion that have the main influence on the secular evolution are the ones related to low order mean-motion resonances. Therefore, if the ratio ${n_2^*}/{n_1^*}$ is close to the rational approximation ${k_1^*}/{k_2^*}$, then the effects due to the harmonics $(k_1^* \lambda _1 -k_2^* \lambda _2)$ should be taken into account in the secular Hamiltonian. Let us also recall that the coefficients of the Fourier expansion decay exponentially with $|\mathbf{k }|_1=|k_1|+|k_2|$, so we just need to consider low order resonances.

Let us go into details. Consider a system close to the $k_2^*:k_1^*$ mean-motion resonance and define the vector $\mathbf{k }^* = (k_1^*, -k_2^*)$ and two integer parameters $K_F=|\mathbf{k }^*|_1$ and $K_S = |\mathcal C _\mathcal I (\mathbf{k }^*)|$. We denote by $\lceil f \rceil _{{\varvec{\lambda }};K_F}$ the Fourier expansion of a function $f$ truncated in such a way that we keep only the harmonics satisfying the restriction $0<|\mathbf{k }|_1\le K_F$. The effect of the near mean-motion resonances is taken into account by choosing the parameters $K_S$ and $K_F$ as the lowest limits that include the corresponding resonant harmonics. Using the Lie series algorithm to calculate the canonical transformations (see, e.g., Henrard 1973 and Giorgilli 1995), we transform the Hamiltonian (4) as $\widehat{\mathcal{H }}^{(\mathcal{O }2)}=\exp \mathcal L _{\mu \,\chi _{1}^{(\mathcal{O }2)}}\,\mathcal{H }^{(\mathcal{T })}$, with the generating function $\mu \,\chi _1^{(\mathcal{O }2)}({\varvec{\lambda }},{\varvec{\xi }},{\varvec{\eta }})$ determined by solving the equation

$$\begin{aligned} \sum _{j=1}^{2}n^*_j \frac{\partial \,\chi _{1}^{(\mathcal O 2)}}{\partial \lambda _j} +\sum _{j_2=0}^{K_S}\left\lceil h_{0,j_2}^{(\mathcal{T })} \right\rceil _{{\varvec{\lambda }};K_F}\quad ({\varvec{\lambda }},{\varvec{\xi }},{\varvec{\eta }})=0. \end{aligned}$$

(6)

Notice that, by definition, the average over the fast angles of $\left\lceil h_{0,j_2}^{(\mathcal{T })}\right\rceil _{{\varvec{\lambda }};K_F}$ is zero, which assures that (6) can be solved provided that the frequencies are non resonant up to order $K_F$. The Hamiltonian $\widehat{\mathcal{H }}^{(\mathcal O 2)}$ has the same form as $\mathcal{H }^{(\mathcal{T })}$ in (4), with the functions $h^{(\mathcal{T })}_{j_1,j_2}$ replaced by new ones, $\hat{h}^{(\mathcal O 2)}_{j_1,j_2}$, generated by expanding the Lie series $\exp \mathcal L _{\mu \,\chi _{1}^{(\mathcal O 2)}}\, \mathcal H ^{(\mathcal{T })}$ and gathering all the terms having the same degree both in the fast actions and in the secular variables.

We now perform a second canonical transformation $\mathcal{H }^{(\mathcal{O }2)}=\exp \mathcal L _{\mu \,\chi _{2}^{(\mathcal{O }2)}}\,\widehat{\mathcal{H }}^{(\mathcal{O }2)}$, where the generating function $\mu \,\chi _{2}^{(\mathcal{O }2)}(\mathbf{L },{\varvec{\lambda }},{\varvec{\xi }},{\varvec{\eta }})$, which is linear with respect to $\mathbf{L }$, is determined by solving the equation

$$\begin{aligned} \sum _{j=1}^{2}n^*_j \frac{\partial \,\chi _{2}^{(\mathcal{O }2)}}{\partial \lambda _j} +\sum _{j_2=0}^{K_S}\left\lceil \hat{h}_{1,j_2}^{(\mathcal{O }2)} \right\rceil _{{\varvec{\lambda }};K_F}\quad (\mathbf{L },{\varvec{\lambda }},{\varvec{\xi }},{\varvec{\eta }})=0. \end{aligned}$$

(7)

Again, (7) can be solved provided the frequencies are non resonant up to order $K_F$ and the Hamiltonian $\mathcal H ^{(\mathcal O 2)}$ can be written in a form similar to (4), namely

$$\begin{aligned} \mathcal{H }^{(\mathcal{O }2)}(\mathbf{L },{\varvec{\lambda }},{\varvec{\xi }},{\varvec{\eta }})= \mathbf{n }^*\cdot \mathbf{L }+ \sum _{j_1=2}^\infty h_{j_1,0}^{(\mathrm{Kep})}(\mathbf{L })+ \mu \sum _{j_1=0}^\infty \sum _{j_2=0}^\infty h_{j_1,j_2}^{(\mathcal{O }2)}(\mathbf{L },{\varvec{\lambda }},{\varvec{\xi }},{\varvec{\eta }};\mu )+\mathcal{O }(\mu ^3)\ ,\nonumber \\ \end{aligned}$$

(8)

where the new functions $h^{(\mathcal{O }2)}_{j_1,j_2}$ are computed as previously explained for $\hat{h}^{(\mathcal{O }2)}_{j_1,j_2}$ and still have the same dependence on their arguments as $h^{(\mathcal{T })}_{j_1,j_2}$ in (4). As we are interested in a second order approximation, we have neglected the contribution of the order $\mathcal{O }(\mu ^3)$ in the canonical transformations associated to (6) and (7). Following a common practice in perturbation theory, we denote again by $(\mathbf{L },{\varvec{\lambda }},{\varvec{\xi }},{\varvec{\eta }})$ the transformed coordinates.

In the following, we will denote by $\mathcal{T }_{\mathcal{O }2}$ the canonical transformation induced by the generating functions $\mu \,\chi _{1}^{(\mathcal{O }2)}$ and $\mu \,\chi _{2}^{(\mathcal{O }2)}$, namely

$$\begin{aligned} \mathcal{T }_{\mathcal{O }2}(\mathbf{L },{\varvec{\lambda }},{\varvec{\xi }},{\varvec{\eta }}) = \exp \mathcal L _{\mu \,\chi _{2}^{(\mathcal{O }2)}} \circ \exp \mathcal L _{\mu \,\chi _{1}^{(\mathcal{O }2)}}(\mathbf{L },{\varvec{\lambda }},{\varvec{\xi }},{\varvec{\eta }})\ . \end{aligned}$$

(9)

Let us remark that the non resonance condition

$$\begin{aligned} \mathbf{k }\cdot \mathbf{n }^* \ne 0 \quad \text{ for }\ \ 0<|\mathbf{k }|_1\le K_F\ , \end{aligned}$$

does not imply that the canonical change of coordinates is convergent. Indeed, the terms $\mathbf{k }\cdot \mathbf{n }^*$ that appear as the denominators of the generating functions, even if they do not vanish, can produce the so-called small divisors. It is well known that the presence of small divisors is a major problem in perturbation theory. Therefore, for each system considered in this work, we check that the canonical transformation $\mathcal{T }_{\mathcal{O }2}$ is near to the identity and only in that case we proceed computing the approximation at order two in the masses.

3.2 Averaged Hamiltonian in diagonal form

Starting from the Hamiltonian $\mathcal{H }^{(\mathcal{O }2)}$ in (8), we just need to perform an average over the fast angles ${\varvec{\lambda }}$. More precisely, we consider the averaged Hamiltonian

$$\begin{aligned} \mathcal{H }^{(\mathrm{sec})}({\varvec{\xi }},{\varvec{\eta }}) = \left\langle \mathcal{H }^{(\mathcal{O }2)}\big |_{\mathbf{L }=0}\right\rangle _{{\varvec{\lambda }}}, \end{aligned}$$

(10)

namely we set $\mathbf{L }=0$ and average $\mathcal{H }^{(\mathcal{O }2)}$ by removing all the Fourier harmonics depending on the angles. This results in replacing the orbit having zero eccentricity with an invariant torus of the unperturbed Hamiltonian. The Hamiltonian so constructed is the secular one, describing the slow motion of the eccentricities and pericenters. Concerning the approximation at order one in the masses, let us recall that we directly average the Hamiltonian $\mathcal{H }^{(\mathcal{T })}$, see Eq. (5).

After the averaging over the fast angles, the secular Hamiltonian has two degrees of freedom and, in view of the d’Alembert rules, contains only terms of even degree in $({\varvec{\xi }},{\varvec{\eta }})$. Therefore, the lowest order approximation of the secular Hamiltonian, namely its quadratic part, is essentially the one considered in the Laplace-Lagrange theory. The origin $({\varvec{\xi }}, {\varvec{\eta }}) = (0, 0)$ is an elliptic equilibrium point, and it is well known that one can find a linear canonical transformation $({\varvec{\xi }},{\varvec{\eta }})=\mathcal D (\mathbf{x },\mathbf{y })$ which diagonalizes the quadratic part of the Hamiltonian, so that we may write $\mathcal{H }^{(\mathrm{sec})}$ in the new coordinates as

$$\begin{aligned} H^{(\mathrm{sec})}(\mathbf{x }, \mathbf{y })= \sum _{j=1}^{2}\nu _j\frac{x_j^2+y_j^2}{2}+ H_{2}^{(0)}(\mathbf{x },\mathbf{y })+H_{4}^{(0)}(\mathbf{x },\mathbf{y })+ \ldots , \end{aligned}$$

(11)

where $\nu _j$ are the secular frequencies in the small oscillations limit and $H_{2s}^{(0)}$ is a homogeneous polynomial of degree $2s+2$ in $(\mathbf{x },\mathbf{y })\,$.

To illustrate the transformations described above, the secular Hamiltonian, $\mathcal{H }^{(\mathrm{sec})}$, of the $\upsilon$ Andromedae extrasolar system (see Sect. 5 for a detailed description of the system and a discussion on its proximity to the 5:1 mean-motion resonance) is reported in the Appendix. First and second order approximations in the masses, including terms up to order 6 in $({\varvec{\xi }},{\varvec{\eta }})$, are given.

4 Secular evolution in action-angle coordinates

Following Libert and Henrard (2006), we now aim to introduce an action-angle formulation, since its associated equations of motion are extremely simple and can be integrated analytically. The secular Hamiltonian (11) has the form of a perturbed system of harmonic oscillators, and thus we can construct a Birkhoff normal form (see Birkhoff 1927) introducing action-angle coordinates for the secular variables, by means of Lie series (see, e.g., Hori 1966; Deprit 1969; Giorgilli 1995). Finally, an analytical integration of the action-angle equations will allow us to check the accuracy of our secular approximation, by comparing it to a direct numerical integration of the Newton equations.

4.1 Birkhoff normal form via Lie series

As the construction of the Birkhoff normal form via Lie series is explained in detail in many previous studies, here we just briefly recall it, adapted to the present context.

First, we define a canonical transformation $(\mathbf{x },\mathbf{y })=\mathcal A (\mathbf{I },{\varvec{\varphi }})$ introducing the usual action-angle variables

$$\begin{aligned} x_j = \sqrt{2 I_j} \cos {\varphi _j}\ ,\quad y_j = \sqrt{2 I_j} \sin {\varphi _j},\quad j=1,2. \end{aligned}$$

(12)

The secular Hamiltonian in these variables reads

$$\begin{aligned} H^{(\mathrm{sec})}(\mathbf{I }, {\varvec{\varphi }})= {\varvec{\nu }}\cdot \mathbf{I }+ H_{2}^{(0)}(\mathbf{I }, {\varvec{\varphi }})+H_{4}^{(0)}(\mathbf{I }, {\varvec{\varphi }})+\ldots . \end{aligned}$$

(13)

In order to remove the dependency of the secular angles ${\varvec{\varphi }}$ in this expression, we compute the Birkhoff normal form up to order $r$,

$$\begin{aligned} H^{\,(r)} = Z_{0}(\mathbf{I })+\cdots +Z_{r}(\mathbf{I }) + \mathcal R ^{(r)}(\mathbf{I }, {\varvec{\varphi }})\ , \end{aligned}$$

(14)

where $Z_{s}$, for $s=0,\ldots ,r$, is a homogeneous polynomial of degree $s/2+1$ in $\mathbf{I }$ and is zero for odd $s$. Only the remainder, $\mathcal R ^{(r)}(\mathbf{I },{\varvec{\varphi }})$, depends also on the angles ${\varvec{\varphi }}$. Again, with a little abuse of notation, we denote by $(\mathbf{I },{\varvec{\varphi }})$ the new coordinates. At each order $s>0$, we determine the generating function $X^{(s)}$, by solving the equation

$$\begin{aligned} \left\{ X^{(s)},{\varvec{\nu }}\cdot \mathbf{I }\right\} + H_{s}(\mathbf{I }, {\varvec{\varphi }})= Z_{s}(\mathbf{I }). \end{aligned}$$

(15)

Using the Lie series, we calculate the new Hamiltonian as $H^{(s+1)}=\exp \mathcal L _{X^{(s+1)}}\,H^{(s)}$, provided that the non-resonance condition

$$\begin{aligned} \mathbf{k }\cdot {\varvec{\nu }}\ne 0 \quad \text{ for }\ \mathbf{k }\in \mathbb Z ^2\ \mathrm{such\ that}\ 0<|\mathbf{k }|_1\le s+2 \end{aligned}$$

(16)

is fulfilled.

Let us remark that, considering the Hamiltonian at order two in the masses, the Birkhoff normal form is not always convergent at high order, especially when the eccentricities are significant or the system is too close to a mean-motion resonance. Indeed, in these cases, the transformation $\mathcal{T }_{\mathcal{O }2}$, which brings the Hamiltonian at order two in the masses, induces a big change in the coefficients of the secular Hamiltonian, that can prevent the convergence of the normalization procedure. On the contrary, the algorithm seems to be convergent at first order in the masses (see the convergence au sens des astronomes in Libert and Henrard (2006)).

Assuming that the non-resonance conditions (16) are satisfied up to an order $r$ large enough, the remainder $\mathcal R ^{(r)}(\mathbf{I }, {\varvec{\varphi }})$ can be neglected and we easily obtain an analytical expression of the secular frequencies. Indeed, the equations of motion for the truncated Hamiltonian are

$$\begin{aligned} \dot{\mathbf{I }}=0 \quad \mathrm{and} \quad \dot{\varvec{\varphi }}= \frac{\partial H^{(r)}}{\partial \,\mathbf{I }}, \end{aligned}$$

(17)

and lead immediately to the expression of the two frequencies $\dot{\varphi }_1$ and $\dot{\varphi }_2$. Let us remark that, as the generating functions of the Lie series depend only on the angular difference $\varphi _1 - \varphi _2$, the frequency of the apsidal difference $\varDelta \varpi = \omega _1-\omega _2$ is equal to $\dot{\varphi }_1 - \dot{\varphi }_2$.

4.2 Analytical integration

Using the equations in (17), we can compute the long-term evolution on the secular invariant torus, namely

$$\begin{aligned} \mathbf{I }(t) = \mathbf{I }(0)\qquad \text{ and }\qquad {\varvec{\varphi }}(t)={\varvec{\varphi }}(0)+t\dot{\varvec{\varphi }}(0), \end{aligned}$$

where $\mathbf{I }(0)$ and ${\varvec{\varphi }}(0)$ correspond to the values of the initial conditions. To validate our results, we will compare our analytical integration with the direct numerical integration of the full three-body problem, by using the symplectic integrator $\mathcal S \mathcal B \mathcal A \mathcal B 3$ (see Laskar and Robutel 2001).

Here we briefly explain how the analytical computation of the secular evolution of the orbital elements is performed. Let us denote by $\mathcal{T }_\mathcal{B }^{(r)}$ the canonical transformation induced by the Birkhoff normalization up to the order $r$, namely

$$\begin{aligned} \mathcal{T }_\mathcal{B }^{(r)}\big (\mathbf{I }, {\varvec{\varphi }}\big ) = \exp \mathcal L _{X^{(r)}}\circ \,\cdots \circ \,\exp \mathcal L _{X^{(1)}} \>\big (\mathbf{I },{\varvec{\varphi }}\big ). \end{aligned}$$

(18)

We denote by $\mathcal C ^{(r)}$ the composition of all the canonical changes of coordinates defined in Sects. 2–4, namely

$$\begin{aligned} \mathcal C ^{(r)}=\mathcal{T }_{F}\circ \mathcal{T }_{\mathcal{O }2}\circ \mathcal D \circ \mathcal A \circ \mathcal{T }_\mathcal{B }^{(r)}. \end{aligned}$$

(19)

Taking the initial conditions $\big (\mathbf{a }(0),{\varvec{\lambda }}(0),\mathbf{e }(0),{\varvec{\omega }}(0)\big )$, we can compute the evolution of the orbital elements by using the following scheme

(20)

where $({\varvec{\varLambda }},{\varvec{\lambda }},{\varvec{\xi }},{\varvec{\eta }}) = \mathcal E ^{-1}(\mathbf{a }(0),{\varvec{\lambda }}(0),\mathbf{e }(0),{\varvec{\omega }}(0))$ is the non-canonical change of coordinates (2). Thus, the analytical integration via normal form actually reduces to a transformation of the initial conditions to secular action-angles coordinates, the computation of the flow at time $t$ in these coordinates, followed by a transformation back to the original orbital elements. Let us stress that, considering only the secular evolution, the scheme above commutes only if $r$ is equal to infinity.

In the following sections, we will compare, for several extrasolar systems, the analytical secular evolution of the eccentricities and apsidal difference with the results of a direct numerical integration. This kind of comparison has been shown to be a very stressing test (see, e.g., Locatelli and Giorgilli 2007 and Sansottera et al. 2013) for the accuracy of the whole algorithm constructing the normal form.

5 Application to the $\upsilon$ Andromedae system

We aim to investigate the improvements of the secular approximation at order two in the masses, introduced in the previous sections, in describing the long-term evolution of extrasolar systems close to a mean-motion resonance. The planetary system $\upsilon$ Andromedae c and d is well known for his proximity to the 5:1 mean-motion resonance. This has notably been confirmed analytically in Libert and Henrard (2007), where the authors argued that a first order approximation gives a good qualitative approximation of the secular dynamics of the system. In the following, we show that a second order approximation can quantitatively enhance the determination of the secular frequencies, as well as the extremal values of the eccentricities and difference in apsidal angles reached during the long-term evolution of the planets. For this study, we use the orbital parameters reported in Wright et al. (2009).³

In order to take into account the proximity of the system to the 5:1 mean-motion resonance, we must include, in the approximation at order two in the masses, the effects of all the terms up to the trigonometric degree 6 in the fast angles and up to degree 4 in the secular variables, namely we set $K_F=6$ and $K_S=4$ (see the definitions in Sect. 3.1). After having constructed the secular approximation, we perform a Birkhoff normal form up to order $r=10$ (see Sect. 4.1), which corresponds to taking into account the secular variables up to order 12.

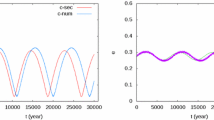
In Fig. 1, we report the long-term evolution of the eccentricities (top panel) and difference of the longitudes of the pericenters (bottom panel) obtained analytically with our second order approximation (red curves). We compare it to the direct numerical integration of the full three-body problem (i.e., including the fast motions) in heliocentric canonical variables (green curves). The agreement between both curves is excellent; the second order theory reproduces qualitatively and quantitatively the results of the numerical integration. A comparison with the first order approximation is also shown (blue curves) and gives evidence of the improvement of the second order approximation for systems close to a mean-motion resonance.

To highlight the dependency on the truncation parameters, we report, in the table below, the values of the secular period for different values of $K_F$ and $K_S$. The period obtained via numerical integration is $\sim$7,000 years. As expected, higher values of the truncation parameters allow to obtain better results, but with a higher computational cost. As already shown in Fig. 1, the main correction on the secular evolution is achieved when considering the terms related to the 5:1 mean-motion resonance, i.e., $K_F=6$ and $K_S=4$. This validates our choice of the truncation limits.

Fig. 1

Long-term evolution of the eccentricities (left panel) and difference of the longitudes of the pericenters (right panel) for the $\upsilon$ Andromedae system ($a_1/a_2=0.328$), obtained in three different ways: (i) direct numerical integration via $\mathcal S \mathcal B \mathcal A \mathcal B 3$ (green curves); (ii) second order approximation (red curves); (iii) first order approximation (blue curves). See text for more details

$K_F$	$K_S$	Secular period
4	2	7,132
6	4	7,035
8	6	6,998

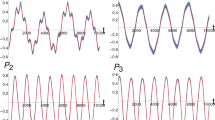
In Fig. 2, we slightly modify the semi-major axis of planet d in such a way that the modified $\upsilon$ Andromedae systems are closer and closer to the 5:1 mean-motion resonance. First we set $a_1/a_2=0.335$ (left panel). In this case the approximation at order one is not good enough, while the one at order two is still suitable for the computation of the long-term evolution of the system, even if the approximation is worst than the one corresponding to the real $\upsilon$ Andromedae in Fig. 1. Finally, setting $a_1/a_2=0.338$ (right panel), both the secular approximations completely fail. Indeed, in this case, the system is too close to the resonance to be qualitatively described by a secular approximation.

Fig. 2

Long-term evolution of slightly different versions of the $\upsilon$ Andromedae system, where the semi-major axis of planet d has been modified to be closer to the 5:1 resonance. For $a_1/a_2=0.335$ (left panel), the secular approximation at order two in the masses is still efficient, while it is no more suitable for $a_1/a_2=0.338$ (right panel)

6 Influence of the mean anomaly on the secular evolution

On the contrary to a first order analytical theory, an expansion to the second order in the masses takes into account the influence of the initial values of the fast angles on the secular evolution of the system. Let us stress that, as the averaging process giving the first order secular Hamiltonian (5) does not involve any canonical transformation, we take as “averaged” initial conditions the original ones⁴.

A change in the mean anomaly of a planet can have a significant impact on the secular period of the system. To show this, we plot, in Fig. 3, the extrasolar system HD 169830 for two different values of the inner planet mean anomaly: $M_1=0^\circ$ and $M_1=160^\circ$, all the other orbital parameters being unchanged and issued from Mayor et al. (2004). The displacement between the two secular evolutions is obvious in the top panel. Let us note that, for both values, our second order averaged Hamiltonian (in red) is very accurate and coincides with the numerical evolution (in green). The limitation of the secular expansion to order one in the masses is pointed out in the bottom panel of Fig. 3. The first order evolution (blue curve) is the same regardless the initial value of the mean anomaly, on the contrary to the approximation at order two in the masses (red curves).

Fig. 3

Influence of the initial mean anomaly, $M$, on the secular evolution of the HD 169830 system. Left: long-term evolution for $M_1=0^\circ$ and $M_1=160^\circ$. In both cases, the second order approximation (red curves) reproduce accurately the numerical integration (green curves). Right: comparison between the evolution at order one (blue curve) and two (red curves) in the masses. See text for more details

7 Evaluation of the proximity to a mean-motion resonance

We now study the proximity to a mean-motion resonance of the two-planet exosystems discovered so far. This represents an extension of the results in Libert and Henrard (2007), previously obtained with an approximation at order one in the masses.

Let us make some heuristic considerations. For systems that are very close to a low-order mean-motion resonance $k_2$:$k_1$, i.e., $k_1 n_1^*-k_2 n_2^*\approx 0$, the generating functions related to the second order approximation (i.e., $\mu \, \chi _1^{(\mathcal{O }2)}$ and $\mu \, \chi _{2}^{(\mathcal{O }2)}$ defined in (6) and (7), respectively) contain the so-called small divisors. The presence of small divisors is a major problem in perturbation theory, and here can prevent the convergence of the second order averaging over the fast angles. Instead, for a system that is only near to a mean-motion resonance, but not too close, the approximation at order two in the masses, including the main effects of the nearest low-order resonance, enables to describe with great accuracy the long-term evolution of the system. Finally, the secular evolution of a system that is far from any low order mean-motion resonance is accurately depicted by the approximation at order one in the masses. Indeed, in this case, we can safely replace the canonical transformation $\mathcal{T }_{\mathcal{O }2}$ with the classical first order average over the fast angles, see Eq. (5).

Let us go into details. To evaluate the proximity of a planetary system to a mean-motion resonance, we introduce a criterion similar to the one in Libert and Henrard (2007). The idea is to rate the proximity to a mean-motion resonance by looking at the canonical change of coordinates induced by the approximation at order two in the masses. Precisely, we consider the low order terms of the canonical transformation induced by $\mathcal{T }_{\mathcal{O }2}$, writing the averaged variables $({\varvec{\xi }}^{\prime },{\varvec{\eta }}^{\prime })$ as

$$\begin{aligned} \xi _j^{\prime }&=\xi _j - \frac{\partial \,\mu \,\chi _1^{(\mathcal{O }2)}}{\partial \eta _j} = \xi _j\,\left( 1-\frac{1}{\xi _j}\frac{\partial \,\mu \,\chi _1^{(\mathcal{O }2)}}{\partial \eta _j}\right) \ , \\ \eta _j^{\prime }&=\eta _j - \frac{\partial \,\mu \,\chi _1^{(\mathcal{O }2)}}{\partial \xi _j} = \eta _j\,\left( 1-\frac{1}{\eta _j}\frac{\partial \,\mu \,\chi _1^{(\mathcal{O }2)}}{\partial \xi _j}\right) \ , \end{aligned}$$

for $j=1\,,\,2\,$. The idea is that the generating function $\mu \, \chi _1^{(\mathcal{O }2)}$ carries the main information about the proximity to a mean-motion resonance, and we will focus here on the coefficients of the functions

$$\begin{aligned} \delta \xi _j = \frac{1}{\xi _j}\frac{\partial \,\mu \,\chi _1^{(\mathcal{O }2)}}{\partial \eta _j} \quad \text{ and }\quad \delta \eta _j = \frac{1}{\eta _j}\frac{\partial \,\mu \,\chi _1^{(\mathcal{O }2)}}{\partial \xi _j}\ . \end{aligned}$$

(21)

In these expressions, we aim to determine the most important periodic terms whose corresponding harmonic $\mathbf{k }\cdot {\varvec{\lambda }}$ identifies the main important mean-motion resonance to the system. For each system, we define a radius ${\varvec{\varrho }}$ of a polydisk $\varDelta _{{\varvec{\varrho }}}$ around the origin of $\mathbb R ^4$,

$$\begin{aligned} \varDelta _{{\varvec{\varrho }}}=\left\{ ({\varvec{\xi }},{\varvec{\eta }})\in \mathbb R ^4: \,\xi _j^2+\eta _j^2\le \varrho _j^2,\quad j=1,\,2 \right\} , \end{aligned}$$

so as to include in that domain the initial conditions. Given an analytic function $f_{0,j_2}({\varvec{\lambda }},{\varvec{\xi }},{\varvec{\eta }})$ of the form (4), that reads

$$\begin{aligned} f({\varvec{\lambda }},{\varvec{\xi }},{\varvec{\eta }}) =\sum _\mathbf{k }f^{(\mathbf{k })}({\varvec{\xi }}, {\varvec{\eta }})\, \begin{array}{l} \sin \\ \cos \\ \end{array} (\mathbf{k }\cdot {\varvec{\lambda }}), \end{aligned}$$

where

$$\begin{aligned} f^{(\mathbf{k })}({\varvec{\xi }}, {\varvec{\eta }})= \sum _{|\mathbf{l }|+|\mathbf{m }|=j_2} f^{(\mathbf{k })}_{\mathbf{l },\mathbf{m }}\,{\varvec{\xi }}^{\mathbf{l }}\,{\varvec{\eta }}^{\mathbf{m }}\ , \end{aligned}$$

we can easily bound the sup-norm of the terms corresponding to the harmonic $\mathbf{k }\cdot {\varvec{\lambda }}$ in $f$, by bounding $f^{(\mathbf{k })}$ in the polydisk $\varDelta _{{\varvec{\varrho }}}$ with the norm

$$\begin{aligned} \Vert f^{(\mathbf{k })}\Vert _{{\varvec{\varrho }}}= \sum _{\mathbf{l },\mathbf{m }} |f^{(\mathbf{k })}_{\mathbf{l },\mathbf{m }}|\,\varrho _1^{l_1+m_1}\,\varrho _2^{l_2+m_2}\ . \end{aligned}$$

(22)

Applying the same criterion, for each angular combination $\mathbf{k }\cdot {\varvec{\lambda }}$, we evaluate $\Vert \delta \xi ^{(\mathbf{k })}_j\Vert _{{\varvec{\varrho }}}$ and $\Vert \delta \eta ^{(\mathbf{k })}_j\Vert _{{\varvec{\varrho }}}$ for $j=1,\,2\,$, and, to identify the closest mean-motion resonance to the system, we define

$$\begin{aligned} \delta \xi _j^* = \max _{\mathbf{k }}(\Vert \delta \xi ^{(\mathbf{k })}_j\Vert _{{\varvec{\varrho }}}) \quad \text{ and }\quad \delta \eta _j^* = \max _{\mathbf{k }}(\Vert \delta \eta ^{(\mathbf{k })}_j\Vert _{{\varvec{\varrho }}}). \end{aligned}$$

For convenience we also introduce the following parameters: $\delta _j = \min (\delta \xi _j^*, \delta \eta _j^*)$ for $j=1,2$ and $\delta =\max (\delta _1, \delta _2)\,$. The parameter $\delta$ is a measure of the change from the original secular variables to the averaged ones. The actual computation of $\delta$ is quite cumbersome, but is more reliable than just looking at the semi-major axes ratio, since it holds information about the non-linear character of the system.

The results for all the extrasolar systems that we have considered are shown in Table 1 and Fig. 4. In Table 1, we report, for each system, the numerical values of the semi-major axes ratio $a_1/a_2$, the mass ratio $\mu$, the small divisor $k_1n_1^*+k_2n_2^*$ (where $k_1$ and $k_2$ correspond to the mean-motion resonance in brackets) and the two aforementioned parameters, $\delta _1$ and $\delta _2$, that will be used to set up a criterion evaluating the proximity to a mean-motion resonance. In Fig. 4, we plot the evolution of the eccentricities obtained by direct numerical integration of the Newton equations (green curves) and the ones obtained with a secular Hamiltonian at order one (blue curves) and two (red curves) in the masses. As in Sect. 5, we limit the Birkhoff normal form at order $r=10$ (i.e., $12$ in the secular variables). Let us stress that, for the HD 128311 and HD 183236 systems, due to their close proximity to the mean-motion resonances 2:1 and 5:1, respectively, the canonical transformation $\mathcal{T }_{\mathcal{O }2}$ performing the second order approximation is not close to the identity. Therefore, we report only their numerical integrations.

Table 1 Evaluation of the proximity to a mean-motion resonance (MMR)

Fig. 4

Long-term evolution of the eccentricities of the extrasolar systems of Table 1, obtained by three different ways: (i) the direct numerical integration via $\mathcal S \mathcal B \mathcal A \mathcal B 3$ (green curves); (ii) the second order approximation (red curves); (iii) the first order approximation (blue curves). See text for more details

Comparing the data in Table 1 and the corresponding plots in Fig. 4, we can roughly distinguish three cases: (i) if $\delta <2.6\times 10^{-3}$, the first order approximation describes the secular evolution with great accuracy, therefore we label these systems as secular; (ii) if $2.6\times 10^{-3}<\delta \le 2.6\times 10^{-2}$, a second order average of the Hamiltonian is required to describe the long-term evolution in detail, we label them as near mean-motion resonance (the $\upsilon$ Andromedae system analyzed in Sect. 5 is the typical example of such category); (iii) if $\delta >2.6\times 10^{-2}$, the system is too close to a mean-motion resonance and a secular approximation is not enough to describe their evolution, then we label them as in mean-motion resonance. In this case it would be worthwhile to consider a resonant Hamiltonian instead of a secular approximation. Let us note that the Sun-Jupiter-Saturn system and HD 108874 are both really close to the border between near mean-motion resonance and in mean-motion resonance categories. Indeed, a much refined secular approximation could be used, for instance increasing the values of $K_F$ and $K_S$, without having to resort to a resonant model.

The criterion introduced above is clearly heuristic and quite rough, nevertheless we think it is useful to discriminate between the different behaviors of planetary systems.

8 Conclusions and outlooks

In this work we have analyzed the long-term evolution of several exoplanetary systems by using a secular Hamiltonian at order two in the masses. The second order approximation, as explained in detail in Sect. 3, includes a careful treatment of the main effects due to the proximity to a low-order mean-motion resonance.

Starting from the secular Hamiltonian, we have computed a high-order Birkhoff normal form via Lie series, introducing action-angle coordinates for the secular variables. This enabled us to compute analytically the evolution on the secular invariant torus and to obtain the long-term evolution of the eccentricities and apsidal difference.

As a result, for all the systems that are not too close to a mean-motion resonance, we have shown an excellent agreement with the direct numerical integration of the full three-body problem (including the fast motions). The influence of the mean anomalies on the secular evolution of the systems has also been pointed out. Furthermore, evaluating the difference between the original and the averaged secular coordinates, we have set up a simple (and rough) criterion to discriminate between three different behaviors: (i) secular system, where a first order approximation is enough; (ii) system near a mean-motion resonance, where an approximation at order two is required; (iii) system that are really close to or in a mean-motion resonance, where a resonant model should be used. In particular, we find that HD 11964, HD 74156, HD 134987, HD 163607, HD 12661 and HD 147018 belong to (i); HD 11506, HD 177830, HD 9446, HD 169830 and $\upsilon$ Andromedae to (ii); HD 108874, HD 128311 and HD 183263 to (iii).

Let us remark that these results could be extended to the spatial case with minor changes. Indeed, after the reduction of the angular momentum, the starting Hamiltonian would have exactly the same form as $\mathcal{H }^{(\mathcal{T })}$, defined in (4).

Moreover, having such a good analytical description of the orbits, even for systems that are near a mean-motion resonance, we can also study the effective stability of extrasolar planetary systems in the framework of the KAM and Nekhoroshev theories. This topic deserves further investigation in the future.

Finally, a natural extension to the present work would be the study of the secular evolution of systems that are really close to or in a mean-motion resonance. As previously said, a resonant Hamiltonian that keeps the dependency on the resonant combinations of the fast angles has to be considered. This study is reserved for future work.

Appendix: Secular Hamiltonian for the \(\upsilon \) Andromedae up to order 6

We report here the expansion of the secular Hamiltonian $\mathcal{H }^{(\mathrm{sec})}$ (Eq. (10)) of the $\upsilon$ Andromedae extrasolar system up to degree $6$ in $({\varvec{\xi }},{\varvec{\eta }})\,$. In particular, we show both the approximations at order one and two in the masses to highlight the differences. A detailed description of the $\upsilon$ Andromedae system is given in Sect. 5. As this system is near the 5:1 mean-motion resonance, the main difference between the two secular approximations affects terms that are at least of order 6 in the canonical secular variables.

$\xi _1$	$\xi _2$	$\eta _1$	$\eta _2$	First order	Second order
0	0	0	0	$-3.8449638957147059 \times 10^{+0}$	$-3.8490132363346130 \times 10^{+0}$
2	0	0	0	$-4.7203675679835364 \times 10^{-4}$	$-4.7442843563932181 \times 10^{-4}$
1	1	0	0	$1.9765062410537654 \times 10^{-4}$	$1.9478085580405423 \times 10^{-4}$
0	2	0	0	$-1.2594397524843563 \times 10^{-4}$	$-1.2389253809188814 \times 10^{-4}$
0	0	2	0	$-4.7203675679835364 \times 10^{-4}$	$-4.7442843563932181 \times 10^{-4}$
0	0	1	1	$1.9765062410537654 \times 10^{-4}$	$1.9478085580405423 \times 10^{-4}$
0	0	0	2	$-1.2594397524843563 \times 10^{-4}$	$-1.2389253809188814 \times 10^{-4}$
4	0	0	0	$1.4338305925091211 \times 10^{-4}$	$1.4383176583648995 \times 10^{-4}$
3	1	0	0	$4.3147125112054390 \times 10^{-4}$	$4.5045949999300181 \times 10^{-4}$
2	2	0	0	$-7.4883810227863515 \times 10^{-4}$	$-7.5868060326294868 \times 10^{-4}$
2	0	2	0	$2.8676611850182422 \times 10^{-4}$	$2.8766295710810365 \times 10^{-4}$
2	0	1	1	$4.3147125112054390 \times 10^{-4}$	$4.5045950531661890 \times 10^{-4}$
2	0	0	2	$-5.1509576520639426 \times 10^{-4}$	$-5.2857952689768168 \times 10^{-4}$
1	3	0	0	$3.3341302753346505 \times 10^{-4}$	$3.2386648540035952 \times 10^{-4}$
1	1	2	0	$4.3147125112054390 \times 10^{-4}$	$4.5045950531661890 \times 10^{-4}$
1	1	1	1	$-4.6748467414448156 \times 10^{-4}$	$-4.6020211054162414 \times 10^{-4}$
1	1	0	2	$3.3341302753346505 \times 10^{-4}$	$3.2386626581402522 \times 10^{-4}$
0	4	0	0	$-9.4514514989701095 \times 10^{-5}$	$-9.0913589478614943 \times 10^{-5}$
0	2	2	0	$-5.1509576520639426 \times 10^{-4}$	$-5.2857952689768124 \times 10^{-4}$
0	2	1	1	$3.3341302753346505 \times 10^{-4}$	$3.2386626581402554 \times 10^{-4}$
0	2	0	2	$-1.8902902997940219 \times 10^{-4}$	$-1.8182716424233877 \times 10^{-4}$
0	0	4	0	$1.4338305925091211 \times 10^{-4}$	$1.4383176583649006 \times 10^{-4}$
0	0	3	1	$4.3147125112054390 \times 10^{-4}$	$4.5045949999300165 \times 10^{-4}$
0	0	2	2	$-7.4883810227863515 \times 10^{-4}$	$-7.5868060326294889 \times 10^{-4}$

$\xi _1$	$\xi _2$	$\eta _1$	$\eta _2$	First order	Second order
0	0	1	3	$3.3341302753346505 \times 10^{-4}$	$3.2386648540035947 \times 10^{-4}$
0	0	0	4	$-9.4514514989701095 \times 10^{-5}$	$-9.0913589478614848 \times 10^{-5}$
6	0	0	0	$8.0737006151169034 \times 10^{-5}$	$1.3917499875750025 \times 10^{-4}$
5	1	0	0	$-1.4728781329895123 \times 10^{-4}$	$-5.7065127472031446 \times 10^{-4}$
4	2	0	0	$-3.8625662439607426 \times 10^{-4}$	$8.8051997114562091 \times 10^{-4}$
4	0	2	0	$2.4221101845350710 \times 10^{-4}$	$4.1753226095492534 \times 10^{-4}$
4	0	1	1	$-1.4728781329895123 \times 10^{-4}$	$-5.7066077231623241 \times 10^{-4}$
4	0	0	2	$4.4154338663068642 \times 10^{-5}$	$3.1718226339201008 \times 10^{-4}$
3	3	0	0	$1.1715817984811095 \times 10^{-3}$	$-9.4757874129889675 \times 10^{-4}$
3	1	2	0	$-2.9457562659790246 \times 10^{-4}$	$-1.1413685872968715 \times 10^{-3}$
3	1	1	1	$-8.6082192611828580 \times 10^{-4}$	$1.1266453489623077 \times 10^{-3}$
3	1	0	2	$9.0270698998234857 \times 10^{-4}$	$-7.3916625373992911 \times 10^{-4}$
2	4	0	0	$-1.0274689835474350 \times 10^{-3}$	$8.0672276683552634 \times 10^{-4}$
2	2	2	0	$-3.4210228573300561 \times 10^{-4}$	$1.1977229419632242 \times 10^{-3}$
2	2	1	1	$1.7093314154786317 \times 10^{-3}$	$-1.3644052823847199 \times 10^{-3}$
2	2	0	2	$-1.4654674698375437 \times 10^{-3}$	$1.2083393139899557 \times 10^{-3}$
2	0	4	0	$2.4221101845350710 \times 10^{-4}$	$4.1753226095492669 \times 10^{-4}$
2	0	3	1	$-2.9457562659790246 \times 10^{-4}$	$-1.1413685872968726 \times 10^{-3}$
2	0	2	2	$-3.4210228573300561 \times 10^{-4}$	$1.1977229419632145 \times 10^{-3}$
2	0	1	3	$9.0270698998234857 \times 10^{-4}$	$-7.3916701878536670 \times 10^{-4}$
2	0	0	4	$-4.3799848629010854 \times 10^{-4}$	$4.0161436876523369 \times 10^{-4}$
1	5	0	0	$3.8723701961918303 \times 10^{-4}$	$-2.8749294965146893 \times 10^{-4}$
1	3	2	0	$9.0270698998234857 \times 10^{-4}$	$-7.3916701878535239 \times 10^{-4}$
1	3	1	1	$-1.1789409945146532 \times 10^{-3}$	$8.1021818828667783 \times 10^{-4}$
1	3	0	2	$7.7447403923836607 \times 10^{-4}$	$-5.7498741718758071 \times 10^{-4}$
1	1	4	0	$-1.4728781329895123 \times 10^{-4}$	$-5.7066077231623220 \times 10^{-4}$
1	1	3	1	$-8.6082192611828580 \times 10^{-4}$	$1.1266453489623106 \times 10^{-3}$
1	1	2	2	$1.7093314154786317 \times 10^{-3}$	$-1.3644052823847082 \times 10^{-3}$
1	1	1	3	$-1.1789409945146532 \times 10^{-3}$	$8.1021818828667317 \times 10^{-4}$
1	1	0	4	$3.8723701961918303 \times 10^{-4}$	$-2.8749285273268994 \times 10^{-4}$
0	6	0	0	$-6.9390702058934342 \times 10^{-5}$	$6.9301447295937329 \times 10^{-5}$
0	4	2	0	$-4.3799848629010854 \times 10^{-4}$	$4.0161436876524556 \times 10^{-4}$
0	4	1	1	$3.8723701961918303 \times 10^{-4}$	$-2.8749285273267357 \times 10^{-4}$
0	4	0	2	$-2.0817210617680304 \times 10^{-4}$	$2.0789708715975659 \times 10^{-4}$
0	2	4	0	$4.4154338663068642 \times 10^{-5}$	$3.1718226339199647 \times 10^{-4}$
0	2	3	1	$9.0270698998234857 \times 10^{-4}$	$-7.3916625373990645 \times 10^{-4}$
0	2	2	2	$-1.4654674698375437 \times 10^{-3}$	$1.2083393139899626 \times 10^{-3}$
0	2	1	3	$7.7447403923836607 \times 10^{-4}$	$-5.7498741718756510 \times 10^{-4}$
0	2	0	4	$-2.0817210617680304 \times 10^{-4}$	$2.0789708715975702 \times 10^{-4}$
0	0	6	0	$8.0737006151169034 \times 10^{-5}$	$1.3917499875750112 \times 10^{-4}$

$\xi _1$	$\xi _2$	$\eta _1$	$\eta _2$	First order	Second order
0	0	5	1	$-1.4728781329895123 \times 10^{-4}$	$-5.7065127472031587 \times 10^{-4}$
0	0	4	2	$-3.8625662439607426 \times 10^{-4}$	$8.8051997114559945 \times 10^{-4}$
0	0	3	3	$1.1715817984811095 \times 10^{-3}$	$-9.4757874129888428 \times 10^{-4}$
0	0	2	4	$-1.0274689835474350 \times 10^{-3}$	$8.0672276683552298 \times 10^{-4}$
0	0	1	5	$3.8723701961918303 \times 10^{-4}$	$-2.8749294965147088 \times 10^{-4}$
0	0	0	6	$-6.9390702058934342 \times 10^{-5}$	$6.9301447295938372 \times 10^{-5}$