1 INTRODUCTION

There are fundamental problems in theoretical physics that we have been trying to understand for centuries. One such problem is whether general relativity can be reconciled with quantum field theory. Already in the approximation dealing with classical gravity and quantum massless field one get problems. It was discovering by Hawking that the Schwarzschild black hole produces radiation like black body.

More specifically, we will discuss the problem of the black hole explosions which is a result of Hawking radiation of black holes. First we will describe what is the black hole explosion problem. The temperature of radiation is inverse proportional to the mass of the black hole. In the process of radiation the mass is decreasing and the temperature is increasing. That are the entropy of radiation and its energy density go to infinity. This is clearly nonphysical. This problem has been mentioned by Hawking in his first publication about black hole radiation [1].

Note also, that there are different options how we can try to resolve this problem. For instance one can argue that one should use the quantum gravity or stop investigation in the Planck scale or include in consideration a modified gravity etc.

In this talk we will consider a viewpoint that complete evaporation is possible. Such point of view is shared by Hawking, Page, Susskind, Maldacena and others. In such an approach we have to explain how to use the semi-classical effective theory of gravity to describe the complete black hole evaporation without blow up of the temperature. Note the recent works on the so-called island approach to the entanglement entropy do not get a solution to this problem [4].

Note that the Schwarzschild metric is regular in the limit \(M \to 0\) there we get the Minkowski space. In [2] it is pointed out that the origin of the singular behaviour of the black hole temperature maybe lie in application of the Kruskal coordinates which are singular for vanishing mass. It has been suggested that by the using another coordinates, the so-called thermal coordinates, it is possible to overcome the problem of getting infinite temperature at \(M \to 0\).

In the case when there are charges, rotation, non-zero cosmological constant, there is other option: one can impose constraints on characteristics of BHs. In particular, we can consider the charged RN BH and demonstrate that if one impose a certain relation between mass and charge then we can avoid the blow up of the temperature. Similar results take place for Kerr, dS-Sch, etc. [3].

2 THERMAL COORDINATES OR OBSERVE RUNNING AWAY

The Schwarzschild metric in the Schwarzschild coordinates is

$$\begin{gathered} d{{s}^{2}} = - \left( {1 - \frac{{2M}}{r}} \right)d{{t}^{2}} + {{\left( {1 - \frac{{2M}}{r}} \right)}^{{ - 1}}}d{{r}^{2}} + {{r}^{2}}d{{\Omega }^{2}}, \\ r > 2M > 0, \\ \end{gathered} $$
(1)

where \(d{{\Omega }^{2}} = d{{\theta }^{2}} + {{\sin }^{2}}\theta d{{\varphi }^{2}}\). It is obvious that the exterior Schwarzschild spacetime (\(r > {{r}_{h}} = 2M\)) admits the \(M \to 0\) limit, that defines the Minkowski spacetime.

The Kruskal coordinates are defined as usual as \(U = - {{e}^{{ - \frac{u}{{4M}}}}},\) \(V = {{e}^{{v/4M}}},\) where \(u = t - {{r}_{*}},v = t + {{r}_{*}},\) \({\kern 1pt} {{r}_{*}} = r + 2M\log \left( {\frac{r}{{2M}} - 1} \right)\), and the Schwarzschild metric becomes

$$\begin{gathered} d{{s}^{2}} = - \frac{{32{{M}^{3}}}}{r}{{e}^{{ - r/2M}}}{\kern 1pt} dUdV + {{r}^{2}}d{{\Omega }^{2}}, \\ {\kern 1pt} {\text{where}}{\kern 1pt} \,\,\,\,\left( {\frac{r}{{2M}} - 1} \right){{e}^{{\frac{r}{{2M}}}}} = - UV. \\ \end{gathered} $$
(2)

Note that the Kruskal coordinates and metric (2) are singular in the limit \(M \to 0\).

We introduce new coordinates as

$$\mathcal{U} = - {{e}^{{ - \frac{u}{{4M + b}}}}},\,\,\,\,\mathcal{V} = {{e}^{{\frac{v}{{4M + b}}}}}.$$
(3)

These coordinates are specified by parameter \(b\) and we call them thermal coordinates (or E-coordinates). The Schwarzschild metric in these coordinates is (\(r > 2M\))

$$\begin{gathered} d{{s}^{2}} = {{(4M + b)}^{2}}\left( {1 - \frac{{2M}}{r}} \right)\frac{{{\kern 1pt} d\mathcal{U}d\mathcal{V}}}{{\mathcal{U}\mathcal{V}}} \hfill \\ + \,\,{{r}^{2}}d{{\Omega }^{2}},{\kern 1pt} \,\,\,\,{\text{here}}\,\,{\text{r}}\,\,{\text{is}}\,\,{\text{defined}}\,\,{\text{b}}y{\kern 1pt} \hfill \\ {{e}^{{2{{r}_{*}}/(4M + b)}}} = - \mathcal{U}\mathcal{V}. \hfill \\ \end{gathered} $$
(4)

It is clear that in the limit \(b \to 0\) the metric in (4), rewritten as

$$\begin{gathered} d{{s}^{2}} = - 16{{(M + {b \mathord{\left/ {\vphantom {b 4}} \right. \kern-0em} 4})}^{2}}{{\left( {2M} \right)}^{{\frac{M}{{M + {b \mathord{\left/ {\vphantom {b 4}} \right. \kern-0em} 4}}}}}} \\ \times \,\,\frac{{{{{(r - 2M)}}^{{\frac{b}{{4M + b}}}}}}}{r}{{e}^{{ - \frac{r}{{2(M + {b \mathord{\left/ {\vphantom {b 4}} \right. \kern-0em} 4})}}}}}{\kern 1pt} d\mathcal{U}d\mathcal{V} + {{r}^{2}}d{{\Omega }^{2}}, \\ \end{gathered} $$
(5)

becomes the Schwarzschild–Kruskal metric (2). At \(M \to 0\) the metric (4) becomes

$$\begin{gathered} d{{s}^{2}} = - {{b}^{2}}{{e}^{{ - \frac{{2r}}{b}}}}d\mathcal{U}{\kern 1pt} d\mathcal{V} + {{r}^{2}}d{{\Omega }^{2}},{\kern 1pt} \\ {\text{here}}\,\,{\text{r}}\,\,{\text{is}}\,\,{\text{defined}}\,\,{\text{by}}{\kern 1pt} {\kern 1pt} - {\kern 1pt} \mathcal{U}\mathcal{V} = {{e}^{{\frac{{2r}}{b}}}}. \\ \end{gathered} $$
(6)

Let us stress that in the previous considerations, we do not change the mass of the Schwarzschild black hole. We keep the original Schwarzschild metric with mass \(M\) and just rewrite the metric in new coordinates \(\mathcal{U} = - {{e}^{{ - u/(4M + b)}}}\), \(\mathcal{V} = {{e}^{{v/(4M + b)}}}\). This is clear from the formula below

$$d{{s}^{2}} = - \left( {1 - \frac{{2M}}{r}} \right)d{{t}^{2}} + {{\left( {1 - \frac{{2M}}{r}} \right)}^{{ - 1}}}d{{r}^{2}} + {{r}^{2}}d{{\Omega }^{2}},$$
(7)
$$ = {{(4M + b)}^{2}}\left( {1 - \frac{{2M}}{r}} \right)\frac{{{\kern 1pt} d\mathcal{U}d\mathcal{V}}}{{\mathcal{U}\mathcal{V}}} + {{r}^{2}}d{{\Omega }^{2}}.$$
(8)

Therefore, the Schwarzschild metric in both forms, (7) and (8) describes the black hole with mass \(M\). The fact that the parameter \(b\) is not an addition to the black hole mass is also evident from the fact that for \(M = 0\) and \(b \ne 0\) we obtain not the Schwarzschild metric with mass \(b\), but the Minkowski metric. Indeed, in this case \(\mathcal{U} = - {{e}^{{(r - t)/b}}},\,\,\mathcal{V} = {{e}^{{(r + t)/b}}}\) and

$$\begin{gathered} {{\left. {d{{s}^{2}}} \right|}_{{{\kern 1pt} (8)\;{\text{for}}\;{\kern 1pt} M = 0}}} = {{b}^{2}}\frac{{{\kern 1pt} d\mathcal{U}d\mathcal{V}}}{{\mathcal{U}\mathcal{V}}} + {{r}^{2}}d{{\Omega }^{2}} \\ = - d{{t}^{2}} + d{{r}^{2}} + {{r}^{2}}d{{\Omega }^{2}}. \\ \end{gathered} $$

In our consideration the parameter \(b\) is an arbitrary positive parameter. Physical meaning of thermal coordinates is that they describe an observer who moves with non-constant acceleration depending on the parameter \(b\), see Section 3.3 in [2].

To show this let us introduce the coordinates \(\mathcal{T} = {{(\mathcal{V} + \mathcal{U})} \mathord{\left/ {\vphantom {{(\mathcal{V} + \mathcal{U})} 2}} \right. \kern-0em} 2}\) and \(\mathcal{X} = {{(\mathcal{V} - \mathcal{U})} \mathord{\left/ {\vphantom {{(\mathcal{V} - \mathcal{U})} 2}} \right. \kern-0em} 2}\) and rewrite the metric as

$$\begin{gathered} ds_{2}^{2} = f(r){{(4M + b)}^{2}}\frac{{ - d{{\mathcal{T}}^{2}} + d{{\mathcal{X}}^{2}}}}{{ - {{\mathcal{T}}^{2}} + {{\mathcal{X}}^{2}}}}, \\ {\text{where}}{\kern 1pt} \,\,\,\,{{\mathcal{X}}^{2}} - {{\mathcal{T}}^{2}} > 0. \\ \end{gathered} $$
(9)

Now let us fix \(\mathcal{X} = {{\mathcal{X}}_{0}}\). This trajectory can be parametrized by \(\mathcal{T}\) and in the Schwarzschild coordinates we have

$$\begin{gathered} t = \frac{{4M + b}}{2}\log \left( {\frac{{\mathcal{T} + {{\mathcal{X}}_{0}}}}{{{{\mathcal{X}}_{0}} - \mathcal{T}}}} \right), \\ {{r}_{*}} = \frac{{4M + b}}{2}\log (\mathcal{X}_{0}^{2} - {{\mathcal{T}}^{2}}). \\ \end{gathered} $$
(10)

For the acceleration along this trajectory we have

$$\begin{gathered} {{w}^{2}} = \frac{{\mathcal{X}_{0}^{2}{{{\left( {\frac{1}{{4M + b}} - \frac{M}{{{{r}^{2}}}}} \right)}}^{2}}}}{{1 - \frac{{2M}}{r}}} \\ \times \,\,{{e}^{{ - 2r/(4M + b)}}}{{\left( {\frac{r}{{2M}} - 1} \right)}^{{ - 4M/(4M + b)}}}. \\ \end{gathered} $$
(11)

For \(M = 0\) we get \({{w}^{2}} = \frac{{\mathcal{X}_{0}^{2}}}{{{{b}^{2}}}}{{e}^{{ - 2r/b}}}\), that in term of Schwarzschild time \(t\) is

$${{w}^{2}} = \frac{1}{{{{b}^{2}}}}\mathop {\cosh }\nolimits^2 \frac{t}{b}.$$

This answer is similar to the Rindler acceleration discussed by Unruh (see more detailed discussion in Section 3.4 in [2]).

To find the temperature of Hawking radiation of Schwarzschild black holes in thermal coordinates let us consider the wave equations for the scalar field \(\phi (u,v) = \Phi (\mathcal{U},\mathcal{V})\) in these coordinate systems

$$\begin{gathered} {{\partial }_{v}}{{\partial }_{u}}\phi = 0,{\kern 1pt} {\kern 1pt} u,v \in \mathbb{R}, \\ {{\partial }_{\mathcal{V}}}{{\partial }_{\mathcal{U}}}{\kern 1pt} \Phi = 0,{\kern 1pt} {\kern 1pt} \,\,\,\,\mathcal{U} < 0,{\kern 1pt} \,\,\,\mathcal{V} > 0. \\ \end{gathered} $$
(12)

Solutions to these equations can be represented as combinations of the left and write modes, \(\phi (u,v) = {{\phi }_{{\text{R}}}}(u) + {{\phi }_{{\text{L}}}}(v)\). For the real right mode (for the left mode all consideration is similar and will be omitted) one has

$$\begin{gathered} {{\phi }_{{\text{R}}}}(u) = \int\limits_0^\infty {d\omega } {\kern 1pt} ({{f}_{\omega }}{{b}_{\omega }} + f_{\omega }^{*}b_{\omega }^{ + }), \\ {{f}_{\omega }}(u) = \frac{1}{{\sqrt {4\pi \omega } }}{{e}^{{ - i\omega u}}}, \\ \end{gathered} $$
(13)

where \([{{b}_{\omega }},b_{{\omega {\kern 1pt} '}}^{ + }] = \delta (\omega - \omega {\kern 1pt} ')\). One also has representation for \(\Phi \)-field \(\Phi (\mathcal{U},\mathcal{V}) = {{\Phi }_{{\text{R}}}}(\mathcal{U}) + {{\Phi }_{{\text{L}}}}(\mathcal{V})\) where for right mode(similar for left ones)

$$\begin{gathered} {{\Phi }_{{\text{R}}}}(\mathcal{U}) = \int\limits_0^\infty {d\mu ({{\mathfrak{b}}_{\mu }}{{\mathfrak{f}}_{\mu }}(\mathcal{U})} + \mathfrak{b}_{\mu }^{ + }\mathfrak{f}_{\mu }^{*}(\mathcal{U})), \\ {{\mathfrak{f}}_{\mu }}(\mathcal{U}) = \frac{1}{{\sqrt {4\pi \mu } }}{{e}^{{ - i\mu \mathcal{U}}}}, \\ \end{gathered} $$
(14)

where \([{{\mathfrak{b}}_{\mu }},{{\mathfrak{b}}_{{\mu {\kern 1pt} '}}}] = \delta (\mu - \mu {\kern 1pt} ')\). Right (and left) modes in different coordinate system are related \({{\phi }_{{\text{R}}}}(u) = {{\Phi }_{{\text{R}}}}(\mathcal{U}(u))\) and therefore,

$$\begin{gathered} \int\limits_0^\infty {d\omega } ({{f}_{\omega }}{{b}_{\omega }} + f_{\omega }^{*}b_{\omega }^{ + }) = \int\limits_0^\infty {d\mu } ({{\mathfrak{f}}_{\mu }}{{\mathfrak{b}}_{\mu }} + \mathfrak{f}_{\mu }^{*}\mathfrak{b}_{\mu }^{ + }), \\ u \in \mathbb{R}. \\ \end{gathered} $$
(15)

Multiplying (15) on \({{f}_{{\omega {\kern 1pt} '}}}(u)\) and integrate the first equation over \(\mathbb{R}\) one getsFootnote 1

$$\begin{gathered} {{b}_{\omega }} = \int d\mu (\beta _{{\omega {\kern 1pt} \mu }}^{*}\mathfrak{b}_{\mu }^{ + } + \alpha _{{\omega {\kern 1pt} \mu }}^{*}{{\mathfrak{b}}_{\mu }}), \\ b_{\omega }^{ + } = \int d\mu ({{\beta }_{{\omega {\kern 1pt} \mu }}}{{\mathfrak{b}}_{\mu }} + {{\alpha }_{{\omega {\kern 1pt} \mu }}}\mathfrak{b}_{\mu }^{ + }), \\ \end{gathered} $$
(16)

where

$$\begin{gathered} {{\beta }_{{\omega {\kern 1pt} \mu }}} = \int\limits_\mathbb{R} {\frac{{du}}{{2\pi }}} \sqrt {\frac{\omega }{\mu }} {{e}^{{ - i\omega u}}}{{e}^{{ - i\mu \mathcal{U}}}}, \\ {{\alpha }_{{\omega {\kern 1pt} \mu }}} = \int\limits_\mathbb{R} {\frac{{du}}{{2\pi }}} \sqrt {\frac{\omega }{\mu }} {{e}^{{ - i\omega u}}}{{e}^{{i\mu \mathcal{U}}}}. \\ \end{gathered} $$
(17)

The thermal-vacuum \(\left| {{{0}_{E}}} \right\rangle \) does not contain \(\mathfrak{b}\) particles, i.e. \({{\mathfrak{b}}_{\omega }}\left| {{{0}_{E}}} \right\rangle = 0\), but it contains the Minkowski \(b\) particles:

$${\kern 1pt} \langle {{0}_{E}}\left| {{{N}_{\omega }}(b)} \right|{{0}_{E}}\rangle \equiv \langle {{0}_{E}}\left| {b_{\omega }^{ + }{{b}_{\omega }}} \right|{{0}_{E}}\rangle = \int\limits_0^\infty {d\mu {{{\left| {{{\beta }_{{\omega \mu }}}} \right|}}^{2}}} .$$
(18)

The Bogoliubov coefficient \({{\beta }_{{\omega \nu }}}\) are given

$$\begin{gathered} {{\beta }_{{\omega {\kern 1pt} \mu }}} = \frac{B}{{2\pi }}\sqrt {\frac{\omega }{\mu }} {\kern 1pt} {{e}^{{ - \frac{{\pi B\omega }}{2}}}}{\kern 1pt} {{(\mu )}^{{ - iB\omega }}}\Gamma (iB\omega ), \\ B = 4M + b. \\ \end{gathered} $$
(19)

Using the formula \({{\left| {\Gamma \left( {ix} \right)} \right|}^{2}} = {\pi \mathord{\left/ {\vphantom {\pi {(x\sinh (\pi x))}}} \right. \kern-0em} {(x\sinh (\pi x))}}\) we get he Planck distribution

$${{\left| {{{\beta }_{{\omega {\kern 1pt} \mu }}}} \right|}^{2}} = \frac{B}{{2\pi \mu }}\frac{1}{{{{e}^{{2\pi B\omega }}} - 1}},$$
(20)

with the temperature [2]

$$T = \frac{1}{{2\pi B}} = \frac{1}{{2\pi (4M + b)}}.$$
(21)

This temperature at \(M = 0\) is \(T = {1 \mathord{\left/ {\vphantom {1 {(2\pi b)}}} \right. \kern-0em} {(2\pi b)}}\) and its corresponds to a non-inertial observer in Minkowski space.

Let us make few remark about information paradox. Note that in semi classical approximation it is impossible to give a sharp formulation of the information loss problem, since it would required an investigation of black hole formation from a pure state and also a description of an evaporation process in term of quantum gravity.

We can have in mind a vague formulation of the problem that we can often see in the current literature. In a such style we can say that in the case of using the E(thermal)-coordinates the black hole life time is infinite. Therefore, formally speaking, the information loss paradox disappears. Sometimes the information paradox is formulated as follows. A collapsing black hole, described by a wave function, completely evaporates and leaves only radiation, described by a dense matrix. So one gets a transformation of pure state to a mixed state, that contradicts to the unitary evolution in quantum mechanics. Thus, a transformation of a pure state into a mixed one is occurred, which contradicts the unitary evolution in quantum mechanics, and means the loss of information. This formulation of the information lost paradox has a meaning only if the black hole time life is finite. In the case of using the E-coordinates the black hole life time is infinite. Therefore, formally speaking, the information loss paradox disappears.

It would be interesting to estimate the entropy balance during the evaporation in the thermal coordinates. It would also be interesting to study the fate of primordial black holes in the thermal coordinates and to use the thermal coordinates for investigation of massive fields of various spins in different dimensions in gravitational backgrounds.

3 COMPLETE EVAPORATION NEAR EXTREME REGIME

We consider a model of complete evaporation of a Reissner–Nordstrom (RN) black hole with the following metric

$$\begin{gathered} d{{s}^{2}} = - f(r)d{{t}^{2}} + f{{(r)}^{{ - 1}}}d{{r}^{2}} + {{r}^{2}}d{{\Omega }^{2}}, \\ f(r) = 1 - \frac{{2M}}{r} + \frac{{{{Q}^{2}}}}{{{{r}^{2}}}}, \\ \end{gathered} $$
(22)

here \(M\) and \(Q\) are mass and charge of the black hole (two independent variables). It is assumed that \({{M}^{2}} \geqslant {{Q}^{2}}\). The blackening function in (22) can be presented as

$$\begin{gathered} f = (r - {{r}_{ + }}){{(r - {{r}_{ - }})} \mathord{\left/ {\vphantom {{(r - {{r}_{ - }})} {{{r}^{2}}}}} \right. \kern-0em} {{{r}^{2}}}}, \\ {\text{where}}\,\,\,{{r}_{ \pm }} = M \pm \sqrt {{{M}^{2}} - {{Q}^{2}}} . \\ \end{gathered} $$
(23)

The temperature of the Reissner–Nordstrom black hole is

$$T = \frac{1}{{2\pi }}\frac{{\sqrt {{{M}^{2}} - {{Q}^{2}}} }}{{{{{(M + \sqrt {{{M}^{2}} - {{Q}^{2}}} )}}^{2}}}}.$$
(24)

Let us take \(Q\) to be a function on \(M\) of the form

$${{Q}^{2}} = {{M}^{2}} - \lambda {{(M)}^{2}},$$
(25)

where \(0 < \lambda (M) < M\). The Hawking temperature \(T\) under this constraint becomes equal to

$$T = \frac{{\lambda (M)}}{{2\pi {{{(M + \lambda (M))}}^{2}}}}.$$
(26)

Depending on the behavior of the function \(\lambda (M)\) we have:

• if \(\lambda (M)\) satisfies for small \(M\) the bounds

$$0 < \lambda (M) \leqslant C{{M}^{\gamma }},\,\,\,\,C > 0,\,\,\,\,\gamma > 2$$
(27)

then \(T \to 0\) as \(M \to 0\) and one gets the complete evaporation of black hole;

• if the function \(\lambda (M)\) satisfies the bounds

$$\begin{gathered} 0 < \lambda (M) \leqslant C\frac{{{{M}^{\gamma }}}}{{A + {{M}^{{\gamma + 1}}}}}, \\ C > 0,\,\,\,\,A > 0,\,\,\,\,{\kern 1pt} \gamma > 2 \\ \end{gathered} $$
(28)

then the temperature \(T \to 0\) also for \(M \to \infty \);

• if the function \(\lambda (M)\) is

$$\lambda (M) = \frac{{{{M}^{\gamma }}}}{{A + {{M}^{{\gamma - 1}}}}},\,\,\,\,A > 0,\,\,\,\gamma > 3,$$
(29)

then the temperature \(T \to 0\) and \(Q \to 0\) also for \(M \to \infty \). Note that the asymptotic of \(T\) at \(M \to \infty \) coincides with the Schwarzschild case.The entropy and the free energy under constraint (25) are equal

$$\begin{gathered} {{S}_{{{\text{RN}}}}} = \pi r_{ + }^{2} = \pi {{(M + \lambda (M))}^{2}}, \\ {{G}_{{{\text{RN}}}}} = M - TS = M - \frac{1}{2}\lambda (M). \\ \end{gathered} $$
(30)

Note that entropy \({{S}_{{{\text{RN}}}}}\) and free energy \({{G}_{{{\text{RN}}}}}\) go to \(0\) as \(M \to 0\) for \(\lambda \) satisfying (27).

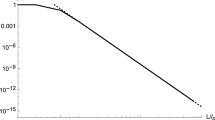
Equation (24) defines the surface \(\Sigma \) of the state equation for Reissner–Nordstrom black hole. This surface is shown in Fig. 1. The 3D curves in Fig. 1 show the dependence of temperature on mass along the curves

$$\lambda (M) = {{\left( {\frac{M}{\mu }} \right)}^{\gamma }}.$$
(31)

with different \(\gamma = 1,1.4,2,2.5,3\). We see that on some curves the temperature tends to infinity as \(M \to 0\) (for these curves \(\gamma < 2\)), while on curves with \(\gamma > 2\) the temperature tends to zero as \(M \to 0\).

Fig. 1.
figure 1

(a) The 3D plot shows the dependencies of the temperature on the mass \(M\) and the charge \(Q\). 3D curves \({{\sigma }_{\gamma }}\) show the dependence of the temperature on the mass along the constrains (25) with \(\lambda (M) = {{M}^{\gamma }}\), \(\gamma = 1,1.4,2,2.5,3\). (b) The graph shows charge \(Q\) (magenta) and temperature \(T\) (red) versus \(M\) for different values of the scaling parameter \(\gamma \), \(\gamma = 1,2,2.5\). (c) The graph shows dependencies of free energy \(G\) (green), black hole entropy \(S\) (blue) and radiation entropy (dark cyan) on \(M\) for scale parameter \(\gamma = 1.2,2.5\). The black lines show the boundaries of the allowed regions for \(M\).

Full size image

Mass dependence of charge \(Q\), temperature \(T\), entropy and free energy at (31) with different \(\gamma \) parameters and the same \(\mu = 1\) parameter are shown in Figs. 1b and 1c. We see that for all \(\gamma > 1\) there is a restriction on \(M\), \(M \leqslant 1\). The temperature and entropy of the radiation tend to zero at \(M \to 0\) for \(\gamma > 2\), to a nonzero constant for \(\gamma = 2\), and to infinity for \(\gamma < 2\). In this case, the temperature and radiation entropy \({{S}_{R}}\) at \(\gamma > 2\), starting from the initial value at \(M = 1\), increase to a certain maximum value, then decrease to zero, i.e. the mass dependencies \(T\) and \({{S}_{R}}\) have deformed bell shapes (the thickest red and dark cyan lines in Figs. 1b and 1c, respectively). In the case of a slow dependence of mass on time during black hole evaporation, the dependence of radiation entropy on mass, represented in Fig. 1b by the dark cyan line, leads to the Page form of the time evolution of radiation entropy. The entropy of a black hole and the free energy tend to zero at \(M \to 0\) for all values of \(\gamma \). We also see, Fig. 1b, that the shape of Q versus \(M\) is a deformed bell (except in the case of \(\gamma = 1\) and \(Q = 0\), which corresponds to the Schwarzschild case). Note that in Fig. 1c one can see that the free energy increases as the black hole mass decreases. This corresponds to the region \(M\), where the charge increases with decreasing mass \(M\).

The loss of the mass and charge during evaporation of RN black hole is a subject of numerous consideration [5, 6] and refs therein. In the case of fixed relations (25), we consider the following system of equations

$$\begin{gathered} \frac{{dM}}{{dt}} = - A\sigma {{T}^{4}} + \frac{Q}{{{{r}_{ + }}}}\frac{{dQ}}{{dt}}, \\ \frac{{dQ}}{{dt}} = \frac{{M - \lambda \lambda {\kern 1pt} '}}{{\sqrt {{{M}^{2}} - {{\lambda }^{2}}} }}\frac{{dM}}{{dt}}, \\ \end{gathered} $$
(32)

where \(A\) is a positive constant and the cross-section \(\sigma \) is proportional to \({{M}^{2}}\) for small \(M\). The first equation in the system of Eqs. (32) coincides with the equation considered in [6], and the second is obtained by simply differentiating the relation (25). From (32) we get

$$\frac{{dM}}{{dt}} = - \frac{{A\sigma {{T}^{4}}(M + \lambda )}}{{\lambda (1 + \lambda {\kern 1pt} ')}}.$$
(33)

For \(\lambda (M) = C{{M}^{\gamma }}\) and small \(M\) one gets

$$\frac{{dM}}{{dt}} = - {{C}_{1}}{{M}^{{3\gamma - 5}}}.$$
(34)

This equation for \(\gamma > 2\) and \(M(0) = {{M}_{0}}\) has a solution

$$M(t) = \frac{{{{M}_{0}}}}{{{{{\left( {1 + B{\kern 1pt} t} \right)}}^{{\frac{1}{{3(\gamma - 2)}}}}}}},\,\,\,\,B = \frac{{3(\gamma - 2){{C}_{1}}}}{{M_{0}^{{6 - 3\gamma }}}},\,\,\gamma > 2,$$
(35)

where \({{M}_{0}}\) and \(B\) are positive constants. For \(\gamma = 2\) we have \(M(t) = {{M}_{0}}{{e}^{{ - {{C}_{1}}t}}}\) and one gets an infinite large time of the complete evaporation of charged black hole under constraint (25).