1 Introduction

The interest in primordial black holes (PBH) started over fifty years ago [1, 2], and the conjecture was soon put forward that they could account for a (possibly significant) fraction of the dark matter [3]. The basic idea is that, in the early radiation dominated Universe, a sufficiently overdense region should collapse into a black hole [4]. Many mechanisms to generate primordial fluctuations of sufficient density have then been proposed and their confrontation with astrophysical and cosmological data has generated a huge literature (for a review, see, e.g. Ref. [5]).

In this work, we are interested in the fundamental issue of the formation of PBH’s. In fact, the importance of the spatial profile of perturbations in classical general relativity has already been pointed out in Refs. [6,7,8]. Our aim here is to show that the quantum nature of primordial fluctuations and the overall process of black hole formation could also be very relevant. For this purpose, we shall consider a simplified scenario in which we can carry out a complete analysis, albeit without the presumption to obtain predictions directly comparable with the observations. For estimating the initial number of PBH’s, we shall then employ the Horizon Quantum Mechanics (HQM) [9,10,11,12,13], which was precisely proposed with the purpose of describing the gravitational radius of spherically symmetric compact sources and determining the existence of a horizon in a quantum mechanical fashion.

2 Quantum primordial black holes

We shall here model a primordial fluctuation as a quantum state of excited gravitons with a thermal distribution above the de Sitter ground state [14], and then employ the (global) HQM [9,10,11,12,13] in order to compute the probability that this fluctuation is a black hole.

The corpuscular picture of gravity [14] was first introduced for describing black holes, but it also applies to cosmology and inflation in particular [15,16,17]. In order to have the de Sitter space-time in general relativity, one must assume the existence of a cosmological constant \(\Lambda \), or vacuum energy density \(\rho _L\), so that the Friedman equation reads Footnote 1

$$\begin{aligned} H^2 \equiv \left( \frac{\dot{a}}{a}\right) ^2 = G_\mathrm{N}\, \rho _L. \end{aligned}$$
(1)

Upon integrating on the volume inside the Hubble radius

$$\begin{aligned} L = H^{-1} = \sqrt{{3}/{\Lambda }}, \end{aligned}$$
(2)

we obtain

$$\begin{aligned} L \simeq G_\mathrm{N}\,L^3\,\rho _L \simeq G_\mathrm{N}\,E_L. \end{aligned}$$
(3)

The length L therefore satisfies a relation exactly like the Schwarzschild radius for a black hole of ADM mass \(E_L\), which supports the conjecture that the de Sitter space-time could likewise be described as a condensate [16, 17]. One can roughly describe the corpuscular model by assuming that the graviton self-interaction gives rise to a condensate of N (soft virtual) gravitons of typical Compton length of the order of L, so that \( E_L \simeq N\,{\ell _\mathrm{p}\,m_\mathrm{p}}/{L} \) and the usual consistency conditions

$$\begin{aligned} N\simeq \frac{E_L^2}{m_\mathrm{p}^2} \end{aligned}$$
(4)

turns out to be a natural consequence [14]. Equivalently, one finds

$$\begin{aligned} L \simeq \frac{\sqrt{N}}{\ell _\mathrm{p}}, \end{aligned}$$
(5)

which shows that for a macroscopic black hole, or universe, one needs \(N\gg 1\). If one wishes to describe the present dark energy dominated Universe [18, 19], one should take \(L\simeq H_0^{-1}\), where \(H_0\sim 70\,(\)km / s) / Mpc is the present value of the Hubble constant, and obtains \(L\sim 10^{27}\,\)m and \(N\sim 10^{120}\). For studying primordial black holes, one should consider values of L corresponding to the size of the inflating patch within which the black hole is forming. For instance, assuming the initial size is of the order of the Planck length and inflation lasts 60 e-foldings, one has \(10^{-35}\,\)m \(\lesssim L\lesssim 10^{-9}\,\)m, corresponding to \(1\lesssim N\lesssim 10^{26}\).

2.1 Schwarzschild-de Sitter space-time

For our analysis of primordial perturbations, we shall employ the spherically symmetric and static Schwarzschild-de Sitter metric

$$\begin{aligned} \hbox {d}s^2 = -f \, \hbox {d}t^2 +f^{-1}\,\hbox {d}r^2 +r^2 \,\hbox {d}\Omega ^2, \end{aligned}$$
(6)

with

$$\begin{aligned} f=1 - \frac{2 \, G_\mathrm{N}\, M}{r} - \frac{r^2}{L^2}. \end{aligned}$$
(7)

This metric represents the exterior of a black hole of mass M as seen by a static observer located at constant radial position r, provided \(R_\mathrm{H}<r<R_\mathrm{L}\), where \(R_\mathrm{H}\) is the black hole horizon and \(R_\mathrm{L}\) the cosmological horizon. For our purpose, we can associate L with the background homogenous space-time undergoing inflation, and the mass M with the energy of the local fluctuation.

As usual, horizons are given by real solutions of the equation \(f(r)=0\), that is

$$\begin{aligned} R_\mathrm{H/L} = \frac{2\,L}{\sqrt{3}}\, \cos \left[ \frac{\pi }{3} \pm \frac{1}{3}\,\arccos \left( \frac{3\,\sqrt{3}\, G_\mathrm{N}\, M}{L}\right) \right] , \end{aligned}$$
(8)

and the nomenclature is then justified by the fact that \(R_\mathrm{H} < R_\mathrm{L}\) for \(L\ge 3\,\sqrt{3}\,G_\mathrm{N}\,M\ge 0\), with the proper metric signature \((-+++)\) in the region \(R_\mathrm{H}< r< R_\mathrm{L}\), as anticipated above. Moreover, for \(L\gg G_\mathrm{N}\,M\), the black hole horizon approaches the usual Schwarzschild radius, that is

$$\begin{aligned} R_\mathrm{H} \simeq 2 \,G_\mathrm{N}\, M \left[ 1 + \left( \frac{R_M}{L}\right) ^2 \right] . \end{aligned}$$
(9)

In the same limit, the cosmological horizon approaches the de Sitter value,

$$\begin{aligned} R_\mathrm{L} \simeq L \left( 1 - \frac{R_\mathrm{M}}{2\,L}\right) . \end{aligned}$$
(10)

Finally, we note that the extremal configuration is

$$\begin{aligned} R_\mathrm{H} =R_\mathrm{L} = 3\,G_\mathrm{N}\,M = {L}/{\sqrt{3}}, \end{aligned}$$
(11)

in which case the coordinate r is always time-like and there are no values of r corresponding to a static observer. Nonetheless, since

$$\begin{aligned} 2\,G_\mathrm{N}\,M\le R_\mathrm{H}(M,L)\le 3\,G_\mathrm{N}\,M, \end{aligned}$$
(12)

in the following we shall consider the case \(R_\mathrm{H}\simeq 3\,G_\mathrm{N}\,M\) for simplicity and for maximising the probability of black hole formation. In fact, one in general finds that the probability for a system to be a black hole is larger when a given value of the mass M corresponds to a larger gravitational radius \(R_\mathrm{H}\). However, since the range (12) is rather limited, from a comparison with cases studied previously [9,10,11,12], we do not expect that this probability is suppressed by more than an exponential factor of the order of \(e^{-3/2}\sim 0.2\).

2.2 Horizon quantum mechanics

According to this approach [9,10,11,12,13], we assume the existence of two observables, the quantum Hamiltonian corresponding to the energy M of the fluctuation which might result in a black hole,

$$\begin{aligned} \hat{H} = \sum _\alpha E_\alpha \mid E_\alpha \,\rangle \langle \, E_\alpha \mid , \end{aligned}$$
(13)

and the gravitational radius corresponding to the black hole horizon, with eigenstates

$$\begin{aligned} \hat{r}_\mathrm{H}\,\mid {r_\mathrm{H}}_\beta \,\rangle = {r_\mathrm{H}}_\beta \,\mid {r_\mathrm{H}}_\beta \,\rangle . \end{aligned}$$
(14)

The cosmological length L, being associated with the background space-time, is instead regarded as a classical parameter here, like the electric charge of the Reissner-Nordström space-time in Refs. [20, 21].Footnote 2

General quantum states for the fluctuation can be described by linear combinations of the form

$$\begin{aligned} \mid \Psi \,\rangle = \sum _{\alpha ,\beta } C(E_\alpha ,{r_\mathrm{H}}_\beta ), \mid E_\alpha \,\rangle \mid {r_\mathrm{H}}_\beta \,\rangle , \end{aligned}$$
(15)

but only those for which the relation (8) between the Hamiltonian and the gravitational radii hold are viewed as physical. In particular, we invert Eq. (9) in order to write

$$\begin{aligned} M(R_\mathrm{H};L) = \frac{R_\mathrm{H}}{2\,G_\mathrm{N}} \left( 1-\frac{R_\mathrm{H}^2}{L^2}\right) , \end{aligned}$$
(16)

and then impose this condition as the weak Gupta–Bleuler constraint

$$\begin{aligned} 0= & {} \left[ \hat{H} - M(\hat{r}_\mathrm{H};L) \right] \mid \Psi \,\rangle \nonumber \\= & {} \sum _{\alpha ,\beta } \left[ E_\alpha - M({r_\mathrm{H}}_\beta ;L) \right] C(E_\alpha ,{r_\mathrm{H}}_\beta )\, \mid E_\alpha \,\rangle \mid {r_\mathrm{H}}_\beta \,\rangle . \end{aligned}$$
(17)

The solution is given by

$$\begin{aligned} C(E_\alpha ,{r_\mathrm{H}}_\beta ) = C\left( E_\alpha ,R_\mathrm{H}(E_\alpha ;L)\right) \delta _{\alpha \beta }, \end{aligned}$$
(18)

which means that Hamiltonian eigenmodes and gravitational radius eigenmodes can only appear suitably paired in a physical state.

By tracing out the gravitational radius, we recover the spectral decomposition of the system,

$$\begin{aligned} \mid {\psi }_\mathrm{S}\,\rangle= & {} \sum _\alpha C\left( E_\alpha ,R_\mathrm{H}(E_\alpha ,L)\right) \mid E_\alpha \,\rangle \nonumber \\\equiv & {} \sum _\alpha C_\mathrm{S}(E_\alpha ,L)\,\mid E_\alpha \,\rangle , \end{aligned}$$
(19)

in which we used the (generalised) orthonormality of the gravitational radius eigenmodes [13]. Conversely, by integrating out the energy eigenstates, we obtain the Horizon Wave-Function (HWF) [9,10,11,12]

$$\begin{aligned} {\psi }_\mathrm{H}({r_\mathrm{H}}_\alpha ) = C_\mathrm{S}(M({r_\mathrm{H}}_\alpha ,L)). \end{aligned}$$
(20)

If the index \(\alpha \) is continuous (again, see Ref. [13] for some important remarks), the probability density that we detect a gravitational radius of size \(r_\mathrm{H}\) associated with the quantum state \({\psi }_\mathrm{S}\) is given by

$$\begin{aligned} \mathcal {P}_\mathrm{H}(r_\mathrm{H}) = 4\,\pi \,r_\mathrm{H}^2\,|{\psi }_\mathrm{H}(r_\mathrm{H})|^2, \end{aligned}$$
(21)

and we can define the conditional probability density that the source lies inside its own gravitational radius \(r_\mathrm{H}\) as

$$\begin{aligned} \mathcal {P}_<(r<r_\mathrm{H}) = P_\mathrm{S}(r<r_\mathrm{H})\,\mathcal {P}_\mathrm{H}(r_\mathrm{H}), \end{aligned}$$
(22)

where

$$\begin{aligned} P_\mathrm{S}(r<r_\mathrm{H})= 4\,\pi \int _0^{r_\mathrm{H}} |{\psi }_\mathrm{S}(r)|^2\,r^2\,\hbox {d}r. \end{aligned}$$
(23)

Finally, the probability that the system in the state \({\psi }_\mathrm{S}\) is a black hole will be obtained by integrating (22) over all possible values of \(r_\mathrm{H}\), namely

$$\begin{aligned} P_\mathrm{BH} = \int _0^\infty \mathcal {P}_<(r<r_\mathrm{H})\,\hbox {d}r_\mathrm{H}. \end{aligned}$$
(24)

2.3 Thermal density fluctuations in de Sitter

As we mentioned above, we assume the spectral decomposition of a primordial perturbation is given by a Planckian distribution at the temperature \(T=k\,T_\mathrm{dS}\), that is

$$\begin{aligned} C_\mathrm{S}^2(E) \simeq \frac{\mathcal {N}^2}{T^{3}}\, \frac{(E-E_L)^2}{{\exp \left\{ (E-E_L)/T\right\} -1}}, \end{aligned}$$
(25)

where \(E_L\) is the background de Sitter energy in Eq. (3) and the de Sitter temperature \(T_\mathrm{dS}\simeq m_\mathrm{p}\,\ell _\mathrm{p}/L\). The mean energy density above the ground state associated to such a fluctuation is thus given by

$$\begin{aligned} \frac{\Delta E}{E_L}\simeq & {} \int _{E_L}^\infty \frac{(E-E_L)}{E_L}\,C_\mathrm{S}^2(E)\,\hbox {d}E \nonumber \\\simeq & {} \frac{\pi ^4\, T}{30\,\zeta (3)\,E_L} \simeq 2.7\,\frac{k}{N} \ , \end{aligned}$$
(26)

which implies that a fluctuation can carry a significant fraction of the energy within the length \(L\sim \sqrt{N}\) only if the temperature is \(k\sim N\) times the de Sitter temperature \(T_\mathrm{dS}\sim 1/\sqrt{N}\). Let us also note that the above result \(\Delta E/E_L\sim 1/N\) for \(k=1\) is analogous to the one for thermal corpuscular black holes [22,23,24].

2.4 Black hole formation

From the spectral decomposition of the whole fluctuation (25), on assuming the extremal relation (11), that is

$$\begin{aligned} r_\mathrm{H}\simeq 3\,\ell _\mathrm{p}\,\frac{E-E_L}{m_\mathrm{p}}, \end{aligned}$$
(27)

one immediately finds the HWF

$$\begin{aligned} {\psi }_\mathrm{H}(r_\mathrm{H}) \simeq \frac{\mathcal {N}_\mathrm{H}\,(L/k)^{5/2}\,r_\mathrm{H}/\ell _\mathrm{p}^{5}}{\sqrt{\exp \{L\,r_\mathrm{H}/3\,k\,\ell _\mathrm{p}^2\}-1}} \ , \end{aligned}$$
(28)

with \(\mathcal {N}_\mathrm{H}= 1/108\,\sqrt{2\,\pi \,\zeta (5))}\simeq 3.6\cdot 10^{-3}\) and where we used \(T=k\,T_\mathrm{dS}=k\,m_\mathrm{p}\,\ell _\mathrm{p}/L\).

In order to proceed, we describe the fluctuation in position space by means of a Gaussian wave-function of width \(\lambda \sim L\),

$$\begin{aligned} \psi (r) = \frac{e^{-\frac{r^2}{2 \, \lambda ^2}}}{\left( \lambda \, \sqrt{\pi }\right) ^{3/2}}, \end{aligned}$$
(29)

from which we then obtain

$$\begin{aligned} \mathcal {P}_<(r<r_\mathrm{H})\simeq & {} \frac{(L/k)^5\,r_\mathrm{H}^4}{5832\,\zeta (5)\,\ell _\mathrm{p}^{10} \left( e^{\frac{L\,r_\mathrm{H}}{3\,k\,\ell _\mathrm{p}^2}}-1\right) ^2}\nonumber \\&\times \left[ \mathrm{Erf}\left( \frac{r_\mathrm{H}}{\lambda }\right) -\frac{2\,e^{-\frac{r_\mathrm{H}^2}{\lambda ^2}}\,r_\mathrm{H}}{\sqrt{\pi }\,\lambda } \right] . \end{aligned}$$
(30)

Upon integrating this expression over \(r_\mathrm{H}\) (numerically) for fixed values of \(\lambda \), L and \(k=T/T_\mathrm{dS}\) one obtains the probability (24) that the fluctuation is a black hole.

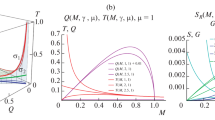
The result as a function of L for \(k=1\) and \(\lambda =L\) is plotted in Fig. 1, and, for \(L\gtrsim 10\,\ell _\mathrm{p}\), it is extremely well approximated by

$$\begin{aligned} P_\mathrm{BH}(L) \simeq K_{\lambda =L,k=1}\left( \frac{\ell _\mathrm{p}}{L}\right) ^6, \end{aligned}$$
(31)

with \(K_{L,1}\simeq 4\cdot 10^3\). For values of \(\lambda <L\), the probability \(P_\mathrm{BH}\) remains of the form in Eq. (31), with \(K_{\lambda =L/2,k=1}\simeq 4\cdot 10^4\) and \(K_{\lambda =L/4,k=1}\simeq 3\cdot 10^5\). For larger values of the temperature (that is, for \(k>1\)), we notice that the function in front of the square brackets in Eq. (30) depends on the effective length L / k. We therefore expect that doubling the temperature is (roughly) equivalent to halving the Hubble scale L. In general, we find that for \(L\gg \ell _\mathrm{p}\), the coefficient in Eq. (31) is very well approximated by

$$\begin{aligned} K_{\lambda ,k} \simeq 4\cdot 10^3 \left( \frac{k\,L}{\lambda }\right) ^3 \ , \end{aligned}$$
(32)

as is shown in Fig. 2. Upon including this result, one finally obtains

$$\begin{aligned} P_\mathrm{BH}(L) \simeq 4\cdot 10^3 \left( \frac{T}{T_\mathrm{dS}}\right) ^3 \left( \frac{\ell _\mathrm{p}}{\lambda }\right) ^3 \left( \frac{\ell _\mathrm{p}}{L}\right) ^3, \end{aligned}$$
(33)

which holds for \(L\gtrsim \lambda \gg \ell _\mathrm{p}\) and \(T\gtrsim T_\mathrm{dS}\).

Fig. 1
figure 1

Black hole probability for \(\lambda =L\) (solid line) vs. analytical approximation (31) (dotted line) with \(T=T_\mathrm{dS}\) (equivalent to \(k=1\))

Full size image
Fig. 2
figure 2

Coefficient \(K_{\lambda =L,k}\) evaluated numerically (solid line) and analytical approximation (32)

Full size image

Since the typical mass M of these PBH is related to L according to Eq. (26), that is \(M\simeq E_\Lambda \simeq m_\mathrm{p}\,{L}/{\ell _\mathrm{p}}\), we can equivalently write

$$\begin{aligned} P_\mathrm{BH}(M) \simeq 30 \left( \frac{T}{T_\mathrm{dS}}\right) ^3 \left( \frac{\ell _\mathrm{p}}{\lambda }\right) ^3 \left( \frac{m_\mathrm{p}}{M}\right) ^3, \end{aligned}$$
(34)

for \(M\gtrsim m_\mathrm{p}/10\). We remark that there appears no sharp threshold in the black hole mass, which is in fact what one expects from the HQM [9,10,11,12]. Upon multiplying this probability for the number of de Sitter patches of size \(L\sim M\), one can estimate the total number of PBH’s inside the visible universe of a given mass,

$$\begin{aligned} N_\mathrm{BH}(M)\simeq & {} \frac{R_0\,m_\mathrm{p}}{3 \, \sqrt{3} \, \ell _\mathrm{p}\,M}\,P_\mathrm{BH}(M) \nonumber \\\simeq & {} 6 \cdot 10^{62} \left( \frac{T}{T_\mathrm{dS}}\right) ^3 \left( \frac{\ell _\mathrm{p}}{\lambda }\right) ^3 \left( \frac{m_\mathrm{p}}{M}\right) ^4, \end{aligned}$$
(35)

in which we used \(R_0\simeq 10^{62}\,\ell _\mathrm{p}\) for the size of the visible Universe. We remark that this counting applies to the initial number PBH’s and neglects both the subsequent evaporation and possible accretion.

The above result can be recast in the following form. First we note that the de Sitter energy density is holographic [18, 19], that is

$$\begin{aligned} \rho _L \simeq \frac{3\, m_\mathrm{p}}{8\, \pi \, \ell _\mathrm{p}\,L^2}, \end{aligned}$$
(36)

whereas the energy density of the fluctuation is given by

$$\begin{aligned} \delta \rho \simeq \frac{\Delta E}{(4\, \pi \, \lambda ^3 / 3)} \simeq \frac{\pi ^3\,T}{40\, \zeta (3)\,{\lambda ^3}} \simeq 0.7 \, \frac{T}{\lambda ^3}. \end{aligned}$$
(37)

Upon recalling that \(T_\mathrm{dS}\simeq m_\mathrm{p}\,\ell _\mathrm{p}/L\), one finds

$$\begin{aligned} \frac{\delta \rho }{\rho _L} \simeq 6 \, \frac{T}{T_\mathrm{dS}} \left( \frac{\ell _\mathrm{p}}{L} \right) ^2 \left( \frac{L}{\lambda } \right) ^3, \end{aligned}$$
(38)

and therefore

$$\begin{aligned} N_\mathrm{BH}(M)\simeq & {} 2\cdot 10^{58} \, \left( \frac{\lambda }{\ell _\mathrm{p}} \right) ^6 \left( \frac{\delta \rho }{\rho _L} \right) ^3 \left( \frac{m_\mathrm{p}}{M} \right) ^7 \nonumber \\\simeq & {} 5 \cdot 10^{62} \left( \frac{\delta \rho }{\rho _L} \right) ^3\frac{m_\mathrm{p}}{M}, \end{aligned}$$
(39)

where we assumed \(\lambda \simeq L\) in the last approximation.

3 Conclusions and outlook

In this work, we have computed the probability of PBH formation in a simple framework for the early Universe and quantum density perturbations. Our results should first and foremost caution that the details of the process of black hole formation still need to be understood better and that quantum effects might not be negligible.

In particular, after a brief review of the HQM, we have provided an explicit computation of the probability of black hole formation by describing the primordial fluctuations in terms of a Planckian distribution of typical temperature \(T \simeq k \, T_\mathrm{dS}\). The factor k was left arbitrary here, but it should be easy be obtained it from any specific models in the literature.

The key result of our analysis is that the mass spectrum of PBH’s (39) appears to be extremely suppressed in this simplified setup. In particular, it seems that a purely quantum mechanical treatment of primordial density perturbations implies a very low likelihood for the formation of PBH’s in the very early Universe, unless one has reasons to consider for the fluctuations some very large values of \(\delta \rho / \rho _L\sim T/T_\mathrm{dS}\).

As we mentioned in the Introduction, much of the present interest stems from PBH’s as candidates for the dark matter [3, 25]. This of course requires a significant production which could occur during inflation only during stages of departure from the (quasi de Sitter) slow-roll evolution, or later on during the radiation dominated era [26,27,28,29,30]. The calculation in the present work should therefore be adapted to such scenarios in order to say something of relevance in this respect. Moreover, it would be interesting to understand if the probability of black hole formation changes significantly when the seeding fluctuation is not spherically symmetric. Preliminary works to extend the HQM to include non-spherical and rotating cases were presented in Refs. [31, 32] but their generalisation to a (quasi) de Sitter space will require further fundamental investigation.