A large class of search and detection tasks for moving objects is reduced to the optimization of their trajectories and velocity laws with an integral optimality criterion specified in terms of the detection risk related to the detection probability, as was proposed in [1–3]. The corresponding mathematical formulations are expressed in terms of variational or optimal control problems, and the solution of these optimization problems relies on the integration of the Euler–Lagrange or adjoint equations, taking into account the maximum condition for the Pontryagin function, as in [4, 5]. Most studies are devoted to the development of numerical algorithms for constructing optimal trajectories of motion. An overview of such algorithms can be found in [6]. and only an insignificant portion of works, Due to the nonlinearity of problem formulations, an analytical derivation, determination, and classification of solutions are addressed in only a small number of works, for example, in [1, 4, 7]. This paper continues [7] and, more specifically, generalizes the formulation considered in [7]. We study the problem of finding optimal trajectories of an object with a nonuniform radiation pattern that moves in the presence of a sensor (detector). A generalized formulation is proposed that covers different types of physical fields used for object detection. As a result, this approach can be used to solve a broad class of search–evasion problems.

1 FORMULATION OF THE PROBLEM

An object moves in the field produced by a search system, which, in the simplest case, represents a single sensor located at the origin. The task is to find optimal trajectories of the object by solving a classical variational problem with an integral risk functional depending on the level of the signal S(t) emitted by the object.

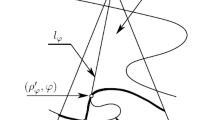
This level of the signal depends on a number of constant characteristics of the moving object and the sensor and on the instantaneous velocity of the object and the distance to the sensor

$$S = {{\left( {\frac{{v}}{r}} \right)}^{\mu }}G\left( \varphi \right)\gamma \left( {r,\varphi } \right)g\left( \beta \right),$$
(1)

where \(G\left( \varphi \right)\) is responsible for the radiation pattern of the sensor’s receiving antenna, g(β) is the radiation pattern of the moving object, r is the current distance between the sensor and the object, \({v}\) is the instantaneous velocity of the object, and \(\gamma \left( {r,\varphi } \right)\) is the attenuation coefficient of the medium. The geometric meaning of the angles ψ and φ is explained in Fig. 1a. Namely, ψ is the angle of rotation of the object’s velocity, and φ is the angle of rotation of the object’s radius vector. The angle \(\psi - \varphi = \beta \) is an angle in the rectangular triangle constructed using the radial \({{{v}}_{r}}\) and transversal \({{{v}}_{\varphi }}\) projections of the object’s velocity, i.e., the angle between the object’s velocity and its projection onto the radius vector, as shown in Fig. 1b. The quantity μ > 1 characterizes the physical field used for detection. The field can be magnetic, thermal, acoustic, or electromagnetic.

Fig. 1.
figure 1

Position of the object on the plane of Cartesian coordinates with the sensor S.

Full size image

The optimization criterion for the problem is the risk R regarded as an integral functional of the signal S in (1). It has the form

$$R = \mathop \smallint \limits_0^T {{\left( {\frac{{v}}{r}} \right)}^{\mu }}G\left( \varphi \right)\gamma \left( {r,\varphi } \right)g\left( \beta \right)dt.$$
(2)

Assume that the radiation pattern of the receiving antenna is uniform \((G\left( \varphi \right) \equiv 1)\) and the signal is not damped by the medium, i.e., \(\gamma \left( {r,\varphi } \right) = 1\).

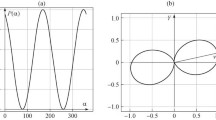
An example of the radiation pattern g(β) is given in Fig. 2.

Fig. 2.
figure 2

Example of the radiation pattern of the moving object.

Full size image

Thus, the problem of finding optimal trajectories can be formulated as follows.

Problem 1. Find a trajectory \((r{\text{*}}(t),\varphi {\text{*}}(t))\) minimizing the functional

$$R = \mathop \smallint \limits_0^T {{\left( {\frac{{v}}{r}} \right)}^{\mu }}g\left( \beta \right)dt,$$
(3)

where \(v\) is the velocity of the object and r is the distance between the sensor and the object. The boundary conditions are fixed:

$$r\left( 0 \right) = {{r}_{A}},\quad r\left( T \right) = {{r}_{B}},\quad \varphi \left( 0 \right) = {{\varphi }_{A}},\quad \varphi \left( T \right) = {{\varphi }_{B}}.$$

The travel time T from the point A to the point B is also fixed.

2 NECESSARY OPTIMALITY CONDITIONS

Lemma 1. The substitution of the variable \(\rho = {\text{ln}}r\) brings functional (3) to the form

$$R\left( \rho (\cdot ),\varphi (\cdot ) \right)=\underset{0}{\overset{T}{\mathop \int }}\,\text{}{{({{\dot{\rho }}^{2}}+{{\dot{\varphi }}^{2}})}^{\mu /2}}g\left( \text{arctan}\frac{{\dot{\varphi }}}{{\dot{\rho }}} \right)dt.$$
(4)

Lemma 1 implies that Problem 1 is equivalent to the two-point boundary variational problem of minimizing functional (4).

Problem 2. Find a trajectory \(\left( {\rho {\text{*}}\left( t \right),\varphi {\text{*}}\left( t \right)} \right)\) minimizing the functional

$$\begin{gathered} R\left( {\rho \left( \cdot \right),\varphi \left( \cdot \right)} \right) = \mathop \smallint \limits_0^T S(\rho ,\dot {\rho },\varphi ,\dot {\varphi },t)\,dt \\ = \int\limits_0^T {{{{({{{\dot {\rho }}}^{2}} + {{{\dot {\varphi }}}^{2}})}}^{{\mu /2}}}g\left( {{\text{arctg}}\frac{{\dot {\varphi }}}{{\dot {\rho }}}} \right)\,} dt \to \mathop {\min }\limits_{\rho ( \cdot ),\varphi ( \cdot )} . \\ \end{gathered} $$
(5)

with boundary conditions

$$\rho \left( 0 \right) = {{\rho }_{A}},\quad \rho \left( T \right) = {{\rho }_{B}},\quad \varphi \left( 0 \right) = {{\varphi }_{A}},\quad \varphi \left( T \right) = {{\varphi }_{B}}.$$

Due to the form of functional (5), it has several first integrals.

Lemma 2. The Lagrangian \(S\left( {\rho ,\dot {\rho },\varphi ,\dot {\varphi },t} \right)\) has a constant value S* on an extremal trajectory \(\left( {\rho {\text{*}}(t),\varphi {\text{*}}(t)} \right)\).

The following theorem provides a necessary condition for the optimality of a trajectory solving Problem 2.

Theorem 1. Suppose that \(g\left( \beta \right)\) is a twice differentiable function of β such that \(0 < {{g}_{1}} < g\left( \beta \right) < {{g}_{2}}\) for all \(\beta \in \left[ {0,2\pi } \right]\), where \({{g}_{1}}\) and \({{g}_{2}}\) are constants. Assume that there exist \(\ddot {\rho }(t)\) and \({\kern 1pt} \ddot {\varphi }(t)\) that are continuous functions of t. Then an extremal trajectory of Problem 2 satisfies the system of equations

$$\begin{gathered} \dot {\rho } = {\text{const}}, \\ \dot {\varphi } = {\text{const}}. \\ \end{gathered} $$
(6)

Corollary 1. Theorem 1 implies that the extremal trajectory has the form of a logarithmic spiral:

$$\begin{gathered} r\left( t \right) = {{r}_{A}}{\text{exp}}\left( {\frac{t}{T}{\text{ln}}\frac{{{{r}_{B}}}}{{{{r}_{A}}}}} \right), \\ \varphi \left( t \right) = {{\varphi }_{A}} + \frac{{{{\varphi }_{B}} - {{\varphi }_{A}}}}{T}t. \\ \end{gathered} $$
(7)

The equation of the extremal trajectory on the polar plane has the form

$$r(\varphi ) = {{r}_{A}}{\text{exp}}\left( {\frac{{\varphi - {{\varphi }_{A}}}}{{{{\varphi }_{B}} - {{\varphi }_{A}}}}{\text{ln}}\frac{{{{r}_{B}}}}{{{{r}_{A}}}}} \right).$$

The following two lemmas determine the velocity law for the object and the risk of its detection while moving along the extremal trajectory.

Lemma 3. The velocity of the object moving along the extremal trajectory (8) obeys the law

$${v}\left( t \right) = \frac{{{{r}_{A}}}}{T}{\text{exp}}\left( {\frac{t}{T}{\text{ln}}\frac{{{{r}_{B}}}}{{{{r}_{A}}}}} \right)\sqrt {{\text{l}}{{{\text{n}}}^{2}}\frac{{{{r}_{B}}}}{{{{r}_{A}}}} + {{{\left( {{{\varphi }_{B}} - {{\varphi }_{A}}} \right)}}^{2}}} .$$
(9)

Lemma 4. The value of the functional (4) on the extremal trajectory (8) is given by

$$R{\text{*}} = \frac{{{{{({{{({{\rho }_{B}} - {{\rho }_{A}})}}^{2}} + {{{({{\varphi }_{B}} - {{\varphi }_{A}})}}^{2}})}}^{{\mu /2}}}}}{{{{T}^{{\mu - 1}}}}}g\left( {\beta {\text{*}}} \right),$$
(10)

where \(\beta {\text{*}} = {\text{arctan}}\frac{{{{\varphi }_{B}} - {{\varphi }_{A}}}}{{{{\rho }_{B}} - {{\rho }_{A}}}}\), and depends only on the boundary conditions.

3 SUFFICIENT CONDITIONS OF OPTIMALITY

Now, we find the conditions under which the resulting extremal trajectory is an optimal solution of Problem 2, i.e., a strong minimizer of functional (4). For this purpose, we consider the Hessian matrix.

Lemma 5. Let \(S\left( {\rho ,\dot {\rho },\varphi ,\dot {\varphi },t} \right) = {{({{\dot {\rho }}^{2}} + {{\dot {\varphi }}^{2}})}^{{\mu /2}}}g\left( \beta \right)\), where g(β) is a three times continuously differentiable function of β. Then the Hessian matrix of the function H has the form

$${\mathbf{H}} = \left( {\begin{array}{*{20}{c}} {{{H}_{{11}}}}&{{{H}_{{12}}}} \\ {{{H}_{{21}}}}&{{{H}_{{22}}}} \end{array}} \right),$$
(11)

where

$$\begin{gathered} {{H}_{{11}}} = \frac{{{{\partial }^{2}}S}}{{\partial {{{\dot {\rho }}}^{2}}}} = ( - 2\dot {\varphi }\dot {\rho }(\mu - 1)g{\kern 1pt} '(\beta ) + \mu ({{{\dot {\varphi }}}^{2}} + {{{\dot {\rho }}}^{2}}(\mu - 1))g(\beta ) \\ \, + g{\kern 1pt} ''(\beta ){{{\dot {\varphi }}}^{2}}){{({{{\dot {\varphi }}}^{2}} + {{{\dot {\rho }}}^{2}})}^{{\frac{\mu }{2} - 2}}}, \\ \end{gathered} $$
$$\begin{gathered} {{H}_{{12}}} = \frac{{{{\partial }^{2}}S}}{{\partial \dot {\rho }\partial \dot {\varphi }}} = (({{{\dot {\rho }}}^{2}} - {{{\dot {\varphi }}}^{2}})(\mu - 1)g{\kern 1pt} '(\beta ) \\ \, + \dot {\rho }\dot {\varphi }(({{\mu }^{2}} - 2\mu )g(\beta ) - g{\kern 1pt} ''(\beta ))){{({{{\dot {\varphi }}}^{2}} + {{{\dot {\rho }}}^{2}})}^{{\frac{\mu }{2} - 2}}}, \\ \end{gathered} $$
$$\begin{gathered} {{H}_{{21}}} = \frac{{{{\partial }^{2}}S}}{{\partial \dot {\varphi }\partial \dot {\rho }}} = (({{{\dot {\rho }}}^{2}} - {{{\dot {\varphi }}}^{2}})(\mu - 1)g{\kern 1pt} '(\beta ) \\ \, + \dot {\rho }\dot {\varphi }(({{\mu }^{2}} - 2\mu )g(\beta ) - g{\kern 1pt} ''(\beta ))){{({{{\dot {\varphi }}}^{2}} + {{{\dot {\rho }}}^{2}})}^{{\frac{\mu }{2} - 2}}}, \\ \end{gathered} $$
$$\begin{gathered} {{H}_{{22}}} = \frac{{{{\partial }^{2}}S}}{{\partial {{{\dot {\varphi }}}^{2}}}} = (2\dot {\varphi }\dot {\rho }(\mu - 1)g{\kern 1pt} '(\beta ) + \mu ({{{\dot {\rho }}}^{2}} + {{{\dot {\varphi }}}^{2}}(\mu - 1))g(\beta ) \\ \, + g{\kern 1pt} ''(\beta ){{{\dot {\rho }}}^{2}}){{({{{\dot {\varphi }}}^{2}} + {{{\dot {\rho }}}^{2}})}^{{\frac{\mu }{2} - 2}}}, \\ \end{gathered} $$

and the Hessian is given by

$$\begin{gathered} {\text{det}}{\mathbf{H}} = {{({{{\dot {\varphi }}}^{2}} + {{{\dot {\rho }}}^{2}})}^{{\mu - 2}}}(\mu - 1)({{g}^{2}}(\beta ){{\mu }^{2}} \\ \, + g(\beta )g{\kern 1pt} ''(\beta )\mu - g{\kern 1pt} {{'}^{2}}(\beta )(\mu - 1)). \\ \end{gathered} $$
(12)

The following theorem provides a sufficient condition for the optimality of a trajectory that is a candidate for the solution of the problem.

Theorem 2. Assume that the conditions of Theorem 1 and Lemmas 2 and 5 are satisfied and detH > 0 for all β. Then an extremal trajectory satisfying (6) is a strong minimizer of functional (4).

Thus, the fact that the determinant of the Hessian matrix is positive guarantees the optimality of the logarithmic spiral as a solution of the problem. For an arbitrary radiation pattern g(β). Theorem 2 gives a definite answer to the question about the optimality of trajectory (8) as a solution of the problem. Indeed, the sign of the Hessian depends on the sign of the third factor in (12), which, for given μ, depends only on the form of g(β). If the sufficient conditions are not satisfied, the desired optimal trajectory has a more complicated form and consists of several logarithmic spirals.

As a more general case, we can consider the motion of an object from one manifold to another. The derivation of the form of trajectories remains valid in this case.

4 EXAMPLE

Consider an example for the special case \(\mu = 2\), which may correspond to a primary acoustic signal propagating in a homogeneous water medium. Suppose that the radiation pattern of the object has the form

$$g\left( \beta \right) = {{K}_{1}} + {{K}_{2}}{\text{co}}{{{\text{s}}}^{2}}\beta .$$

The coefficients K1 and K2 determine the character of the radiation; they are strictly positive and normalized, i.e., \({{K}_{1}} + {{K}_{2}} = 1\). Figure 2 shows a radiation pattern of this form for \({{K}_{1}} = 0.25\) and \({{K}_{2}} = 0.75\). The Hessian is computed using Lemma 5:

$${\text{det}}{\mathbf{H}} = 4{{K}_{1}}\left( {{{K}_{1}} + {{K}_{2}}} \right) = 4{{K}_{1}}.$$

Obviously, the Hessian is strictly positive. Then, by Theorem 2, the logarithmic spiral (8) is the optimal minimum-risk trajectory in the motion between two points on the plane. This statement can be checked by varying functional (4):

$$\begin{gathered} \delta R = 2\dot {\rho }\delta \rho {\text{|}}_{0}^{T} + \dot {\varphi }\delta \varphi {\text{|}}_{0}^{T} - 2\int\limits_0^T {(\ddot {\rho }\delta \rho + \ddot {\varphi }\delta \varphi )\,dt} \\ + \,\int\limits_0^T {(\delta {{\rho }^{2}} + {{K}_{1}}\delta {{\varphi }^{2}})dt = \int\limits_0^T {(\delta {{\rho }^{2}} + {{K}_{1}}\delta {{\varphi }^{2}})} } \,dt, \\ \end{gathered} $$

where δρ and δφ are the variations of the coordinates, which are sufficiently smooth functions of time. The first and the second terms vanish due to the fixed boundary conditions for the variations, while the third term vanishes, because, on the extremal trajectory, the Euler–Lagrange equations hold, which imply (6). The only thing left is the weighted sum of squares, which is obviously positive. Thus, any variation of the trajectory (logarithmic spiral) increases the value of the risk functional, which proves its optimality. By Lemma 4, the risk value on this trajectory is given by

$$R{\text{*}} = \frac{1}{T}\left( {{\text{l}}{{{\text{n}}}^{2}}\frac{{{{r}_{B}}}}{{{{r}_{A}}}} + K_{1}^{2}{{{\left( {{{\varphi }_{B}} - {{\varphi }_{A}}} \right)}}^{2}}} \right)$$

and depends only on the boundary conditions.