Two Optimal Path Planning Problems for a Moving Object in the Case of Degeneration of Necessary Extremum Conditions

Abstract

The path planning problem for a controlled moving object with a nonuniform radiation pattern is considered for the case in which the necessary path optimality conditions are degenerate. Additional constraints are introduced, and two optimization problems are formalized, one of finding an optimal speed mode for a given path of the object and the other of finding an optimal path when moving at a constant speed. Methods and algorithms for constructing optimal paths and finding speed modes are proposed; for the second problem, the analytical domain of existence of a solution for arbitrary parameters is found. The analytical results are illustrated with examples.

1. INTRODUCTION

The widespread use of unmanned vehicles operating in various environments and autonomously solving civilian and military tasks necessitates planning their missions and solving path control problems based on available information arriving through measurement and communication channels [1,2,3]. The onboard decision making on the sequence of actions or the routing of a controlled moving object (CMO) should be based on the optimization of some performance criterion associated with a particular application. Since there is often a lack of measurement and information channels and data, one has to use mathematical models describing the onset and evolution of physical field signals in space prior to the formation of an information feature determining the criterion. In particular, in the problem of evading detection by a fixed detection system, the criterion is formed on the basis of the CMO detection failure probability [4,5,6]. The onboard algorithms and software must take into account the specific features of the path planning problem, including the nonuniqueness of its solution in the general case [7,8,9]. Therefore, CMO path planning is a science-intensive and topical problem [10, 11].

Analytical solutions for the CMO reference paths in the detection evasion problem have been obtained for the cases of constant speed [12] and variable speed [13]. A numerical algorithm has been developed for radar evasion by a CMO with a nonuniform scattering pattern [14] and sensor evasion by a CMO with a nonuniform radiation pattern [7, 15]. The papers [14, 16] also deal with settings taking into account the presence of a radar in the CMO motion region.

The present paper continues the studies [17,18,19] on path planning for CMOs operating in a conflict environment and solving the detection system evasion problem; here we consider the mathematical aspects of planning. Conditions for the degeneracy of necessary and sufficient optimality conditions for the paths of a CMO that has a nonuniform radiation pattern and evades a stationary detector on the plane were obtained and studied in [7]. An explicit form of the radiation pattern that leads to degeneration of the optimality conditions was found in [7].

In the present paper, we consider two statements of path planning problems and the corresponding solution methods for the case of a degenerate radiation pattern. These are the problem of finding an optimal speed mode for a given path of a CMO with zero Hessian and the problem of finding an optimal path for a CMO with zero Hessian in the case of a constant speed whose value must be determined in the course of the solution.

2. STATEMENT OF THE PROBLEM

Consider the path planning problem for a moving object with a nonuniform radiation pattern evading a single stationary detector on a plane. We assume that the CMO moves in the sensor field of a detection system consisting of a single sensor located at the origin. Thus, we deal with the problem of planning a CMO path minimizing the risk functional given in [7]. The task of the moving object is to move from a starting point $A$ to a terminal point $B$ in given time with minimum possible risk on the path.

Problem 1.

Find a path $(\rho ^*(t), \varphi ^*(t))$ minimizing the functional

$$ R\big (\rho (\cdot ),\varphi (\cdot )\big ) = \int \limits _{0}^{T} S(\rho ,\dot {\rho },\varphi ,\dot {\varphi }) dt =\int \limits _{0}^{T}\left (\dot {\rho }^2+\dot {\varphi }^2\right )^{\mu /2} G\left (\arctan \frac {\dot {\varphi }}{\dot {\rho }}\right )dt \rightarrow \min _{\rho (\cdot ),\varphi (\cdot )} $$

(2.1)

with the boundary conditions

$$ \begin {gathered} \rho (0) = \rho _A,\quad \rho (T) = \rho _B,\quad \varphi (0) = \varphi _A,\quad \varphi (T) = \varphi _B.\end {gathered} $$

Here we have introduced coordinates $(\rho ,\varphi )$ determining the position of the CMO relative to the sensor, $\rho =\ln r$, where $r$ is the distance between the sensor and the CMO, and $\varphi$ is the polar angle. Assume that $\mu =2$ and consider the degenerate case of zero Hessian [7]. The radiation pattern $G(\beta )$ is related to the CMO radiation profile. To be concise, from now on we omit the dependence of functions on their arguments unless this dependence needs to be refined.

Definition 1.

The profile $P(\alpha )$ is the function representing the dependence of the emitted signal power on the angle between a given axis (which coincides with the direction of motion of the object in what follows) and the direction towards the observer.

Fig. 1.

Radiation profile for the case of zero Hessian: (a) unfolding of the radiation profile; (b) radiation profile on the Cartesian plane.

Fig. 2.

Geometry of the direction of motion and the CMO and sensor positions.

It was shown in [7] that the normalized profile $P(\alpha )$ corresponding to the zero Hessian has the form

$$ P(\alpha ,\nu ) = \cos ^2 (\alpha -\nu ), $$

(2.2)

where $\nu$ is an arbitrary constant defining various possible profiles. Figure 1 depicts the object profile for the case of $\nu =15^{\circ }$.

Definition 2.

The radiation pattern $G(\beta )$ is the power of the signal emitted in the direction of the sensor when the object deviates by an angle $\beta$ from the direction to the position of the object relative to the sensor.

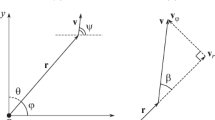
The relationship between the radiation profile and the radiation pattern is explained in Fig. 2.

In Fig. 2, the sensor is at the origin. The CMO velocity forms an angle $\beta$ with the segment connecting the sensor and the object. The value of the radiation pattern towards the sensor is indicated by the segment $G(\beta )$. The angle $\beta$, as can be seen from the figure, is determined by the formula

$$ \beta = \arctan \left (\frac {\dot {\varphi }\cdot r}{\dot {r}}\right ). $$

(2.3)

The angles $\alpha$ and $\beta$ are related by $\alpha =-\beta$. In this case, the radiation pattern $G(\beta ,\nu )$ will have the form

$$ G(\beta ,\nu ) = P (-\beta ,\nu )=\cos ^2 (-\beta -\nu ) =\cos ^2 (\nu +\beta ). $$

(2.4)

After the change of variables $\rho =\ln r$, the angle $\beta$ becomes $\beta = \arctan \left (\frac {\dot {\varphi }}{\dot {\rho }}\right )$. Then the integrand in (2.1) can be rewritten as

$$ \displaystyle S=(\dot {\rho }^2 +\dot {\varphi }^2 )\cdot \cos ^2 (\nu + \beta )= (\dot {\rho }^2 +\dot {\varphi }^2 )\cdot \left (\cos \nu \cdot \cos \beta -\sin \nu \cdot \sin \beta \right )^2. $$

(2.5)

In view of the equalities

$$ \displaystyle \sin \beta =\frac {\dot {\varphi } }{\sqrt {\dot {\rho }^2 + \dot {\varphi }^2}}, \quad \cos \beta =\frac {\dot {\rho } } {\sqrt {\dot {\rho }^2 + \dot {\varphi }^2}}, $$

(2.6)

the expression (2.5) acquires the form

$$ S=(\dot {\rho }\cdot \cos \nu -\dot {\varphi }\cdot \sin \nu )^2 =\cos ^2(\nu +\beta )\frac {V^2}{r^2}, $$

(2.7)

where $V$ is the absolute value of the CMO velocity.

Now Problem 1 can be restated as follows.

Problem 2.

Find a path (a vector of time dependences) $(\rho ^*(t), \varphi ^*(t))$ minimizing the functional

$$ R(\rho (\cdot ),\varphi (\cdot )) = \int \limits _{0}^{T}(\dot {\rho }\cdot \cos \nu -\dot {\varphi }\cdot \sin \nu )^2 dt $$

(2.8)

with the boundary conditions

$$ \begin {gathered} \rho (0) = \rho _A,\quad \rho (T) = \rho _B,\quad \varphi (0) = \varphi _A,\quad \varphi (T) = \varphi _B.\end {gathered} $$

Problem 2 has the specific feature that, owing to a special form of the radiation pattern, $\varphi _B$ is not uniquely determined. The boundary conditions for the point $B$ may differ by $2K\pi$. In the simplest case, one can move around the sensor on different sides. This case is considered in more detail when solving the problem of finding an optimal path with a constant speed.

3. SPECIFIC FEATURES OF EXTREMAL PATHS IN PROBLEM 2

The Euler equations of Problem 2 have the form

$$ \begin {cases} \displaystyle \frac {\partial S}{\partial \dot {\rho }}=2\cdot \cos \nu \cdot (\dot {\rho }\cdot \cos \nu -\dot {\varphi }\cdot \sin \nu )=\mathrm {const} \\[1em] \displaystyle \frac {\partial S}{\partial \dot {\varphi }} =-2\cdot \sin \nu \cdot (\dot {\rho }\cdot \cos \nu -\dot {\varphi }\cdot \sin \nu )=\mathrm {const}. \end {cases} $$

(3.1)

Since the function $S(\rho ,\dot {\rho },\varphi ,\dot {\varphi })$ in Eq. (2.7) does not explicitly depend on $t$, we can write an expression for the first integral of the Euler equations of Problem 2 in the form of a generalized Hamiltonian function that coincides with $S$; namely,

$$ \begin {aligned} \displaystyle \dot {\rho }\cdot \frac {\partial S}{\partial \dot {\rho }} + \dot {\varphi }\cdot \frac {\partial S}{\partial \dot {\varphi }} - S&= 2\cdot \dot {\rho }\cdot \cos \nu \cdot (\dot {\rho }\cdot \cos \nu -\dot {\varphi }\cdot \sin \nu ) \\[.3em] &\qquad {}-2\cdot \dot {\varphi }\cdot \sin \nu \cdot (\dot {\rho } \cdot \cos \nu -\dot {\varphi }\cdot \sin \nu )-S=S=\mathrm {const}. \end {aligned} $$

(3.2)

Since $S =\mathrm {const}$ and the value of the functional in the optimal case is equal to $S\cdot T$, where $T$ is the time of motion, it follows that the expression $\dot {\rho }\cdot \cos \nu -\dot {\varphi }\cdot \sin \nu$ coincides with $\sqrt S$ up to sign. Set $C=\sqrt {S}$ and write this equation as

$$ \dot {\rho }\cdot \cos \nu -\dot {\varphi }\cdot \sin \nu = \sigma \cdot C, $$

(3.3)

where $\sigma =\{-1,1\}$. In view of (2.7), this equation can also be written in the form

$$ \cos \big (\nu +\beta (t)\big ) = \frac {\sigma \cdot C\cdot r(t)}{V(t)}, $$

(3.4)

where $V$ is the velocity of motion. We integrate Eq. (3.3) and obtain

$$ \big (\rho (t)-\rho (0)\big )\cdot \cos \nu -\big (\varphi (t)-\varphi (0)\big )\cdot \sin \nu =\sigma \cdot C\cdot t. $$

(3.5)

Substituting the time of motion $t=T$ into (3.5), we obtain the value of the constant,

$$ C= \frac {\big (\rho (T)-\rho (0)\big )\cdot \cos \nu -\big (\varphi (T)-\varphi (0)\big )\cdot \sin \nu }{\sigma \cdot T}. $$

(3.6)

Equation (3.5) can be viewed as parametrically setting the time of motion along a given parametric path $(\rho (p),\varphi (p))$,

$$ \big (\rho (p)-\rho (0)\big )\cdot \cos \nu -\big (\varphi (p)-\varphi (0)\big )\cdot \sin \nu =\sigma \cdot C\cdot t(p), $$

(3.7)

where $\rho (p)$, $\varphi (p)$, and $t(p)$ are continuous functions, $p\in [0,1]$, and the value of $C$ is determined by (3.6). A “simple” solution satisfying (3.3) is given by the linear dependences $\dot {\rho }=\frac {\rho (T)-\rho (0)}{T }$ and $\dot {\varphi }=\frac {\varphi (T)-\varphi (0)}{T}$. First, they are a solution for all values of the angle $\nu$; second, the radiation pattern for these dependences is constant on the entire path, and the motion path in the coordinates ( $\rho , \varphi$) is the straight line segment connecting the initial and terminal points. In the Cartesian coordinate system, the solution is a logarithmic spiral. Therefore, in what follows we often compare the solutions obtained for paths and velocities with this basic solution and the value of the risk functional with its minimum value on the spiral [7]. Since there is only one independent Euler equation for finding the extremal, we can introduce additional conditions to solve the variational problem uniquely. The additional problem can be stated in quite a few ways, but in the present paper we focus on the following two statements. First, for an arbitrary path we study the possibility of ensuring the motion along it in such a way that the value of the functional be minimal. If this is possible, we find an optimal speed mode. Further, in the second problem we find a path minimizing the risk functional in class of constant-speed motions.

4. PROBLEM OF FINDING AN OPTIMAL SPEED MODE OF MOTION ALONG A GIVEN PATH

This section considers Problem 2 for the case of a given path of the CMO, that is, the problem of finding an optimal speed mode of motion along a given path so as to minimize the risk for a CMO with the radiation profile (2.2) corresponding to the zero Hessian and a parameter $\nu$. In the general case, we can assume that the path is given parametrically. Consider the class of smooth paths. The paths are specified as $(x(p), y(p))$, $p\in [0, 1]$, in the Cartesian coordinate system or $(r(p), \varphi (p))$, $p\in [0, 1]$, in the polar coordinate system. We fix the path in the Cartesian coordinate system as shown in Fig. 3.

Fig. 3.

Sample path: (a) coordinates as functions of the parameter, (b) path in the Cartesian coordinates.

Let us proceed to the coordinate system $(\rho , \varphi )$ with the initial coordinates $(\rho _A, \varphi _A)$. This coordinate system is convenient because the main variables included in the equations correspond to the coordinate axes and $\beta$ is the slope angle of the path constructed in this coordinate system.

If the angles are defined parametrically, then we use a time-like parameter $p$ instead of the variable $t$. The path $(\rho (p),\varphi (p))$ and the parametric dependence $\beta (p)$ are shown in Fig. 4.

Remark 1.

It follows from Eq. (3.4) that the sum $\nu +\beta (t)$ of angles along the entire path must be such that the sign of the function $\cos (\nu +\beta ( t))$ does not change.

Fig. 4.

Graphs of the path and the derivative $\beta (p)$: (a) path in the coordinates $(\rho , \varphi )$, (b) values of the angle $\beta$ on the path.

Remark 2.

Let $(\rho (p), \varphi (p))$ be a smooth path. Then the function $t(p)$ in (3.7) is smooth as well. Moreover, if the condition in Remark 1 is satisfied, then $t(p)$ is a monotone increasing function. In particular, it has an inverse function $p(t)$.

We define $\beta _{\max }$ and $\beta _{\min }$ as the maximum and minimum values of the angle $\beta (p)$ on the path and $\Delta \beta = \beta _{\max }- \beta _{\min }$ as the range of angles. Then the following corollary of Remark 1 obviously holds.

Corollary 1.

If $\Delta \beta > 180^{\circ }$ , then the motion along such a path with risk equal to the risk on the optimal logarithmic spiral is impossible.

Paths satisfying Corollary 1 are not considered in this paper.

In the above example, $\beta _{\min }=1{.}938^{\circ }$, $\beta _{\max }=125{.}43^{\circ }$, and when moving along the path, the angle $\beta$ crosses the value 90 $^{\circ }$, as shown in Fig. 4, where the angles of the tangent to the path become equal to 90 $^{\circ }$. Zones of violation of Remark 1 are marked with a dashed line. However, $\Delta \beta =123{.}492^{\circ }<180^{\circ }$, and hence there exists a range of the parameter $\nu$ for which the motion at an optimal speed is possible. To this end, we find the maximum angle $\beta _{kr}$ from the set of angles $90^{\circ }+k\cdot 180^{\circ }\leqslant \beta _{\max }$, $k\in Z$. Then the range of possible values of the parameter $\nu$ for which Remark 1 holds lies in the interval $(\beta _{kr}-\beta _{\min }+k\cdot 180^{\circ }, \beta _{kr} +180^{\circ }-\beta _{\max } + k\cdot 180^{\circ })$. For the path shown in Fig. 4, $\beta _{kr}=90^{\circ }$, and hence the angles lie in the range $\nu \in (88{.}062^{\circ };144{.}57^{\circ })$. The next range of angles is for $\nu \in (268{.}062^{\circ };324{.}57^{\circ })$, but it corresponds to the same profile.

The algorithm for solving the problem studied in this section has the following form.

Algorithm 1 (for finding $V(t)$).

• 1. Set the parameters $\nu$ and $T$ and the path $(\rho (p),\varphi (p))$.

• 2. Check Remark 1 for the given value of $\nu$ and the fixed path.

• 3. If Remark 1 is valid, then do the following.

• 4. Calculate the constant $C$ using Eq. (3.6).

• 5. Calculate $t(p)$ using Eq. (3.7).

• 6. Calculate the speed by the formula $V(p)=\left |\frac {C\cdot r(p)}{\cos (\nu +\beta (p))}\right |$.

• 7. Perform the inverse change of time and find the dependence $V(t)=V(p(t))$.

Fig. 5.

Solution for the angle $\nu$ equal to $125^{\circ }$: (a) $t(p)$, (b) $V(p)$, (c) $V (t)$.

As an illustration, take the angle $\nu =125^{\circ }$, which falls within the range of admissible values of $\nu$. The functions $t(p)$, $V(p)$, and $V(t)$ found by Algorithm 1 are presented in Fig. 5.

5. PROBLEM OF FINDING AN OPTIMAL CONSTANT-SPEED PATH

In Sec. 4, to regularize the problem, parametrized motion paths were used as an additional second equation. In this section, we use the condition of constant speed as an additional equation. Then the system of equations has the form

$$ \left \{ \begin {array}{l} \displaystyle \dot {\rho }\cdot \cos \nu -\dot {\varphi }\cdot \sin \nu =\sigma \cdot C \\[.3em] \displaystyle \dot {r}^2+\dot {\varphi }^2\cdot r^2=V_0^2, \end {array} \right . $$

(5.1)

where $\rho =\ln r$ and $V_0$ is the constant speed on path. Consider the following example. Let sensor $S$ be located on the Cartesian plane at the point $(0,0)$, and assume that the CMO has to perform a transition from point $A(50,0)$ to point $B(-60,180)$, as shown in Fig. 6. The given time of motion along the path is $T=4$. The value of the angle $\nu$ in the profile is $12^\circ$.

Fig. 6.

Positions of sensor $S$, initial point $A$, and terminal point $B$.

Fig. 7.

Possible positions 1, 2, 3, 4 of the object.

On the plane $(x,y)$, the distances from the sensor are $r_A=50$ for the starting point and $r_B=189{.}737$ for the terminal point; on the plane $(\rho ,\varphi )$, these distances are $\rho _A=3{.}912$ and $\rho _B=5{.}2456$. Points $A$ and $B$ on the plane $(x,y)$ are mapped to the points $(0,0)$ and $(\rho (T)-\rho (0),\varphi (T)-\varphi (0))$ on the plane $(\rho -\rho (0),\varphi -\varphi (0))$, as shown in Fig. 7. Point $A$ is mapped uniquely, and point $B$ can be mapped to a set of points lying on the vertical line with coordinate $\rho (T)-\rho (0)$, the distance between the points along the $\varphi$-axis being $2\pi k$ and the distance between neighboring points along the $\varphi$-axis being $2\pi$. Figure 7 shows four possible points $1$, $2$, $3$, $4$. The values of the angle $\varphi$ for these points are $(-4{.}3906; 1{.}8925; 8{.}1757; 14{.}4589)$ radians, respectively.

Figure 7 shows the projections of the vectors issuing from the origin and ending at points 1–4 onto the vector $(\cos \nu , -\sin \nu )$, denoted by the dashed line. These projections are 2.217, 0.911, 0.3954, and 1.7017, respectively. The projection of the vector ending at point 3 is minimal, followed in ascending order by the projections of the vectors ending at points 2, 4, and 1. Another point $\varphi _0$ is marked in the figure, for which the value of the product is $C\cdot T=0$, because it lies on the perpendicular to the axis $(\cos \nu , -\sin \nu )$ through the point $(0,0)$. For any point with coordinates ( $\rho (T)-\rho (0),\varphi$) outside the interval $({\varphi _0-\pi },\varphi _0+\pi )$, there exists a point lying inside the interval, determining the terminal point in the Cartesian coordinate system, and having a smaller value of the functional. Let us refer to this interval as the workspace. The maximum value of the product in the workspace is $C\cdot T= |\pi \cdot \sin \nu |$.

The logarithmic spiral paths for all of the above cases are shown in Fig. 6. The line thickness corresponds to the projection size. The minimum thickness corresponds to the path with the largest projection and hence with the largest value of the functional; the maximum thickness corresponds to the path with the smallest projection (the smallest value of the functional). The minimum risk is attained on the transition from the starting point to point 3 lying in the workspace. The same four paths for transitions are shown in Fig. 7. Therefore, to solve the problem, one first needs to choose the value of the angle $\varphi (T)$ and a logarithmic spiral in the vicinity of which the desired path will be constructed. The value of $\varphi _B$ must be inside the workspace. Now we assume that the value of $\varphi _B$ has been chosen and proceed to solving the problem.

5.1. Special Cases of $r_B=r_A$ and $C=0$

Let us start solving the problem by considering the special case in which $r(T)=r(0)=r_A=r_B$. Then a special case of motion along a logarithmic spiral is the motion along a circle at a constant speed, which is a solution of the problem considered in [12],

$$ \begin {cases} \displaystyle r(t)=\mathrm {const} \\[.3em] \displaystyle \varphi (t)=\varphi _A+\frac {\varphi _B-\varphi _A}{T}\cdot t. \end {cases} $$

(5.2)

Another special case is one where $r_B\neq r_A$, while $C=0$ in the expression (3.5). In this case, the angle $\nu$ is equal to $\nu _0=\arctan \frac {\rho _B-\rho _A}{\varphi _B-\varphi _A}$. Then the path is a straight line passing through the origin in the coordinate system $(\rho -\rho (0),\varphi -\varphi (0))$ and accordingly a logarithmic spiral in the Cartesian coordinates $(x,y)$. Since the value of the radiation pattern is zero, it is possible to move at any speed, including a constant one. In this case, the speed is determined by the length of the logarithmic spiral and the time of motion. The value of the functional is zero. The solution of the equation $\dot {r}=\pm \sin ({\nu }_0)\cdot V_0$ determines the radial component of the path,

$$ r(t)=\pm \sin (\nu _0)\cdot V_0\cdot t+r_A, $$

(5.3)

where the value of the velocity is ${ V_0=\left |\frac {r_B-r_A}{T\cdot \sin (\nu _0)}\right |}$. From Eq. (3.5) we obtain the angular component

$$ \varphi (t)=\cot (\nu _0)\cdot \ln \left (\frac {t}{T} \cdot \Big ( \exp \big (\tan \nu _0\cdot (\varphi _B-\varphi _A)-1\big )\Big )+1\right )+\varphi _A. $$

(5.4)

The expressions (5.3) and (5.4) determine the path.

5.2. General Case

Let us proceed to the study of the general case. We assume that $C\neq 0$. We also assume that $\sin \nu \neq 0$ and $\cos \nu \neq 0$. These cases are considered below.

Lemma 1.

The changes of variables $w=\arcsin \left (\frac {C\cdot r}{V_0}\right )$ and $\tau =C\cdot \cos \nu \cdot t$ reduce system (5.1) to the differential equation

$$ \frac {dw}{d\tau }=\sigma \cdot \tan w\pm \tan \nu . $$

(5.5)

Proof. Let us express $\dot {\varphi }$ from the first equation in system (5.1),

$$ \begin {gathered} \displaystyle \dot {\varphi }=\frac {\dot {r}\cdot \cos \nu -\sigma \cdot C\cdot r}{r\cdot \sin \nu }.\end {gathered} $$

Let us substitute $\dot {\varphi }$ into the second equation. The solution of the quadratic equation for $\dot {r}$ has the form

$$ \dot {r}=\sigma \cdot C\cdot r\cdot \cos \nu \pm \sin \nu \cdot \sqrt {V_0^2-(C\cdot r)^2}. $$

(5.6)

We divide both sides of equation (5.6) for $\dot {r}$ by $V_0$ and obtain the equation

$$ \frac {\dot {r}}{V_0}=\frac {\sigma \cdot C\cdot r}{V_0}\cdot \cos \nu \pm \sin \nu \cdot \sqrt {1-\left (\frac {C\cdot r}{V_0}\right )^2}. $$

(5.7)

Further, we make the change of variables $u=\frac {C\cdot r}{V_0}$ in (5.7) and obtain

$$ \frac {\dot u}{C}=\sigma \cdot u\cdot \cos \nu \pm \sin \nu \cdot \sqrt {1-u^2}. $$

(5.8)

Dividing both sides of the equation by $\cos \nu$, we obtain

$$ \frac {\dot u}{C\cdot \cos \nu }=\sigma \cdot u\pm \tan \nu \cdot \sqrt {1-u^2}. $$

(5.9)

Let us make the change of time $\tau =C\cdot \cos \nu \cdot t$,

$$ \frac {du}{d\tau }=\sigma \cdot u\pm \tan \nu \cdot \sqrt {1-u^2}. $$

(5.10)

Note that the equation is defined in the domain $|u|\leqslant 1$; making the final change of variables $w=\arcsin u$, we arrive at Eq. (5.5), as claimed in Lemma 1. The proof of Lemma 1 is complete. $\quad \blacksquare$

Lemma 2.

Equation (5.5) can be integrated in implicit form,

$$ c_1+\frac {2\cdot \tau }{\cos ^2 \nu }\mp 2\cdot \sigma \cdot \tan \nu \cdot w-\ln \Big (\big ((\tan w\pm \sigma \cdot \tan \nu )\cdot \cos w\big )^2\Big )=0. $$

(5.11)

Here $c_1$ is an integration constant.

The assertion of Lemma 2 can be verified by a straightforward differentiation of the expression (5.11).

We make the inverse change of time $\tau =C\cdot \cos \nu \cdot t$ and rewrite the solution (5.11) in the form

$$ c_1+\frac {2\cdot \sigma \cdot t}{\cos \nu }\mp 2\cdot \sigma \cdot \tan \nu \cdot w-\ln \Big (\big ((\tan w\pm \sigma \cdot \tan \nu )\cdot \cos w\big )^2\Big )=0. $$

(5.12)

The value of the constant $c_1$ is found from the initial conditions at $t=0$; namely,

$$ c_1=\pm 2\cdot \sigma \cdot \tan \nu \cdot w(0)+\ln \Big (\big ((\tan w(0)\pm \sigma \cdot \tan \nu )\cdot \cos w(0)\big )^2\Big ), $$

(5.13)

where $w(0)=\arcsin \left (\frac {C\cdot r(0)}{V_0}\right )$. Substituting (5.13) into (5.12) and transforming the expression, we obtain the solution for the function $w(t)$ in the implicit form

$$ \pm \sin \nu \cdot \big (w(t)-w(0)\big )+\sigma \cdot \cos \nu \cdot \ln \left (\frac {\sin \big (\nu \pm \sigma \cdot w(t)\big )}{\sin \big (\nu \pm \sigma \cdot w(0)\big )}\right )=C\cdot t. $$

(5.14)

Further, multiplying both sides of the equation by $\sigma$, we obtain

$$ \pm \sigma \cdot \big (w(t)-w(0)\big )\cdot \sin \nu +\cos \nu \cdot \ln \left (\frac {\sin \big (\nu \pm \sigma \cdot w(t)\big )}{\sin \big (\nu \pm \sigma \cdot w(0)\big )}\right )=\sigma \cdot C\cdot t. $$

(5.15)

The equations for the motion speed $V_0$ are obtained for time equal to the time of motion, $t=T$. The value $V_0$ must satisfy at least one of the equations below,

$$ \begin {aligned} \displaystyle +\sigma \cdot \big (w(T)-w(0)\big )\cdot \sin \nu +\cos \nu \cdot \ln \left (\frac {\sin \big (\nu +\sigma \cdot w(T)\big )}{\sin \big (\nu +\sigma \cdot w(0)\big )}\right )&=\sigma \cdot C\cdot T, \\[.6em] \displaystyle -\sigma \cdot \big (w(T)-w(0)\big )\cdot \sin \nu +\cos \nu \cdot \ln \left (\frac {\sin \big (\nu -\sigma \cdot w(T)\big )}{\sin \big (\nu -\sigma \cdot w(0)\big )}\right )&=\sigma \cdot C\cdot T, \end {aligned} $$

(5.16)

where $w(0)=\arcsin \left (\frac {C\cdot r_A}{V_0}\right )$ and $w(T)=\arcsin \left (\frac {C\cdot r_B}{V_0}\right )$.

Essentially, Eqs. (5.16) are two parametric dependences on $V_0$, and to find the speed mode on the entire path, one must find the root of at least one of the above functions. Note that the values of $w(0)$ and $w(T)$ are related to each other. For example, if $r_B<r_A$, then $w(T)=\arcsin \left (\frac {r_B}{r_A}\cdot \sin w(0)\right )$; otherwise, $w(0)=\arcsin \left (\frac {r_A}{r_B}\cdot \sin w(T)\right )$.

We define $r_{\max }=\max \{r_A,r_B\}$ and $r_{\min }=\min \{r_A,r_B\}$ and introduce the new variable

$$ z=\sigma \arcsin \left (\frac {C\cdot r_{\max }}{V_0}\right ). $$

(5.17)

Using the values of the function $z$, we determine the values of $w(0)$ and $w(T)$. One of these values is equal to $z$, and the other is $\arcsin \left (\frac {r_{\min }}{r_{\max }}\cdot \sin z\right )$. This function is convenient, because its values lie in the range $[-\pi /2, \pi /2]$ and both equations for $V_0$ involving $w(0)$ and $w(T)$ are written in the same way.

If $\sigma =1$, then the first equation in (5.16) formally determines the behavior on the interval $z\in [\nu ,\pi /2+\nu ]$, while the second equation (5.16) determines the behavior on the interval $z\in [-\pi /2+\nu ,\nu ]$. In the general case, the resulting solutions must be reduced to the interval $z\in [-\pi /2, \pi /2]$.

If $\sigma =-1$, then the equations in (5.16) are just interchanged, which does not affect the procedure for finding the root.

Lemma 3.

The optimal value $V_0$ of the speed on the path is determined by the solution of the equation

$$ \displaystyle F(z)=\sigma \cdot \sigma _r\cdot C\cdot T, $$

(5.18)

where the function $F(z)$ is given by

$$ F(z)=\big (z-\arcsin (k_r\cdot \sin z)\big )\cdot \sin \nu +\cos \nu \cdot \ln \left (\frac {\sin (\nu +z)} {\sin \big (\nu +\arcsin (k_r\cdot \sin z)\big )}\right ), $$

(5.19)

$$ k_r=\frac {r_{\min }}{r_{\max }},\quad \text {and}\quad \sigma _r=\mathrm{sign}\, (r_B-r_A). $$

Proof. Set $k_r= \frac {r_{\min }}{r_{\max }}$ and $\sigma _r=\mathrm{sign}\, (r_B-r_A)$. If $r_{\max }=r_B$; then Eq. (5.16) has the form

$$ \begin {gathered} \big (z-\arcsin (k_r\cdot \sin z)\big )\cdot \sin \nu +\cos \nu \cdot \ln \left (\frac {\sin (\nu +z)} {\sin \big (\nu +\arcsin (k_r\cdot \sin z)\big )}\right )=\sigma \cdot C\cdot T.\end {gathered} $$

On the other hand, if $r_{\max }=r_A$, then

$$ \begin {gathered} \big (\arcsin (k_r\cdot \sin z)-z\big )\cdot \sin \nu +\cos \nu \cdot \ln \left (\frac {\sin \big (\nu +\arcsin (k_r\cdot \sin z)\big )} {\sin (\nu +z)}\right )=\sigma \cdot C\cdot T.\end {gathered} $$

We multiply this by ( $-1$) and make some transformations to obtain the dependence

$$ \begin {gathered} \big (z-\arcsin (k_r\cdot \sin z)\big )\cdot \sin \nu +\cos \nu \cdot \ln \left (\frac {\sin (\nu +z)} {\sin \big (\nu +\arcsin (k_r\cdot \sin z)\big )}\right )=-\sigma \cdot C\cdot T.\end {gathered} $$

Therefore, with the use of the constant $\sigma _r$, Eq. (5.16) can be written in the form

$$ \begin {gathered} \displaystyle \big (z-\arcsin (k_r\cdot \sin z)\big )\cdot \sin \nu +\cos \nu \cdot \ln \left (\frac {\sin (\nu +z)} {\sin \big (\nu +\arcsin (k_r\cdot \sin z)\big )}\right )=\sigma \cdot \sigma _r\cdot C\cdot T.\end {gathered} $$

Now, defining the function $F(z)$ by (5.19), we arrive at the assertion in Lemma 3. The proof of Lemma 3 is complete. $\quad \blacksquare$

Let us find the domain of the function $F(z)$. Note once more that the domain lies in the interval $z\in [-\pi /2,\pi /2]$. For the value of the function to exist, it is necessary that the functions $\sin (\nu +z)$ and $\sin (\nu +\arcsin (k_r\cdot \sin (z)))$ in the argument of the logarithm have the same sign and do not vanish. By the original assumptions, $\sin \nu \ne 0$, and on the interval $[-\pi /2,\pi /2]$ there exists a point $z=\nu _0=-\nu$ where $\sin (\nu +\nu _0)=0$ and a point $z=z_{\mathrm {gr}}$ where $\sin (\nu +\arcsin (k_r\cdot \sin (z_{\mathrm {gr}}) )=0$.

Lemma 4.

• 1. If $z_{\mathrm {gr}}$ exists and $z_{\mathrm {gr}}\leqslant \nu _0$ , then the domain of the function $F(z)$ is $z\in [-\pi /2,z_{\mathrm {gr}})\cup (\nu _0,\pi /2]$ ; otherwise, $z\in (\nu _0,\pi /2]$ .

• 2. If $z_{\mathrm {gr}}$ exists and $z_{\mathrm {gr}}\geqslant \nu _0$ , then the domain of $F(z)$ is $z\in [-\pi /2,\nu _0)\cup (z_{\mathrm {gr}},\pi /2]$ ; otherwise, $z\in [-\pi /2,\nu _0)$ .

Proof. The conditions for the existence of a value of the function $F(z)$ are written in the form $\arcsin (k_r\cdot \sin z)<\nu _0$ and $z<\nu _0$ or $\arcsin (k_r\cdot \sin z)>\nu _0$ and $z>\nu _0$. If the point $z_{\mathrm {gr}}$ is to the left of $\nu _0$, then for $\frac {\sin \nu _0}{k_r}<-1$ the function is undefined in this domain, because $z_{\mathrm {gr}}$ does not exist, and hence $z\in (\nu _0,\pi /2]$. Otherwise, $z_{\mathrm {gr}}=\arcsin \left (\frac {\sin \nu _0}{k_r}\right )$, and the domain is $z\in [-\pi /2,z_{\mathrm {gr}})\,\cup \,(\nu _0-\nu ,\pi /2]$.

The second assertion in Lemma 4 can be proved in a similar way. The proof of Lemma 4 is complete. $\quad \blacksquare$

To obtain a less cumbersome form of the function $F(z)$, we introduce the variable

$$ \displaystyle \hat {z}=\arcsin \big (k_r\cdot \sin (z)\big ). $$

(5.20)

We find $V_0$ in two stages. First, we find $z$ from Eq. (5.19), because $V_0$ does not explicitly occur in the equation, and then we determine $V_0$ corresponding to $z$. In the new notation, the function $F(z)$ takes the form

$$ F(z)=(z-\hat {z})\cdot \sin \nu +\cos \nu \cdot \ln \left (\frac {\sin (\nu +z)}{\sin (\nu +\hat {z})}\right ). $$

(5.21)

Lemma 5.

Under the condition $\sin \nu \neq 0$ , the function $F(z)$ is a monotone function on each connected part of its domain specified by Lemma 4 except for the points $z=\pm ~\pi /2$ .

Proof. Let us find the derivative $\frac {dF(z)}{dz}$. Note that $\frac {d\hat {z}}{dz}=k_r\cdot \frac {\cos z}{\cos \hat {z}}$. The following chain of equalities holds:

$$ \begin {aligned} \displaystyle \frac {dF(z)}{dz}&=\left (1-k_r\cdot \frac {\cos z}{\cos \hat z}\right )\cdot \sin \nu + \cos \nu \cdot \frac {\sin (\nu +\hat {z})}{\sin (\nu +z)}\\[.7em] &\qquad \qquad {} \times \left (\frac {\cos (\nu +z)}{\sin (\nu +\hat {z})}-\frac {\sin (\nu +z)\cdot \cos (\nu +\hat {z})\cdot k_r\cdot \cos z}{\sin ^2(\nu +\hat {z})\cdot \cos \hat {z}}\right ) \\[.7em] &{} =\sin \nu + \cos \nu \cdot \frac {\cos (\nu +z)}{\sin (\nu +z)}-\frac {k_r\cdot \cos z}{\cos \hat {z}}\cdot \left (\sin \nu +\frac {\cos \nu \cdot \cos (\nu +\hat {z})}{\sin (\nu +\hat {z})}\right ) \\[.6em] &{} =\frac {\cos z}{\sin (\nu +z)}-\frac {k_r\cdot \cos z}{\sin (\nu +\hat {z})} \\[.6em] &{}=\frac {\cos z}{\sin (\nu +z)\cdot \sin (\nu +\hat {z})} \\[.6em] &\qquad \qquad {}\times (\sin \nu \cdot \cos \hat {z}+\cos \nu \cdot \sin \hat {z}-k_r\cdot \sin \nu \cdot \cos z-k_r\cdot \cos \nu \cdot \sin z) \\[.6em] &{}=\frac {\cos z\cdot \sin \nu }{\sin (\nu +z)\cdot \sin (\nu +\hat {z})}\cdot (\cos \hat {z}-k_r\cdot \cos z).\end {aligned} $$

Since $\cos z >0$ for $z\in (-\pi /2,\pi /2)$, we have $\sin (\nu +z)\cdot \sin (\nu +\hat {z})>0$, because $\sin (\nu +z)$ and $\sin (\nu +\hat {z})$ are of same sign by the assumption in Lemma 4, $\cos (\hat {z})-k_r\cdot \cos z\!=\!\sqrt {1-(k_r\cdot \sin z)^2 }-\sqrt {k_r^2-(k_r\cdot \sin z)^2 }>0$, $0<k_r<1$, and the sign of the derivative is determined by the sign of $\sin \nu$. If $\sin \nu >0$, then the function is monotone increasing on each connected part of its domain; on the opposite, if $\sin \nu <0$, then the function is monotone decreasing on each connected part of its domain. The proof of Lemma 5 is complete. $\quad \blacksquare$

Lemma 5 makes it easy to determine the presence of a root inside the domain $F(z)$, since the value of the function tends to $+\infty$ or $-\infty$ on one of the boundaries of the domain. The value of the function on the other boundary of the domain and the behavior of the function $F(z)$ make it possible to determine whether there exists a solution and find it.

Theorem.

If Eq. (5.18) has a solution and $k_r<1$, then this solution is unique.

Proof. Let us show that the solution is unique. If the domain consists of a single half-interval, then the solution is unique by Lemma 5, because the function $F(z)$ is monotone increasing or decreasing and the right-hand side of the equation is constant. Let there be two half-intervals in the domain. Then, by Lemma 4, $k_r>\sin \nu$ and each of the half-intervals is adjacent to one of the boundaries of the possible values of $z$. Consider the difference $\Delta F=F(\pi /2)-F(-\pi /2)$ of values of the function at the boundaries. Note that $\Delta F=0$ for $k_r=1$. We have the chain of equalities

$$ \begin {aligned} \displaystyle \Delta F&=(\pi /2-\arcsin k_r)\cdot \sin \nu +\cos \nu \cdot \ln \left (\frac {\sin (\nu +\pi /2)}{\sin (\nu +\arcsin k_r)}\right ) \\[.6em] &\qquad {}\displaystyle -(-\pi /2+\arcsin k_r)\cdot \sin \nu -\cos \nu \cdot \ln \left (\frac {\sin (\nu -\pi /2)}{\sin (\nu -\arcsin k_r)}\right ) \\[.6em] &{}\displaystyle =(\pi -2\arcsin k_r)\cdot \sin \nu +\cos \nu \cdot \ln \left (\frac {\sin (\nu +\pi /2) \cdot \sin (\nu -\arcsin k_r)}{\sin (\nu -\pi /2)\cdot \sin (\nu +\arcsin k_r)}\right ) \\[.6em] &{}\displaystyle =(\pi -2\arcsin k_r)\cdot \sin \nu +\cos \nu \cdot \ln \left (\frac {\sin (\arcsin k_r-\nu )}{\sin (\arcsin k_r+\nu )}\right ). \end {aligned} $$

(5.22)

Now let us find the derivative $\displaystyle \frac {d\Delta F}{d k_r}$,

$$ \begin {aligned} \displaystyle \frac {d\Delta F}{d k_r}&=-\frac {2\sin \nu }{\sqrt {1-k_r^2}}+\frac {\cos \nu \cdot \sin (\arcsin k_r+\nu )}{\sqrt {1-k_r^2}\cdot \sin (\arcsin k_r-\nu )} \\[.3em] &\qquad {}\displaystyle \times \frac {\cos (\arcsin k_r-\nu )\cdot \sin (\arcsin k_r+\nu )-\cos (\arcsin k_r-\nu )\cdot \sin (\arcsin k_r+\nu )}{\sin ^2(\arcsin k_r+\nu )} \\[.3em] &{}\displaystyle =\frac {1}{\sqrt {1-k_r^2}}\cdot \left (-2\sin \nu +\frac {\cos \nu \cdot \sin (2\cdot \nu )}{\sin (\arcsin k_r-\nu )\cdot \sin (\arcsin k_r+\nu )}\right ) \\[.3em] &{}\displaystyle =\frac {\sin \nu }{\sqrt {1-k_r^2}}\cdot \left (\frac {\cos (2\arcsin k_r)-\cos (2\nu )+2\cos ^2 \nu }{\sin (\arcsin k_r-\nu )\cdot \sin (\arcsin k_r+\nu )}\right ) \\[.3em] &{}\displaystyle =\frac {\sin \nu \cdot (1+\cos (2\arcsin k_r)}{\sin (\arcsin k_r-\nu )\cdot \sin (\arcsin k_r+\nu )\cdot \sqrt {1-k_r^2}}=\frac {2\sin \nu \cdot \sqrt {1-k_r^2}}{k_r^2-\sin ^2\nu }.\end {aligned} $$

The sign of the derivative $\frac {d\Delta F}{d k_r}$ coincides with the sign of $\sin \nu$, because $k_r>\sin \nu$ by Lemma 4. If $\nu >0$, then the minimum value of $F(z)$ for the left domain corresponds to $z_1=-\pi /2$. The value of this function is maximum for the right domain at $z_2=\pi /2$, and $\Delta F$ is maximum at $k_r=1$ and equals zero. This means that the values of the function in the left domain are greater than the values of the function in the right domain. The situation is similar for $\nu <0$, where the values of the function in the left domain are less than the values in the right domain. Thus, if there exists a solution, then it is unique. The proof of the Theorem is complete. $\quad \blacksquare$

By way of example, consider the transition depicted in Fig. 6 along path 3. The upper part of Fig. 8 shows the behavior of the function $\sin (\nu +z)$.

Fig. 8.

Functions $\sin {\nu +z}$ and $F(z)$.

The point where this function crosses zero determines the position of the value of the angle $\nu _o$. The vertical segment marks the position of the value $\nu _0=-12^{\circ }$. The graph of $F(z)$ is displayed at the bottom of the figure. The value of $z_{\mathrm {gr}}$ is marked with a vertical dashed line. The domain of $F(z)$ consists of two half-intervals $[-\pi /2,z_{\mathrm {gr}})$ and $(\nu _0,\pi /2]$. For the example under consideration,

$$ k_r=\frac {r_A}{r_B}=\frac {50}{189{.}737}=0{.}2635\quad \text {and}\quad z_{\mathrm {gr}}=\arcsin \left (\frac {\sin \nu _0}{k_r}\right ) =\arcsin \left (\frac {\sin (-12^{\circ })}{k_r}\right )=- 52{.}089^{\circ }. $$

This point is marked with a vertical dashed line in the lower part of the figure; the horizontal line marks the value of the right-hand side of Eq. (5.18), equal to $0.3954$, which is used to determine the constant $C=0{.}09885$ at $T =4$. Then the solution of Eq. (5.18) is the point of intersection of the corresponding function graphs, and the value of the variable is $z=-4{.}755^{\circ }$. The optimal speed value is found from the established values of the variables $V_0=\left |\frac {C\cdot r_{\max }}{\sin z}\right |=226{.}25$.

Fig. 9.

Extremal paths (left) and the speed mode on them (right).

Fig. 10.

Extremal paths (left) and the speed mode on them (right).

In Fig. 9, the path of motion and the speed graph are shown in solid lines. For comparison, the dashed line shows the path in the form of a logarithmic spiral and the optimal speed mode on this path. The value of the functional is $R=0{.}039$ and coincides with the value of the functional on the logarithmic spiral.

For comparison, in Fig. 10 we present the paths and speeds for the case of transition to point 2 on the plane $(\rho ,\varphi )$. The value of the functional is $R=0{.}2075$; it is much greater than the minimum value but coincides with the value of the functional on logarithmic spiral 2.

It remains to consider a few special cases of the values of $\nu$. Let us start investigating these.

5.3. Special Case of $\sin \nu =0$

Consider the case of $\sin \nu =0$. Then $\cos \nu =\pm 1$ and system (5.1) becomes

$$ \begin {cases} \displaystyle \dot {r}={\pm \sigma \cdot C}\cdot r\\[.3em] \displaystyle \dot {r}^2+(\dot {\varphi }\cdot r)^2=V_0^2.\\ \end {cases} $$

(5.23)

Lemma 6.

The solution of system (5.23) has the form

$$ \displaystyle r(t)=r_A\cdot \exp \left (\pm \sigma \cdot C\cdot t\right ), $$

(5.24)

$$ \varphi (t)-\varphi _A=\pm \big (\cot w(t)+w(t)-\cot w(0)-w(0)\big ), $$

(5.25)

where $w(t)=\arcsin \left (\frac {C\cdot r(t)}{V_0}\right )$.

Proof. Integrating the first equation in (5.23), we obtain the dependence (5.24). Set $\tilde {C}={\pm C\cdot \sigma }$; then $r(t)=r_A\cdot \exp (\tilde {C}\cdot t)$. Substituting $\tilde {C}$ into the second equation in system (5.23), we obtain

$$ \begin {gathered} \tilde {C}^2\cdot r^2+\dot {\varphi }^2\cdot r^2=V_0^2.\end {gathered} $$

Since $\tilde {C}^2=C^2$, we write the differential equation for $\dot \varphi (t)$ in the form

$$ \begin {gathered} \dot {\varphi }=\pm \sqrt {\frac {V_0^2}{r^2(t)}-C^2}=\pm \sqrt {\frac {V_0^2}{r^2_A}\cdot \exp (-2\cdot \tilde {C}\cdot t)-C^2}.\end {gathered} $$

We make the change of variables $\tau =\exp (\tilde {C}\cdot t)$ to obtain

$$ \begin {gathered} d\varphi =\pm \frac {1}{\tau ^2}\cdot \sqrt {\left (\frac {V_0}{r_A\cdot C}\right )^2-\tau ^2}\cdot d\tau .\end {gathered} $$

After the integration of the last equation, the dependence $\varphi (\tau )$ with some integration constant $C_2$ takes the form

$$ \begin {gathered} \displaystyle \varphi (\tau )=\pm \left (-\frac {1}{\tau }\cdot \sqrt {\left (\frac {V_0}{r_A\cdot C}\right )^2-\tau ^2}-\arcsin \left (\frac {\tau \cdot \ r_A\cdot C}{V_0}\right )\right )+C_2.\end {gathered} $$

The inverse change of time yields the dependence $\varphi (t)$,

$$ \begin {gathered} \displaystyle \varphi (t)=\pm \left (-\sqrt {\left (\frac {V_0}{r(t)\cdot C}\right )^2-1}-\arcsin \left (\frac {r(t)\cdot C}{V_0}\right )\right )+C_2.\end {gathered} $$

The value of $C_2$ is found from the initial conditions,

$$ \begin {gathered} C_2=\varphi _A\mp \left (-\sqrt {\left (\frac {V_0}{r_A\cdot C}\right )^2-1}-\arcsin \left (\frac {r_A\cdot C}{V_0}\right )\right ).\end {gathered} $$

If we pass to the variables $w(t)=\arcsin \left (\frac {C\cdot r(t)}{V_0}\right )$, then we obtain the dependence $\varphi (t)$ in the form (5.25). The proof of Lemma 6 is complete. $\quad \blacksquare$

By Lemma 6, when substituting the boundary condition into relations (5.24)–(5.25), we obtain an equation for $V_0$, which has the form

$$ |\varphi _B-\varphi _A|=\big |\cot (w(T))+w(T)-\cot (w(0))-w(0)\big |. $$

(5.26)

The function $\cot (w)+w$ is monotone decreasing on the interval $(0,\pi /2)$ with increasing $w$, because

$$ \begin {gathered} \displaystyle \frac {d(\cot w+w)}{dw}=\frac {-\sin ^2 w-\cos ^2 w}{\sin ^2 w}+1=-\cot ^2 w;\end {gathered} $$

therefore, the right-hand side of Eq. (5.26) is equal to $\cot w(0)+w(0)-\cot w(T)-w(T)$ if $w(T)>w(0)$ and $\cot w(T)+w(T)-\cot w(0)-w(0)$ otherwise. In terms of the functions $z$ in (5.17) and $\hat {z}$ in (5.20), Eq. (5.26) becomes

$$ |\varphi _B-\varphi _A|=\cot \hat {z}+\hat {z}-\cot z-z. $$

(5.27)

Lemma 7.

There exists a unique solution of Eq. (5.27) provided that

$$ |\varphi _B-\varphi _A|\geqslant \cot (\arcsin k_r)+\arcsin k_r-\pi /2. $$

(5.28)

Proof. The variable $z$, just as the function $V_0$, is monotone and assumes the values $z\in (0,\pi /2]$. The minimum value of the right-hand side of Eq. (5.27) is attained at $z=\pi /2$ and accordingly $\hat {z}=\arcsin k_r$ and is equal to

$$ \begin {gathered} \displaystyle \cot (\arcsin k_r)+\arcsin k_r-\pi /2.\end {gathered} $$

Therefore, there exists a unique solution if (5.28) is satisfied. The proof of Lemma 7 is complete. $\quad \blacksquare$

Consider Fig. 7 for the sample path shown in Fig. 6. Since $\nu =0$, it follows that the projection onto the horizontal axis is the same for all points, which means that the value of the functional is the same for all transitions. However, the speeds for these cases are very different. It is natural to choose the path with minimum speed. First, consider the motion in the vicinity of path 2. Then $|\varphi _B-\varphi _A|=1{.}8925$ radians, $k_r=r_B/r_A=50/189{.}737=0{.}2635$, and the expression (5.28) takes the value $\cot (\arcsin k_r)+\arcsin k_r-\pi /2=2{.}3565>|\varphi _B-\varphi _A|$. There is no path along which the CMO moves at a constant speed and which corresponds to the minimum risk value on path 2. However, if we take path 1 for which $|\varphi _B-\varphi _A|=4{.}3906$ radians, then the motion at a constant speed is possible.

Fig. 11.

Extremal paths (left) and the speed mode on them (right).

The solution is shown in Fig. 11. For this case, $V_0=104{.}65$, and the value of the functional is $R=0{.}44463$. Thus, in the case of $\sin \nu =0$ and $r_A\neq r_B$, one can always choose a shift by $2k\pi$ so that the value $|\varphi _B-\varphi _A|$ satisfies Lemma 7.

5.4. Special Case of $\cos \nu =0$

Consider the second special case where $\cos \nu =0$. Then $\sin \nu =\pm 1$ and system (5.1) acquires the form

$$ \begin {cases} \displaystyle \dot {\varphi }=\mp \sigma \cdot C\\[.6em] \displaystyle \dot {r}^2+(\dot {\varphi }\cdot r)^2=V_0^2. \end {cases} $$

(5.29)

Lemma 8.

The solution of system (5.29) has the form

$$ \displaystyle \varphi (t)-\varphi _A=\mp \sigma \cdot C\cdot t, $$

(5.30)

$$ \displaystyle r(t)=\frac {V_0}{C}\sin \left (\arcsin \left (\frac {C\cdot r_A}{V_0}\right )\pm C\cdot t\right ). $$

(5.31)

Proof. Integrating the first equation in system (5.29), we obtain (5.30). Let us solve the second equation in (5.29) for $\dot {r}$,

$$ \displaystyle \dot {r}=\pm V_0\cdot \sqrt {1-\left (\frac {C\cdot r(t)}{V_0}\right )^2}. $$

(5.32)

The change of variables $u=\frac {C\cdot r(t)}{V_0}$ brings Eq. (5.32) to the form $\frac {\dot {u}}{C}=\pm \sqrt {1-u^2}$. Integrating the latter, we conclude that $\arcsin u=\pm C\cdot t+C_3$, where $C_3$ is the integration constant. The inverse change of variables gives $\arcsin \left (\frac {C\cdot r(t)}{V_0}\right )=\pm C\cdot t+C_3$. The constant $C_3$ is found from the initial conditions,

$$ \begin {gathered} C_3=\arcsin \left (\frac {C\cdot r_A}{V_0}\right ).\end {gathered} $$

This implies (5.31). The proof of Lemma 8 is complete. $\quad \blacksquare$

The substitution of the boundary conditions into (5.31) gives an equation for the speed,

$$ \displaystyle \Bigg |\arcsin \left (\frac {C\cdot r_B}{V_0}\right )-\arcsin \left (\frac {C\cdot r_A}{V_0}\right ) \Bigg |=C\cdot T. $$

(5.33)

In terms of the variables $z$ in (5.17) and $\hat {z}$ in (5.20), Eq. (5.33) becomes

$$ z-\hat {z}=C\cdot T. $$

(5.34)

Lemma 9.

Equation (5.34) has a unique solution provided that the boundary conditions satisfy the inequality

$$ \displaystyle |\varphi _B-\varphi _A| \leqslant \pi /2-\arcsin k_r. $$

(5.35)

Proof. Since $\cos \nu =0$, we have $F(z)=z-\hat {z}$, which is a monotone function by Lemma 5. The minimum value of the left-hand side of Eq. (5.34) is zero, and the maximum value is ( $\pi /2-\arcsin k_r$). Therefore, Eq. (5.34) has a solution for the value of $C\cdot T$ that, in turn, is found from (5.30) and equals $|\varphi _B-\varphi _A|$. Then condition (5.35) must be satisfied for the existence of a solution, which is unique owing to the monotonicity of $F(z)$. The proof of Lemma 9 is complete. $\quad \blacksquare$

Corollary 2.

If condition (5.35) is satisfied, then the value of the speed is equal to

$$ \displaystyle V_0=\frac {1}{T}\frac {\varphi _B-\varphi _A}{\sin (\varphi _B-\varphi _A)}\cdot \sqrt {r_A^2-2\cdot r_A\cdot r_B\cdot \cos |\varphi _B-\varphi _A|+r_B^2 }. $$

(5.36)

Proof. The following chain of transformations leads to determining $V_0$ and finding such a path:

$$ \begin {aligned} \arcsin \left (\frac {C\cdot r_{\max }}{V_0}\right )&=\arcsin \left (\frac {C\cdot r_{\min }}{V_0}\right )+C\cdot T, \\[.3em] \sin \left (\arcsin \left (\frac {C\cdot r_{\max }}{V_0}\right )\right )&=\sin \left (\arcsin \left (\frac {C\cdot r_{\min }}{V_0}\right )+C\cdot T\right ), \\[.3em] \frac {C\cdot r_{\max }}{V_0}&=\frac {C\cdot r_{\min }}{V_0}\cdot \cos (C\cdot T)+\sqrt {1-\left (\frac {C\cdot r_{\min }}{V_0}\right )^2}\cdot \sin (C\cdot T), \\[.3em] \frac {C\cdot r_{\max }}{V_0}-\frac {C\cdot r_{\min }}{V_0}\cdot \cos (C\cdot T)&=\sqrt {1-\left (\frac {C\cdot r_{\min }}{V_0}\right )^2}\cdot \sin (C\cdot T),\end {aligned} $$

$$ \begin {aligned} &\frac {C^2\cdot \big (r_{\max }^2-2\cdot r_{\min }\cdot r_{\max }\cdot \cos (C\cdot T)+r_{\min }^2\cdot \cos ^2(C\cdot T)\big )}{V_0^2}&{} \\[.3em] &\qquad \qquad \qquad \qquad \qquad \quad {}=\sin ^2(C\cdot T)-\left (\frac {C\cdot r_{\min }}{V_0}\right )^2\cdot \sin ^2(C\cdot T).\end {aligned} $$

From the last expressions, we conclude that

$$ \begin {gathered} \displaystyle V_0=\frac {C}{\sin (C\cdot T)}\cdot \sqrt {r_{\max }^2-2\cdot \cos (C\cdot T)\cdot r_{\max }\cdot r_{\min }+r_{\min }^2},\end {gathered} $$

or $V_0$ can be represented in the form (5.36). If $C=0$, then the motion occurs along the radius and

$$ \begin {gathered} V_0=\frac {1}{T}\cdot |r_B-r_A|.\end {gathered} $$

As an example, consider the transition depicted in Fig. 6. We conclude that

$$ {\pi /2-\arcsin k_r=\pi /2-\arcsin 0{.}2635=1{.}304<\varphi _B-\varphi _A=1{.}8925}, $$

and so there is no solution in this case. $\quad \blacksquare$

5.5. Solution Existence Domain

Above, we considered the solution of the problem of finding the possibility of constructing a path of motion at a constant speed and finding the value of such a speed. Now we study the set of points on the plane for which there exists a solution of this problem. Let us make a few clarifying remarks.

Remark 3.

For convenience of description, we will consider the domain of existence of the solution in a coordinate system with the initial position of the object on the $X$-axis. Then $\varphi _A=0$.

Remark 4.

The pattern $G(\beta ,\nu )$ is symmetric, because $G(\beta ,\nu \pm \pi )= G(\nu ,\beta )$. Therefore, any parameter $\nu$ can be replaced by its value $\nu \in [0,\pi ]$.

Remark 5.

In addition, when $\nu _1=\pi -\nu$, the problem of transition from the starting point to the terminal point with the boundary conditions $\rho (T)=\rho _B$ and $\varphi (T)=\varphi _B$ with angle $\nu _1$ coincides with the problem of going to a point with the boundary conditions $\rho (T)=\rho _B$ and $\varphi (T)=-\varphi _B$ with angle $\nu$. Hence, for all values of $\nu$, only the values $\nu \in [0,\pi /2]$ can be used. Then for $\nu \in [0,\pi /2]$ the function $F(z)$ will always be increasing, because $\sin \nu >0$.

In addition, there is another symmetry.

Remark 6.

To construct the domain of existence of a solution, it suffices to construct it inside the circle $r\leqslant r_A$.

Let us illustrate Remark 6 with an example.

Fig. 12.

Symmetry solution in the plane $(\rho , \varphi )$.

Let the point $A$ have the coordinates $r_A=50$, $\varphi _A=0^{\circ }$, $r_B=80$, $\varphi _B = 100^{\circ }$, and let $\nu =35^{\circ }$. On one graph, consider one more transition from point $A$ to the point $C$ with the coordinates $r_C = 31{.}25$, $\varphi _C = -100^{\circ }$. The points $B$ and $C$ are shown in Fig. 12 in the coordinate system $(\rho (t)-\rho _A, \varphi (t)-\varphi _A)$. The figure shows that the points $B$ and $C$ are located symmetrically, and the projections onto the axis ( $\cos \nu ,-\sin \nu$) have the same absolute values but opposite signs; i.e., the right-hand side of (5.18) has opposite signs for transitions to these points. Since $r_C < r_A$ and $r_B > r_A$, it follows that the values of $k_r$ for these points are the same, $k_r=\frac {r_A}{r_B}=\frac {r_C} {r_A}$; this means that the solutions are the same. Thus, the information about the entire domain of existence of a solution is contained inside the disk of radius $r_A$.

The existence of a solution is based on the definition of the solvability of Eq. (5.18), where the main role is played by the values $F(-\pi /2)$ and $F(\pi /2)$.

Lemma 10.

In the disk $r<r_A$ , the set of points $(r_B,\varphi _B)$ or $(k_r,\varphi _B)$ , where $k_r=r_B/r_A$ , at which there exists a solution of Problem 2 is determined by the following two systems of inequalities:

$$ \begin {cases} \displaystyle \ln k_r\cdot \cot \nu -\pi \leqslant \varphi _B\\[.03em] \displaystyle \frac {\pi }{2}-\arcsin k_r+\cot \nu \cdot \ln \left (\frac {\cos \nu }{\sin (\nu +\arcsin k_r)}\right )\geqslant -\ln k_r\cdot \cot \nu +\varphi _B; \end {cases} $$

(5.37)

$$ \qquad \quad \enspace {} \begin {cases} \displaystyle \varphi _B\leqslant \ln k_r\cdot \cot \nu +\pi \\[.03em] k_r > \sin \nu \\[.03em] \displaystyle -\frac {\pi }{2}+\arcsin k_r+\cot \nu \cdot \ln \left (\frac {-\cos \nu }{\sin (\nu -\arcsin k_r)}\right )\leqslant -\ln k_r\cdot \cot \nu +\varphi _B.\\ \end {cases} $$

(5.38)

Proof. As was mentioned earlier, the problem of finding the boundary of the domain of existence can be reduced to the problem for which $\nu > 0$, $\nu < 90^{\circ }$ ( ${\sin \nu >0})$, and $r_B < r_A$. Based on Lemmas 3 and 4 as well as the chosen range of values of $\nu$, we rewrite the conditions for finding the solution as

$$ \displaystyle F(\pi /2)\geqslant -\sigma \cdot C\cdot T, $$

(5.39)

$$ \displaystyle F(-\pi /2)\leqslant -\sigma \cdot C\cdot T \mbox { if } k_r > \sin \nu . $$

(5.40)

For the chosen range of values in Eq. (3.5), assuming that $\varphi _A = 0$, we obtain

$$ \begin {gathered} \sigma \cdot C\cdot T = \ln k_r\cdot \cos \nu - \varphi _B \cdot \sin \nu .\end {gathered} $$

This range of angles is within the workspace, which gives the first inequalities in (5.37) and (5.38). Dividing Eq. (5.39) and (5.40) by $\sin \nu$, we obtain the second inequality in (5.37) and the third inequality in (5.38), each of them related to its own range of values defined by the first inequalities in these systems. The proof of Lemma 10 is complete. $\quad \blacksquare$

Fig. 13.

Boundaries of the domain of existence of a solution in polar (left) and Cartesian (right) coordinates normalized to the initial distance.

The polar angle $\varphi _0$ for which $C\cdot T = 0$ is determined as

$$ \displaystyle \varphi _0=\ln k_r\cdot \cot \nu . $$

(5.41)

The domain boundary values must fall within the working range ( ${\varphi _0-\pi }, { \varphi _0+\pi }$), as shown in Fig. 13. For given values of $\nu$ and $k_r$, these equations define the boundaries of the domain of existence of a solution,

$$ \begin {aligned} \varphi _{1}&=\pi /2-\arcsin k_r+\cot \nu \cdot \ln \left (\frac {\cos \nu }{\sin (\nu +\arcsin k_r)}\right )+\varphi _0(k_r,\nu ), \\[.3em] \varphi _{2}&=-\pi /2+\arcsin k_r+\cot \nu \cdot \ln \left (\frac {-\cos \nu }{\sin (\nu -\arcsin k_r)}\right )+\varphi _0(k_r,\nu ).\end {aligned} $$

These curves pairwise intersect with the curves $\varphi _0\pm \pi =0$. One point of intersection $\varphi _{g1}$ is determined by the joint solution of the equation $\varphi _1 =\varphi _0-\pi$, and the other point $\varphi _{g2}$ is found from the joint solution of the equation $\varphi _2 =\varphi _0+\pi$.

An example of calculating the domain of existence of a solution for the maximum distance from the sensor equal to $300$ units is shown in Fig. 14a. Recall that the sensor is located at the point with coordinates $(0,0)$, and the initial point is $A=(50,0)$. The domain of existence of a solution is marked in gray, and the black lines correspond to the special cases of $r_A = r_B$ and $C = 0$.

Fig. 14.

Domain of existence of a solution for $\nu =35^{\circ }$: (a) $r_B \in [0; 300]$; (b) $r_B < r_A$.

Fig. 15.

Domain of existence of a solution for $\nu =90^{\circ }$: (a) $r_B \in [0; 300]$; (b) $r_B < r_A$.

Figure 14b shows the domain of existence of a solution for the interior of the domain $r_B < r_A$ provided that the coordinates are normalized. The distance is defined in relative units $k_r=r_B / r_A$. The starting point $A$ has the coordinates $(1,0)$. The shape of the domain in Fig. 14b naturally coincides with the shape of the domain inside the disk of radius $r_A$ in Fig. 14a. Let us explain by an example how the existence of a point for a distance greater than $r_A$ is determined based on the domain in Fig. 14b. For example, let us take a point $D_1$ located at distance $210$ with direction angle ( $-60^{\circ }$) (point $D_1$ is indicated in Fig. 14a). For this point, the ratio is $k_r=50/210=0{.}2381$. Data on the possibility of solution for this point can be obtained by setting the distance equal to $k_r$ at the angle $60^{\circ }$ (point $D_2$ is indicated in Fig. 14b).

Finally, consider the special case of $\cos \nu =0$. Since the reachability condition is the validity of Eq. (5.35), the boundary of the domain is easily calculated. For the case of $r_B \geqslant r_A$, one has the value $k_r= r_A / r_B$, and the boundary coordinate is ${x=r_B\cdot \cos (\pi /2-\arcsin k_r)=r_B\cdot k_r= r_A}$. The entire half-plane is mapped into the disk with center and radius $r_A / 2$. This domain is presented in Fig. 15.

6. CONCLUSIONS

The two path planning problems for autonomous and manned CMOs considered in the article point to the common features characteristic of this class of problems. It turns out that optimization criteria naturally introduced in the formalization of path planning problems do not allow one to obtain a solution for all boundary conditions. For the problem of motion along a given path, the conditions for the existence of an optimal speed mode were proposed and an algorithm for finding it was developed. For the problem of finding the optimal path of motion at a constant speed, the domains of existence of a solution with the value of the risk functional equal to the minimum value on the path corresponding to the logarithmic spiral with the optimal law of velocity change on it were found, a method for constructing this domain was proposed, and an analytical form of the optimal path was established.

Further research can be aimed at solving the path planning problem for the case of several speed modes of a CMO with a radiation pattern for which the necessary conditions for the optimality of the risk functional degenerate.