Method to Construct Periodic Solutions of Controlled Second-Order Dynamical Systems

Abstract

Nonconservative mechanical systems with one degree of freedom are considered. The goal is to provide the existence of steady-state oscillations with the prescribed properties. The system’s behavior is modeled by a second-order autonomous dynamical system with one variable parameter describing the amplifying coefficient of the control action. A numerical-analytic method to find the amplifying coefficient is proposed. Conditions of the orbital stability are obtained for the steady-state oscillations. An example of the application of the method is provided. The proposed approach can be applied to solve control problems and to find periodic solutions of second-order autonomous dynamical systems.

INTRODUCTION

The problem to generate oscillations with the a priori given properties is actual for various applications; it is discussed in many contemporary papers, in particular, for the case of systems with one degree of freedom, e.g. [1–9].

The efficiency of control strategies providing the existence of steady-state oscillations with a priori determined properties is frequently verified on the example of the control problem for a heavy pendulum. In [5], the stabilization problem for oscillations of a mathematical pendulum is solved by the passification method (see [10]), where the control depends on the coordinate and velocity. In [6], the following two approaches to the control of nonautonomous pendulum systems are considered: the active control with nonlinear saturation (see [11]) and passive damping assuming that an additional object with one degree of freedom is added to the mechanical system. In the cited papers, the structure of the constructed control is rather complicated: feedback with respect both to the coordinate and velocity is presented.

In order to construct a control providing the existence of periodic oscillations, one can use approaches to search for periodic solutions of nonconservative systems and modify them. For example, in [7–9], approaches close to the method proposed in [12] are used to control the oscillator under small nonconservative actions. In [13], to construct a periodic motion of a vibration system, a corollary of the averaging method of [14] is applied; this corollary establishes a correspondence between fixed points of the averaged system and periodic solutions of the complete system. If there are no small parameters, then methods using the numerical integration of the system (the shooting method) and numerical-analytical procedures can be used to find periodic solutions. Examples of numerical-analytical procedures are methods for nonautonomous systems with a periodic dependence on time, e.g., the methods proposed in [15, 16] (to extend such approaches to autonomous systems, we have to change variables in advance (as a rule, this substitution is nontrivial) and the projection methods (see, e.g., [17, 18]). The latter are sensitive to the influence of high harmonics.

In this paper, we consider an autonomous pendulum-type mechanical system with one degree of freedom. Conservative and nonconservative forces act on the system. Also, a control action with a feedback and one varied parameter is presented, e.g., by the moment linear with respect to the angular velocity or proportional to the sign of the angular velocity, where the proportionality factor is to be selected to provide the desired properties of the system’s motion. Assume that the requirements to the steady-state oscillation mode are formulated. For example, the steady-state oscillations are to enclose the known equilibrium state and possess the given value of the mean mechanical energy. The posed problem is to select an amplifying coefficient of the control action which ensures the existence of such a steady-state mode (an attracting one is preferable).

Such control problems arise, e.g., in tuning operating duties for mechanisms and technical systems. In particular, the control of the external load in the local chain of a small-scale wind power unit can be reduced to such a problem (see [2]).

In this paper, we propose a numerical-analytical method to construct a control providing the existence of a steady-state oscillation mode with the prescribed properties for a nonconservative system without small parameters. This method is a numerical-analytical iteration procedure. The first iteration coincides with the result of the application of the criterion constructed in [12]. The new method extends the method proposed in [19] to the case of systems without the central symmetry properties. Apart from constructing a control, the method can be applied to searching for periodic solutions of second-order autonomous nonconservative dynamical systems.

We consider an example of the application of the proposed method to the oscillation problem for a controlled heavy pendulum in the air flow. The control action is presented by the moment in the pendulum hinge which is proportional to the sign of the angular velocity of the pendulum. The proportionality factor is a varied parameter. Using the proposed method, we solve the problem to find an amplifying coefficient of the control action which ensures the existence of steady-state oscillations with the prescribed value of the mean mechanical energy (the oscillations enclose the lower equilibrium of the pendulum). For attracting periodic motions, basins of attraction are described.

We discuss specific features of the new method and its advantages over the well-known methods.

1. PROBLEM POSING AND FORMALIZATION

Consider a mechanical system with one degree of freedom such that its motion is described by the dimensionless equations of the following kind:

$$\begin{gathered} \dot {x} = \frac{{\partial H(x,y)}}{{\partial y}}, \\ \dot {y} = - \frac{{\partial H(x,y)}}{{\partial x}} + a\left( {Q(x,y) - u(x,y)} \right), \\ u(x,y) = bf(x,y). \\ \end{gathered} $$

((1.1))

Here, the dot denotes the derivative with respect to the dimensionless time, x is the dimensionless generalized coordinate, y is the dimensionless momentum, $H(x,y) = 0.5{{k}^{{ - 1}}}(x){{y}^{2}} + P(x)$ is the Hamilton function describing the total mechanical energy of the system, $k(x) > 0$ is an analytical function defined by the structure of the kinetic energy of the system, $P(x) \geqslant 0$ is an analytical function describing the potential energy of the system, a > 0 is a dimensionless coefficient, $Q(x,y)$ is the dimensionless generalized force corresponding to external nonconservative forces (an analytical function), and $u(x,y)$ is the control. It is assumed that the control is the product of coefficient b to be selected and the given function $f(x,y)$ characterizing the feedback structure such that $yf(x,y) > 0$ provided that$y \ne 0$. Thus, the control is selected in the form of a dissipative or antidissipative function (depending on the sign of b). For example, the control might be of the form $u = by$ or $u = b\operatorname{sgn} (y)$.

The problem is to select a suitable amplifying coefficient b for the control action in order to generate in system (1.1) attracting periodic oscillations with the prescribed time mean $h$ of the function $H(x,y)$ if this is possible; this correspond to a certain average mechanical energy. It is assumed that the oscillation modes have to “enclose” the prescribed equilibrium of system (1.1). Also, we need to describe the basin of attraction of the “constructed” oscillation mode and to find the range of values of h accessible under the control of the selected structure. The method proposed below can be easily generalized for the case where the value of the oscillation amplitude is to be prescribed and for other similar problems to construct oscillations with prescribed properties.

The goal of this paper can be formalized as follows: for a given h, find sufficient conditions for the existence of a value $b = \tilde {b}(h)$ such that, for $b = \tilde {b}(h)$, system (1.1) has a periodic solution enclosing an isolated equilibrium $({{x}_{0}},0)$ and such that the mean value (with respect to time) of the function $H(x,y)$ along this solution is equal to h. If such $b = \tilde {b}(h)$ exists, then the goal is to find it, to find out whether the corresponding periodic solution is attracting; and to describe the basin of attraction, if the solution is attracting.

2. FINDING AN AMPLIFYING COEFFICIENT PROVIDING THE EXISTENCE OF A CYCLE

Assume that fixed points of system (1.1) are found and an isolated fixed point $({{x}_{0}},0)$ is selected such that it is to be enclosed by periodic solutions. Further, we assume that ${{x}_{0}} = 0$ (for brevity). Consider system (1.1) in the band $- {{A}_{0}} < x < C$, where A₀ and C are positive constants to be selected such that the cycle corresponding to the given value h of the function H(x, y) is located in the band $- {{A}_{0}} < x < C$(if such a cycle exists).

We start from an auxiliary problem. Let A be such that $0 < A < {{A}_{0}}$. The value ${{h}_{0}} = P( - A)$ corresponds to the phase point $( - A,0)$. We look for a value $\hat {b}(A)$ of parameter b, providing the existence of a periodic solution of system (1.1), passing through the phase point $( - A,0)$. Define successive approximations of the following kind:

$$\begin{gathered} y_{0}^{ + }(x;A) = \operatorname{Re} \sqrt {2k(x)({{h}_{0}} - P(x))} ,\quad y_{0}^{ - }(x;A) = - \operatorname{Re} \sqrt {2k(x)({{h}_{0}} - P(x))} , \\ {{b}_{0}}(A) = {{\left( {\int\limits_{ - A}^A {(f(x,y_{0}^{ + }(x;A)) - f(x,y_{0}^{ - }(x;A)))} dx} \right)}^{{ - 1}}}\int\limits_{ - A}^A {(Q(x,y_{0}^{ + }(x;A)) - Q(x,y_{0}^{ - }(x;A)))} dx; \\ \end{gathered} $$

((2.1))

$$\begin{gathered} y_{n}^{ + }(x;A) = \operatorname{Re} \sqrt {2k(x)\left( {{{h}_{0}} - P(x) + a\int\limits_{ - A}^x {(Q(s,y_{{n - 1}}^{ + }(s;A)) - {{b}_{{n - 1}}}f(s,y_{{n - 1}}^{ + }(s;A)))} ds} \right)} , \\ x_{n}^{ + } = \overline {\mathop {\lim }\limits_{z \in ( - A,C)} } \{ \left. {z\;} \right|y_{n}^{ + }(x;A) > 0\quad {\text{for}}\quad x \in ( - A,z)\} ; \\ \end{gathered} $$

$$\begin{gathered} y_{n}^{ - }(x;A) = - \operatorname{Re} \sqrt {2k(x)\left( {{{h}_{0}} - P(x) + a\int\limits_{ - A}^x {(Q(s,y_{{n - 1}}^{ - }(s;A)) - {{b}_{{n - 1}}}f(s,y_{{n - 1}}^{ - }(s;A)))} ds} \right)} ; \\ x_{n}^{ - } = \overline {\mathop {\lim }\limits_{z \in ( - A,\;C)} } \{ \left. {z\;} \right|y_{n}^{ - }(x;A) < 0\quad {\text{for}}\quad x \in ( - A,z)\} , \\ \end{gathered} $$

((2.2))

and

$$\begin{gathered} {{x}_{n}} = \max (x_{n}^{ + },x_{n}^{ - }); \\ {{b}_{n}}(A) = \frac{{\int\limits_{ - A}^{{{x}_{n}}} {Q(x,y_{n}^{ + }(x;A))} dx - \int\limits_{ - A}^{{{x}_{n}}} {Q(x,y_{n}^{ - }(x;A))} dx}}{{\int\limits_{ - A}^{{{x}_{n}}} {f(x,y_{n}^{ + }(x;A))} dx - \int\limits_{ - A}^{{{x}_{n}}} {f(x,y_{n}^{ - }(x;A))} dx}},\quad n \geqslant 1, \\ \end{gathered} $$

where $y_{n}^{ + }(x;A)$ and $y_{n}^{ - }(x;A)$ are the n-step approximations of the phase curves describing the parts of the desired cycle lying in the upper and lower half-planes of the phase plane, respectively, $x_{n}^{ + }$ and $x_{n}^{ - }$ are the n-step approximations of the value of variable x at the right-most point of the desired phase cycle, and ${{b}_{n}}(A)$ is the n-step approximation of the desired value of the amplifying coefficient.

The zero iteration (2.1) coincides with the result of the formal application of the method proposed in [12] to system (1.1): it is formal in the sense that it is required in [12] for parameter a to be small but the fulfillment of this condition is not guaranteed in the specified problem.

If system (1.1) possesses the central symmetry property, then we obtain $y_{n}^{ + }(x;A) = - y_{n}^{ - }( - x;A)$ and $x_{n}^{ + } = x_{n}^{ - } = A$ on each step; in this case, the numerical implementation of the method and the proof of the assertions on the limit of sequences (2.2) are substantially simplified (see [19]). In the present paper, no central symmetry of system (1.1) is assumed. Then the upper and lower parts of the desired cycle are constructed as limits of sequences such that each one consists of parts of the trajectories of the Hamilton systems which are different for the upper and lower half-planes. To obtain each consequent “generating” Hamilton system, we substitute the preceding approximation $y_{{n - 1}}^{ + }(x;A)$ and $y_{{n - 1}}^{ - }(x;A)$ for a part of the periodic trajectory in the right-hand side of system (1.1). On the nth step, the Hamiltonians of these generating systems have the form

$$\begin{gathered} H_{n}^{ + }(x,y) = \frac{{{{y}^{2}}}}{{2k(x)}} + P(x) - a\int\limits_{ - A}^x {(Q(s,y_{{n - 1}}^{ + }(s;A)) - {{b}_{{n - 1}}}f(s,y_{{n - 1}}^{ + }(s;A)))} ds; \\ H_{n}^{ - }(x,y) = \frac{{{{y}^{2}}}}{{2k(x)}} + P(x) - a\int\limits_{ - A}^x {(Q(s,y_{{n - 1}}^{ - }(s;A)) - {{b}_{{n - 1}}}f(s,y_{{n - 1}}^{ - }(s;A)))} ds. \\ \end{gathered} $$

The next approximations $y_{n}^{ + }(x;A)$ and $y_{n}^{ - }(x;A)$ are the trajectories of the systems determined by the Hamiltonians $H_{n}^{ + }(x,y)$ and $H_{n}^{ - }(x,y)$ (respectively) for the Hamiltonian level h₀.

If both sequences $y_{n}^{ + }(x;A)$ and $y_{n}^{ - }(x;A)$ converge for all x, then the sequences $x_{n}^{ + }$, $x_{n}^{ - }$, and ${{b}_{n}}(A)$ converge. Let these sequences converge. Let the relation $y_{n}^{ + }(x_{n}^{ + };A) = y_{n}^{ - }(x_{n}^{ - };A) = 0$ holds provided that n is sufficiently large, and the limits $\tilde {x}_{{}}^{ + }$ and $\tilde {x}_{{}}^{ - }$ of the sequences $x_{n}^{ + }$ and $x_{n}^{ - }$ (respectively) coincide with each other, i.e., $\tilde {x}_{{}}^{ + } = \tilde {x}_{{}}^{ - }$. Then the limit of the sequence of ${{b}_{n}}(A)$ is the desired value $\hat {b}(A)$ and the part of the cycle existing in system (1.1) for $b = \hat {b}(A)$, lying in the upper half-plane, is described by the limit $\tilde {y}_{{}}^{ + }(x;A)$ of the sequence of $y_{n}^{ + }(x;A)$, while its part lying in the lower half-plane is described by the limit $\tilde {y}_{{}}^{ - }(x;A)$ of the sequence of $y_{n}^{ - }(x;A)$.

If the sequences of (2.2) do not converge, then this does not mean the nonexistence of the desired value of the parameter $b = \hat {b}(A)$; it just means that it cannot be found by the proposed method (the corresponding examples can be provided). Thus, the convergence of the method is a sufficient (but not necessary) existence condition for the desired coefficient $b = \hat {b}(A)$.

By the properties similar to the properties of vector field rotation (see [20]), if $\hat {b}(A)$ exists, then it is unique (for centrally symmetric systems, a similar property is discussed in [19]).

Assume that the sequences of (2.2) converge for a given A. Then, to solve the main problem, compute the mean value $\tilde {h}(A)$ of the function $H(x,y)$ along the found periodic trajectory $(\tilde {X}(t;A),\tilde {Y}(t;A))$ existing in system (1.1) for $b = \hat {b}(A)$ (this trajectory is described by the functions $\tilde {y}_{{}}^{ + }(x;A)$ and $\tilde {y}_{{}}^{ - }(x;A)$):

$$\begin{gathered} \tilde {h}(A) = \frac{1}{T}\int\limits_0^T {H(\tilde {X}(t;A),\tilde {Y}(t;A))} dt \\ = {{\left( {\int\limits_{ - A}^{{{{\tilde {x}}}^{ + }}(A)} {\frac{1}{{\tilde {y}_{{}}^{ + }(x;A)}}} dx - \int\limits_{ - A}^{{{{\tilde {x}}}^{ + }}(A)} {\frac{1}{{\tilde {y}_{{}}^{ - }(x;A)}}} dx} \right)}^{{ - 1}}}\left( {\int\limits_{ - A}^{{{{\tilde {x}}}^{ + }}(A)} {\frac{{H(x,\tilde {y}_{{}}^{ + }(x;A))}}{{\tilde {y}_{{}}^{ + }(x;A)}}} dx - \int\limits_{ - A}^{{{{\tilde {x}}}^{ + }}(A)} {\frac{{H(x,\tilde {y}_{{}}^{ - }(x;A))}}{{\tilde {y}_{{}}^{ - }(x;A)}}} dx} \right). \\ \end{gathered} $$

((2.3))

Note that to compute the value $\tilde {h}(A)$, the value $b = \hat {b}(A)$ found above is used.

Apply algorithm (2.1)–(2.3) to all values of A such that $0 < A < {{A}_{0}}$ (for the numerical implementation, a step with respect to A is selected). Assuming that the sequences of (2.2) converge for all such values of A, we obtain a dependence between the mean level h of the mechanical energy on steady-state oscillations and the value of coefficient b. This dependence is parametrized by value A. In other words, $\tilde {b}(h) = \{ \left. {\hat {b}(A)} \right|\tilde {h}(A) = h\}$.

The monotonicity of the dependence $\tilde {h}(A)$ is not guaranteed and thus it is not guaranteed that the dependence $\tilde {b}\left( h \right)$ is one-valued. If it is not one-valued, then each value of $\tilde {b}\left( h \right)$ can be taken as the desired amplifying coefficient of the control signal; e.g., we can take the value with the broadest basin of attraction of the corresponding cycle.

3. STABILITY AND BASIN OF ATTRACTION

The following assertion takes place providing possibility to check the stability of a cycle: if for A = A₁ the derivative of the function $\hat {b}(A)$ is negative, then, for $b = \hat {b}({{A}_{1}})$, the cycle of system (1.1) passing through the point $( - {{A}_{1}},0)$ is attracting; if the derivative of the function $\hat {b}(A)$ is positive for $A = {{A}_{1}}$, then, for $b = \hat {b}({{A}_{1}})$, the cycle of system (1.1) passing through the point $( - {{A}_{1}},0)$ is repelling. This assertion follows from the properties of the vector field rotation.

To describe basins of attraction of cycles existing for various values of parameter b, apply method (2.1)–(2.3) for all A such that $0 < A < {{A}_{0}}$ (for the numerical implementation, a step with respect to A is selected). This yields dependence $b = \hat {b}(A)$ describing cycles existing in system (1.1) for various values of b. In particular, if the corresponding values of $\hat {b}(A)$ coincide each other for more than one value of A then more than one cycle exists for such a value $b = \hat {b}(A)$ and unstable cycles bound basins of attraction of orbitally stable cycles. If procedure (2.2) converges for all the corresponding values of A, then the description obtained this way is complete. In other words, the convergence of the method in a sufficiently broad range of values of A is a sufficient condition for obtaining exhausting information on the basins of attraction of the constructed orbitally stable cycles.

Consider an example of the application of method (2.1)–(2.3), including the analysis of basins of attraction of the constructed periodic solutions, to a particular mechanical system.

4. METHOD APPLICATION: EXAMPLE

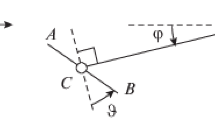
Consider a heavy aerodynamic pendulum in a stationary horizontal airflow (see Fig. 1). Similar problems are considered in [21–23] in relation to the search of self-oscillating and autorotation modes of pendulum systems in flow-energy conversion problems. Our example differs from the mentioned ones by the orientation of the blade with respect to the holder and by the character of the location of the object’s center of mass. In [24], the oscillation amplitude is maximized for a heavy pendulum with a viscous friction, where the control is the location of a heavy point on the holder; the constructed control has a relay form, and switchings occur if the sign of the angular coordinate or angular speed of the pendulum changes.

Fig. 1.

Scheme of aerodynamic pendulum.

The aerodynamic pendulum is a rigid body that can rotate around a fixed horizontal axis O. It consists of the holder OG and the blade, which is a plate orthogonal to the holder. The center of mass of the pendulum coincides with point G. The pendulum is located in the gravitational field in the horizontal airflow. The vector ${\mathbf{V}}$ of the flow velocity lies in the plane of oscillation of the pendulum.

In the sequel, the following notation is used: $\varphi$ is the rotation angle of the holder OG, counted from the vertical axis, r is the length of the holder OG, $m$ is the mass of the pendulum, and J is the pendulum’s moment of inertia with respect to the axis of rotation.

Introduce the following kinematic characteristics of the motion: $\omega = r{{V}^{{ - 1}}}d\varphi {\text{/}}dt$ is the dimensionless angular speed of the pendulum, V is the value of the flow speed, U is the airspeed of point G, and $\alpha = {\text{arctan}}({\text{sin}}\varphi {\text{/}}(\omega - {\text{cos}}\varphi ))$ is the instantaneous angle of attack (the angle between vector U and the plate).

The aerodynamic action on the pendulum is described by the quasi-steady approach

$$D = \frac{1}{2}\rho S{{U}^{2}}{{C}_{D}}(\alpha ),\quad L = \frac{1}{2}\rho S{{U}^{2}}{{C}_{L}}(\alpha )$$

(see [25, 26]), where D is the drag force, L is the lift force, $\rho$ is the air density, S is the reference area of the plate, and ${{C}_{D}}(\alpha )$ and ${{C}_{L}}(\alpha )$ are the dimensionless coefficients of the drag force and the lift force.

The aerodynamic coefficients are approximated by the following functions which reflect their specific properties:

$${{C}_{D}}(\alpha ) = 0.1 + {{\sin }^{2}}\alpha \quad {\text{and}}\quad {{C}_{L}}(\alpha ) = \sin 2\alpha .$$

It is assumed that the moment of value $T = - {{T}_{0}}{\text{sgn}}\omega$ is applied at hinge О. It can be treated as a relay control torque. If T is a dissipative moment (i.e., ${{T}_{0}} > 0$), then it can also be interpreted as dry friction in the hinge.

In dimensionless variables, the equations of motion of the system can be represented by a system of type (1.1), where angle $\varphi$ corresponds to variable x, $\omega$ corresponds to variable y, and the dot denotes the derivative with respect to the dimensionless time $\tau = Vt{\text{/}}r$:

$$\begin{gathered} \dot {\varphi } = \omega , \\ \dot {\omega } = - p\sin \varphi + a\left( {Q(\varphi ,\omega ) - b\operatorname{sgn} \omega } \right), \\ Q(\varphi ,\omega ) = \sqrt {{{{(\omega - \cos \varphi )}}^{2}} + {{{\sin }}^{2}}\varphi } \left( {{{C}_{L}}(\alpha )\sin \varphi - {{C}_{D}}(\alpha )(\omega - \cos \varphi )} \right), \\ a = \frac{{\rho S{{r}^{3}}}}{{2J}},\quad b = \frac{{2{{T}_{0}}}}{{\rho Sr{{V}^{2}}}},\quad p = \frac{{mg{{r}^{3}}}}{{J{{V}^{2}}}}. \\ \end{gathered} $$

((4.1))

Further, we assume that p = 1. Since system (4.1) has a cylindrical phase space, it suffices to consider $\varphi$ on the interval $[ - \pi ,\pi )$.

For $a < {{a}_{1}} \approx 2.1$, the pendulum has two equilibriums. Further, we consider a in this range. Due to the actions of aerodynamic forces (in the case where b = 0), the lower equilibrium of the heavy pendulum is displaced along the flow, the upper one is displaced against the flow, the fixed point $({{\varphi }_{1}},0)$ corresponding to the upper equilibrium remains a saddle, and the fixed point $({{\varphi }_{0}},0)$ corresponding to the lower one is asymptotically stable. If the value of b is different from zero, then the right-hand side of system (4.1) has a discontinuity along line ω = 0. This leads to the following effect: on line ω = 0, in the punctured neighborhood of each equilibrium $({{\varphi }_{i}},0)$, a special set ${{\wp }_{i}}$ appears such that $\left| {Q(\varphi ,0)} \right| \leqslant \left| b \right|$ for all points $(\varphi ,0)$ of this set.

Apply procedure (2.1)–(2.3) to find coefficient b providing the existence of an oscillation mode of a pendulum with the prescribed mean (with respect to time) mechanical energy. For positive values of b, such a problem can be interpreted as the description of the dependence of the mean energy of steady-state oscillations on the dry friction coefficient in the axis of the pendulum. Note that, unlike the aerodynamic pendulum which periodic motions are described in [27], this system is not centrally symmetric.

If there exists a cycle of system (4.1), then it encloses the equilibrium $({{\varphi }_{0}},0)$. According to the proposed algorithm, we start from the auxiliary problem to find a cycle passing through the point $( - A,0)$, where $- \pi < A < {{\varphi }_{0}}$. For the numerical implementation of the method, the following criterion of the “practical” convergence is used: if there exists an iteration such that the value ${{\Delta }_{n}} = \mathop {\max }\limits_x \left| {y_{n}^{ \pm }(x;A) - y_{{n - 1}}^{ \pm }(x;A)} \right|$ on this iteration is less that the threshold value (in our case, the value 0.001 is selected), then we suppose that the iteration process is completed.

For all values A for which sequences (2.2) converge, compute h along the numerically constructed phase curves $\tilde {y}_{{}}^{ + }(x;A)$ and $\tilde {y}_{{}}^{ - }(x;A)$ using relation (2.3).

Figure 2 provides the dependence $\tilde {b}\left( h \right)$ obtained for the numerical realization of the method (2.1)–(2.3) for the following two values of parameter a: a = 0.01 and a = 1. Figure 3 provides graphs $(n,{{\Delta }_{n}})$ characterizing the convergence speed of the method for several different values of h and a.

Fig. 2.

Dependence of value of h on coefficient b for a = 0.01 and a = 1. Dense curves denote families of attracting cycles, while dotted curves denote families of unstable cycles.

Fig. 3.

Dependence of residual on iteration number for a = 0.01 and a = 1, corresponding to various values of h.

The dense branches of the curves in Fig. 2 correspond to families of attracting steady-state oscillations, while the dotted branches correspond to families of repelling steady-state oscillations. In Fig. 2, the bifurcation values of parameter b are shown for the case where a = 1 (for other values of a, they can be introduced in the same way). The following bifurcation occurs, while parameter b moves from the right to the left through value $b = {{b}_{c}} = 0$: the attracting special set ${{\wp }_{0}}$ surrounding the lower equilibrium shrinks to a point generating an orbitally stable cycle. For each arbitrarily small negative b there exist a new special set ${{\wp }_{0}}$ surrounding the isolated equilibrium $({{\varphi }_{0}},0)$; however, it is a repelling set. All the region inside the generated cycle, including the set ${{\wp }_{0}}$, but excluding the equilibrium itself, is a part of the basin of attraction of the cycle. From the outside, the basin of attraction of the generated cycle is bound by the unstable cycle. For $b = {{b}_{d}}$ (${{\left. {{{b}_{d}}} \right|}_{{a = 1}}} \approx - 0.082$), the attracting and repelling cycles merge with each other. Attracting cycles with values $h$ such that ${{h}_{c}} < h < {{h}_{d}}$ are realized for negative values of coefficient b.

If an attracting cycle with values h such that ${{h}_{e}} < h < {{h}_{f}}$ exists, then its basin of attraction is bounded from inside by an unstable cycle. From outside, it is bounded by the phase trajectory passing through an edge point of the special set ${{\wp }_{1}}$. Such cycles are realized for positive values of coefficient b (the case of the control simulating dry friction). For $b = {{b}_{e}}$ (${{\left. {{{b}_{e}}} \right|}_{{a = 1}}} \approx 0.158$), the attracting and repelling cycles merge with each other. For $b = {{b}_{f}}$ (${{\left. {{{b}_{f}}} \right|}_{{a = 1}}} \approx 0.137$), the attracting cycle is destroyed, reaching the boundary of the special set ${{\wp }_{1}}$ surrounding the fixed point $({{\varphi }_{1}},0)$. The corresponding point on the curve $\tilde {b}\left( h \right)$ is denoted by F (see Fig. 2). The values satisfying the inequality $h > {{h}_{f}}$ correspond to pendulum rotations (not to oscillations).

Consider the behavior of system (4.1) for the case where a = 1 and the amplifying coefficient $b = - 0.07$. In Fig. 2, points P and R correspond to this case. Figure 4 displays the corresponding cycles (the pairs of curves $\tilde {y}_{n}^{ + }(x;A)$ and $\tilde {y}_{n}^{ - }(x;A)$) obtained by method (2.1) and (2.2) (the attracting one is shown by the bold dense curve, while the repelling one is shown by the dotted curve) and the phase trajectories of system (4.1) constructed by the Runge–Kutta method (shown by the thin dense curve) for $b = - 0.07$. We see that the results of numerical implementation of the new method are entirely coordinated with the results of the direct numerical integration of the system.

Fig. 4.

Elements of phase portrait of system (4.1) for a = 1 and $b = - 0.07$, numerically constructed by method (2.1) and (2.2) (attracting cycle is denoted by bold dense curve, while repelling cycle is denoted by dotted curve) and by Runge–Kutta method (this is denoted by thin dense curves).

Consider the behavior of system (4.1) for the case where a = 1 and the amplifying coefficient b = 0.14. In Fig. 2, points K and M correspond to this case. Figure 5 displays the corresponding cycles obtained by method (2.1)–(2.2) and the phase trajectories of system (4.1) constructed by the Runge–Kutta method. The results of the numerical application of the new method are entirely coordinated with the results of the direct numerical integration of the system.

Fig. 5.

Elements of phase portrait of system (4.1) for a = 1 and b = 0.14, numerically constructed by method (2.1) and (2.2) (attracting cycle is denoted by bold dense curve, while repelling cycle is denoted by dotted curve) and by Runge–Kutta method (this is denoted by thin dense curves).

Figure 6 provides an example of the form of iterative approximations for cycle K, i.e., the curves $y_{n}^{ + }(x;A)$ and $y_{n}^{ - }(x;A)$ for a = 1. The zero iteration is determined by the method proposed in [12]; it coincides with the cycle of the mathematical pendulum.

Fig. 6.

Examples of iteration curves $y_{n}^{ + }(x;A)$ and $y_{n}^{ - }(x;A)$ for cycle K (a = 1).

Thus, to implement the desired program control for various values of h, the values of the amplifying coefficient b such that ${{b}_{d}} < b < {{b}_{e}}$ are to be used. Thus, to provide a possibility to implement the program control, the restriction for the value of the control torque is to be greater than or equal to $\max (\left| {{{b}_{d}}} \right|,\left| {{{b}_{e}}} \right|)$. Assume that the exact instantaneous information about the current angle and angular speed of the pendulum is always available and the restriction for the control coincides with $\max (\left| {{{b}_{d}}} \right|,\left| {{{b}_{e}}} \right|)$, i.e., with ${{b}_{e}}$ (for the considered example). Then, the following strategy is preferable in order to achieve a neighborhood of the program trajectory as soon as possible. Assume that the phase point corresponding to the initial-value conditions is located inside (outside) the program cycle. First, we assign $b = - {{b}_{e}}$ ($b = {{b}_{e}}$). Once the trajectory $(\varphi (t),\omega (t))$ intersects the curve $\tilde {y}_{{}}^{ + }(\varphi ;\tilde {A}(h))$ or $\tilde {y}_{{}}^{ - }(\varphi ;\tilde {A}(h))$, the value of the amplifying coefficient b is to be changed for b = $\tilde {b}(h)$. For a = 1, examples of the corresponding transitional processes are displayed by the dotted curves in Fig. 7.

Fig. 7.

Examples of reaching of cycle R from various initial-value conditions for case of one-switching controls.

Thus, for a = 1, the data on the program values of the control torque and program trajectories obtained by algorithm (2.1)–(2.3) are sufficient to reach the program mode with values $h \in ({{h}_{c}},{{h}_{d}}) \cup ({{h}_{e}},{{h}_{f}})$ from the wide range of initial-value conditions.

5. DISCUSSION OF RESULTS

Implementing method (2.1)–(2.3) numerically, we describe the dependence of the mean value of the mechanical energy of steady-state oscillations of the aerodynamic pendulum on the amplifying coefficient b of the relay control action. The stability properties of the found cycles are described. In particular, it is clear from Fig. 2 that, under the considered relay control, attracting oscillation modes with relatively low (${{h}_{c}} < h < {{h}_{d}}$) and relatively high (${{h}_{e}} < h < {{h}_{f}}$) values of the mean energy can be implemented. Oscillations with intermediate energy values are unstable under this kind of control. They divide basins of attraction of orbitally stable periodic modes.

The considered example shows the efficiency of the proposed method for constructing periodic solutions of a system of type (1.1), including the case of a discontinuous right-hand side. A significant difference of the proposed method from the already known numerical-analytic iterative procedures for constructing periodic solutions (e.g., [15–18]) is the nonlinearity of the generating zero-approximation system. Regarding the generation of oscillations of an autonomous system, the advantages of the proposed method in comparison with known approaches are as follows: no transition to nonautonomous equations is required (unlike [15, 16]), the presence of high harmonics in the program periodic solution has no a priori influence on the convergence speed (unlike projection methods), and it is possible to solve the problem under specific restrictions on the control structure, e.g., under the condition that the control depends only on the phase velocity (unlike [5, 6]).

Note that the value of parameter а affects the convergence speed and the fact of the convergence of procedure (2.1) and (2.2) itself. Examples of the numerical implementation of the method show that the iterative process (2.2) converges rapidly for sufficiently small values of a and near the merging points of the cycles (see Fig. 3), i.e., in the cases where methods for finding periodic solutions based on direct numerical integration work relatively slowly.

However, as a rule, the convergence of the method is lost once the values of а become sufficiently large. The slowest convergence of method (2.1) and (2.2) and the absence of convergence are observed near the bifurcation points corresponding to $b = {{b}_{c}}$ and $b = {{b}_{f}}$, i.e., in the case where the cycle is located close to the special sets ${{\wp }_{0}}$ or ${{\wp }_{1}}$.

CONCLUSIONS

For dynamical systems with one degree of freedom, a numerical-analytic method for the construction of a control is proposed such that the constructed control guarantees the existence of a steady-state oscillation mode with the prescribed value of the mean mechanical energy. Unlike many other approaches, the method is applicable for searching for a control depending only on the phase speed.

The method is based on the search for an amplifying coefficient of the control action (which is a varied parameter of the model), providing the existence of a periodic trajectory passing through the given point of the phase plane of the system. The orbital stability conditions are obtained for steady oscillations. The advantages of the method compared with other numerical-analytic approaches applicable for similar problems are described.

Using the problem on a heavy aerodynamic pendulum, we demonstrate the capabilities of the method, provide results of the numerical simulation illustrating the convergence speed, and describe the range of the parameters of the problem in which the method is preferable to the approach based on the direct numerical integration of the system.