Method for Generating Asynchronous Self-Sustained Oscillations of a Mechanical System with Two Degrees of Freedom

Abstract

An autonomous nonconservative mechanical system with two degrees of freedom is studied. The system is subject to a feedback control with two control impact gain factors. It is required to select the values of these factors in such a way as to ensure existence of asynchronous self-sustained oscillations with prescribed properties. An iterative method is proposed to search for the corresponding values of control impact gain factors. This approach is based on constructing auxiliary second-order systems and generating limit cycles in these systems. The algorithm that is used for this purpose represents a modification of the Andronov–Pontryagin method, but does not require the presence of a small parameter in the system. The efficiency of this approach is illustrated on a problem of generating asynchronous self-sustained oscillations/rotations in a model of an aerodynamic pendulum. The applicability conditions of the algorithm and the possible modifications are discussed.

INTRODUCTION

The term “self-sustained oscillations” was introduced by A.A. Andronov in the beginning of the 20th century for describing a process which in the mathematical model may be put in correspondence to the Poincaré limit cycle of the autonomous system of differential equations. Firstly, he considered the case of a nonconservative second-order system. Introducing the concept, Andronov proposed an idea for searching the cycles corresponding to self-sustained oscillations [1]. Somewhat later, this idea was formalized by Pontryagin [2]. The proposed approach is closely related to the Krylov–Bogolyubov method; it is inferior to the latter in terms of the dimension of suitable systems, but is more convenient for second-order systems. Thus, the Andronov–Pontryagin method is being intensively developed and applied in modern research on planar dynamical systems [3–11], including when solving problems related to the 16th problem of Hilbert [12, 13].

As the Krylov–Bogolyubov averaging method, the Andronov–Pontryagin method presupposes the presence of a small parameter in the system. However, for both methods there are modifications with an iterative procedure that allow releasing the requirement concerning the presence of a small parameter: for the first method in [14, 15] and for the second method in [16–18]. For these methods, the convergence rate and the convergence itself are dependent on the Lipschitz constant of the function describing the non-Hamiltonian terms in the system.

The concept of self-sustained oscillations can be naturally extended to the case of a mechanical system with two degrees of freedom described by an autonomous fourth-order dynamical system. However, in this system, self-sustained oscillations may correspond both to the limit cycle or to the attractor of a more complex structure, for instance, the quasi-periodic trajectory.

Compared to the case of one degree of freedom, the methods for studying the self-sustained oscillations for systems with two or more generalized coordinates become substantially more sophisticated. Among them we may distinguish the approaches based on the direct integration of dynamical equations, the projection methods, the methods based on averaging, etc. A brief survey of the algorithm for searching the periodic solutions is given in [18]; for the case of quasi-periodic solutions, see [19]; among the newest methods, we may note works [20–24]. The realization of the methods intended to describe the quasi-periodic solutions requires, as a rule, highly complicated computational algorithms.

In this work we propose a numerical-analytical method for searching (for generating) self-sustained oscillations, which is relatively simple in its implementation and does not require additional replacement of variables. The approach is based on consideration of two auxiliary second-order systems and application of the method based on the Andronov–Pontryagin method [17] to each of them. Moreover, the algorithm allows detecting self-sustained oscillations (generating them if we assume the presence of the control parameter) which correspond to attractors not being periodic trajectories. However, the method usually does not detect the periodic trajectories of the system, because it does not take into account the effects associated with synchronization. Note that there are several well-known approaches to forming periodic self-sustained oscillations for certain classes of systems with two or more degrees of freedom (for instance, the approach in [25]).

Earlier, the authors of [26, 27] proposed a method for constructing trajectories close to periodic ones (but not periodic) which is intended to generate the asynchronous modes of self-sustained rotation of a mechanical system with two rotational degrees of freedom. They considered the class of systems narrower than the class of systems in the current work: in [26, 27] the cross links between the subsystems depend only on the phase velocities, but not on the coordinates; moreover, in [27] this dependence is assumed to be linear. In the current work the cross links between the subsystems are dependent both on the phase coordinates and on the phase velocities (in the general case, the dependence is nonlinear). Therefore, the method for constructing a solution close to the periodic one becomes more sophisticated (the method of [26] substantially relies on the absence of cross links in coordinates whereas the approach in [27] in addition principally uses the linear character of the cross links in velocities). The additional technical sophistication in the present work is associated with the fact that we consider the solutions corresponding not only to self-sustained rotations, but also to self-sustained oscillations.

We illustrate the efficiency of the algorithm proposed below on an example of the problem about the formation of self-sustained oscillations of an aerodynamic pendulum. We determine the coefficients in the control law for which there exists a trajectory close to the periodic one and corresponding to the oscillations with a prescribed amplitude.

1 PROBLEM FORMULATION

Consider an autonomous nonconservative mechanical system with two degrees of freedom. Suppose that in the dimensionless variables the equations of motion of the system have the following form (a dot denotes the derivative with respect to dimensionless time τ):

$$\begin{gathered} {{{\dot {\varphi }}}_{1}} = {{\omega }_{1}}, \\ {{{\dot {\omega }}}_{1}} = \sum\limits_{k = 0}^N {{{F}_{{1k}}}\left( {{{\varphi }_{1}},{{\omega }_{1}},{{G}_{{2k}}}({{\varphi }_{2}},{{\omega }_{2}})} \right)} + {{u}_{1}}({{\varphi }_{1}},{{\varphi }_{2}},{{\omega }_{1}},{{\omega }_{2}}), \\ {{{\dot {\varphi }}}_{2}} = {{\omega }_{2}}, \\ {{{\dot {\omega }}}_{2}} = \sum\limits_{k = 0}^N {{{F}_{{2k}}}\left( {{{\varphi }_{2}},{{\omega }_{2}},{{G}_{{1k}}}({{\varphi }_{1}},{{\omega }_{1}})} \right)} + {{u}_{2}}({{\varphi }_{1}},{{\varphi }_{2}},{{\omega }_{1}},{{\omega }_{2}}). \\ \end{gathered} $$

(1.1)

We consider the control of the form

$$\begin{gathered} {{u}_{1}} = - {{b}_{1}}{{f}_{1}}({{\varphi }_{1}},{{\omega }_{1}}) + {{g}_{2}}({{b}_{2}},{{\varphi }_{2}},{{\omega }_{2}}), \\ {{u}_{2}} = - {{b}_{2}}{{f}_{2}}({{\varphi }_{2}},{{\omega }_{2}}) + {{g}_{1}}({{b}_{1}},{{\varphi }_{1}},{{\omega }_{1}}). \\ \end{gathered} $$

Here, φ_i are the generalized coordinates and ω_i are the corresponding generalized velocities. From now on, i = 1, 2. The functions F_ik are determined from the expression for the mechanical energy of the system and from the external forces and moments, including nonconservative ones, the functions G_ik describe the interaction in the system, u_i are the control components, and b_i are the control impact gain factors to be selected according to the control problem. The functions f_i are responsible for the control impact intended to vary the behavior of the variables φ_i and ω_i. The function g₂ describes the indirect effect of the control impact in φ₂ and ω₂ on the variation in the variables φ₁ and ω₁, and a similar role is played by the function g₁.

We select the functions f_i so that the following property is satisfied: ${{\omega }_{i}}{{f}_{i}}({{\varphi }_{i}},{{\omega }_{i}}) > 0$ for ${{\omega }_{i}} \ne 0$ (for instance, ${{f}_{i}} = {{\omega }_{i}}$). All functions in (1.1) are supposed to be analytic.

Suppose that, using the control, we need to organize the mode of self-sustained oscillations in the mechanical system described by Eqs. (1.1) and this mode is such that the amplitude of oscillations in each variable φ_i remains near some prescribed values $\varphi _{i}^{ * }$ and the time averages (on a long time period) of the oscillation frequencies in two variables are incomparable (there occurs no synchronization). Note that asynchronous oscillations are of interest for several applied problems [28, 29].

We assume that the right-hand sides of system (1.1) depend on the coordinates φ_i with a period of 2π. In addition to the already formulated problem, we further consider two particularly close problems: generating a mode at which in both coordinates there occur rotations with near-constant mutually incomparable angular velocities $\omega _{i}^{ * }$ and generating a mode at which in one of the coordinates there occur oscillations with an amplitude close to the prescribed one whereas in the second coordinate there occurs rotation with an angular velocity close to the prescribed one.

2 PARTIALLY AVERAGED SYSTEMS

We construct two auxiliary partially averaged second-order systems with as yet undetermined parameters:

$$\begin{gathered} {{{\dot {\varphi }}}_{1}} = {{\omega }_{1}}, \\ {{{\dot {\omega }}}_{1}} = \sum\limits_{k = 1}^N {{{F}_{{1k}}}({{\varphi }_{1}},{{\omega }_{1}},\bar {G}_{{2k}}^{j})} + \bar {g}_{2}^{j} - b_{1}^{j}{{f}_{1}}({{\varphi }_{1}},{{\omega }_{1}}), \\ \end{gathered} $$

(2.1)

$$\begin{gathered} {{{\dot {\varphi }}}_{2}} = {{\omega }_{2}}, \\ {{{\dot {\omega }}}_{2}} = \sum\limits_{k = 1}^N {{{F}_{{2k}}}({{\varphi }_{2}},{{\omega }_{2}},\bar {G}_{{1k}}^{j})} + \bar {g}_{1}^{j} - b_{2}^{j}{{f}_{2}}({{\varphi }_{2}},{{\omega }_{2}}). \\ \end{gathered} $$

(2.2)

Here, $\bar {G}_{{ik}}^{j}$, $\bar {g}_{i}^{j}$, $b_{i}^{j}$ are the unknown parameters to be determined; their computation is performed by the method of successive approximations. The upper index j ($j \geqslant 0$) corresponds to the number of the iteration step.

The coefficient $b_{i}^{j}$ in system (2.i) corresponds to the rotation of the vector field (due to the abovementioned property of the function f_i: ${{\omega }_{i}}{{f}_{i}}({{\varphi }_{i}},{{\omega }_{i}}) > 0$). This control impact gain factor must be selected so that in system (2.i) there occurs a limit cycle passing through the point ($- \varphi _{i}^{ * }$, 0). In the following, we denote such cycle by ($\tilde {\varphi }_{i}^{j}(t)$, $\tilde {\omega }_{i}^{j}(t)$). We assume that the sought value $b_{i}^{j}$ exists. To determine the value of $b_{i}^{j}$, we may apply different methods for generating/searching for periodic trajectories, see the survey on them, e.g., in [18]. When needed, the localization of the regions of existence of limit cycles may be carried out using the methods given in [30, 31]. In the current work we use the method of [16] to determine the values of $b_{i}^{j}$ in the case if the system possesses the central symmetry, the method of [17] for the system without central symmetry, or the method of [18] in the case if self-sustained rotation occurs in some coordinate instead of self-sustained oscillations. All the mentioned cases are illustrated below on the problem of the aerodynamic pendulum.

The parameters $\bar {G}_{{ik}}^{j}$ and $\bar {g}_{i}^{j}$ are determined as follows

$$\bar {G}_{{2k}}^{0} = \bar {g}_{2}^{0} = 0,\quad \bar {G}_{{2k}}^{{j + 1}} = \frac{1}{{T_{2}^{j}}}\int\limits_0^{T_{2}^{j}} {{{G}_{{2k}}}(\tilde {\varphi }_{2}^{j}(t),\tilde {\omega }_{2}^{j}(t))dt} ,$$

$$\bar {g}_{2}^{{j + 1}} = \frac{1}{{T_{2}^{j}}}\int\limits_0^{T_{2}^{j}} {{{g}_{2}}(b_{2}^{j},\tilde {\varphi }_{2}^{j}(t),\tilde {\omega }_{2}^{j}(t))dt;\quad } j \geqslant 0,$$

$$\bar {G}_{{1k}}^{j} = \frac{1}{{T_{1}^{j}}}\int\limits_0^{T_{1}^{j}} {{{G}_{{1k}}}(\tilde {\varphi }_{1}^{j}(t),\tilde {\omega }_{1}^{j}(t))dt} ,\quad \bar {g}_{1}^{j} = \frac{1}{{T_{1}^{j}}}\int\limits_0^{T_{1}^{j}} {{{g}_{1}}(b_{1}^{j},\tilde {\varphi }_{1}^{j}(t),\tilde {\omega }_{1}^{j}(t))dt;\quad } j \geqslant 0.$$

Here, $T_{i}^{j}$ is the period of the limit cycle ($\tilde {\varphi }_{i}^{j}(t)$, $\tilde {\omega }_{i}^{j}(t)$) of system (2.i) constructed at the jth step. To apply the algorithm, it is convenient to use the formulas eliminating time dependence in the computation of $\bar {G}_{{ik}}^{j}$; the same applies to the computation of $\bar {g}_{i}^{j}$,

$$\bar {G}_{{ik}}^{{j + i - 1}} = \frac{1}{{T_{i}^{j}}}\left( {\int\limits_{ - \varphi _{i}^{ - }}^{\varphi _{i}^{ + }} {\frac{{{{G}_{{ik}}}(\varphi ,\omega _{i}^{{j + }}(\varphi ))}}{{\omega _{i}^{{j + }}(\varphi )}}d\varphi } - \int\limits_{ - \varphi _{i}^{ - }}^{\varphi _{i}^{ + }} {\frac{{{{G}_{{ik}}}(\varphi ,\omega _{i}^{{j - }}(\varphi ))}}{{\omega _{i}^{{j - }}(\varphi )}}d\varphi } } \right),$$

$$T_{i}^{j} = \left( {\int\limits_{ - \varphi _{i}^{ - }}^{\varphi _{i}^{ + }} {\frac{1}{{\omega _{i}^{{j + }}(\varphi )}}d\varphi } - \int\limits_{ - \varphi _{i}^{ - }}^{\varphi _{i}^{ + }} {\frac{1}{{\omega _{i}^{{j - }}(\varphi )}}d\varphi } } \right);\quad j \geqslant i - 1.$$

Here, $\varphi _{i}^{ - } = \varphi _{i}^{ * }$. The point ($\varphi _{i}^{ + }$, 0) is the rightmost point of the periodic trajectory ($\tilde {\varphi }_{i}^{j}(t)$, $\tilde {\omega }_{i}^{j}(t)$) on the phase plane (${{\varphi }_{i}}$, ${{\omega }_{i}}$); $\omega _{i}^{{j \pm }}({{\varphi }_{i}})$ is the function describing the dependence of ω_i on φ_i along the upper/lower part of the limit cycle ($\tilde {\varphi }_{i}^{j}(t)$, $\tilde {\omega }_{i}^{j}(t)$), respectively (that is, in the upper/lower half-plane), and $\omega _{i}^{{j \pm }}(\varphi _{i}^{ + })$ = $\omega _{i}^{{j \pm }}(\varphi _{i}^{ - })$ = 0. In the case of periodic trajectory $\omega _{i}^{j}(\varphi )$, corresponding to the self-sustained rotation along the angular coordinate, the formulas similar in their meaning are valid; then, $\omega _{i}^{j}({{\varphi }_{i}})$ is a 2π-periodic function of φ_i and, because such trajectory is entirely situated in the upper/lower part of the phase cylinder, the index ± is not needed for it,

$$\bar {G}_{{ik}}^{{j + i - 1}} = \frac{1}{{T_{i}^{j}}}\int\limits_0^{2\pi } {\frac{{{{G}_{{ik}}}(\varphi ,\omega _{i}^{j}(\varphi ))}}{{\omega _{i}^{j}(\varphi )}}d\varphi } ,\quad T_{i}^{j} = \int\limits_0^{2\pi } {\frac{1}{{\omega _{i}^{j}(\varphi )}}d\varphi } ;\quad j \geqslant i - 1.$$

The proposed algorithm allows not computing the explicit dependence of the variables on time on the limit cycle; it is enough to determine the dependence of ω_i on the coordinate φ_i along the upper/lower part of the cycle. This radically reduces the amount of necessary computations when generating limit cycles of auxiliary systems. As an example, we may compare the description of limit cycles of a perturbed Duffing oscillator expanding [32] and not expanding [11] the time dependence: in the latter case the number of computations is reduced many times.

Thus, at the jth step of the algorithm, using the previous step, we construct the periodic trajectory of system (2.1) passing through the point ($- \varphi _{1}^{ * }$, 0) as a two-valued function $\omega _{1}^{{j \pm }}({{\varphi }_{1}})$ on the coordinate. We determine the corresponding value of $b_{1}^{j}$ which provides the existence of such trajectory. Along the trajectory we compute the values $\bar {G}_{{1k}}^{j}$ and $\bar {g}_{1}^{j}$ of the functions G_1k and g₁ time-averaged over the period. These values are substituted into the right-hand side of system (2.2), after which we similarly perform the jth step of the algorithm for system (2.2). The average values $\bar {G}_{{2k}}^{{j + 1}}$ and $\bar {g}_{2}^{{j + 1}}$ of the functions G_2k and g₂ obtained at the jth step are used for the (j + 1)th step in system (2.1) and so on until for each i the difference between the values $\bar {G}_{{ik}}^{j}$, $\bar {g}_{i}^{j}$, and $b_{i}^{j}$ obtained at the jth and (j + 1)th steps becomes less than some prescribed threshold value (the criterion of practical convergence of the algorithm).

Below, when discussing the attraction properties of solutions, we use the designation $db_{i}^{j}{\text{/}}d\varphi _{i}^{ * }$ = ${{\left. {db_{i}^{j}{\text{/}}d\varphi _{i}^{0}} \right|}_{{\varphi _{i}^{0} = \varphi _{i}^{ * }}}}$, where $b_{i}^{j}(\varphi _{i}^{0})$ is the value of $b_{i}^{j}$ providing the presence of limit cycle passing through the point ($- \varphi _{i}^{0}$, 0) for fixed values $\bar {G}_{{ik}}^{j}$, $\bar {g}_{i}^{j}$$\bar {G}_{{ik}}^{j}$, $\bar {g}_{i}^{j}$. According to the properties of the rotation of the vector field for $db_{i}^{j}{\text{/}}d\varphi _{i}^{ * }$ < 0, the limit cycle $\omega _{i}^{{j \pm }}({{\varphi }_{i}})$ is orbitally stable. In the case of trajectory 2π‑periodic in φ_i, the similar statement is valid for $db_{i}^{j}{\text{/}}d\omega _{i}^{ * }$ < 0. The corresponding theorems are discussed in detail in [16–18].

Suppose that, in the numerical realization of the method, at each jth step the values of $b_{i}^{j}$ are determined and the values of $\bar {G}_{{ik}}^{j}$, $\bar {g}_{i}^{j}$, and $b_{i}^{j}$ converge to some limit values as $j \to \infty$. Furthermore, if, beginning from some j, it is true that $db_{i}^{j}{\text{/}}d\varphi _{i}^{ * }$ < 0, then for sufficiently weak cross links between the subsystems we may expect that in system (1.1) with ${{b}_{i}}$ = $b_{i}^{ * }$ = $\mathop {\lim }\limits_{j \to \infty } b_{i}^{j}$ there exists an attracting near-periodic solution corresponding to self-sustained oscillations in the coordinates φ_i with the amplitudes close to $\varphi _{i}^{ * }$. In the case when in some coordinate we consider rotation and $db_{i}^{j}{\text{/}}d\omega _{i}^{ * }$ < 0, a similar statement holds.

If this hypothesis is confirmed, then the projections of the near-periodic trajectory of system (1.1) on the plane (${{\varphi }_{i}}$, ${{\omega }_{i}}$) are approximately characterized by the curves $\omega _{i}^{ \pm }({{\varphi }_{i}})$, which are the periodic trajectories existing in systems (2.i) at limit values $\bar {G}_{{ik}}^{ * }$, $\bar {g}_{i}^{ * }$, and $b_{i}^{ * }$ of the parameters. Due to continuous dependence of the trajectory on the parameters, the functions $\omega _{i}^{ \pm }({{\varphi }_{i}})$ are determined and are the limits of the functional sequences $\omega _{i}^{{j \pm }}({{\varphi }_{i}})$ as $j \to \infty$. These functions are computed in addition to $b_{i}^{ * }$ in the course of the algorithm execution.

We formulate the sufficient conditions of formation of asynchronous oscillations at finite cross links between the variables in system (1.1).

Theorem 1. Suppose that for each j ≥ 0 the periodic trajectories $\omega _{i}^{{j \pm }}({{\varphi }_{i}})$ and the corresponding values $\bar {G}_{{ik}}^{j}$, $\bar {g}_{i}^{j}$, and $b_{i}^{j}$ in systems (2.i) are determined. Suppose that all these sequences converge as $j \to \infty$ to some limits $\omega _{i}^{ \pm }({{\varphi }_{i}})$ is an attracting limit cycle of the system (2.i) at $\bar {G}_{{ik}}^{ * }$, $\bar {g}_{i}^{ * }$, and $b_{i}^{ * }$ and $db_{i}^{*}{\text{/}}d\varphi _{i}^{*}$ < 0. In addition, suppose that there exist the regions Ω_i on the planes (${{\varphi }_{i}}$, ${{\omega }_{i}}$) containing the curves $\omega _{i}^{ \pm }({{\varphi }_{i}})$ and such that at $({{\varphi }_{i}},{{\omega }_{i}}) \in {{\Omega }_{i}}$ the values of the right-hand side of the (2i)th equation of system (1.1) is different from the values of the right-hand side of the second equation of system (2.i) at $\bar {G}_{{ik}}^{ * }$, $\bar {g}_{i}^{ * }$, and $b_{i}^{ * }$ by the value Γ_i bounded in its absolute value by some constant A_i. Suppose that in the regions Ω_i there exist auxiliary curves $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\omega } _{i}^{ \pm }({{\varphi }_{i}})$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } _{i}^{ \pm }({{\varphi }_{i}})$ whose determination is given in the text of the proof. Then there exists an attractor in system (1.1) and the projection of this attractor onto the plane (${{\varphi }_{i}}$, ${{\omega }_{i}}$) is situated inside the strip limited by the curves $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\omega } _{i}^{ \pm }({{\varphi }_{i}})$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } _{i}^{ \pm }({{\varphi }_{i}})$ (that is, the attractor projections are located in the neighborhood of the curves $\omega _{i}^{ \pm }({{\varphi }_{i}})$).

Proof. At $({{\varphi }_{i}},{{\omega }_{i}}) \in {{\Omega }_{i}}$ the first two equations of system (1.1) become

$$\begin{gathered} {{{\dot {\varphi }}}_{1}} = {{\omega }_{1}}, \\ {{{\dot {\omega }}}_{1}} = \sum\limits_{k = 1}^N {{{F}_{{1k}}}({{\varphi }_{1}},{{\omega }_{1}},\bar {G}_{{2k}}^{*})} + \bar {g}_{2}^{*} - b_{1}^{*}{{f}_{1}}({{\varphi }_{1}},{{\omega }_{1}}) + \Gamma _{1}^{{}}({{\varphi }_{1}},{{\omega }_{1}},{{\varphi }_{2}},{{\omega }_{2}}); \\ \left| {{{\Gamma }_{1}}({{\varphi }_{1}},{{\omega }_{1}},{{\varphi }_{2}},{{\omega }_{2}})} \right| \leqslant {{A}_{1}}. \\ \end{gathered} $$

We formally consider the following nonautonomous system in the space of arbitrary values ${{\varphi }_{1}}$, ${{\omega }_{1}}$ for which we know that $\left| {{{U}_{1}}(t)} \right| \leqslant {{A}_{1}}$:

$$\begin{gathered} {{{\dot {\varphi }}}_{1}} = {{\omega }_{1}}, \\ {{{\dot {\omega }}}_{1}} = \sum\limits_{k = 1}^N {{{F}_{{1k}}}({{\varphi }_{1}},{{\omega }_{1}},\bar {G}_{{2k}}^{*})} + \bar {g}_{2}^{*} - b_{1}^{*}{{f}_{1}}({{\varphi }_{1}},{{\omega }_{1}}) + {{U}_{1}}(t). \\ \end{gathered} $$

(2.3)

For each trajectory of system (1.1) there exists a function U₁, $\left| {{{U}_{1}}(t)} \right| \leqslant {{A}_{1}}$, such that at $({{\varphi }_{i}},{{\omega }_{i}}) \in {{\Omega }_{i}}$ the projection of this trajectory of system (1.1) onto the plane (${{\varphi }_{1}}$, ${{\omega }_{1}}$) coincides with some trajectory of system (2.3).

The function U₁ in system (2.3) may be treated as the control impact, and we can formulate the problem of selection of the control impact U₁ which maximally deviates the solution from the curve $\omega _{1}^{ \pm }({{\varphi }_{1}})$, that is, simulate the worst possible perturbations caused by cross links.

Consider the case ${{U}_{1}} = {{A}_{1}}{\text{sgn}}{{\omega }_{1}}$. At this choice of U₁ system (2.3) is autonomous and the function U₁ in this system provides rotation of the vector field by a positive angle; at such rotation of the vector field of the system on the plane/cylinder, the attracting limit cycles expand, the repulsive ones shrink, and both limit cycles can collapse, for instance, by merging together [33].

At ${{U}_{1}} \equiv 0$ in system (2.3) there exists an attracting periodic trajectory $\omega _{1}^{ \pm }({{\varphi }_{1}})$. Suppose that, in transition to system (2.3) with ${{U}_{1}} = {{A}_{1}}{\text{sgn}}{{\omega }_{1}}$, this periodic trajectory is not destroyed, but, expanding, transits to some limit cycle $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } _{1}^{ \pm }({{\varphi }_{1}})$ and the curve $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } _{1}^{ \pm }({{\varphi }_{1}})$ is situated in the region Ω₁.

We similarly consider ${{U}_{1}} = - {{A}_{1}}{\text{sgn}}{{\omega }_{1}}$. Such a function provides the rotation of the field by a negative angle. Assume that, in transition to system (2.3) with ${{U}_{1}} = - {{A}_{1}}{\text{sgn}}{{\omega }_{1}}$, the periodic trajectory is not destroyed, but, expanding, transits to some attracting trajectory $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\omega } _{1}^{ \pm }({{\varphi }_{1}})$ and the curve $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\omega } _{1}^{ \pm }({{\varphi }_{1}})$ is situated in the region Ω₁.

To build the cycles $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\omega } _{1}^{ \pm }({{\varphi }_{1}})$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } _{1}^{ \pm }({{\varphi }_{1}})$, for instance, we may use the method of [17].

Then, for an arbitrary function U₁ given the condition $\left| {{{U}_{1}}(t)} \right| \leqslant {{A}_{1}}$, the trajectory of system (2.3) beginning at the strip limited by the curves $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\omega } _{1}^{ \pm }({{\varphi }_{1}})$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } _{1}^{ \pm }({{\varphi }_{1}})$ never leaves this strip. If we assume the contrary, then, at the point of intersection between the trajectory of system (2.3) and some of the strip boundaries, we obtain a contradiction: on the one side, the functions ${{U}_{1}} = \pm {{A}_{1}}{\text{sgn}}{{\omega }_{1}}$ provides the maximum/minimum value of the angle of the tangent inclination in system (2.3), and, on the other side, at the point of intersection between the trajectory and the strip boundary, the value of the angle of inclination of the tangent to the trajectory is larger/less than the angle of inclination of the tangent to the boundary.

We perform the analogous considerations for ${{\varphi }_{2}}$, ${{\omega }_{2}}$. Assume that the corresponding curves $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\omega } _{2}^{ \pm }({{\varphi }_{2}})$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } _{2}^{ \pm }({{\varphi }_{2}})$ exist and are located in Ω₂.

Under the assumption of existence of the curves $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\omega } _{i}^{ \pm }({{\varphi }_{i}})$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } _{i}^{ \pm }({{\varphi }_{i}})$ at $({{\varphi }_{i}},{{\omega }_{i}}) \in {{\Omega }_{i}}$, we find that the perturbations caused by the bounded cross links in system (1.1) do not destroy the near-periodic solution that exists when the functions describing the interaction are formally replaced by their averaged values $\bar {G}_{{ik}}^{ * }$ and $\bar {g}_{i}^{ * }$. This generating solution in the complete system transits to some attractor whose projection onto the plane (${{\varphi }_{i}}$, ${{\omega }_{i}}$) is situated inside the strip bounded by the curves $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\omega } _{i}^{ \pm }({{\varphi }_{i}})$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } _{i}^{ \pm }({{\varphi }_{i}})$.

Theorem 1 is proved.

In the case when in one of two systems (2.i) the periodic trajectory describes rotations, not oscillations, we may weaken the theorem conditions by considering the case when the upper and lower boundaries for the functions Γ_i describing the cross links are different from each other.

The choice of the control impact U₁ that maximally expands/narrows the limit cycle on the plane is carried out by analogy to the approach proposed in [34] and applied to the problem of the swing oscillations in [35].

In addition, we note that system (2.3) may be treated as a system with transient perturbations. The modern methods for studying controlled systems with transient perturbations are discussed and applied, e.g., in [36, 37]. In particular, in [36] an approach is developed at which the averaging is applied to construct the first approximation of the Lyapunov function.

Testing the conditions of Theorem 1 is nontrivial; nevertheless, it requires working only with second-order systems, not with fourth-order systems. In the case of fulfillment of the sufficient conditions, we localize a region inside which we definitely have an attractor of the complete fourth-order system. This attractor may have a small region of attraction; therefore, it can be substantially more difficult to find it by simple search of the initial conditions in the four-dimensional space than to verify that the conditions of Theorem 1 are satisfied.

As an example in which the conditions of Theorem 1 are realized, we consider one of the modes of asynchronous self-sustained rotation in a system with two degrees of freedom, the approximation for which was found in paper [26] (by the method being a special case of the algorithm proposed here). This is the mode of self-sustained rotation in a model of the double Darrieus wind turbine. The dynamic equations in the form of system (1.1) and the parameter values are given in work [26]. The mode is characterized by the program values of the dimensionless angular velocities $\omega _{1}^{ * }$ = $\omega _{2}^{ * }$ = 9.4. For such $\omega _{i}^{ * }$ the trajectories 2π‑periodic in φ_i for the partially averaged systems of type (2.i) are determined together with the corresponding values $b_{i}^{ * }$ ($b_{i}^{ * }$ ≈ 0.11). For the given $\omega _{i}^{ * }$ the conditions of Theorem 1 are satisfied, for instance, at ${{\Omega }_{i}}$ = $\{ {\kern 1pt} |{\kern 1pt} {{\omega }_{i}} - \omega _{i}^{ * }{\kern 1pt} |$ < 0.01}.

In the case when the cross links between the subsystems of Eqs. (1.1) are bounded by a small value, the conditions of Theorem 1 may be weakened. Let us present the corresponding result.

Theorem 2. Suppose that for each $j \geqslant 0$ the periodic trajectories $\omega _{i}^{{j \pm }}({{\varphi }_{i}})$ and the corresponding values $\bar {G}_{{ik}}^{j}$, $\bar {g}_{i}^{j}$, and $b_{i}^{j}$ in systems (2.i) are determined. Suppose that all these sequences converge as $j \to \infty$ to some limits $\omega _{i}^{ \pm }({{\varphi }_{i}})$ is an attracting limit cycle of the system (2.i) at $\bar {G}_{{ik}}^{ * }$, $\bar {g}_{i}^{ * }$, and $b_{i}^{ * }$. In addition, suppose that there exist finite regions Ω_i on the planes (${{\varphi }_{i}}$, ${{\omega }_{i}}$) containing the curves $\omega _{i}^{ \pm }({{\varphi }_{i}})$ and such that at $({{\varphi }_{i}},{{\omega }_{i}}) \in {{\Omega }_{i}}$ the values of the right-hand side of the (2i)th equation of system (1.1) are different from the values of the right-hand side of the second equation of system (2.i) at $\bar {G}_{{ik}}^{ * }$, $\bar {g}_{i}^{ * }$, and $b_{i}^{ * }$ by a value bounded in its absolute value by some arbitrarily small ε. In other words, the cross links in system (1.1) are small at least if ${{\varphi }_{i}}$, ${{\omega }_{i}}$ take their values from finite neighborhoods of the curves $\omega _{i}^{ \pm }({{\varphi }_{i}})$. Then, in system (1.1) there exists some attractor whose projection onto the plane (${{\varphi }_{i}}$, ${{\omega }_{i}}$) tends to the curve $\omega _{i}^{ \pm }({{\varphi }_{i}})$ as ε → 0.

Proof. Consider the system of the form (2.3) with ${{U}_{1}} = \varepsilon {\text{sgn}}{{\omega }_{1}}$ at $({{\varphi }_{1}},{{\omega }_{1}}) \in {{\Omega }_{1}}$. In the case ε = 0 this system has an attracting stable cycle $\omega _{1}^{ \pm }({{\varphi }_{1}})$. At sufficiently small ε > 0 such a cycle is not destroyed, but transits to the attracting cycle $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } _{1}^{{\varepsilon \pm }}({{\varphi }_{1}})$ situated outside the region bounded by the curves $\omega _{1}^{ \pm }({{\varphi }_{1}})$ (by the property of rotation of the vector field) and contracting to $\omega _{1}^{ \pm }({{\varphi }_{1}})$ as ε → 0. Similarly, at ${{U}_{1}} = \varepsilon {\text{sgn}}{{\omega }_{1}}$ in system (2.3) there exists an attracting cycle $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\omega } _{1}^{{\varepsilon \pm }}({{\varphi }_{1}})$ situated inside the region bounded by the curves $\omega _{1}^{ \pm }({{\varphi }_{1}})$ and contracting to $\omega _{1}^{ \pm }({{\varphi }_{1}})$ as ε → 0. At sufficiently small ε, both cycles $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\omega } _{1}^{{\varepsilon \pm }}({{\varphi }_{1}})$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } _{1}^{{\varepsilon \pm }}({{\varphi }_{1}})$ lie in the finite region Ω₁.

Consider the trajectory of system (1.1) with the initial conditions in (${{\varphi }_{i}}$, ${{\omega }_{i}}$) lying on the curve $\omega _{i}^{ \pm }({{\varphi }_{i}})$. The projection of this trajectory onto the plane (${{\varphi }_{1}}$, ${{\omega }_{1}}$) cannot get outside the tube bounded by the curves $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\omega } _{1}^{{\varepsilon \pm }}({{\varphi }_{1}})$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } _{1}^{{\varepsilon \pm }}({{\varphi }_{1}})$ while $({{\varphi }_{2}},{{\omega }_{2}}) \in {{\Omega }_{2}}$, because at the point of intersection with this tube the condition $\left| {{{U}_{1}}(t)} \right| \leqslant \varepsilon$ would be violated, which is impossible for $({{\varphi }_{i}},{{\omega }_{i}}) \in {{\Omega }_{i}}$. The similar property holds for the projection of this trajectory on the plane (${{\varphi }_{2}}$, ${{\omega }_{2}}$). Thus, the trajectory under consideration tends to some attractor whose projection onto each of the planes (${{\varphi }_{i}}$, ${{\omega }_{i}}$) occurs inside the tube bounded by the curves $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\omega } _{i}^{{\varepsilon \pm }}({{\varphi }_{i}})$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } _{i}^{{\varepsilon \pm }}({{\varphi }_{i}})$ and tends to the curve $\omega _{i}^{ \pm }({{\varphi }_{i}})$ as ε → 0.

Theorem 2 is proved.

For comparison’s sake, we note that in [38] the stability property of the solution was used to prove the preservation of asynchronous oscillations at small cross links in a fourth-order system characteristic for models of neural networks. On the basis of such considerations, we probably can substantially sharpen the result of Theorem 2 (for instance, by extending it to the near-periodic trajectories of system (1.1) which are not attracting both in direct and reverse time), but this is outside the scope of this work.

3 ON NUMERICAL TESTING, STABILITY QUESTIONS, AND AREA OF ALGORITHM APPLICABILITY

In the case when the conditions of Theorem 1 are not satisfied, the presence in the complete system of a near-periodic solution generated by periodic trajectories of the partially averaged systems requires additional testing, for instance, by direct numerical integration of system (1.1) with the initial conditions taken on the limit curves $\omega _{i}^{ \pm }({{\varphi }_{i}})$ or in their neighborhood (for instance, ${{\varphi }_{i}}(0)$ = $\varphi _{i}^{ * }$ and ${{\omega }_{i}}(0) = 0$). Note that a situation is possible in which in system (1.1) there exists a trajectory which is close to the periodic one whose projections onto the phase planes are situated near the constructed curves $\omega _{i}^{ \pm }(\varphi )$, but it is not attracting in both direct and reverse time. In the latter case the presence of such a solution will not be confirmed by numerical testing. It is possible to further develop the method by constructing the control impact stabilizing such trajectories.

The applicability area of the method is determined by the region of convergence of the iterative procedure and by the region in which the interaction of subsystems can be qualitatively described by averaged values of the cross-link functions.

Below, we provide an example demonstrating the efficiency of the proposed method for an underactuated system in which the cross links are not weak.

4 AN EXAMPLE OF APPLICATION TO A PROBLEM OF THE AERODYNAMIC PENDULUM

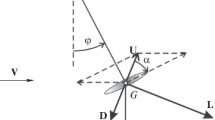
Consider a pendulum consisting of a support OC mounted in a fixed hinged joint O (the joint axis is vertical) and a plate AB mounted in a joint C (Fig. 1). The plane of the plate is vertical. The system is in a horizontal air flow with a velocity V and a density ρ. The system has two degrees of freedom which are described by the angle φ of rotation of the support OC measured in the counterclockwise direction relative to the wind direction and by the angle ϑ of the relative orientation of the plate measured in the counterclockwise direction from the direction perpendicular to the support OC. In the joint C, a spiral springis installed, whose undeformed state corresponds to the value ϑ = 0, and a moment of linear viscous friction is applied. In the joint O some control moment M_u is applied.

Fig. 1.

Suppose r is the length of the support OC, J₁ is the moment of inertia of the support with respect to the point O, m is the plate mass, the center of mass of the plate is situated at the point C, and J₂ is the moment of inertia of the plate with respect to the point C. The kinetic energy of the system has the form (here, a dot denotes the derivative with respect to time t):

$$T = 0.5({{J}_{1}} + m{{r}^{2}}){{\dot {\varphi }}^{2}} + 0.5{{J}_{2}}{{(\dot {\varphi } + \dot {\vartheta })}^{2}}.$$

The aerodynamic forces from the air flow act on the plate. We assume that they are represented by the drag force D and the lift force L applied at the point C and given by

$$L = 0.5\rho S{{U}^{2}}{{C}_{l}}(\alpha ),\quad D = 0.5\rho S{{U}^{2}}{{C}_{d}}(\alpha ).$$

Here, S is the area of the plate, α is the instantaneous angle of attack, that is, the angle between the air velocity of the point C and the plate plane, ${{C}_{d}}(\alpha )$ and ${{C}_{l}}(\alpha )$ are the coefficients of the drag and lift (lateral) forces, respectively, and U is the value of the air velocity of the point C:

$${{U}^{2}} = {{(V\cos \varphi )}^{2}} + {{(r\dot {\varphi } - V\sin \varphi )}^{2}},\quad \tan (\alpha - \vartheta ) = \frac{{V\cos \varphi }}{{r\dot {\varphi } - V\sin \varphi }}.$$

A similar model of the aerodynamic impact was considered in [9, 10] for a pendulum with one degree of freedom ($\vartheta \equiv 0$) and in [17, 18] for other structures of one-link pendulums in a flow; a similar model was applied in [39] for an alternative scheme of a two-link pendulum. This quasi-static approach to describing the pendulum aerodynamics in a flow goes back to work [40]. The authors of works [41, 42] proposed more complicated modifications.

In numerical calculations we use the simplest approximations for the aerodynamic coefficients which reflect the qualitative properties of evenness/oddness of these functions:

$${{C}_{d}}(\alpha ) = 0.1 + {{\sin }^{2}}\alpha ,\quad {{C}_{l}}(\alpha ) = \sin (2\alpha ).$$

We introduce the following designations for the dimensionless variables and time: $\omega = {{V}^{{ - 1}}}rd\varphi {\text{/}}dt$, w = V^–1rdϑ/dt, and $\tau = {{r}^{{ - 1}}}Vt$.

The generalized force with respect to the coordinate φ representing the aerodynamic load is given by

$${{Q}_{\varphi }} = 0.5\rho S{{V}^{2}}F(\varphi ,\vartheta ,\omega ),$$

$$F(\varphi ,\vartheta ,\omega ) = \sqrt {{{{\cos }}^{2}}\varphi + {{{(\omega - \sin \varphi )}}^{2}}} \left( {{{C}_{l}}(\alpha )\cos \varphi - {{C}_{d}}(\alpha )(\omega - \sin \varphi )} \right),$$

$$\alpha = {\text{arctan}}\left( {\frac{{\cos \varphi }}{{\omega - \sin \varphi }}} \right) + \vartheta .$$

We write the function $F(\varphi ,\vartheta ,\omega )$ as

$$F(\varphi ,\vartheta ,\omega ) = P(\varphi ) + ({{F}_{0}}(\varphi ,\omega ) - P(\varphi )) + {{F}_{1}}(\varphi ,\omega )\vartheta + 0.5{{F}_{2}}(\varphi ,\omega ){{\vartheta }^{2}} + O({{\vartheta }^{3}}),$$

where we have used the following designations:

$$P(\varphi ) = F(\varphi ,0,0),\quad {{F}_{0}}(\varphi ,\omega ) = F(\varphi ,0,\omega ),$$

$${{F}_{1}}(\varphi ,\omega ) = {{\left. {\frac{{\partial F(\varphi ,\vartheta ,\omega )}}{{\partial \vartheta }}} \right|}_{{\vartheta = 0}}},\quad {{F}_{2}}(\varphi ,\omega ) = {{\left. {\frac{{{{\partial }^{2}}F(\varphi ,\vartheta ,\omega )}}{{\partial {{\vartheta }^{2}}}}} \right|}_{{\vartheta = 0}}}.$$

We will seek the self-sustained oscillations with relatively low amplitude in the angle ϑ and restrict ourselves for the function $F(\varphi ,\vartheta ,\omega )$ by the expansion terms up to the order $O({{\vartheta }^{2}})$ inclusive. Then, each term in the right-hand side of the system of the equations of motion is a product of the functions each of which depends either only on φ and ω or only on ϑ and w.

Thus, in the dimensionless designations, the equations of motion of the system have the structure similar to (1.1):

$$\dot {\varphi } = \omega ,$$

$$\dot {\vartheta } = w,$$

$$\dot {\omega } = a\sum\limits_{k = 0}^2 {\frac{1}{{k!}}{{F}_{k}}(\varphi ,\omega )} {{\vartheta }^{k}} + p(\kappa \vartheta + \chi w) + u,$$

(4.1)

$$\dot {w} = - a\sum\limits_{k = 0}^2 {\frac{1}{{k!}}{{F}_{k}}(\varphi ,\omega )} {{\vartheta }^{k}} - \kappa \vartheta - \chi w - u,$$

$$a = \frac{{\rho S{{r}^{3}}}}{{2({{J}_{1}} + m{{r}^{2}})}},\quad p = \frac{{{{J}_{2}}}}{{{{J}_{1}} + m{{r}^{2}} + {{J}_{2}}}}.$$

(4.1)

Here, a is the parameter characterizing the aerodynamic load, p is the coefficient characterizing the inertial parameters, κ is the dimensionless stiffness coefficient of the spring mounted in the joint C, and χ is the dimensionless viscous friction coefficient in the joint С. We choose the dimensionless control impact u in the form

$$u = - {{b}_{1}}\omega + {{b}_{2}}\operatorname{sgn} w.$$

(4.2)

In the designation of system (1.1), we obtain ${{f}_{1}}({{\varphi }_{1}},{{\omega }_{1}}) = {{\omega }_{1}}$, ${{f}_{2}}({{\varphi }_{2}},{{\omega }_{2}})$ = $\operatorname{sgn} ({{\omega }_{2}})$, ${{g}_{1}}({{\varphi }_{1}},{{\omega }_{1}})$ = ${{b}_{1}}{{\omega }_{1}}$, and ${{g}_{2}}({{\varphi }_{2}},{{\omega }_{2}})$ = ${{b}_{2}}\operatorname{sgn} ({{\omega }_{2}})$.

We need to adjust the values of the parameters b_i so that in system (4.1) there exists a near-periodic trajectory corresponding to self-sustained oscillations (self-sustained rotations) whose amplitude in φ is approximately equal to φ* (the frequency of which in φ is approximately equal to ω*) and whose amplitude in $\vartheta$ is approximately equal to ϑ* and such that in this mode there is no synchronization between the angles φ and ϑ.

Note that the system has deficient control impacts; the difficulties related with this fact are described, for instance, in [34].

4.1 Asynchronous Self-Sustained Oscillations of a Double Pendulum

Consider the problem of generating asynchronous self-sustained oscillations. System (4.1) has the property of central symmetry. We seek the solutions of the oscillatory type which has central symmetry. Accounting for the symmetry properties, some of the terms in the construction of auxiliary partially averaged systems (2.1) and (2.2) vanish:

$$\begin{gathered} \dot {\varphi } = \omega , \\ \dot {\omega } = aP(\varphi ) + [a({{F}_{0}}(\varphi ,\omega ) - P(\varphi )) + 0.5a{{F}_{2}}(\varphi ,\omega )\bar {G}_{{22}}^{j} - b_{1}^{j}\omega ], \\ \end{gathered} $$

(4.3)

$$\begin{gathered} \dot {\vartheta } = w, \\ \dot {w} = - (a\bar {G}_{{11}}^{j} + \kappa )\vartheta + [ - b_{2}^{j}\operatorname{sgn} w - \chi w]. \\ \end{gathered} $$

(4.4)

The remaining terms do not enter the partially averaged systems, because, due to the properties of central symmetry, the averaged values $\bar {G}_{{ik}}^{j}$ of the corresponding functions are zero at each step of the algorithm.

The square brackets in the partially averaged systems denote all terms, except for the conservative part (note that we must not include exactly P(φ) from ${{F}_{0}}(\varphi ,\omega )$ in the conservative terms, but this is one of the most natural possible options).

We illustrate the operation of the proposed algorithm. We set a = 0.2, $p = 0.005$ (a small value of the parameter p is essential, and it agrees with the physical meaning), κ = 10, and $\chi = 0.04$. We consider the following sets of program values of the amplitudes: (1) $\varphi \text{*} = 0.2$ and $\vartheta \text{*} = 0.2$ and (2) $\varphi \text{*} = 2.5$ and $\vartheta \text{*} = 0.1$.

In Figs. 2 and 3, we draw in black color the curves ${{\omega }^{ \pm }}(\varphi )$ and ${{w}^{ \pm }}(\vartheta )$ plotted approximately during application of the proposed algorithm to auxiliary systems. Gray is used to plot the approximations for the projections of the attractor of system (4.1) on the planes ($\varphi$, $\omega$) and ($\vartheta$, $w$); they are constructed by direct numerical integration of system (4.1) by the Runge–Kutta method with initial conditions from the neighborhoods of the curves ${{\omega }^{ \pm }}(\varphi )$ and ${{w}^{ \pm }}(\vartheta )$ (the projection of the trajectory fills some area). The system and the determined solutions have the central symmetry. The corresponding values of the coefficients in the control law obtained as a result of application of the algorithm are equal to (1) $b_{1}^{ * } \approx 0.818$, $b_{2}^{ * } \approx - 0.097$ and (2) $b_{1}^{ * } \approx 0.216$, $b_{2}^{ * } \approx - 0.050$.

Fig. 2.

Fig. 3.

The dashed line on the plane ($\varphi$, $\omega$) in Fig. 2 shows the Poincaré section for the constructed trajectory by the hyperplane $\vartheta = 0$ (in the direction of increase in ϑ). The qualitative form of the constructed Poincaré section suggests that the found attractor is a two-dimensional invariant torus: the characteristic form of the Poincaré sections corresponding to different types of attractors is given, for instance, in [43].

In the considered examples, in constructing the periodic trajectories ${{\omega }^{ \pm }}(\varphi )$ and ${{w}^{ \pm }}(\vartheta )$ of systems (4.3) and (4.4), we performed five iterative approximations of the method of [16] for each step j, and in total we carried out three steps ($j = 0,1,2$).

4.2 Asynchronous Mode at which Self-Sustained Rotation of the First Link Is Accompanied by Self-Sustained Oscillations of the Second Link.

When the plate is rigidly mounted to the support at the right angle ($\vartheta \equiv 0$), the considered pendulum is an element of the Darrieus rotor. Self-sustained rotation in a flow is characteristic for this rotor, and instead of rotation there occur oscillations only for a relatively large additional dissipation [10]. Consider the problem of generating the asynchronous mode of system (4.1) characterized by rotation in φ and oscillations in ϑ. We seek the control, as above, in the form (4.2). When the first link performs self-sustained rotations, we cannot use the properties of central symmetry in computation of average values of the functions of variables φ and ω. As a result, in both partially averaged systems there arise additional terms in comparison to the previous case.

$$\begin{gathered} \dot {\varphi } = \omega , \\ \dot {\omega } = aP(\varphi ) + p\kappa \bar {G}_{{21}}^{j} + p\chi \bar {G}_{{20}}^{j} + \bar {g}_{2}^{j} \\ + \;[a({{F}_{0}}(\varphi ,\omega ) - P(\varphi )) + a{{F}_{1}}(\varphi ,\omega )\bar {G}_{{21}}^{j} + 0.5a{{F}_{2}}(\varphi ,\omega )\bar {G}_{{22}}^{j} - b_{1}^{j}\omega ], \\ \end{gathered} $$

(4.5)

$$\begin{gathered} \dot {\vartheta } = w, \\ \dot {w} = - a\bar {G}_{{10}}^{j} - (a\bar {G}_{{11}}^{j} + \kappa )\vartheta - 0.5a\bar {G}_{{12}}^{j}{{\vartheta }^{2}} + \bar {g}_{1}^{j} + [ - b_{2}^{j}\operatorname{sgn} w - \chi w]. \\ \end{gathered} $$

(4.6)

The parameters responsible for cross links have also entered both the nonconservative and conservative parts of auxiliary systems. The values $\bar {g}_{i}^{j}$ in this case depend on $b_{i}^{j}$.

The correspondence between the functions averaged over the periodic trajectories of systems (4.5) and (4.6) and the auxiliary parameters is as follows: ${{F}_{0}}(\varphi ,\omega ) \to \bar {G}_{{10}}^{j}$, ${{F}_{1}}(\varphi ,\omega ) \to \bar {G}_{{11}}^{j}$, ${{F}_{2}}(\varphi ,\omega ) \to \bar {G}_{{12}}^{j}$, $b_{1}^{j}\omega \to \bar {g}_{1}^{j}$, $w \to \bar {G}_{{20}}^{j}$, $\vartheta \to \bar {G}_{{21}}^{j}$, ${{\vartheta }^{2}} \to \bar {G}_{{22}}^{j}$, and $b_{2}^{j}{\text{sgn}}w \to \bar {g}_{2}^{j}$.

We use the algorithm described above. At each step of the algorithm, to system (4.5) we apply the modification [18] of the method of [16] intended to generate self-sustained rotations in the second-order system. Moreover, for system (4.6) we use the modification [17] of the approach of [16] intended to generate self-sustained oscillations in the system without central symmetry.

With $\omega \text{*} = 2$ and $\vartheta \text{*} = 0.2$ we obtain $b_{1}^{ * } \approx - 0.057$ and $b_{2}^{ * } \approx 0.099$.

In Fig. 4, by black curves we present the generating periodic trajectories of systems (4.5) and (4.6) plotted by the proposed iterative method; by gray color we present the projections of the approximation for the attractor of system (4.1) onto the phase planes which are constructed by the Runge–Kutta method at ${{b}_{i}} = b_{i}^{ * }$ (the trajectory fills some area); the dashed curve in Fig. 4 depicts the Poincaré section by the hyperplane $\vartheta = 0$ (in the direction of increase in ϑ) for the trajectory obtained by the Runge–Kutta method. As in the previous example, the qualitative form of the Poincaré section indirectly indicates that the found attractor is the two-dimensional invariant torus.

Fig. 4.

The values of the auxiliary parameters $\bar {G}_{{10}}^{j}$, $\bar {G}_{{11}}^{j}$, $\bar {G}_{{12}}^{j}$, $\bar {G}_{{22}}^{j}$, $\bar {g}_{1}^{j}$, $b_{1}^{j}$, and $b_{2}^{j}$ for three steps of the algorithm (j = 0, 1, 2) almost cease changing. The values $\bar {G}_{{20}}^{j}$, $\bar {G}_{{21}}^{j}$, and $\bar {g}_{2}^{j}$ remain nearly zero in all iterations, because, although the periodic trajectory of system (4.6) is not centrally symmetric, it is little different from such.

The modification of the approach intended to form the asynchronous self-sustained rotations in the system with two rotational coordinates was proposed and illustrated in examples in [26, 27]. In these works there were some additional restrictions on the form of the system which are released in the current work. In particular, in [26, 27] the cross links between the subsystems are independent of the coordinates φ_i. As a result, in [26] the parameters similar to $\bar {G}_{{ik}}^{j}$ and $\bar {g}_{i}^{j}$ must not be sought iteratively, because they are determined in advance, before the construction of the limit cycles of the auxiliary systems (in other words, the parameters responsible for the cross links are independent of j). Due to additional restrictions on the form of the system, in [27] the parameters similar to $\bar {G}_{{ik}}^{j}$ and $\bar {g}_{i}^{j}$ are absent, and the average values of the phase velocities on the trajectory corresponding to the self-sustained rotation serve as the coefficients $b_{i}^{*}$, which substantially simplifies the algorithm for searching such a trajectory. In the case of self-sustained rotations, the method for generating 2π-periodic trajectories [18] is used in both coordinates at each step of the algorithm execution for the second-order auxiliary systems.

5 DISCUSSION

Let us point out some of the features of the algorithm execution detected when considering the mechanical example presented above and describe the possible directions of the further development of the general problem.

A relatively large stiffness κ of the spring in the joint C is substantial for the algorithm efficiency. In the limit case, if this coefficient is far larger than the remaining coefficients of system (4.1), the system is close to completely integrable. In this case, we may anticipate expansion of the applicability area of the algorithm. If the stiffness is small, then the area of parameters with synchronization where the system approaches the periodic mode expands substantially. We can suggest that strengthening the nonconservative impacts compared to conservative ones is one of the factors promoting synchronization.

Note that the interaction of the elements of the system significantly affects not only the oscillations of the variables near the average values (smearing of the attractor), but also the form of generating periodic solutions of auxiliary systems. To confirm this, we can compare the solutions obtained in the above-discussed examples with the periodic solutions in the problem of the pendulum with a plate rigidly fixed at the first link ($\vartheta \equiv 0$). The latter were described in [10] (but in the case of system with a small parameter).

The proposed algorithm allows rapidly constructing the approximation for asynchronous oscillations, which in several cases turns out to be rather rough. For instance, for the considered values $\varphi \text{*} = 0.2$ and $\vartheta \text{*} = 0.2$ the amplitude in φ for the generated self-sustained oscillations considerably deviates from φ*. However, the constructed rough approximation may be used as a starting point to determine, by the parameter continuation, the control impact gain factors which provide the more accurate tracking of the program values of the amplitudes.

Among the possible modifications of the proposed method, we need to point out, first of all, the algorithm for seeking the asynchronous self-sustained oscillations of the system without control. To generalize the method to this problem, we need to artificially add the terms of the form ${{b}_{i}}{{f}_{i}}({{\varphi }_{i}},{{\omega }_{i}})$ to the system and execute the algorithm for a larger set of pairs $(\varphi _{1}^{ * },\varphi _{2}^{ * })$, seek the pairs $(\varphi _{1}^{ * },\varphi _{2}^{ * })$ at which $b_{i}^{ * } = 0$, numerically test such pairs for the presence of the trajectory close to the periodic trajectory in the original system. Such an approach allows in fact searching through the initial conditions for the original trajectory not in the four-dimensional, but in the two-dimensional, space, and only in the neighborhood of suspicious pairs $(\varphi _{1}^{ * },\varphi _{2}^{ * })$ adjusting the initial conditions in the space of all four variables.

In addition, we note that for a controlled system it is advisable to develop a modification of the method which proposes a special choice of functions ${{f}_{i}}({{\varphi }_{i}},{{\omega }_{i}})$ for providing the attraction properties of the trajectory generated by the periodic solutions of the auxiliary systems or for extending the range of values $(\varphi _{1}^{ * },\varphi _{2}^{ * })$ for which the iterative process converges.

The additional modifications of the proposed algorithms may be obtained by applying alternative methods for constructing periodic solutions to the auxiliary systems (2.i), for instance, the methods of [14, 15], the iterative method based on the direct numerical integration or on the expansion of the solution into the harmonic series, and the methods based on studying the bifurcations of cycle initiation in the neighborhood of the equilibrium positions and the parameter continuation [44, 45]. The application of the particular approach in dependence on the context of the specific problem may allow extending the convergence region and increasing the convergence rate.

CONCLUSIONS

In this work we considered an autonomous nonconservative mechanical system with two degrees of freedom. We assumed that in this system there are control impacts in the form of feedback. We proposed a method for generating asynchronous self-sustained oscillations by adjusting the control impact gain factors. The similar approach to form the self-sustained rotations were proposed earlier in [26, 27]. The efficiency of the algorithm operation was illustrated on an example of the problem of generating self-sustained oscillations of the aerodynamic pendulum. The application area of the proposed approach and the possible directions of its further development were discussed.