Introduction

Today, design and description of nanostructured metamaterials with the purpose of realizing their optical properties that are not available in natural materials is an important and interesting field of research in various sciences [1,2,3,4,5,6,7,8,9]. A class of these synthetic structures that have attracted a lot of attention is epsilon-near-zero (ENZ) metamaterials where the real part of one or two components of effective permittivity becomes zero. The near-zero permittivity can be found at the infrared and optical frequencies. Some examples of these are polar dielectrics (silicon carbide), semiconductors (indium antimonide), Ag, and Au, near their plasma frequencies [2]. ENZ behavior can be realized in fabricated metamaterials. One main approach to achieve the desired ENZ metamaterials is utilizing multilayer metal-dielectric nanostructures, which are actually attractive because of their simple fabrication. Experimental realization and theoretical investigation of an ENZ metamaterial at visible wavelength have been reported recently [3, 10, 11].

Up to now, many unique applications have been discovered for these kinds of nanostructures such as negative refraction [12, 13], subwavelength imaging [14,15,16], cloaking [17, 18], super absorbing [19, 20], wave guiding [21, 22], and spontaneous [23, 24] and thermal emission engineering [25, 26].

The ENZ metamaterials are introduced as angular filters [27, 28]. Alu et al. [27] showed that an ENZ planar stack allows transmission just for a particular narrow angular width, not far from the normal incidence, by acting as an angular filter for the transverse magnetic (TM) polarization. Alekseyev et al. [28] concluded that an array of silver nanowires in anodic alumina matrix can function as a narrowband angular transmittance filter and polarizer. However, to date, filtering has not been reported for multilayer (two sublayers) metamaterials. Hence, in this work, we designed a multilayer metamaterial stack which consists of three sublayers instead of two sublayers in conventional multilayer metamaterials. The sublayers can be either metal, dielectric, or semiconductor. The effective permittivity of multilayer metamaterials with three sublayers is derived based on the Bloch theory and transfer matrix method for the TM mode at normal and transverse electric (TE) mode at oblique incident lights. In these metamaterials, we have more control to obtain the ENZ wavelength, namely just by changing the thickness of one of the sublayers, we can have an ENZ wavelength anywhere in the visible range. Indeed in our proposed multilayer stack, one can obtain ENZ wavelength in the broader range that is not accessible in conventional multilayer stacks.

Also, the propagation properties of terahertz (THz) waves passing through the multilayer stacks have been theoretically explored via the calculated transmission, reflection, and absorption spectra at different angles of incidence. We demonstrate that the loss can be reduced and kept under control as an important issue in nanostructured metamaterials. In addition, we show that our proposed structure can act as a band-pass filter in the visible range, namely passes wavelengths within a narrow range and rejects wavelengths outside that range.

Finally, we showed that the number of depth in reflection spectra (peak in transmission spectra) is enhanced by increasing the number of periodic triple layers. Actually, there is one depth in reflection spectra (peak in transmission spectra) for each boundary between periodic triple layers. There are two, three, and four depths in the reflection spectra, for three, four, and five triple layers respectively.

It is noteworthy that all our analytical results are in good agreement with the results obtained from numerical simulations. Our numerical simulations are performed by using the finite difference time domain (FDTD) method with the software computer simulation technology (CST, Microwave Studio).

Formulas and Theoretical Analysis

Because of the subwavelength feature of the multilayer metamaterial stacks, their electromagnetic properties can be described by effective medium theory (EMT). Therefore, the effective permittivity only depends on the frequency. However, the components of permittivity depend on the frequency and wave vector due to the variation of electromagnetic field on a unit nanostructure. Then, the optical nonlocality effects with spatial dispersion occur in the multilayer stacks. Recently, the nonlocal effective parameters of metal-dielectric multilayer metamaterials have been determined based on various analyses of optical nonlocalities. These effects have been studied around the ENZ wavelength [10, 11, 29, 30].

In this study, the nonlocal effective permittivity of multilayer metamaterial stacks with three sublayers is derived based on the Bloch theory and transfer matrix method for the TM mode at normal and TE mode at oblique incident lights.

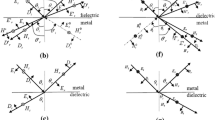
A one-dimensional nonmagnetized periodic nanostructure is considered with three sublayers by utilizing an incident plane wave with the wave vector \( \overrightarrow{k}=\left({k}_x,0,{k}_z\right) \) and field components (Ex, Hy, Ez) at normal incidence for the TM mode and the field components (Hx, Ey, Hz) at arbitrary angle of incidence for TE mode. The permittivity and the thickness of the three sublayers are symbolized as ε1, d1; ε2, d2; and ε3, d3 respectively. When the geometric parameters are much smaller than the free-space wavelength (λ0) of the incident electromagnetic wave, the underlying structure can be considered as an effective medium. Effective permittivity of the multilayer metamaterial stacks can be homogenized via Maxwell-Garnett formulas [31, 32]. For TM mode, we derived and obtained the permittivity components parallel and perpendicular to the stack layers as

$$ {\varepsilon}_{\mathrm{eff}}^x={\varepsilon}_{\mathrm{eff}}^y={f}_1{\varepsilon}_1+{f}_2{\varepsilon}_2+{f}_3{\varepsilon}_3 $$
(1)
$$ {\varepsilon}_{\mathrm{eff}}^z=\frac{\varepsilon_1{\varepsilon}_2{\varepsilon}_3}{f_1{\varepsilon}_2{\varepsilon}_3+{f}_2{\varepsilon}_1{\varepsilon}_3+{f}_3{\varepsilon}_1{\varepsilon}_2} $$
(2)

and for TE mode, the permittivity component can be obtained as

$$ {\varepsilon}_{\mathrm{eff}}^y={f}_1{\varepsilon}_1+{f}_2{\varepsilon}_2+{f}_3{\varepsilon}_3 $$
(3)

where\( {f}_1=\frac{d_1}{d_1+{d}_2+{d}_3} \), \( {f}_2=\frac{d_2}{d_1+{d}_2+{d}_3} \), and \( {f}_3=\frac{d_3}{d_1+{d}_2+{d}_3} \) are the filling fraction of the three sublayers respectively. In this approach, EMT, the effective permittivity is a function of the frequency. But if we consider stack layers as a one-dimensional photonic crystal along the z direction, the dispersion relation was derived based on the Bloch theory and transfer matrix method as below

$$ {\displaystyle \begin{array}{c}\cos \left({k}_zd\right)=\cos \left({k}_1{d}_1\right)\cos \left({k}_2{d}_2\right)\cos \left({k}_3{d}_3\right)-{\gamma}_{12}\sin\;\left({k}_1{d}_1\right)\;\sin \left({k}_2{d}_2\right)\cos\;\left({k}_3{d}_3\right)\\ {}-{\gamma}_{13}\;\sin \left({k}_1{d}_1\right)\;\mathit{\cos}\left({k}_2{d}_2\right)\sin\;\left({k}_3{d}_3\right)-{\gamma}_{23}\cos\;\left({k}_1{d}_1\right)\sin \left({k}_2{d}_2\right)\sin \left({k}_3{d}_3\right)\end{array}} $$
(4)

where \( {k}^{(l)}=\sqrt{k_0^2{\varepsilon}_l-{k}_x^2};l=1,2,3 \) and the polarization-specific parameters are given by

$$ {\displaystyle \begin{array}{c}{\gamma_{12}}^{\left(\mathrm{TM}\right)}=\frac{1}{2}\left(\frac{k_1{\varepsilon}_2}{k_2{\varepsilon}_1}+\frac{k_2{\varepsilon}_1}{k_1{\varepsilon}_2}\right)\kern0.5em {\gamma_{13}}^{\left(\mathrm{TM}\right)}=\frac{1}{2}\left(\frac{k_1{\varepsilon}_3}{k_3{\varepsilon}_1}+\frac{k_3{\varepsilon}_1}{k_1{\varepsilon}_3}\right)\kern0.5em \\ {}\kern0ex {\gamma_{23}}^{\left(\mathrm{TM}\right)}=\frac{1}{2}\left(\frac{k_2{\varepsilon}_3}{k_3{\varepsilon}_2}+\frac{k_3{\varepsilon}_2}{k_2{\varepsilon}_3}\right)\end{array}} $$
(5)
$$ {\gamma_{12}}^{\left(\mathrm{TE}\right)}=\frac{1}{2}\left(\frac{k_1}{k_2}+\frac{k_2}{k_1}\right)\kern0.5em {\gamma_{13}}^{\left(\mathrm{TE}\right)}=\frac{1}{2}\left(\frac{k_1}{k_3}+\frac{k_3}{k_1}\right)\kern0.5em {\gamma_{23}}^{\left(\mathrm{TE}\right)}=\frac{1}{2}\left(\frac{k_2}{k_3}+\frac{k_3}{k_2}\right) $$
(6)

On the other hand, if we consider the multilayer as an anisotropic stack, composed of a single material with the same total thickness, the dispersion relations of the TM and TE modes propagating in the x-z plane can be written as

$$ \frac{k_z^2}{\varepsilon_{\mathrm{eff}}^x}+\frac{k_x^2}{\varepsilon_{\mathrm{eff}}^y}={k}_0^2 $$
(7)
$$ \frac{k_z^2}{\varepsilon_{\mathrm{eff}}^y}+\frac{k_x^2}{\varepsilon_{\mathrm{eff}}^y}={k}_0^2 $$
(8)

It is worth mentioning that this conventional regime with effective permittivities given in Eqs. (7) and (8) can be obtained from Eq. (4) through the Taylor expansion up to the second order in |k1d1| <  < 1; |k2d2| <  < 1; |k3d3| <  < 1; |kzd| <  < 1.

Due to the Eq. (4) for TM mode at normal incidence (kx = 0) and TE mode at different angles of incidence, the nonlocal effective permittivity can be derived as

$$ {\displaystyle \begin{array}{c}{\varepsilon}_{\mathrm{eff}}^x=\frac{1}{d^2{k}_0^2}\left[{\operatorname{arccos}}^2\right[\cos \left(\sqrt{\varepsilon_1}{k}_0{d}_1\right)\cos \left(\sqrt{\varepsilon_2}{k}_0{d}_2\right)\cos \left(\sqrt{\varepsilon_3}{k}_0{d}_3\right)\\ {}-\frac{1}{2}\left(\sqrt{\frac{\varepsilon_1}{\varepsilon_3}}+\sqrt{\frac{\varepsilon_3}{\varepsilon_1}}\right)\sin \left(\sqrt{\varepsilon_1}{k}_0{d}_1\right)\cos \left(\sqrt{\varepsilon_2}{k}_0{d}_2\right)\sin \left(\sqrt{\varepsilon_3}{k}_0{d}_3\right)\\ {}-\frac{1}{2}\left(\sqrt{\frac{\varepsilon_1}{\varepsilon_2}}+\sqrt{\frac{\varepsilon_2}{\varepsilon_1}}\right)\sin \left(\sqrt{\varepsilon_1}{k}_0{d}_1\right)\sin \left(\sqrt{\varepsilon_2}{k}_0{d}_2\right)\cos \left(\sqrt{\varepsilon_3}{k}_0{d}_3\right)\\ {}-\frac{1}{2}\left(\sqrt{\frac{\varepsilon_2}{\varepsilon_3}}+\sqrt{\frac{\varepsilon_3}{\varepsilon_2}}\right)\cos \left(\sqrt{\varepsilon_1}{k}_0{d}_1\right)\sin \left(\sqrt{\varepsilon_2}{k}_0{d}_2\right)\sin \left(\sqrt{\varepsilon_3}{k}_0{d}_3\right)\left]\right]\end{array}} $$
(9)

and

$$ {\displaystyle \begin{array}{c}\begin{array}{c}{\varepsilon}_{\mathrm{eff}}^y=\frac{1}{d^2{k}_0^2}\left[{\operatorname{arccos}}^2\right[\cos \left({k}_1{d}_1\right)\cos \left({k}_2{d}_2\right)\cos \left({k}_3{d}_3\right)\\ {}-\frac{1}{2}\left(\frac{k_1}{k_3}+\frac{k_3}{k_1}\right)\sin \left({k}_1{d}_1\right)\cos \left({k}_2{d}_2\right)\sin \left({k}_3{d}_3\right)\\ {}-\frac{1}{2}\left(\frac{k_1}{k_2}+\frac{k_2}{k_1}\right)\sin \left({k}_1{d}_1\right)\sin \left({k}_2{d}_2\right)\cos \left({k}_3{d}_3\right)\\ {}-\frac{1}{2}\left(\frac{k_3}{k_2}+\frac{k_2}{k_3}\right)\cos \left({k}_1{d}_1\right)\sin \left({k}_2{d}_2\right)\sin \left({k}_3{d}_3\right)\end{array}\\ {}+{\sin}^2\left(\theta \right)\end{array}} $$
(10)

respectively. As illustrated in Fig. 1(b), θ is the angle of incidence in free space and kx = k0 sin(θ). To confirm the results, the effective permittivity of the multilayer metamaterials with two sublayers is obtained by setting one of the three sublayers’ thicknesses to zero.

Fig. 1
figure 1

Schematic illustration of multilayer metamaterial with three layers forming its period. The incident light is (a) TM mode along the z direction with the component of Ex and Hyand (b) TE mode with the components of Ey, Hx, and Hz

Full size image

In the following, one type of ENZ metamaterial stacks, dielectric-semiconductor-metal (DSM), is introduced to study their unique optical properties and locate the ENZ wavelengths at visible frequencies.

Dielectric-Semiconductor-Metal Multilayer Metamaterials

Here multilayer metamaterial stacks based on dielectric-semiconductor-metal (DSM) including Al2O3 − Ge − Ag triples are considered and introduced to study their unique optical properties and obtain the ENZ wavelengths at visible frequencies. Figure 1 shows the schematic diagram of these kinds of nanostructures with two multilayers as we used in our calculations. The DSM multilayer stacks composed of Al2O3, Ge, and Ag are considered for the TE mode of incident light with fAg = 0.46 (filling fraction of Ag) and total thickness of 65 nm in each period. The permittivities of Al2O3, Ge, and Ag are assumed to be \( {\varepsilon}_{\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3}=3.12, \)εGe = 16.2, and \( {\varepsilon}_{\mathrm{Ag}}={\varepsilon}_{\infty }-\frac{\omega_p^2}{\omega \left(\omega +i{\gamma}_c\right)} \) (Drude model), for the entire frequency region of our interest. For Ag, the high-frequency permittivity, the bulk plasma frequency, and the collision frequency are ε∞ = 5, ωp = 13.4 × 1015rad/s, and γ = 0.14 × 1015rad/s respectively. The thickness of the sublayers are labeled as dAg = d1, dGe = d2, and\( {d}_{\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3}={d}_3 \). For the given constant filling fraction of Ag, the effective permittivity with respect to wavelength, at different thicknesses of Al2O3, is plotted in Fig. 2. The ENZ wavelengths of Al2O3 − Ge − Ag are shown by solid points where these wavelengths vary from 420 to 750 nm. While according to this figure, by considering the semiconductor-metal (d3 = 0) multilayer of Ge − Ag or dielectric-metal (d2 = 0) multilayer of Al2O3 − Ag with the same conditions (the total thickness of 65 nm in each period and fAg = 0.46), the ENZ occurs at only one wavelength for each case. Therefore, in our multilayer metamaterials, we have more control to obtain the ENZ wavelength. In fact, an ENZ wavelength can be obtained anywhere in the visible range just by changing the thickness of one of the sublayers. Indeed, in our proposed multilayer stack, one can obtain ENZ wavelength in the broader range that is not accessible in conventional multilayer stacks.

Fig. 2
figure 2

The effective permittivity against the wavelength, at different thicknesses of  Al2O3 for the total thickness of 65 nm in each period and fAg = 0.46. The solid points show the ENZ wavelength. The dashed red curve represents simulation and the blue solid curve represents analytical results

Full size image

According to Eq. (10), the effective permittivity of Al2O3(10nm) − Ge(25nm) − Ag(30nm) stack at different angles are plotted in Fig. 3. It is shown that the nonlocal ENZ wavelength of the DSM multilayer depends on the angle of incident light for the TE mode. Also, by increasing the angle of incidence, the ENZ wavelength goes down to shorter wavelengths. The ENZ wavelength difference, ΔλENZ, due to optical nonlocality can be calculated as

$$ \Delta {\lambda}_{\mathrm{ENZ}}={\lambda}_{\mathrm{ENZ}}^{\mathrm{nonlocal}}-{\lambda}_{\mathrm{ENZ}}^{\mathrm{EMT}} $$
(11)
Fig. 3
figure 3

The effective permittivity against the wavelength, at different angles of incidence for Al2O3(10nm) − Ge(25nm) − Ag(30nm) stack

Full size image

To clarify the optical nonlocality in the multilayer stacks, the variation of ENZ wavelength difference with respect to the thickness of sublayers and angle of incidence is plotted in Fig. 4. In these plots, the total thickness is assumed to be constant. It is clear that the difference of ENZ wavelength and thereby the optical nonlocality increase by increasing the thickness of the silver and germanium sublayers and decrease by increasing the thickness of Al2O3 (Fig. 4(a)–(c)). In Fig. 4(d), the dependency of ΔλENZ on the angle of incidence is presented for TE mode. It is shown that ΔλENZ decreases by increasing the incident angle; therefore, the optical nonlocality is maximum for normal incidence.

Fig. 4
figure 4

The ENZ wavelength difference versus the thickness of (a) Al2O3, (b) Ag, (c) Ge, and (d) angle of incidence

Full size image

Reduced loss is another advantage in these multilayer metamaterials. Actually, by choosing the appropriate third sublayer, loss can be reduced and are kept under control in proposed nanostructures. In Fig. 5, the absorption of the multilayer stack with respect to wavelength for different thicknesses of Al2O3 is illustrated while the total thickness and fAg are constant. In this case, by adding Al2O3 layer to the Ge − Ag multilayer as the third layer, the absorption and consequently the loss are reduced in the visible range.

Fig. 5
figure 5

The reduction trend of absorption of Ge − Ag multilayer by adding Al2O3 as a third layer with different thicknesses while the total thickness and fAg are constant. The dashed red curve represents simulation and blue curve represents analytical results

Full size image

As we know, the amplitude of electric field in the multilayer metamaterials decays due to the optical loss. So the electric field amplitude becomes too low after crossing the stack [10]. To confirm the reduction of loss in our three-layer stack, we have calculated the electric field distribution along the propagation direction at the ENZ wavelength via simulation method. The results showed that in DSM multilayer stack, the amplitude of electric field relatively increases by increasing the d3layer which means the electric field decreases slowly (Fig. 6).

Fig. 6
figure 6

The electric field distribution along the propagation direction for DSM multilayer at the ENZ wavelength of (a) 750 nm, (b) 720 nm, (c) 690 nm, and (d) 640 nm. By increasing the thickness of the d3 layer, the electric field amplitude is increased due to the reduction of optical loss

Full size image

Filtering by Dielectric-Semiconductor-Metal Multilayer Metamaterials

In this section, it is shown that the dielectric-semiconductor-metal multilayers can be introduced as a band-pass filter in the visible range and various conditions are examined for suitable filtering. Figure 7(a)–(d) illustrates transmission and reflection spectra of Al2O3 − Ge − Ag stack for different thicknesses of Al2O3 and Ge where the total thickness of the stack and silver thickness are assumed to be the same. As the figure show, the reflection spectra have a relatively narrow depth (transmission spectra have a peak) in the visible range. Also, as the thickness of Al2O3 layer is increasing, the depth in reflection (peak in transmission spectra) becomes deeper (higher) and wider. These effects are happening because by increasing the thickness of the Al2O3 layer, the thickness of the Ge layer reduces and since the refractive index of Al2O3 is less than that of Ge, the optical path is reduced in the total thikness; therefore, the electric field decays less. In addition, with the same reason and according to Bragg’s law, the position of the depth in reflection (peak in transmission spectra) decreases and takes place at shorter wavelengths.

Fig. 7
figure 7

The transmission and reflection spectra of Al2O3 − Ge − Ag for (a) d3 = 0 nm, (b) d3 = 5 nm, (c) d3 = 10 nm, and (d) d3 = 15 nm. The dashed curves represent simulation and solid curves represent analytical results

Full size image

The effect of the type of third layer in each period on filtering is calculated and plotted in Fig. 8. It should be mentioned that the filtering is only achieved if the third layer in each period should be either Al2O3 or Ge. As Fig .8 shows, if the third layer is Ge, the band width of filtering is narrower and the suitable filter will be obtained.

Fig. 8
figure 8

The effect of the third layer in each period on filtering. The dashed curve represents transmission and reflection of Ge − Al2O3 − Ag multilayer stack. The solid curve represents transmission and reflection of Al2O3 − Ge − Ag multilayer stack

Full size image

In Fig. 9, the effect of the thickness enhancement of the metal layer on filtering is investigated. As shown in this figure, if the thickness of the silver layer increases in each period, a thinner with smaller height for transition is obtained; therefore, the loss in the system is relatively high. In the reflection spectra, a similar behavior occurred but with less variation in the depths. According to the results obtained in this section and the trend of the thickness variations of sublayers, optimal filtering conditions can be achieved from dielectric-semiconductor-metal multilayers.

Fig. 9
figure 9

(a) The transmission and (b) reflection versus wavelength of incident light at different Ag thicknesses

Full size image

Another essential point in the dielectric-semiconductor-metal multilayers is the number of triple layers in the structure. As it is mentioned before, our results are obtained for two triple layers. Here we have calculated the transmission and reflection for more than two triple layers. Figure 10 shows the reflection spectra of the stack containing three, four, and five triple layers. As can be seen, there is one depth in reflection spectra (peak in transmission spectra) for each boundary between periodic triple layers. For example, there are two, three, and four depths in the reflection spectra for three, four, and five triple layers respectively. It should be noted that the transmission and reflection spectra are obtained for TM and TE mode at normal incidence. According to our calculations, this trend is also observed for both modes at oblique incidence; however, by increasing the incident angle, the depths in the reflection spectra (peaks in transmission spectra) take place at shorter wavelengths.

Fig. 10
figure 10

The effect of periodic triple layer number in reflection spectra. The reflection spectra of Al2O3 − Ge − Ag for (a) 3, (b) 4, and (c) 5 triple layers. The dashed red curve represents simulation results and solid blue curve represents analytical results

Full size image

These depths in the reflection spectra (peaks in transmission spectra) are related to the Bragg’s law. To make it clear, the normalized real part of the band structure, together with the transmission and reflection spectra of the multilayer stack, with respect to the normalized frequency, is plotted in Fig. 11. The normalized wave vector kz/kp and normalized frequency ω/ωp are used in the band structure. Where kz is obtained from Eq. (4), the plasma frequency of Ag is ωp = 13.4 × 1015rad/s and plasma wave vector is defined as kp = ωp/c. As shown in these figures, the peaks of the transmission spectra (depths in the reflection spectra) are quite consistent with the zigzag points in the band structure diagram that satisfy the Bragg’s law.

Fig. 11
figure 11

The real part of the band structure together with the transmission and reflection of Al2O3 − Ge − Ag for (a) 3, (b) 4, and (c) 5 triple layers

Full size image

Conclusion

In summary, we designed a new epsilon-near-zero metamaterial theoretically based on multilayer metamaterial stacks which consist of three sublayers instead of two sublayers in conventional multilayer metamaterials. We derived the effective permittivity of multilayer metamaterials based on the Bloch theory and transfer matrix method for TM mode at normal and TE mode at oblique incident lights. It is shown that one can obtain ENZ wavelength in the broader range by changing the thickness of one of the sublayers that is not accessible in conventional multilayer stack. The results of variation of ENZ wavelength show that the optical nonlocality in the multilayer metamaterial stacks decreases with increasing thickness of Al2O3 and incident angle. The propagation properties of terahertz (THz) waves passing through the multilayer stack show that DSM multilayer metamaterials can be introduced as a band-pass filter and these results are dependent on the number of periodic triple layers which is in full agreement with Bragg’s law.